1.
Introduction
In the last two decades there have been a number of theoretical, computational and experimental studies of the dynamics of the rotationally driven jet flows [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26] that were for the inviscid, Newtonian viscous and non-Newtonian flow cases. An essential and relevant assumption for the theoretical investigations has been the so-called slender jet theory, where as in the experimental observation and technological applications the aspect ratio for the fiber jet is considered to be sufficiently small.
Decent et al. [1] developed and studied a model for an inviscid jet that was generated by a rotating drum, which was considered as a very simplified and idealistic model for the cases in some applications such as, for example, the one on the manufacturing of pellets. The authors included the effects of both gravity and surface tension, and their investigation was based on asymptotic and numerical techniques. For their determined steady solutions, they calculated only the jet centerline for different values of the parameters and found that the effect of the gravity was to push down the centerline of the inviscid jet in the downward direction.
Wallwork et al. [2] and Decent et. al. [5] developed horizontal models for slender curved inviscid and Newtonian viscous jets, respectively, which were generated by a rotating orifice in a liquid zone. As was explained in [1], two-dimensional assumption for their jet system meant that the jet centerline was restricted to lie in a fixed two-dimensional plane. In both studies [2,5] the effect of gravity was neglected. For their determined steady solutions, which were based on asymptotic method, the jet trajectory was calculated in [2] and in [5] viscous effect on the jet was found to be weak, and it made the steady solution tightly coiled.
Marheineke and Wegener [6] developed an asymptotic one-dimensional model for a Newtonian fiber jet, which was produced by a rotating cylindrical drum. The authors carried out some numerical calculations, which were restricted under certain conditions on the range of values of the parameters. By numerically damping the jet instabilities due to the surface tension effect, they calculated jet centerline, cross sectional area and the jet velocity for given values of the parameters.
Padron et al. [8] carried out theoretical and numerical modeling of a horizontal inviscid rotating jet and in the presence of surface tension. Their horizontal inviscid modeling system was based on the original Euler and Continuity equations [27] and the corresponding boundary conditions for the jet system. Their modeling system was a simplified version of a centrifugal spinning system for the production of fiber jet, and their more experimentally developed and completed system is referred to as forcespinning process. They solved their resulting modeling system numerically and calculated the fiber jet trajectory and the jet radius as a function of the jet arc length and for different values of the parameters that represented the effects due to the rotational forces and the surface tension. They found that jet trajectory was contracted as the surface tension was increased, and the value of the jet radius was reduced as the rotation rate was increased.
Padron et al. [12] carried out experiments using the forcespinning process to produce mico- and nano-fiber jets. Using high speed photography in their forcespinning experimental set up, they were able to improve some understanding of the mechanisms on which the fiber jets were produced during the forcespinning. They found, in particular, that the fiber jet diameter was decreased with increasing the rotational forces, and using different weight percentages of PEO (Polyethylene oxide) concentration in water, they found that the fiber jet velocity decreased with increasing the fluid viscosity. The authors also studied the effect of changing the spinneret's orifice orientation on the jet direction and the subsequent fiber diameter. They found that higher value of the orifice exit angle with respect to the direction of rotation led to smaller fiber diameter. In addition, the authors acknowledged that presence of gravity force was evident and contributed some effects on the formation of fiber jet, but any explanations or reasoning on the type of such effects on the jet quantities were not reported in their paper.
Alsharif and Uddin [18] investigated rotating viscoelastic curved liquid jet flows with surfactants. They used the Oldroyd-B constitutive equation for the non-Newtonian stress modeling part and applied asymptotic analysis to reduce the governing equations into one-dimensional ones. They determined their steady solution by using a Runge-Kutta numerical procedure and calculated the jet trajectory and the jet radius for different values of the initial surfactant concentrations. They found, in particular, that the jet radius decreases with increasing the arc length but increases with the surfactant concentration.
Riahi [25] studied a horizontal polymeric fiber jet during the forcespinning by implementing a phenomenological viscosity type model for the fluid. He considered a main feature of the polymeric fluid [28], which was due to the variation of the elongational viscosity of the polymer fluid that can produce, in particular, the so-called extensional thinning. Riahi [25] simplified the rheological aspects of polymeric fluid by considering only the viscous aspects of the extensional thinning rheology part of the polymeric jet. He then applied an empirical formula to complete the modeling for the polymeric jet. A similar empirical formula was first proposed by Song and Xia [29] and later was implemented by Feng [30] for modeling of an electrified non-Newtonian jet. Similar to the considerations made in [2,5], Riahi [25] studied the case for a horizontal jet and neglected the effect of gravity. The horizontal restriction for the fiber jet meant that the jet centerline lied on a fixed horizontal plane. As a simple modeling for the non-Newtonian jet during the forcespinning process, the author in [25] made use of the already described polymeric fluid model for the rotating fiber jet by first deriving the simplified governing equations and the boundary conditions for such jet model. The author then determined and calculated, in particular, the steady solutions for different jet quantities. He found that as compared to the Newtonian viscous jet case, the presence of the extensional thinning of the polymeric fiber jet made the jet speed larger and the radius smaller. In addition, the curvature of the horizontal jet trajectory, which is inversely related to radius of curvature of the trajectory curves, was found to be decreased with increasing the jet relaxation time.
Riahi et al. [26] studied theoretical modeling of a horizontal rotating polymeric fiber jet that was similar to that investigated in [25] but took into account both extensional thinning and thickening of the polymeric jet flow. The authors also carried out some experimental study for several types of polymeric fiber jets during the forcespinning process. Their experimental work provided some qualitative results, which indicated that as the fiber velocity increases or polymeric jet viscosity decreases, then the fiber diameter decreases. These experimental results were in qualitative agreement with their corresponding theoretical results.
In addition to the rotationally driven forces, there were also some research studies that made use of the centrifugal forces generated by an externally imposed rotational constraint and combined with a newly developed pressurized melt gyration approach [16,17,19,20,21,22,23,24]. Such studies, which were done either experimentally or by using fitting type models that involved many parameters, enabled their authors to produce polymeric fibers and other types of morphologies under the restrictions that a specific experimental setup is needed first before a fitting type modeling be implemented. In addition, the effects of some main physical properties of the polymeric jet such as surface tension and viscosity were not possible to take into account in the fitting type modeling part of their studies.
It should be noted that the aim of the present investigation was, in particular, to include for the first time two main realistic effects, which are the jet inclination shape case, which can be realized experimentally [12] if the spinneret's orifice orientation was set on an inclined direction during forcespinning, and the presence of gravity force. Such, a model is also constructed to aid in the experimentally studies for the fiber jet production using the forcespinning process [12,26], which is known in the fiber production technologies to have more advantages over other fiber processing. For example, its advantages over the electrospinning process [30,31] are known to be higher fiber production rate capability and applicability to produce micro- and nano-fibers from different types of materials.
2.
Governing modeling system
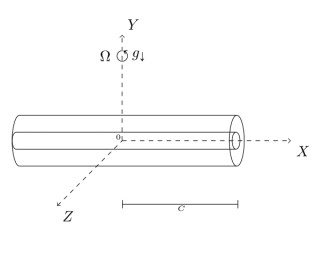
Our present modeling for the rotating polymeric jet flow is initially based on the original fluid dynamics equations for the momentum and mass conservation [28] in a rotating coordinate system. As in the forcespinning process [8,12], we assume that such a rotating coordinate system to be attached and embedded on the rotating spinneret (Figure 1) for a rotating system such as that of the forcespinning system [8]. In this figure the coordinate system is attached to the rotating spinneret. The magnitude of the angular velocity of the rotating spinneret as shown in this figure, whose axis is anti-parallel to the force of gravity, is a given constant. Also in this figure C designates a constant representing the half-length of the spinneret. As in the forcespinning process [12], the centerlines of the produced fibers are curved due to the rotational forces (centrifugal and Coriolis forces).
The original governing equations for the mass continuity and the momentum in the rotating coordinate system [25,28] are given below
where the definition of each symbol in the above equations are the same as those given in [25,26], but we provide those definitions here that make the present paper somewhat more self-explanatory to the readers. Here u is the relative velocity vector of the fiber jet, P is the pressure, T is the stress tensor, ρ is the density of the melt or solution, g is the force of gravity per unit mass, t is the time variable, ω is the angular velocity vector with magnitude Ω of the rotating spinneret whose orifice emits fiber jet from the melt or solution in the fluid container [8,12], and r is a position vector of a point on the fiber. Here, the rotating coordinate system is designated by Cartesian coordinate system (X, Y, Z), which as was described before, is attached to the rotating spinneret, and we refer to it hereafter as the rotating coordinated system. This coordinate system is fixed relative to the rotating spinneret. In contrast to the earlier two-dimensional studies [2,25,26], we consider a model that includes the force of gravity, and the fiber jet's arc length condition that needs to be satisfied here is given below
where s is the arc length along the jet's centerline. Thus, we assume that the components of a position vector of a point on the jet's centerline with respect to the rotating Cartesian coordinate (X, Y, Z) system are, respectively, X, Y and Z.
The governing equations (1.1)–(1.3) are considered with the following kinematic and dynamic boundary conditions at the free surface of the jet [28]:
Here as also defined and given in [25,26], n and ϕ are the radial variable and azimuthal angle, respectively, that represent the variables in the so-called polar coordinate that are in a plane perpendicular to the centerline of the jet, n is a unit normal vector that is perpendicular to the boundary surface of the jet pointing out of the jet, I is a unitary matrix, R is the radius of the jet, σ is surface tension, and κ≡∇.n is twice mean curvature of the jet boundary. Similar to the earlier treatment [2,25,26], we presented (1d) and (1e) in terms of the independent variables (s, n, ϕ). In addition, here the following main boundary conditions at the orifice where the jet exits are satisfied:
where u is the centerline component of the jet velocity vector, U is the centerline velocity of the jet at the exit section and ro is the radius of the orifice at the jet exit section.
As in [25,26], we consider a phenomenological viscosity model due to [29] to represent the extension thinning for our non-Newtonian polymeric fluid flow case. So, the viscous stress term in the momentum equation (1b) is modeled in the following form
where μ is a reference (constant) dimensional dynamic viscosity and the expression for η is turned out to be a function of the strain rate [29,30]. It represents an empirical formula, whose expression will be given later, for the viscosity function of the extensional behavior of the present polymeric jet.
As in the experimental observation [12], we investigate the rotating polymeric jet that has curved centerline. We consider the already described local orthogonal curvilinear coordinate system that can describe the location of any point on the jet. Our governing system (1.1)–(1.6) and (2) will then be investigated in such an orthogonal curvilinear coordinate system, where one coordinate is the arc-length s along the jet's centerline and the other two coordinates are the polar ones (n, ϕ) in a plane perpendicular to the jet's centerline.
We now make the system (1.1)–(1.5) and (2) in the orthogonal coordinate system (s, n, ϕ) dimensionless by using scaling U for velocity vector u = (u, v, w), ρU2for pressure, ro for n and R, C for s and (X, Y, Z), and C/U for t. For simplicity of notation, we express the resulting dimensionless variables in the governing system in terms of the same original symbols. The dimensionless form of the governing system contains some dimensionless parameters that are given as follows. Rossby number Rb = U/(ΩC) that represents the rotational parameter, Froude number F = U/(Cg)0.5 that represents the gravity parameter, Weber number We = ρU2ro/σ that represents the surface tension parameter, Reynolds number Re = ρUC/μ that represents the viscosity parameter, Deborah number De = λU/C that represents the non-Newtonian parameter and a small aspect ratio parameter ε = ro/C (ε < < 1), where g is acceleration due to gravity and λ is the relaxation time.
Similar to the previous studies [2,25], the present dimensionless system that contains ε, is under the relevant assumption that the fiber jet is a long and very slender object, so that ε is considered a very small parameter (ε < < 1) for our scaling analysis and with the following related expansions for the dependent variables:
We then apply the scaling analysis with these expansions in the dimensionless system, where ε is used to scale the variables properly in the system. Following similar approach to [25,26], the system is then simplified and only the leading order terms in the system are retained and further simplifications are made to have a final system only for u0, R0, X0, Y0 and Z0. Dropping the subscripts for simplicity of notations, the resulting system of our constructed model under no imposed condition on the jet shape is given in Appendix (A1.1–A1.6).
In this paper our main investigation is by considering steady solutions and for the jet inclination shape case where Y = m Z, where m is a constant in the range m > 0. This simplification corresponds to the case where the jet's centerline is in the plane, which contains the line Y = m Z and the X-axis in the rotating coordinate system. The constant m can be written as m = tan (θ), where θ in the angle between the inclined plane and the horizontal plane (0 < θ < π/2). Most of the results to be presented in the next section are for m = 1, but we will also describe the results for other values of m as well. But referring to Figure 1, such plane in the rotating frame corresponds to a very wide domain in the fixed coordinate system in the three-dimensional space. It can also be seen that for the present system, the jet's centerline location provides a much wider and more realistic domain in three-dimensional space for the jet centerline than the two-dimensional horizontal counterpart case can provide.
With the described justification for our simplification that turns out to notably reduce the complexity of the modeling system (A1.1–A1.6), the resulting simplified form of the steady system for the jet model becomes
where the expression for the empirical formula η [29,30] for the extension thinning of the polymeric fluid flow that we consider here is given below
where De = λU/C is the Deborah number, λ is the relaxation time, and n is a constant power law index.
3.
Solutions and results
3.1. Solutions and general results
We now investigate and determine the solutions to (4.1)–(4.7) for m = 1, which we mostly consider to determine the results, both asymptotically for very small arc length and numerically for arbitrary arc length. Considering the asymptotic form of the solutions of (4.1)–(4.5) for very small s, we find
where the constants a1, a2 and b1 were found to satisfy the following relations
The asymptotic solutions and the results given by (5.1)–(5.6) are also useful for providing some needed initial conditions for the computation that is similar to the procedure described in [25,26]. Thus, we use such conditions to be described further below for the initial value problems that are solved numerically to determine the solutions of the full nonlinear solutions to (4.1)–(4.6).
We solved the nonlinear system (4.1)–(4.6) numerically by considering it as an initial value problem with all the dependent variables as functions of s. Similar to the cases in [25,26], the viscous stress terms in (4.1) and (4.4) contain second derivative for u and third derivatives for X and Z. Thus, we used the solutions given in (5.1)–(5.6) at s = 0 that require knowing the values of the two constants a1 and b1 given in (5.5)–(5.6). But, (5.5)–(5.6) contain also additional constant a2. Following [25,26], we applied an iterative approach for given value of a2 and calculate iteratively a1 from (5.5) and then used the values of a1 and a2 in (5.6) to find the value of b1. We did such iterative procedure for several prescribed values of a2 and found that the solution for the rate of change of the strain rate at s = 0 is very small of order 10-3. We then found that the result is rather insensitive with respect to the value of a2 that is used in (5.5)–(5.6) to evaluate a1 and b1. We, thus, did our actual computation by setting a2 = 0. To solve the actual initial value problem numerically, we first converted the system (4.1)–(4.6) into a system of 8 first order ordinary differential equations with independent variable s and then determined the numerical solutions by using an efficient Runge-Kutta scheme [27,33].
We generated data for the jet quantities for different values of s and the parameters Re, De, F, Rb, We and n. As was also determined by previous horizontal jet case studies [2,25,26] for the effects of surface tension on the jet properties, we found that for the present inclined jet flow case, jet speed decreases and jet radius increases with decreasing We, but the rate of changes of these quantities with respect to the jet arc length were found to be notably higher than the corresponding ones in the horizontal jet case counterpart. These results about the effect of the Weber number are reasonable since as the Weber number decreases, it increases the stabilizing effect of the surface tension to resist the thinning of the fiber. However, in contrast to the horizontal jet case result [25], the curvature of the centerline jet was found to increase locally as surface tension decreases.
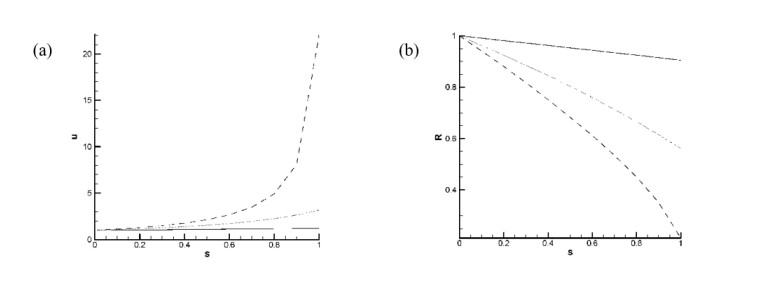
3.2. Results with variation of Rossby number
Figure 2 presents jet speed (a) and jet radius (b) versus arc length for We = 1.5, Re = 1.0, F = 5.0, De = 1.0, n = 0.8 and three different values 0.8, 1.0 and 2.0 of the Rossby number. It can be seen from Figure 2a that the effect of rotational forces is destabilizing in the sense that the jet speed increases with the rotation rate. Such destabilizing effect of the rotation is also seen to be enhanced rapidly with increasing the arc length. Our additional generated data for higher values of the Deborah number and smaller index values indicated that the polymeric effect has similar destabilizing effect as the one due to the rotational forces. We also find that the curvature of the jet trajectory increases with the rotation rate. As compared with the corresponding results in the two-dimensional case [25,26], the rate of increase of jet speed with respect to the rotation rate and the arc length in the present inclined jet system were found to be notably higher than the corresponding ones in the horizontal jet case. Figure 2b which is for the jet radius versus arc length, shows that the jet radius decreases with increasing the rotation rate and such decrease is enhanced with increasing the arc length. It is again evident about the significant destabilizing effect by the rotational forces on the jet radius. The present results for the jet speed and its rate of increase with respect to the arc length and the rotation rate were found to be higher than those in horizontal jet case (m = 0) [25].
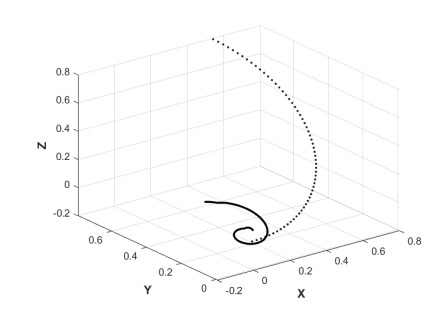
Figure 3 presents a typical result for the jet trajectory with given values of Re, F, De, n and We and for two different values of the Rossby number. It can be seen from this figure that the local curvature of the trajectory curve and the tightness of the curve increases with rotation rate, which is due to destabilizing effect of the rotational forces. We also calculated the jet trajectory for given values of the parameters Re, Rb, We, n (n < 1) and F and for different values of De and found that the curvature of the jet trajectory increases locally with increasing the Deborah number.
3.3. Results with variation of Deborah number
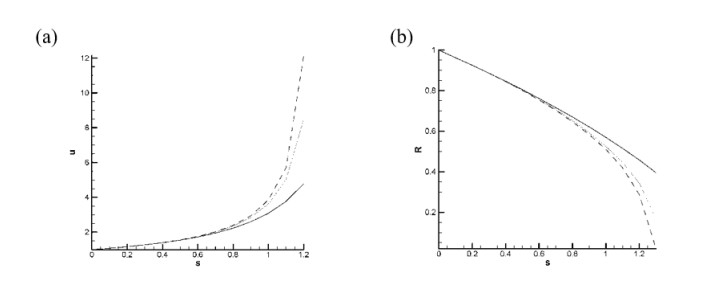
Figure 4 presents the jet speed (a) and jet radius (b) versus arc length for Rb = 1.0, Re = 1.0, F = 5.0, We = 1.5 and for different values of the Deborah number and the index n. It can be seen from figure 4a that the jet speed increases both with increasing the arc length and the extensional thinning effect, which indicate the presence of the destabilizing role played by the extensional polymeric fluid flow. It also shows that the polymeric jet speed enhances more rapidly with increasing the jet arc length away from a short from the jet exit, while the jet speed for the Newtonian fluid flow is notably smaller than those for the corresponding non-Newtonian fluid flow cases. Our additionally generated data indicated that the inclined jet speed is notability higher than the corresponding one for the horizontal jet, and this result enhances with increasing the jet arc length.
Figure 4b is the same as Figure 6 but for the jet radius versus arc length. As can be seen from this figure, the effect of the extensional thinning of the polymeric fluid flow is to decreases the jet radius, and such effect appears to increase with increasing the jet arc length. Our additional generated data indicated that the radius of the inclined jet is notably smaller than the corresponding one for the horizontal jet case, and such result enhances with increasing the arc length.
3.4. Results with variation in Froude number
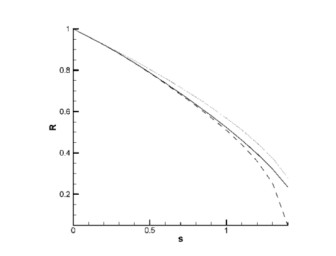
Figure 5 presents jet radius versus arc length for Rb = 1.0, Re = 1.0, We = 1.5 and for inclined non-Newtonian case (De = 1.0, n = 0.8, F = 0.6; dashed line), horizontal polymeric case (De = 1.0, n = 0.8, F = ∞; dotted line) and Newtonian viscous case (De = 0.0, n = 1.0, F = 0.6; solid line). It can be seen from this figure that the value of the jet radius decreases with increasing the arc length in each of these three cases, but its value is smaller in the present inclined polymeric case as compared with the other two values for the horizontal polymeric and Newtonian viscous cases.
In order to gain more insight into the role of inclined jet case, we also carried out some numerical simulation for case where no imposed restriction was imposed on the jet shape case. For such numerical simulation, we consider Y as additional dependent variable, where Y = m Z is not assumed. We used system (A1.1)–(A1.6) and convert this system into a system of 11 first order ordinary differential equations and solved such system using standard Runge-Kutta scheme of fourth order and with all the related procedure similar to what we described in details for the present inclined jet case.
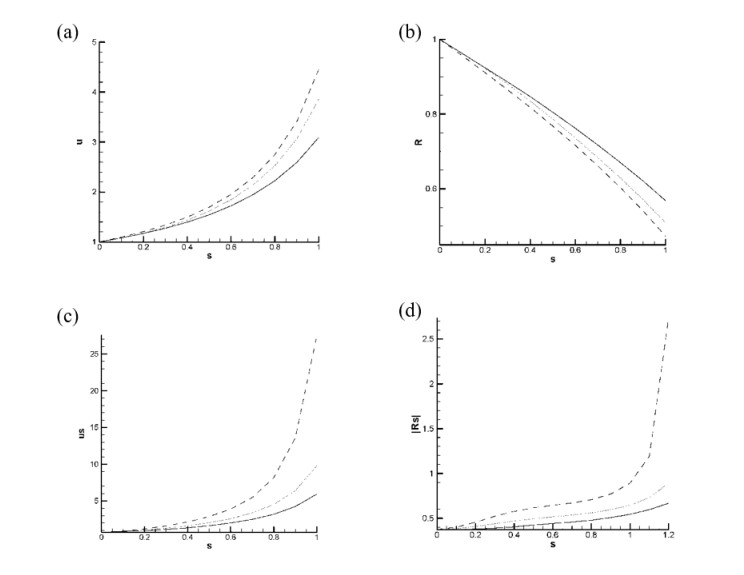
Figure 6 presents typical results about the jet speed (a), jet radius (b), strain rate (c) and stretching rate (d) versus arc length for given finite values of Rb, Re, We, n, F and De and for inclined jet case, horizontal jet case with no gravity effect (F = ∞), and the general case with no imposed restriction on the jet shape. It can be seen from figure 6a that the jet speed is higher than that for either inclined or horizontal jet case, which jet speed value is intermediate between the values of the jet speed for both horizontal case and the case under no imposed conditions on the jet shape. This result also indicates the important effect of the presence of the gravity as well as the role of the jet shape on the fiber jet speed.
Figure 6b, which presents the jet radius versus arc length, shows that in the present inclined jet case, the value of the jet radius is an intermediate value between the horizontal jet shape and no imposed shape case. It can also be seen that the presence of the gravity force can significantly lower down the value of the fiber jet radius.
Figure 6a, b present strain rate (∂u/∂s) and the stretching rate (|∂R/∂s|), respectively, versus the arc length for We = 1.5, Rb = 1.0, Re = 1.0, De = 1.0, n = 0.8, and for two cases of inclined jet with different values of the Froude number [F = 0.3 (dashed line); 1.0 (dotted line)] and for one case of horizontal jet (no gravity effect, solid line). It can be seen from Figure 6c that inclined nature of the jet system and the presence of the gravity force have both destabilizing effect on the strain rate in the sense that the value of the strain rate is notably higher for the inclined jet as compared with the corresponding one for the horizontal jet case. In addition, as the arc length increases and the value of the Froude number decreases, then the destabilization effect of the gravity force is amplified either with increasing the arc length or with decreasing the value of the Froude number. Our additional generated data for the strain rate in the case jet with no imposed restriction on its shape indicated qualitatively similar results to the one for inclined jet but with larger values. It can be seen from Figure 6d that similar behavior to that of the strain rate is apparent for the stretching rate, where the rate of jet stretching increases with the arc length as well as with the destabilizing effects of both inclined nature of the jet system and the presence of the gravity force. Our generated data for the stretching rate in the case of jet with no imposed condition on its shape indicated qualitatively similar results to the ones for the inclined jet but with higher values.
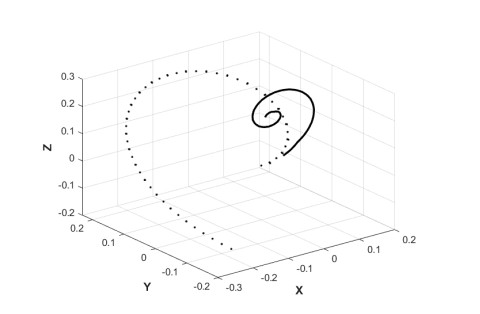
Figure 7 presents the jet trajectory for given values of the parameters Re, Rb, We, n, De and two different values of the Froude number 0.3 and 5.0. It can be seen from this figure that the force of gravity, which is in the direction along the negative Y-axis, pushes further the jet centerline in such downward direction. Thus, the force of gravity exerts a force along negative Y-axis causing the jet moves faster mostly in that direction.
3.5. Results with variations of other parameters
In the previous several sub-sections of this section we presented and discussed results for the cases where one parameter can be varied, while the rest of the parameters were held at fixed values in those results in all such sub-sections. In the following paragraphs that are provided in this sub-section, we provide results and discussions based on our generated computational data for variation of each of those parameters that was held fixed so far.
Our generated data with variation of the Weber number We and fixed values of the other parameters indicated that jet speed, strain rate, centerline curvature and stretching rate decrease, while jet radius increases as We decreases, which is due to the force resisting the thinning of the jet. Clearly the present results for the stabilizing effect of the surface tension are consistent with the role that the effect of the surface tension has on the jet.
Our generated data with variation of the power law index n and fixed values of the other parameters indicated as is also known in previous studies of electrically driven jet [30], the range of values of such index is 0 < n < 1 for polymeric non-Newtonian jet and n = 1 corresponds to Newtonian jet flow case. For the present polymeric jet case, the extensional thinning of the jet increases with decreasing the power law index n, which is reasonable as jet radius, strain rate, centerline curvature and stretching rate of the jet were found to increase and the jet radius decrease with decreasing n.
Our calculated and generated data with variation of Reynolds number Re and fixed values of the other parameters indicated that the jet speed, stretching rate, centerline curvature and strain rate increase, while jet radius decreases with increasing Re. Clearly such results indicate that there is stabilizing effect of viscosity, which is consistent with the role that such effect has on the jet flow.
Similar to the case m = 1 that we calculated the inclined jet quantities for different values of the parameters and already described the results in details in this section, we also carried out calculations for cases with several different values of m (m > 0) and find the corresponding results were qualitatively similar to the case m = 1. Based on several cases of the values of m that we did our calculations, we found that jet speed, stretching rate, strain rate and centerline curvature increased with m, while jet radius decreased with increasing m. In addition, the jet radius was found to smallest for the jet with no imposed condition on its shape. These results were found to agree with the available experimental results [12].
4.
Conclusions and remarks
Modeling of a rotating inclined nonlinear polymeric fiber jet system with the gravity effect was developed and investigated theoretically and numerically, where an empirical formula for the viscosity of the polymeric jet was implemented. The effects due to the inclination of the jet system in the presence of the gravity force on the jet quantities were found to be notable. It was found that as compared with the previous horizontal jet case studies, which were in the absence of gravity effect, the values of the jet speed, strain rate and the stretching rate and their rates of increase with respect to the jet arc length are higher by the inclination of the jet flow and the presence of the gravity force, and these results are enhanced with increasing the arc length distance from the orifice and with increasing the effects due to the extensional thinning and the rotational forces. Also as compared to the horizontal jet cases, the value of the jet radius is smaller due to the presence of the gravity and the inclination nature of the jet system, and the jet radius becomes smaller with increasing the effects due to the rotation rate and the extensional thinning of the polymeric fluid flow. In addition, in contrast to the horizontal jet case, the curvature of the inclined jet trajectory was found to increase locally with increasing the values of the rotation rate and the extensional thinning, but it decreases locally with increasing the values of the surface tension and the viscosity. However, a jet with no imposed condition on its shape was found to have smaller radius and larger values for its speed, strain rate, curvature and stretching rate as compared to the ones for an inclined jet.
It is worthwhile to note that as was described before in the section 2, the present type of jet inclination assumption means that the jet's centerline lies in an inclined plane in the rotating coordinate system, but in the fixed three-dimensional space the jet's centerline can lie in a very large three-dimensional domain. This is in sharp contrast to the previously assumed horizontal case [2,3,4,5,8,25,26], where the jet's centerline can lie only in the horizontal plane in the fixed coordinate system since such fixed horizontal plane coincides with the horizontal plane in the rotating frame (Figure 1).
It should be noted that the parameters values used in the present paper all lie within the typical range of values that are known in both theoretical and experimental applications [1,12,26,30]. Here we provide a collection of such range of values of the parameters, which are 0.01 < Re < O(1), 0.0001 < Rb < O(1), 0.00001 < We < O(1), 0.001 < F < O(1), 0.3 < n < 1, m > 0 and 0 < De < 100. Thus, in particular, the values of the parameters that were chose in the present paper, such as those in sub-sections 2–4 of section 3 with We = 1.5, Re = 1.0 and n = 0.8 lie in such range of values, which mostly correspond to those values taken in real experiments and applications [12].
It is of interest to make some comparison the present results with those of the related investigations that were done in the past. Decent et al. [1] derived a mathematical model for the inviscid liquid. For the steady case they calculated only the jet centerline for different values of the Weber number, Rossby number and the Froude number. They found that the more tightly coiled centerline curves corresponded to higher values of the Weber number, lower values of the Rossby number or higher values of the Froude number. These results agree qualitatively with the corresponding results in the present non-Newtonian inclined jet flow case. However, in contrast to the present work, no results were reported in their paper about the effects of these parameters on the important jet quantities such as the jet speed, jet radius, strain rate and the stretching rate.
Marheineke and Wegener [6] derived and investigated a restricted asymptotic model for the dynamics of the spinning Newtonian fiber jet at some discrete values of time and for different values of the surface tension but with fixed values of the other parameters in their problem. They first calculated the cross sectional area, velocity and centerline of the fiber jet for a one-dimensional jet in the direction along the gravity vector and in the limit where the Rossby number was infinity. Next, they carried out some simulations under very restricted conditions on the parameters. Their result that the curvature of the jet centerline increased locally with decreasing the value of the surface tension is in agreement with the present result.
Padron et al. [12] used high speed photography to provide some understanding on the mechanisms involved for the production of fiber jets through FS. They determined the effects of controllable parameters such as, in particular, angular velocity of the rotating spinneret and viscosity effect of the polymeric solution, which was a weight percentage of PEO (Polyethylene oxide) concentration in water, on the fiber jet speed and jet diameter. These results are qualitatively in agreement with the corresponding results of the present study. The authors also studied experimentally the effects that the changing the orientation spinneret's orifice can have on the jet shape and the fiber radius. They used needles with different exit angles were constructed to select the orifice at particular orientation. They found the fiber radius is smaller if the angle θ is higher (0 < θ < π/2), but the fiber radius is smaller if no orientation is imposed on the orifice. These results are in agreement with the present results.
About the modeling results given in [25,26] for the horizontal rotating polymeric jet that we described in details in the introduction section, it should be emphasized that there are significant differences between the type of the jet system and the corresponding results in the previous modeling work [25,26] and the corresponding ones in the present work. In the present study we uncovered new results about the presence and the destabilizing effects of the inclination of the jet system and the gravity force on the jet quantities, while the previous modeling work [25,26] was for a horizontal jet and the gravity effect was completely neglected. The values of the jet speed, strain rate and stretching rate in the present inclined case are higher than those in the horizontal case, and their rate of increase with respect to rotation rate, relaxation time and arc length are higher than those in the horizontal approximation case. The jet radius is smaller in the present case than that in the horizontal case, and its rate of decrease with respect to the rotation rate, relaxation time and the arc length are found to be higher than the ones in the horizontal case. In contrast to the horizontal case, the curvature of the jet trajectory in the present three-dimensional case is higher locally for higher values of the rotation rate and the relaxation time and for lower values of the surface tension and the viscosity.
About the benefit of the present investigation, the present model is relevant in the forcespinning process to generate fiber at micro- and nano-scales. An important advantage of the forcespinning process over other processes [23,24,32,33], which confirmed both experimentally and in fiber production technology, is in its higher production rate as well as its applicability to produce fibers from different types of materials. We also stated in the section 1 about the disadvantages of fitting type modeling for the processing using rotational constraint combined with the pressurized melt gyration [23,24] that is highly dependent to specific experimental design and unable to take into consideration some of the essential physical properties including the viscosity and the surface tension. The other fiber production processing that is known as electrospinning [32,33] has the main disadvantage that the fiber radius increases with the relaxation time of the polymeric jet and its rate decrease with respect to the arc length decreases with increasing the arc length, while as we explained in the previous section our present modeling, which is relevant for the forcespinning process, predicated that the fiber radius decreases with increasing the relaxation time and its rate of decrease with respect to the arc length increases with the arc length. Thus, our present approach has significant benefit for production of fibers with sufficiently small radius at the scales that can be demanded by the fiber production technologies, which mostly desire to have higher quality and applicability of the polymeric fibers that are produced at higher relaxation time.
In regard to the stability of the present non-Newtonian inclined fiber jet, it should be noted that in the horizontal case, which was carried out in [25], only linear stability of the steady solutions with respect to infinitesimal disturbances was carried out. However, it should be noted that for particular cases that the fiber jet instability was detected, the amplitude of the growing perturbation increases until such the linear stability analysis becomes no longer valid, and, thus, a nonlinear stability analysis will be required to be performed, which we will leave it for a future investigation in both horizontal and inclined cases. Other possible extensions of the present study in the near future can be to investigate the effects due to the presence of extensional thickening and the viscoelasticity on the inclined fiber jet driven by the rotational forces.
Acknowledgments
S.O would like to thank Cristina Villalobos, Timothy Huber and Elda Leal for the office space and hospitality at the University of Texas Rio Grande Valley (UTRGV) during the summer of 2021.
Conflict of interest
The authors declare no conflict of interest.
Appendix
The completed governing equations and the boundary conditions for the jet modeling system under no imposed restriction on the jet flow is given below:









 DownLoad:
DownLoad: