Recently, non-singular fractional operators have a significant role in the modeling of real-world problems. Specifically, the Caputo-Fabrizio operators are used to study better dynamics of memory processes. In this paper, under the non-singular fractional operator with exponential decay kernel, we analyze the Ambartsumian equation qualitatively and computationally. We deduce the result of the existence of at least one solution to the proposed equation through Krasnoselskii's fixed point theorem. Also, we utilize the Banach fixed point theorem to derive the result concerned with unique solution. We use the concept of functional analysis to show that the proposed equation is Ulam-Hyers and Ulam-Hyers-Rassias stable. We use an efficient analytical approach to compute a semi-analytical solution to the proposed problem. The convergence of the series solution to an exact solution is proved through non-linear analysis. Lastly, we present the solution for different fractional orders.
Citation: Shabir Ahmad, Aman Ullah, Ali Akgül, Manuel De la Sen. A study of fractional order Ambartsumian equation involving exponential decay kernel[J]. AIMS Mathematics, 2021, 6(9): 9981-9997. doi: 10.3934/math.2021580
| [1] | Kangqun Zhang . Existence and uniqueness of positive solution of a nonlinear differential equation with higher order Erdélyi-Kober operators. AIMS Mathematics, 2024, 9(1): 1358-1372. doi: 10.3934/math.2024067 |
| [2] | Naimi Abdellouahab, Keltum Bouhali, Loay Alkhalifa, Khaled Zennir . Existence and stability analysis of a problem of the Caputo fractional derivative with mixed conditions. AIMS Mathematics, 2025, 10(3): 6805-6826. doi: 10.3934/math.2025312 |
| [3] | H. H. G. Hashem, Hessah O. Alrashidi . Qualitative analysis of nonlinear implicit neutral differential equation of fractional order. AIMS Mathematics, 2021, 6(4): 3703-3719. doi: 10.3934/math.2021220 |
| [4] | Abdelatif Boutiara, Mohammed M. Matar, Jehad Alzabut, Mohammad Esmael Samei, Hasib Khan . On ABC coupled Langevin fractional differential equations constrained by Perov's fixed point in generalized Banach spaces. AIMS Mathematics, 2023, 8(5): 12109-12132. doi: 10.3934/math.2023610 |
| [5] | Shuqin Zhang, Jie Wang, Lei Hu . On definition of solution of initial value problem for fractional differential equation of variable order. AIMS Mathematics, 2021, 6(7): 6845-6867. doi: 10.3934/math.2021401 |
| [6] | Özge Arıbaş, İsmet Gölgeleyen, Mustafa Yıldız . On the solvability of an initial-boundary value problem for a non-linear fractional diffusion equation. AIMS Mathematics, 2023, 8(3): 5432-5444. doi: 10.3934/math.2023273 |
| [7] | Xiaoping Li, Dexin Chen . On solvability of some p-Laplacian boundary value problems with Caputo fractional derivative. AIMS Mathematics, 2021, 6(12): 13622-13633. doi: 10.3934/math.2021792 |
| [8] | Kishor D. Kucche, Sagar T. Sutar, Kottakkaran Sooppy Nisar . Analysis of nonlinear implicit fractional differential equations with the Atangana-Baleanu derivative via measure of non-compactness. AIMS Mathematics, 2024, 9(10): 27058-27079. doi: 10.3934/math.20241316 |
| [9] | Thanin Sitthiwirattham, Rozi Gul, Kamal Shah, Ibrahim Mahariq, Jarunee Soontharanon, Khursheed J. Ansari . Study of implicit-impulsive differential equations involving Caputo-Fabrizio fractional derivative. AIMS Mathematics, 2022, 7(3): 4017-4037. doi: 10.3934/math.2022222 |
| [10] | Lakhlifa Sadek, Tania A Lazǎr . On Hilfer cotangent fractional derivative and a particular class of fractional problems. AIMS Mathematics, 2023, 8(12): 28334-28352. doi: 10.3934/math.20231450 |
Recently, non-singular fractional operators have a significant role in the modeling of real-world problems. Specifically, the Caputo-Fabrizio operators are used to study better dynamics of memory processes. In this paper, under the non-singular fractional operator with exponential decay kernel, we analyze the Ambartsumian equation qualitatively and computationally. We deduce the result of the existence of at least one solution to the proposed equation through Krasnoselskii's fixed point theorem. Also, we utilize the Banach fixed point theorem to derive the result concerned with unique solution. We use the concept of functional analysis to show that the proposed equation is Ulam-Hyers and Ulam-Hyers-Rassias stable. We use an efficient analytical approach to compute a semi-analytical solution to the proposed problem. The convergence of the series solution to an exact solution is proved through non-linear analysis. Lastly, we present the solution for different fractional orders.
Precisely regulated cell proliferation is essential for embryonic development as well as homeostasis in adult organs and tissues, whereas uncontrolled cell proliferation is a hallmark of cancer [1]. Thus, understanding how the cell cycle machinery is controlled is an important area of research in normal development and cancer cell biology. Extensive research has led to current models of cell cycle control [2]. In quiescent cells, E2F transcription factors are repressed by their association with hypo-phosphorylated Retinoblastoma (Rb) protein family members [3]. A key mechanism to switch E2Fs from a repressed state to an active state is the phosphorylation of Rb protein by cell cycle-associated cyclin-dependent kinases (CDKs) [3]. This results in the disruption of Rb-E2F complexes due to reduced interaction of E2Fs with hyper-phosphorylated Rb. Transcription of E2F target genes is required for cell cycle progression [4].
Our previous studies show the human homolog of Drosophila ecdysoneless protein (ECD) as a novel Rb binding partner [5]. The ecdysone hormone is responsible for coordinating embryogenesis, larval molting and metamorphosis. The “ecdysoneless” phenotype of Drosophila has been known for decades, is caused by “Ecd” mutations and emanates from reduced secretion of ecdysone [6]. Only recently however did the cloning of Drosophila Ecd gene lead to an appreciation that the ECD protein plays a cell-autonomous role in development and oogenesis separate from its role in ecdysone production [7].
Homozygous Ecd deletion in mice is early embryonic lethal and ex vivo Cre-mediated Ecd deletion in mouse embryonic fibroblasts (MEFs) or knockdown in human epithelial cells induces cell cycle arrest [5], implicating ECD as a novel cell cycle regulator. We demonstrated that the C-terminus of ECD directly binds to retinoblastoma (Rb) protein at the pocket domain, and competes with E2F for binding to hypo-phosphorylated Rb [5]. ECD binds to p53, stabilizes it and enhances p53 function when overexpressed [8]. Further studies demonstrated that ECD is overexpressed in breast [9], and pancreatic [10] cancers; and its overexpression correlates with poor survival in breast cancer patients [9]. Furthermore, co-overexpression of ECD with mutant Ras rendered immortal epithelial cells fully tumorigenic, through mechanisms that involve an elevation of the autophagy program [11].
Recent studies demonstrate ECD phosphorylation on two serine residues by Casein Kinase-2 (CK2) creates a motif for binding of PIH1D1 (also called NOP17), a component of the HSP90-associated co-chaperone R2TP complex [12]. The R2TP complex is composed of PIH1D1, RPAP3 (also known as hSPAGH), RUVBL1 (has multiple names-Pontin, RVB1, TIP49A, TAP54alpha, ECP-54, TIH1, p50) and RUVBL2 (also known as Reptin, RVB2, TIP49B, TAP54 beta, ECP-51, TIH2, p47) proteins [13], and is involved in the assembly of large protein-protein or protein-RNA complexes, such as RNA polymerase, small nucleolar ribonucleoproteins (snoRNPs), and phosphatidylinositol 3-kinase-related kinases (PIKKs) [14,15]. Recent data shows that the N-terminus of ECD independently associates with RUVBL1, and this interaction is required for its cell cycle regulatory function [16]. Phosphorylation of six ECD serine residues is important for its cell cycle regulation function [16]. ECD has also been shown to interact with TXNIP and helps in p53 stabilization [17]. A recent study by Claudius et al demonstrated that human ECD can rescue splicing defects in drosophila induced by deletion of fly Ecd and Ecd also interacts with a complex containing Prp8, Aar2, Brr2 and Snu114 proteins[18]. The interaction of human ECD with human PRPF8 has been confirmed [16].
Here we have characterized ECD protein structure by circular dichroism measurements and sequence analysis software. These analyses suggest that the majority of ECD is composed of α-helices and that the C-terminal 100 or so amino acids are disordered in the absence of binding partners. Small angle X-ray scattering (SAXS) analysis showed that deletion fragments, ECD(1-432) and ECD(1-534) are both well-folded and reveals that the first 400 residues are globular and the next 100 residues are in an extended cylindrical structure. The majority of ECD residues are within 30 to 35 Å of each other with a maximal dimension for ECD(1-432) and ECD(1-534) of 92 and 122 Å, respectively. It is noteworthy that the extended C-terminus of ECD contains CK2 sites where PIH1D1 and Rb interact. Finally, a theoretical structural model for ECD (1-432) was calculated that suggests ECD acts like a structural hub or scaffolding protein to associate with its protein partners. This hypothetical model and function of ECD will be tested experimentally in the future.
ECD(1-432) and ECD(1-534) sequences were subcloned into a pET28a vector with a C-terminal 6X-His tag. Plasmids were transformed into BL21(DE3) cells, grown in LB medium at 37 °C to an OD600 of 0.7, and induced with 0.5 mM IPTG overnight in an 18°C shaking incubator. Cells were collected by centrifugation, suspended in lysing buffer (2X PBS pH 7.8, 1% Triton X-100, 20 mM imidazole, 2 mM β-mercaptoethanol and protease inhibitor cocktail), lysed using an Emulsiflex-C3 (Avestin, Inc.), and purified by nickel affinity chromatography (5 mL His-Trap FF; GE Healthcare) using an ÄKTAfplc program for a linear gradient from 20 to 400 mM imidazole in basic buffer (2X PBS pH 7.8, 2 mM β-mercaptoethanol). Nearly pure sample eluted at approximately 150 mM imidazole.The product was polished by passing over a Superdex75 HiLoad 16/60 column (GE Healthcare) using isocratic elution into 20 mM HEPES pH 7.5, 250 mM NaCl, 5 mM β-mercaptoethanol. Dynamic light scattering (DynaPro MX/S; Wyatt Technology Corp.) was used to select monodisperse fractions for CD and SAXS experiments. For CD, aliquots of protein were dialyzed into 1X PBS using a 3500 MWCO Slide-A-Lyzer Dialysis Cassette (Thermo Pierce). At all steps, identity and purity of the proteins were assessed by SDS-PAGE analysis.
CD experiments were performed on a JASCO J-815 CD spectrometer fitted with a Peltier temperature control system (Easton, MD). Each spectrum was the average of five scans collected in the far UV (260-195 nm), with a 0.1 mm path length quartz cell, using a bandwidth of 1 nm, an integration time of 1 sec, and a scan rate of 50 nm/min. All spectra were corrected by subtracting the solvent spectrum acquired under identical conditions. The protein concentration for each sample was between 35 and 45 μM, in 1X PBS. All CD data were processed from mDeg to mean residue ellipiticity (MRE; deg cm2 dmol-1) using the Spectra Analysis function of Jasco Manager Version 2, to account for the concentration differences. Secondary structure composition of each spectrum was analyzed using the K2D method provided by the online program DichroWeb [19]. Thermal stability data were collected in the far UV at 222 nm (loss of secondary structure), at the same concentrations and in the same condition as for the CD experiments. CD values were recorded every 1 °C from 25 to 80 °C, after the temperature equilibrated for 5 sec at ± 0.1 °C from target temperature. The thermal unfolding temperature was determined by fitting the curve to a Boltzmann sigmoidal equation using a nonlinear least squares fitting algorithm (GraphPad Prism software).
Data from monodisperse samples at three concentrations were collected at room temperature on a Rigaku BioSAXS 1000 system with an FR-E rotating anode X-ray generator (λ = 1.54 Å). Concentrations were determined by Bradford protein assays. Images were collected for 90 min and subframes were taken every ten min to examine the data for radiation damage. No radiation damage was observed in the data. The data were processed using the Automated Analysis Pipeline in the SAXSLab software (Rigaku). SAXSLab provides a GUI for the ATSAS Package [20], transparently creating scripts and running the associated ATSAS programs and then presenting the results back to the user. The SAXSLab software automatically subtracts the buffer and calculates the Guinier plot, radius of gyration, molecular weight and volume, pair distribution function, Kratky plot, an infinite dilution scattering curve, and ab initio bead model fits to the data. Dmax was calculated from the X-intercept of the P(r) curve. For both the ECD(1-432) and ECD(1-534) proteins, nine bead models were generated from the calculated infinite dilution scattering curves using the slow annealing option. Shannon analysis was performed by Shanum software [21]. Two bead models, one for each protein, with the lowest normalized spatial discrepancy (NSD) value were aligned using the Colores program from the Situs package to dock the smaller ECD(1-432) bead model into the ECD(1-534) bead model [22,23]. This program performs an exhaustive search of the rotational and translational degrees of freedom using the linear cross-correlation as the fitting criterion. Figures were generated with PyMOL (Schrödinger, LLC).
Given that the three-dimensional structure of ECD is not known, a secondary structure prediction was performed with Protean software from the DNAstar Lasergene 10 core suite (see Supplementary Figure S1 line 1 and line 2). Disordered protein structure was also predicted with PONDR (see Supplementary Figure S1 line 4)[24,25,26]. Full length ECD(1-644) was predicted to have 60% α-helix. Also, 35% was predicted to be disordered and the most disordered region was in the last 100 C-terminal residues. Based on this information, two deletion fragments, ECD(1-432) and ECD(1-534), were generated. These proteins were purified to homogeneity (Figure 1A) and shown to be monodisperse and of monomeric quaternary structure by dynamic light scattering analysis [27]. Circular dichroism (CD) data were measured (Figure 1B) and fitted with Dichroweb to estimate secondary structure content. ECD(1-432) contained 41% α-helix, 17% β-sheet and 42% random coil, whereas ECD(1-534) contained 38% α-helix, 16% β-sheet and 46% random coil. Predicting protein secondary structure from amino acid sequence calculates that ECD(1-432) is 62.5% α-helix, 3.7% β-sheet, 16.4% turns, and 17.6% coil [28]. However, the CD data indicated less α-helix than the observed and more β-sheet structure, indicating that the Protean prediction software over predicted the amount of α-helix for ECD.
 Figure 1. Characterization of ECD(1-432) and ECD(1-534) samples. (A) Purity shown with Coomassie-stained SDS-PAGE. (B) Secondary structure measured with circular dichroism at 25 °C (B).
Figure 1. Characterization of ECD(1-432) and ECD(1-534) samples. (A) Purity shown with Coomassie-stained SDS-PAGE. (B) Secondary structure measured with circular dichroism at 25 °C (B).
To get an estimate for how tightly ECD is folded we measured the melting temperature (Tm) of ECD(1-432) and ECD(1-534). CD analysis was used to observe the unfolding of ECD. The data indicate that in the absence of binding partners, ECD has a very low Tm with values of 39.5 °C for ECD(1-432) and 41.4 °C for ECD(1-534) (Figure 2). The α-helices and β-strands convert to random coils upon unfolding. These data indicate that the folded domains within the ECD fragments are loosely held together. Limited proteolysis experiment using trypsin on ECD(1-432) showed release of a 10 kDa domain(s) (data not shown). Furthermore, N-terminal amino acid sequencing showed a mixture and indicated that these domains were from both the N- and C-termini of ECD(1-432).
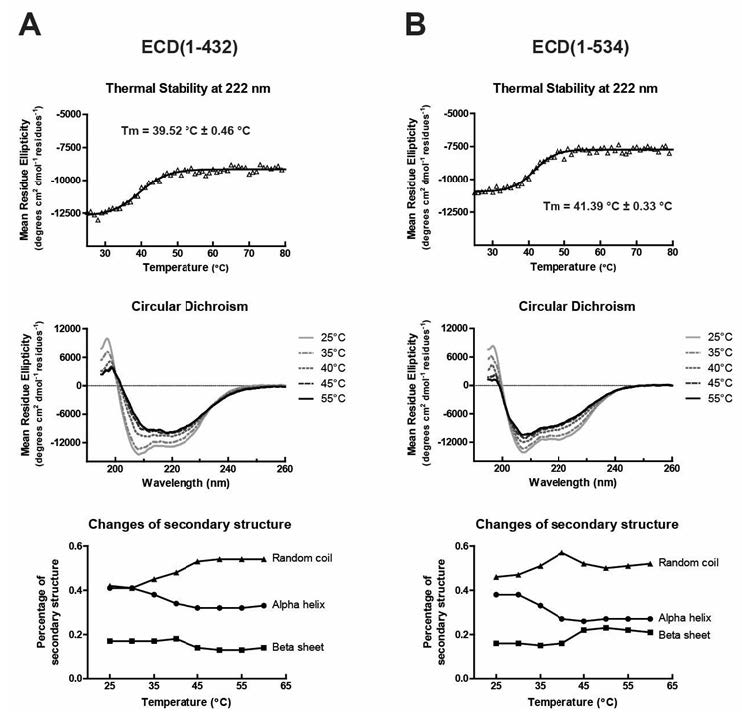 Figure 2. Thermal stability study of ECD fragments by CD. Tm of (A) ECD(1-432) and (B) ECD(1-534) were measured by the change of CD signal at 222 nm from 25 to 80 °C (upper panel). The Tm was determined by nonlinear least squares fitting. In the middle panel, only spectra obtained at 25 (pale grey solid line), 35 (grey dot-dashed line), 40 (grey dotted line), 45 (dark grey dashed line), and 55 °C (black solid line) are displayed for clarity. In the bottom panel, the percentage changes of the random coiled (triangle), α-helix (dot), and β-sheet (square) composition were estimated by DichroWeb and plotted as a function of temperature.
Figure 2. Thermal stability study of ECD fragments by CD. Tm of (A) ECD(1-432) and (B) ECD(1-534) were measured by the change of CD signal at 222 nm from 25 to 80 °C (upper panel). The Tm was determined by nonlinear least squares fitting. In the middle panel, only spectra obtained at 25 (pale grey solid line), 35 (grey dot-dashed line), 40 (grey dotted line), 45 (dark grey dashed line), and 55 °C (black solid line) are displayed for clarity. In the bottom panel, the percentage changes of the random coiled (triangle), α-helix (dot), and β-sheet (square) composition were estimated by DichroWeb and plotted as a function of temperature.
Thousands of crystallization experiments of the ECD fragments produced only clear drops or precipitation. Perhaps this was due to the flexibility of the fold. Therefore, we performed small angle X-ray scattering (SAXS) measurements to determine a low resolution ECD structure. SAXS is commonly used for the investigation of conformation, shape, and dimension of biopolymers in solution (Figure 3). Data were collected over three concentrations. The concentrations used were required to be from monodisperse samples as defined by DLS (dynamic light scattering) analysis [27]. Note that higher protein concentrations could be achieved for ECD(1-432) and thus the SAXS curves had better signal to noise. The scattering curves indicate strong data to q of about 0.2 for ECD(1-432) or 0.15 Å−1 for ECD(1-534) (Figure 3A & D), where q = 4πsin(θ)/λ and 2θ is the angle between the incident and scattered radiation of wavelength λ. Data beyond q of 0.3 (not shown) are weaker and noisy but still useful in the calculations according to Shanum software which gave optimal q of 0.65 for ECD(1-432) and 0.67 for ECD(1-534) [21]. All data were included in calculations.
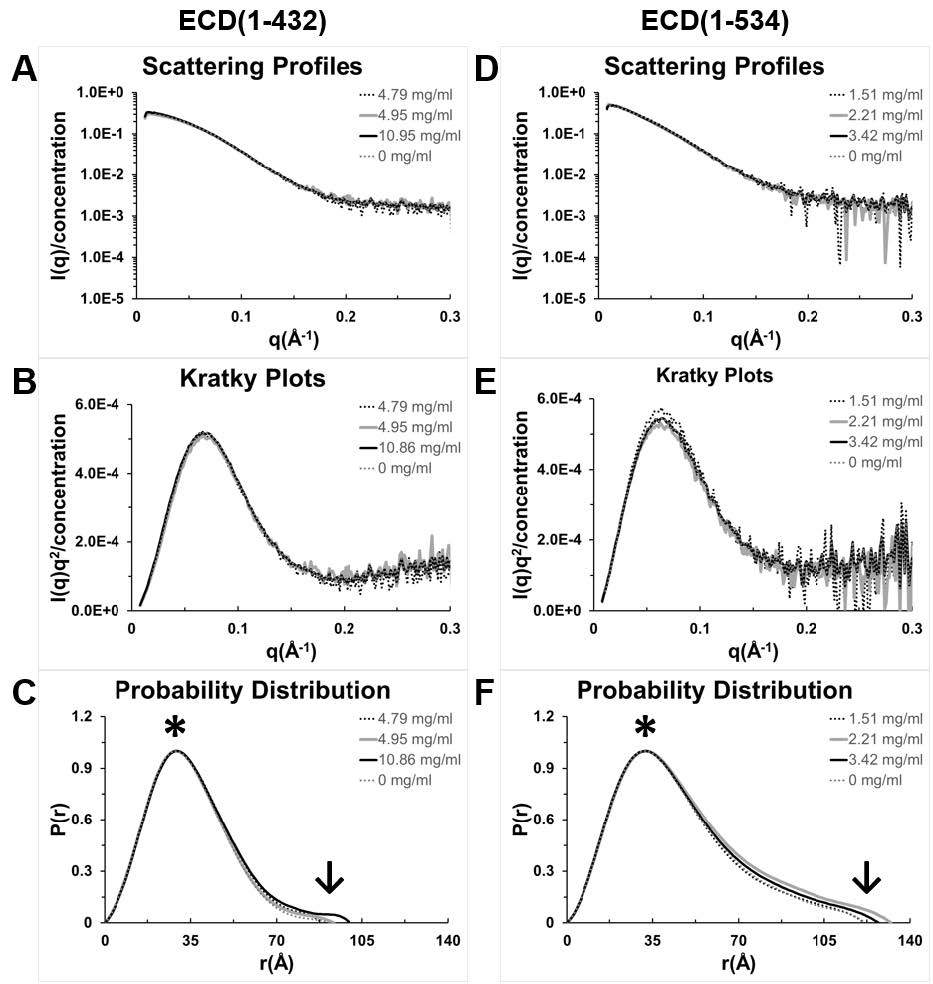 Figure 3. SAXS data and analysis for ECD(1-432) and ECD(1-534). Values for the most common interatomic distance are indicated with an asterisk and the maximum dimension (Dmax) with an arrow.
Figure 3. SAXS data and analysis for ECD(1-432) and ECD(1-534). Values for the most common interatomic distance are indicated with an asterisk and the maximum dimension (Dmax) with an arrow.
Analysis of the scattering curves using the Guinier approximation gives information about the radius of gyration (Rg). ECD(1-432) has an Rg of 26.3 Å and ECD(1-534) has Rg of 34.8 Å (Table 1). Presentation of the scattering data in the form of a Kratky plot provides information about the globularity (packing density) and conformation of a protein [29]. An unfolded protein will tend toward a horizontal asymptote while a well-folded globular protein will reach a peak and return to zero; a partially folded protein will be intermediate, reaching a peak, but not returning to zero and tending to increase at higher q values. Kratky plots of both fragments of ECD (Figure 4B & E) shows that they are both globular and folded.
| Sample | ECD(1-432) | ECD(1-534) | ||||||
| Concentration (mg ml-1) | 4.79 | 4.95 | 10.86 | ∞-1 | 1.51 | 2.21 | 3.42 | ∞-1 |
| I(0) (Normalized concentration; cm-1) | 0.33 | 0.32 | 0.35 | 0.32 | 0.52 | 0.54 | 0.52 | 0.50 |
| Rg Guinier (Å) | 27.7 | 27.2 | 28.5 | 26.3 | 34.7 | 37.8 | 36.3 | 34.8 |
| Rg P(r) (Å) | 27.3 | 27.0 | 28.5 | 26.4 | 35.6 | 38.8 | 37.1 | 35.6 |
| Dmax (Å) | 89.0 | 93.0 | 100.0 | 92.0 | 121 | 132 | 127 | 122 |
| Porod volume (Å3) | 90,302 | 86,625 | 93,368 | 87,266 | 114,882 | 126,440 | 117,895 | 116,206 |
| DAM volume (Å3) | 109,400 | 104,900 | 111,100 | 105,300 | 145,700 | 159,300 | 149,200 | 145,400 |
| MW Porod (kDa) | 53.1 | 51.0 | 54.9 | 51.3 | 67.6 | 74.4 | 69.4 | 68.4 |
| MW DAMa (kDa) | 54.7 | 52.5 | 55.6 | 52.7 | 72.9 | 79.7 | 74.6 | 72.7 |
| a where DAM is Dummy Atom Model | ||||||||
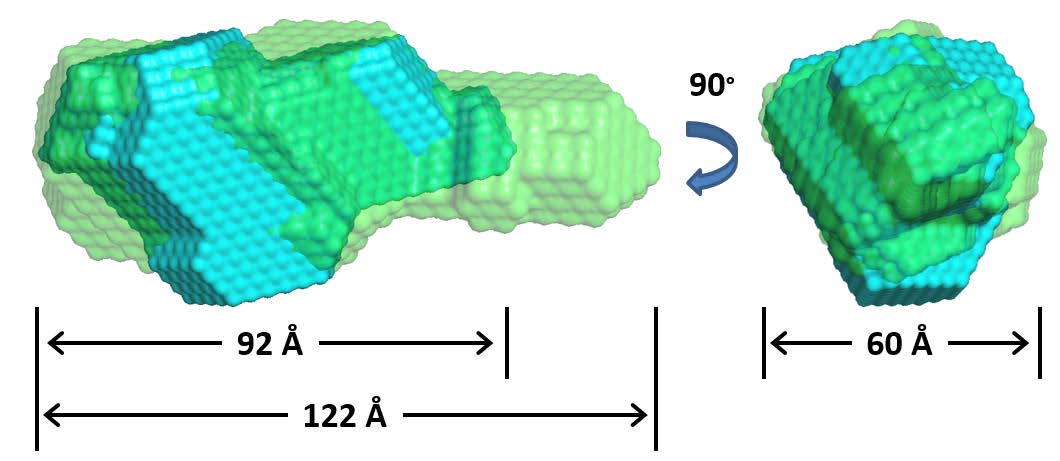 Figure 4. Ab initio bead models of ECD(1-432) (blue) and ECD(1-534) (green) with the lowest NSD values. For ECD(1-432) the best NSD value was 0.606 and from 9 models the maximum value was 0.675, mean was 0.633 and standard deviation was 0.023. For ECD(1-534) the best NSD value was 0.636 and from 9 models the maximum value was 0.750, mean was 0.665 and standard deviation was 0.041.
Figure 4. Ab initio bead models of ECD(1-432) (blue) and ECD(1-534) (green) with the lowest NSD values. For ECD(1-432) the best NSD value was 0.606 and from 9 models the maximum value was 0.675, mean was 0.633 and standard deviation was 0.023. For ECD(1-534) the best NSD value was 0.636 and from 9 models the maximum value was 0.750, mean was 0.665 and standard deviation was 0.041.
The probability distribution function, P(r), plot gives the pairwise distance between atoms and the maximum dimensions (Dmax) for the molecule at the X-intercept (see arrow Figure 3C & F). The majority of ECD residues are within 30 to 35 Å of each other (asterisk Figure 3C & F). For ECD(1-432) the maximum dimension is 89-100 Å and for ECD(1-534) it is 121-132 Å (Table 1). Ab initio bead models for the molecular envelop were fit to the P(r) function [29] and the relative topology of the different domains was observed (Figure 4). The bead models show that the first 400 residues are globular and the next 100 residues are in an extended cylindrical structure. It is noteworthy that the C-terminus of ECD contains the CK2 consensus phosphorylation sites, Rb binding site, and PIH1D1 binding sites. These results show that ECD(1-432) forms the base of the scaffold that tethers various complexes to ECD. We calculated models using Gasbor software and obtained similar results (see Supplementary Figure 2A).
Theoretical models for ECD(1-432) were calculated using molecular modeling tools and the best model was selected using the SAXS scattering data (Figure 3A). The I-TASSER webserver was used to predict structures. The I-TASSER method was introduced as a webserver after winning a community-wide protein structure prediction contest [30]. In addition to being a state-of-the-art prediction method, I-TASSER was chosen because it is completely automated, freely available online, has been used extensively, and its predictions come with reasonable estimates of model accuracy. Furthermore, it can be used to predict the structure of protein sequences as large as 1,500 amino acids by simply providing a single protein sequence in FASTA format and returns predicted models within 48 hours or less. For complete details of the methodology, please refer to the original publications [30,31,32,33]. I-TASSER uses a composite homology/ab initio methodology, wherein the structures of parts of the target sequence that can be confidently aligned to sequences of known structure are predicted using homology modeling, and ab initio loop modeling is used to fill in the gaps. I-TASSER also uses the structure-function paradigm to predict the biological function of a protein based on local and global similarity of the predicted structure to proteins of known structure and function.
I-TASSER makes use of PSIPRED [34,35] to predict the secondary structure of the target sequence. ECD(1-432) was predicted to be 47% helix, 11% beta-sheet, and 42% random coil, and is in good agreement with CD data (Figure 1B). To perform tertiary structure prediction, I-TASSER identifies template structures using multiple threading programs and takes only the most highly significant match from each method and ranks them according to each threading method’s past performance in benchmark experiments. The top template match for ECD(1-432), generated by the FFAS-3D threading algorithm [36], is PDB ID 4xgcA. Despite being the top match, ECD(1-432) and 4xgcA have a low sequence identity in the aligned region (0.13). Another measure of threading quality is the Z-score, where Z-scores greater than 1 indicate a good alignment. ECD(1-432) has a Z-score of 1.01 when threaded over 4xgcA. The highest threading Z-score among all of the top 10 templates (1.40) was obtained by threading the ECD(1-432) sequence over the second ranked template, PDB ID 5bq9A, which was identified by the PROSPECT2 threading algorithm [37]. The identities of the other 8 top templates range from 0.08 to 0.11, and the Z-scores range from 0.58 to 1.37. Taken together, these results indicate that ECD(1-432) is a hard target for protein structure prediction due to its large size, which complicates pure ab initio modeling, and lack of good structural templates, which complicates homology modeling. Finally, I-TASSER provides confidence scores (“C-scores”) for the top 5 predicted 3D models. C-scores can range from −5 to 2, with a C-score of greater than −1.5 being typically indicative of an overall correctly predicted global topology. In the case of ECD(1-432), the C-scores of the top 5 predicted models ranged from −3.42 to −2.39, all of which fall outside the range of C-scores that are usually taken to indicate a good overall prediction. The top 2 models deviated by 2.7 and 1.5 Å, respectively, from their template structures 4xgcA and 5bq9A [38].
Because no single model stood out, all 5 top models were used to calculate theoretical SAXS scattering curves, and these curves were compared to the available experimental data (Figure 5). Atomic models were fit against the scattering data using Crysol [39]. Model 2, created by threading over 5bq9, had the best fit to the SAXS data (Figure 5A). Model 2 had a nice fit to the data from q = 0.0-0.2 Å−1 and reasonable fit from q = 0.2-0.3 Å−1 relative to the noise in the SAXS data. The calculated data for the worst model against the observed SAXS data is shown for comparison (Figure 5B).
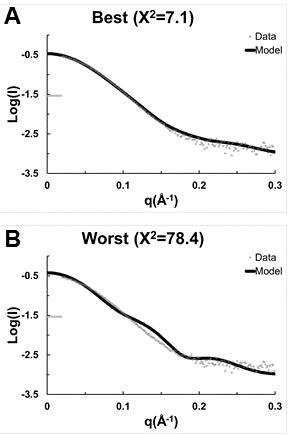 Figure 5. Representative samples of SAXS data calculated using the ECD(1-432) theoretical atomic models compared to the observed SAXS data; (A) the best model threaded with PDB ID 5bq9A, and (B) the worst model.
Figure 5. Representative samples of SAXS data calculated using the ECD(1-432) theoretical atomic models compared to the observed SAXS data; (A) the best model threaded with PDB ID 5bq9A, and (B) the worst model.
The best theoretical model for ECD(1-432) was docked into the best ab initio bead model (lowest NSD) using Situs (Figure 6). The second model threaded with PDB ID 5bq9 gave the best fit to the bead model. Please note, 5bq9 is an uncharacterized protein lpg1496 from Legionella pneumophila subspecies pneumophila. So this threading experiment does not yield further clues into ECD function at this point in time. The secondary structure of this model (Supplementary Figure S1 line 3) is also in good agreement with the predicted secondary structures (Supplementary Figure S1 line 2) and predicted disordered regions (Supplementary Figure S1 line 4). The N-terminus of this model is positioned approximately where the N-terminus of ECD is most likely to be located from the interpretation of the SAXS bead models of ECD(1-432) and ECD(1-534) (Figure 4). The model fills the Dammin SAXS bead model well and has similar dimensions (Figure 6A). The model overlaid with the Gasbor SAXS model gives similar results (see Supplementary Figure 2B). The model has two domains composed of helices and strands with a flexible linker between them (Figure 6B). Of particular interest is the LxxLL motif. It is located on a helical region near the C-terminus (Figure 6C). This helical structure is probably loosely tethered and becomes elongated upon interaction with other proteins, as observed in the crystal structure of other proteins with the LxxLL protein-protein interaction peptide motif [40]. It may extend into the cylindrical region observed in the ECD(1-534) bead model (Figure 4).
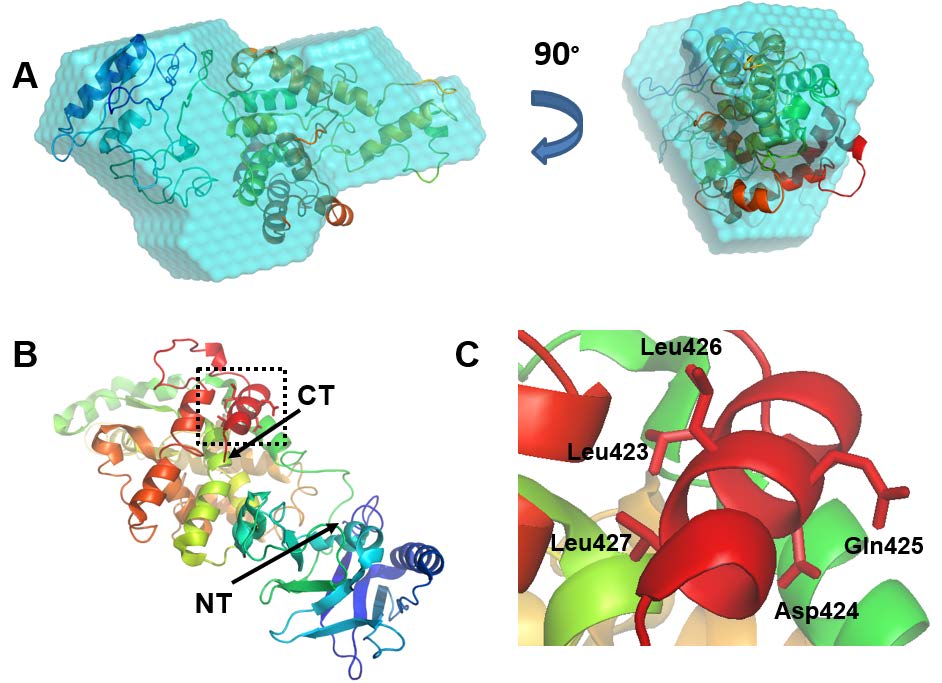 Figure 6. The best theoretical model of ECD(1-432). (A) Docked into the ab initio bead model using Situs software. (B) Ribbon drawing of the bilobal domain structure rainbow colored from N-terminus (Blue) to C-terminus (red); and (C) zoom-in on the C-terminal LxxLL motif (dotted box in part B).
Figure 6. The best theoretical model of ECD(1-432). (A) Docked into the ab initio bead model using Situs software. (B) Ribbon drawing of the bilobal domain structure rainbow colored from N-terminus (Blue) to C-terminus (red); and (C) zoom-in on the C-terminal LxxLL motif (dotted box in part B).
CD, thermal, and SAXS analysis of ECD(1-432) and ECD(1-534) reveals that they have a folded globular structure that is loosely held together. The Kratky plot and the ab initio bead models show a globular structure for each protein and ECD(1-534) includes an extended cylindrical structure. The “best” theoretical model, produced by I-TASSER calculations, appears reasonable and, in the future, will be tested experimentally (e.g. FRET). This extended structure houses the Rb binding site and some of the CK2 sites where PIH1D1 binds (Supplementary Figure S1). Based on these results we conclude that ECD may form a base, or scaffold, for tethering of various protein partners and thus be a critical component for the formation of these complexes. This is consistent with the idea that in partially-condensed proteins the structured N-terminal domain (SNTD) organizes the remaining protein chain by intramolecular interaction [41]. Moreover an interspersed pattern of SNTD-docked regions and free loops can coordinate the assembly of sub-complexes in a defined loop section and enable novel regulatory mechanisms, one of which may be phosphorylation of docked regions.
Work is supported by the National Institute of Health (NIH) grants CA96844 & CA144027 to VB, CA87986 & CA99163 to HB, and Department of Defense Grants W81XWH-07-1-0351 & W81XWH-11-1-0171 to VB; and the Fred & Pamela Buffett Cancer Center Support Grant (P30CA036727).GB also thanks support from National Center for Research Resources grant 5P20RR016469, the National Institute for General Medical Science grant 8P20GM103427 and the Protein Structure Core Facility for N-terminal sequencing data of limited proteolysis.
The authorsdeclare no conflict of interests.
 Supplementary Figure 1. Ecd sequence analysis summary. The first row indicates the amino acid sequence of Ecd: capitols indicate residues that are identical between human, mouse and cow; lower case are homologous; underlined are not conserved. Second row the Garnier Robson predictions for alpha helix (a), beta (b), coil (c) and turns (t) are indicated.Third row alpha helix (H), beta (S), and coil (C) from molecular modeling of ECD(1-432) are indicated. Last row PONDR VL-XT disordered regions are indicated with D. The LxxLL residues 423-427 are highlighted in light blue; acidic residues 499-527 are highlighted in green; CK2 sites 503, 505, and 518 are highlighted in magenta, CK2 sites 572, 579, and 584 are highlighted in red. The ends of deletion constructs are highlighted in yellow. Note, there is a small deletion in mouse at 531-533 and a small insertion in mouse at 568-569.
Supplementary Figure 1. Ecd sequence analysis summary. The first row indicates the amino acid sequence of Ecd: capitols indicate residues that are identical between human, mouse and cow; lower case are homologous; underlined are not conserved. Second row the Garnier Robson predictions for alpha helix (a), beta (b), coil (c) and turns (t) are indicated.Third row alpha helix (H), beta (S), and coil (C) from molecular modeling of ECD(1-432) are indicated. Last row PONDR VL-XT disordered regions are indicated with D. The LxxLL residues 423-427 are highlighted in light blue; acidic residues 499-527 are highlighted in green; CK2 sites 503, 505, and 518 are highlighted in magenta, CK2 sites 572, 579, and 584 are highlighted in red. The ends of deletion constructs are highlighted in yellow. Note, there is a small deletion in mouse at 531-533 and a small insertion in mouse at 568-569.
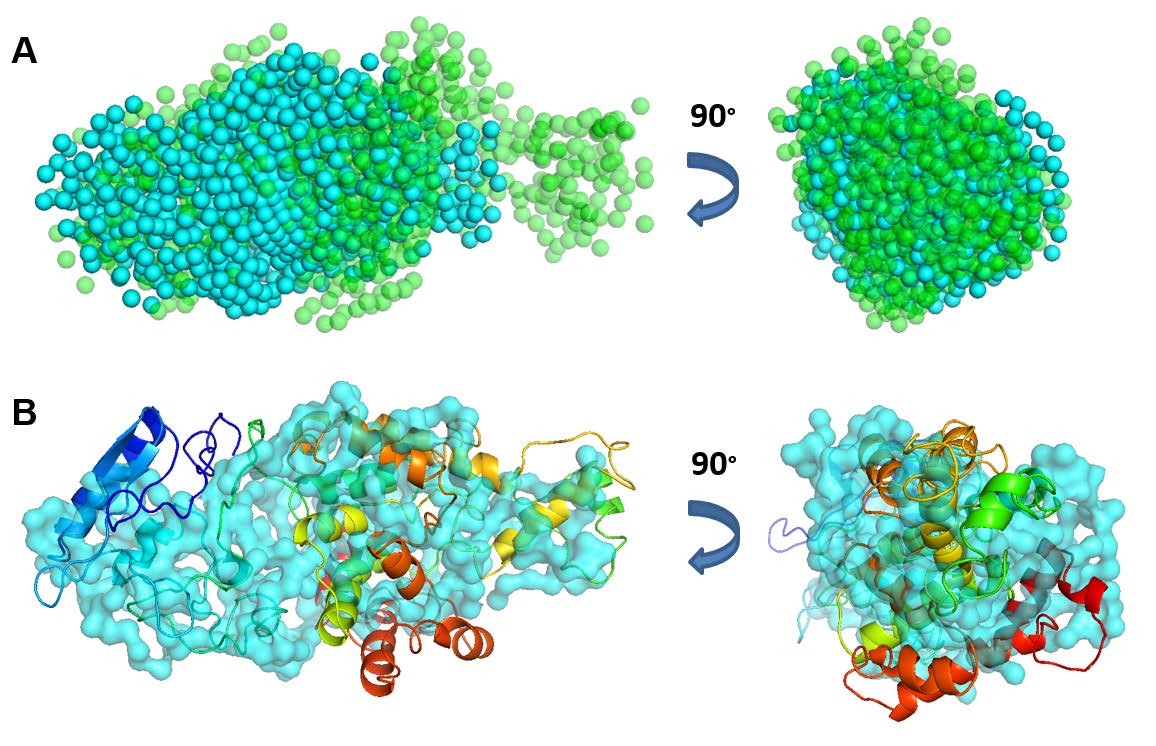 Supplementary Figure 2. Gasbor ab initio calculations. (A) SAXS model for ECD(1-432) in blue and ECD(1-534) in green. For ECD(1-432) the best NSD value was 0.866 and from 6 models the maximum value was 1.060, mean was 0.932 and standard deviation was 0.098. For ECD(1-534) the best NSD value was 1.271 and from 6 models the maximum value was 1.414, mean was 1.271 and standard deviation was 0.137. (B) The best theoretical model of ECD(1-432) docked into the GASBOR model using Situs software.
Supplementary Figure 2. Gasbor ab initio calculations. (A) SAXS model for ECD(1-432) in blue and ECD(1-534) in green. For ECD(1-432) the best NSD value was 0.866 and from 6 models the maximum value was 1.060, mean was 0.932 and standard deviation was 0.098. For ECD(1-534) the best NSD value was 1.271 and from 6 models the maximum value was 1.414, mean was 1.271 and standard deviation was 0.137. (B) The best theoretical model of ECD(1-432) docked into the GASBOR model using Situs software.
| [1] | V. A. Ambartsumian, On the fluctuation of the brightness of the milky way, Dokl. Akad. Nauk. USSR, 44 (1994), 223-226. |
| [2] | T. Kato, J. B. McLeod, The functional-differential equation y0(x) = ay(lx) + by(x), B. Am. Math. Soc., 77 (1971), 891-935. |
| [3] | J. Patade, S. Bhalekar, On analytical solution of Ambartsumian equation, Natl. Acad. Sci. Lett., 40 (2017), 291–293. |
| [4] | V. Daftardar-Gejji, S. Bhalekar, Solving fractional diffusion-wave equations using the new iterative method, Fract. Calc. Appl. Anal., 11 (2008), 193-202. |
| [5] | H. Fatoorehchi, H. Abolghasemi, Finding all real roots of a polynomial by matrix algebra and the Adomian decomposition method, J. Egypt. Math. Soc., 22 (2014), 524-528. |
| [6] | A. Alshaery, A. Ebaid, Accurate analytical periodic solution of the elliptical Kepler equation using the Adomian decomposition method, Acta Astronaut., 140 (2017), 27-33. |
| [7] | Y. Cherruault, G. Adomian, Decompostion methods: a new proof of convergence, Math. Comput. Model., 18 (1993), 103-106. |
| [8] | H. O. Bakodah, A. Ebaid, Exact solution of Ambartsumian delay differential equation and comparison with Daftardar-Gejji and Jafari approximate method, Mathematics, 6 (2018), 331. |
| [9] | A. A. Alatawi, M. Aljoufi, F. M. Alharbi, A. Ebaid, Investigation of the surface brightness model in the milky way via homotopy perturbation method, J. Appl. Math. Phys., 8 (2020), 434-442. |
| [10] | D. Kumar, J. Singh, D. Baleanu, S. Rathore. Analysis of a fractional model of the Ambartsumian equation, Eur. Phys. J. Plus, 133 (2018), 259. |
| [11] | A. A. Kilbas, H. Srivastava, J. J. Trujillo, Theory and application of fractional differential equations, North Holland Mathematics Studies, Amsterdam: Elseveir, 204 (2006), 1–523. |
| [12] | M. M. Khader, K. M. Saad, Z. Hammouch, D. Baleanu, A spectral collocation method for solving fractional KdV and KdV-Burgers equations with non-singular kernel derivatives, Appl. Numer. Math., 161 (2021), 137–146. |
| [13] |
K. M. Saad, M. Alqhtani, Numerical simulation of the fractal-fractional reaction diffusion equations with general nonlinear, AIMS Mathematics, 6 (2021), 3788–3804. doi: 10.3934/math.2021225

|
| [14] | K. M. Saad, E. H. F. AL-Sharif, Comparative study of a cubic autocatalytic reaction via different analysis methods, Discrete Cont. Dyn. S, 12 (2019), 665–684. |
| [15] | A. Shah, R. A. Khan, A. Khan, H. Khan, J. F. Gómez-Aguilar, Investigation of a system of nonlinear fractional order hybrid differential equations under usual boundary conditions for existence of solution, Math. Methods Appl. Sci., 44 (2021), 1628–1638. |
| [16] | H. Khan, J. F. Gomez-Aguilar, T. Abdeljawad, A. Khan, Existence results and stability criteria for ABC-fuzzy-Volterra integro-differential equation, Fractals, 28 (2020), 2040048. |
| [17] | A. Khan, H. Khan, J. F. Gómez-Aguilar, T. Abdeljawad, Existence and Hyers-Ulam stability for a nonlinear singular fractional differential equations with Mittag-Leffler kernel, Chaos Soliton. Fract., 127 (2019), 422–427. |
| [18] | T. Abdeljawad, A. Atangana, J. F. Gómez-Aguilar, F. Jarad, On a more general fractional integration by parts formulae and applications, Physica A., 536 (2019), 122494. |
| [19] | A. Ullah, T. Abdeljawad, S. Ahmad, K. Shah, Study of a fractional-order epidemic model of childhood diseases, J. Funct. Space., 2020 (2020), 5895310. |
| [20] | K. K. Nisar, S. Ahmad, A. Ullah, K. Shah, H. Alrabaiah, M. Arfan, Mathematical analysis of SIRD model of COVID-19 with Caputo fractional derivative based on real data, Results Phys., 21 (2021) 103772. |
| [21] | R. A. Khan, K. Shah, Existence and uniqueness of solutions to fractional order multi-point boundary value problems, Commun. Appl. Anal., 19 (2015), 515-526. |
| [22] |
K. Shah, M. A. Alqudah, F. Jarad, T. Abdeljawad, Semi-analytical study of Pine Wilt Disease model with convex rate under Caputo-Fabrizio fractional order derivative, Chaos Soliton. Fract., 135 (2020), 109754. doi: 10.1016/j.chaos.2020.109754

|
| [23] | M. Caputo, M. Fabrizio, A new definition of fractional derivative without singular kernel, Progr. Fract. Differ. Appl., 1 (2015), 73–85. |
| [24] | V. F. Morales-Delgado, M. A. Taneco-Hernández, J. F. Gómez-Aguilar, On the solutions of fractional order of evolution equations, Eur. Phys. J. Plus., 132 (2017), 47. |
| [25] | L. X. Vivas-Cruz, A. González-Calderón, M. A. Taneco-Hernández, D. P. Luis, Theoretical analysis of a model of fluid flow in a reservoir with the Caputo-Fabrizio operator, Commun. Nonlinear Sci., 84 (2020), 105186. |
| [26] | D. Baleanu, A. Jajarmi, H. Mohammadi, S. Rezapour, A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative, Chaos Soliton. Fract., 134 (2020), 109705. |
| [27] | D. Baleanu, H. Mohammadi, S. Rezapour, A mathematical theoretical study of a particular system of Caputo-Fabrizio fractional differential equations for the Rubella disease model, Adv. Differ. Equ., 2020 (2020), 184. |
| [28] |
F. Gao, X. L. Li, W. Q. Li, X. J. Zhou, Stability analysis of a fractional-order novel hepatitis B virus model with immune delay based on Caputo-Fabrizio derivative, Chaos Soliton. Fract., 142 (2021), 110436. doi: 10.1016/j.chaos.2020.110436

|
| [29] | S. Ahmad, A. Ullah, K. Shah, A. Akgül, Computational analysis of the third order dispersive fractional PDE under exponential-decay and Mittag-Leffler type kernels, Numer. Meth. Part. D. E., 2020, DOI: 10.1002/num.22627. |
| [30] | R. K. Pandey, H. K. Mishra, Homotopy analysis Sumudu transform method for time\textemdash Fractional third order dispersive partial differential equation, Adv. Comput. Math., 43 (2017), 365-383. |
| [31] |
D. Baleanu, B. Shiri, Collocation methods for fractional differential equations involving non-singular kernel, Chaos Soliton. Fract., 116 (2018), 136-145. doi: 10.1016/j.chaos.2018.09.020

|
| [32] | H. Jafari, C. M. Khalique, M. Nazari, Application of the Laplace decomposition method for solving linear and nonlinear fractional diffusion-wave equations, Appl. Math. Lett., 24 (2011), 1799-1805. |
| [33] | M. Z. Mohamed, T. M. Elzaki, Comparison between the Laplace decomposition method and Adomian decomposition in time-space fractional nonlinear fractional differential equations, Appl. Math., 9 (2018), 448–458. |
| [34] |
K. Shah, F. Jarad, T. Abdeljawad, On a nonlinear fractional order model of dengue fever disease under Caputo-Fabrizio derivative, Alex. Eng. J., 59 (2020), 2305–2313. doi: 10.1016/j.aej.2020.02.022

|
| [35] | M. Sher, K. Shah, Z. A. Khan, H. Khan, A. Khan, Computational and theoretical modeling of the transmission dynamics of novel COVID-19 under Mittag-Leffler Power Law, Alexandria Eng. J. 59 (2020), 3133–3147. |
| [36] | D. H. Hyers, On the stability of the linear functional equation, Proc. Natl. Acad. Sci. USA, 27 (1941), 222-224. |
| [37] |
T. M. Rassias, On the stability of the linear mapping in Banach spaces, P. Am. Math. Soc., 72 (1978), 297-300. doi: 10.1090/S0002-9939-1978-0507327-1

|
| [38] |
A. Khan, H. Khan, J. F. Gomez-Aguilar, T. Abdeljawad, Existence and Hyers-Ulam stability for a nonlinear singular fractional differential equations with Mittag-Leffler kernel, Chaos Soliton. Fract., 127 (2019), 422-427. doi: 10.1016/j.chaos.2019.07.026

|
| [39] |
H. Khan, T. Abdeljawad, M. Aslam, R. A. Khan, A. Khan, Existence of positive solution and HyersUlam stability for a nonlinear singular-delay-fractional differential equation, Adv. Differ. Equ., 2019 (2019), 104. doi: 10.1186/s13662-019-2054-z

|
| [40] | T. A. Burton, T. Furumochi, Krasnoselskiis fixed point theorem and stability, Nonlinear Anal.-Theor., 49 (2002), 445–454. |
| Sample | ECD(1-432) | ECD(1-534) | ||||||
| Concentration (mg ml-1) | 4.79 | 4.95 | 10.86 | ∞-1 | 1.51 | 2.21 | 3.42 | ∞-1 |
| I(0) (Normalized concentration; cm-1) | 0.33 | 0.32 | 0.35 | 0.32 | 0.52 | 0.54 | 0.52 | 0.50 |
| Rg Guinier (Å) | 27.7 | 27.2 | 28.5 | 26.3 | 34.7 | 37.8 | 36.3 | 34.8 |
| Rg P(r) (Å) | 27.3 | 27.0 | 28.5 | 26.4 | 35.6 | 38.8 | 37.1 | 35.6 |
| Dmax (Å) | 89.0 | 93.0 | 100.0 | 92.0 | 121 | 132 | 127 | 122 |
| Porod volume (Å3) | 90,302 | 86,625 | 93,368 | 87,266 | 114,882 | 126,440 | 117,895 | 116,206 |
| DAM volume (Å3) | 109,400 | 104,900 | 111,100 | 105,300 | 145,700 | 159,300 | 149,200 | 145,400 |
| MW Porod (kDa) | 53.1 | 51.0 | 54.9 | 51.3 | 67.6 | 74.4 | 69.4 | 68.4 |
| MW DAMa (kDa) | 54.7 | 52.5 | 55.6 | 52.7 | 72.9 | 79.7 | 74.6 | 72.7 |
| a where DAM is Dummy Atom Model | ||||||||
| Sample | ECD(1-432) | ECD(1-534) | ||||||
| Concentration (mg ml-1) | 4.79 | 4.95 | 10.86 | ∞-1 | 1.51 | 2.21 | 3.42 | ∞-1 |
| I(0) (Normalized concentration; cm-1) | 0.33 | 0.32 | 0.35 | 0.32 | 0.52 | 0.54 | 0.52 | 0.50 |
| Rg Guinier (Å) | 27.7 | 27.2 | 28.5 | 26.3 | 34.7 | 37.8 | 36.3 | 34.8 |
| Rg P(r) (Å) | 27.3 | 27.0 | 28.5 | 26.4 | 35.6 | 38.8 | 37.1 | 35.6 |
| Dmax (Å) | 89.0 | 93.0 | 100.0 | 92.0 | 121 | 132 | 127 | 122 |
| Porod volume (Å3) | 90,302 | 86,625 | 93,368 | 87,266 | 114,882 | 126,440 | 117,895 | 116,206 |
| DAM volume (Å3) | 109,400 | 104,900 | 111,100 | 105,300 | 145,700 | 159,300 | 149,200 | 145,400 |
| MW Porod (kDa) | 53.1 | 51.0 | 54.9 | 51.3 | 67.6 | 74.4 | 69.4 | 68.4 |
| MW DAMa (kDa) | 54.7 | 52.5 | 55.6 | 52.7 | 72.9 | 79.7 | 74.6 | 72.7 |
| a where DAM is Dummy Atom Model | ||||||||