A minimizing-movements approach to GENERIC systems

1.   Introduction

The aim of this note is to discuss a new variational time-discretization scheme adapted to the structure of General Equations for Non-Equilibrium Reversible-Irreversible Coupling (GENERIC). Introduced by Grmela & Öttinger, this formulation provides a unified frame for describing the time evolution of physical systems out of equilibrium in presence of reversible and irreversible dynamics ^[37].

Let $y$ denote the state of a closed, nonequilibrium physical system and let $E(y)$ and $S(y)$ be the corresponding total energy and total entropy, respectively. The GENERIC formulation of the time evolution of the system reads

Here, $y'$ denotes the time derivative, $L$ is the antisymmetric Poisson operator, and $K$ is the symmetric and positive definite Onsager operator (details in Section 2).

The gist of the GENERIC system (1.1) is that conservative and dissipative dynamics are clearly separated. Under a specific compatibility condition, see (2.4) below, this entails that a solution $t\mapsto y(t)$ to (1.1) conserves energy and accumulates entropy in a quantifiable way, namely

The conservation of energy and the quantified dissipative character are the distinguishing traits of the GENERIC system (1.1). To replicate these properties at the discrete level leads to so-called structure-preserving approximations. These have drawn interest in the last years, giving rise to different numerical solutions adapted to diverse applicative contexts.

In the last years, GENERIC has attracted increasing attention and has been applied to a number of situations ranging from complex fluids ^[18], to dissipative quantum mechanics ^[32], to thermomechanics ^{[5,21,22,23,31]}, to electromagnetism ^[24], to shape-memory alloys ^[3], to the Vlasov-Fokker-Planck ^[13,14,20] and the Boltzmann equation ^[35], and to large-deviation limits of reversible stochastic processes ^[26,27].

Numerical schemes conserving energy can be found for instance in ^{[16,41,43,44,45,48]}; see ^[8] for a review and ^[50] for a contribution explicitly focusing on GENERIC formulations. These schemes are often discrete-gradient methods, where gradients of functionals are specifically modified in order to fulfill a discrete chain rule and exactly replicate conservation ^{[16,17,19,30]}. In the thermomechanical context, structure-preserving discretizations either in terms of the absolute temperature ^[9,10,15,39] or of the internal energy or the entropy ^[5,6] have been obtained. The reader is referred to ^[28] for an approach to open systems.

GENERIC integrators able to conserve energy and accurately describe entropy accumulation have been proposed in ^[38], where however some limitations are also mentioned. In particular, energy and Onsager operators have to be suitably modified in a time-step dependent manner in order energy conservation to hold. Integrators are actually constructed in case of a single dissipation mechanism only (were $K$ be a matrix, it would have to have rank one) and no convergence theory is provided. The discretization of the damped harmonic oscillator is addressed in ^[38], where nonetheless the temperature is given by a prescribed heat bath. In this case, explicit solutions have to be used in order to specify the GENERIC integrator.

To the best of our knowledge, all available numerical schemes directly target GENERIC systems in their differential form (1.1). Our focus is here on a time-discretization of variational nature instead, fitting into the general scheme of so-called minimizing movements ^[1,2]. In particular, at all discrete steps we aim at solving a specific minimization problem. We start by defining the entropy-production potential $\Psi(y, \xi) = \langle\xi, K(y)\xi \rangle/2$ and denoting by $\Psi^*(y, \cdot)$ its conjugate in the second variable. Then, the GENERIC relation (1.1) in $[0, T]$ can be equivalently rewritten in terms of the scalar equation

for all $t\in [0, T]$. The reformulation of dissipative systems in terms of scalar equations as (1.2) is usually referred to as De Giorgi's Energy-Dissipation Principle ^[12,29,33]. This principle has already been applied in a variety of different contexts, including generalized gradient flows ^[4,47], curves of maximal slope in metric spaces ^[2,11], rate-independent systems ^[34,42], and optimal control ^[40]. For GENERIC systems, the reformulation of (1.1) in terms of such variational principle has been already presented in ^[14].

Our new minimizing-movements approach to (1.1) consists in tackling a discrete version of relation (1.2). Assume to be given a time partition $0 = t_0 < t_1 < \dots < t_N = T$ with steps $\tau_i = t_i - t_{i-1}$, and an initial state $y^0$. We define the time-discrete trajectory $\{ y_i \}_{i = 0}^N$ by letting $y_0 = y^0$ and subsequently perform the minimization

for $i = 1, \dots, N$ where $y^\phi : = \phi y + (1-\phi) y_{i-1}$ for some fixed $\phi \in [0, 1]$. The latter is nothing but a localized and discretized version of the De Giorgi's Energy-Dissipation Principle (1.2).

The minimizing-movements scheme above has been introduced in ^[25]. The theory in ^[25] is however restricted to $\phi = 1$ and to the case of state-independent operators $L$ and $K$, which severely limits the applicability to real GENERIC systems. In addition, the convergence analysis in ^[25] relies on a suitable set of a priori assumptions, leaving open the discussion whether these can be met in practice.

The aim of this note is then threefold. First, we extend the reach of the numerical method to include the case of state dependent operators $L(y)$ and $K(y)$, hence covering the full extent of the GENERIC theory (Section 2). In addition, we investigate the general case $\phi\in[0, 1]$. Our main result is the conditional convergence of Theorem 2.1. Second, we provide the detailed analysis in the classical case of the damped harmonic oscillator for the choice $\phi = 1/2$. In this case, the above-mentioned convergence assumptions can actually be proved to hold (Section 3). Eventually, we present numerical experiments assessing the performance of the minimizing-movements scheme (Subsection 3.4). In particular, we show that the scheme conserves the energy.

2.   The minimizing-movements scheme for GENERIC systems

In this section, we recall the structure of a GENERIC system ^[37] by specifying the assumptions on functionals and operators that will be used throughout. Moreover, we formulate our minimizing-movements scheme and present a conditional convergence result, namely Theorem 2.1.

The GENERIC system

is defined by specifying the quintuple $(Y, E, S, L, K)$. In the following, the state space $Y$ is assumed to be a reflexive Banach space. The functionals $E$ and $S$ represent the total energy and the total entropy of the system, respectively. We assume $E$ to be Fréchet differentiable, with strongly-weakly continuous differential $\mathrm{D} E$, and $-S:Y \to (-\infty, \infty]$ to be proper and lower semicontinuous with single-valued and strongly-weakly continuous Fréchet subdifferential $\partial(-S)$ ^[36]. Recall that one has $\xi \in \partial(-S)(y)$ iff $S(y) > -\infty$ and

In the following, we also make use of the obvious notation $-\partial S = \partial (-S)$.

The operators $L$ and $K$ define a Poisson and an Onsager geometric structure on $Y$, respectively. In particular, for all states $y\in Y$ we assume that $L(y)$ and $K(y)$ are linear and continuous from $Y^*$ to $Y$. Moreover, $L(y)$ is required to be antisymmetric, $L^*(y) = -L(y)$, and to fulfill the Jacobi identity $\{ \{g_1, g_2\}, g_3 \}+\{ \{g_2, g_3\}, g_1 \}+\{ \{g_3, g_1\}, g_2 \} = 0$. Here, $g_i$ denotes any differentiable function on $Y$ and the Poisson bracket is defined as $\{g, \tilde g\}(y) = \langle \mathrm{D} g(y), L(y) \mathrm{D} \tilde g(y) \rangle$, where $\langle \cdot, \cdot \rangle$ denotes the duality pairing between $Y^*$ (dual) and $Y$. Moreover, we assume the strong-weak continuity

The mapping $K(y)$ is asked to be symmetric and positive definite, namely $K(y) = K^*(y)\geq 0$. We associate with $K$ the so-called entropy-production potential $\Psi: Y \times Y^* \to [0, \infty)$ given by $\Psi(y, \xi) = \langle \xi, K(y)\xi \rangle/2$ and let $\Psi^*$ be its conjugate in the second variable, namely $\Psi^*(y, \eta) = \sup_{\xi}(\langle \xi, \eta \rangle - \Psi(y, \xi))$. We also assume the lower semicontinuity of the sum of the entropy-production potential and its dual, that is

In addition, functionals and operators are asked to satisfy the crucial noninteraction condition

This condition ensures that the system of dissipative actions $K(y)\, \partial S(y)$ does not spoil energy conservation and the system of conservative actions $L(y)\, \mathrm{D} E(y)$ does not contribute to dissipation. Indeed, by assuming sufficient smoothness one checks that

The noninteraction condition (2.4) hence implies that trajectories $y$ solving (2.1) have constant total energy, and that the entropy rate is $\langle \partial S(y), K(y) \partial S(y) \rangle$. In particular, the entropy is nondecreasing and entropy production results solely from irreversible processes. In computing (2.5) we have used the chain rule $(\mathrm{d}/ \mathrm{d} t)S(y) = \langle \partial S(y), y' \rangle$ almost everywhere. This is classical in case $-S$ is (a regular perturbation of) a convex functional [7,Prop. 3.3,p. 73]. The reader is referred to ^[46] for a general discussion out of the convex case.

Before moving on, let us remark that the structure of GENERIC is geometric in nature. Indeed, it is invariant by coordinate changes. Let $y = \phi(\tilde y)$ for $\tilde y \in \tilde Y$ and define $\tilde E(\tilde y) = E(\phi(\tilde y))$, $-\tilde S(\tilde y) = -S(\phi(\tilde y))$, $\tilde L(\tilde y) = \mathrm{D} \phi(\tilde y)^{-1} L(\phi(\tilde y)) \mathrm{D} \phi(\tilde y)^{-*}$, and $\tilde K(\tilde y) = \mathrm{D} \phi(\tilde y)^{-1} K(\phi(\tilde y)) \mathrm{D} \phi(\tilde y)^{-*}$, where $\mathrm{D} \phi(\tilde y) ^{-*}: \tilde Y^* \to Y^*$ is the adjoint of the inverse of $\mathrm{D} \phi(\tilde y) : \tilde Y \to Y$. Then, the quintuple $(\tilde Y, \tilde E, \tilde S, \tilde L, \tilde K)$ satisfies the above structural assumptions and the GENERIC structure (2.1) can be rewritten as $\tilde y' = \tilde L(\tilde y)\, \mathrm{D} \tilde E(\tilde y) + \tilde K (\tilde y)\, \partial \tilde S(\tilde y)$.

We now reconsider the discussion leading to (1.2) and specify it further by remarking that relation (2.1) is actually equivalent to the inequality

for all $t \in [0, T]$. The equivalence between (2.1) and (2.6) follows from Fenchel's relations. Applied to the entropy-production potential $\Psi$, these relations read

where the subdifferential is taken in the second variable only. By noting that $\partial \Psi(y, \partial S(y)) = K(y)\, \partial S(y)$ and using (2.7) and (2.8), one can prove the equivalences

In particular, the last left-to-right implication follows by integration while the right-to-left counterpart from the nonnegativity of the integrand, given (2.4) and (2.7).

The minimizing-movements scheme corresponds to a discretization of inequality (2.6). To each time partition $0 = t_0 < t_1 < \dots < t_{N} = T$, we associate the time steps $\tau_i = t_i - t_{i-1}$ and the diameter $\tau = \max \tau_i$. Given the vector $\{y_i\}_{i = 0}^N\in Y^{N+1}$, we introduce the backward piecewise constant and piecewise linear interpolations $\overline y:[0, T] \to Y$ and $\widehat y:[0, T] \to Y$,

We define the incremental functional by $G : (0, \infty) \times Y\times Y \to (-\infty, \infty]$ as

where $y^\phi = \phi y + (1-\phi)\eta$ and $\phi \in [0, 1]$ is fixed throughout. By letting $y_0 = y^0$ we find the discrete solution $\{y_i\}_{i = 0}^{N}$ by subsequently solving the minimization problem

The state dependence in $\Psi$, $\Psi^*$, and $\mathrm{D} E$ can be made implicit or explicit suitably choosing the parameter $\phi\in[0, 1]$, and our analysis is independent from such a specific choice.

For all $\tau > 0$ and $y_{i-1}\in Y$ with $S(y_{i-1}) > -\infty$, the map $y \mapsto G(\tau_i, y_{i-1};y)$ is strongly lower semicontinuous because of the lower semicontinuity of $-S$, the lower semicontinuity (2.3) of $\Psi^*+\Psi$, the weak-strong continuity of $\mathrm{D} E$ and $\partial S$, and the continuity (2.2) of $L$. In order to solve problem (2.9) one has hence to check that $y \mapsto G(\tau_i, y_{i-1};y)$ is strongly coercive.

The main result of this section is the following conditional convergence result.

Theorem 2.1 (Conditional convergence). Under the above assumptions, let a sequence of partitions $0 = t_0^n < \dots < t_{N^n}^n = T$ be given with $\tau^n\to 0$ as $n \to \infty$, and let $\{y_i^n\}_{i = 1}^{N^n}$ be such that $y_0^n = y^0$, not necessarily being minimizers from (2.9). Assume that

Then, up to a subsequence, $\widehat y^n \rightharpoonup y$ in $H^1(0, T; H)$, where $y$ is a solution of the $\text{GENERIC}$ system (2.1) in the sense of inequality (2.6).

Proof of Theorem 2.1. We infer from the Aubin-Lions lemma [49,Cor. 7], upon extracting not relabeled subsequences, that

As $\partial S$ is strongly-weakly closed, we have that $s = \partial S(y)$ almost everywhere. On the other hand, the strong-weak continuity of $\mathrm{D} E$ and the continuity (2.2) of $L$ imply that $L(\overline y^n)\, \mathrm{D} E(\overline y^{\phi n}) \to L(y)\, \mathrm{D} E(y)$ pointwise in time, so that $\ell = L(y)\, \mathrm{D} E(y)$ almost everywhere.

Fix any $t\in (0, T]$ and let $t^n_m$ be such that $t \in (t^n_{m-1}, t^n_m]$. The discrete sequence of solutions $\{y_i^n\}_{i = 0}^{N^n}$ fulfills

As $\Psi(\tilde y, \cdot)\geq \Psi(\tilde y, 0) = 0$ for all $\tilde y$, we conclude that $\Psi^*\geq 0$ as well. By restricting integrals to the interval $[0, t] \subset [0, t^n_m]$ equation (2.16) implies that

We now pass to the limit inferior as $n\to \infty$ in relation (2.17). By using convergence (2.10), the lower semicontinuity of $-S$, convergences (2.14) and (2.15), and the lower semicontinuity (2.3), we readily obtain that the limit $y$ fulfills inequality (2.6).

The conditional convergence result of Theorem 2.1 relies on the possibility of solving the inequality $G(\tau_i^n, y_{i-1}^n; y_i^n)\leq 0$ up to a small, controllable error, and establishing some a priori bounds on the discrete solution. The validity of these conditions has to be checked on the specific problem at hand. In the upcoming Section 3 we give an example of a situation where (2.10)–(2.13) actually hold.

In case $-S$ is convex, an example of $\{y_i^n\}_{i = 0}^{N^n}$ fulfilling (2.10) are the solutions of the Euler scheme

with $y_i^{\phi n} = \phi y_i^n + (1-\phi) y^n_{i-1}$. Indeed, such $\{y_i^n\}_{i = 0}^{N^n}$ fulfills

where the last equality follows from (2.8) and (2.18).

In the purely dissipative case $L = 0$, the existence of a solution to the minimization problem (2.9) is ensured as soon as $\tau^* > 0$ exists, such that, for all $\tau\in (0, \tau^*)$ and $y_{i-1}\in Y$ with $S(y_{i-1}) > -\infty$, the function

is strongly coercive. The latter follows whenever $-S$ has strongly compact sublevels. Note however that the specific example of the damped harmonic oscillator from Section 3 does not fall into this class, as it is not purely dissipative and $-S$ does not have strongly compact sublevels. Still, existence for the minimization problem (2.9) can be directly checked.

Let us mention that, in specific applications, the bounds (2.11)–(2.13) may follow from (2.10). For instance, this would be the case if the coercivity

holds for some $c > 0$ and all $\tilde y, \, \eta\in Y$ and $\xi \in Y^*$, namely in case $K(\tilde y)$ is positive definite and bounded, uniformly with respect to $\tilde y$. This however does not apply to the example of the damped harmonic oscillator from Section 3, for $K$ is singular there.

The quadratic nature of the entropy-production potential could be generalized to the case of $p$-growth with $p > 1$ without any specific intricacy. In particular, one could consider the polynomial case $\partial \Psi(\tilde y, \xi) = K(\tilde y) \| \xi\|^{p-2}_{Y^*}\xi$ and coercivity (2.20) would then read

for $1/p+1/p' = 1$. This setting would correspond to the case of doubly-nonlinear GENERIC continuous dynamics, namely

Again, under the noninteraction condition (2.4), suitably regular solutions conserve energy, since $\langle \mathrm{D} E(y), \partial \Psi(y, \partial S(y)) \rangle = \| \partial S(y)\|_{Y^*}^{p-2} \langle \partial S(y), K^*(y)\, \mathrm{D} E(y) \rangle = 0$, and have entropy rate $(\mathrm{d}/ \mathrm{d} t)(S(y)) = \| \partial S(y)\|_{Y^*}^{p-2} \langle \partial S(y), K(y)\, \mathrm{D} S(y) \rangle \geq 0$.

Let us further remark that the conditional convergence result of Theorem 2.1 can serve as an a-posteriori tool to check the convergence of time-discrete approximations $\{y^n_i\}$, regardless of the method used to generate them. Indeed, as already mentioned in the statement of Theorem 2.1, $\{y_i^n\}$ need not be a minimizer. In particular, the case of suitable approximate minimizers can be treated as well. In essence, relation (2.10) can be seen as a sort of a-posteriori error estimator.

3.   The minimizing-movements scheme for the damped harmonic oscillator

In this section, we analyze the simplest GENERIC system fulfilling conditions (2.10)–(2.13). We consider the case of the damped harmonic oscillator, namely

Here, $q\in {\mathbb R}$ represents the position of the harmonic oscillator and $\theta > 0$ is its absolute temperature. Note that the case of $\theta$ being the given, constant temperature of a surrounding heat bath is considered in ^[38] instead. The positive constants $m$, $\nu$, $\kappa$, $\lambda$ and $c$ are the mass of the oscillator, the viscosity of the medium, the elastic modulus, the thermal-exchange coefficient, and the heat capacity, respectively.

By letting $p\in {\mathbb R}$ be the momentum of the harmonic oscillator, we rewrite (3.1)–(3.2) as the first-order system

System (3.3)–(3.5) can be written in the GENERIC form (2.1) by letting $y = (q, p, \theta)\in Y = {\mathbb R}^2\times(0, \infty)$ represent the state of the harmonic oscillator and by defining the total energy and the total entropy as

These definitions comply with the classical Helmholtz relations under the choice for the free energy

In particular, $S = -\partial_\theta \Phi$ and $E = p^2/(2m) + \Phi + \theta S$. Note that both $E$ and $S$ are smooth, $-S$ is convex, and $S(y) > -\infty$ iff $\theta > 0$.

The operators $L, \, K : {\mathbb R}^3 \to {\mathbb R}^{3\times 3}$ are given by

One readily checks that $L$ is antisymmetric and a tedious computation shows that the Jacobi identity holds. On the other hand, $K$ is symmetric and positive semidefinite, while not being invertible. Note that $K(y)$ has rank two for all $p\not = 0$, so that the construction in ^[38] does not apply here.

By computing the gradients $\mathrm{D} E(y) = (\kappa q, p/m, c)$ and $\mathrm{D} S(y) = (-\lambda, 0, c/\theta),$ one can easily check that the noninteraction condition (2.4) holds.

Letting $\xi = (\xi_q, \xi_p, \xi_\theta)\in {\mathbb R}^3$, $\eta = (\eta_q, \eta_p, \eta_\theta) \in {\mathbb R}^3$, and $\tilde y = (\tilde q, \tilde p, \tilde \theta) \in {\mathbb R}^2 \times (0, \infty)$, the entropy-production potential and its dual read

We now choose $\phi = 1/2$, so that the state dependences in $\Psi$, $\Psi^*$, and $\mathrm{D} E$ are evaluated at the midpoint. With the definitions above, the incremental functional $G:(0, \infty)\times {\mathbb R}^3 \times {\mathbb R}^3 \to (-\infty, \infty]$ for $y = (q, p, \theta)$ and $\overline y = (\overline q, \overline p, \overline \theta)$ takes the form

Assume to be given the time partition $0 = t_0 < \dots < t_N = T$ with $\tau_i = t_i - t_{i-1}$ for $i = 1, \dots, N$. By letting $\overline y = (q_{i-1}, p_{i-1}, \theta_{i-1})$ and defining $(q_0, p_0, \theta_0) = (q^0, p^0, \theta^0)$ for some given initial state $(q^0, p^0, \theta^0)\in {\mathbb R}^2 \times (0, \infty)$, the incremental minimization problem (2.9) becomes

Note in particular that the constraint (3.9) is nothing but the conservation of energy, namely

This property is of course of great physical relevance and plays a crucial role in the a priori estimates. In particular, one has that

This entails the bound

where, here and in the following, the symbol $C$ denotes a generic positive constant depending on the initial data $y^0$ and on material parameters, but not on the time partition and, in particular, not on $i$. In addition, bound (3.10) entails that there exists $\theta_{\text min} > 0$ independent of the time partition such that $\theta_i \geq \theta_{\text min}$, see (3.19) below. Note that energy conservation is specific of the current choice $\phi = 1/2$ and hinges on the quadratic nature of $E$.

We devote the remainder of this section to prove that the convergence result of Theorem 2.1 applies to the scheme (3.6)–(3.9), namely that conditions (2.10)–(2.13) are fulfilled. In particular, we check that the minimization problem admits a solution $\{y_i\}_{i = 0}^N = \{(q_i, p_i, \theta_i)\}_{i = 0}^N$ (Subsection 3.1) and that each such solution fulfills condition (2.10) in the stronger sense $G(\tau_i, y_{i-1};y_i) \leq 0$ (Subsection 3.2), and that the bounds (2.11)–(2.13) can be established, independently of the partition (Subsection 3.3). Eventually, numerical simulations are presented in Subsection 3.4.

3.1.   Existence of minimizers

Assume to be given $\overline y = (q_{i-1}, p_{i-1}, \theta_{i-1})\in {\mathbb R}^2\times(0, \infty).$ As $y \mapsto G(\tau_i, \overline y; y)$ is smooth on its domain, in order to prove that the scheme (3.6)–(3.9) admits a solution, we just need to check coercivity, namely that sublevels of $y \mapsto G(\tau_i, \overline y; y)$ are bounded.

By using the constraints (3.8)–(3.9) we can express $q_i$ and $\theta_i$ in terms of $p_i$ and the values $(q_{i-1}, p_{i-1}, \theta_{i-1})$ in the form

where the second-order polynomial $f$ in $p_i$ is defined by

By substituting the two expressions in the minimum problem (3.6)–(3.9), we can reduce it to a minimization in the variable $p_i$ only. Indeed, problem (3.6)–(3.9) is equivalent to

where we have defined

As $F$ is smooth on its domain, in order to solve the minimization problem (3.12) we just need to prove that $F$ has bounded sublevels. This follows from the fact that $F(p_i)\to \infty$ if $f(p_i)\to 0^+$. Hence, it remains to prove that $f(p_i) > 0$ holds on a bounded interval only, depending on $(q_{i-1}, p_{i-1}, \theta_{i-1})$, for $\tau_i$ chosen to be small enough. Since $f$ has the form $f(p_i) = \alpha p_i^2 + \beta p_i +\gamma$, it suffices to check that $\alpha < 0$ and $\gamma > 0$, for $\tau_i$ small enough. In fact, $\alpha < 0$ as soon as $\tau^2 < 4m/\kappa$. On the other hand, under the same upper bound on $\tau_i$ we have

where $C$ is the constant in (3.10). In particular, $\gamma > 0$ if $\tau_i$ is chosen such that $\tau_i < 2mc\theta_{\text min}/(\kappa C^2)$.

We have hence proved that, for all given $(q_{i-1}, p_{i-1}, \theta_{i-1})\in {\mathbb R}^2\times (0, \infty)$, we can find a solution $p_i$ of (3.12). We conclude from (3.11) that for $\tau_i$ small enough there exists $(q_i, p_i, \theta_i)$ solving (3.6)–(3.9). In particular, we have that $\theta_i > 0$.

3.2.   Minimizers fulfill condition (2.10)

Moving from relation (2.19), the convexity of $-S$ ensures that condition (2.10) holds, for minimizers can be compared with solutions of the Euler scheme (2.18)

for $i = 1, \dots, N$.

By adapting the argument from Subsection 3.1, an elementary but tedious computation ensures that the Euler scheme (3.13)–(3.15) admits indeed a solution $y^e_i = (q_i, p_i, \theta_i)$.

Let now $y_i$ be a solution to the incremental minimization problem (3.6). Owing to (2.19), we conclude that

where we have also used the fact that $y^e_i$ fulfills the constraints (3.7)–(3.9). In particular, condition (2.10) holds in the even stronger form

3.3.   A priori bounds

We now prove that condition (2.11)–(2.13) of Theorem 2.1 hold. This will follow by checking a priori bounds on minimizers $\{y_i\}_{i = 0}^N$ of (3.6), independently from the time partition.

Bound (3.10) and constraint (3.8) imply that

Moreover, we readily check that

Let us take the sum for $i = 1, \dots, j$ for $j \leq N$ in (3.16), getting

where

As $\psi^*_j$ and $\psi_j$ are nonnegative, we infer that $S(y_i)$ is nondecreasing. In particular,

and consequently,

for some given $\theta_{\text min}$ depending just on $y^0$ and the material parameters. This ensures that

It follows from the bound (3.10) on $q_i$ and $\theta_i$ that $S(y_i) = -\lambda q_i + c + c \ln \theta_i \leq C$ for all $i = 1, \dots, N$. We conclude that $\psi_N^* \leq -S(y^0)+S(y_N)\leq C$ and

Using the fact that $\theta_i$ is uniformly bounded by (3.10), we can hence bound

Eventually, we infer from constraint (3.9) that

where the last inequality follows from bounds (3.10), (3.17), and (3.22).

Bounds (3.10)–(3.17) and (3.22)–(3.23) imply condition (2.11) from Theorem 2.1. On the other hand, bounds (3.18) and (3.20) imply conditions (2.12) and (2.13), respectively. Hence, the convergence statement of Theorem 2.1 holds. In particular, given initial values $(q^0, p^0, \theta^0)\in {\mathbb R}^3$ with $\theta^0 > 0$, a sequence of partitions $0 = t_0^n < \dots < t^n_{N^n} = T$ with $\tau^n = \max_i(t^n_i - t^n_{i-1})\to 0$, and corresponding minimizers $\{(q_i^n, p_i^n, \theta_i^n)\}_{i = 0}^N$ of (3.6), it follows that

where $(q, p, \theta)$ solves the damped harmonic oscillator system (3.3)–(3.5) with initial value $(q(0), p(0), \theta(0)) = (q^0, p^0, \theta^0)$. Note that solutions of (3.3)–(3.5) are unique. Hence, convergence (3.24) holds for the whole sequence of discrete solutions, not just for a subsequence.

3.4.   Numerical tests

We record here some illustration of the performance of the minimizing-movements scheme (3.6)–(3.9). All computations are made in Matlab. In the following, we choose

Given a uniform time-partition with time step $\tau = T/N$, we find a solution $\{y_i\}_{i = 0}^N$ of the minimizing-movements scheme (3.6)–(3.9) via Newton's method. The numerical reference solution $t\mapsto y(t)$ is calculated by means of the Matlab solver ode45 choosing $10^{-4}$ for the maximal time step and $10^{-8}$ for the absolute tolerance.

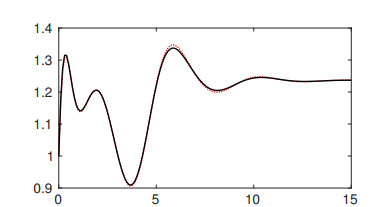
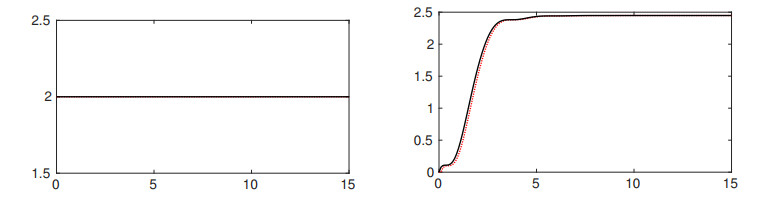
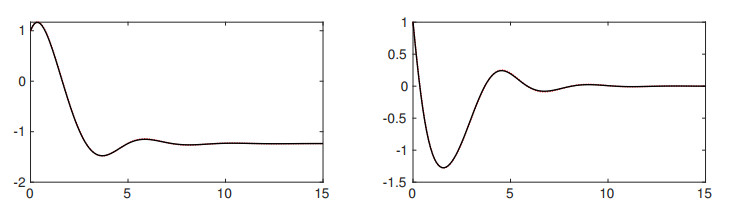
Figures 1–3 illustrate the numerical reference solution and the time-discrete solution for $\tau = 1/4$. As expected, the minimizing-movement scheme conserves energy, see Figure 3 left, while entropy is nondecreasing, see Figure 3 right. A second set of experiments is illustrated in Figure 4. For the same choices in (3.25) and different time steps

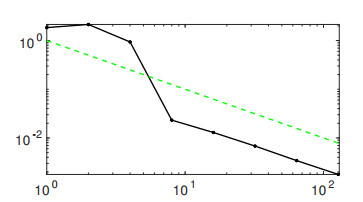
we compute the uniform errors of the temperature component of the solution with respect to the numerical reference solution.

As $\tau$ converges to $0$, our computations confirm that the minimizing-movements is of order $\tau$. Let us mention that a proof of first-order convergence for the minimizing-movements scheme in the nondissipative regime ($L = 0$, $K$ independent of the state) is given in [25,Prop. 4.3].

Acknowledgements

The Authors gratefully acknowledge a remark by Alexander Mielke on an earlier version of this work, which eventually inspired the design of the numerical scheme for the damped harmonic oscillator. This research is supported by Austrian Science Fund (FWF) project F 65 and W 1245. AJ is supported by the FWF projects P 30000 and P 33010. US is supported by the FWF projects I 4354 and P 32788 and by the Vienna Science and Technology Fund (WWTF) through Project MA14-009.

Conflict of interest

The authors declare no conflict of interest.