1. Introduction
T cells use the T cell receptor (TCR) to recognize antigens; i.e. peptides presented by major histocompatibility complexes (pMHC) on antigen-presenting cells (APCs). A striking feature of T cells is the capability of discriminating between antigens of various affinity during their thymic development as well as during immune responses of mature T cells. Another hallmark of the antigen recognition by the TCR is its enormous sensitivity, which enables the T cell to respond to only a few cognate antigen molecules presented by an APC [1,2].
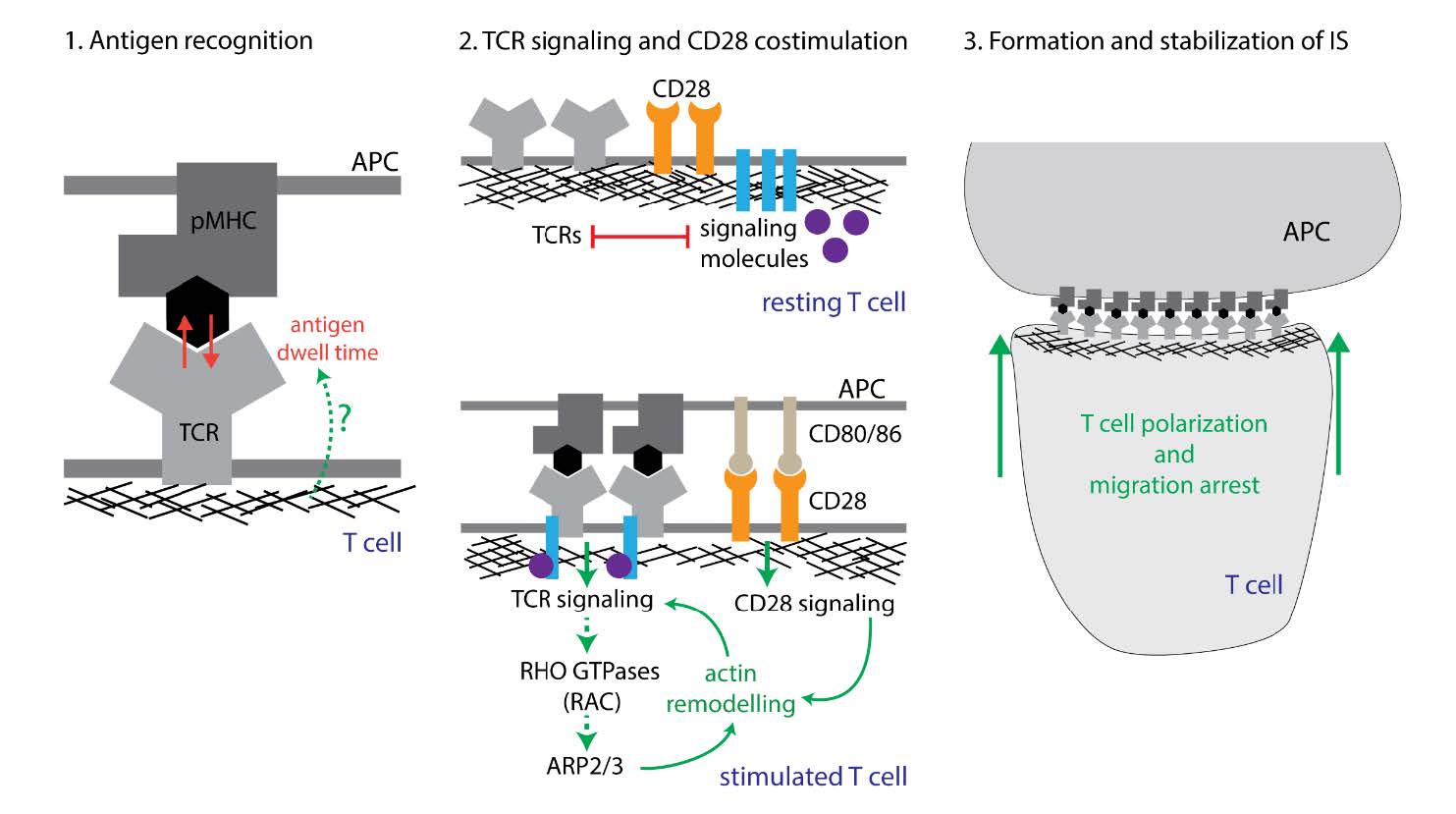
Antigen binding to the TCR triggers the TCR signaling pathway, which eventually leads to the formation of the immunological synapse (IS) between the T cell and the APC. During the IS formation, the T cell polarizes certain plasma membrane components and cytosolic structures (e.g. cytoskeleton, Golgi apparatus, and centrosome) towards the APC [3]. Proteins involved in TCR signal transduction, including kinase ZAP70, signaling adaptors LAT and SLP76, and actin modulators WASP, VAV, RAC, and CDC42 are recruited to the IS, whereas tyrosine phosphatases CD45 and CD148 are excluded from the T cell:APC contact site, which leads to the amplification of TCR signals [4,5,6,7,8,9,10].
Actin cytoskeleton is a dynamic filamentous network that drives the cell shape changes during cell growth and migration. Cellular actin exists in two forms, monomeric and filamentous (F-actin). Dynamic transition between these two forms is a characteristic feature of actin remodeling and actin flow during the various cellular processes [11]. TCR signals induce remodeling of actin cytoskeleton, which facilitates the polarization of the T cell towards the APC [8,12]. Actin rearrangement is required for efficient TCR signal transduction, yet the mechanism is not completely understood [13,14,15,16,17].
2. Role of actin in the antigen recognition
The interaction of the TCR with its cognate antigen initiates the TCR triggering. The TCR has the intrinsic ability to measure the antigen affinity, which is critical for discrimination between self and foreign antigens and for the establishment of the immunological tolerance. Only antigens above the antigen affinity threshold induce strong T cell responses [18,19,20]. A recent study focused on the role of mechanical force on the TCR binding to the antigen [21]. Liu et al. used an ex vivo experimental setup where T cells interacted with antigen-coated beads upon application of tensile forces of defined intensities. The results indicate that the interaction between the TCR and a strong antigen forms a so called “catch-bond”. Catch-bond is a type of non-covalent intermolecular interaction, that is stabilized by weak mechanical forces, most likely via a force-induced conformational change of either of the interaction partners [22]. The more stimulatory the antigen was, the more pronounced catch-bond with a longer lifetime was produced. In contrast, interactions between TCRs and weak antigens formed “slip bonds”, which exhibit shortened lifetimes when force is applied [21]. Because TCRs use a “kinetic proofreading” mechanism to estimate the antigen dwell time [20,23], the force-induced amplification of the differences between low-and high-affinity antigens (i.e. antigen with short and long dwell times) might contribute to the antigen discrimination and maintenance of self-tolerance. In accordance with this view, Liu and colleagues observed robust calcium signaling induced by a high-affinity antigen only when the force was imposed to the TCR-pMHC pair [21].
In live cells, the mechanical force might be exerted by the growing actin meshwork pushing against the plasma membrane [24]. Accordingly, it has been shown recently that TCR signals generate local mechanical force inside the T cell via active rearrangement of actin cytoskeleton [25]. Interestingly, T cells with disrupted actin cytoskeleton do not generate the mechanical force and exhibit impaired downstream TCR signaling upon TCR stimulation. Application of external periodical force on the TCR rescued the intracellular signaling when actin cytoskeleton was disrupted [25].
Huppa and colleagues used single-molecule fluorescence resonance energy transfer (FRET) to estimate the antigen dwell time in situ using antigens presented in an artificial lipid bilayer [26]. This experimental system mimics the T cell:APC membrane interphase (2D). Disruption of actin cytoskeleton by latrunculin A substantially prolonged dwell time of a strong antigen on the TCR about 10-fold, but had a milder effect on a weaker antigen. Overall, F-actin destabilized the interaction of TCR and strong antigen in these experiments, which does not support the idea that actin cytoskeleton exerts the force stabilizing the TCR-pMHC catch-bond in live cells.
Actin disruption had only minor effects on the antigen dwell-time when a single molecule tracking approach was employed in a similar experimental setup [27]. O’Donoghue and colleagues provided a possible explanation that actin dynamics affects the TCR-pMHC conformation as suggested before [28]. In this scenario, actin-induced conformational changes would interfere with the FRET measurements, but not with the single molecule tracking. Even if the actin cytoskeleton does not modulate the antigen dwell time, the conformational changes in the TCR induced by actin cytoskeleton could regulate the initiation of the down-stream TCR signaling. Liu et al., Huppa et al. and O’Donoghue et al. did not investigate how disruption of the actin cytoskeleton modulates TCR signal transduction in their 2D experimental setups. Collectively, F-actin plays an important role in the TCR signal transduction via generation of local force upon TCR engagement, but the direct role of F-actin in the antigen recognition and kinetics of the TCR:antigen interaction is not clear. It remains to be clarified whether actin cytoskeleton modulates lifetimes of the interaction between TCRs and high-or low-affinity antigens and/or whether actin cytoskeleton regulates the conformation of the TCR-antigen pair.
3. Role of actin in TCR triggering
Antigen binding eventually initiates the TCR signaling cascade. The very first biochemical step in the TCR signaling pathway is tyrosine phosphorylation of the TCR-associated CD3 and zeta chains, which activates ZAP70 kinase [29,30], leads to phosphorylation of LAT and SLP-76 [31,32], and eventually results in the triggering of downstream signaling pathways [33,34].
TCR and LAT molecules have been shown to exist in separated clusters, which are brought together upon antigen-induced TCR signal initiation [35]. The same group suggested previously that the clusters of plasma membrane proteins are attached to actin cytoskeleton [36]. Thus, it would be conceivable that actin cytoskeleton represents the barrier physically separating individual components of the TCR signaling cascade in resting T cells. Since TCR signals induce substantial actin remodeling [15], the barrier would be released and facilitate the assembly of the TCR signaling pathway.
In B cells, it has been shown that inhibition of F-actin increases BCR diffusion in the membranes and initiates BCR signaling even in the absence of cognate antigen [37,38]. In resting B cells, actin cytoskeleton therefore acts as an essential diffusional constrain between the BCR and a costimulation molecule, CD19, which keeps the B cell quiescent in the absence of its cognate antigen [39].
However, in case of T cells, disruption of actin cytoskeleton is not sufficient to initiate TCR signaling on its own [40]. Tan and colleagues created a mouse strain carrying an engineered version of a negative regulator of TCR signaling, CSK, which can be rapidly inhibited by a small chemical compound. Inhibition of CSK activity in T cells triggered proximal TCR signals, but did not activate more distal signaling pathways including calcium mobilization and ERK activation in the absence of TCR stimulation. Noticeably, a combination of CSK inhibition with the disruption of actin cytoskeleton stimulated calcium influx and ERK phosphorylation to levels comparable to α-CD3 induced TCR triggering in preselection thymocytes. Similarly, concomitant inhibition of CSK together with engagement of costimulatory receptor CD28 also triggered calcium and ERK signaling pathways. CD28 signaling has been shown to induce actin rearrangement [41]. Tan et al. proposed that the efficient antigenic response of a T cell depends on CD28-mediated actin remodeling. These data suggest that actin cytoskeleton contributes to the maintenance of the T cell quiescence in the absence of the antigenic stimulation.
4. Actin in TCR signaling and IS formation
Actin cytoskeleton is actively involved in the TCR signal transduction cascade. TCR signaling induces actin rearrangement, which subsequently facilitates and amplifies downstream signaling pathways.
The TCR signaling cascade leading to actin remodeling involves activation of VAV1, (a GTP/GDP exchange factor), RHO-family GTPases (e.g. RAC1, CDC42), actin nucleation promoting factors (WAVE2, WASP, HS1), and finally induces ARP2/3-dependent polymerization of F-actin [42,43,44,45,46]. F-actin is polarized towards the APCs which enables formation of the immunological synapse and stabilizes the T cell:APC conjugates [8,12,47,48].
TCR triggering induces rapid dephosphorylation of actin binding ezrin-radixin-moesin (ERM) proteins through the VAV1-RAC1 pathway [44,49]. Phosphorylated ERM proteins provide a molecular linkage between the cortical F-actin and plasma membrane proteins and are essential for cell shape determination and cell:cell adhesion [50]. Transient dephosphorylation of ERM proteins during the early phase of TCR signaling leads to their release from the cortical F-actin. This facilitates T cell repolarization, migration arrest, and formation of the T cell:APC conjugates [44,49].
The retrograde actin flow carries the engaged TCR microclusters from the periphery to the center of the IS via the actomyosin network [13,15,51]. The actin flow is dependent on continuous polymerization of F-actin, which drives segregation of TCR microclusters from adhesion molecules and further facilitates downstream TCR signaling, e.g. PLCγ activation [15,52]. Myosin II mediates movement of the TCR microclusters along the actin filaments [15,53]. Activity of myosin II contributes to the association of ZAP70 with the TCR and, calcium signaling upon TCR triggering [53,54]. Inhibition of myosin II reduced TCR-induced phosphorylation of a focal adhesion scaffolding protein and mechanosensor, NEDD9/CASL, indicating that myosin II and NEDD9/CASL might couple mechanical forces to the TCR signal transduction [53,55,56].
The adaptor protein LAT was recently shown to act as a clustering hub by promoting phase separation of signaling molecules and enhancing F-actin formation in situ [10]. The elevated levels in cytosolic calcium, a hallmark of TCR signaling, further enhance actin polymerization, which results in reduced TCR mobility [57]. Thus, actin dynamics during IS formation is essential for the organization of signaling molecules but also for mechanical stabilization of the T cell:APC conjugate. Chemical blocking of the TCR-induced F-actin polymerization impairs LAT clustering and its association with SLP-76, calcium mobilization, and is overall detrimental to T cell activation [13,14,15,58,59]. Accordingly, loss of an actin nucleation promoting protein, HS1, results in impaired F-actin polarization and VAV1 recruitment to IS, loss of calcium signaling, and IL-2 production [60].
It has been shown that WASP is dispensable for generation of the IS [61,62], but plays a crucial role in the TCR-induced de novo formation of F-actin foci in the region of the IS [61]. The F-actin foci facilitate relatively distal TCR signaling events including PLCγ1 activation and calcium influx [61]. Moreover, WASP is required for sequential formation of multiple immunological synapses [62].
Besides de novo actin polymerization, bundling and crosslinking of actin microfilaments by L-plastin and TAGLN2 are involved in the formation of the IS. L-plastin and TAGLN2 promote the enrichment of F-actin in the IS and facilitate full T cell activation [63,64].
F-actin cytoskeleton is further required for the activation of LFA-1, an integrin mediating T cell:APC contacts [65,66,67]. LFA-1 is activated through binding to talin, an actin binding protein that anchors the cytoplasmic domain of LFA-1 to the actin cytoskeleton [68]. Activated LFA-1 has 10-fold higher affinity to its ligand ICAM-1 exposed on the surface of APC [69]. LFA-1 activation further amplifies F-actin formation via the VAV1 signaling pathway [70].
5. Actin in CD28 signaling
CD28-mediated costimulation is required for the IS formation and for full T cell activation [9,71]. CD28 engagement by its ligands CD80/CD86 leads to VAV1/CDC42/WASP-dependent actin reorganization and activation of the PLCγ/calcium signaling pathways [41,71]. Absence of CD28 signaling can be compensated by the expression of constitutively active RAC1 and cofilin mutants, indicating that these proteins link the CD28 signaling pathway to actin remodeling [9]. CD28 interacts with an F-actin uncapping protein RLTPR, which recruits PKCθ to the IS. RLTPR knockout mice mimic the CD28 knock-out phenotype, indicating that CD28-mediated actin remodeling regulates propagation of CD28 signals [72]. RLTPR binds the actin capping protein CAPZIP, which has been recently shown to be involved in CD28 costimulation-dependent IL-2 production [73].
Filamin A (FLNa) is an actin binding protein that binds to CD28 and is recruited to the IS upon antigenic stimulation [74]. CD28-FLNa association promotes activation of CDC42 and downstream targets of CD28 signaling (e.g. NF-AT) [74]. In addition, CD28-FLNa association promotes localization of PKCθ at the synaptic plasma membrane [75,76], which is required for the activation of the NF-κB and AP-1 signaling pathways. Accordingly, the absence of FLNa does not affect the proximal TCR signaling and the F-actin content, but abrogates the downstream PKCθ and calcium signaling [75]. Thus, FLNa seems to integrate the CD28-mediated actin remodeling with the CD28-triggered signaling pathways.
CD28 costimulation was shown to enhance the activity of the phosphatidylinositol-4, 5-bisphosphate 3-kinase (PI3K) [77]. PI3K catalyzes conversion of the second messenger PIP2 to PIP3, whichpromotes activation and membrane docking of the actin nucleating factor VAV1 [78]. Recent studies showed that the kinase activity of the phosphatidylinositol 4-phosphate 5-kinase α and β (PIP5Kα and PIP5Kβ) is required for CD28-mediated actin remodeling and T cell polarization [79,80]. Similar to PI3K, PIP5 kinases are also involved in the PIP2/PIP3 turnover at the plasma membrane. Here, VAV1 acts together with CD28 to recruit PIP5Kα and PIP5Kβ to the IS, which stimulates CD28-induced downstream signaling [79,80]. PIP2 is enriched in the lipid microdomains, which contain factors necessary for transduction of the TCR signal. Upon CD28 engagement PIP5Kβ together with FLNa facilitate assembly of these microdomains into the IS [74,80].
6. Actin in affinity discrimination
Formation of a stable T cell:APC conjugate results in a long-lasting T cell stimulation, which is required for the generation of effector T cells [81]. High-affinity antigens produce stable T cell:APC contacts in lymph nodes, while low affinity antigens induce only brief contact, kinapses, ex vivo and in vivo [19,82]. Recent studies suggest that T cell polarization is involved in establishing the antigen affinity threshold for effector responses. Antigens with subthreshold affinities fail to polarize actin cytoskeleton towards the immunological synapse, do not induce formation of long-lasting T cells:APC conjugates, and do not promote differentiation of the T cells into cytotoxic effectors [19,20]. Suboptimal antigens cause only slight deceleration of migrating T cells, whereas high-affinity antigens completely inhibit T cell migration and stimulate formation of stable IS [83]. Interestingly, inhibition of an actin modulating complex, ARP2/3, does not affect the T cell deceleration by suboptimal antigens, but prevents the T cell arrest mediated by high-affinity antigens [83].
The above-mentioned evidence suggests that the T cell choice between migration and arrest on the APC determines the subsequent T cell fate (i.e. eventual formation of cytotoxic effectors). Interestingly, actin cytoskeleton and actin modulators including RAC and CDC42 are involved in two mutually exclusive processes: T cell migration and T cell conjugation with an APC. Remarkably, inhibition of ARP2/3, RAC, or CDC42 reduce the T cell discrimination between high-and low-affinity antigens, whereas expression of a hyperactive form of RAC1 has the opposite effect [8]. We proposed that RAC and CDC42 contribute to the antigenic discrimination by promoting T cell migration and detachment from the APC in the absence of strong antigenic stimulation. In addition, RAC and CDC42 enhances the T cell:APC conjugation when a high-affinity antigen is recognized [8]. However, because the effects of the treatments used in the study were rather mild, it remains to be addressed how much actin signaling contributes to the affinity-based antigenic discrimination. This would require sophisticated tools for modulating actin cytoskeleton, that are yet to be developed.
Recently, a kinase WNK1 has been shown to negatively regulate T cell adhesion and promote T cell migration [25]. Thus, it would be interesting to investigate whether WNK1 contributes to the establishment of the antigen affinity threshold by balancing migration vs. conjugation to APCs.
7. Conclusion
Actin cytoskeleton controls T cell activation at multiple levels (Figure 1). Actin filamentous network is essential for the formation of stable T cell:APC conjugates and proper architecture of the IS, it contributes to the inhibition of spontaneous T cell activation, it actively contributes to the TCR signal transduction, and it might be involved in the antigen recognition by the TCR. Moreover, actin cytoskeleton plays crucial roles in many other cellular processes including T cell migration. The multifuncionality of the actin cytoskeleton and actin modulating proteins makes it very challenging to understand the role of actin cytoskeleton at the particular levels of T cell stimulation. Development of novel experimental tools for precise manipulation with actin cytoskeleton in a spatio-temporal manner is required to obtain a more complete picture of the role of actin in the antigen recognition, TCR triggering, T cell:APC conjugation, and the formation of the antigen affinity threshold.
Acknowledgement
This article was supported by a grant by the Czech Science Foundation [16-09208Y] to O.S.
Conflicts of interest
Both authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: 


