1. Introduction
Structural components made from brittle materials such as ceramics, intermetalics, glasses or carbon steels at low temperatures must be designed regarding flaws, holes and inclusions in structure. The load applied on the component causes the local stress concentrations around these defects followed by micro-cracking. If these micro-cracks extend and interact witch each other so that they grow unstably, then a macroscopic failure may arise. The usual combination of high strength and low fracture toughness of brittle materials leads to relatively small critical crack size very difficult detected by current non-destructive evaluation methods. As a result, service reliability of components made from brittle materials is very sensitive to microstructural parameters such as micro-cracks size distribution, micro-cracks shape, orientation and theirs spatial allocations in component stress field.
Low-temperature transgranular cleavage of carbon structural steels has been experimentally proved to be initiated by micro-cracking of carbides [1,2,3]. Local heterogeneity in deformation may result in the initiation of micro-cracks and their propagation into matrix whenever the applied stress σexceeds the local cleavage strength f [4]:
where kIa=[2Eγeff/(1−ν2)]1/2 is micro-crack arrest toughness introduced by Hahn [4], dp is the micro-crack size, β is a micro-crack shape factor; β = π for penny shaped and β = 4/π for trough thickness micro-crack [14], E is Young’s modulus, ν is Poisson ratio and γeff is the effective surface energy.
Experimental investigations of low temperature brittle fracture in steels have been over the past years complemented by attempts to model the fracture process by statistical methods [14], using local criteria for the initiation of micro-cracks. These approaches can reveal the relationship between the microstructural parameters and macroscopic mechanical properties. From size distribution of carbides using the Weibull’s weakest link statistical theory the integral probability of cleavage failure and the temperature dependence of scatter in fracture toughness was computed [15].
Some parameters affecting probability of fracture as character of stress field, shape and orientation of micro-cracks or the volume where micro-cracking process is activated have not yet been discussed in detail. This paper is concerned with probability of brittle fracture in steels loaded under conditions of non-homogenous elastic and elastic-plastic stress field and provides method how to calculate the effect of these conditions on the fracture instability.
2. Probability of Micro-Cracking
The initiated micro-crack obeying criterion given in Eq. (1) propagates further more easily if the cleavage planes in the matrix of the steel are favorably orientated relative to the acting stress. Substantial misalignment between these planes, or when micro-cracks are too small to satisfy the propagation criterion, causes stable micro-cracks formation. Similarly, deviation between applied stress direction and perpendicular to the cleavage plane α makes micro-crack propagation into matrix difficult and the local cleavage strength σf given by Eq. (1) is 1/cos2α times higher [16]. Then for every magnitude of local stress σ there is a certain critical size of micro-crack at which they can spread into the steel matrix:
|
dpf(σ)=βk2Ia2σ2cos4α.
|
(2)
|
Probability of such event is given by:
|
pf(σ)=Pr(dp⩾dpf(σ))=∞∫dpf(σ)π/2∫0ξ(α)ψ(dp)dαddp
|
(3)
|
Where:
|
ψ(dp)=δ0d−δ0p0d(δ0−1)pexp[−(dp/dp0)δ0]
|
(4)
|
is the common Weibull’s probability density function of micro-cracks with size dp0 and shape δ0parameters,
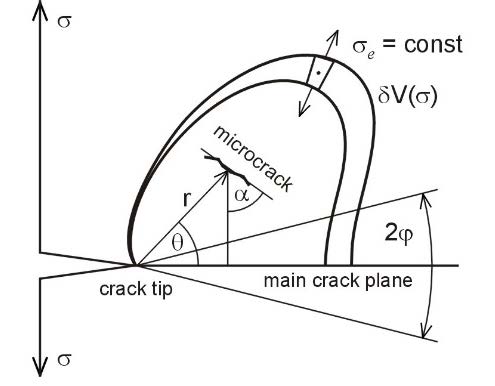
is the probability density of misalignment or disorientation angle α (Figure 1) received from uniform projection of perpendiculars to the cleavage plane [9] and Aα is a constant.
The elementary probability that at least one carbide within isostressed volume element δV(σ), e.g., ahead of macrocrack tip (see Figure 1) can be investigated from the sum:
|
δPf(σ)=1−∞∑i=0ζ(δV,i)[1−pf(σ)]i= 1−exp[−NVδVpf(σ)]
|
(6)
|
where ζ(δV, i) = 1/i!(NVδV)i·exp(−NVδV) is the probability that i microcracks initiate in the volume element δV(σ) corresponding to Poissonxs distribution and [1 - pf(s)]i is a complementary probability that imicro-cracks will be initiated into the considered volume element. For homogenously stressed volume V the final brittle fracture probability Pf is easy to calculate from Eq. (6) replacing δV by V and Pf = Pf(σ).
Non homogenous stress field around the sharps macro-crack tip at small scale yielding conditions satisfy the HRR singular solution [12]:
|
σij(r,θ)=σ0[(1−ν2In)(KIσ0√r)2]1/(n+1)˜σij(n,θ), i,j=r,θ
|
(7)
|
where σ0 is the yield stress, n is the work hardening exponent following from the constitutive law of ε/ε0 = α0(σ/σ0)n, ε0 is the yield strain, α0 is a material constant of order unity, In is dimensionless parameter weakly dependent upon the work hardening exponent n, ˜σij(n,θ) are angular functions of n and KI, is Mode I stress intensity factor. At low temperatures, because the plasticity is small, stress field around macro-crack tip approximates the linear elastic asymptotic solution by Williams [12]:
|
σij(r,θ)=KI√2πrhij(θ), i,j=r,θ
|
(8)
|
where hij(θ) are dimensionless function of θ. Effective stress field around crack tip σe(r,θ) has been considered as the maximum eigenvalue calculated from HRR and elastic stress tensors given by Eqs. (7) and (8).
Isostressed volume element is easily an integral of σe(r,θ) in the following form (see Figure 1):
where φ is an angle of the wedge active region ahead of the macro-crack tip and b is the characteristic width of the crack front [17]. The total probability of brittle fracture initiation can now be established by integrating Eq. (6) within the limits of the lowest σfmin and the highest σfmax local strengths. These extreme values of the local cleavage strength calculated using Eq. (1) from the largest dpmax and smallest dpmin micro-cracks given by statistical distribution of them (Eq. (4)). Integrated Eq. (6) within the active region in non-homogenous stress field around the crack tip enables to calculate the total fracture probability Pf as a function of the stress intensity factor KI. At the fracture instability KI = KIc and KIc represents 100Pf% quantile of experimentally assessed statistical distribution of fracture toughness.
3. Results
The model of brittle fracture was applied on experimental results of Ni-Cr steel [12]. The steel was heat treated to give a structure of tempered martensite and roughly spherical carbides. Transmission electron microscopy at magnification of 13, 500 was employed to investigate the distribution of carbides and their area density. The studied steel was mechanically tested. True stress-strain curves, yield stress σ0 and strain hardening exponent n were assessed from uniaxial tensile tests at low temperatures where brittle fracture prevails. The Young’s modulus and Poisson ratio were taken as E = 207 GPa and ν= 0.3, respectively.
Plane strain fracture toughness, KIc was evaluated in the lower bound temperature range on fatigue pre-cracked single-edge-notched specimens 25 mm thick tested in three point bending in accordance with standard ASTM E 399-90. Fractography investigation using SEM indicated that over the tested temperature range from 93 K to 153 K the fracture surface was mainly created by cleavage facets initiated at larger carbides. The brittle fracture zone of the fracture surface beyond the ductile zone consisted of cleavage facets. Carbides at fracture surfaces of the investigated steel were identified to act as subsidiary sources of cleavage facets formation. Frequent star shaped cleavage facets at fracture surfaces of broken specimens were evidently initiated by local stress concentration in their centres where carbides triggering the facets were recognized (see Figure 2). The direction of river markings from the centre of a star shaped facet to its periphery clearly shows that observed micromechanism of the initiation of micro-cracks are controlled by local stress in the area around carbides.
The relative frequencies of face sizes were subjected to the statistical processing of the least squares method and the parameters of the Weibull’s statistical distribution given by Eq. (4) has been found to be, dp0 = 26.3 mm and δ0 = 2.28. Good agreement obtained between the analytically determined shape of the probability density and the experimentally ascertained distribution was confirmed by a statistical coincidence test.
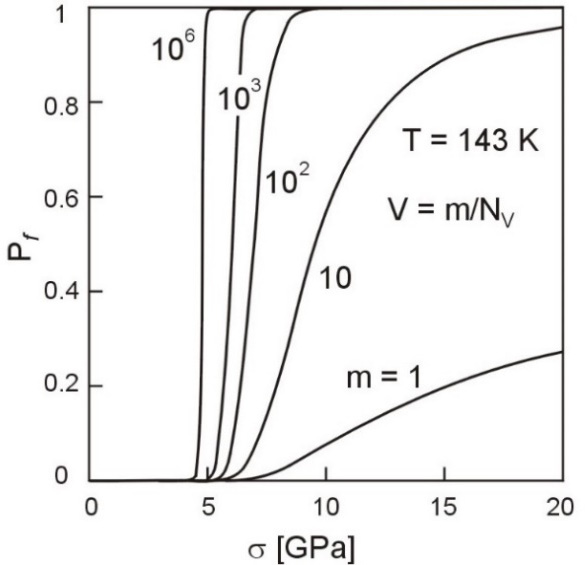
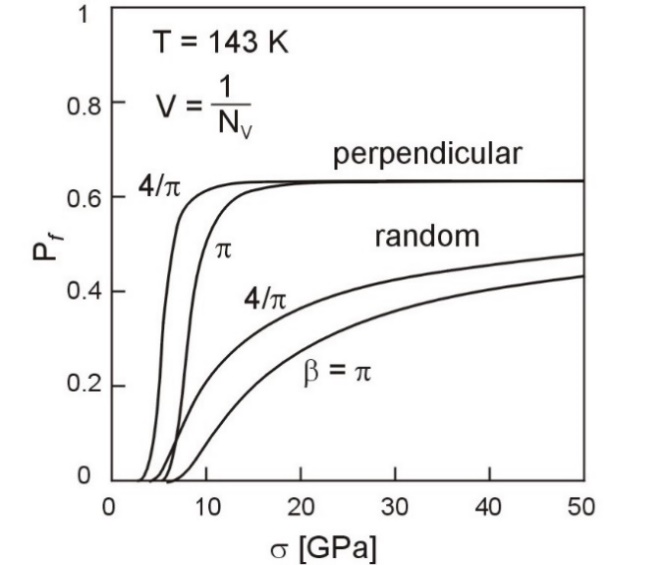
The entirely testing procedure of Ni-Cr steel and its results are published elsewhere [12]. The statistical distribution of micro-crack sizes given by Eq. (4) was employed for numerical calculation of the total fracture probability Pf as a function of homogenous acting stress σ. Calculated curves of Pf for homogenously stressed volumes m/NV in average containing m = 1, 10, 102, 103, and 106 micro-cracks are given in Figure 3. Increasing volume m/NV lovers the strength σf of the body and the curve is getting straight so that the transition from Pf = 0 to Pf = 1 state is jumped. The influence of the micro-crack shape factor β and the way of space array on the total fracture probability Pf is illustrated on Figure 4. The probability Pf is calculated according to Eq. (6) for the volume corresponding to one cracked carbide V = 1/NV, then Pf = 1 = exp[−pf(σ)].
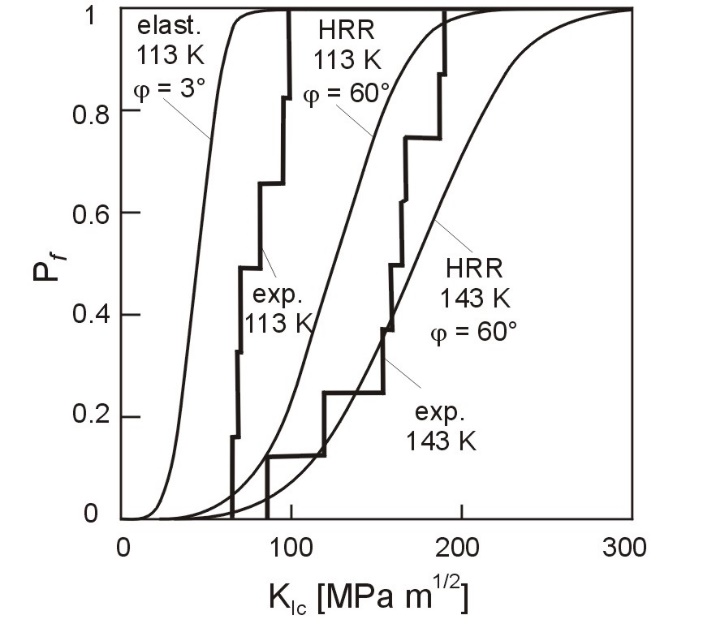
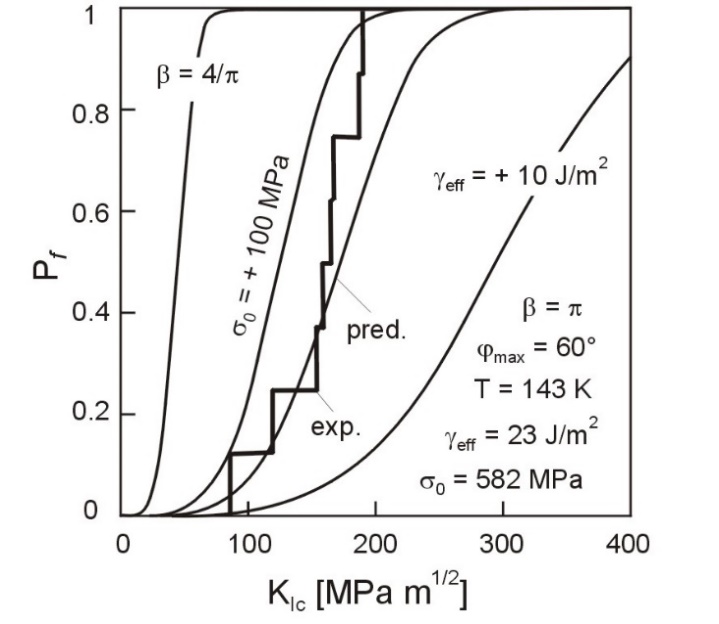
Comparison of Pf(σ) curves for elastic and HRR stress field at 113 K clearly demonstrates affirmative effect of small scale yielding on the growth of the fracture toughness. Figure 5 illustrates how the probability of fracture Pf depends on the stress field singularity around a sharp crack tip. Experimentally assessed statistical distribution of fracture toughness KIc of the investigated steel at temperatures 113 K and 143 K are predicted using integral form of Eq. (6) for HRR (Eq. (7)) or elastic (Eq. (8)) stress field. The following Figure 6 shows the influence of changes in micro-cracks shape expressed by parameter β, yield stress σ0and effective surface energy γeff on the total fracture probability Pf as a function of fracture toughness considering HRR stress field action at the temperature of 143 K. It is obvious from the curves that lowering yield stress σ0 and increasing effective surface energy γeffsuppress the brittle fracture.
4. Discussion
Micro-cracking is connected with main crack propagation in steels under brittle condition, and considerably affects the mechanical behavior of engineering parts. Clarifying the effect of micro-cracking, and interactions of micro-cracks in the field of macro-crack tip is the key to a clear understanding of cracking behaviors of brittle materials generally. Sometimes very complicated description of arrays of microcracks demands simplified statistical treatment of this problem.
The proposed solution applied to Ni-Cr steel at very low temperatures evinces how micro-cracking originated bear on fracture instability of the main crack in a body. Not only the size of the nucleated micro-cracks, but also the way the orientation of cleavage planes in the matrix affects the total probability of fracture is taking into account. It is shown in Eq. (3), that this factor can substantially increase the critical size of micro-crack, and then randomly orientated micro-cracks diminishes the brittle fracture probability. This micro-cracks orientation effect is stronger in homogenously loaded body than in nonhomogenous stress field such as around macro-crack tip. Increasing effective surface energy, lowering yield stress and localized plasticity in the nearness of the macro-crack tip reduce the risk of brittle fracture creation. The solution put on the stress singularity described by the stress intensity factor enables to predict statistical distribution of fracture toughness. Elastic stress field singularity ahead of crack tip promotes much more brittle fracture then small scale yielding HRR stress field and diminishes fracture toughness. Through thickness micro-cracks when β = 4/π are more sensitive to create brittle fracture instability than penny shaped micro-cracks nucleated with β = π. All these general conclusions can be directly utilized in microstructural design of steels operating at low temperatures or at conditions evoking an embrittlement.
As it has been analyzed earlier, the actual strength or fracture toughness of the material could vary depending on microstructural parameters. In addition, it is usually difficult to precisely predict the external loads acting on the component made from the material under actual service conditions. The risk of the brittle fracture can be expressed in terms of statistical distributions of local maximum effective stress σemax = σ of the brittle fracture can be φ1(σ1) and local cleavage strength φ2(σ2) as follows [17]:
|
Pf=Pr(σ⩾σf)=+∞∫0ϕ1(σ)σ∫0ϕ2(σf)dσfdσ.
|
(10)
|
On the other hand the safety factor locally defined as, kp = σf/σemax, behaves due to variability of sσf and σemax randomly with statistical probability density:
|
K(kp)=+∞∫0σϕ1(σ)ϕ2(kpσ)dσ
|
(11)
|
and Pr (kp ≤ 1) equals to the probability Pf. This relationship is an attempt how to span differences between deterministic and probabilistic approaches in design of engineering components. Furthermore, utilizing Eq. (6) in the integral form, the microstructural and macroscopical factors affecting failure of the component can be link together to acquire more precise estimation of its reliability. Fundamentally, designing to prevent service failures made from brittle material is a statistical problem including its defects array and loading of components.
5. Conclusions
A statistical model for prediction of brittle fracture probability has been developed. Considering the critical event is micro-crack initiation, its elementary probability has been quantified as a function of size and shape distributions of micro-cracks, theirs orientation, elastic and plastic characteristics of material. From the weakest link statistical theory, the total brittle fracture probability has been computed for homogenously and nonhomogenously loaded part of an engineering component. Applying the model to nonhomogenous stress field described by KI—singularity around sharp crack tip, the statistical distribution of fracture toughness has been predicted. Increasing effective surface energy, lowering yield stress and localized plasticity ahead of the macro crack tip reduce the brittle fracture probability and increase brittle fracture toughness. The model has been proved on Ni-Cr steel having microstructure of tempered martensite and precipitated carbides acting as micro-cracks initiation origins. Calculated total probability of brittle fracture can be exploited not only for microstructural design of brittle materials but also for new formulation in probabilistic design of components.
Acknowledgements
This paper was created under support of the Project No. SP2016/184—Characteristics of fracture surfaces in carbon steels cracked by high dynamical loading by financial support of the MŠMT of the Czech Republic.
Conflict of Interest
The authors declare that there is no conflict of interest regarding the publication of this manuscript.









 DownLoad:
DownLoad: