Effects of elongation delay in transcription dynamics

1.   Introduction

Infectious disease outbreaks remain a major threat to global health. This is especially the case for highly pathogenic and transmissible diseases with pandemic potential. These global threats were recently exemplified by the 2009 swine flu outbreak and the ongoing COVID-19 pandemic caused by the novel Severe Acute Respiratory Syndrome coronavirus 2 (SARS-CoV-2). To effectively mitigate and control the spread of an epidemic, it is paramount for public health decision-making to be informed by an accurate understanding of the dynamics of disease transmission and the potential impact of intervention measures.

To this end, epidemic models have become an important tool to help better understand epidemic dynamics, predict its future trends, evaluate the effectiveness of intervention measures, such as lock-down or vaccination, and ultimately control the epidemic.

Mathematical epidemiology models can be broadly divided into two main types: compartmental models and agent-based models. An agent-based model is a very detailed stochastic model where the agent represent single individuals within a population ^{[1,2,3,4,5,6,7,8]}. Such models are generally complex and computationally expensive. In compartmental models, the population is subdivided into epidemiological compartments with each compartmental generally representing a health or disease progression stage ^{[9,10,11,12,13,14,15,16]}. Thus compartmental models are computationally simple, scalable, and capable of describing the dynamics of the number of people in each compartment throughout the course of an epidemic. In this work, we propose a nonlinear state-space compartmental model.

Compartmental model date back to the early twentieth century, most notably to the work by ^[17], whose susceptible, infected, and recovered (SIR) model was used for modeling the plague (London 1665–1666, Bombay 1906) and cholera (London 1865) epidemics ^[10]. More specifically, it is a weighted directed graph representation of a dynamic system. The susceptible refers to those healthy people who are susceptible to the disease and may get infected; the infected refers to those under infection; the recovered refers to those who recovered from infection and will be temporarily or permanently immune to the disease. However, there are several drawbacks in the original SIR model:

$ 1) $ It is a deterministic model, meaning the model always performs the same for a given initial condition, which cannot explain the unknowable randomness in the observations ^[12,16,18];

$ 2) $ It is only a temporal model, which does not consider the spread in geographical regions, e.g., human interaction induced by modern transportation ^[19];

$ 3) $ It assumes that all the parameters are known, which is not realistic. Parameter estimation from noisy observations is needed for better understanding and forecasting epidemics ^[18].

Many researchers have proposed variants of the basic SIR model to address some of these issues, such as ^[20], who considered the age dependence of social structure; ^[21], who used hyperbolic compartmental models to solve the large uncertainty in the values reported by official sources; ^[22,23], who applied multiscale kinetic transport equations to describe the transport dynamic of the commuters and non-communting population; but accurate state and parameter estimation from partial and noisy observations remains an open problem. To handle this issue, our proposed framework embeds the classical compartmental model within a nonlinear state-space model. The state model is a spatial-temporal stochastic dynamic model that allows hidden states in a given location to change over time and the disease dynamics in one location to affect neighbouring locations through human movements between locations. The proposed framework consists of a multinomial state model based on a variant of the SIR model --- the SEIRD model ^[24,25,26] --- and an observation model to allow the assimilation of publicly available data, including daily testing rate, daily test positivity rate, specificity and sensitivity of the tests. In addition, the model considers the differential testing rate between symptomatic patients and asymptomatic and healthy individuals. The proposed framework is employed to estimate i) the hidden epidemic state vector $ X^t = (S^t, E^t, I^t, R^t, D^t) $ and ii) epidemiological parameters, such as infection rate and the average infectious period, using noisy incomplete time series epidemic data. Accurate estimation of the true epidemic state and parameters is paramount for designing and evaluating the effectiveness of control strategies.

2.   Mathematical model

2.1.   Classical SEIRD model

The SEIRD model predicts the time evolution of epidemic. It models the dynamic interaction of people between five different compartments, namely, the susceptible (S), the exposed (E), the infected (I), the recovered (R) and the deceased (D). The classic discrete-time SEIRD model can be described by the following equations:

with $ S_t + E_t + I_t + R_t + D_t \, = \, 1 $, where $ S_t $, $ E_t $, $ I_t $, $ R_t $, $ D_t $ are the fraction of the population (the size of which is assumed to be constant over the time interval of interest) at time $ t $ that, respectively, $ S $ is not yet infected with the disease; $ E $ has been exposed to the virus but does not show symptoms yet; $ I $ is infective after the virus incubation period; $ R $ has been infected and then recovered; and $ D $ is deceased due to the epidemic.

The model is governed by the following parameters:

● $ \lambda_S $ is the infection rate, which is the probability that an individual moves from the S to the E compartment. The nonlinear term $ \lambda_S S_tI_t $ models the infection speed, which depends not only on the infection rate, but also on the fraction of susceptible and infected people at time $ t $;

● $ \lambda_E $ is the probability that an individual moves from the E to the I compartment. It can be understood as the inverse of the average incubation time;

● $ \lambda_R $ is the recovery rate, which is the probability than an individual moves from the I to the R compartment. It can be understood as the inverse of the average recovery time;

● $ \lambda_D $ is the mortality rate, which is the probability than an individual moves from the I to the D compartment.

2.2.   Covid-19 epidemic metapopulation state-space model

Given the complexity and reality of epidemics, many different implementations of the classical SEIRD model have been proposed ^{[24,25,26,27]}. Two clear drawbacks of the classical SEIRD model is the inability to model variation over a geographic area, and the fact that that the SEIRD values are assumed to be directly observable. In this paper, we address these drawbacks by means of a novel nonlinear metapolulation state-space framework, where the state process provides a spatial-temporal discrete-time stochastic model of the evolution of the number of individuals in the SEIRD compartments over several geographical regions, while the observation process models noisy time series of reported epidemiological data, considering the accuracy of tests and different testing rates for symptomatic and asymptomatic people.

2.2.1.   State model

Consider a discrete-time state process $ \{{{\bf X}}_i^t; i = 1, \dots, G; t = 0, 1, \dots\} $, where $ {{\bf X}}_i^t = (S_i^t, E_i^t, I_i^t, R_i^t, D_i^t) $ is a state vector, containing the number of individuals in the SEIRD compartments in geographical area $ i $ at time $ t $, where the unit of time is typically day or week. At time $ t $, the total number of individuals in region $ i $ is $ N_i = S_i^t + E_i^t + I_i^t + R_i^t + D_i^t $. We assume that this number stays constant over the time interval of interest (e.g., no significant amounts of migration is assumed to occur during the time interval of interest; plus, births and non-specific deaths are assumed to approximately balance out). This results in a good approximation provided that the interval of time in consideration consists of weeks or a few months, especially in the case of a full-blown outbreak when, the impact of migration is negligible.

Before proceeding, we recall the definition of the binomial and multinomial probability distributions. A random variable $ Z $ has a binomial distribution with parameters $ n\geq 1 $ and $ 0 < p < 1 $, denoted by $ Z \sim {\rm Binomial}(n, p) $, if

Variable $ Z $ is the number of $ k $ occurrences of an outcome among $ n $ identical independent trials that can result in the outcome with probability $ p $. The expected value and variance of this variable are $ E[Z] = np $ and $ {\rm Var}(Z) = np(1-p) $, respectively. More generally, we define a random vector $ (Z_1, \ldots, Z_M) $ to have a multinomial distribution with parameters $ n\geq 1 $ and $ p_1, \ldots, p_M\geq 0 $ such that $ \sum p_i \leq 1 $, denoted by $ (Z_1, \ldots, Z_M) \sim {\rm Multinomial}(n, p_1, \ldots, p_M) $, if

Variables $ Z_1, \ldots, Z_M $ are the number of occurrences of each of $ M $ outcomes over $ n $ identical independent trials that can result in outcome $ m $ with probability $ p_m $. It is clear that $ Z_m \sim {\rm Binomial}(n, p_m) $, for $ m = 1, \ldots, M $ (thus $ E[Z_m] = np_m $ and $ {\rm Var}(Z_m) = np_m(1-p_m) $). In addition, the case $ M = 1 $ results in the binomial distribution.

In our model, the state vector $ {{\bf X}}_i^t = (S_i^t, E_i^t, I_i^t, R_i^t, D_i^t) $ is assumed to evolve according to the following nonlinear stochastic model:

for $ t = 0, 1, \ldots $, where $ N^{t}_{S_{i, j}} $ is the number of susceptible individuals at time $ t $ in region $ i $ who will become exposed at time $ t+1 $ due to contact with an infective individual from region $ j $, $ N^{t}_{E_i} $ is the number of exposed people at time $ t $ in region $ i $ who will become infective at time $ t+1 $, while $ N^{t}_{R_i} $ and $ N^{t}_{D_i} $ are the numbers of infected people at time $ t $ in region $ i $ who will become recovered or deceased at time $ t+1 $, respectively.

We assume that each susceptible individual in region $ i $ becomes exposed due to contact with an infective individual from region $ j $ at time $ t $ independently with a probability $ \lambda_{S}c_{ij}I_j^t/N_j $ (these parameters are explained below). Therefore, the distribution of the numbers of new infections over the regions is multinomial:

The infection rate $ \lambda_S > 0 $ is disease-specific, but also affected by public policies, such as mask wearing and social distancing. We assume that these factors are constant over the geographical area (e.g., a single political unit, such as a state or country) and time interval in the study, so that $ \lambda_S $ is the same for all regions. If $ i = j $, then the contact is internal to region $ i $, and $ c_{ii} = 1 $. If $ i \neq j $, then $ 0\leq c_{ij} \leq 1 $ models the relative amount of transient interchange of individuals between regions $ i $ and $ j $, due to commuting, tourism, and so on. If regions $ i $ and $ j $ are far apart, or one of them is not economically important, then $ c_{ij} $ is close to zero. Note that $ c_{ij} = c_{ji} $. The values of $ c_{ij} $ are selected in our study based on the gravity model, which is a model of population movement between discrete locations, based on the populations of the origin and destination and the distance between them ^[28,29,30]. Namely, the $ c_{ij} $ values are determined by a proportional factor (the so-called "gravitational constant") multiplied by the product of the populations of both regions and divided by the square of their distance from one another. Finally, the ratio $ I_j^t/N_j $ indicates that if there are more infective individuals in region $ j $, they will spread the disease with higher probability. Note that the expected value of the (normalized) $ j $-th flux is $ E[N_{S_{i, j}}^t/N_i] = \lambda_{S}c_{ij}(S_i^t/N_i)(I_j^t/N_j) $. This may be contrasted to the flux $ \lambda_{S}S(t)I(t) $ in the classical case.

In our model, an exposed individual in region $ i $ becomes infective at time $ t $, independently of the other regions, with probability $ \lambda_E $. Hence,

The expected number of exposed individuals who become infective at time $ t $ is thus $ E[N_{E_i}^{t}] = \lambda_E E_i^t $. Note also that the distribution of the total time until an exposed individual becomes infective is geometric with parameter $ \lambda_E $, so that the expected number of time units until an exposed individual becomes infective is $ \lambda_E^{-1} $.

Finally, each infective individual in region $ i $ becomes recovered or deceased at time $ t $, independently of the other regions, with probabilities $ \lambda_R $ and $ \lambda_D $, respectively. Hence,

The expected numbers of infective individuals who become recovered or deceased at time $ t $ are $ E[N_{R_i}^{t}] = \lambda_R I_i^t $ and $ E[N_{D_i}^{t}] = \lambda_D I_i^t $, respectively. The expected numbers of time units until an infective individual becomes recovered or deceased are $ \lambda_R^{-1} $ and $ \lambda_D^{-1} $, respectively.

2.2.2.   Observation model

The observation model is a major contribution of this work. We model reported epidemiological data, namely confirmed new cases and cumulative recorded deaths, as noisy observations on the true state of the pandemic, as defined in the previous section. The proposed observation model addresses the uncertainty introduced by imperfect testing and the imbalance in testing of symptomatic and asymptomatic individuals (the former cohort is tested more ^[31]).

We model the reported data as a time series $ \{{{\bf Y}}_i^t; i = 1, \dots, G; t = 0, 1, \dots\} $ where $ {{\bf Y}}_i^t = (P_i^t, Q_i^t) $ contains the numbers $ P_i^t $ and $ Q_i^t $ of new confirmed cases and deaths, respectively, in geographical area $ i $ at time $ t $. The number of reported new cases contain both false and true positives,

for $ t = 0, 1, ,\ldots $, where $ N_{TP_i}^t $ and $ N_{FP_i}^t $ are the number of false and true testing positives, respectively. Let $ \alpha $ and $ \beta $ be the false positive and true positive rates, respectively, of the COVID-19 test under consideration (multiple tests of different accuracy can be introduced by splitting the populations according to the test received). True positives come from the exposed and infective populations. In addition, a percentage of the infective population is asymptomatic; we assume that those are tested at a smaller rate than the symptomatic ones. Accordingly, we split the number of new true positives at time $ t $ as the sum of the number of positive-tested symptomatic infective people and the number of positive-tested asymptomatic infective and exposed individuals:

where $ \varepsilon^t_1 $ and $ \varepsilon^t_2 $ are the testing rates of asymptomatic and symptomatic individuals at time $ t $, respectively, while $ \varepsilon^t_4 $ is the percentage of infective individuals who are asymptomatic at time $ t $. These parameters are assumed to be the same over all regions. As shown later, these parameters can be calculated from the overall testing and positivity rates, which are available from public records.

Similarly, the false positives come from the susceptible and recovered populations, and here we have to distinguish between symptomatic individuals (who are not infected by COVID-19 but instead by other similar viruses, such as Influenza) and asymptomatic individuals:

where $ \varepsilon^t_3 $ is the percentage of non-specific symptomatic individuals at time $ t $.

Finally, we assume that the reported cumulative recorded deaths in each region is a fraction of the true number $ D_i^t $, according to

Even though there might be a number of non-COVID-19 deaths falsely reported as COVID-19, we are assuming that this number is small and can be ignored. Notice that (2.11) implies that COVID-19 deaths are underreported, which is widely assumed to be the case.

Let $ R_T^t $ be the testing rate, i.e., the percentage of the population that is tested at time $ t $, and let $ R_P^t $ the positivity rate at time $ t $. Both these parameters are reported by health authorities. Next, we show how the parameters $ \varepsilon^t_1 $, $ \varepsilon^t_2 $, $ \varepsilon^t_3 $, and $ \varepsilon^t_4 $ can be calculated from $ R_T^t $ and $ R_P^t $

The test positivity rate ($ R_P^t $) is the percentage of positive tests $ P^t $ over the total number of tests $ N_{T}^t $ in a given region; it can be written as

where $ A = (1 - \varepsilon^t_3)(S^t + R^t) $, $ B = \varepsilon^t_3 (S^t + R^t) $, $ C = (1 - \varepsilon^t_4) I^t $, and $ D = \varepsilon^t_4 I^t + E^t $.

Similarly, the testing rate $ R_T^t $ is the percentage of total tests over the total population, which can be written as

Using the previous two equations, we can solve for $ \varepsilon^t_1 $ and $ \varepsilon^t_2 $ in terms of $ \varepsilon^t_3 $ and $ \varepsilon^t_4 $:

Now, $ \varepsilon^t_1 $ and $ \varepsilon^t_2 $ are the testing rates of asymptomatic and symptomatic individuals at time $ t $, and can be related to each other. According to ^[31], we have

where $ \zeta $ is uniformly distributed in the interval $ [2, 4.3] $ to account for various non-specific symptoms (e.g., fever, cough, loss of taste, smell) that are shared by COVID-19 and other common viral diseases. Substituting (2.15) into (2.14) results, after some algebra, in the following expression for $ {\varepsilon^t_3} $

In addition, according to ^[32], the percentage of asymptomatic infective people $ \varepsilon^t_4 $ is around 20% and from this the other parameters $ \varepsilon^t_1 $, $ \varepsilon^t_2 $, $ \varepsilon^t_3 $ can be calculated.

3.   Covid-19 epidemic state and parameter estimation

In this section, we describe state-of-the-art estimators for the state and parameters of the metapopulation state-space model introduced in the previous section. These estimators use as input the noisy time series $ {{\bf Y}}_i^t = (P_i^t, Q_i^t) $ of reported new cases and deaths in the several geographical regions in the study. The state vector $ {{\bf X}}_i^t = (S_i^t, E_i^t, I_i^t, R_i^t, D_i^t) $ is estimated at each time $ t $ by using the Unscented Kalman Filter (UKF) ^[33], which is the state-of-the-art estimator for stochastic nonlinear state-space models, while the parameters $ \lambda_S, \lambda_R, \lambda_D $ are estimated by maximum-likelihood, by using the metaheuristic optimization - fish school search algorithm ^[34,35,36].

First, we write the state-space model in the previous section in the standard form

where $ {f} $ and $ {h} $ are nonlinear mappings, and $ \{{\bf{n}}_i^t; i = 1, \dots, G; t = 0, 1, \dots\} $ and $ \{{\bf{v}}_i^t; i = 1, \dots, G; t = 0, 1, \dots\} $ are white-noise (i.e., uncorrelated in time) transition and observation noise processes, respectively, which are independent of each other and independent of the initial state $ \{{{\bf X}}_i^0; i = 1, \ldots, G\} $.

The proposed state-space model can be put in the standard form (3.1) by rewriting the state equations as:

where the transition noise terms are:

Similarly, the observation model can be rewritten in the standard form (3.1):

where the observation noise terms are:

3.1.   Unscented Kalman filter

With the state-space model in the standard format (3.2), one can apply the Unscented Kalman Filter (UKF) algorithm ^[33,37,38] to estimate the state variables $ (S_i^t, E_i^t, I_i^t, R_i^t, D_i^t) $ from the noisy data $ (P_i^t, Q_i^t) $ of new cases and cumulative deaths in geographical area $ i $ at time $ t $. The UKF assumes that the statistics of the state variables at time $ t = 0 $ are known (in practice, these values need to be only very roughly guessed since, as the time $ t $ increases, the UKF generally "forgets" the information in the initial state). It also assumes that all the parameters are known; however, in the next section we describe a methodology to estimate the parameters from the data as well.

In the UKF algorithm, $ {\bf{m}}_{t|t} $ and $ {\bf{P}}_{t|t} $ denote the estimates at time $ t $ of the mean and error covariance matrix, respectively, of the state vector $ {\bf{X}}^t = (S^t, E^t, I^t, R, D^t) $ using all observed data up to time $ t $ (for brevity, the subscript $ i $ used previously to discriminate the region is omitted throughout this section, since the same process is applied to all regions separately). We initalize the mean vector via $ E[I^0] = E[E^0] = P^0 $, $ E[R^0] = 0 $, $ E[D^0] = Q^0/\beta $, and $ E[S^0] = N-E[I^0+E^0+R^0+D^0] $, while the covariance matrix is initialized to the identity matrix. The UKF estimate of the state $ {\bf{X}}^t $ is $ {\bf{m}}_{t|t} $, with uncertainty given by $ {\bf{P}}_{t|t} $. These estimates are computed by the following iteration:

Initialization: Given the initial observation $ {\bf{Y}}^0 = (P^0, Q^0) $, let

For $ t = 1, 2, \ldots $ repeat:

Prediction:

1) Generate (2n+1) sigma points,

where $ \left[ \sqrt{n{\bf{P}}_{t-1|t-1}}\right]_i $ is the i-th column of the matrix square root.

2) Propagate the sigma points through the state equation:

3) Compute predicted mean and predicted error covariance:

where $ {\bf{Q}}_{t-1} $ is the covariance matrix of the transition noise (see the Supplementary Information for its derivation).

Update:

1) Update sigma points based on the predicted mean and error covariance:

2) Propagate the sigma point through the observation equation:

3) Compute predicted measurement mean, measurement covariance matrix, and cross-covariance matrix:

where $ {\bf{R}}_{t-1} $ is the covariance matrix of the observation noise (see the Supplementary Information for its derivation).

4) Compute the filter gain and new state error covariance matrix. Assimilate the observation $ {\bf{Y}}^t $ at time $ t $ to find new state mean vector $ {\bf{m}}_{t|t} $:

3.2.   Maximum-likelihood adaptive filtering

The UKF algorithm requires that all parameter values be known. The parameters that govern the proposed model in (3.2) and (2.8) are $ \lambda_S $, $ \lambda_E $, $ \lambda_R $, $ \lambda_D $, $ \alpha $, $ \beta $, $ \varepsilon_1 $, $ \varepsilon_2 $, $ \varepsilon_3 $, and $ \varepsilon_4 $. Of these, $ \alpha $ and $ \beta $ are known, while $ \varepsilon_1 $ through $ \varepsilon_4 $ can be obtained using the procedure described in Section 2.2.2. Among the $ \lambda $ parameters, some may be known a priori, but others may be unknown. Let $ \mathit{\boldsymbol{\theta}} $ be a vector containing these parameters. Accurate estimation of $ \mathit{\boldsymbol{\theta}} $ from the observed data is key to make the proposed methodology useful in practice. We estimate $ \mathit{\boldsymbol{\theta}} $ using maximum-likelihood method in combination with the UKF, which is known as maximum-likelihood adaptive filtering ^[39,40,41].

Let $ {{\bf Y}}^{0:t} = \{{{\bf Y}}^0, {{\bf Y}}^1, \ldots, {{\bf Y}}^t\} $ denote the observed data up to time $ t $. The log-likelihood of the model parameters $ \mathit{\boldsymbol{\theta}} $ at time $ t $ is given by:

where

with $ {\bf{V}}_t \, = \, {{\bf Y}}^t - \mathit{\boldsymbol{\mu}}_t $. The quantities $ \mathit{\boldsymbol{\mu}}_t $ and $ {\bf{S}}_t $ are calculated in the UKF recursion. Then, the target is to maximize the log-likelihood $ L_t(\theta) $,

There are several possible ways to address this optimization problem. For example, one can apply the Expectation-Maximization (EM) algorithm, which is especially effective when there is a closed-form solution for the "M" maximization step, which avoids recursive gradient calculation. However, there is no such closed-form solution in our case. Other gradient-based optmization methods did not produce good results. Instead, we used biology-inspired metaheuristic optimization, in this case, the Fish School Search (FSS) algorithm ^[34,35], which we had already applied in our previous work ^[36]. Metaheuristic optimization algorithms, such as FSS, can find good solutions, in a reasonable amount of time, of complex, non-linear, and multi-dimensional problems, where traditional gradient-descent optimization is not effective ^[42,43,44]. A brief description of the FSS algorithm is found in the Supplementary Information. For more details about the FSS algorithm, please see ^[34,35,36].

4.   Numerical experiments

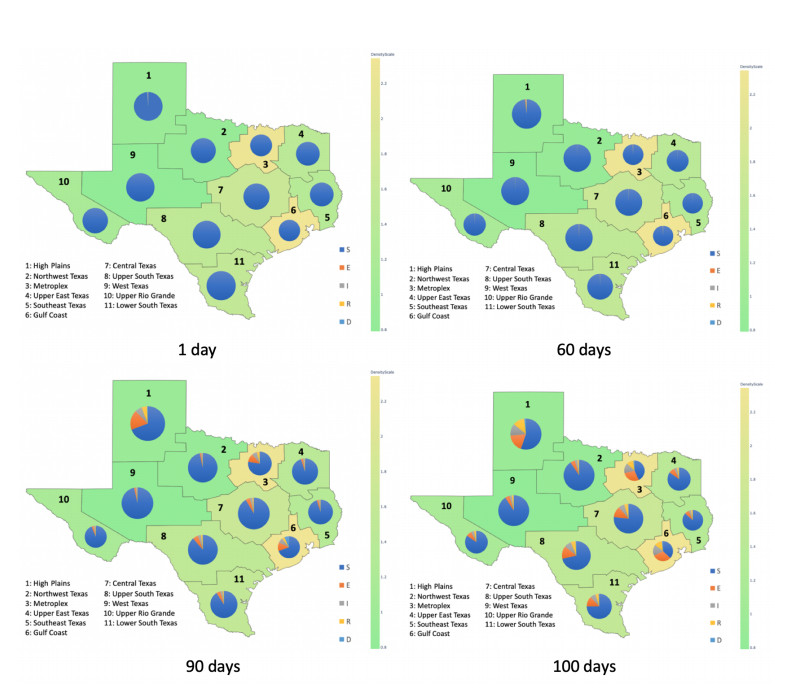
In this section, we present the results of numerical experiments, using synthetic and real data from the state of Texas in the United States. We divided Texas into 11 regions, based on the Texas Health and Human Services (HHS) regional map.

Sections 4.1 and 4.2 assume the parameter values displayed in Table 1 (unless stated otherwise). We initialize 100 individuals in the exposed state in region 1. The COVID-19 test false positive rate $ \alpha $ and false negative rate $ 1 - \beta $ are based on ^[45]; the infection rate $ \lambda_S $ is an assumption; mean incubation period $ 1/\lambda_E $, and mean recovery time $ 1/\lambda_R $ are consistent with the Center for Disease Control and Prevention (CDC) data ^[46,47]; while the mortality rate $ \lambda_D $ is based on publicly reported data ^[48]. The values for $ \varepsilon^t_1 $ through $ \varepsilon^t_4 $ are computed as described in Section 2.2.2. On the other hand, in Section 4.3, the methodology was applied to real COVID-19 epidemic data.

4.1.   Forward prediction of epidemic dynamics

Here we illustrate the proposed model's ability to predict the spatial and temporal dynamics of epidemic, assuming the parameter values displayed in Table 1. We ran the model for a period of 200 days. Figure 1 displays the results at day 1, day 60, day 90, and day 100. In this simulation, the epidemic is assumed to have originated in region 1 with only a few infective individuals, as can be seen in the upper left diagram of Figure 1. After 60 days, the pandemic has spread to other regions, but it is still very limited. However, after 90 days, i.e., only 30 days after the previous snapshot, the epidemic has spread much more widely, especially in the originating region 1, as well as regions with large populational density, e.g., region 3 and region 6, which is where Dallas and Houston are located, respectively. Finally, after only another 10 days, the number of infected individuals has almost doubled. These results are in agreement with the fact that an epidemic is easier to control at an early stage, and will spread at an exponential rate if not controlled early ^[49,50,51]. These predictions underscore the need for early-stage public health interventions, such as social distancing, mask wearing, or a limited lockdown in the critical originating region 1.

4.2.   State and parameter estimation from synthetic data

In this section, we investigate the ability of the proposed maximum-likelihood adaptive filtering methodology in recovering both the hidden state and all unknown parameters of the pandemic from a synthetic time series of reported new cases and deaths. The synthetic data allow us to evaluate the performance of the methodology against the simulated ground truth.

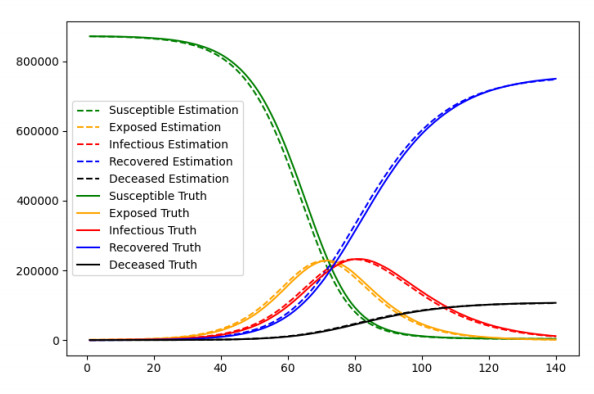
In the first experiment, we assume that the parameter values are known (see Table 1) and evaluate the ability of the filtering methodology to recover the hidden SEIRD state from the synthetic times series. Although in practice not all parameters would be known, this experiment allows us to evaluate the pure state estimation capabilities of the algorithm. Figure 2 displays the results over region 1 (the behavior was similar over all other regions). We can see that the maximum-likelihood adaptive filter can track the state evolution remarkably well. This is confirmed quantitatively by the relative error, defined as

which is displayed in Table 2 for a few time snapshots. We can see that the errors are small, with the exception of early in the epidemic, when not enough data has been accumulated yet.

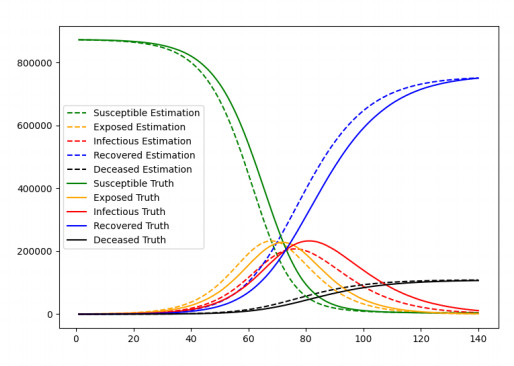
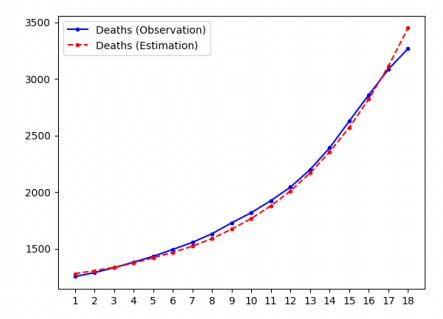
In the second experiment, we remove the assumption that the infection rate, mean recovery time, and mortality rate parameters are known, and evaluate the performance of the methodology in recovering the values of these parameters. This is a difficult problem, since the states are also unknown, and the algorithm must perform simultaneous state and parameter estimation. Table 3 shows that the algorithm produced estimated parameter values that are close to the groundtruth values. Figure 3 displays state estimation results when the estimated parameters are plugged in for the unknown parameters. We can see that the results are not quite as good as the case where all parameters are known in Figure 2, but the proposed methodology is still able to track the state evolution relatively well. The relative errors in Table 4 is still very small in many cases. Once again, the error tends to be larger early in the epidemic because not enough data has been accumulated. In addition, some of the states, such as number of susceptible and exposed individuals, become very small near the end of the time interval, which makes the relative error increase.

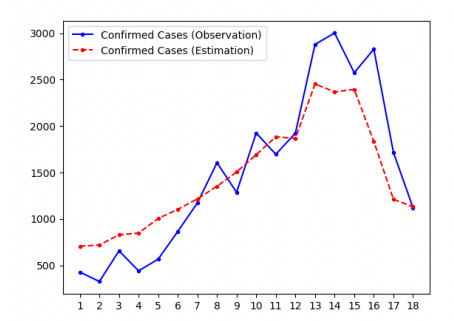
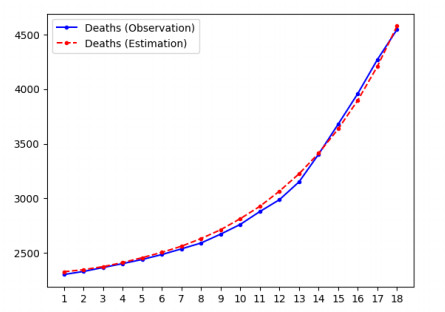
4.3.   State and parameter estimation using Johns Hopkins University COVID-19 data

In this experiment, we demonstrate the performance of the proposed algorithm on Texas COVID-19 data from the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU) ^[52]. Due to the presence of delayed reporting, there is often incorrect data in the early part of the week and corrections at the end of the week. To address this, we consider the time unit to be week, not day, and average the daily reported data (from Sunday to Saturday) to produce one data point for the week. The data used in this experiment is from the week of Oct 4th, 2020 to the week of Feb 1st, 2021, which is from the third (Fall 2020) wave of the COVID-19 epidemic in the United States.

In this experiment, we only use data from four large regions (3, 6, 7, 8), which contain Dallas, Houston, Austin and San Antonio, which are the most reliable data available. The population movement parameters $ c_{ij} $ of those four areas were calculated using the gravity model, as explained in Section 2.2.1, where the "gravitational constant" is set such that the probability of an individual moving between regions on a given day is equal to 1%. This produced the following calculated values for $ c_{ij} $:

We assume that only the test false positive rate, false negative rate and the mean incubation time are known. However, the value of the latter in Table 1 is based on a daily time unit, so here the value used is $ \lambda_E = 10/7 = 0.7 $. If desired, all estimated rates obtained by the algorithm in this experiment can be divided by 7 in order to obtain daily rates.

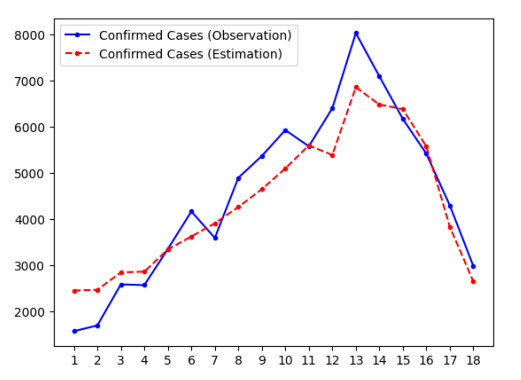
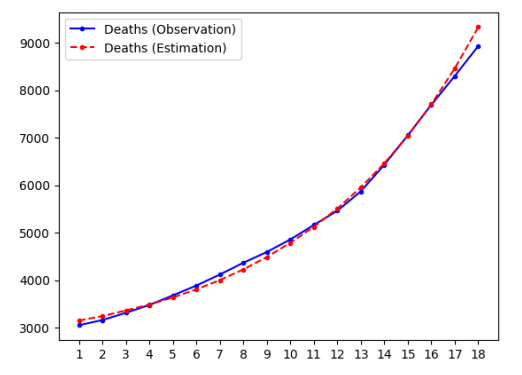
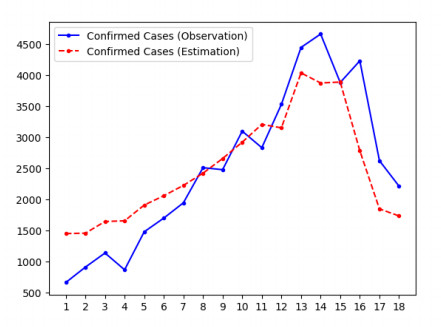
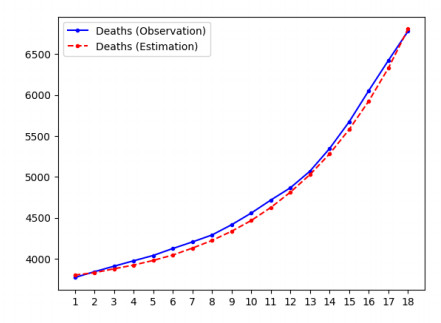
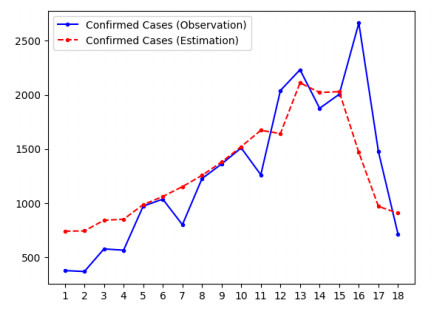
In addition, unlike in the experiment with synthetic data, we have no groundtruth for the states or parameters. In order to evaluate the performance of the algorithm, we use the estimated values of states and parameters to predict the time series of observed data and check its agreement with the actual JHU data. These plots are displayed in Figures 4 and 5 for region 3 (the plots for other regions are in the Supplementary Information). In all cases, the state vector was initialized using the procedure described in Section 3.1, which produced the value $ {\bf{m}}_{0|0} = (7717644, 1574, 1574, 0, 3591) $. Table 5 displays the estimated values of the parameters. These results indicate that our model can accurately estimate the hidden states and unknown parameters. The value for the infection rate is the same over all regions, by assumption; however, Figures 4 and 5 provide evidence that this is a reasonable assumption.

4.4.   Discussion

Compared with the standard SEIRD model, which assumes that the states of the epidemic can be observed directly, our stochastic state-space model realistically treats these states as hidden and only indirectly observed from the reported data. The proposed methodology is also able to incorporate detailed information about the testing procedure, such as false positive and false negative test rates and differential testing rate between symptomatic and asymptomatic patients. Contrary to standard models which consider reported cases as the true state of the epidemic, our model accounts for the impact of unobserved, undiagnosed cases on epidemic prediction. In so doing, our model provides a more accurate understanding of epidemic dynamics than models that ignore the effect of unobserved variables.

Our model has limitations, which can be addressed by future work. First, our model does not consider vital dynamics such as birth and death from other causes. Provided that the model is run over a short interval of time, such as an isolated wave in the epidemic, the results will not be affected too much; in addition, new born play an insignificant role in COVID-19 spread. Second, we assume that individuals infected with COVID-19 will develop life-long immunity. Though some epidemiological data have indicated evidence of COVID-19 reinfections, in most cases immunity persist for at least eight months. Therefore, we believe that this assumption has a marginal impact on our results, provided once again that the model is run over a short enough time interval. Third, our model ignored the impact of age on COVID-19 epidemiological parameters such as infection rate, disease severity (symptomatic vs asymptomatic), mortality rate, recovery rate, and testing rate. Age-specific infection rate and disease-induced complications have been observed during the ongoing COVID-19 pandemic and considered to play an import role in disease transmission and the design of public health policies. Fourth, our model in its current form assumes that connection between the different regions can be modeled with a simple gravity commuting model ^[28,29,30]. This limitation can be addressed by using empirical population mobility data. Finally, Our model did not consider potential temporal changes of parameters over time, e.g., the mortality rate may be be high and recovery rate low at the beginning of an outbreak because of lack of effective treatments, or public behavior, such as social distancing and mask wearing, may vary over time. Also, in the case of the Fall 2020 wave, it is known that mass vaccination began at the end of this wave (December 2020), which very likely had a major impact in the disease transmission parameters. Hence, the estimated parameter values reflect average rates over the time interval in consideration.

5.   Conclusions

We proposed a novel stochastic metapopulation state-space model for COVID-19 transmission, based on a discrete-time SEIRD model, which is able to estimate the hidden epidemic states and transmission parameters from a noisy time series of reported epidemiological data, by applying unscented Kalman filtering (UKF), Maximum Likelihood (ML) adaptive filtering, and metaheuristic optimization. We reported results from a comprehensive set of experiments, using synthetic data and real epidemic data to demonstrate that our model can estimate parameters and predict future trends accurately and effectively. The proposed framework was applied to the state of Texas in the United States, using data from the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University. It can also be applied to any city, state, and nation by providing the necessary time series data (e.g., reported cases, deaths, and testing rates). The proposed methodology may provide a valuable tool for revealing the current epidemic status through accurate estimated states and disease transmission parameters, improving the ability of authorities to make informed decisions on public health measures to contain the disease.

Conflict of interest

The authors declare that they have no conflicts of interest.

Acknowledgements

Martial Ndeffo-Mbah acknowledges funding from the National Science Foundation RAPID Award [grant number DEB-2028632].

Supplementary Information

1. Calculation of the covariance matrix Q of the process noise.

Covariance matrix $ Q_t $ is a 5 by 5 square matrix giving the covariance between each pair of elements of the state process noise vector $ (n^t_{S_i}, n^t_{E_i}, n^t_{I_i}, n^t_{R_i}, n^t_{D_i}) $ for a specific region $ i $ at time $ t $.

Diagonal elements of the covariance matrix contain the variances of each variable, which are calculated as:

The off-diagonal elements contain the covariances of each pair of variables, which are calculated as:

The remaining elements will be zero.

2. Covariance of the observation noise (R)

Covariance matrix $ R_t $ is a 2 by 2 square matrix giving the covariance between each pair of elements of the observation noise vector $ ({v_p}_i^t, {v_q}_i^t) $ for a specific region $ i $ at time $ t $.

Similarly, diagonal elements of the covariance matrix contain the variances of each variable, but all the off-diagonal elements will be zero.

3. Fish school search algorithm

Fish school search (FSS) is a population-based continuous optimization algorithm, which is inspired by the collective behavior of natural fish schools that expand and contract while searching for food. In the FSS algorithm, the objective is to find a model that maximizes a given score or fitness. Each candidate model, i.e., each candidate parameter vector $ \theta $, corresponds to a particle or "fish". An ensemble of candidate solutions is a "school, " which is iteratively updated by a series of biologically-inspired moves, namely, (1) an individual movement operator for each fish (a small random perturbation), (2) a feeding operator that updates the weight of all fish based on the fitness improvement from the previous step, (3) a collective instinctive movement operator that makes the fish that had successful individual movements influence the collective direction of movement of the school, and (4) a collective volitive movement operator when the fish move in concert, depending on whether the fish school is successful after the previous steps, i.e., its total weight increases, or not. If the fish school is successful, then it should contract, changing from exploration to exploitation mode. Otherwise, it should expand in order to explore the space more. This process is repeated for either a fixed number of iterations or until there is no significant improvement in the score.

4. State and parameter estimation using Johns Hopkins University COVID-19 data