1. Introduction
Transcription is one of the most fundamental cell biology processes. Gene transcription regulation is also one of the central topics in modern molecular biology. With the advent of MS2 tagging and single molecule RNA fluorescence in situ hybridisation technologies, detecting mRNA production in a single cell has come true. The measurement results reveal that mRNA copy number presented in an individual cell is low and mRNA level can vary significantly across cells in isogenic or clonal populations exposed to the same environment [5,10,12,13,15,26,32,40]. This variability may affect many important processes in cellular biology, such as response to apoptosis-inducing factors [3,45], bet-hedging in bacterial phenotypes [14,29], information processing [33], cellular decision-making [2,35,42,53], stem-cell fate decisions [8,9,10,35,36], the effectiveness of clinical treatment [30], and even cancer development [7]. Thus, understanding the origins of gene expression variabilities and establishing theoretical model to describe these variabilities have become very important in cell biology.
There is a large body of literature devoted to mean transcript level and transcription noise [5,6,12,13,14,19,28,31,32,33,46,47,48,49,54,55]. The models include Poisson expression statistics, two-state model of gene regulation [5,37,41], multi-state model of gene regulation [49], and so on. Additionally, reaction rates can also fluctuate because of stochastic variation in the global pool of housekeeping genes or because of fluctuations in environmental conditions that affect all genes [5,10,12,15]. For example, substrates, enzymes and regulatory molecules can also fluctuate and further randomize expression rates. All these lead to considerable intercellular variation in the mRNA levels in genetically identical cell populations.
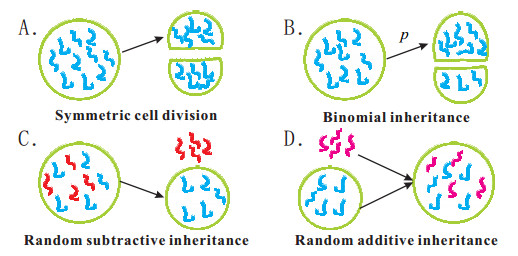
Cell division is an integral part of life activity by which a single-celled fertilized egg develops into a mature organism, as well as the process by which blood cells, hair, skin, and some internal organs are renewed. Life growth and development are driven by the continuous cell divisions. It is a stochastic and complex process. The volume-based division and the time-based division are two common methods to describe cell division. For the former, when the volume of a cell is growing twice the original volume, the cell begins to divide [16,34,38]. But the time-based division is different from the volume-based cell division. A cell might divide before its volume reaching double the original volume or not divide although its volume reaches double the original volume. The time at which the cell divides is deterministic or random depending on cellular environments or cellular physiological states [17,18,38,50]. Cell division modes contain both symmetric and asymmetric ones, where asymmetric cell division contains binomial inheritance, random subtractive inheritance and random additive inheritance, etc. Symmetric cell division yields two daughter cells with equal cellular components. However, asymmetric cell division is different. Biological experiments have provided evidence for division times, but the mechanism how symmetric and asymmetric cell division, as well as cell cycle affect gene expression has not been fully elucidated. The cell cycle between adjacent divide times has global effects on mRNA synthesis. Recent experiments have suggested that it is also an important source of transcription noise [4,11,51]. At the end of cell cycle, stochastic partitioning of mRNA molecules can also create further fluctuations at cell division, it is also a vital source of transcription noise. For example, in Drosophila melanogaster, asymmetric cell division plays an important role in neural development. Elucidating the stochastic kinetics of cell division is crucial to comprehensively understanding gene expression.
Although there has been much work focused on cell divisions [4,11,16,17,18,24,34,38,43,50,51,52], there is little work of quantitative analysis exploring the effects of symmetric and asymmetric cell divisions as well as cell cycle on mean transcript level and transcription noise. In this paper, we consider the time-based division and merge cell division as well as a variety of inheritance regimes into a two-state model of gene transcription. We derive the dynamic mean transcript level and transcription noise with cell divisions. The analytical solutions agree exactly with stochastic simulations. The mathematical formalism we explored provides an effective method to get explicit moment formula for mRNA number and provides an insight into gene expression.
2. Model description
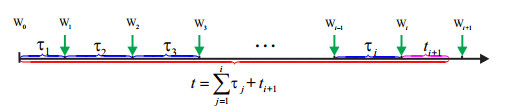
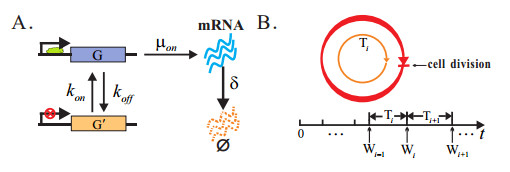
We construct the following theoretical model to describe the random transcription with cell division (Figure 1). The model is built on the most prevailing stochastic model for gene transcription, the so-called two-state model commonly used in the literature [15,23,26,44]. It has been postulated that the durations in the gene active (G) and inactive (G′) states are independent exponentially distributed, and mRNA copy numbers are controlled by a random birth and death process. Each copy of the gene switches stochastically with rates kon and koff between active and inactive states in a cell cycle. In the active state, transcription is initiated stochastically with rate μon. Mature mRNA is degraded stochastically with rate δ (Figure 1. A). The model includes two additional features: the cell cycle and the partitioning of mRNA molecules effects. Since we are concerned with the effects of cell division on mean transcript level and transcription noise, we don't distinguish several phases in the cell cycle but merge them into one stage (Figure 1. B). It should be pointed out that this simplification does not influence the qualitative conclusions reached in this paper. The ith cell cycle is from Wi−1 to Wi, Ti=Wi−Wi−1 is the ith cell cycle duration, where W0=0. T1,T2,T3,⋯ are assumed to be the independent and identically distributed random variables and the division is a transient process, the duration for division is not counted. Cell goes from the ith cell cycle into the (i+1)th cell cycle. At the end of the cell cycle, each mRNA molecule has the same probability to be segregated to one daughter cell which is regarded as the mother cell in the next cell division (for convenience, we call it the aim daughter cell), or a number of mRNA molecules are lost or gained at each cell division, and this number is itself a random variable. We focus on exploring the analytic expressions of mean transcript level and transcription noise.
3. Analytical results
3.1. The mean and noise within a cell cycle
In this subsection, we derive the analytical expressions of the dynamic mean transcript level and the dynamic transcription noise corresponding to the reaction network (Figure 1. A) within a cell cycle. Let M(t) be the copy number of the mRNA molecules at time t. Suppose that the initial copy number of the mRNA molecules is m0 and the gene in a single cell is inactive initially. Let
quantify the probability that there are m mRNA molecules at time t. The mean transcript level m(t) and the second moment μ(t) are defined as
|
m(t)=∞∑m=0mP(m,t), μ(t)=∞∑m=0m2P(m,t).
|
The stochastic fluctuations of transcription in cell populations have been characterized by noise η2(t), the variance normalized by the square of m(t) and noise strength, and the ratio between the variance and the mean [5,12,28,46,47]
Clearly, the noise is completely determined by the mean m(t) and the second moment μ(t).
For the convenience of the reader, we add Appendix A to give proofs of the next (1) and (2).
and
|
μ(t)=m20h2(t)+m0r(t)+s(t),
|
(2)
|
where
|
h(t)=e−δt,g(t)=μonkon(kon+koff)(kon+koff−δ)e−(kon+koff)t−μonkonδ(kon+koff−δ)e−δt+μonkonδ(kon+koff),r(t)=(2μonkonδ(kon+koff)+1)(e−δt−e−2δt)−2μonkon(kon+koff)(δ−kon−koff)(e−(kon+koff+δ)t−e−2δt),s(t)=−μonkon(2δ2+(2μon−kon−koff)δ−2μonkoff)δ(kon+koff)(kon+koff−δ)(kon+koff−2δ)(e−(kon+koff)t−e−2δt)−μonkon(δ(kon+koff)+2μonkon)δ2(kon+koff)(kon+koff−δ)(e−δt−e−2δt)+μonkonδ(kon+koff)(1+δμon+μonkonδ(kon+koff+δ))(1−e−2δt)−2μ2onkonkoffδ(kon+koff)((kon+koff)2−δ2)(e−(kon+koff+δ)t−e−2δt).
|
(1) and (2) are the basis for the dynamic mean transcript level and the noise with cell divisions.
3.2. The mean and noise with cell divisions
In this section, we detail the approach by which we obtain the first two moments of M(t) with any number of cell cycles and stochastic partitioning mRNA molecules at cell divisions. For consistency reasons, we stipulate ∑ij=kaj=0 and ∏ij=kaj=1 for i<k throughout this paper.
Now, we consider the stochastic model of transcription with a series of cell divisions. The ith cell cycle is from Wi−1 to Wi, Ti=Wi−Wi−1 is the ith cell cycle duration, where W0=0. The most common distributions to model the cell cycle Ti are exponential distribution, Erlang distribution [1], log-normal distribution [18], uniform distribution, etc. Let τi be the value of the ith cell cycle Ti, after which a division occurs. A variable ti+1 measures the elapsed time since the ith cell division (Figure 2), then ti+1∈[0,τi+1). Time is accounted for throughout this hybrid model in the following manner. If the ith (the recent) cell division has occurred, the total elapsed time can be written as ∑ij=1τj+ti+1. Hence for any t≥0 there exists an (i+1)-dimension vector (τ1,τ2,⋯,τi,ti+1) such that
where i stands for the number of the cell division before the time t, and ti+1 measures the elapsed time since the ith (the recent) cell division.
In order to obtain mean mRNA level m(t) and transcription noise η2(t) in each cell cycle stage, we need the following definitions and notations.
● m−i: the copy number of mRNA molecules just before the ith cell division;
● m+i: the copy number of mRNA molecules right after the ith cell division;
● Pκ(m+i|m−i): the probability that there are m+i mRNA molecules in the daughter cell after the ith cell division, given m−i mRNA molecules in the mother cell before the ith cell division;
● Pj(m,ti+1|m+i−j): the probability that there are m mRNA molecules at time t after the ith cell division, given m+i−j mRNA molecules right after the (i−j)th cell division;
● Φj=Pκ(m+j|m−j)P0(m−j,τj|m+j−1);
● θj(m−i)=∑m−im+i=0(m+i)jPκ(m+i|m−i);
● ϑj(m−i)=∑∞m+i=m−i(m+i)jPκ(m+i|m−i);
● ∑′i,j=∑∞m−i=0∑m−im+i=0∑∞m−i−1=0∑m−i−1m+i−1=0⋯∑∞m−j=0∑m−jm+j=0;
● ∑″i,j=∑∞m−i=0∑∞m+i=m−i∑∞m−i−1=0∑∞m+i−1=m−i−1⋯∑∞m−j=0∑∞m+j=m−j;
● Ai=∑′i,1m0(τi+1|m+i)∏ij=1Φj, A0=m0(τ1);
● Ci=∑″i,1m0(τi+1|m+i)∏ij=1Φj, C0=m0(τ1);
● Bi=∑′i,1μ0(τi+1|m+i)∏ij=1Φj, B0=μ0(τ1);
● Di=∑″i,1μ0(τi+1|m+i)∏ij=1Φj, D0=μ0(τ1).
Define
|
mj(ti+1|m+i−j)=∞∑m=0mPj(m,ti+1|m+i−j), i=0,1,2,⋯, j=0,1,2,⋯,i
|
and
|
μj(ti+1|m+i−j)=∞∑m=0m2Pj(m,ti+1|m+i−j), i=0,1,2,⋯, j=0,1,2,⋯,i.
|
The aim in the following is to obtain the expressions of mi(ti+1|m0) and μi(ti+1|m0). For symmetric division and binomial inheritance, based on the total probability formula, Pi(m,ti+1|m0) can be decomposed into the following form [25]
|
Pi(m,ti+1|m0)=∞∑m−i=0m−i∑m+i=0Pi−1(m−i,τi|m+0)Pκ(m+i|m−i)P0(m,ti+1|m+i).
|
(3)
|
By induction, one can get
|
Pi(m,ti+1|m0)=′∑i,1(P0(m,ti+1|m+i)i∏j=1Φj).
|
(4)
|
From (1) and (2), we have by noting m+0=m−0=m0
|
m0(t1|m0)=m(t1)=m0h(t1)+g(t1)
|
(5)
|
and
|
μ0(t1|m0)=μ(t1)=m20h2(t1)+m0r(t1)+s(t1),
|
(6)
|
respectively. Taking advantage of (4)-(6), we obtain
|
mi(ti+1|m0)=′∑i,1m0(ti+1|m+i)i∏j=1Φj =h(ti+1)′∑i−1,1∞∑m−i=0θ1(m−i)P0(m−i,τi|m+i−1)i−1∏j=1Φj +g(ti+1)′∑i−1,1∞∑m−i=0θ0(m−i)P0(m−i,τi|m+i−1)i−1∏j=1Φj
|
(7)
|
and
|
μi(ti+1|m0)=′∑i,1μ0(ti+1|m+i)i∏j=1Φj=h2(ti+1)′∑i−1,1∞∑m−i=0θ2(m−i)P0(m−i,τi|m+i−1)i−1∏j=1Φj +r(ti+1)′∑i−1,1∞∑m−i=0θ1(m−i)P0(m−i,τi|m+i−1)i−1∏j=1Φj +s(ti+1)′∑i−1,1∞∑m−i=0θ0(m−i)P0(m−i,τi|m+i−1)i−1∏j=1Φj.
|
(8)
|
3.3. The mean and noise with some specific divisions
In this subsection, we will derive the specific expressions of (7) and (8) for some specific cell divisions. Usually, there are two distinct types of cell divisions, i.e., symmetric division and asymmetric division, where asymmetric cell division includes binomial inheritance, random subtractive inheritance and random additive inheritance, etc.
3.3.1. Symmetric cell division
For symmetric cell division, the mRNA molecules in mother cell are equally divided into two daughter cells [20,21,22,27]. Note that m+i is a nature number, Pκ(m+i|m−i) can be expressed as
|
Pκ(m+i|m−i)=1{m−i/2}(m+i)+1{(m−i±1)/2}(m+i),
|
where 1Ω is the indicator function of Ω.
For convenience, let m+i take real numbers, we obtain
|
mi(ti+1|m0)=12h(ti+1)Ai−1+g(ti+1)
|
and
|
μi(ti+1|m0)=h2(ti+1)4Bi−1+r(ti+1)2Ai−1+s(ti+1),
|
where
|
Ai−1=2m0i∏j=1(h(τj)2)+i∑k=1(g(τk)i∏j=k+1(h(τj)2))
|
and
|
Bi−1=4m20i∏j=1(h(τj)2)2+i∑k=1(i∏j=k+1(h(τj)2)2(r(τk)2Ak−2+s(τk))).
|
3.3.2. Binomial inheritance
For binomial inheritance, every mRNA molecule in mother cell can be assigned into the daughter cell with the equal probability pi. The number of mRNA molecules assigned into the daughter cell obeys binomial distribution. Hence
|
Pκ(m+i|m−i)=(m−im+i)pm+ii(1−pi)m−i−m+i, i=0,1,2,⋯,
|
where pi∈(0,1). In this case, we obtain
|
mi(ti+1|m0)=pih(ti+1)Ai−1+g(ti+1)
|
and
|
μi(ti+1|m0)=p2ih2(ti+1)Bi−1+((pi−p2i)h2(ti+1)+pir(ti+1))Ai−1+s(ti+1),
|
where
|
Ai−1=m0pii∏j=1(pjh(τj))+i∑k=1(pkg(τk)pii∏j=k+1pjh(τj))
|
and
|
Bi−1=m20p2ii∏j=1(pjh(τj))2+i∑k=1(((pk−1−p2k−1)h2(τk)+pk−1r(τk))Ak−2i∏j=k+1(pjh(τj))2)+i∑k=1(s(τk)i∏j=k+1(pjh(τj))2),
|
where p0≡0.
3.3.3. Random subtractive inheritance
We now consider the case where a number of mRNA molecules are lost at each cell division. This number is a random variable and obeys binomial distribution with population size 2ηi and probability 0.5, then the average loss number is ηi. Hence
|
Pκ(m+i|m−i)=(2ηim−i−m+i)2−2ηi.
|
In this case, we obtain
|
mi(ti+1|m0)=h(ti+1)Ai−1+g(ti+1)−ηih(ti+1)
|
and
|
μi(ti+1|m0)=h2(ti+1)Bi−1+(r(ti+1)−2ηih2(ti+1))Ai−1+h2(ti+1)(η2i+ηi2)−ηir(ti+1)+s(ti+1),
|
where
|
Ai−1=m0i∏j=1h(τj)+i∑k=1((g(τk)−ηk−1h(τk))i∏j=k+1h(τj))
|
and
|
Bi−1=m20i∏j=1h2(τj)+i∑k=1((r(τk)−2ηk−1h2(τk))Ak−2i∏j=k+1(h(τj))2)+i∑k=1((h2(τk)(η2k−1+ηk−12))i∏j=k+1(h(τj))2)+i∑k=1((−ηk−1r(τk)+s(τk))i∏j=k+1(h(τj))2).
|
3.3.4. Random additive inheritance
We now consider the case where a number of mRNA molecules are gained at the ith cell division. This number is a random variable and obeys binomial distribution with population size 2ζi and probability 0.5, then the average loss number is ζi. Hence
|
Pκ(m+i|m−i)=(2ζim+i−m−i)2−2ζi.
|
We firstly decompose Pi(m,ti+1|m0) into the following form
|
Pi(m,ti+1|m0)=∞∑m−i=0∞∑m+i=m−iPi−1(m−i,τi|m+0)Pκ(m+i|m−i)P0(m,ti+1|m+i).
|
It follows by induction that
|
Pi(m,ti+1|m0)=″∑i,1(P0(m,ti+1|m+i)i∏j=1Φj).
|
Similarly to the random subtractive inheritance, we obtain
|
mi(ti+1|m0)=h(τi+1)Ci−1+g(τi+1)+ζih(τi+1)
|
and
|
μi(ti+1|m0)=h2(ti+1)Di−1+(r(ti+1)+2ζih2(ti+1))Ci−1+h2(ti+1)(ζ2i+ζi2)+ζir(ti+1)+s(ti+1),
|
where
|
Ci−1=m0i∏j=1h(τj)+i∑k=1((g(τk)+ζk−1h(τk))i∏j=k+1h(τj))
|
and
|
Di−1=m20i∏j=1h2(τj)+i∑k=1((r(τk)+2ζk−1h2(τk))Ck−2i∏j=k+1(h(τj))2)+i∑k=1(h2(τk)(ζ2k−1+ζk−12)i∏j=k+1(h(τj))2)+i∑k=1((ζk−1r(τk)+s(τk))i∏j=k+1(h(τj))2).
|
4. Numerical results
In this section, we will present our numerical results. For a given cell cycle distribution (exponential distribution, Erlang distribution [1], log-normal distribution [18], uniform distribution, etc.), we first randomly generate a series of division cycles τ1,τ2,⋯,τi whose mean is denoted by τ (representing the mean cell-cycle length). mi(ti+1|m0) and μi(ti+1|m0) denote respectively the mean and noise of mRNA numbers with the generating fixed cell division cycles τ1,τ2,⋯,τi. By averaging the different mi(ti+1|m0) and μi(ti+1|m0) corresponding to the different series of division cycles τ1,τ2,⋯,τi, we obtain the time-evolutional analytic mean and noise of mRNA number, respectively. Similarly, with a series of division cycles τ1,τ2,⋯,τi, by using the Gillespie stochastic simulation algorithm, we generate 10000 run at every time point and calculate the stochastic trajectory. By averaging these trajectory data, we obtain the time-evolutional numerical mean mRNA number.
For the narrative convenience, we introduce the following abbreviations:
● S: symmetric cell division;
● BF: binomial inheritance with fixed probability p=0.5;
● BR: binomial inheritance with random probability p∈[0.4,0.6];
● RA: random additive inheritance;
● AS: random additive and subtractive inheritance;
● RS: random subtractive inheritance.
For S, m+i=m−i2 if m−i is even, otherwise m+i takes randomly between m−i−12 and m−i+12. For BF, m+i obeys the binomial distribution with parameters m−i and p=0.5. For BR, each mRNA molecule is assigned to the daughter cell with the probability p at the end of a given cell cycle, but p may be different at the ends of the different cell cycles, which can be randomly selected from the interval [0.4, 0.6]. For AS, m+i takes randomly between m−i+n and m−i−n where n obeys the binomial distribution with parameters m−i and p=0.5. For constant cycle, we take the average in a few cycles as the steady-state mRNA mean or steady-state mRNA noise, otherwise we average the values in the time interval [200,800] as the steady-state mRNA mean or steady-state mRNA noise. The parameters kon=koff=1, μon=10, δ=0.0529 [52]. The initial mRNA molecule number m0=4. By (1) and (2) we know the steady-state mRNA mean and the steady-state mRNA noise with no cell division are ¯m=94.5180 and ¯η=0.0363, respectively.
The analytic solutions agree exactly with Gillespie stochastic simulation using plausible parameters kon=koff=1, μon=10, δ=0.0529 [52]. Figure 4 shows the analytic solutions and the numerical solutions of mean transcript level with BR and AS, where the cell cycle obeys log-normal distribution with the mean τ=120.
Table 1 shows the steady-state mean transcript level (the steady-state mRNA noise) with S, BF, BR and different cell cycle distributions, where the mean of cell cycle is τ=120.
Table 1. The steady-state mean transcript level (the steady-state mRNA noise) with S, BF, BR, and different cell cycle distributions, where the mean of the cell cycle is τ=120.
|
S |
BF |
BR |
| Constant cell cycle |
86.4910 (0.0402) |
86.4910 (0.0408) |
86.4924 (0.0408) |
| Exponential distribution |
87.2826 (0.0395) |
87.2826 (0.0401) |
87.2840 (0.0401) |
| Log-normal distribution |
86.7222 (0.0402) |
86.7222 (0.0407) |
86.7257 (0.0408) |
| Erlang distribution |
86.8273 (0.0400) |
86.8273 (0.0406) |
86.8276 (0.0407) |
| Uniform distribution |
86.7222 (0.0402) |
86.7222 (0.0407) |
86.7257 (0.0408) |
Table 2 shows the steady-state mean transcript level (the steady-state mRNA noise) with BA, BS, AS and different cell cycle distributions, where the mean of cell cycle is τ=120.
Table 2. The steady-state mean transcript level (the steady-state mRNA noise) with RA, AS, RS and different cell cycle distributions, where the mean of the cell cycle is τ=120.
|
RA |
AS |
RS |
| Constant cell cycle |
96.0226 (0.0353) |
94.1360 (0.0367) |
92.2314 (0.0381) |
| Exponential distribution |
95.9311 (0.0356) |
94.1327 (0.0367) |
92.3301 (0.0379) |
| Log-normal distribution |
95.7876 (0.0354) |
94.1105 (0.0367) |
92.4612 (0.0379) |
| Erlang distribution |
95.9445 (0.0354) |
94.1248 (0.0367) |
92.3034 (0.0380) |
| Uniform distribution |
95.9698 (0.0353) |
94.1229 (0.0367) |
92.2841 (0.0381) |
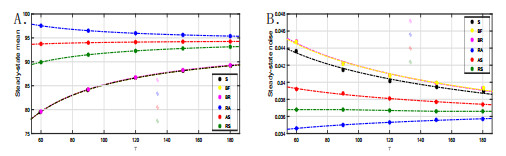
From Table 1 and Table 2 we can see that the steady-state mRNA noise with S is less than that with BF, and the steady-state mean transcript levels with the two modes are same. The steady-state mean transcript levels (the steady-state mRNA noises) with BF and BR are almost same. The steady-state mean transcript levels with S, BF and BR fall by about 7.65%-8.5% compared with no cell division. The steady-state mean transcript level with RA rises by about 1.5%-1.9%. The steady-state mean transcript levels with AS and RS fall by 0.4%-0.43% and 2.18%-2.42% respectively, compared with no cell division. All division modes except RA raise the steady-state mRNA noises.
In the case of the same cell cycle distribution, Figure 5 show that the steady-state mRNA noise with S is less than that with BF, but the steady-state mean transcript level with S is always equal to that with BF; The steady-state mean transcript levels (the steady-state mRNA noises) with BF and BR are almost same; The steady-state mean transcript levels (the steady-state mRNA noises) with S, BF and BR increase (decrease) with the average cell cycle duration, while the steady-state mean transcript level (the steady-state mRNA noise) with RA decreases (increases) with the average cell cycle duration; The steady-state mean transcript level is almost constant although the steady-state mRNA noise with AS decreases with the average cell cycle duration; The steady-state mean transcript level with RS increases with the average cell cycle duration although the steady-state mRNA noise with RS is almost constant. By fitting we obtain the relationship between the steady-state mean transcript level (the steady-state mRNA noise) and the cell cycle duration is very close to the power function with the form f(x)=axb+c. From the fitting we can predict the steady-state mean transcript level (the steady-state mRNA noise) in different cycles.
5. Conclusion and discussion
Gene transcription is a complex stochastic process, which result in high variability in gene expression. The sources of transcription noise come about in two ways, intrinsic source and extrinsic source. Intrinsic noise results from the inherent stochasticity of biochemical processes. The extrinsic noise originates from the cellular environmental perturbations or from extracellular signals regulating intracellular processes. Although there is a large body of literature devoted to mean transcript level and transcription noise [5,6,12,13,14,19,28,31,32,33,46,47,48,49,54,55] even cell divisions [4,11,16,17,18,24,34,38,43,50,51,52], there is little work of quantitative analysis exploring the effects of symmetric and asymmetric cell divisions as well as cell cycle on mean transcript level and transcription noise. Here, we have constructed a theoretical model to describe the random transcription with cell division. We merge several phases in a cell cycle into one stage and derive the analytical formulas for mean transcript level and mRNA noise corresponding to our model. By analysis, we have shown that symmetric cell division and binomial inheritance not only decrease mean transcript level but also increase transcription noise. For symmetric cell division and binomial inheritance, the steady-state mean mRNA level increases with the average cell cycle duration. All results are confirmed by Gillespie stochastic simulation using plausible parameters. The mathematical formalism we explored provides a method for yielding explicit formula of each moment of mRNA. Our method can be extended to more complex cases of gene expression. Our next step is to take gene replication into account and investigate the effects of specific phase of cell cycle on mean transcript level and transcription noise.
Appendix A. Proofs of (1) and (2)
Let U(t) be the number of active gene in a single cell at time t. Then U(t) is a random process. U(t)=0 and U(t)=1 denote the gene is inactive and active, respectively. By the assumption, we know
Let
|
P(j)(m,t)=Pr{M(t)=m,U(t)=j}, m=0,1,2,⋯, j=0,1
|
denote the probability that there are m mRNA molecules and j active genes. The initial conditions are
|
P(j)(m,0)={1, m=m0, j=0,0, otherewise.
|
(9)
|
Then
|
P(m,t)=Pr{M(t)=m}=P(0)(m,t)+P(1)(m,t).
|
We can derive the following chemical master equations
|
{∂∂t(P(0)(m,t))=−(kon+δm)P(0)(m,t)+koffP(1)(m,t)+δ(m+1)P(0)(m+1,t),∂∂t(P(1)(m,t))=konP(0)(m,t)−(koff+μon+mδ)P(1)(m,t)+μonP(1)(m−1,t)+δ(m+1)P(1)(m+1,t).
|
(10)
|
To obtain the mean transcript level m(t) and second moment μ(t), we define
|
m(0)(t)=∞∑m=0mP(0)(m,t), m(1)(t)=∞∑m=0mP(1)(m,t)
|
and
|
μ(0)(t)=∞∑m=0m2P(0)(m,t), μ(1)(t)=∞∑m=0m2P(1)(m,t).
|
Then we have
|
m(t)=m(0)(t)+m(1)(t), μ(t)=μ(0)(t)+μ(1)(t),
|
which together with (9) yields
Set
Then by [39,52], we have
|
P(1)(t)=konkon+koff−konkon+koffe−(kon+koff)t.
|
(12)
|
Multiplying both sides of each equation in (10) by m, and summing m from 0 to ∞, respectively, we obtain
|
{m(0)′(t)=−(kon+δ)m(0)(t)+koffm(1)(t),m(1)′(t)=konm(0)(t)−(koff+δ)m(1)(t)+μonP(1)(t).
|
(13)
|
It follows by summing its both sides that
|
m′(t)+δm(t)=μonP(1)(t).
|
(14)
|
Combining (14) with the initial condition (11) we get (1).
By eliminating m(0)(t) from (13) we can get the differential equation
|
m(1)′(t)+(kon+koff+δ)m(1)(t)=konm(t)+μonP(1)(t).
|
(15)
|
Combining with (9) we obtain the initial condition of m(1)(t)
Solving equation (15) with the initial condition (16) we get
|
m(1)(t)=m0konkon+koff(e−δt−e−(kon+koff+δ)t)+μonkon(δ−koff)δ(kon+koff)(kon+koff−δ)e−(kon+koff)t−k2onμonδ(kon+koff)(kon+koff−δ)e−δt−μonkonkoffδ(kon+koff)(kon+koff+δ)e−(kon+koff+δ)t+μonkon(kon+δ)δ(kon+koff)(kon+koff+δ).
|
Now multiplying both sides of each equation in (10) by m2, and summing m from 0 to ∞, respectively, we get the differential equations
|
{μ(0)′(t)=−(kon+2δ)μ(0)(t)+koffμ(1)(t)+δm(0)(t),μ(1)′(t)=konμ(0)(t)−(koff+2δ)μ(1)(t)+(2μon+δ)m(1)(t)+μonP(1)(t).
|
(17)
|
Adding the two equations in (17) yields
|
μ′(t)+2δμ(t)=δm(t)+2μonm(1)(t)+μonP(1)(t).
|
(18)
|
Combining (18) with (1), (12) and the condition (11), we can get (2).
Acknowledgments
We would like to thank the two anonymous reviewers for their valuable and precious comments and suggestions.









 DownLoad:
DownLoad: