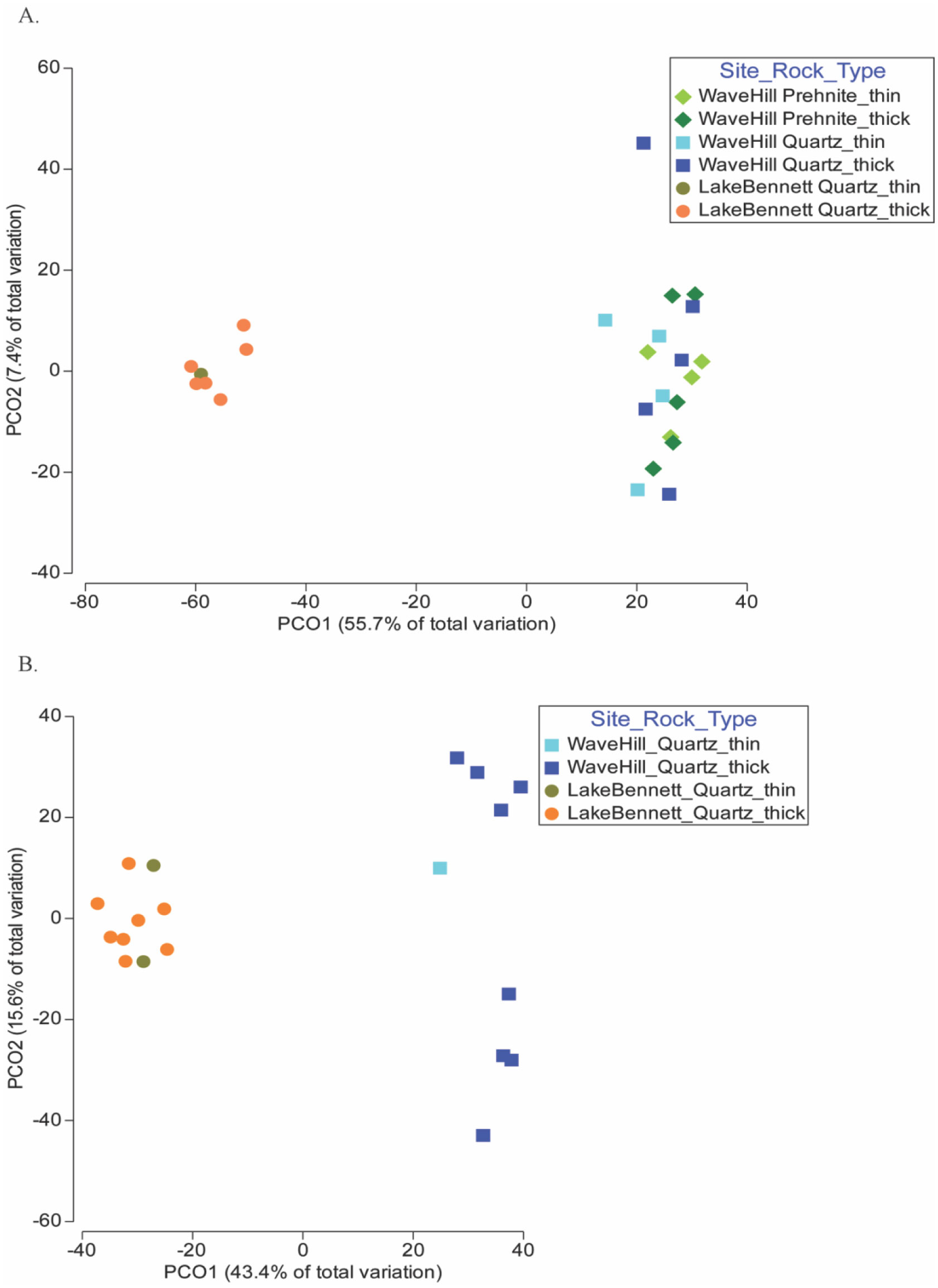
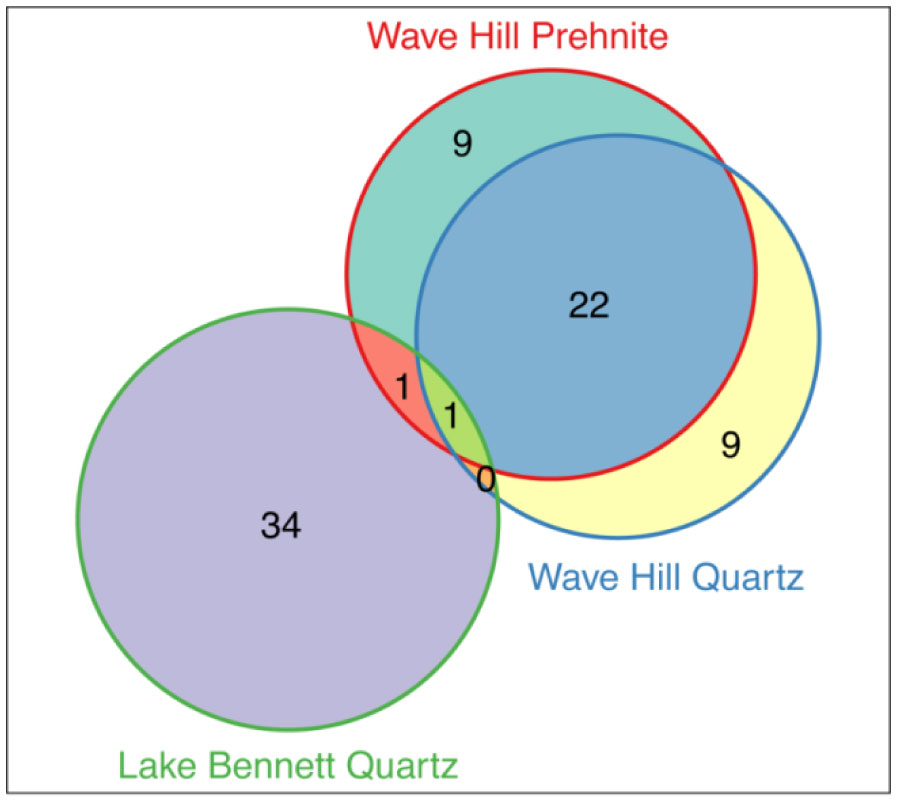
Hypolithic communities (under translucent rocks) were compared between a semi-arid site (Wave Hill) and a site with considerably higher rainfall (Lake Bennett) to test the hypothesis that the communities at the higher rainfall site would be more diverse. A total of 153 cyanobacteria operational taxonomic units (OTUs) were identified, and only 50 of those were found at both sites. Of these, only two were core OTUs, as defined as being present in ≥90% of samples, highlighting the extreme differences in the cyanobacterial communities at the two sites. At Wave Hill, we compared the composition of the cyanobacterial components under two different rock types (quartz and prehnite) to determine if the different minerals would result in different hypolithic communities, but no differences were found. Of the 42 core OTUs found at Wave Hill, 22 (52%) were shared between the two rock types. As hypothesised, the diversity of both cyanobacteria and eukaryotes in the hypolithic communities was significantly higher at Lake Bennett. Some hypolithic communities were thin and tightly adhered to the rock surface, but others were thicker and could be peeled off the rock in sheets. However, the two types were not significantly different in OTU composition. Metazoans, primarily nematodes, were ubiquitous, raising the possibility that nematodes may act as vectors to transport the components of hypolithic communities from rock to rock as a mechanism of colonization.
1.
Introduction
For a multi-node network system, consensus problems play a particular significance role in both theories and applications. Such problems are broadly investigated in fields of distributed computing [7], management science [1], flocking/swarming theory [16], distributed control [2] and sensor networks [11], and so on. Such systems also seem to have remarkable capability to regulate the flow of information from distinct and independent nodes to achieve a prescribed performance. As previous observations in both simulation and theory, the connectedness of the adjacency matrix and the processing delay play key roles to make the system achieve the emergent feature. The main motivation in current work is to analyze and explain the dynamical consensus patterns in a multi-node system, while the connectedness of the adjacency matrix is absent and the distributed processing delays are also involved in.
In this paper, we consider a $ N $-node network system with the distributed processing delay, reading as,
where $ {x}_i\in{R^n} $ denotes the $ n $ dimensional state of $ i $-th node at time $ t $. $ \lambda $ is a constant measured the coupling strength. $ \bar{x}_j(t) = \int_{-\tau}^0\varphi(s)x_j(t+s)ds $ measures the average of $ v_j $ on $ [t-\tau, t] $, where $ \tau $ denotes the maximum processing delay from $ j $ to $ i $, $ \varphi $ is a (positive) normalized distributed function so that $ \int_{-\tau}^0\varphi(s)ds = 1 $. $ \bar{x}_i(t) $ is defined similarly. In physically, a more realistic model should include a delay distribution over the time that depicts the human behavior in average. Usually, the traffic flow models are inherently time delayed because of the limited sensing and acting capabilities of drivers against velocity and position variations [9]. As we known, the delays usually follow the uniform distribution, the exponential distribution and discrete distribution. And $ \varphi(s) = \frac{1}{\tau} $ for the case of the unform distribution and $ \varphi(s) = \frac{\alpha}{1-e^{-\alpha\tau}}e^{\alpha s} $ for the exponential distribution, where $ \alpha $ is a positive constant. The constant $ a_{ij}\geq 0 $ is the strength of the influence of node $ j $ on $ i $ and $ a_{ii} = 0 $. In this model, the interaction involves delayed information processing, where the difference of the average states $ x_j-x_i $ influences the dynamics of the nodes after some time delay $ \tau $.
In the previously published works, consensus problems have often been studied with discrete processing delays [5,6,11], time-varying processing delays [8,12] and $ \gamma $-distribution delays [9,10] and the references therein. The case of discrete delay is always viewed as a delay with Bernoulli distribution. Mathematically, there have been many contributions to the stability of network system with processing delays, see [3,14,15] for examples.
To understand the dynamical consensus patterns better, we assume the adjacency matrix $ A = (a_{ij})_{N\times N} $ is a symmetric matrix. Let $ C = \sum_{i,j = 1}^Na_{ij} $ be the volume of the system and $ a_{ij} $ be normalized by
Let $ \tilde{\lambda} = \lambda C $, then we can rewrite the system (1) in the form
It is easy to find that the system (1) and system (2) have the same dynamical behaviors.
Let $ \tilde{A} = (\tilde{a}_{ij})_{N\times N} $, then $ \tilde{A} $ is a one-row-sum matrix and stochastic matrix [13]. Also it is a diagonalizable matrix, $ 1 $ is one of its eigenvalues and all other eigenvalues are real. Throughout the paper, we assume the eigenvalue $ 1 $ of stochastic matrix $ \tilde{A} $ is semi-simple with algebraic multiplicity $ n_0 $. And all different eigenvalues of $ \tilde{A} $ are $ \mu_i (i = 1, 2,\cdots,{m_0}) $ with the algebraic multiplicity $ p_i $. All eigenvalues of $ \tilde{A} $ satisfy the order
Naturally, if $ n_0 = 1 $, then the matrix $ \tilde{A} $ is a connected matrix. And when $ n_0>1 $, the connectedness of matrix $ \tilde{A} $ will be absent. From the matrix theory, we see that there is an orthogonal matrix $ {T}_0 $ such that $ \tilde{A} = {T}_0 {J}_0 {T}_0^{-1} $, where $ {J}_0 $ is a diagonal matrix with the first block $ I_{n_0} $, say $ {J}_0 = \left (In000J∗
\right ) $, where $ \mathbf{0} $ is zero matrix with matchable dimension. Define the norm of a real matrix $ {S}\in R^{N\times m} $ by $ \| {S}\| = \sup_{|\mathbf{\alpha}|\neq 0}\frac{| {S}\mathbf{\alpha}|}{|\mathbf{\alpha}|}, \ \ \mathbf{\alpha}\in R^m, $ then $ \|{T}_0\| = \|{T}_0^{-1}\| = 1 $.
To find the qualitative behaviors, we finish this section by considering the equation
and its characteristic equation is
Lemma 1.1. ([4], Corollary 6.1, P215) If $ a_0 = \max\{Re z: h_0(z) = 0\} $, then, for any $ c_0>a_0 $, there is a constant $ K = K(c_0) $ such that the fundamental solution $ S_w(t) $ of the equation (3) satisfies the inequality
2.
Main results
To specify a solution for the network system (1), we need to specify the initial conditions
where $ {f}_i $ is a given continuous vector-value function.
Definition 2.1. Suppose $ \{{x}_i (t)\}_{i = 1}^N $ is a solution to (1) and (5). The above system is said to achieve a weak periodic consensus, if there are periodic functions $ \phi_{pi}(t) $ with a same period such that
If $ {x_{i\infty}} = {x}_\infty $ for all $ i $, then the system is said to achieve a periodic consensus, where $ {x}_\infty \in {R^n} $ is a constant vector; If all $ \phi_{pi}(t) = 0 $, the system (1) is said to achieve a weak consensus. If both $ {x_{i\infty}} = {x}_\infty $ and $ \phi_{pi}(t) = 0 $ hold, it is said to achieve a consensus.
Let $ f_{max} = \max\{\|\mathbf{f}(\theta)\|: \theta\in[-\tau,0]\} $ for $ \mathbf{f}(\theta) = (f_1(\theta),\cdots,f_N(\theta))^T $ and
where $ y_{im} $ is a minimum positive root of equation
Set
then we obtain the following results and the details of proof will be given in sequel.
Lemma 2.2. Let $ \tilde{\lambda}>0 $. If $ 0\leq\tilde{\lambda}\tau(1-\mu_{m_0})<k^* $, then all other roots of the equation (4) have negative real parts and $ c_1<0 $. If $ \tilde{\lambda}\tau(1-\mu_{m_0}) = k^* $, then all other roots, except the pure imaginary roots, of the equations $ z+\tilde{\lambda}(1- \mu_i)\int_{-\tau}^0\varphi(s)e^{z s}ds = 0 $ $ (i = 2,\cdots,m_0-1) $ have negative real parts and $ c_2<0 $.
Theorem 2.3. Let $ \mathbf{X}(t) = (x_1(t),\cdots,x_N(t))^T $ be a solution of system (1) and $ 1 $ be a $ n_0 $-multiple eigenvalue of the matrix $ \tilde{A} $.
(1) Assume $ 0\leq\tilde{\lambda}\tau(1-\mu_{m_0}) <k^* $, then the system achieves a weak consensus with
and, for all $ \varepsilon\in(0,-c_1) $, there is constant $ K_1 $ such that
Especially, when $ n_0 = 1 $, the system achieves a consensus.
(2) Assume $ \tilde{\lambda}\tau(1-\mu_{m_0}) = k^* $, then the system achieves a weak periodic consensus with
and, for all $ \varepsilon\in(0,-c_2) $, there is constant $ K_2 $ such that
where $ \mathbf{X}_p(t) $ is formulated by (16). Especially, when $ n_0 = 1 $, the system achieves a periodic consensus.
Remark 1. For the case of uniform distribution, the distributed function is $ \varphi(s)\equiv \frac{1}{\tau} $. By direct computation, we see that $ k^* = \frac{\pi^2}{2} $ and $ y_{im} = \frac{\pi}{\tau} $. The values of $ k^* $ and $ y_{im} $ for typical distributions are listed in following table.
3.
Proof of main results
Proof of Lemma 2.1 Assume $ z = x+yi $ $ (y>0) $ is a root of $ z+\tilde{\lambda}(1- \mu_i)\int_{-\tau}^0\varphi(s)e^{z s}ds = 0 $. Then we have
Next, we show that $ x\leq 0 $ for $ y\in [0,y_{im}] $. Indeed, assume $ x>0 $, then $ \int_{-\tau}^0\varphi(s)e^{xs}\cos(ys)ds<0 $. {Let $ \tau_i(i = 1,2,\cdots,k) $ be all the roots of equation $ \cos(ys) = 0 $ on $ [-\tau,0] $. Also, we assume that
Set
then
Noting that $ y\in[0,y_{im}) $ and $ r = y_{im} $ is a minimum positive root of equation $ \int_{-\tau}^0\varphi(s)\cos(rs)ds = 0, $ we see that $ \int_{-\tau}^0\varphi(s)\cos(ys)ds>0 $ and $ \sum_{i = 0}^{l}(-1)^{i}A_i>0 $ for $ l = 1,2,\cdots,k $.
By direct computation, for $ x>0 $, we have $ \tilde{A}_0-\tilde{A}_1>e^{x\tau_1}({A}_0-{A}_1)>0 $ and
For generally, we have
It contradicts with $ \int_{-\tau}^0\varphi(s)e^{xs}\cos(ys)ds<0 $. Thus all other roots of the equation $ z+\tilde{\lambda}(1- \mu_i)\int_{-\tau}^0\varphi(s)e^{z s}ds = 0 $ have negative real parts when $ y\in [0,y_{im}) $. When $ y = y_{im} $, except the pure imaginary roots, the equation $ z+\tilde{\lambda}(1- \mu_{i})\int_{-\tau}^0\varphi(s)e^{z s}ds = 0 $ have negative real parts when $ i = 2,\cdots, m_0-1 $.
On the other hand, combining
and the fact $ \tau y_{im}+k^*\int_{-\tau}^0\varphi(s)\sin(y_{im}s)ds = 0, $ we see that $ y\in [0,y_{im}) $ if and only if $ 0\leq\tilde{\lambda}\tau(1-\mu_{m_0})<k^* $. Also $ y = y_{im} $ if and only if $ \tilde{\lambda}\tau(1-\mu_{m_0}) = k^* $. Since $ \tilde{\lambda}\tau(1-\mu_{i})\leq\tilde{\lambda}\tau(1-\mu_{m_0})<k^* $ holds for $ i = 2,\cdots, m_0 $, we conclude that all other roots of the equation (4) have negative real parts when $ 0\leq\tilde{\lambda}\tau(1-\mu_{m_0})<k^* $. Also, if $ \tilde{\lambda}\tau(1-\mu_{m_0}) = k^* $, except the pure imaginary roots, the equation $ z+\tilde{\lambda}(1- \mu_{i})\int_{-\tau}^0\varphi(s)e^{z s}ds = 0 $ have negative real parts when $ i = 2,\cdots, m_0-1 $.
Noting that the set $ \{Re(z):z = -\tilde{\lambda}(1-\mu_i)\int_{-\tau}^0\varphi(s)e^{z s}ds\} $ is up-bounded when $ 0\leq\tilde{\lambda}\tau(1-\mu_{m_0})<k^* $, and from above arguments, we see that the supremum
Assume that $ c_1 = 0 $, then there is a sequence $ \{z_n\} $ $ (z_n = x_n+iy_n, y_n>0) $ with
Thus
and
Then, for $ x_n\leq 0 $, the sequence $ \{y_n\} $ is bounded by $ y_{im} $. Thus there is a convergent subsequence of $ \{y_n\} $. Without loss of generality, we assume $ \{y_n\} $ is a convergent sequence with the limit $ y_\infty $ satisfying $ y_\infty\leq y_{im} $. For $ \lim_{n\rightarrow\infty}x_n = 0 $, we see that
If $ y_\infty< y_{im} $, then it contradicts that $ r = y_{im} $ is a minimum positive root of equation $ \int_{-\tau}^0\varphi(s)\cos(rs)ds = 0. $ If $ y_\infty = y_{im} $, for $ \tilde{\lambda}(1-\mu_i)<\tilde{\lambda}\tau(1-\mu_{m_0})<k^* $, then it contradicts with $ \tau y_{im}+k^*\int_{-\tau}^0\varphi(s)\sin(y_{im}s)ds = 0. $ Thus $ c_1<0 $. Similar arguments yield $ c_2<0 $. This completes the proof.
Proof of Theorem 2.1 Let $ \mathbf{X} = (x_1,x_2,\cdots,x_N)^T $ and $ \mathbf{\bar{X}}(t) = \int_{-\tau}^0\varphi(s)\mathbf{X}(t+s)ds $. Thus the system (1) can be rewritten with the vector form, reading as,
Recalling $ \tilde{A} = T_0\left (In000J∗
\right )T_0^{-1} $ and let
then the equation of (10) yields
That is, $ \dot{y}_i(t) = 0 $ for $ i = 1,2,\cdots,n_0 $, and $ \mathbf{y}^*(t) $ solves the equation (3). And then the characteristic equation $ h_0(z) = 0 $ becomes
where $ p_i $ is the algebraic multiplicity of $ \mu_i $, $ m_0 $ is the number of the different eigenvalues of $ {P}_0 $.
Let $ \mathbf{{S}}^*(t) $ be a fundamental solution operator of the equation (3). Then the solution $ \mathbf{X}(t) $ of the equation (10) becomes
Let
By using the equalities (12) and (13), we have
CASE Ⅰ: $ \tilde{\lambda}\tau(1-\mu_{m_0})<k^* $. Following Lemma 2.1, we see that all roots of the characteristic equation (11) have negative real parts. And from Lemma 1.1, there are a constant $ K_1>0 $ such that
Thus $ \|\mathbf{S}^*(t)\|\leq K_1e^{-(|c_1|-\varepsilon)t} \ \mbox{ for all}\ \varepsilon\in(0,-c_1) $ and
This implies that
It means that $ \lim_{t\rightarrow\infty}\mathbf{X}(t+\theta) = \mathbf{{X}}_{a}(\theta). $ On the other hand, noting that $ \dot{y}_i(t) = 0 $ for $ i = 1,2,\cdots,n_0 $ and $ \lim_{t\rightarrow\infty}\mathbf{y}^*(t) = \mathbf{{0}} $, we conclude that
Thus, we have
and
Thus, from Definition 2.1, the system (1) achieves a weak consensus.
Especially, when $ n_0 = 1 $, for $ T_0 $ is an orthogonal matrix, then $ \mathbf{{X}}_{\infty} $ are formulated by
where $ \otimes $ denotes the Kronecker product. Thus the system (1) reaches a consensus.
CASE Ⅱ: $ \tilde{\lambda}\tau(1-\mu_{m_0}) = k^* $. Consider the equation
and its characteristic equation is given by $ z = -\tilde{\lambda}(1-\mu_{m_0})\int_{-\tau}^0\varphi(s)e^{zs}ds $. From the definition of $ k^* $, we see that $ \pm y_{im}i $ are two pure imaginary roots of above equation. Thus both $ e^{ty_{im}i} $ and $ e^{-ty_{im}i} $ are solutions of the given equation, and then both $ \cos(y_{im}t) $ and $ \sin(y_{im}t) $ are also solutions. Thus the periodic solution $ y(t) $ would be formulated by $ y(t) = c_1\cos(y_{im}t)+c_2\sin(y_{im}t) $. Substituting the initial values, we find that the basic periodic solution is
Let
and rewrite the diagonal matrix $ J $ as
Similarly, let $ \mathbf{{S}}_p^*(t) $ be a fundamental solution operator of the equation
Then the solution $ \mathbf{X}(t) $ in (10) becomes
for $ t\in [0,+\infty), \theta\in [-\tau,0]. $
To find the asymptotic behaviors, we consider the characteristic equation corresponding to (17), reading as
By direct computation, the above equation becomes
Noting $ \tilde{\lambda}\tau(1-\mu_{j})<k^* $ for $ j = 2,\cdots, m_0-1, $ and all roots of $ h_1(z) = 0 $ are also the roots of $ h_0(z) = 0 $, following Lemma 2.1, we see that all roots of the characteristic equation (19) have negative real parts when $ \tilde{\lambda}\tau(1-\mu_{m_0}) = k^* $.
Following Lemma 1.1, there is a constant $ K_2>0 $ such that
Thus $ \|\mathbf{S}^*_p(t)\|\leq K_2e^{-(|c_2|-\varepsilon)t} \ \mbox{for all}\ \varepsilon\in(0,-c_2) $ and
This implies that
Thus
Furthermore, when $ n_0 = 1 $, all the components of $ \mathbf{{X}}_{\infty} $ are same. Also, all the components of $ \mathbf{{X}}_{p}(t) $ are periodic functions with a same period $ \frac{2\pi}{y^*} $ and
Thus it follows from Definition 2.1 that the system (1) achieves a periodic consensus when $ n_0 = 1 $. When $ n_0>1 $, the system (1) achieves a weak periodic consensus. This completes the proof.
4.
Numerical simulation
In this section, we verify our main conclusions by a series of numerical simulations. We consider the system (1) with 10 nodes. The initial velocities are given as follows:
Case Ⅰ. Consider the adjacency $ A = (a_{ij})_{N\times N} $ satisfying $ a_{ij} = 1(j\neq i) $ and $ a_{ii} = 0 $. Then $ \tilde{A} = (\tilde{a}_{ij})_{N\times N} $ satisfies $ \tilde{a}_{ij} = \frac{1}{N(N-1)}(j\neq i) $ and $ \tilde{a}_{ii} = \frac{N-1}{N} $. Direct calculation yields
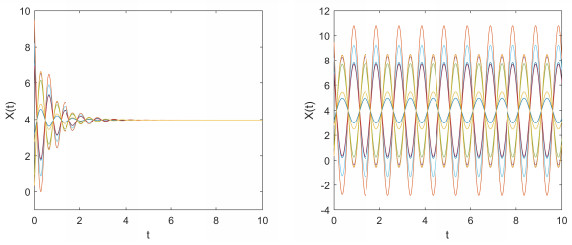
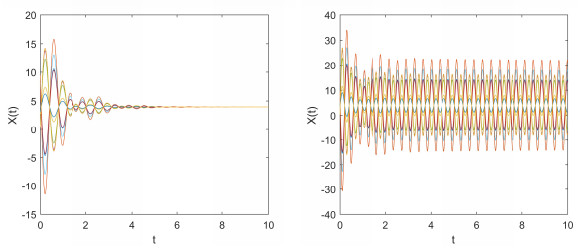
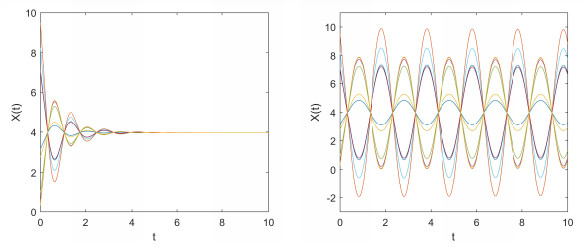
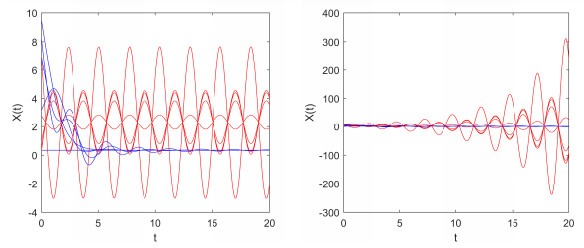
Let $ N = 10 $, we obtain $ \mu_1 = 1(n_0 = p_1 = 1) $ and $ \mu_2 = \frac{8}{9}(p_2 = 9) $. The simulation results and values of $ \tilde{\lambda} $ and $ \tau $ for different distribution function are listed in Table 3.
Case Ⅱ. In order to understand the dynamical behaviours when the parameter $ \tilde{\lambda} $ is changing, we consider the case $ A = \left( A100A2
\right)_{2N\times2N} $, where $ A_1 = (a_{ij}^{(1)})_{N\times N} $ satisfies $ a_{ij}^{(1)} = 1(j\neq i) $ and $ a_{ii}^{(1)} = 0 $, $ A_2 = (a_{ij}^{(2)})_{N\times N} $ satisfies $ a_{ij}^{(2)} = 1(j>i) $ and $ a_{ii}^{(2)} = 0 $. Then $ \tilde{A} = (\tilde{a}_{ij})_{2N\times2N} $ satisfies $ \tilde{a}_{ij} = \frac{2}{3N(N-1)}(j\neq i) $ and
Direct calculation yields
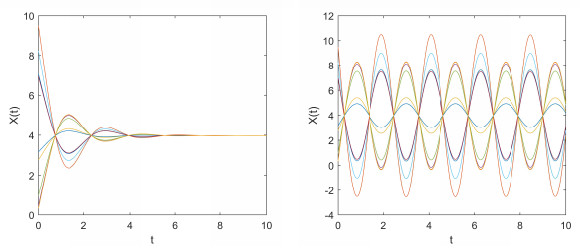
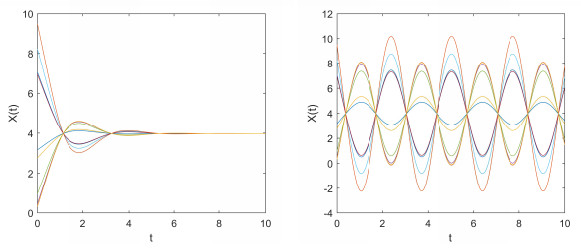
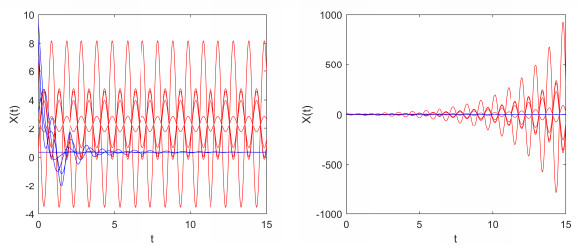
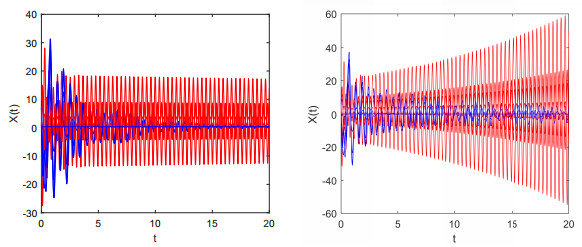
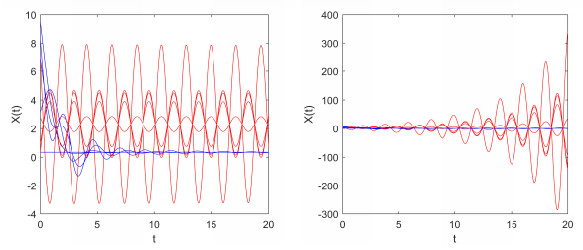
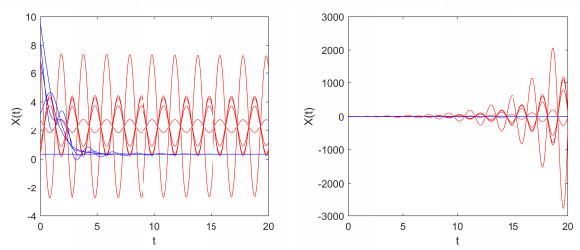
Take $ N = 5 $, we obtain $ \mu_1 = 1(n_0 = p_1 = 2) $, $ \mu_2 = \frac{29}{30}(p_2 = 1) $, $ \mu_3 = \frac{14}{15}(p_3 = 1) $, $ \mu_4 = \frac{9}{10}(p_4 = 1) $, $ \mu_5 = \frac{13}{15}(p_5 = 1) $ and $ \mu_6 = \frac{5}{6}(p_6 = 4) $. Let $ x_i(i = 6,7,...,10) $ be in Group 1 (blue line) and the others $ x_i(i = 1,2,...,5) $ in Group 2 (red line). In this case, the numerical simulations results are listed in Table 4.
Acknowledgments
We would like to thank the editors and the reviewers for their careful reading of the paper and their constructive comments.









 DownLoad:
DownLoad: