Citation: Vasiliki Panagopoulou, Athina Kalokairinou, Foteini Tzavella, Styliani Tziaferi. A survey of Greek women’s satisfaction of postnatal care[J]. AIMS Public Health, 2018, 5(2): 158-172. doi: 10.3934/publichealth.2018.2.158
| [1] | Valentina Contrò, John R. Basile, Patrizia Proia . Sex steroid hormone receptors, their ligands, and nuclear and non-nuclear pathways. AIMS Molecular Science, 2015, 2(3): 294-310. doi: 10.3934/molsci.2015.3.294 |
| [2] | William M. Scovell, Sachindra R. Joshi . The changing paradigm: estrogen receptor α recognition on DNA and within the dynamic nature of nucleosomes. AIMS Molecular Science, 2015, 2(2): 48-63. doi: 10.3934/molsci.2015.2.48 |
| [3] | Geovanni Alberto Ruiz-Romero, Carolina Álvarez-Delgado . Effects of estrogens in mitochondria: An approach to type 2 diabetes. AIMS Molecular Science, 2024, 11(1): 72-98. doi: 10.3934/molsci.2024006 |
| [4] | Maria Kristina Parr, Anna Müller-Schöll . Pharmacology of doping agents—mechanisms promoting muscle hypertrophy. AIMS Molecular Science, 2018, 5(2): 131-159. doi: 10.3934/molsci.2018.2.131 |
| [5] | Carson C. Chow, Karen M. Ong, Benjamin Kagan, S. Stoney Simons Jr. . Theory of partial agonist activity of steroid hormones. AIMS Molecular Science, 2015, 2(2): 101-123. doi: 10.3934/molsci.2015.2.101 |
| [6] | Alicja Florczak, Aleksandra Królikowska, Mateusz Mazurek, Sławomir Woźniak, Zygmunt Domagała . Most relevant genetic factors in ovarian cancer development. AIMS Molecular Science, 2025, 12(1): 1-25. doi: 10.3934/molsci.2025001 |
| [7] | Laura Serna . Crosstalk among hormones and signaling networks during stomatal development in Arabidopsis hypocotyls. AIMS Molecular Science, 2016, 3(4): 550-559. doi: 10.3934/molsci.2016.4.550 |
| [8] | James R. Lambert, Steven K. Nordeen . A role for the non-conserved N-terminal domain of the TATA-binding protein in the crosstalk between cell signaling pathways and steroid receptors. AIMS Molecular Science, 2015, 2(2): 64-76. doi: 10.3934/molsci.2015.2.64 |
| [9] | Mohamed Amine Ben Mlouka, Thomas Cousseau, Patrick Di Martino . Application of fluorescently labelled lectins for the study of polysaccharides in biofilms with a focus on biofouling of nanofiltration membranes. AIMS Molecular Science, 2016, 3(3): 338-356. doi: 10.3934/molsci.2016.3.338 |
| [10] | Amedea B. Seabra, Halley C. Oliveira . How nitric oxide donors can protect plants in a changing environment: what we know so far and perspectives. AIMS Molecular Science, 2016, 3(4): 692-718. doi: 10.3934/molsci.2016.4.692 |
Microbes respond to various chemical signals by altering their phenotype. This change in response to specific chemical signals falls under the rubric of quorum sensing [1]. The autoinducers of this signaling are typically one of two classes of compounds, i.e., homoserine lactones and oligopeptides [2,3,4,5]. Most recently, insulin, a phylogenetically ancient molecule, has been demonstrated to function as a cross-kingdom quorum chemical signal [6,7]. Although steroids have not been described as part of the autoinducer family of quorum chemical signals, they demonstrate a concentration specific bi-functionality with regards to their effect on microbial phenotype. At one end of the spectrum, steroid hormones enhance microbial pathogenicity. In contrast, they also inhibit microbial growth and toxin production, both directly and indirectly, in a manner reminiscent of host factors associated with the innate immune system. The focus of this review is to describe the interkingdom pleiotropic effects human steroid hormones have on microbes.
Microbial colonization of host tissues, abiotic and mucosal surfaces is a prerequisite for infection and disease. For microbe-mediated disease processes to occur, a microbe must colonize host surfaces and elicit an immune response. A prerequisite for colonization and microbial spread is adherence to biologic or abiotic surfaces, formation of biofilms, and subsequent dispersal of organisms from those biofilms (Figure 1) [8,9,10,11,12,13]. A requirement for biofilm formation is replication. For microbes to shift from a planktonic state, adhere and replicate, there needs to be microbial recognition of an advantageous environment for their sessile survival. Steroid hormones can serve as these signals. They can function as interkingdom chemical signaling compounds that trigger concentration-specific phenotypic changes in microbes. The mechanism via which this signal recognition occurs is referred to as quorum sensing [1]. The autoinducers for this process include chemical signals of the lactone class (homoserine lactones), oligopeptides and the polypeptide insulin [6,7]. Interestingly, steroid hormones can function as interkingdom quorum signaling molecules, even though they have not been identified as members of the autoinducer families. Of the interkingdom steroid hormone signals, the ones most studied are estrogen, progesterone, testosterone and dehydroepiandosterone (DHEA).
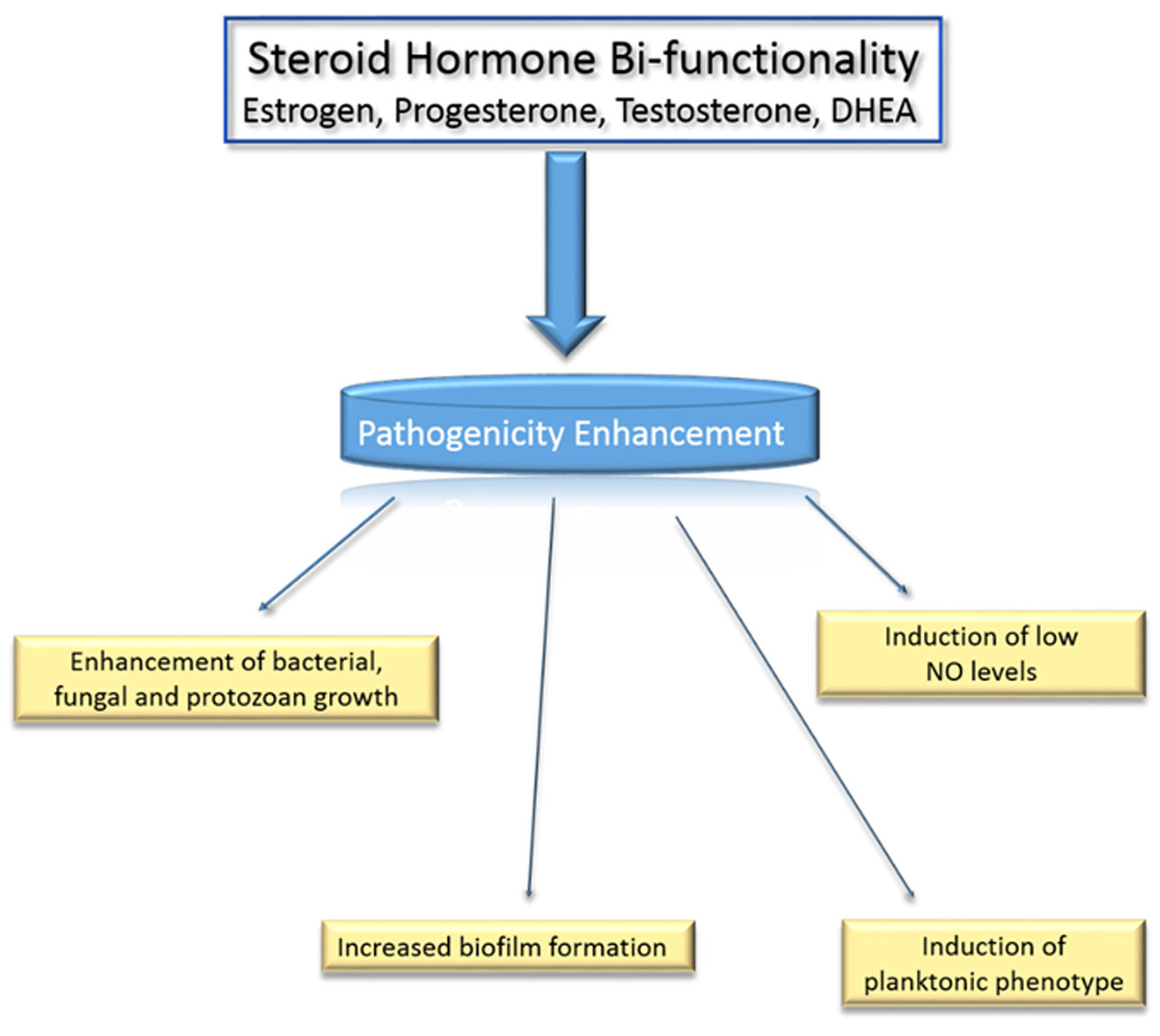Figure 1. Effects of steroid hormones on the various aspects of pathogenicity.Estrogen and its analogs regulate various aspects of fungal, protozoal and bacterial morphogenesis in a concentration-specific manner [14,15]. Estrogen and 17β-estradiol stimulate Coccidiodes immitis hyphal growth rates, as well as spherule maturation with endospore release rate [16]. In a similar fashion, norethisterone, an estrogen mimic, improves growth rates of Aspergillus species, including A. clavatus, A. fumigatus and A. niger, as well as Microsporum canis and Trichophyton mentagrophytes in a concentration-specific manner; low steroid levels increase fungal growth, while high concentrations depress mold growth [17]. The most well studied effects of estrogen on fungal growth and morphogenesis were done with Candida albicans [18].
Morphogenic conversion of C. albicans from blastospore to hyphal state is associated with its virulence and biofilm formation capabilities. Zhang et al. reported that the growth rate of three C. albicans variants increased in response to 17β-estradiol [19]. In addition, there was an increase in the number and overall length of the Candida germ tubes, a change associated with increased biofilm formation and virulence [20,21,22,23]. This hyphal conversion would assist Candida in maintenance of colonization and biofilm status despite epithelial cell shedding [20,21,22,23]. These findings support in vivo findings that estrogen is important in susceptibility to and maintenance of candidal vaginitis, a functionality that includes a ligand-estrogen-binding protein interaction in the yeast [24,25].
Indirect effects of estrogen that affect fungal virulence-associated factors include hormone up-regulation of expression of efflux pumps associated with multidrug resistance [19,20,26,27,28]. Interestingly, estrogen upregulates candidal CDR1 and CDR2 genes which are associated with drug resistance. Furthermore, 17β-estradiol increased expression of PDR16, an alternative gene also correlated with increased anti-fungal drug resistance [20]. Mechanistically, the response to estrogen and drug resistance appears as the result of estrogen and antifungal agents sharing efflux pumps [20]. However, in contrast to the number of studies examining estrogen and its analog's effects on fungi, their effects on bacteria are less well studied.
Estrogen has been shown to enhance the growth and survival of several Gram-negative bacteria. In Bacteroides melaninogenicus, estrogen can replace menadione, an essential growth factor [29]. Estradiol's interaction with Pseudomonas aeruginosa results in both in vitro and in vivo enhancement of the virulent mucoid biofilm phenotype [30]. Clinically, the significance of P. aeruginosa shifting from a nonmucoid phenotype to an alginate producer, is an exacerbation in women with cystic fibrosis of pneumonia with associated parenchymal damage [31,32]. The mechanism for this shift appears related to a P. aeruginosa constitutive cytosolic estrogen-binding protein, which plays a role in the selection of mutations in the alginate synthesis negative regulator (mucA) [30]. The binding specificity of this protein for steroids is estradiol >estrone >dihydrotestosterone >estriol >testosterone >progesterone >promegestone [33]. In Chlamydia trachomatis, estradiol downregulates a significant portion of genes involved in nucleotide metabolism and fatty acid biosynthesis, and upregulates genes associated with the chlamydial stress response [34]. Estradiol upregulation of yggV, pyk, omcB, trpB, cydA and cydB genes appears to be associated with enhanced chlamydial survival and persistence. This estradiol-mediated alteration in gene expression may explain why chlamydial infections are more common in the estrogen-dominant phase of menstruation.
Progesterone, like estrogen, increases the pathogenesis of microorganisms in a concentration-specific manner. The survival and intracellular replication of Neisseria gonorrhoeae within human cervical epithelial cells is enhanced by the presence of progesterone [35]. Mechanistically, progesterone aids gonococcal phospholipase D-mediated adherence and invasion of cervical cells. Metabolically, progesterone induces expression of N. gonorrhoeae anaerobic respiratory detoxification pathway. This phenotypic change augments N. gonorrhoeae growth in cervical fluid [35]. Progesterone also affects the metabolism of Chlamydia trachomatis [34]. In C. trachomatis, progesterone upregulates genes involved in both the citric acid cycle and glycolytic pathway. Replication of C. pneumoniae, a common cause of respiratory tract infections in humans, is modulated by its progestin receptor [36,37,38]. Intracellular replication of C. pneumoniae in human epithelial cells is inhibited by mifepristone, a progestin receptor antagonist. In addition, mifepristone inhibited C. pneumoniae growth during a natural infectious process, but failed to inhibit growth during a persistent infection [36,37,39]. Clinically, this metabolic shift may have a role in induction of, or maintenance of chlamydial persistence [34]. Similarly, progesterone directly influences Bacteroides melaninogenicus metabolic pathways since progesterone, like estrogen, can substitute for menadione, an essential growth factor [29]. The interchangeability of progesterone or estrogen with menadione raises the possibility that either hormone could directly affect B. melaninogenicus in vivo [29]. In addition, progesterone was also similar to estrogen in its ability to stimulate growth and morphogenesis of Coccidioides immitis [16].
From a pathogen's perspective, recognition of a host-derived quorum signaling compound that is universally present would have immense advantages for survival. Interestingly, although DHEA is present at various concentrations in humans throughout life, it exhibits the narrowest microbial species spectrum [40,41,42]. DHEA had no effect on any Gram-negative pathogens tested i.e., Escherichia coli, Salmonella paratyphi or Alcaligenes faecalis [43]. The sole pathogen affected was Staphylococcus aureus, both methicillin-sensitive and methicillin-resistant strains (MSSA and MRSA, respectively) [44,45,46]. In S. aureus, DHEA triggered a shift to a phenotype which shares characteristics with S. aureus heteroresistant and small colony variants e.g., cell wall scaffolding changes, increases in peptidoglycan thickness, cross-linkage and carotenoid production [44,47,48]. In addition, DHEA mediates an increase in cell surface positive electrostatic charge, surface hydrophobicity and capsule production, which would permit a closer association with mammalian cell surfaces [44,49]. DHEA also induces a fourfold increase in resistance to vancomycin, as well as other positively charged antimicrobials and host-derived compounds e.g., lysozyme and beta-defensins [50]. The mechanism for these phenotypic changes occurs via DHEA effects on the sarA global regulator [44]. Taken together, this DHEA-mediated phenotype could increase a host carrier state, and may explain vancomycin clinical treatment failures [51,52,53].
The hormone concentration-specific bi-functionality on microbe pathogenicity-associated phenotypes is perhaps most pronounced for testosterone. For example, Microsporum canis growth ranged from being inhibited to stimulated, depending on testosterone concentration [17]. This bi-functionality is postulated due to hormone concentration-specific allosteric interference with gene transcription or translation and intercalation into the fungal cell membranes [17]. Testosterone also inhibited the rate of Trichomonas vaginalis growth while it stimulated Coccidiodes immitis growth [14,16,54]. Similar to its impact on fungi, testosterone also exhibited opposing effects on various microbial species. For example, at 1.0 µM S. aureus' and E. coli's doubling rate was increased, while that of E. faecalis and P. aeruginosa was slowed [45]. How this testosterone effect on microbial growth translates into alteration in virulence remains to be determined.
Similar to the findings for steroid hormones' role in pathogenicity enhancement, estrogen, progesterone, testosterone and DHEA also function as members of the innate immune system in a concentration specific manner (Figure 2). One commonality shared by these hormones is their ability to inhibit microbial growth. Yotis and Williams demonstrated that progesterone, estrogen and testosterone are comparable in their ability to inhibit the growth of Staphylococcus aureus, Staphylococcus epidermidis, Streptococcus faecalis, Micrococcus conglomeratus, Gaffkya tetragena, Listeria monocytogenes, Bacillus subtilis, Bacillus cereus, Candida albicans and Saccharomyces cerevisiae [55]. Methyl testosterone was also shown to have a fungistatic effect on the growth of Trichophyton purpureum and Trichophyton gypseum, as well as inhibit the rate of Trichomonas vaginalis growth [14,54,56]. Of this group of steroids, progesterone exhibited the highest activity as an inhibitor of gonococcal respiration [57]. The ability of progesterone to inhibit N. gonorrhoeae oxygen uptake is thought to be related to its molecular configuration i.e., the greater the number of steroid-associated lipophilic groups, the more respiration inhibition [57]. Mechanistically, this inhibition is the result of steroid diffusion through the N. gonorrhoeae outer membrane, facilitated by the presence of lipophilic groups. This progesterone sensitivity is limited to pathogenic Neisseria species i.e., N. gonorrhoeae and N. meningitidis [58]. Beyond its effect on growth, progesterone has also been shown to reduce staphylococcal alpha toxin cytolytic action and affect staphylococcal alpha toxin activity via an undefined mechanism [59].
Although DHEA is best known of the steroid hormones for its effect on immune function and disease resistance, testosterone (as testosterone propionate) promoted increased resistance to Streptococcus pneumoniae disease in a murine model, staphylococcal furunculosis and integumental Trichophyton purpureum infections in castrated rabbits [43,56,60,61]. In related studies, steroid receptor co-activator 3 (SRC-3) is shown to play a role in protection against Gram-negative bacteria; SRC-3 deficient mice are more susceptible to E. coli infections, possibly the result of depression in phagocytic function [62,63,64].
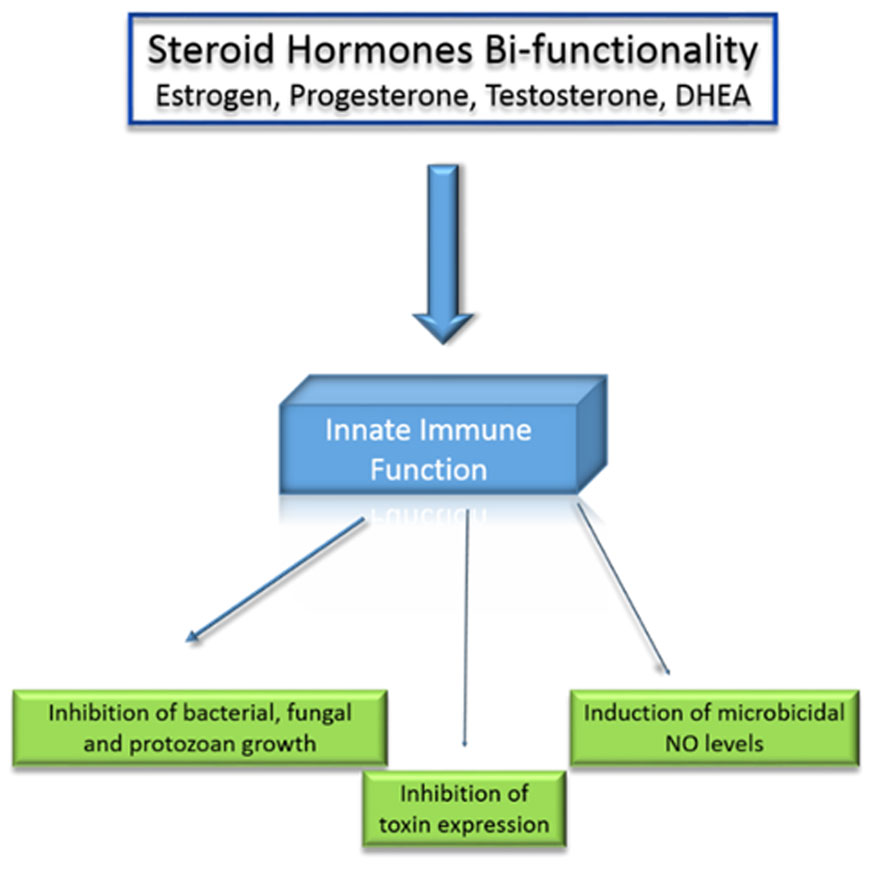Figure 2. Innate immune functions of steroid hormones.As a chemical signal, nitric oxide (NO) is a highly diffusible, global interkingdom signaling molecule [65,66,67,68]. In humans, NO is an essential component of the innate immune system, in addition to its other functions in the regulation of multiple aspects of metabolism [69,70,71,72]. There are three NO synthases (NOS) which are responsible for the production of NO. These include neuronal, or brain constitutive nitric oxide synthase (nNOS), inducible nitric oxide synthase (iNOS) and endothelium constitutive nitric oxide synthase (eNOS) [73,74]. Production of NO is regulated, in part, by the steroid hormones estrogen, progesterone, testosterone and DHEA [75,76,77,78]. A commonality these hormones share is that all have been shown to induce iNOS. For example, DHEA treatment of rats increases iNOS levels, while 17β-estradiol and estrogen increase iNOS expression and NO release in RAW 264.7 cells, a monocyte-like cell line [40,79,80,81]. In addition, both estrogen via receptor α and progesterone induce activation of eNOS via the non-genomic pathway [82,83,84]. The steroid induction of multiple NOS isoforms likely results in microenvironments with variable NO concentrations present. Interestingly, like that of steroid concentration-specific effects on microbial phenotype expression, NO levels also have polygenic effects on microbial phenotypes, most significantly those associated with biofilm formation [85].
Microbial biofilms play an essential role in the majority of infectious processes, particularly chronic infections, and are known to change structure and/or composition to enhance microbe survival (Figure 3) [9,10,12,86,87]. Depending on NO concentration present, four biofilm-associated phenotypes are induced that could be detrimental for microbial survival i.e., increased adherence in the absence of biofilm, defective biofilm formation, shift to planktonic cells (biofilm dissolution), and direct NO-mediated cell lysis. These NO-mediated phenotypic changes are, in part, mediated through NosP, a NO binding protein shown to regulate biofilm formation and dissolution for prokaryotic and eukaryotic microbes, including E. coli, Pseudomonas aeruginosa, Group B Streptococcus, MRSA and Candida albicans [88,89,90]. Mechanistically, nanomolar levels of NO stimulate phosphodiesterase activity, lowering microbial intracellular levels of cyclic GMP (cGMP). During the initial step in biofilm formation i.e., adherence, low cGMP levels increase attachment to surfaces [91]. The binding of microbes to a solid surface prior to the formation of the protective biofilm would increase microbe vulnerability to phagocytosis [92]. As the process of biofilm formation continues, NO stimulated low cGMP levels cause incomplete biofilm maturation, with loss of biofilm integrity [85,93]. Inevitably, metabolic changes due to the numerous downstream effects of cGMP, result in microbe dispersal from their biofilm, as has been demonstrated for P. aeruginosa, Serratia marcescens, Vibrio cholerae, Escherichia coli, Fusobacterium nucleatum, Bacillus licheniformis, Staphylococcus epidermidis and C. albicans [90,94,95]. Both the NO-mediated formation of defective biofilm, and return of cells to a planktonic state would expose organisms to the actions of soluble immune components e.g., lysozyme, complement and immunoglobulin. The role steroids can play in this process is exemplified by progesterone [96]. Via the nongenomic NO-inducible pathway, progesterone induces release of picomolar to nanomolar levels of NO, which subsequently causes the dispersal of N. gonorrhoeae and P. aeruginosa from their respective biofilms [84,94,97,98,99]. Thus, low physiologic concentrations of NO cause biofilm dispersal; however, NO's effects are dichotomous when concentrations increase from the micromolar to the millimolar range.
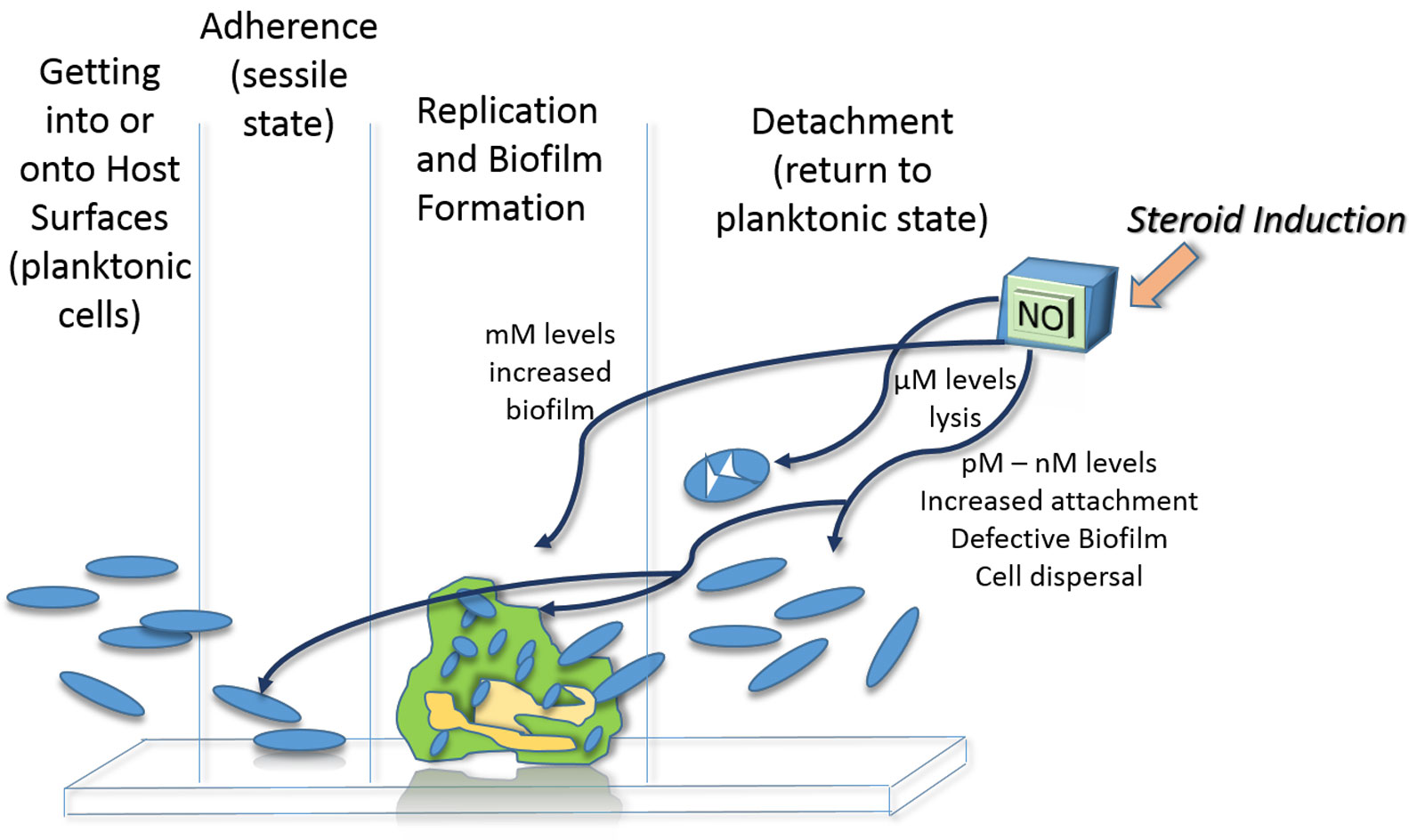Figure 3. Interaction of steroid hormones with nitric oxide in the formation of biofilms.At concentrations of 200 ppm or greater, NO can form a variety of cytotoxic reactive nitrogen species (RNS) such as peroxynitrite, via a diffusion-limited reaction with superoxide [100]. NO at these concentrations are microbicidal for clinical isolates of E. coli, P. aeruginosa, S. agalactiae, methicillin resistant S. aureus (MRSA) and C. albicans [95]. Clinically, trials using wound dressings adapted to release micromolar amounts of NO have shown promise in keeping patients free from infection [85,101]. The role of NO in immune protection is further indicated in naturally acquired malaria where disease severity exhibits an inverse association with NO levels [102]. Paradoxically, although picomolar and nanomolar NO levels cause biofilm dispersal and micromolar levels can be cytotoxic, millimolar NO concentrations appear to stimulate an increase in biofilm growth [72]. An increase in biofilm formation levels was measured for P. aeruginosa exposed to sodium nitroprusside at 2.5 mM to 75 mM, while Nitrosomonas europaea and Burkholderia cenocepacia were induced to form biofilms [94,98,103]. The increase in biofilm formation could result from a metabolic shift from aerobic respiration to anaerobic respiration in the mM range which appear to promote microbial survival phenotypes [104]. Thus overall, steroid hormone induction of NO release is host protective below mM NO levels [105].
Steroids function as concentration-specific double-edged swords in host-pathogen interactions. Host-derived steroidal hormones may promote the rate of microbial replication and enhance their adherence to surfaces, a prerequisite for biofilm formation and colonization. Moreover, bacteria can utilize these compounds e.g., DHEA, as a quorum-like signal triggering biofilm formation. Conversely, steroid hormones can function as components of the host innate immune system. Depending on the concentration present, steroid hormones can directly slow, or completely inhibit microbial growth. This is the case even for steroid derivatives from environmental extremophiles e.g., Pseudoalteromonas [106,107]. Interestingly, their inhibitory activity appears to be more microbe species dependent than hormone effects resulting in stimulation of microbial growth. Furthermore, their activity as an integral part of the innate immune system is not limited to direct steroid-microbial actions. Their function in immune protection can also occur via induction of secondary signaling chemicals e.g., NO, a global interkingdom signaling molecule. This induction can occur via both genomic and non-genomic pathways. NO levels that are host protective lie in a relatively narrow concentration range, with excess NO levels pathogen promoting. Taken together, these findings support the contention that steroid hormone functions are interwoven into the fabric of the innate immune system, and that care must be exercised to maintain the concentration-specific homeostatic balance required for protective immunity.
The authors thank the Midwestern University Office of Research and Sponsored Programs for its generous support. The authors also wish to thank Amber Kaminski for her editorial assistance.
All authors declare no conflicts of interest in this paper.
| [1] |
Wilkins C (2006) A qualitative study exploring the support needs of first-time mothers on their journey towards intuitive parenting. Midwifery 22: 169–180. doi: 10.1016/j.midw.2005.07.001
|
| [2] |
Emmanuel EN, Creedy DK, St JW (2011) Maternal role development: The impact of maternal distress and social support following childbirth. Midwifery 27: 265–272. doi: 10.1016/j.midw.2009.07.003
|
| [3] |
Leahy-Warren P, Mccarthy G (2011) Maternal parental self-efficacy in the postpartum period. Midwifery 27: 802–810. doi: 10.1016/j.midw.2010.07.008
|
| [4] | Hynes L (1999) The puererium, In: Bennett RV, Brown LK, Myles textbook for midwives, 13th Ed., Edinburgh: Churchill Livingston Ltd, 589–628. |
| [5] | Abbott H, Bick D, Mcarthur C (1997) Health after birth, In: Henderson C, Jones K, Essential midwifery, London: Mosby, 285–318. |
| [6] |
Tavoulari EF, Benetou V, Vlastarakos PV, et al. (2016) Factors affecting breastfeeding duration in Greece: What is important? World J Clin Pediatr 5: 349–357. doi: 10.5409/wjcp.v5.i3.349
|
| [7] |
Bouras G, Mexi-Bourna P, Bournas N, et al. (2013) Mothers' expectations and other factors affecting breastfeeding at six months in Greece. J Child Health Care 17: 387–396. doi: 10.1177/1367493512468358
|
| [8] |
Koutra K, et al. (2018) Pregnancy, perinatal and postpartum complications as determinants of postpartum depression: The Rhea mother-child cohort in Crete,Greece. Epidemiol Psychiatr Sci 27: 244–255. doi: 10.1017/S2045796016001062
|
| [9] |
Gonidakis F, Rabavilas AD, Varsou E, et al. (2008) A 6-month study of postpartum depression and related factors in Athens Greece. Compr Psychiatry 49: 275–282. doi: 10.1016/j.comppsych.2007.05.018
|
| [10] | United Nations (2015) Every Woman Every Child. Saving lives, protecting futures: Progress report on the Global Strategy for Women's and Children's Health. United Nations, New York. |
| [11] |
Bick DE, Rose V, Weavers A, et al. (2011) Improving inpatient postnatal services: Midwives views and perspectives of engagement in a quality improvement initiative. BMC Health Serv Res 11: 293. doi: 10.1186/1472-6963-11-293
|
| [12] |
Bick D, Murrells T, Weavers A, et al. (2012) Revising acute care systems and processes to improve breastfeeding and maternal postnatal health: A pre and post intervention study in one English maternity unit. BMC Pregnancy Childbirth 12: 41. doi: 10.1186/1471-2393-12-41
|
| [13] |
Schmied V, Cooke M, Gutwein R, et al. (2009) An evaluation of strategies to improve the quality and content of hospital-based postnatal care in a metropolitan Australian hospital. J Clin Nurs 18: 1850–1861. doi: 10.1111/j.1365-2702.2008.02746.x
|
| [14] |
Beake S, Rose V, Bick D, et al. (2010) A qualitative study of the experiences and expectations of women receiving in-patient postnatal care in one English maternity unit. BMC Pregnancy Childbirth 10: 70. doi: 10.1186/1471-2393-10-70
|
| [15] |
Brown SJ, Davey MA, Bruinsma FJ (2005) Women's views and experiences of postnatal hospital care in the Victorian Survey of Recent Mothers 2000. Midwifery 21: 109–126. doi: 10.1016/j.midw.2004.09.006
|
| [16] |
Rudman A, Waldenström U (2007) Critical views on postpartum care expressed by new mothers. BMC Health Serv Res 7: 178. doi: 10.1186/1472-6963-7-178
|
| [17] |
Razurel C, Kaiser B, Dupuis M, et al. (2013) Validation of the postnatal perceived stress inventory in a French speaking population of primiparous women. J Obstet Gynecol Neonat Nurs Jognn 42: 685–696. doi: 10.1111/1552-6909.12251
|
| [18] |
Smith MP (1989) Postnatal concerns of mothers: An update. Midwifery 5: 182–188. doi: 10.1016/S0266-6138(89)80005-1
|
| [19] | Kirca N, Ozcan S (2018) Problems experienced by puerperants in the postpartum period and views of the puerperants about solution recommedations for these problems: A qualitative research. Int J Car Sci 11: 360–370. |
| [20] |
Sapountzi-Krepia D, Tsaloglidou A, Psychogiou M, et al. (2011) Mothers' experiences of pregnancy, labour and childbirth: A qualitative study in Northern Greece. Int J Nurs Pract 17: 583–590. doi: 10.1111/j.1440-172X.2011.01975.x
|
| [21] | Chaniotakis IE, Lymperopoulos C (2009) Service quality effect on satisfaction and word of mouth in the health care industry. J Serv Theory Pract 19: 229–242. |
| [22] | Tsetsila E, Lavdaniti M, Psychogiou M, et al. (2010) New mothers' perceptions regarding maternity care services provided in a prefecture of Northern Greece. Int J Car Sci 3: 129–135. |
| [23] |
Al-Abri R, Al-Balushi A (2014) Patient satisfaction survey as a tool towards quality improvement. Oman Med J 29: 3–7. doi: 10.5001/omj.2014.02
|
| [24] |
Faley H, Enguidanos ER, Coletti CM, et al. (2014) Patient satisfaction surveys and quality of care: An information paper. Ann Emerg Med 64: 351–357. doi: 10.1016/j.annemergmed.2014.02.021
|
| [25] | Smith LF (2011) Postnatal care: Development of a psychometric multidimensional satisfaction questionnaire (the WOMBPNSQ) to assess women's views. Br J Gen Pract 61: e628–e637. |
| [26] | Panagopoulou V, Hancock J, Tziaferi S (2016) Women's Satisfaction of Postnatal Care- A Pilot Study in a District Hospital in Greece. 9th Panhellenic, 8th Pan-European Scientific & Professional Nursing Congress, Kalamata,Greece(in Greek). |
| [27] | Forster DA, Mclachlan HL, Davey MA, et al. (2016) Continuity of care by a primary midwife (caseload midwifery) increases women's satisfaction with antenatal, intrapartum and postpartum care: Results from the COSMOS randomised controlled trial. BMC Pregnancy Childbirth 16: 28. |
| [28] |
Barimani M, Vikström A (2015) Successful early postpartum support linked to management, informational, and relational continuity. Midwifery 31: 811–817. doi: 10.1016/j.midw.2015.04.009
|
| [29] |
Martin A, Horowitz C, Balbierz A, et al. (2014) Views of women and clinicians on postpartum preparation and recovery. Matern Child Health J 18: 707–713. doi: 10.1007/s10995-013-1297-7
|
| [30] | Bailey S (2010) Postnatal care: Exploring the views of first-time mothers. Comm Pract 83: 26–29. |
| [31] |
Rudman A, Waldenström U (2007) Critical views on postpartum care expressed by new mothers. BMC Health Serv Res 7: 178. doi: 10.1186/1472-6963-7-178
|
| [32] |
Cronin C (2003) First-time mothers-identifying their needs, perceptions and experiences. J Clinl Nurs 12: 260–267. doi: 10.1046/j.1365-2702.2003.00684.x
|
| [33] |
Hajimiri K, Shakibazadeh E, Mehrizi AAH, et al. (2018) The impact of general health and social support on health promoting lifestyle in the first year postpartum: The structural equation modelling. Electron Physician 10: 6231–6239. doi: 10.19082/6231
|
| [34] |
Cornell A, Mccoy C, Stampfel C, et al. (2016) Creating New Strategies to Enhance Postpartum Health and Wellness. Matern Child Health J 20: 39–42. doi: 10.1007/s10995-016-2182-y
|
| [35] |
Fahey JO, Shenassa E (2013) Understanding and meeting the needs of women in the postpartum period: The perinatal maternal health promotion model. J Midwifery Womens Health 58: 613–621. doi: 10.1111/jmwh.12139
|
| [36] |
Mckee M, Stukler D (2016) Health effects of the financial crisis: Lessons fromGreece. Lancet Public Health 1: e40–e41. doi: 10.1016/S2468-2667(16)30016-0
|
| [37] | Filipidis F, Gerovasili V, Millett C, et al. (2017) Medium-term impact of the economic crisis on mortality, health-related behaviours and access to healthcare in Greece. Sci Rep 7: 464223. |
| [38] |
Nunes S, Rego G, Nunes R (2015) The impact of economic recession on health-care and the contribution by nurses to promote individuals' dignity. Nurs Inquiry 22: 285–295. doi: 10.1111/nin.12100
|
| [39] | Kerasidou A, Kingori P, Legido-Quigley H (2016) "You have to keep fighting": Maintaining healthcare services and professionalism on the frontline of austerity inGreece. Int J Equity Health 15: 118. |
| [40] | ICMJE (2017) International Committee of Medical Journal Editors Form for Disclosure of Potential Conflicts of Interest. Available from: http://www.icmje.org/conflicts-of-interest/. |
| 1. | Jeanne Kagle, Small talk: chemical conversations with bacteria, 2020, 6, 2199-3793, 10.1007/s40828-020-0102-7 | |
| 2. | Niyati Hede, Lidita Khandeparker, Extracellular polymeric substances mediate the coaggregation of aquatic biofilm-forming bacteria, 2020, 847, 0018-8158, 4249, 10.1007/s10750-020-04411-x | |
| 3. | Fatemehalsadat Tabatabaeifar, Elham Isaei, Davood Kalantar-Neyestanaki, José Rubén Morones-Ramírez, Antimicrobial and Antibiofilm Effects of Combinatorial Treatment Formulations of Anti-Inflammatory Drugs—Common Antibiotics against Pathogenic Bacteria, 2022, 15, 1999-4923, 4, 10.3390/pharmaceutics15010004 | |
| 4. | Madhusudhanarao Katiki, Neetu Neetu, Shivendra Pratap, Pravindra Kumar, Biochemical and structural basis for Moraxella catarrhalis enoyl-acyl carrier protein reductase (FabI) inhibition by triclosan and estradiol, 2022, 198, 03009084, 8, 10.1016/j.biochi.2022.02.008 | |
| 5. | Yingying Chen, Hui Gong, Donge Tang, Lan Yu, Shoubin Long, Bao Zheng, Dixian Luo, Anji Cai, Liver proteomic analysis reveals the key proteins involved in host immune response to sepsis, 2023, 11, 2167-8359, e15294, 10.7717/peerj.15294 | |
| 6. | Ali Abdul Hussein S. AL-Janabi, Ruaa Kadhim Mohammed Jawad, Abdul Razzak Kalaf Hassan, Impact of the type of breast cancer on the biodiversity of the vaginal Candida represented by estrogen receptor and its levels, 2023, 2692-3106, 878, 10.37349/emed.2023.00183 |
Vasiliki Panagopoulou, Athina Kalokairinou, Foteini Tzavella, Styliani Tziaferi. A survey of Greek women’s satisfaction of postnatal care[J]. AIMS Public Health, 2018, 5(2): 158-172. doi: 10.3934/publichealth.2018.2.158
DownLoad: 