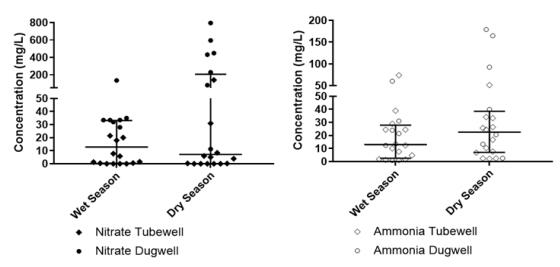
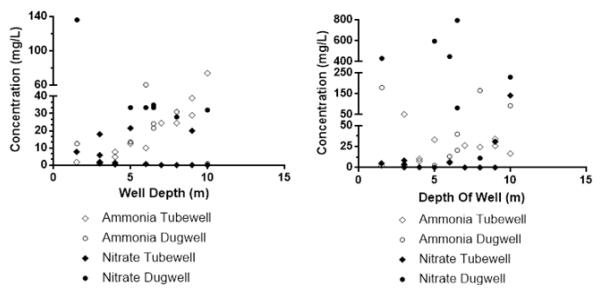
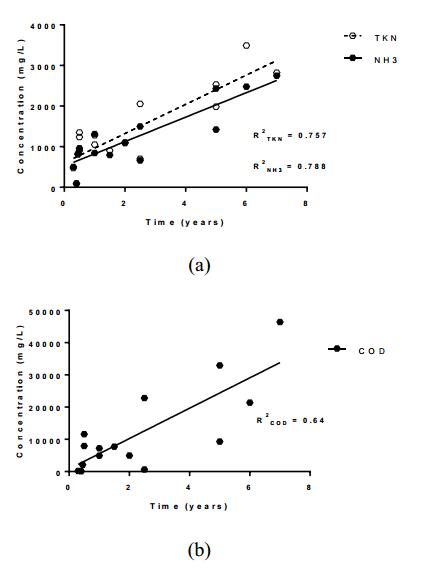
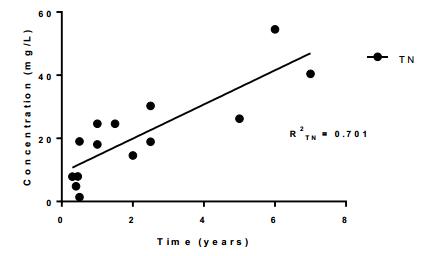
Leaching of nitrogen-containing compounds (e.g., ammonia, nitrate) from pit latrines and seepage tanks into groundwater may pose health risks, given that groundwater is a significant source for drinking water in many low-income countries. In this study, three communities within Kathmandu, Nepal (Manohara, Kupondole, and Lokanthali) were visited to investigate the impact of pit latrines on groundwater quality, with a focus on understanding the fate of nitrogen-containing compounds specifically. Well water samples were analyzed over two seasons (wet and dry) for their nitrogen content, dissolved oxygen (DO), chemical oxidation demand (COD), and oxidation-reduction potential (ORP), and samples collected from within the nearby pits were also analyzed to determine nitrogen content and COD. Hand dug wells were found to be more likely receptors of contamination than tube wells, as expected, with inter-well variations related to the relative redox conditions in the wells. Increased pit-emptying frequency was related to lower levels of nitrogen in the latrines and in the nearest wells, suggesting this may be an effective strategy for reducing the risks of groundwater contamination in such settings, all else being equal.
1.
Introduction
The Pythogorean theorem states as follows: For any right-angled triangle, the square of the hypotenuse c equals the sum of squares of/on the two (shorter) legs lengths a and b, which is written as a2+b2=c2 and is among the Diophantine equations [1]. Several different proofs have been given for the Pythagorean theorem, see e.g., [2,3,4]. It was also shown that the converse of the theorem to be true. Indeed, Euclid (C. 300 B.C.) proved that a triangle with sides a, b and c that satisfies the equation a2+b2=c2 is necessarily a right-angled triangle [5]. The generalisation of Pythagorean theorem by Dijkstra and the shorter proof by Bhaskara are among the hundreds of proofs reported in the literature so far [6].
In the case where a, b and c are all natural numbers different from zero, the triple (a,b,c) is called a Pythagorean triple. Therefore, finding Pythagorean triples is equivalent to finding right triangles with integral sides. The problem for rational numbers is clearly the same up to a scale factor. The notion of Pythagorean triple, and its relation to the Pythagorean theorem, is a cornerstone of several areas of pure mathematics, including number theory, elementary and algebraic geometry, as well as applied mathematics. In particular, a new stream of literature flourished in the past decade on the topic of generation of Pythagorean triples in view of its relevance in areas such as cryptography and random number generation algorithms. Given the large number of contributions in these areas, it would be impossible to quote even only a fraction of the relevant references, and we consequently direct the interested reader to the monographs [4] and [7], which provide surveys of the extensive literature in these areas, and to the papers [8,9,10] along with the references cited therein.
The formula by Euclid forms the basis for generating Pythagorean triples from an arbitrary pair of non-zero natural numbers u,v. According to Euclid's formula, all primitive Pythagorean triples (a,b,c) in which b is even are obtained from the following equations
where u>v, and u and v being all pairs of relatively prime (co-prime) numbers. The important property to note is that one of the numbers u,v is even and the other is odd. In addition, each primitive Pythagorean triple (a,b,c) where b is even is obtained in this way only once.
Thomas Harriot, an English mathematician and scientist, was one of the pioneers to suggest that Pythagorean triples exist in series [11]. Many of the classical formulae/parameterisations available in the literature are known to generate all primitive triples but they do not generate all possible triples, in particular the non-primitive triples [12,13]. More recent works have explored methods to generate both primitive and non-primitive triples [14,15,16]. Some properties of a Pythagorean triangle such as the difference between the length of the hypotenuse and one side of the triangle being distinctly dependent on the length of the other side have been used to generate them. In [17], a relation is presented between the rational points on a circle and the Pythagorean triples. In [18], a parameterisation is derived for all perfect parallelograms, and as a special case establishes how the perfect rectangles correspond to Pythagorean triples. In [19], a representation is provided of Fibonacci numbers. In comparison to these, in [20], a different enumeration is used, which is based on two simple geometric parameters, called the height and the excess, to discuss some known results about the set of primitive Pythagorean triples. On the other hand, in [21], the perfect cuboid problem is related to a parametric solution using Pythagorean triples. However, no general form in terms of a series to characterise Pythagorean triples was given. This gap in literature forms the prime motivation of this paper.
We propose a new method to express Pythagorean triples in terms of odd and even series, which comprise the triangles in which the difference between the hypotenuse and a side is odd and/or even. With Euclid's formula, the significance of odd and even sides has been described in [8, Lemma 1]. In this paper, a complete formula for the parameterisation of the Pythagorean triples without repetitions in terms of odd and even series is proposed and discussed. Further, the generation of all Pythagorean triples (primitive as well as non-primitive) with this parameterisation is established in this paper. While it may be considered that there are many established methods for the generation of all Pythagorean triples, the more interesting and challenging problem is in developing a parameterization that can generate all the triples (not only the primitive ones) without repetitions. This constitutes the key contribution of the paper.
2.
Theory and methods
Several properties of Pythagorean triples have been studied over many centuries. Nevertheless, not all fundamental mathematical aspects have been fully explored. Modular ring theory and number theory have been used in the literature to extend several existing methods to generate families of Pythagorean triples [22,23]. We begin with the fundamental definition of a generic Pythagorean triple, which is denoted as the triple
where a,b,c∈N∖{0}, with c>max{a,b}, i.e., a and b denote the sides of a right triangle, and c denotes the length of the hypothenuse. The set of all Pythagorean triples is denoted by P. A Pythagorean triple (a,b,c) is said to be primitive if a, b and c are relatively prime (co-prime). We denote by P0 the set of all primitive Pythagorean triples. Next, we use the Euclid's formula for parameterising a family of Pythagorean triples given an arbitrary pair of natural numbers u,v∈N∖{0} with u>v.
Lemma 1. [Euclid's Formula]
For any u,v∈N∖{0} with u>v,
is a Pythagorean triple.
We refer to the Pythagorean triples generated by (2.2) as Euclidean triples. Let us denote the set of such triples by E. It is known that Euclid's formula generates all primitive Pythagorean triples, and we establish a relationship between Euclidean triples and Pythagorean triples with the following important proposition, see [4].
Proposition 1. There holds P⊃E⊃P0. Further, a Euclidean triple generated with (2.2) is primitive if and only if u and v are relatively prime (co-prime) and u−v is odd.
The inclusion of E⊃P0 in Proposition 1 shows that Euclid's formula generates all primitive Pythagorean triples. We observe that such inclusion is strict as it can be seen that (2.2) generates also a subset of P∖P0. Let us consider the following case when the triple, (a,b,c) is not primitive:
"If both u and v are odd, then a=u2−v2, b=2uv and c=u2+v2 are even".
To illustrate, consider u=6 and v=3, which are not co-prime, and u−v is odd. In this case the corresponding Euclidean triple is (27,36,45), which is not primitive. In addition, since the inclusion P⊃E in Proposition 1 is also strict, E is a proper subset of the set P of all Pythagorean triples. Indeed, while it is true that every primitive Pythagorean triple is an element of E, some non-primitive Pythagorean triples are not in E. For example, for the non-primitive Pythagorean triple (9,12,15)∈P∖P0, there exists no set of values of u,v∈N∖{0} with u>v such that (u2−v2,2uv,u2+v2)=(9,12,15).
It is established in [4] that if (a,b,c) is a primitive Pythagorean triple, then exactly one between a, b is odd, and c is odd. In addition, we observe that the converse is not necessarily true. In other words, there are Pythagorean triples that are not primitive for which one value between a and b is odd and c is odd, as can be seen from the Pythagorean triple (27,36,45).
The above observations form a key motivation for this study. In this paper, we explore the subset of the set of Euclidean triples, that we denote by the symbol C, which consists of triples with the property that exactly one value between a and b is odd and c is odd. We can easily establish that exactly one between a and b is odd if and only if exactly one between u and v is odd, so that
Following Proposition 1, we arrive at the chain of inclusions
A straightforward assumption is that the order of the elements of a triple in C is the one induced by the order imposed in E. Thus, a is odd and b is even for any (a,b,c)∈C. Therefore, for every (a,b,c)∈C, the difference c−b is odd and the difference c−a is even.
Overall, we have established that with the standard Euclidean formula, it is not possible to generate all the Pythagorean triples and some interesting odd-even properties have been identified.
3.
Proposed method to generate all Pythagorean triples
We observe that many methods that have been used to generate the Pythagorean triples have adopted different representations of the numbers that were generated. The representation of Fibonacci numbers [19], the geometrical representation of Dicksons method [1] and other forms of parametrisation of Pythagorean triples [22,23,24] are commonly adopted in the literature. However, they do not provide a unique expression for finding all triples. In this section, we propose a new parametrisation of Pythagorean triples which generates all triples, both primitive and non-primitive, in a simple manner. The following is the key to obtain a parameterisation of the set of Pythagorean triples in a convenient form [15]. We establish some preliminary results on the intersection of the sets of Pythagorean and Platonic right angle triangles [15] to the end of determining all primitive and non-primitive Pythagorean triples in the following section.
Lemma 2. For any Pythagorean triple (a,b,c)∈C
● there exists m∈N∖{0} such that c−b=(2m−1)2;
● there exists n∈N∖{0} such that c−a=2n2.
Conversely, given m,n∈N∖{0}, there exists (a,b,c)∈C such that c−b=(2m−1)2 and c−a=2n2.
Proof. Firstly, it is shown that given (a,b,c)∈C, the difference c−b can be written as (2m−1)2 for some m∈N∖{0}. From Lemma 1 and the definition of C, there exist u,v∈N∖{0} with u>v and u−v odd such that a=u2−v2, b=2uv and c=u2+v2. We can write
Thus, c−b can be written as (2m−1)2 for some m∈N∖{0} if and only if u−v is odd, which is true.
Secondly, given (a,b,c)∈C, the difference c−a can be shown to be equal to 2n2 for some n∈N∖{0}. Indeed, using again Lemma 1, it is found that
Then, n=v is a solution. To prove the converse, in view of Lemma 1, it suffices to prove that the equations
can be solved in u,v∈N∖{0} with u>v, and where u−v is odd. It is straightforward to verify that u=n+2m−1 and v=n is a solution.
Loosely, in view of Lemma 2, for every Pythagorean triple (a,b,c)∈C, the difference c−b is constrained to be an odd integer in {1,9,25,49,....}. Similarly, the difference c−a is constrained to be equal to one of the even numbers in {2,8,18,32,....}. This simple consideration enables the introduction of the following definition.
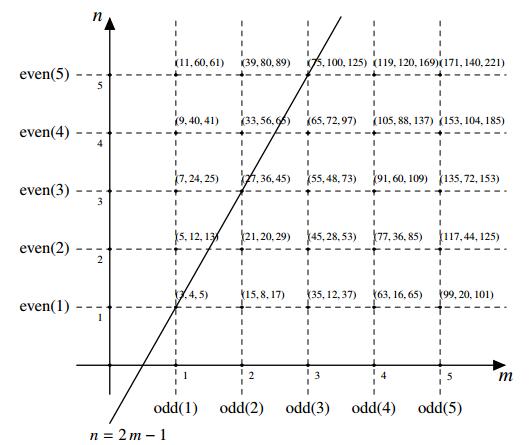
Definition 1. For every m,n∈N∖{0}, the series of odd Pythagorean triples of C is defined as
and the series of even Pythagorean triples of C is defined as
For example, (3,4,5),(5,12,13),(7,24,25)∈odd(1) and (3,4,5),(15,8,17),(35,12,37)∈even(1).
As a consequence of Lemma 2, the following results hold.
Theorem 1. The following facts hold true:
1. There holds
2. For any m1,m2∈N∖{0} with m1≠m2, there holds odd(m1)∩odd(m2)=∅. Likewise, for any n1,n2∈N∖{0} with n1≠n2, there holds even(n1)∩even(n2)=∅.
3. For every (a,b,c)∈C there exists n,m∈N∖{0} such that (a,b,c)∈odd(m)∩even(n). Conversely, for every n,m∈N∖{0} the intersection odd(m)∩even(n)∈C contains a single Pythagorean triple.
4. Let m,n∈N∖{0}. Then, the triple (a,b,c)∈C such that c−b=(2m−1)2 and c−a=2n2 can be written in a unique way as the Diophantine equations in m,n
Proof. The points 1-3 are a simple consequence of Lemma 2. We only need to prove the last point. From the last part of the proof of Lemma 2 it is found that
which immediately lead to (3.1-3.3). It is now shown that (a,b,c)∈C is written in a unique way as a function of n,m∈N∖{0}. To this end, using (3.1) yields
which, once substituted in (3.2), gives the biquadratic equation (2m−1)4+2b(2m−1)−a2=0, which is easily seen to admit only one positive solution
Replacing the latter into (3.4) yields
This shows that given (a,b,c)∈C, the values of the natural numbers m and n such that (3.1-3.3) hold are uniquely determined.
Remark 1. Notice that (3.1-3.3) can be written as
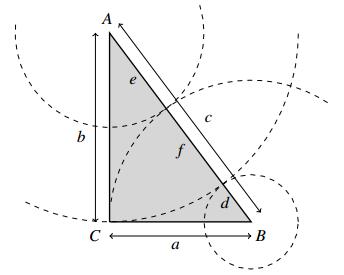
Consider the right triangle in Figure 1.
Let a=¯BC, b=¯AC and c=¯AB. Suppose d=c−b is odd and e=c−a is even. Then, defining f=a−d, the three relations
are obtained. From the non-singularity of [011110111] it follows that e=2n2 and d=(2m−1)2.
Remark 2. The Pythagorean triples obtained in this way are all such that c is odd. However, if m is allowed to also take the values 1/2,3/2,5/2...., then a, b, c are still in N∖{0} and (a,b,c) is still a Pythagorean triple, but a, b and c are all even. This means that C comprises all the triples of E except for those for which a,b,c are even. Stated differently, denoting N1/2 def=N∪{p+12|p∈N}, and defining
there holds ˆC=E. Indeed, defining s=2m, the equations in the proof of Theorem 1 become
so that by setting u=n+s−1 and v=n it is seen that (a,b,c)∈E.
As a result of Lemma 2 and Theorem 1, every Pythagorean triple (a,b,c) in C can be expressed in a unique way as a function p of m and n, i.e., we can write
In view of the considerations above, all triples in C can be represented in terms of m and n into a lattice as shown in Figure 2.
From Figure 2, it is clear that C also contains non-primitive triples. For example, all triples lying on the line n=2m−1 can be expressed as p2(3,4,5) where p∈N is odd. More in general, the following result holds.
Theorem 2. Let (a,b,c)∈C and let m,n∈N∖{0} such that (a,b,c)=p(m,n). Then, (a,b,c) is primitive if and only if n and 2m−1 are co-prime.
Proof. Let μ def=2m−1. Writing (3.1-3.3) as a function of n and μ yields
Firstly, it is shown that if n and μ have a common factor, (a,b,c) is not primitive. Let us write n=q˜n and μ=q˜μ, where q,˜n,˜μ∈N∖{0}. Substituting these expressions into (3.7-3.9) yields
which show that (a,b,c)∈C∖P0.
It is now shown that if (a,b,c) is not primitive in C, then n and μ are not co-prime. If (a,b,c) is not primitive, it can be written as (a,b,c)=k(α,β,γ) where k∈N∖{0} and (α,β,γ)∈P0. Therefore, there exist ˆn,ˆμ∈N∖{0} such that (α,β,γ)=p(ˆn,ˆμ), which, by taking (3.7-3.9) into account, gives
The first and the third equations give k=n2/ˆn2, which, once substituted into the second equation, yields
Notice that ℓ∈N and ℓ2=k. Thus, ℓ is a common factor of n and μ, which are therefore not co-prime.
Remark 3. From the considerations in Remark 2, the set of Pythagorean triples in ˆC=E can be represented as the lattice in Figure 3.
Remark 4. Particularly important special cases of the parameterisation given in Theorem 1 are:
1. the so-called Pythagorean family of odd triples (2n+1,2n2+2n,2n2+2n+1), which can be obtained as p(1,n)=odd(1)={(3,4,5),(5,12,13),(7,24,25)…}, i.e.,
which follows also from (3.6) by setting m=1;
2. the so-called Platonic family of even triples (4m2−1,4m,4m2+1), which can be obtained as p(m,1)=even(1)={(3,4,5),(15,8,17),(35,12,37)…}, i.e.,
which follows from (3.6) with n=1.
The only Pythagorean triple that simultaneously belongs to the set of Pythagorean family of triples and to the Platonic family of triples is obviously the Pythagorean triple (3,4,5). There holds p(1,1)=(3,4,5).
From the above parameterisation, we observe that to generate the Pythagorean triples, the Platonic method proceeds from even numbers and the Pythoagorian method proceeds from odd numbers. In simple terms, it takes a given even number as one of the sides about the right angle triangle, divides it by two and squares the half, then by adding one to the square gets the subtending side, and by subtracting one from the square gets the other side about the right angle and thus it has constructed the same triangle that was obtained by the Pythagorean method.
We combine Pythagorean and Platonic families of triples to obtain the following expression, which generates all the Pythagorean triples:
From this expression, we obtain the following equations:
4.
Concluding remarks
An important body of works has been produced, over the centuries, around the properties of Pythagorean triples. In more recent times, a renewed interest in the generation of Pythagorean triples has been motivated by their various real-life applications, including (but not limited to) cryptography and information security. The set of triples that can be generated using the classical Euclid's formula does not include the non-primitive Pythagorean triples (a,b,c) where a, b and c are all even. While several methods have been explored to find alternatives to characterise and generate Pythagorean triples, the majority of these focuses on primitive triples only. This paper has presented a new approach for generating all Pythagorean triples, both primitives and non-primitives. A new parameterisation of Pythagorean triples has been introduced in the general form of odd and even series.
New properties of co-prime right angle triangles in the Euclidean field have been established by exploring the intersection of the Pythagorean and Platonic families for generating all Pythagorean triples. The parameterisation presented in this paper has already been successfully exploited to obtain faster computations of the golden ratio and silver ratio, see [26,27]. Future work entails exploring further applications to areas such as data encryption and decryption [28,29].
Acknowledgements
This work was supported by the Australian Research Council under the grant DP160104994. The authors wish to thank the affiliated educational institutions for the encouragement and support given to this research work.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: