Titanium implant osseointegration can be enhanced by surface modifications that include hydroxyapatite from Ca3(PO4)2. However, CaO may provide more surface calcium (w/w) to induce cellular responses. Therefore, the purpose of this study was to compare responses to novel CaO and Ca3(PO4)2-enriched titania-polyester (PPC) nanocomposite coatings, which were created by an electrostatic ultrafine dry powder coating technique. EDX confirmed the presence of a base polymer scaffold, biocompatible titanium, and CaO or Ca3(PO4)2. SEM showed that human embryonic palatal mesenchymal cells (ATCC CRL-1486) had attached and spread out onto all surfaces within 24 hours. Cell attachment assays showed that there was a progressive increase in cell numbers with surface CaO incorporation (0–5%), such that the PPC + 5% CaO coatings supported the most cells. Furthermore, the PPC + 5% CaO had significantly more (P = 0.006) cells attached to their surfaces than the PPC + 5% CaP coatings and titanium controls, at 24 hours. The PPC + 5% CaO also had more cells that had proliferated on their surfaces over 72 hours, although these differences were not significant (P > 0.05). Similarly, MTT assays showed that the cells had sustained metabolic activity on all surfaces. Again, metabolic activities were highest on the PPC + 5% CaO, and they were significantly higher (P < 0.05) on all CaO-enriched surfaces (1/3/5% CaO) than on the PPC + 5% CaP. Subsequently, Alizarin Red-S staining detected the initiation of biomineralization within 2 weeks, and abundant mineral deposits after 4 weeks of growth on PPC + 5% CaO and PPC + 3% CaO. These nanocomposite coatings have shown that CaO enrichments may provide a heightened cell response when compared to conventional hydroxyapatite.
1.
Introduction
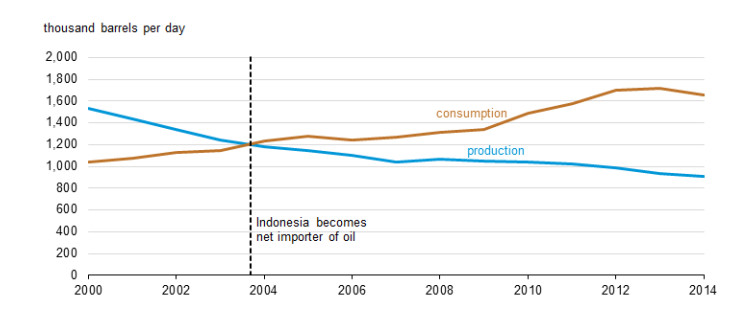
Energy is a basic human requirement without which a national economy cannot develop because no goods and services can be produced or transported between locations. Energy sources are categorized as one of two types; renewable or non-renewable. The latter is derived from fossil fuels and natural minerals, while its renewable counterpart, comprising solar, geothermal, wind and biomass energy, can be continuously replenished. Modern society remains highly dependent on non-renewable energy. Until the end of 2017, the use of renewable energy globally is estimated at 26.5%, and this has increased by 5% due to the use of renewable energy in 2016 only 20.5% from total energy consumption [1]. We can see that the use of renewable energy still very little compared to fossil energy. On the other hand, petroleum production is decreasing, for example in Indonesia (see Figure 1), population growth requires increased consumption patterns, but over the past ten years production increases of 1 million barrels per day in 2006 to 737 thousand barrels per day in 2016 or increased by 26.3% [2]. Since fossil fuels will run out in the future, humankind has been forced to look for alternative energy sources [3]. Therefore, increasing the exploitation of renewable energy represents a major economic objective for every nation.
Because the need for renewable energy development is increasing, countries in the world have a target percentage of renewable energy use of the total energy used. Over these few years, countries around the world have set renewable energy utilization targets. For example, Scotland has declared that 11% of national electricity requirements will be produced from renewable sources such as geothermal energy by the end of 2020. As for other countries, Finland intends to increase renewable energy utilization from 28.5% in 2005 to 38% in 2020 and Italy from 5.2% in 2005 to 17% in 2020 [5]. Meanwhile, Turkey estimates that, by 2023, 30% of its electricity generation will be renewable energy-based [6] and the Republic of Serbia has declared that by 2020 renewable energy must account for 27% of its total national energy consumption [7]. In 2016, 6.3% of the total energy consumption of France was produced from renewable energy sources, a figure set to increase to 23% by 2020 [8].
In particular, Indonesia also targeted a percentage of the use of renewable energy to the total energy used. Government Regulation No.79 (2014) stipulated that national renewable energy consumption should increase to 23% by 2025, with 26% of such renewable energy is produced from biofuels sourced from organic sources [9]. In addition to promoting energy security, the development of renewable energy in Indonesia is in line with the COP21 Agreement of 2016, signed in Paris, which seeks to reduce carbon emissions, replace fossil fuels with renewable energy sources and implement follow-up initiatives which address the issue of global warming [10]. Under the terms of the agreement, Indonesia committed itself to introduce measures designed to reduce emissions. One such government initiative involves implementing policies related to the exploitation of renewable energy produced from biomass.
To achieve the target percentage of renewable energy use, the government has implemented a mandated policy on the use of renewable energy since 2006 in the form of using biodiesel and bioethanol as a mixture of fuel oil. One of government-introduced policy of 2018 authorized the use of a mixture of biofuel and diesel fuel, specifical utilization of 20% biodiesel as a mixture with diesel fuel in all sectors of fossil fuel users (B20). Biodiesel is a diesel engine fuel made from vegetable resources. Commercial products from biodiesel from palm oil and other first-generation sources are called FAME (Fatty Acids Methyl Ester) [11]. Such government intervention was prompted because of the poor price competitiveness of biofuels vis-a-vis that of fossil fuels [12]. This policy is regarded as offering numerous advantages for the economic and social sectors within Indonesia, one of which is that biodiesel produced in-country involves the processing of palm oil, an indigenous raw material. The B20 mandatory policy has a significant impact in biodiesel consumption because from the total energy consumption, 30% of the consumption came from the transportation sector [13]. In 2018, the total consumption of diesel oil in Indonesia for the transportation sector was around 32000 KL [14]. Therefore, this compulsory 20% biodiesel component will increase the demand for palm oil, while simultaneously improving the welfare of its domestic producers.
The importance of biofuel usage besides the depletion of fossil energy, its also by the use of fossil energy in the transportation and industrial sectors which can cause more emissions in the air compared to the use of biofuels. The dominant use of fossil fuels has led to emerging risks of global warming, the greenhouse effect and ozone depletion [15]. Because the use of fossil energy produces harmful exhaust gasses that have caused millions of people to suffer from severe diseases such as cancer, respiratory problems, etc., the reduction of fossil fuels will directly affect human health [16,17]. Clearly, there is a necessity to reduce fossil fuel usage because utilization of biodiesel can cause significant emissions reduction to air quality. Biodiesel is a better choice of alternative fuel due to its similar function properties with diesel fuel, renewable and can be produced directly and environmentally friendly characteristic. Furthermore, biofuels will improve the quality of fuel when mixed with conventional fuels [18].
Overall, existing policies have many advantages in Indonesia. However, during future implementation, developed policies are likely to encounter numerous challenges and opportunities. There is an urgent need in assessing the feasibility of biodiesel policies and the factors that make these policies successful. In addition to the urgent need to meet biodiesel renewal targets, there are several technical issues related to the projected implementation of mandatory biodiesel policy. With the aims of filling such a gap, a comprehensive review on biodiesel development in Indonesia is conducted. Therefore, this study will review the history of biodiesel usage in Indonesia, recent policy initiatives, the development of the palm oil sector, the current status biodiesel usage and, finally, the challenges and opportunities that lie ahead. This review aims to answer whether, why, and how biodiesel should be developed in Indonesia. The review is organized as follows. Section two describes a literature review about biodiesel research and section three describe the methodology. The next two section describes historical and current status. Section six analyzed barriers and opportunities and the final section concludes the whole review.
This research constitutes a descriptive study of the challenges and opportunities surrounding the development of biodiesel in Indonesia which focuses more on what happens, rather than why it happens [19]. In accordance with the implementation of a descriptive study methodology, data was collected through a combination of observation and interviews. The study involved collating data and reports on biodiesel dating from 2006 to the present. Each report was analyzed to extract facts relating to the development of biodiesel in Indonesia since its initiation. In order to enhance the rigour of this study, the sources referred to were enriched by interviews conducted with the chairs of the Indonesian Association of Biofuel Producers (Aprobi) and the Indonesian Bioenergy Expert Association. Each interview, 90 minutes in duration, covered the history and current state of the Indonesian biodiesel sector, together with its present opportunities and challenges.
2.
Literature review
At the global level, 66 countries have implemented the policy of mixing biofuels and fossil fuels: 14 in the Americas, 12 in the Asia Pacific region, 11 in Africa and the Indian Ocean, as well as two non-EU members in Europe [20]. Indonesia is one of the countries that apply this policy with the intention of promoting renewable energy use within the country.
The Indonesian government's policy on the use of renewable energy since 2006 in the form of the use of biodiesel and bioethanol as a mixture of fuel oil has become the topic of research carried out to support the policy. Some study conduct research to see the opportunities to achieve government targets and scenarios to achieve them. Putrasari et al. (2016) [21] pessimistic that the Indonesian government's target of 5% of biodiesel consumption from total national energy consumption in 2025 can be achieved seeing in the period 2006 to 2016 the development of Indonesian biofuels is not well developed. A study by Rahmadi et al. (2013) stated that Indonesian target to have at least 5% biofuel of the total primary energy mix in 2025 could be achieved with maximum blending alternative based on constant energy demand growth of 6% [22]. Mayasari et al. (2019) calculate a projection of biodiesel production in Indonesia to achieve national mandatory and shows that there are three scenarios to increase biodiesel production: palm oil cultivation land, palm oil productivity and refined CPO shared [23]. With a different analysis, the study by Sukarno et al. (2016) [13] and Widyaparaga et al. (2020) [24] recommended that to fulfil national and oil reduction targets, one example policy that we can apply is implementing vehicle retirement policy.
Research has begun to focus on second and third-generation biofuels. However, biodiesel in Indonesia is still derived from the first generation of plants, which is palm oil, of which the country is the largest global producer [25]. Intense criticism levelled at the palm oil sector focuses on the expansion of plantations, land conversion and the negative impact in the areas of biodiversity loss, threats to food security and damage to the ecosystem [26]. In fact, together with Malaysia, Indonesia accounts for 85% of global palm oil production [27]. However, increased palm oil production achieved through an expansion in the area of cultivated land remains the subject of debate. Rulli et al. (2019) [28] stated the negative impact of a large number of lands uses for biodiesel. They quantified the impact of the increasing use of land for palm oil plantations as a means of satisfying the demand for biofuels, foodstuffs and other commodities through such indicators as deforestation, carbon emissions resulting from changes in land use and air pollution caused by fertilizers. This study concluded that increased CO2 emissions and the pollution of clean water are caused by the increasing demand for palm oil. In line with that research, Nugroho and Zhu (2019) [29] argued that using palm oil as a biodiesel feedstock is non-sustainable due to competing with household demand.
To answer the challenges regarding land use for first-generation biodiesel, some researchers began to search for biodiesel raw materials sourced from the second generation or third generation with a case study in Indonesia. Both the use of biomass as a biofuel and exploitation of its potential sources in Indonesia have increasingly become subjects for investigation. Nugroho and Zhu (2019) [29] conducted a case study of supply chains relating to biofuels sourced from rice straw and waste cooking oil in Indonesia. Khalil et al. (2019) investigated the potential for biogas production from animal waste [30] and conclude that prospective sources of raw material for biogas comprise: livestock manure, rumen and blood or other matter derived from slaughtered poultry. Astuti and Mufrodia (2019) conducted research to utilize waste cooking oil into biodiesel [31]. Sasmita (2019) doing a pilot project in a region in Indonesia to develop Kemiri Sunan plant as biodiesel feedstock [32]. Soegiantoro et al. (2019) use waste cooking oil and chicken fat as biodiesel feedstock [33]. However, the studies that have been carried out are still in the research and development stage and have not yet entered the commercialization stage.
Even though it is associated with land-use problems, other studies have emphasized that increased palm oil production in Indonesia has a positive social effect. For example, research by Euler et al. (2017) [34] confirmed that the increasing involvement of small-scale farmers has contributed to economic development in Indonesia, with a concomitant positive effect on household welfare due to enhanced nutrition through the availability of healthy food. Khrisna [35] analyzed the economic and social impacts of palm oil farming by smallholder farm households and found the living standard of households significantly increased. Dib et al. [36] suggest that oil palm contributes to Indonesia economic development where farm households have higher profit from oil palm cultivation, and non-farm households have new lucrative employment opportunities. Alwarritzi et al. (2016) shows that palm expansion by smallholder have a great performance for improving the livelihood of the rural community and help in reducing the problem of job opportunity and poverty in Indonesia [37]. Furthermore, the United Nations also acknowledges that palm oil-based agriculture has reduced poverty in Indonesia [38].
In 2018, in response to the alleged environmental impacts resulting from the allocation of land for palm oil plantations, the Government of Indonesia implemented a moratorium on the issuing of permits. The policy constituted an instruction to evaluate the effectiveness of such licenses in increasing palm oil plantation productivity. It is necessary to improve both the quality of palm oil and the technology employed to meet the growing domestic demand without increasing the amount of land allocated to plantations. Research by Afriyanti et al. (2016) into meeting palm oil demands during the period up to 2050 concluded that, even without intensive logging and the conversion of peatlands to palm oil plantations, Indonesia is capable of meeting the projected demand in the Asian region [39]. Furthermore, Harahap and Khatidawa (2019) investigated opportunities to increase the competitiveness of the palm oil-based biodiesel industry in Indonesia by configuring its biodiesel production system [40] so that biodiesel needs can be met without expansion of forest land.
3.
The historical perspective
The history of government programs, financial incentives and official authorization of biofuel mix for the development of biodiesel in the transportation sector in Indonesia will be summarized in this section.
3.1. The historical background to the government program
In 2006, the President of the Republic of Indonesia issued Presidential Instruction (Inpres) No.1 concerning the supply and applications of biofuels or Bahan Bakar Nabati (BBN) in relation to other fuels [41]. In order to reinforce these instructions, the government issued Presidential Regulation No.5 (2006) which officially promoted the domestic use of biofuel and set a target of 5% for the proportion of ethanol and biodiesel use within national energy consumption by 2025 [42]. The summary of policy documents on biodiesel development in Indonesia is shown in Table 1.
In order to support growth in renewable energy, the government issued Regulation No.30 (2007) concerning the supply and utilization of new and renewable energy, including biofuels [43]. In 2008, the Ministry of Energy and Mineral Resources issued a directive governing the mixture of biofuels during the period 2008–2025 through the Ministry of Energy and Mineral Resources Regulation No.32 (2008) [44]. The regulation stipulated the minimum volume of biofuels utilized in the transportation, industrial and commercial sectors, as well as for electricity generation. Global consumption of renewable energy is increasing. For this reason, under Government Regulation No.79 of 2014, Indonesia targeted a 23% increase in the proportion of renewable energy within national energy production, with 26% provided by biofuels [9]. In order to maintain biofuel price stability, in 2014 the government issued an ESDM (Energy and Mineral Resources) Ministry Decree regarding the determination of the Market Index Price (HIP) for biofuels mixed with oil derived from fossils [45]. Between 2013 and 2015, amendments were made to government Regulation No. 32 of 2008 governing the minimum amount of biofuel which could be mixed with fossil fuels [46,47,48]. The policy regarding biofuel use was introduced in 2006 with B2.5 and discontinued in 2013 with B7.5. In 2014, the policy issuing B10 and continued with B15 during the following year.
To ensure the sustainability of the development of oil palm plantations which are the raw material for biodiesel in Indonesia, the government established a palm oil fund management agency that charges levies on each ton of palm oil exported through Presidential Regulation no. 61/2015 [49]. The provision of incentives forms part of the policy to utilize biodiesel mixed with diesel fuel since its price has proved uncompetitive with that of fossil fuel-derived diesel. A fee of USD 50 per tonne of palm oil is collected by BPDPKS at the point of export in accordance with Ministry of Finance regulation No.114 of 2015 [50]. This fee is collected to reduce the gap between the price of biodiesel and that of diesel fuel. The verification process introduced by this regulation enables BPDPKS to channel funds to producers. Moreover, the application of this fee also finances R & D activities.
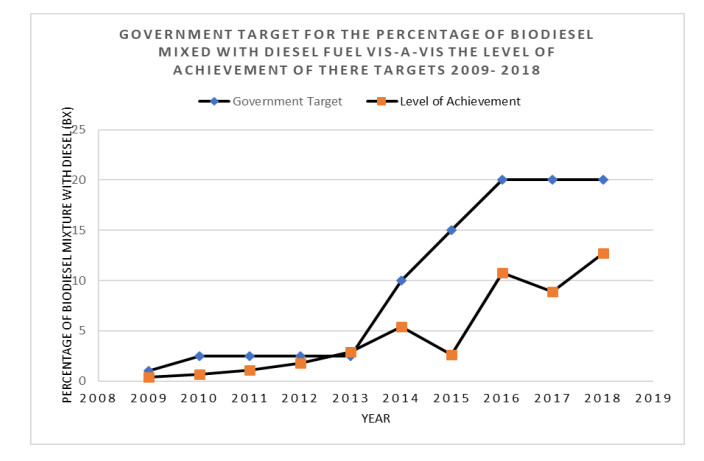
In 2018, the government issued ESDM Ministerial Regulation No.41 governing the supply and utilization of biodiesel biofuel [51]. This edict established the obligation of commercial entities across all economic sectors to use B20 and sanctions for those which do not obey it. The annual targets and performance levels are shown in Figure 2.
In fact, the set target was only achieved in 2013 (Figure 2). Furthermore, later in the same year, the government accelerated implementation of the mixing directive from 2.5% in 2013 to 10% in 2014 through the Ministry of Energy and Mineral Resources Regulation No. 25. This initiative resulted in the failure to meet government targets even though the use of biodiesel in Indonesia had increased significantly year-on-year. The decline in consumption of biodiesel used solely for transportation occurred in 2015. This decline was because the policy was implemented due to weakening world oil prices resulting in biodiesel prices becoming uncompetitive [52].
3.2. Biofuel resources in Indonesia
Based on the source of raw materials used, there are four generations of biofuels. The first generation is biofuel with raw materials derived from food crops. Examples of the first-generation biofuel are sugar drops, coconut and corn and any sugar or starch [53,54]. Because the sources of first-generation raw materials compete with food, first-generation biofuels often debate whether these raw materials are better used as fuel or used as food. For this reason, the second generation to fourth generation fuel is developed as a response to the controversy that occurs in first-generation biofuel [55]. Second-generation fuels are fuels sourced from feedstock or lignocellulose and non-food materials such as forest residues and straw. First-generation fuels have been commercially produced globally, but second-generation fuels are still produced in only five regions until 2016, namely the US, China, Canada, EU and Brazil [56]. The third generation of biofuels are fuels sourced from Algae and are still in the research stage to date [53]. The fourth-generation biofuel is using genetically modified algae biomasses to enhance biofuel production [57]. At this time of writing, there is no commercialization of third and fourth generation biofuels.
There are several types of biofuels available, but biofuels that are already popular globally are biodiesel and bioethanol [21]. At this time, biofuels that have been successfully commercialized in Indonesia are biodiesel with raw materials from palm oil and ethanol, which are made from molasses (see Table 2). For biofuels originating from other biomass, they are still in the development stage. For example, in 2007, Indonesia government have been launch Jatropha Energy Self-Sufficient Village project and allocated USD 1.1 million. But Jatropha failed to sustain in Indonesia [58]. Therefore, until this time of writing other biomass is still in the research and development stage before being commercialized.
3.3. Biodiesel production process
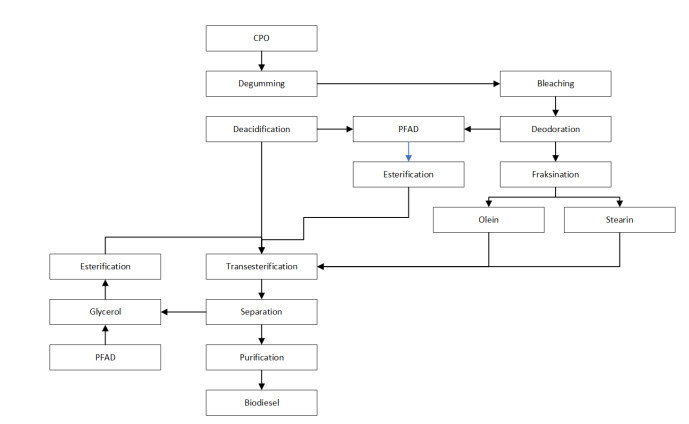
Biodiesel is an automotive diesel engine fuel derived from vegetable resources, with commercial products from generation 1 biodiesel referred to as FAME (Fatty Acids Methyl Ester) [11]. The raw material of oil palm biodiesel comes from the derivatives of Crude Palm Oil (CPO) processed by refinery industry. Technologies commonly used commercially in producing biodiesel are esterification and/or transesterification of oil. Transesterification process is done by adding alcohol (methanol) and catalyst to produce biodiesel (fatty acid methyl ether-FAME) as the main product and glycerol as a by-product [60].
Raw materials that can be used to produce biodiesel from oil palm refinery process are RPO, Palm Fatty Acid Distillate (PFAD), stearin, and olein [61]. Glycerol is a by-product of RPO that can be used to produce biodiesel after being coupled with PFAD through esterification process [61]. PFAD is a by-product of oil palm refinery process [61]. Stearin an Olein is derivative of CPO refinery from palm oil by degumming, bleaching and fractionation process [11]. Flow chart of palm oil to biodiesel production process is depicted in Figure 3.
3.4. Development of the palm oil sector and biodiesel industry in Indonesia
The development of the Indonesian biofuel industry was initiated with the issuance of presidential directives on the domestic use of biofuels and focuses on the production of biodiesel which exploited palm oil as the raw material. Consequently, palm oil constitutes one plantation commodity playing a vital role within the national economy. Moreover, together with oil and gas, it represents a major export commodity and foreign exchange earner for Indonesia [62]. The country ranks as the largest global producer and exporter of palm oil whose potential to support the policy of developing bioenergy (involving the use of biodiesel) remains highly significant.
Indonesian biodiesel production capacity has expanded from approximately 4.9 billion liters in 2012 to in the region of 11.5 billion liters in 2017 with the number of refineries increasing from 22 to 31. While capacity has grown significantly since 2012, the actual expansion in production has been much slower resulting in a current marked estimated decline in capacity utilization of approximately 30 percent [50]. This shows that the capacity of the biodiesel industry in Indonesia is sufficiently expansive to satisfy domestic needs.
4.
Current status
The latest regulations regarding the biodiesel mandate, the mechanism of cash flow and the flow of goods in the biodiesel supply chain and the current mandate implementation will be explained in this section.
4.1. Government program
Under Regulation No.12 of the Ministry of Energy and Mineral Resources issued in 2015 the economic sectors within which biofuels must be applied include micro-businesses, fisheries, agriculture, industrial and commercial transportation, public services/PSO (Public Service Obligation) and non-PSO entities [63]. The programme has been implemented with particular success in the transportation sector (PSO) [50]. Following a directive issued by the President of the Republic of Indonesia, as of September 1st, 2018, the B20 regulation has been extensively implemented across all economic sectors.
From the contents of Table 3, it is evident that biodiesel production in Indonesia increased dramatically from 2009 to 2018. This rise is in line with domestic demand for B20. The policy change requires technological readiness and coordination with biodiesel providers (biodiesel industry) and diesel fuel suppliers (in this case, represented by Pertamina, a state-owned company that manages oil and gas production, distribution and sales in Indonesia). The achieving of B20 has only reached 92% [64] because the prospective distribution points (fuel terminals) remain under configuration. To date, Pertamina operates 112 service points to which B100 was initially dispatched for mixing. However, subsequent distribution of B100 to the eastern regions of Indonesia has been rendered problematic due to the biodiesel industry being predominantly located in the west of the country. Consequently, the delivery points were then reconfigured with the result that B100 was sent to only 29 terminals to be subsequently distributed to all Pertamina-owned terminals [64].
4.2. Biodiesel actor and fund mechanism
Following is the mechanism of the flow of goods, the flow of funds, and the mandate of biodiesel mixing that occurs in Indonesia.
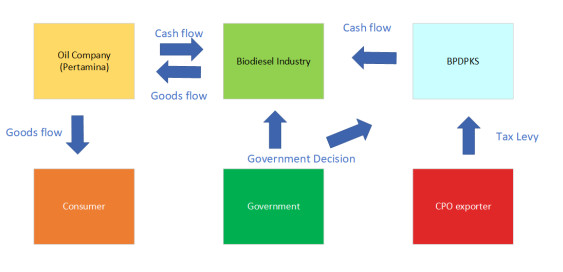
There are five actors involved in the Indonesian biodiesel industry (Figure 4). They are: (1) the government that represented by the ministry of energy and mineral resources, (2) the biodiesel industry, (3) oil companies that mix biodiesel with diesel and distributing oil to consumers (in this paper the oil company is represented by Pertamina, which is a state-owned enterprise that mostly controls the sale of fuel oil in Indonesia), (4) BPDPKS as fund managers and (5) consumers (consisting of Indonesian consumers and CPO exporters). In general, the government will fulfill domestic biodiesel before finally being exported. For the remainder of the exported CPO, a levy of USD 50 per ton was made [50]. The results of this levy will be used to pay the gap between the cost of diesel oil prices and biodiesel oil prices. The difference between the production price and the market price is given in the form of incentives. It the beginning, the government announced an assignment to the biodiesel industry to meet the needs of B20 in the country (flow of regulations). Furthermore, the biodiesel industry will ship B100 to Pertamina and get paid from the amount sent according to the index price of diesel fuel. The difference between the biofuel market index price and the diesel fuel index price will be replaced from the funds in BPDPKS. Furthermore, Pertamina blends and distributes it to consumers.
The mechanism for determining the capacity of biodiesel from industry and the flow of funds is as follows. First, Pertamina determines the amount of diesel capacity to be produced and then publishes biodiesel requirements to the government. The government then issues requirements that must be met by industry to become a biodiesel supplier. Then, the government selects producers who meet the requirements and determines the capacity that must be met by each industry. For example, Decree of the Minister of Energy and Mineral Resources of the Republic of Indonesia No. 3756 k/10/MEM/2017 describe government decision to assign 20 biorefineries for the procurement of biodiesel from November 2017–April 2018 [65]. Finally, the government through the ministry of energy and mineral resources is responsible for verifying the delivery of biodiesel from producers to oil companies. Furthermore, BPDPKS uses the results of verification to provide funding to the biodiesel industry [14].
4.3. Current mandate implementation
As of the end of 2018, the level of biodiesel blends in Indonesia stood at 11.3% (see Table 3), a figure falling well short of the government’s aspiration of 20%. In order to achieve the target of 20% by 2019 with the same level of demand as 2018, which is approximately 26,146 million liters of diesel fuel (see Table 3), around 5,229 million litres of biodiesel are required for domestic consumption.
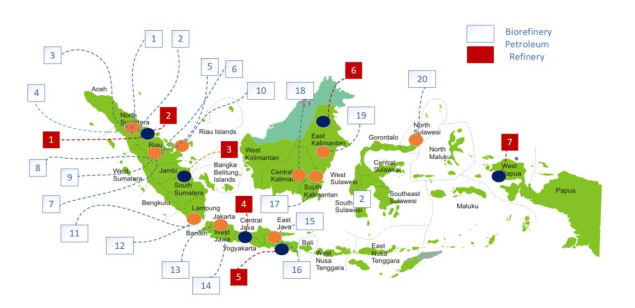
In addition to the quantity of biodiesel that must be supplied, the location of biodiesel plants, diesel plants and mixing terminals must be optimal to enable the shipping process to proceed smoothly and transportation costs to be minimized. It should be noted that transportation is a vital consideration because the costs involved, especially those relating to biodiesel transportation, represent a determining factor in the number, capacity and location of biodiesel plants [66]. At present, biodiesel providers with a total capacity of 11,357 million Liters are distributed across 31 locations [14] to satisfy domestic and export demand and diesel providers are spread across seven different locations (Figure 5), while the fuel terminals are located in 112 sites distributed throughout Indonesia. Indonesia, as an archipelagic country, renders biodiesel supply chain transportation more challenging since it encompasses both land and sea routes.
5.
Discussion on barriers and opportunities
Nationally, the B20 policy has many benefits for Indonesia. In economic terms, the use of biodiesel constituting a mixture of diesel oil fuels has resulted in a decrease in oil imports, thus avoiding a reduction in the country’s foreign currency reserves.
In order to successfully implement this policy, all interrelated actors must cooperate and the B20 supply chain must be capable of meeting demand punctually and at minimal cost. Although the Indonesian government has implemented a policy intended to maximize the optimal use of biodiesel to promote energy security, several challenges and opportunities described in the section below persist.
a. Using biodiesel as a fuel
The implementation of mixing biodiesel with diesel oil through the mandatory Indonesian B20 in 2019 has increased sharply compared to the previous period, although it has not been fully realized. In general, Indonesia's biodiesel managed to save USD 937.84 Million within a period of four months in 2018 [67]. In addition, reducing the use of fossil energy has reduced emissions in this country and have substantial direct health benefits, such as preventing many thousands of air-pollutions—induced deaths annually worldwide from both indoor and outdoor sources [17].
b. Raw materials of palm oil
One widely discussed issue related to the use of palm oil as a biodiesel feedstock is that of the proliferation of palm oil plantations which allegedly contributes to deforestation and compromises national food security. Deforestation can threaten the sustainability of global ecosystems. Indeed, it is estimated that the trees felled in Indonesia, Malaysia, and Papua New Guinea between 2001 and 2016 amounted to approximately 40% of the total number available [68]. Consequently, those areas whose exploitation was governed by the issuing of permits have suffered habitat degradation and other forms of damage [68]. For this reason, recommendations constituting part of a long-term plan are required in order to prevent further deforestation. In the case of Indonesia, such proposals could be in the form of improving palm oil quality, thereby increasing production without expanding the amount of ground dedicated to plantation use further into the forests.
Despite these challenges, biodiesel from palm oil production has resulted in both beneficial economic and social impacts, in particular improved welfare and living standards for local farmers in Indonesia [34,35,36,37]. Moreover, the United Nations also acknowledges that palm oil-based agriculture has reduced poverty within the country [38].
c. The biodiesel-processing industry
The production of biofuels is currently based on food crops (first-generation biofuels). If the governmental edict to mix 20% of diesel fuel is observed, domestic biodiesel consumption is expected to amount to 5,229 million litres by 2019, while a directive to implement a 30% mix is expected to increase such consumption to 7,843 million litres. The capacity of the biofuel industry in Indonesia is sufficient, at 11.6 million litres, to achieve B20 and B30, (see Table 3). This target can be achieved without a further expansion of palm oil plantations into forest areas.
The significant price difference between biodiesel and subsidized diesel represents a significant challenge for the biodiesel industry. The existence of BPDPKS, which provides incentives to the biodiesel industry, has stimulated biodiesel production. However, because the funds obtained by BPDPKS depend on palm oil export levies, it is feared that significant domestic biodiesel consumption will reduce BPDPKS revenue, while also further reducing the incentives relating to biodiesel development. For this reason, there should be a harmonization of the subsidies applied to both diesel and biodiesel.
d. Biodiesel distribution
According to the Managing Director of Pertamina in 2014, the pattern of distribution of fuel oil (BBM) in Indonesia was the most complex in the world. This is due to the geographic nature of the country which is an archipelago whose constituent islands are scattered along the equator [69]. The presence of biodiesel fuel sources that must be mixed with diesel from fossil fuels before being distributed to consumers exacerbates the complexity of this distribution pattern. As of February 2019, the implementation level of B20 had reached only 92%. According to the Director General of New and Renewable Energies Indonesia, the figure had not yet reached the target of 100% due to supply chain problems [64].
Successful implementation of the B20 mandate across all sectors requires collaboration synergy between the actors involved in distribution aspect who also have to maximize the profits of their respective commercial enterprises. Three parties contribute to the success of this policy in distribution aspect: the suppliers of raw materials (individuals, private sector and state-owned enterprises); the biodiesel industry, which currently has 31 companies spread throughout Indonesia, and oil companies that will mix and distribute fuel to consumers. These commercial enterprises include: Pertamina, AKR, Shell and Total, although, the actor discussed in this study was Pertamina alone. Consumers have no stake in this mandate because they still pay the same price as that for diesel fuel due to the price of biodiesel being subsidized by BPDPKS.
At the supply chain level, the economic performance of the biodiesel supply chain can be optimized by strategic choices regarding production capacity, supply chain configuration, transportation mode and conversion location [70]. A critical factor in cost-efficient supply chain design is that high production capacity saves investment and operational costs, but this increases the need to mobilize biomass and B100 raw materials at a considerable distance. The introduction of distributed supply chain configurations which reduce biomass transportation costs are proposed in this paper.
The total number of biodiesel distribution points, Terminal Bahan Bakar Minyak (TBBM), owned by Pertamina as of 2019 is 112 terminals distributed throughout the territory of Indonesia (Figure 3). Biodiesel will be sent from 20 biorefineries (the number of this biorefineries is in accordance with the decision of the assignment from the government in 2018 [65]) and diesel will be delivered from seven oil refineries to be mixed before being distributed to all Pertamina terminals and, subsequently, to the public. However, the biodiesel/diesel mixing site still requires recalculation and reconfiguration. In September 2018, Pertamina determined 10 TBBMs as mixing points [71]. This means that B100 from the biofuel industry will be sent to 10 TBBM to be mixed with diesel fuel and distributed to 102 other TBBMs. As of February 2019, 29 installations have been designated as mixing points [64]. The change in the number of points has been introduced because due to persistent problems in the on-time distribution of fuel oil supply chains at minimum cost. Changes in the mixing point scheme will disrupt the timely availability of raw materials and the costs that must be imposed on the biofuel and BBM industries. If biofuel containing B100 is to be sent to 112 TBBMs, for the conveying vessels to reach TBBMs via sea transportation routes will require a minimum of twice the time. In the opinion of the Chair of Aprobi, this fact represents something of a dilemma for the biofuel industry because the cost of renting ships is extremely high. If it is necessary to send biofuel to only a limited number of locations, Pertamina must provide a tank with a capacity large enough to accommodate B100 and then mix it with diesel fuel before distributing it to other TBBMs. Provision of these tanks involves both investment and operational costs. From this, it can be concluded that there is still a non-fixed distribution pattern between government regulations, the biofuel industries and oil companies.
The complexity surrounding distribution can be solved by making a model that can optimize the distribution of biodiesel, i.e., the number and locations of mixing points, and the quantity that must be distributed from the biodiesel industry to Pertamina. It should be noted that Indonesian palm oil plantations proliferate in western Indonesia, while numerous biodiesel plants are also located in that region. The biodiesel plant will be distributed to Pertamina terminals throughout Indonesia. Determination of the mixing point must pay attention to the demand of consumers around the terminal due to the uneven distribution of the country’s inhabitants, of whom around 70% reside in central and western Indonesia. In general, for the upstream sector supply chain, the location of the biofuel plant and its optimum capacity can be determined by adjusting it to the site of the palm oil plantation which supplies the necessary raw materials. Such optimization must minimize transportation costs while also ensuring that available supplies arrive on time. Furthermore, the necessary size of the biodiesel industry must be estimated. Therefore, when the target amount of biodiesel to be mixed increases from B20 to B30, the industrial capacity must be capable of implementing the policy. Consequently, a mathematical model that can successfully solve this distribution problem is required.
6.
Conclusions
In this descriptive study, the status of palm oil-based biodiesel policies together with their associated challenges and opportunities have been analyzed. This study finds that Indonesia has been promoting biodiesel commercialization using national strategy by make government regulation mandatory blending and providing financial incentives. Indonesia’s policy in supporting the use of renewable energy through the mandatory use of biodiesel as a mixture for diesel fuel has a significant impact in increasing the use of biodiesel although this target has not been reached 100%. Several contributions of this investigation offer the potential of becoming suggestions for policy improvement and future research opportunities that can be developed to support the use of biodiesel in Indonesia.
1. Indonesian government policies supportive of the development of domestic biodiesel has been described. Because of its success, the officially-mandated use of biodiesel increased from its initial targets of 5% for PSO and 7% for non-PSO in 2018 [44] to 20% use of biodiesel across all sectors in 2018 [47]. This study found that the policy of rendering compulsory the use of biodiesel as a mixture of diesel fuel had a significant impact at economic, social and environmental. This policy also has a positive impact on industry because even though biodiesel prices have, to date, proved unable to compete with those of diesel fuel derived from fossils, the government provides economic incentives to compensate producers for such differences in price.
2. The latest policy during 2018 regarding the B20 mandate in all sectors (PSO and non-PSO) has yet to prove completely successful [64] because problems persist with the distribution channels between the biofuel industry and Pertamina. This distribution pattern is complicated since Indonesia constitutes an archipelagic country in which the distribution process involves seaborne modes of transportation. At the time of writing, the government has consistently attempted to reconfigure biofuel industry-Pertamina delivery points. This distribution pattern constitutes a potential future research opportunity which would involve the application of a mathematical model capable of calculating the number of delivery points and transportation schemes required. Doing so would ensure that raw materials arrive punctually, thereby avoiding consumption of pure diesel fuel from fossil fuel. Furthermore, the resulting distribution model must be capable of further development if government policies are to evolve into a B30 mandate.
3. Significant price differences between biodiesel and subsidized diesel pose a challenge for the biodiesel industry. The existence of BPDPKS that provide incentives to the biodiesel industry has stimulated biodiesel production. However, since the funds obtained by BPDPKS depend on palm oil export levies, the high level of domestic biodiesel utilization is feared to reduce BPDPKS revenues and can further reduce the allocation of incentives for biodiesel development. For this reason, there should be a harmonization of subsidies relating to diesel and biodiesel.
4. The capacity of the biodiesel industry in Indonesia is currently sufficient to meet the needs of B20 and B30. In order to meet the needs of B30 and minimize the further incursion of palm oil plantation into forests, attention should be focused on the research that can improve biodiesel production technology and increase the productivity of Indonesian palm oil plantations which is currently far below that of their counterparts in Malaysia [72].
Acknowledgement
This study was partly supported by a research grant from the Ministry of Research, Technology and Higher Education of the Republic of Indonesia.
Conflict of interest
The authors declare that there is no conflict of interest.









 DownLoad:
DownLoad: