Figure 1.
Schematic diagram of the HGW.
Citation: Eduardo Mercado III. Learning-Related Synaptic Reconfiguration in Hippocampal Networks: Memory Storage or Waveguide Tuning?[J]. AIMS Neuroscience, 2015, 2(1): 28-34. doi: 10.3934/Neuroscience.2015.1.28
| [1] | Chuanda Cai, Changgen Peng, Jin Niu, Weijie Tan, Hanlin Tang . Low distortion reversible database watermarking based on hybrid intelligent algorithm. Mathematical Biosciences and Engineering, 2023, 20(12): 21315-21336. doi: 10.3934/mbe.2023943 |
| [2] | Qichao Ying, Jingzhi Lin, Zhenxing Qian, Haisheng Xu, Xinpeng Zhang . Robust digital watermarking for color images in combined DFT and DT-CWT domains. Mathematical Biosciences and Engineering, 2019, 16(5): 4788-4801. doi: 10.3934/mbe.2019241 |
| [3] | Shaozhang Xiao, Xingyuan Zuo, Zhengwei Zhang, Fenfen Li . Large-capacity reversible image watermarking based on improved DE. Mathematical Biosciences and Engineering, 2022, 19(2): 1108-1127. doi: 10.3934/mbe.2022051 |
| [4] | Wenfa Qi, Wei Guo, Tong Zhang, Yuxin Liu, Zongming Guo, Xifeng Fang . Robust authentication for paper-based text documents based on text watermarking technology. Mathematical Biosciences and Engineering, 2019, 16(4): 2233-2249. doi: 10.3934/mbe.2019110 |
| [5] | Shanqing Zhang, Xiaoyun Guo, Xianghua Xu, Li Li, Chin-Chen Chang . A video watermark algorithm based on tensor decomposition. Mathematical Biosciences and Engineering, 2019, 16(5): 3435-3449. doi: 10.3934/mbe.2019172 |
| [6] | Kaimeng Chen, Chin-Chen Chang . High-capacity reversible data hiding in encrypted images based on two-phase histogram shifting. Mathematical Biosciences and Engineering, 2019, 16(5): 3947-3964. doi: 10.3934/mbe.2019195 |
| [7] | Hongyan Xu . Digital media zero watermark copyright protection algorithm based on embedded intelligent edge computing detection. Mathematical Biosciences and Engineering, 2021, 18(5): 6771-6789. doi: 10.3934/mbe.2021336 |
| [8] | Qiuling Wu, Dandan Huang, Jiangchun Wei, Wenhui Chen . Adaptive and blind audio watermarking algorithm based on dither modulation and butterfly optimization algorithm. Mathematical Biosciences and Engineering, 2023, 20(6): 11482-11501. doi: 10.3934/mbe.2023509 |
| [9] | Haoyu Lu, Daofu Gong, Fenlin Liu, Hui Liu, Jinghua Qu . A batch copyright scheme for digital image based on deep neural network. Mathematical Biosciences and Engineering, 2019, 16(5): 6121-6133. doi: 10.3934/mbe.2019306 |
| [10] | Rong Li, Xiangyang Li, Yan Xiong, An Jiang, David Lee . An IPVO-based reversible data hiding scheme using floating predictors. Mathematical Biosciences and Engineering, 2019, 16(5): 5324-5345. doi: 10.3934/mbe.2019266 |
As an important technology to protect database security [1], database watermarking technology was firstly introduced and applied to database copyright protection by IBM Almaden Research Center in 2002 [2]. Since then, a variety of database watermarking techniques emerge, such as a relational database watermark based on a special tag tuple method [3,4], a digital fingerprint watermark based on the idea of multimedia watermark block [5] and a method of watermarking relational database based on optimization techniques [6]. These methods may cause permanent distortion of the data in the original host when watermark is embedded. If the distortion ratio is small, it will not affect the usage of the database, but if the distortion ratio is large, it will become unacceptable in some specific fields (such as financial, medical, legal, military, etc.). Therefore reducing data distortion and recovering data are important aspects the researchers will concern. To solve such problems, the researchers have proposed a reversible database watermarking method [7,8,9,10] which is a technique for hiding the watermark information into the original data and recovering the original data without loss after extracting the watermark.With reversible database watermark method, data can be recovered after being attacked by insertion, deletion and modification. But not every user with legal identity has the right to recover data. The lower the distortion ratio of the database data is used, the better will be. Under such circumstance mentioned above, the reversible database watermarking method with low distortion is proposed to effectively reduce the data distortion. Therefore, it is of practical significance to carry out research on reversible database watermarking methods with low distortion.
The reversible database watermarking methods can be divided into method with data distortion and method with no data distortion. In the followings, we mainly introduce the robust watermarking method with data distortion. In [7], it proposes the reversible database watermarking method based on histogram shifting watermarking. The reference [11,12] use a difference expansion based watermarking (DEW) to restore the original database, and realizes the reversible watermarking mechanism of the relational database. The reference [13] groups the tuples and then uses DEW to embed the watermark. Based on GADEW method, the reference [14] combines genetic algorithm (GA) and DEW, and proposes a robust reversible database watermarking solution which improves the DEW capacity while maintaining a certain distortion. The reference [15] proposes a Prediction-Errors Expansion Watermarking (PEEW) reversible database watermarking method which has a better result in the aspect of anti-agammaession. The reference [16], for numerical databases, proposes a Robust and Reversible Watermarking (RRW) method which can effectively resist various attacks like insertion, deletion and modification, and can better protect the quality of data. In [17], the authors proposes A New Robust Approach for Reversible Database Watermarking with Distortion Control) which is abbreviated as GAHSW (Genetic Algorithm and Histogram Shifting Watermarking) for numerical relation data. The method combines GA with a newly proposed Histogramfting of prediction error Watermarking (HSW) method to minimize distortion and improve r obustness for database watermarking. The characteristic of GAHSW is to realize the optimized group ing with GA and to embed a watermark bit in each group consequently with HSW by which the robu Shi stness of watermarked database can be ensured. Compared with previous methods, this method can not only significantly improve the capacity of the watermark embedded and reduce the data distortion, but also acquire higher robustness. However, since the histogram [18,19,20,21,22,23,24,25] will be wholly shifted when the watermark is embedded, the data distortion is still serious.
To solve above problems, we propose a low distortion reversible database watermarking method using histogram gap, which is abbreviated as HGW (Histogram-Gaps based Watermarking). The traditional histogram shift method is improved as followings: finding a vacant position that can introduce minimum distortion since the histogram contains gaps to determine the shift direction and the shift distance, and then moving necessary parts of the columns in the histogram to reduce the number of columns to be shifted when the watermark is embedded, and therefore the modification of the carrier database data will be lowered, which also meets the need of reducing data distortion.
This paper concludes altogether four parts. Section 2 elaborates the basic ideas and main steps of the proposed method. Section 3 performs experimental verification and analysis of results. Section 4 gives conclusions and proposes future research directions.
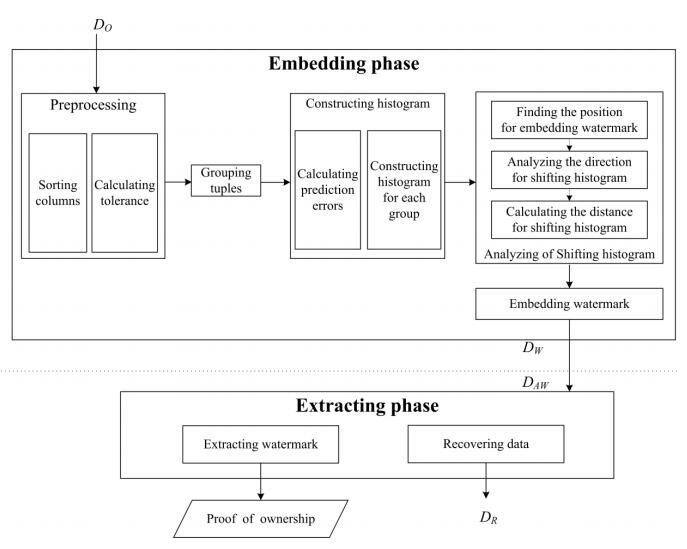
The HGW method consists of two parts which concludes watermark embedding and watermark extraction. As showed in the figure 1, ${D_O}$ is an original database, ${D_W}$ is the database embedded with watermark, ${D_{AW}}$ is the attacked database after insertion, deletion and modification, and ${D_R}$ is the restored database same as the initial database. Specific steps are as follows:
Step1. Data preprocessing.
Step1.1. selecting multiple integer columns from the database that can identify the features of things and then sorting the selected columns in ascending order
Step1.2. defining the semantic distortion range of the $j{\text{th}}$ column as $[min[j], max[j]]$ according to the value of the column and calculating the tolerance of the prediction error of the $j{\text{th}}$ column. The equation of calculating the tolerance is
| $\hat y = \left\lfloor {(max[j] + min[j])/2} \right\rfloor $ | (2.1) |
In the Eq. (2.1), $max[j]$ and $min[j]$ individually represent the maximum and minimum values of the $j{\text{th}}$ column. $\hat y$ is the value determined by the maximum and minimum of the column.
Step 2. Grouping tuples. $K{\text{s}}$, a secret grouping key, is set by a random method and the tuples in the database are divided into a set of non-overlapping groups, and the value of ${N_{\text{g}}}$ is determined by the number of the bits of the watermark to be embedded. Eq. (2.2) should be used to determine the group in which each tuple is located.
| ${n_u} = H(K{\text{s|}}H(K{\text{s|}}{t_u}.PK))\bmod {N_g}$ | (2.2) |
In the Eq. (2.2), ${n_u}$ represents the group number, '|' represents the concatenation operation, $H()$ is a hash function, $K{\text{s}}$ is the secret grouping key and ${t_u}.PK$ is the primary key of the tuple as parameters.
Step 3. Constructing histogram.
Step 3.1. Calculating ${p_e}$ and ${p_h}$ with Eq. (2.3) and Eq. (2.4) respectively
| ${p_e} = y - \hat y$ | (2.3) |
| ${p_h} = |{p_e}|$ | (2.4) |
In the Eq. (2.3) and Eq. (2.4), $y$ represents the value located in $j{\text{th}}$ column and in certain tuple, ${p_e}$ represents the prediction error value corresponding to y. ${p_h}$ is the absolute value of the prediction error of the original database.
Step 3.2. Constructing a histogram for each group with ${p_h}$ and marking the ${p_h}$ occurring most frequently as ${p_i}$ in $i{\text{th}}$ group (i.e., the peak bin in the histogram) and storing ${p_i}$ to array pa.
Step 4. Shifting and embedding.
That related research found that the discrete database has histogram with gaps. Take the right shift as an example. For the histogram column, you don't need to move all on the right side of ${p_i}$ Just clear the side of ${p_i}$ a vacant position and then embed the watermark at ${p_i}$.
Step4.1. In the $i{\text{th}}$ group, the method will start from ${p_i}$ and search the left side and the right side, find the first ${p_h}$ whose frequency is zero, record the corresponding position as ${p_{iL}}$ and ${p_{iR}}$, record the sum of heights of rectangles from ${p_{iL}}$ to ${p_i}$ as $h{s_{iL}}$, record the sum of heights of rectangles from ${p_i}$ to ${p_{iR}}$ as $h{s_{iR}}$, and then respectively calculate the distance from the position of ${p_i}$ to ${p_{iL}}$ and to ${p_{iR}}$. The equations are as follows:
| $d_{i L}=\left|p_{i}-p_{i L}\right|, \quad d_{i R}=\left|p_{i}-p_{i R}\right|$ | (2.5) |
In the Eq. (2.5), ${d_{iL}}$ is the value calculated by the distance from the position of ${p_i}$ to ${p_{iL}}$. ${d_{iR}}$ is the value calculated by the distance from the position of ${p_i}$ to ${p_{iR}}$.
Step4.2. Shifting histogram and embedding watermark. According to the results of comparing $h{s_{iL}}$ with $h{s_{iR}}$, the Eq. (2.6) and Eq. (2.7) can be concluded.
if $h{s_{iL}} \geqslant h{s_{iR}}, $
|
${p'_h} = \left\{ ph+1, p<ph<pi+diRph+w, ph=piph, otherwise \right.$
|
(2.6) |
if $h{s_{iL}} < h{s_{iR}}, $
|
${p'_h} = \left\{ ph−1, pi−diL<ph<piph−w, ph=piph, otherwise \right.$
|
(2.7) |
In the Eq. (2.6) and Eq. (2.7), ${p'_h}$ is the absolute value of new prediction error of watermarked database. According to Eq. (2.4), if ${p_e} \geqslant 0$, ${p_h}$ equals to ${p_e}$. if ${p_e} < 0$, ${p_h}$ equals to $ - {p_e}$. Then substituting the two results respectively into the Eq. (2.6) and Eq. (2.7), the followings Eq. will be concluded.
if $h{s_{iL}} \geqslant h{s_{iR}}$ and ${p_e} \geqslant 0$,
|
${p'_e} = \left\{ pe+1, pi<pe<pi+diRpe+w, pe=pipe, otherwise \right.$
|
(2.8) |
if $h{s_{iL}} \geqslant h{s_{iR}}$ and ${p_e} < 0$,
|
${p'_e} = \left\{ pe−1, −(pi+diR)<pe<−pipe−w, pe=−pipe, otherwise \right.$
|
(2.9) |
if $h{s_{iL}} < h{s_{iR}}$ and ${p_e} \geqslant 0$,
|
${p'_e} = \left\{ pe−1, pi−diL<pe<pipe−w, pe=pipe, otherwise \right.$
|
(2.10) |
if $h{s_{iL}} < h{s_{iR}}$ and ${p_e} < 0$,
|
${p'_e} = \left\{ pe+1, −pi<pe<−(pi−diL)pe+w, pe=−pipe, otherwise \right.$
|
(2.11) |
In the Eq. (2.8)–(2.11), ${p'_e}$ is the new prediction error of watermarked database. According to different situations, the histogram shifting and watermark embedding can be finally solved with Eq. (2.8), Eq. (2.9), Eq. (2.10), and Eq. (2.11). Besides, there are two special situations which should be noted. If ${p_i} = 0$, Eq. (2.8) is the only one which should be used to solve the situation. If ${p_i} = 1$, Eq. (2.8) and Eq. (2.9) should be the only choice. This reduces the data distortion caused by the shifted.
Step5. Watermark extraction and data recovery.
Step5.1. The method selects the columns in which the watermark is embedded, and sorts the columns. The selection method and the sorting method are the same as Step1. Using the secret grouping key generated from the watermark embedding stage, the tuples are divided into non-overlapping groups by Eq. (2.2). Calculating ${p'_e}$ and ${p'_h}$ with Eq. (2.12) and Eq. (2.13) respectively. The histogram is constructed with ${p'_h}$ on each group.
| ${p'_e} = y' - \hat y$ | (2.12) |
| ${p'_h} = |{p'_e}|$ | (2.13) |
In the Eq. (2.12), $y'$ represents any value in ${D_W}$, $\hat y$ which can be calculated with Eq. (2.3) represents the tolerance of the column including $y'$. ${p'_e}$ is the prediction error corresponding to $y'$. After the histogram is constructed, the method will scan ${p'_e}$ one by one, judge the position in the histogram, extract the watermark and restore the database.
Step5.2. Watermark extraction. Each watermark is extracted by using the distance and direction of the shifting in each histograms stored in the array pa. The method performs the above detection on all tuples of the same group, and separately records the number of all '0' and '1' detected in the group, and then use the majority voting mechanism to determine the final watermark bit of the group. The watermark bit which has a larger number is treated as the final detected watermark bit.
If $|{p'_e}| = {p_i}$, meaning the attribute value is not modified and there is a gap at the side of the histogram, the detected watermark bit is '0'. If $h{s_{iL}} < h{s_{iR}}$, two situations will appear. If ${p'_e} > 0$ and ${p'_e} = {p_i} - 1$, the detected watermark bit is '1' and if ${p'_e} < 0$ and ${p'_e} = {p_i} + 1$, the detected watermark bit is '1'. If $h{s_{iL}} \geqslant h{s_{iR}}$, two situations will also appear. If ${p'_e} > 0$ and ${p'_e} = {p_i} + 1$, the detected watermark bit is '1' and if ${p'_e} < 0$ and ${p'_e} = {p_i} - 1$, the detected watermark bit is '1'. Corresponding to the embedded watermark, two special situations will appear while detecting watermark bit '1'. If ${p_i} = 0$ and ${p'_e} = {p_i} + 1$, the detected watermark bit is '1'. If ${p_i} = 1$, if ${p'_e} > 0$ and ${p'_e} = {p_i} + 1$, the detected watermark bit is '1' and if ${p'_e} < 0$ and ${p'_e} = {p_i} - 1$, the detected watermark bit is '1'. It has been verified by experiments that the watermark bits extracted by the majority voting mechanism can also be used to prove the owner of the copyright.
Step5.3. Data recovery. According to the positive and negative values of ${p'_e}$, and the results of comparing $h{s_{iL}}$ with $h{s_{iR}}$, the following data recovery is performed.
if $h{s_{iL}} \geqslant h{s_{iR}}$ and ${p'_e} \geqslant 0$,
|
${y^r} = \left\{ y′−1, pi+1<p′e⩽pi+diRy′−1, p′e=pi+1,w=1y′, otherwise \right.$
|
(2.14) |
if $h{s_{iL}} \geqslant h{s_{iR}}$ and ${p'_e} < 0$,
|
${y^r} = \left\{ y′+1, −(pi+diR)⩽p′e<−(pi+1)y′+1, p′e=−(pi+1),w=1y′, otherwise \right.$
|
(2.15) |
if $h{s_{iL}} < h{s_{iR}}$ and ${p'_e} \geqslant 0$,
|
${y^r} = \left\{ y′+1, pi−diL⩽p′e<pi−1y′+1, p′e=pi−1,w=1y′, otherwise \right.$
|
(2.16) |
if $h{s_{iL}} < h{s_{iR}}$ and ${p'_e} < 0$,
|
${y^r} = \left\{ y′−1, −(pi−1)<p′e⩽−(pi−diL)y′−1, p′e=−(pi−1),w=1y′, otherwise \right.$
|
(2.17) |
In the above equations, ${y^r}$ is the restored attribute value. Corresponding to the special situation while embedding the watermark, if ${p_i} = 0$, Eq. (2.14) is the only one which should be used to solve the situation. If ${p_i} = 1$, Eq. (2.14) and Eq. (2.15) should be the only choice.
Experiments were conducted on a workstation with Intel Core i5 with CPU of 2.40 GHz and RAM of 8 GB. The method is implemented and tested.
The test database is the Forest Cover Type dataset provided by the University of California. The dataset contains 581, 012 tuples and 54 properties. In this paper, 10 integer-type columns are selected for experiments and compared with the existing GAHSW reversible watermarking method. For the sake of comparison, the method of this paper, same as the experiment of GAHSW in [17], will generate a synthetic column as the primary key. All of the following experiments embed watermarks under the same conditions.
In this section, the data distortion rate (DDR) is used to evaluate the distortion effects of the HGW and GAHSW on the database after embedding the watermark. The DDR is calculated as followings:
| $DDR = \frac{{{T_{dis}}}}{{TD}}$ | (3.1) |
In the Eq. (3.1), ${T_{dis}}$ is the total amount of data distorted and TD is the total amount of data in the database. The larger the DDR, the greater the distortion of the data will appear. Conversely, the distortion of the data is small. Experiments verify that the distortion rate of HGW is much smaller than the distortion rate of GAHSW.
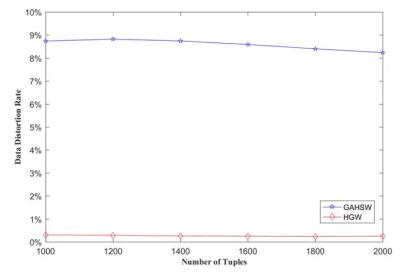
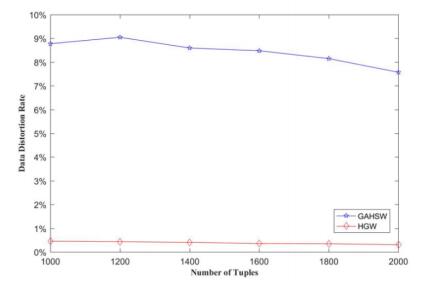
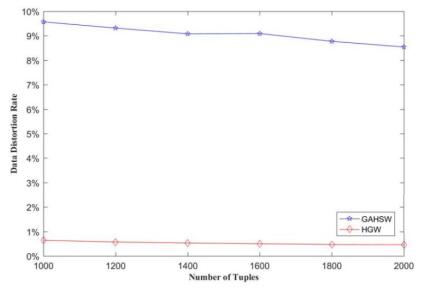
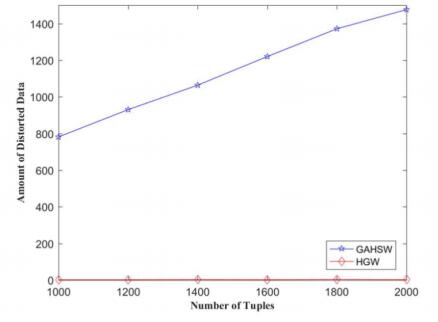
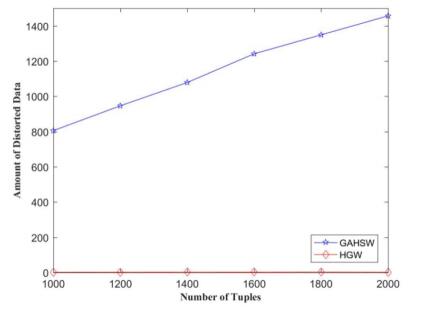
With different length of the watermark (the number of groups) which are 24, 48 and 72, the distortion rates of HGW and GAHSW were compared. During each comparing process, the total number of tuples of 1000, 1200, 1400, 1600, 1800, and 2000 are respectively verified with same length of the watermark (the number of groups), and the results are plotted in Figure 2, 3 and 4. In the figure, the vertical axis is DDR which indicates the ratio of data distortion. When DDR is zero, it means that the data of the database is not distorted and the horizontal axis represents the different number of the tuples. Since both HGW and GAHSW rely on stochastic optimization, the distortion rate is the average of the 10 runs of the two methods.
As can be seen from the figure 2, 3 and 4, when the same watermark information is embedded in the same database, the DDR generated by the HGW method is much lower than the GAHSW, which is less than 0.7%.
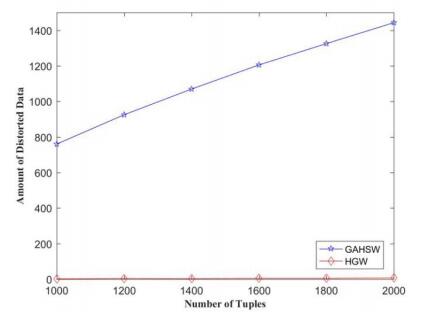
In this section, the total amount of distortion data from the shift (without the distortion caused by embedding the watermark bits) is used to evaluate the distortion effects of the HGW and GAHSW on the database after embedding the watermark.
With different length of the watermark (the number of groups) which are 24, 48 and 72, the distortion rates of HGW and GAHSW were compared. During each comparing process, the total number of tuples of 1000, 1200, 1400, 1600, 1800, and 2000 are respectively verified with same length of the watermark (the number of groups), and the results are plotted in Figure 5, 6 and 7. In the figure, the vertical axis is the total amount of distortion data, indicating the number of data of distortion. When the total amount of translation distortion data is zero, it means that the data of the database is not distorted and the horizontal axis represents the different number of the tuples. Since both HGW and GAHSW rely on stochastic optimization, the total amount of distortion data is the average of the results of 10 runs of the two methods. It can be seen from the figure 5, 6 and 7 that when the same watermark information is embedded in the same database, the total amount of translational distortion data generated by the HGW method is much lower than GAHSW, which is at least 1.5 and 7 at the maximum and almost overlaps with the horizontal axis.
In this section, the robustness of the HGW watermarking method under well-known database attacks is reported. For convenience, the article carries on the comparing test by setting the length of the watermark (the number of groups) as 48 just like the test mentioned in the reference [17]. With analyzing the attack results, this paper verifies the robustness of the HGW method. This article mainly tests three types of attacks: inserts, deletes, and changes. Robustness is evaluated by using bit error rate (BER). That is, the ratio of the number of bits extracted by error to the number of embedded watermark bits. The BER is calculated as follows:
| $BER = \frac{{\sum _{i = 1}^{{N_g}} {{w_i} \oplus w_i^{det}} }}{{{N_g}}}$ | (3.2) |
In the Eq. (3.2), ${w_i}$ is the embedded watermark bit and $w_i^{det}$ is the detected watermark bit. We can see that the lower the BER value appears, the higher the watermark robustness will be. It is verified by experiments that the robustness of HGW is comparable to that of GAHSW. In the followings, we conduct attack experiments under the best situation and the worst situation, demonstrate watermark detection and data recovery results, and compare the two results.
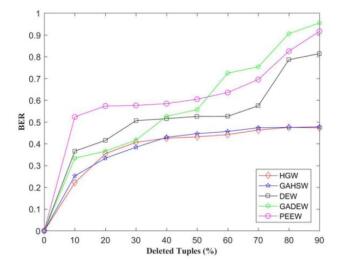
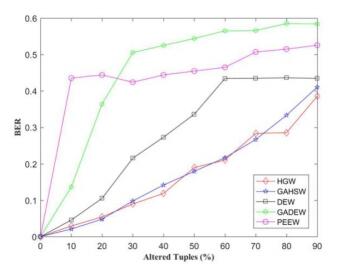
Simulating as an attacker, this article attempts to insert, delete, and modify data for 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, and 90%, and the results are plotted respectively in Figures 8 and 9. The vertical axis in the figure is BER, indicating that the ratio of watermarks has not been successfully detected. When the BER is close to zero, it means that the watermark is correctly detected from the database. The horizontal axis represents the changes' percentage (%) of the tuples in the database after attacking. Since the HGW relies on random optimization, the BER of the watermark extraction is the average of 10 runs of the method.
Both GAHSW and HGW are robust to insertion attacks, and the BER under the insertion attack is always zero no matter how many tuples are inserted. To this end, the comparison diagram of the insertion attacks will not be drawn. It can be seen from Figure 8 and Figure 9 that the robustness of the GAHSW and HGW methods is roughly equivalent under the Deletion attack and modification attacks. As the attack strength increases, the BER of the watermark extracted by these two methods also increases. The experiments also show that the performance of HGW and GAHSW have better watermark detection rate under this attack compared with other methods.
Deletion attack is to randomly delete the tuple to destroy the watermark. Figure 8 shows the BER of the watermark extracted by the HGW, GAHSW, PEEW, DEW and GADEW methods after the Deletion attack. When the database is suffered from severe deletion attack, for example, the number of tuples deleted in the database becomes 90%, DEW, GADEW, and PEEW extract the watermark with the BER value of 0.814, 0.955 and 0.915, respectively. However, the BER of the HGW extraction watermark is 0.472, and the BER of the GAHSW watermark extraction is 0.477. The HGW can also recover at least half of the watermark. If most of the watermark contained in the tuples is deleted, the watermark will not be able to be recovered. Deletion attacks have the greatest impact on database watermarks.
Modification attacks are to randomly modify the attributes of the database. Figure 9 shows the BER of the watermark extracted by the HGW, GAHSW, PEEW, DEW and GADEW methods after modification attacks. We can see that the BER of the extracted watermark increases as the amount of data modification increases. The number of tuples modified in the database becomes 90%, DEW, GADEW, and PEEW extract the watermark with the BER value of 0.434, 0.584 and 0.526, respectively. However, the BER of the HGW extraction watermark is 0.383, and the BER of the GAHSW watermark extraction is 0.411. The HGW can also recover at least half of the watermark. If the watermark contained in most tuples is modified, then the watermark tuple affected by this attack will be difficult to extract from the remaining unaffected data.
In general, the HGW method, comparing to GAHSW, produces a lower BER when embedding the same watermark information into the same database. It is worth noting that the HGW method sorts the names of the attribute columns in alphabetical order before the watermark is embedded and extracted, and groups the tuples according to the primary key of the tuple. Therefore, the rearrangement has no effect on the database.
In order to reduce the data distortion rate of the carrier, a reversible database watermarking method based on histogram gap low distortion is proposed in this article. With this method, the vacancy provided by the histogram gap is used to reduce the number of columns which are shifted when the watermark is embedded, and therefore the modification of the carrier database data will be reduced, which also meets the need of reducing data distortion. The characteristic of HGW significantly reduces the number of histogram column shift while embedding watermarks, greatly reduces the changes to the carrier data, and effectively reduces the database data distortion caused by watermark embedding. Comparing HGW with GAHSW, the results show that HGW is superior to GAHSW in the aspects of reducing the amount of the histogram shifting and the data distortion. In the case of no attack, the watermark extraction error rate of HGW is better than that of GAHSW. In the face of attack, the bit error rate of watermark extraction of HGW nearly equals to that of GAHSW. Basing on the present methods, my future work is to propose better methods to maximally reduce the total amount of distortion data.
The work presented in this paper is supported by the National Natural Science Foundation of China (No.U1536104, 61572052, U1636219, 61772549, U1736214, U1804263, ), the National Key R & D Program of China (No. 2016QY01W0105, 2016YFB0801303), and Plan for Scientific Innovation Talent of Henan Province (No.2018JR0018).
The authors declare no conflict of interest.
| [1] | Lomo T (1966) Frequency potentiation of excitatory synaptic activity in the dentate area of the hippocampal formation. Acta Physiol Scand 68: 128. |
| [2] | Shors TJ, Matzel LD (1997) Long-term potentiation: What's learning got to do with it? Behav Brain Sci 20: 597-614; |
| [3] |
Baudry M, Bi X, Gall C, et al. (2011) The biochemistry of memory: The 26 year journey of a 'new and specific hypothesis'. Neurobiol Learn Mem 95: 125-133. doi: 10.1016/j.nlm.2010.11.015
|
| [4] |
Buzsaki G (2010) Neural syntax: Cell assemblies, synapsembles, and readers. Neuron 68:362-385. doi: 10.1016/j.neuron.2010.09.023
|
| [5] |
Squire LR, Wixted JT (2011) The cognitive neuroscience of human memory since H.M. Annu Rev Neurosci 34: 259-288. doi: 10.1146/annurev-neuro-061010-113720
|
| [6] |
Rissman J, Wagner AD (2012) Distributed representations in memory: Insights from functional brain imaging. Annu Rev Psychol 63: 101-128. doi: 10.1146/annurev-psych-120710-100344
|
| [7] | Rudy JW (2014) The neurobiology of learning and memory. Sunderland, MA: Sinauer Associates. |
| [8] |
Mitsushima D (2015) Contextual learning requires functional diversity at excitatory and inhibitory synapses onto CA1 pyramidal neurons. AIMS Neurosci 2: 7-17. doi: 10.3934/Neuroscience.2015.1.7
|
| [9] | Mitsushima D, Sano A, Takahashi T (2013) A cholinergic trigger drives learning-induced plasticity at hippocampal synapses. Nat Commun 4: 2760. |
| [10] | Takeuchi T, Duszkiewicz AJ, Morris RG (2014) The synaptic plasticity and memory hypothesis: Encoding, storage and persistence. Philos Trans R Soc Lond B Biol Sci 369: 20130288. |
| [11] |
Whitlock JR, Heynen AJ, Shuler MG, et al. (2006) Learning induces long-term potentiation in the hippocampus. Science 313: 1093-1097. doi: 10.1126/science.1128134
|
| [12] |
Bakin JS, Weinberger NM (1996) Induction of a physiological memory in the cerebral cortex by stimulation of the nucleus basalis. Proc Natl Acad Sci U S A 93: 11219-11224. doi: 10.1073/pnas.93.20.11219
|
| [13] |
Mercado E, III, Bao S, Orduna I, et al. (2001) Basal forebrain stimulation changes cortical sensitivities to complex sound. Neuroreport 12: 2283-2287. doi: 10.1097/00001756-200107200-00047
|
| [14] | Froemke RC, Carcea I, Barker AJ, et al. (2013) Long-term modification of cortical synapses improves sensory perception. Nat Neurosci 16: 79-88. |
| [15] |
Froemke RC, Merzenich MM, Schreiner CE (2007) A synaptic memory trace for cortical receptive field plasticity. Nature 450: 425-429. doi: 10.1038/nature06289
|
| [16] |
Marrosu F, Portas C, Mascia MS, et al. (1995) Microdialysis measurement of cortical and hippocampal acetylcholine release during sleep-wake cycle in freely moving cats. Brain Res 671:329-332. doi: 10.1016/0006-8993(94)01399-3
|
| [17] | Newman EL, Gupta K, Climer JR, et al. (2012) Cholinergic modulation of cognitive processing: Insights drawn from computational models. Front Behav Neurosci 6: 24. |
| [18] |
Rokers B, Mercado E, III, Allen MT, et al. (2002) A connectionist model of septohippocampal dynamics during conditioning: Closing the loop. Behav Neurosci 116: 48-62. doi: 10.1037/0735-7044.116.1.48
|
| [19] |
Manseau F, Goutagny R, Danik M, et al. (2008) The hippocamposeptal pathway generates rhythmic firing of GABAergic neurons in the medial septum and diagonal bands: An investigation using a complete septohippocampal preparation in vitro. J Neurosci 28: 4096-4107. doi: 10.1523/JNEUROSCI.0247-08.2008
|
| [20] |
Zhang H, Lin SC, Nicolelis MA (2010) Spatiotemporal coupling between hippocampal acetylcholine release and theta oscillations in vivo. J Neurosci 30: 13431-13440. doi: 10.1523/JNEUROSCI.1144-10.2010
|
| [21] |
Vandecasteele M, Varga V, Berenyi A, et al. (2014) Optogenetic activation of septal cholinergic neurons suppresses sharp wave ripples and enhances theta oscillations in the hippocampus. Proc Natl Acad Sci U S A 111: 13535-13540. doi: 10.1073/pnas.1411233111
|
| [22] |
Ajemian R, D'Ausilio A, Moorman H, et al. (2013) A theory for how sensorimotor skills are learned and retained in noisy and nonstationary neural circuits. Proc Natl Acad Sci U S A 110: E5078-5087. doi: 10.1073/pnas.1320116110
|
| [23] |
Routtenberg A (2013) Lifetime memories from persistently supple synapses. Hippocampus 23:202-206. doi: 10.1002/hipo.22088
|
| [24] |
Routtenberg A (2008) Long-lasting memory from evanescent networks. Eur J Pharmacol 585:60-63. doi: 10.1016/j.ejphar.2008.02.047
|
| [25] |
Routtenberg A (2008) The substrate for long-lasting memory: If not protein synthesis, then what? Neurobiol Learn Mem 89: 225-233. doi: 10.1016/j.nlm.2007.10.012
|
| [26] |
Richards BA, Frankland PW (2013) The conjunctive trace. Hippocampus 23: 207-212. doi: 10.1002/hipo.22089
|
| [27] |
Chen N, Sugihara H, Sharma J, et al. (2012) Nucleus basalis-enabled stimulus-specific plasticity in the visual cortex is mediated by astrocytes. Proc Natl Acad Sci U S A 109: E2832-2841. doi: 10.1073/pnas.1206557109
|
| [28] |
McKenzie IA, Ohayon D, Li H, et al. (2014) Motor skill learning requires active central myelination. Science 346: 318-322. doi: 10.1126/science.1254960
|
| [29] |
Patel J, Fujisawa S, Berenyi A, et al. (2012) Traveling theta waves along the entire septotemporal axis of the hippocampus. Neuron 75: 410-417. doi: 10.1016/j.neuron.2012.07.015
|
| [30] |
Lubenov EV, Siapas AG (2009) Hippocampal theta oscillations are travelling waves. Nature 459:534-539. doi: 10.1038/nature08010
|
| [31] |
Benchenane K, Peyrache A, Khamassi M, et al. (2010) Coherent theta oscillations and reorganization of spike timing in the hippocampal- prefrontal network upon learning. Neuron 66:921-936. doi: 10.1016/j.neuron.2010.05.013
|
| [32] |
Siapas AG, Lubenov EV, Wilson MA (2005) Prefrontal phase locking to hippocampal theta oscillations. Neuron 46: 141-151. doi: 10.1016/j.neuron.2005.02.028
|
| [33] |
Sirota A, Montgomery S, Fujisawa S, et al. (2008) Entrainment of neocortical neurons and gamma oscillations by the hippocampal theta rhythm. Neuron 60: 683-697. doi: 10.1016/j.neuron.2008.09.014
|
| [34] |
Buzsaki G (2005) Theta rhythm of navigation: Link between path integration and landmark navigation, episodic and semantic memory. Hippocampus 15: 827-840. doi: 10.1002/hipo.20113
|
| [35] |
Landfield PW, McGaugh JL, Tusa RJ (1972) Theta rhythm: A temporal correlate of memory storage processes in the rat. Science 175: 87-89. doi: 10.1126/science.175.4017.87
|
| [36] | Miller R (1989) Cortico-hippocampal interplay: Self-organizing phase-locked loops for indexing memory. Psychobiol 17: 115-128. |
| [37] | Palmer JH, Gong P (2014) Associative learning of classical conditioning as an emergent property of spatially extended spiking neural circuits with synaptic plasticity. Front Comput Neurosci 8: 79. |
| [38] | Battaglia FP, Benchenane K, Sirota A, et al. (2011) The hippocampus: Hub of brain network communication for memory. Trends Cogn Sci 15: 310-318. |
| [39] |
Lansdell B, Ford K, Kutz JN (2014) A reaction-diffusion model of cholinergic retinal waves.PLoS Comput Biol 10: e1003953. doi: 10.1371/journal.pcbi.1003953
|
| [40] |
Wester JC, Contreras D (2012) Columnar interactions determine horizontal propagation of recurrent network activity in neocortex. J Neurosci 32: 5454-5471. doi: 10.1523/JNEUROSCI.5006-11.2012
|
| [41] | Pavlov IP (1927) Conditioned reflexes. London: Oxford University Press. |
| [42] | Griffen TC, Wang L, Fontanini A, et al. (2012) Developmental regulation of spatio-temporal patterns of cortical circuit activation. Front Cell Neurosci 6: 65. |
| [43] | Wang L, Fontanini A, Maffei A (2011) Visual experience modulates spatio-temporal dynamics of circuit activation. Front Cell Neurosci 5: 12. |
| [44] |
Blankenship AG, Feller MB (2010) Mechanisms underlying spontaneous patterned activity in developing neural circuits. Nat Rev Neurosci 11: 18-29. doi: 10.1038/nrn2759
|
| [45] |
Palagina G, Eysel UT, Jancke D (2009) Strengthening of lateral activation in adult rat visual cortex after retinal lesions captured with voltage-sensitive dye imaging in vivo. Proc Natl Acad Sci U S A 106: 8743-8747. doi: 10.1073/pnas.0900068106
|
| [46] | Ponulak F, Hopfield JJ (2013) Rapid, parallel path planning by propagating wavefronts of spiking neural activity. Front Comput Neurosci 7: 98. |
| [47] |
Mercado E, III (2014) Relating cortical wave dynamics to learning and remembering. AIMS Neurosci 1: 185-209. doi: 10.3934/Neuroscience.2014.3.185
|
| [48] | Heitmann S, Gong P, Breakspear M (2012) A computational role for bistability and traveling waves in motor cortex. Front Comput Neurosci 6: 67. |
| [49] |
Gong P, van Leeuwen C (2009) Distributed dynamical computation in neural circuits with propagating coherent activity patterns. PLoS Comput Biol 5: e1000611. doi: 10.1371/journal.pcbi.1000611
|
| 1. | Yan Li, Junwei Wang, Xiangyang Luo, A reversible database watermarking method non-redundancy shifting-based histogram gaps, 2020, 16, 1550-1477, 155014772092176, 10.1177/1550147720921769 | |
| 2. | Yan Li, Junwei Wang, Hongyong Jia, A Robust and Reversible Watermarking Algorithm for a Relational Database Based on Continuous Columns in Histogram, 2020, 8, 2227-7390, 1994, 10.3390/math8111994 | |
| 3. | Heyan Chai, Shuqiang Yang, Zoe L. Jiang, Xuan Wang, Yiqun Chen, Hengyu Luo, 2020, Chapter 11, 978-3-030-38990-1, 153, 10.1007/978-3-030-38991-8_11 | |
| 4. | Ali Hamadou, Lanciné Camara, Abdoul Aziz Issaka Hassane, Harouna Naroua, Reversible Fragile Watermarking Scheme for Relational Database Based on Prediction-Error Expansion, 2020, 2020, 1024-123X, 1, 10.1155/2020/1740205 | |
| 5. | Rizwan Taj, Feng Tao, Shahzada Khurram, Ateeq Ur Rehman, Syed Kamran Haider, Akber Abid Gardezi, Saima Kanwal, Reversible Watermarking Method with Low Distortion for the Secure Transmission of Medical Images, 2022, 130, 1526-1506, 1309, 10.32604/cmes.2022.017650 | |
| 6. | Sapana Rani, Raju Halder, An efficient format-independent watermarking framework for large-scale data sets, 2022, 208, 09574174, 118085, 10.1016/j.eswa.2022.118085 | |
| 7. | Qianwen Li, Xiang Wang, Qingqi Pei, Kwok-Yan Lam, Ning Zhang, Mianxiong Dong, Victor C. M. Leung, Database Watermarking Algorithm Based on Decision Tree Shift Correction, 2022, 9, 2327-4662, 24373, 10.1109/JIOT.2022.3188631 | |
| 8. | Sapana Rani, Raju Halder, Comparative Analysis of Relational Database Watermarking Techniques: An Empirical Study, 2022, 10, 2169-3536, 27970, 10.1109/ACCESS.2022.3157866 | |
| 9. | Qiang Liu, Hequ Xian, Jiancheng Zhang, Kunpeng Liu, 2023, Chapter 22, 978-3-031-25537-3, 413, 10.1007/978-3-031-25538-0_22 | |
| 10. | Asmaa Alqassab, Mafaz Alanezi, 2023, Chapter 49, 978-981-19-1411-9, 563, 10.1007/978-981-19-1412-6_49 | |
| 11. | Yexing Zhang, Zihou Wang, Zhaoguo Wang, Chuanyi Liu, 2022, Chapter 1, 978-981-16-9228-4, 3, 10.1007/978-981-16-9229-1_1 | |
| 12. | De Li, Chi Ma, Haoyang Gao, Xun Jin, LBP feature and hash function based dual watermarking algorithm for database, 2023, 148, 0169023X, 102228, 10.1016/j.datak.2023.102228 | |
| 13. | Cheng Li, Xinhui Han, Wenfa Qi, Zongming Guo, 2023, An Improved Reversible Database Watermarking Method based on Histogram Shifting, 9798400700545, 103, 10.1145/3577163.3595091 | |
| 14. | Wenfa Qi, Cheng Li, Xinhui Han, Research on blind reversible database watermarking algorithm based on dual embedding strategy, 2024, 0010-4620, 10.1093/comjnl/bxae080 | |
| 15. | Zhiwen Ren, Zehua Ma, Weiming Zhang, Nenghai Yu, 2023, SPSW: Database Watermarking Based on Fake Tuples and Sparse Priority Strategy, 979-8-3503-8199-3, 896, 10.1109/TrustCom60117.2023.00128 | |
| 16. | Wenling Li, Ning Li, Jianen Yan, Zhaoxin Zhang, Ping Yu, Gang Long, Secure and High-Quality Watermarking Algorithms for Relational Database Based on Semantic, 2022, 1041-4347, 1, 10.1109/TKDE.2022.3194191 | |
| 17. | Jiang Han, Xiaowei Peng, Hequn Xian, Dalin Yang, 2024, A Distortion Free Watermark Scheme for Relational Databases, 979-8-3503-8461-1, 1, 10.1109/ICCCN61486.2024.10637516 | |
| 18. | Zhiwen Ren, Han Fang, Jie Zhang, Zehua Ma, Ronghao Lin, Weiming Zhang, Nenghai Yu, A Robust Database Watermarking Scheme That Preserves Statistical Characteristics, 2024, 36, 1041-4347, 2329, 10.1109/TKDE.2023.3324932 | |
| 19. | Chuanda Cai, Changgen Peng, Jin Niu, Weijie Tan, Hanlin Tang, Low distortion reversible database watermarking based on hybrid intelligent algorithm, 2023, 20, 1551-0018, 21315, 10.3934/mbe.2023943 | |
| 20. | Chundong Wang, Yue Li, 2023, A Copyright Authentication Method Balancing Watermark Robustness and Data Distortion, 979-8-3503-3168-4, 1178, 10.1109/CSCWD57460.2023.10152729 | |
| 21. | Yantao Tan, Zhiwen Ren, Zehua Ma, Weiming Zhang, Nenghai Yu, 2024, Low Distortion Database Watermarking Based on Attribute Prediction, 979-8-3315-0707-7, 62, 10.1109/ICCC62609.2024.10941885 | |
| 22. | Dharmapuri Siri, S. Sangeetha, P. Kalaiselvi, Devayanai V C, Haassan M.M. AlJawahry, Ritin Behl, 2025, A Strong and Adaptable Watermarking Methodology for Relational Databases, 979-8-3315-2749-5, 1243, 10.1109/IC363308.2025.10956503 | |
| 23. | Peng Zuo, Shiqiang Xu, Yang Wang, Peiyu Xiao, Peiyi Han, 2025, Chapter 25, 978-981-96-4508-4, 371, 10.1007/978-981-96-4509-1_25 | |
| 24. | Wenhao Xu, Hequn Xian, 2025, Chapter 22, 978-981-96-4730-9, 444, 10.1007/978-981-96-4731-6_22 |
Eduardo Mercado III. Learning-Related Synaptic Reconfiguration in Hippocampal Networks: Memory Storage or Waveguide Tuning?[J]. AIMS Neuroscience, 2015, 2(1): 28-34. doi: 10.3934/Neuroscience.2015.1.28
DownLoad:
