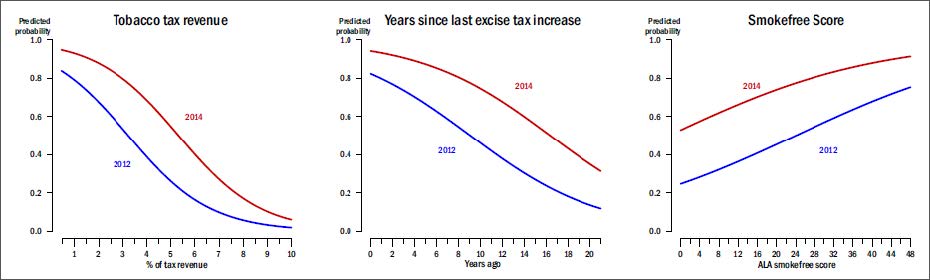
The Family Smoking Prevention and Tobacco Control Act (FSPTCA) give the U.S. Food and Drug Administration (FDA) unprecedented power to regulate tobacco products. One of the most significant provisions of the law allows state and local governments to adopt and enforce tobacco control legislation restricting the time, place, and manner (but not the content) of tobacco advertising. However, there is still reluctance among states and localities for mass adoption of laws due to challenges associated with legal feasibility and lack of U.S.-based evidence in effectiveness. The Center for Public Health Systems Science conducted interviews with key tobacco control contacts in 48 states at two time points (2012 and 2014) since the passage of the FSPTCA to assess the influence of the law on point-of-sale policy development in their state tobacco programs. Logistic regression results show that point-of-sale policy importance is growing post-FSPTCA, and that key influencers of this importance are states' tobacco control histories and environments, including that related to excise taxes and smoke free air policies. The adoption of smokefree and tax policies has become commonplace across the U.S., and the quality and extent of these laws and prevailing political will increasingly impact the ability of states to work in emerging tobacco control policy areas including those directed at the point of sale.
1.
Introduction
In 2008, Bhattacharya et al. [5] and Bell et al. [4] discovered that bipartite chain graphs whose largest eigenvalues within the connected bipartite graph is maximal, and named therein as double nested graphs. After that, many scholars began to study some mathematical properties of chain graphs. Andelic et al. provide that some upper and lower bounds on index of chain graphs [3]. And Alazemi et al. proved that any chain graph has its least positive eigenvalue greater than $ \frac{1}{2} $ [2]. Hence Zhang et al. proposed that upper bounds on Laplacian spectral radius of chain graphs [13]. Das et al. studied the energy and Laplacian energy of chain graphs [8]. In this paper, we further study some bounds of energy and Laplacian energy of chain graphs.
We consider finite undirected connected graphs without loops and multiple edges. Let $ G $ be a such graph with vertex set $ V(G) = \{v_{1}, v_{2}, \dots, v_{n}\} $ and edge set $ E(G) $, where $ |E(G)| = m $. Let $ d_{i} $ be the degree of the vertex $ v_{i} $ for $ i = 1, 2, \dots, n $. The minimum vertex degrees of $ G $ are denoted by $ \delta(G) $. Let $ N_{G}(v_{i}) $ be the adjacent set of the vertex $ v_{i} $, then $ d_{i} = |N_{G}(v_{i})| $. If $ G $ has distinct vertices $ v_{i} $ and $ v_{j} $ with $ N_{G}(v_{i}) = N_{G}(v_{j}) $, then $ v_{i} $ and $ v_{j} $ are duplicates and $ (v_{i}, v_{j}) $ is a duplicate pair.
Let $ A(G) $ be the adjacency matrix of $ G $, and $ rank(G) $ be the rank of the adjacency matrix $ A(G) $. Let $ \lambda_{1}\geq\lambda_{2}\geq\cdots\geq\lambda_{n} $ the eigenvalues of $ A(G) $. We denote $ S(G) = \{\lambda_{1}, \lambda_{2}, \dots, \lambda_{n}\} $ as the spectrum of $ G $. The energy of graph $ G $ is defined as [11]
For its basic properties and application, including various lower and upper bounds, see the [17], the recent paper [1,7,8,11,12,20] and the references cited therein.
The Laplacian matrix of graph $ G $ is defined as $ L(G) = D(G)-A(G) $, where $ D(G) $ is the diagonal matrix of vertex degrees. The matrix $ L(G) $ has non-negative eigenvalues $ \mu_{1}\geq\mu_{2}\geq\cdots\geq\mu_{n-1}\geq\mu_{n} = 0 $, and the Laplacian spectrum of graph $ G $ be denoted by $ LS(G) = \{\mu_{1}, \mu_{2}, \dots, \mu_{n}\} $. The Laplacian energy of $ G $ is defined as [10]
It can also be defined as
where $ \sigma \; (1\leqslant\sigma\leqslant n) $ be the largest positive integer such that $ \mu_{\sigma}\geq\frac{2m}{n} $ and $ S_{k}(G) = \sum\limits_{i = 1}^{k}\mu_{i} $.
For its basic properties, including various lower and upper bounds, see [7,8,10,18,19] and the references cited therein. The Laplacian energy found applications not only in theoretical organic chemistry [12,21], but also in image processing [22] and information theory [16].
In the class of bipartite graphs of fixed order and size those having maximal spectral radius of adjacency/Laplacian/signless Laplacian matrix are chain graphs. Thus, they can be significant in modeling some bipartite networks with large spectral radius. Their applications involve ecological networks, in which graphs with nested properties are considered [14] and are used in some applications for economic network modeling.
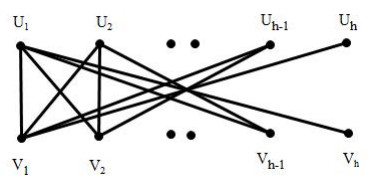
We now introduce the structure of a (connected) chain graph. The vertex set of any chain graph consists of two color classes, which are $ U $ and $ V $. Both of them are divided into $ h $ non-empty units $ U_{1}, U_{2}, \dots, U_{h} $ and $ V_{1}, V_{2}, \dots, V_{h} $, respectively. All the vertices in $ U_{s} $ are joined by edges to all vertices in $ \bigcup_{k = 1}^{h+1-s}V_{k} $, for $ s = 1, 2, \dots, h $. Therefore, if $ u_{i}\in U_{s+1} $ and $ u_{j}\in U_{s} $, then $ N_{G}(u_{i})\subset N_{G}(u_{j}) $, or if $ v_{i}\in V_{t+1} $ and $ v_{j}\in v_{t} $, then $ N_{G}(v_{i})\subset N_{G}(v_{j}) $.
If $ n_{s} = |U_{s}| $ and $ m_{s} = |V_{s}| $ for $ s = 1, 2, \dots, h $, then $ G $ is denoted by $ G(m_{1}, \dots, m_{h}; n_{1}, \dots, n_{h}) $, as shown in Figure 1. And
where
Moreover,
The second smallest Laplacian eigenvalue of a graph is well known as the algebraic connectivity. It has been proved that the second smallest Laplacian eigenvalue $ \mu_{n-1} = 0 $ if and only if $ G $ is disconnected. The algebraic connectivity is often applied in theoretical chemistry, control theory, combinatorial optimization and other fields [15].
As usual, $ K_{n} $, $ K_{p, q}(p+q = n) $ and $ K_{1, n-1} $, denote, respectively, the complete graph, the complete bipartite graph and the star on $ n $ vertices. For other undefined notations and terminology from graph theory, the readers are referred to [6].
The paper is organized as follows. In Section 2, we list some previously known results. In Section 3, we get some upper and lower bounds on $ \varepsilon(G) $ of a chain graph $ G $. In Section 4, we establish an upper bound on $ LE(G) $ of the chain graphs in terms of vertex cover number. In Section 5, we attain the maximal Laplacian energy of the bicyclic chain graph $ G $ by comparing the algebraic connectivity.
2.
Preliminaries
This section lists some known results to be used in this paper.
Lemma 2.1. [8] Let $ B $ be a $ p\times p $ real symmetric matrix and $ B_{k} $ be its leading $ k\times k $ submatrix. Then for $ i = 1, 2, \dots, k $,
where $ \lambda_{i}(B) $ is the $ i $-th largest eigenvalue of $ B $.
Lemma 2.2. [9] Let $ G $ be a graph with vertices $ \{v_{1}, v_{2}, \dots, v_{k}\}\subseteq V(G) $ having same set of adjacent vertices, then $ G $ has at least $ k-1 $ equal eigenvalues $ 0 $.
Lemma 2.3. [18] Let $ G\ncong K_{n} $. Then $ \mu_{n-1}\leqslant \delta(G) $.
Lemma 2.4. [10] Let $ A $ and $ B $ be real symmetric matrices of order $ n $. Then for any $ 1\leqslant k\leqslant n $,
where $ \lambda_{i}(M) $ denotes the $ i $-th largest eigenvalue of the matrix $ M $.
Lemma 2.5. [1] If $ G $ is a connected bipartite graph of rank $ r $, then
Lemma 2.6. [11] If $ G $ is a connected bipartite graph of rank $ r $, then
Lemma 2.7. [8] Let $ G\cong G(m_{1}, \dots, m_{h}; n_{1}, \dots, n_{h}) $ be a chain graph of order $ n $. Then
with equation holds if and only if $ G\cong K_{1, n-1} $.
Lemma 2.8. [8] Let $ G $ be a graph with vertex set $ V(G) = \{v_{1}, v_{2}, \dots, v_{n}\} $. If $ G $ has $ k-1 $ duplicate pairs $ (v_{i}, v_{i+1}) $, where $ i = 1, 2, \dots, k-1 $, then $ G $ has at least $ k-1 $ equal Laplacian eigenvalues and they are all equal to the cardinality of the neighbor set.
3.
Bounds on the energy of chain graphs
Theorem 3.1. Let $ G\cong G(m_{1}, \dots, m_{h}; n_{1}, \dots, n_{h}) $ be a chain graph of order $ n $. Then
with equation holds if and only if $ G\cong K_{n_{1}, m_{1}} $, where $ n_{1}+m_{1} = n $.
Proof. By Lemma 2.2, the eigenvalue $ 0 $ with multiplicity $ \sum\limits_{i = 1}^{h}(n_{i}+m_{i}-2) $ of $ A(G) $, and the remaining eigenvalues are the eigenvalues of the following matrix,
Let $ \lambda_{1}\geq\lambda_{2}\geq\cdots\geq\lambda_{2h} $ be the eigenvalues of $ C $. Then
Since $ G $ be a bipartite graph, we have $ \lambda_{i} $ and $ -\lambda_{i} $ are eigenvalues of $ G $. Thus we have
Obviously,
that is,
So
First we assume that $ h = 1 $. Then $ G\cong K_{n_{1}, m_{1}} $, where $ n_{1}+m_{1} = n $. So $ S(G) = \{\pm\sqrt{m_{1}n_{1}}, 0, \cdots, 0\} $ and $ \varepsilon(G) = 2\sqrt{m_{1}n_{1}} = 2\sqrt{m} $. Hence the equation holds in (3.1).
Next we assume that $ h\geq2 $. By the definition of chain graph, $ G(1, 1;1, 1) $, that is, $ P_{4} $ is an induced subetaaph of $ G $. By Lemma 2.1, we get $ \lambda_{2}(G)\geq\lambda_{2}(P_{4}) > 0 $. Since $ G $ is connected, by Perron-Frobenius theorem we have $ \lambda_{1}(G) > \lambda_{2}(G) $. Hence the inequality $ 2\sum\limits_{1\leqslant i < j\leqslant h}\lambda_{i}\lambda_{j} \leq \sum\limits_{i = 1}^{h}(h-1)\lambda_{i}^{2} $ is strict. This completes the proof.
Theorem 3.2. Let $ G\cong G(m_{1}, \dots, m_{h}; n_{1}, \dots, n_{h}) $ be a chain graph of order $ n $. Then
Proof. By calculating the matrix $ C $ in the proof of Theorem 3.1, we get
Therefore, all the eigenvalues of matrix $ C $ are non-zero. Hence $ r(G) = 2h $. Using Lemma 2.5, we can get result in (3.2).
4.
Bounds on the Laplacian energy of chain graphs
In this section, we give an upper bound on $ LE(G) $ of chain graphs in terms of vertex cover number. Also, the lower bound follows from a known lower bound for Laplacian energy of any graph in terms of rank and energy.
Theorem 4.1. Let $ G\cong G(m_{1}, \dots, m_{h}; n_{1}, \dots, n_{h}) $ be a chain graph of order $ n $, and $ a_{1}\geq b_{1} $. Then
with equation holds if and only if $ G\cong K_{1, n-1} $.
Proof. Let $ \Gamma = \{v_{11}, v_{12}, \ldots, v_{1m_{1}}, v_{21}, v_{22}, \ldots, v_{2m_{2}}, \ldots, v_{h1}, v_{h2}, \ldots, v_{hm_{h}}\} $ be a vertex cover set of the graph $ G $, where $ v_{ij} $ is the $ j $-th vertex in $ V_{i} $. Hence $ \{v_{i1}, v_{i2}, \ldots, v_{im_{i}}\}\in V_{i} $. We can assume that $ G_{ij} $ are spanning subetaaphs of $ G $ such that $ V(G) = V(G_{i1}) = V(G_{i2}) = \cdots = V(G_{im_{i}}) $, and the edge set of $ G_{ij} $ is defined as
Since $ |N_G(v_{i1})| = |N_G(v_{i2})| = \cdots = |N_G(v_{im_{i}})| = a_{i} $,
we have
so
By Figure 1,
then we can see easily that
Note that
where $ S_{k}(G) $ is the sum of the $ k $ largest Laplacian eigenvalues of graph $ G $.
By Lemma 2.4, we get
So from (1.1), we get
Since $ G $ is connected, $ 1\leq \sigma\leq n-1 $. So it suffices to consider the following two cases.
Case1. $ \frac{2m}{n}\geq b_{1} $.
Then we have
Case2. $ \frac{2m}{n} < b_{1} $.
By Lemma 2.3, we get $ \mu_{n-1}\leq \delta(G)\leq \frac{2m}{n} $. Thus it must be $ 1\leq \sigma\leq n-2 $. Hence
Next we prove that the equality holds.
If $ G\cong K_{1, n-1} $, we get $ b_{1} = m_{1} = 1, n_{1} = n-1 $, and $ S(G) = \{0, 1^{n-2}, n\} $. Then
Theorem 4.2. Let $ G\cong G(m_{1}, \dots, m_{h}; n_{1}, \dots, n_{h}) $ be a chain graph of order $ n $. Then
Proof. By Theorem 3.2, we get $ r(G) = 2h $. Using Lemmas 2.6 and 2.7, we get result in (4.2).
5.
Laplacian energy of bicyclic chain graphs
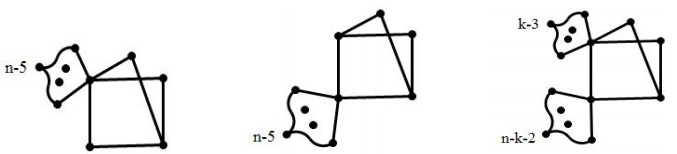
Let $ G $ be a connected bicyclic chain graph. We have $ m = n+1 $, and $ h = 2 $ or $ h = 3 $. If $ h = 2 $, then $ G\cong G(1, 1;3, n-5) $ or $ G\cong G(1, 2;2, n-5) $. If $ h = 3 $, then $ G\cong G(1, 2, k-3;1, 1, n-k-2) $, where $ 4\leq k\leq n-3 $ (Figure 2). In this section, we will attain the maximal Laplacian energy of all connected bicyclic chain graphs.
Lemma 5.1. Let G be a connected bicyclic chain graph $ (n\geq8) $.
(1) If $ G\cong G(1, 1;3, n-5) $, then $ LE(G) = 6+\frac{2(n-4)(n+1)}{n}-2\mu_{n-1} $.
(2) If $ G\cong G(1, 2;2, n-5) $, then $ LE(G) = 10+\frac{2(n-6)(n+1)}{n}-2\mu_{n-1} $.
(3) If $ G\cong G(1, 2, k-3;1, 1, n-k-2) $, where $ 4\leq k\leq n-3 $, then $ LE(G) = 10+\frac{2(n-6)(n+1)}{n}-2\mu_{n-1} $.
Proof. (1) Let $ G\cong G(1, 1;3, n-5) $. By Lemma 2.8, we conclude that $ 2, 2, \underbrace{1, 1, \cdots, 1}_{n-6} $ are the Laplacian eigenvalues of $ G $ and the remaining Laplacian eigenvalues of $ G $ are satisfying the equation $ f_{1}(x) = 0 $, where $ f_{1}(x) $ is the characteristic polynomial of the matrix
that is, $ f_{1}(x) = x\left(x^{3}-(4+n)x^{2}+(5n-2)x-3n\right). $
Let $ h_{1}(x) = x^{3}-(4+n)x^{2}+(5n-2)x-3n $. Then we obtain $ h_{1}(0) = -3n < 0 $, $ h_{1}(1) = n-5 > 0 $, $ h_{1}(2) = 3n-12 > 0 $, $ h_{1}(n-1) = -3 < 0 $ and $ \lim\limits_{x\rightarrow\infty}h_{1}(x) = \infty $. Thus the Laplacian eigenvalues of $ G $ are $ \mu_{1}, \mu_{2}, 2, 2, \underbrace{1, 1, \dots, 1}_{n-6}, \mu_{n-1}, 0 $, where $ \mu_{1}\geq n-1 $, $ 2\leq\mu_{2}\leq n-1 $, $ \mu_{n-1} < 1 $ and $ \mu_{1}+\mu_{2}+\mu_{n-1} = n+4 $.
Therefore
(2) Let $ G\cong G(1, 2;2, n-5) $. By Lemma 2.8, we conclude that $ 3, 2, \underbrace{1, 1, \cdots, 1}_{n-6} $ are the Laplacian eigenvalues of $ G $ and the remaining Laplacian eigenvalues of $ G $ are satisfying the equation $ f_{2}(x) = 0 $, where $ f_{2}(x) $ is the characteristic polynomial of the matrix
that is, $ f_{2}(x) = x\left(x^{3}-(3+n)x^{2}+(5n-8)x-2n\right). $
Let $ h_{2}(x) = x^{3}-(3+n)x^{2}+(5n-8)x-2n $. Then we obtain $ h_{2}(0) = -2n < 0 $, $ h_{2}(1) = 2n-10 > 0 $, $ h_{2}(3) = 4n-24 > 0 $, $ h_{2}(n-2) = -4 < 0 $ and $ \lim\limits_{x\rightarrow\infty}h_{2}(x) = \infty $. Thus the Laplacian eigenvalues of $ G $ are $ \mu_{1}, \mu_{2}, 3, 2, \underbrace{1, 1, \dots, 1}_{n-6}, \mu_{n-1}, 0 $, where $ \mu_{1}\geq n-2 $, $ 3\leq\mu_{2}\leq n-2 $, $ \mu_{n-1} < 1 $ and $ \mu_{1}+\mu_{2}+\mu_{n-1} = n+3 $.
Therefore
(3) Let $ G\cong G(1, 2, k-3;1, 1, n-k-2) $. When $ 4\leq k\leq \lceil\frac{n}{2}\rceil $, by Lemma 2.8, we conclude that $ 2, \underbrace{1, 1, \cdots, 1}_{n-7} $ are the Laplacian eigenvalues of $ G $ and the remaining laplacian eigenvalues of $ G $ are satisfying equation $ f_{3}(x) = 0 $, where $ f_{3}(x) $ is the characteristic polynomial of the matrix
that is
Let $ g(x) = x^{4}-(n+6)x^{3}+(kn+5n-k^{2}+10)x^{2}-(4kn+5n-4k^{2}+12)x+6n $. Then we obtain $ g(0) = 6n > 0 $, $ g(1) = 3k^{2}-3kn+5n-7 < 0 $, $ g(2) = 4(k-2)(2+k-n) < 0 $, $ g(k) = -(k-2)(k-3)(2k-n)\geq 0 $. Since when $ n $ is odd, $ g(x) $ is same for $ k = \lceil\frac{n}{2}\rceil $ and $ k = \lfloor\frac{n}{2}\rfloor $, we take a smaller value $ k = \lfloor\frac{n}{2}\rfloor $. $ g(n-k) = (2+k-n)(2k-n)(-n+3+k)\leq 0 $ and $ \lim\limits_{x\rightarrow\infty}g(x) = \infty $. Thus the Laplacian eigenvalues of $ G $ are $ \mu_{1}, \mu_{2}, \mu_{3}, 2, \underbrace{1, 1, \cdots, 1}_{n-7}, \mu_{n-1}, 0 $, where $ \mu_{1}\geq n-k $, $ k\leq\mu_{2}\leq n-k $, $ 2 < \mu_{3} < k $, $ \mu_{n-1} < 1 $.
Since $ \sum\limits_{i = 1}^{n}\mu_{i} = 2m = 2(n+1) = 2n+2 $, we get $ \mu_{1}+\mu_{2}+\mu_{3}+\mu_{n-1} = n+6 $, that is, $ \mu_{1}+\mu_{2}+\mu_{3} = n+6-\mu_{n-1} $.
Therefore
When $ \lceil\frac{n}{2}\rceil < k < n-3 $, letting $ k = n-k $ in the Eq (5.3) we get the same characteristic polynomial, so it is equal to the Laplacian energy when $ 4\leq k\leq \lceil\frac{n}{2}\rceil $.
When $ k = n-3 $, $ f_{3}(x) = x(x-1)(x-3)\left(x^{3}-(3+n)x^{2}+(5n-8)x-2n\right) $, so it is equal to the Laplacian energy of $ G(1, 2;2, 5) $.
This completes the proof.
Lemma 5.2. Let $ G_{n, k}\cong G(1, 2, k-3;1, 1, n-k-2) $, where $ 4\leq k\leq \lceil\frac{n}{2}\rceil $. Then $ \mu_{n-1}(G_{n, k})\geq \mu_{n-1}\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) $, with equation holds if and only if $ k = \lceil\frac{n}{2}\rceil $. In particular, if $ n $ is odd, then $ \mu_{n-1}\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) = \mu_{n-1}\left(G(1, 2, \lceil\frac{n}{2}\rceil-4;1, 1, \lfloor\frac{n}{2}\rfloor-1)\right) $.
Proof. If $ k = \lceil\frac{n}{2}\rceil $, then $ \mu_{n-1}(G_{n, k}) = \mu_{n-1}\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) $. By Lemma 5.1, we obtain that $ \mu_{1}, \mu_{2}, \mu_{3}, \mu_{n-1} $ are the roots of the equation $ P(G_{n, k}, x) = 0 $, where
and $ \mu_{1}\geq n-k $, $ k\leq\mu_{2}\leq n-k $, $ 2 < \mu_{3} < k $, $ \mu_{n-1} < 1 $.
We need to prove that
Since
we get $ P(G_{n, k+1}, x)-P(G_{n, k}, x)\leq0 $. Hence $ P(G_{n, k+1}, x)\leq P(G_{n, k}, x) $. So when $ n $ is odd and $ k = \lceil\frac{n}{2}\rceil-1 $, the equation holds.
Thus we have $ \mu_{n-1}(G_{n, k}) > \mu_{n-1}(G_{n, k+1}) $, that is,
Hence $ \mu_{n-1}(G_{n, k}) > \mu_{n-1}(G_{n, \lceil\frac{n}{2}\rceil}) = \mu_{n-1}\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) $.
This completes the proof.
Lemma 5.3. Let $ G $ be a bicyclic graph of order $ n\ge 8 $. Then $ \mu_{n-1}(G(1, 2;2, n-5)) > \mu_{n-1}\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right). $
Proof. When $ k = 3 $, we get $ P(G_{n, k}, x) = f_{2}(x) $, that is $ \mu_{n-1}(G_{n, 3}) = \mu_{n-1}\left(G(1, 2;2, n-5)\right) $.
By Lemma 5.2, we have $ P(G_{n, k+1}, x)\leq P(G_{n, k}, x) $, and $ P(G_{n, 4}, x)\leq P(G_{n, 3}, x) $ still hold.
By inequation (5.5), we obtain
Hence $ \mu_{n-1}\left(G(1, 2;2, n-5)\right) > \mu_{n-1}(G_{n, \lceil\frac{n}{2}\rceil}) = \mu_{n-1}\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) $ for $ n\geq8 $.
Lemma 5.4. Let $ G $ be a bicyclic graph of order $ n\ge 8 $. Then $ \mu_{n-1}(G(1, 1;3, n-5))- \mu_{n-1}\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) > \frac{2}{n}. $
Proof. For $ n = 8 $ and $ n = 9 $, it can be verified by using Maple.
Let $ n = 8 $, $ \mu_{n-1}(G(1, 1;3, n-5)) = 0.8377 $ and $ \mu_{n-1}\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) = 0.5858 $. Then $ \mu_{n-1}(G(1, 1;3, n-5))- \mu_{n-1}\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) = 0.2519 > \frac{1}{4} $, so the conclusion is correct.
Let $ n = 9 $, $ \mu_{n-1}(G(1, 1;3, n-5)) = 0.8169 $ and $ \mu_{n-1}\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) = 0.5344 $. Then $ \mu_{n-1}(G(1, 1;3, n-5))- \mu_{n-1}\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) = 0.2825 > \frac{2}{9} $, so the conclusion is correct.
Next we prove when $ n\geq10 $, the inequality holds.
By Lemma 5.3, we get $ \mu_{n-1}(G(1, 2;2, n-5))\geq \mu_{n-1}\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) $, so we can prove $ \mu_{n-1}(G(1, 1;3, n-5))-\mu_{n-1}(G(1, 2;2, n-5)) > \frac{2}{n} $. Let $ \alpha = \mu_{n-1}(G(1, 1;3, n-5)) $, $ \beta = \mu_{n-1}(G(1, 2;2, n-5)) $. Then it is satisfying
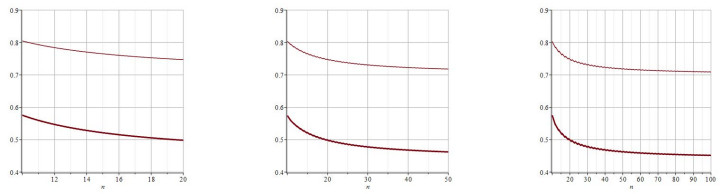
By the implicit function existence theorem and Figure 3, when $ G\cong G(1, 1;3, n-5) $, the relation between the decreases of $ \alpha $ and the increase of $ n $, and $ h_{1}(x) $ is monotonically increasing on the interval $ [0, 1] $. Hence $ h_{1}(0.81) = -3.713+0.39n > 0 $, $ h_{1}(0.69) = -2.956-0.26n < 0 $, so $ 0.69 < \alpha < 0.81 $.
Similarly, $ h_{2}(0.58) = -5.454+0.56n > 0 $, $ h_{2}(0.43) = -3.915-0.035n < 0 $, so $ 0.43 < \beta < 0.58 $. Therefore, $ \alpha-\beta > 0.11 > \frac{2}{19} $, that is, when $ n\geq19 $, hence the conclusion is correct.
When $ 10\leq n\leq18 $, $ \alpha-\beta > \frac{2}{n} $ is obvious. The results are shown in Table 1.
So we conclude that when $ n\geq8 $,
Theorem 5.1. Let $ G $ be a connected bicyclic chain graph of order $ n\geq8 $. Then $ G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2) $ attains the maximal Laplacian energy. In particular, when $ n $ is odd, $ LE\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) = LE\left(G(1, 2, \lceil\frac{n}{2}\rceil-4;1, 1, \lfloor\frac{n}{2}\rfloor-1)\right) $.
Proof. By Lemma 5.1, we can attain the maximal Laplacian energy by comparing $ \mu_{n-1} $ in equations (5.1), (5.2) and (5.4). It is obvious that $ LE(G(1, 2;2, n-5)) < LE\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) $. In particular, when $ n $ is odd, $ LE\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) = LE\left(G(1, 2, \lceil\frac{n}{2}\rceil-4;1, 1, \lfloor\frac{n}{2}\rfloor-1)\right) $. So
Hence by Lemma 5.4, $ LE\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right)-LE(G(1, 1;3, n-5)) > 0 $, that is, $ LE\left(G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2)\right) > LE(G(1, 1;3, n-5)) $. In conclusion, we get $ G(1, 2, \lceil\frac{n}{2}\rceil-3;1, 1, \lfloor\frac{n}{2}\rfloor-2) $ has the maximal Laplacian energy among all connected bicyclic chain graphs $ (n\geq8) $.
6.
Conclusions
In this paper, we introduced the definition of chain graph. We obtain some bounds on $ \varepsilon(G) $ of the chain graphs. Since the rank of the chain graphs is $ 2h $, we can get some bounds on $ \varepsilon(G) $ and $ LE(G) $ of the chain graphs. We present the upper bound on $ LE(G) $ of the chain graphs in terms of vertex cover number. In order to attain the maximal Laplacian energy of bicyclic chain graphs, we compare algebraic connectivity of each kind of bicyclic chain graphs. The problem is still open to discuss what chain graphs give the maximal Laplacian energy for given $ n $ and whether it is still related to algebraic connectivity.
Acknowledgment
This work was supported by National Nature Science Foundation of China (Grant No. 61774137). The authors express their sincere thanks to the anonymous referee for many valuable comments and suggestions.
Conflict of interest
The authors declare that they have no conflict of interest in this paper.









 DownLoad:
DownLoad: