Convergence of discrete duality finite volume schemes for the cardiac bidomain model

1.   Introduction

As has well known, with the rapid development of the global economy and society, water eutrophication has become a global water environmental problem^[1,2]. Furthermore, in order to economically and efficiently assess and respond to natural environmental challenges, theoretical ecologists and mathematicians have delved into complex ecosystems by developing some ecological mathematical models, so that the interactions between prey and predator have consistently been a focal point of ecological research^[3].

In the 1920s, Lotka^[4] and Volterra^[5] introduced the first predator-prey model. Since then, scholars have investigated the interactions between predator and prey influenced by various ecological factors, such as environmental pollution, fishing practice, prey refuge, fear, supplementary food sources, and diseases^{[6,7,8,9,10,11,12,13]}, and obtained some excellent research results. The paper^[6] examined dynamical behaviors of a predator-prey system with foraging facilitation and group defense, and found that both foraging facilitation and group defense mechanisms could play an important role in promoting the balance and diversity of researchers. The researchers ^[7] proposed a two-species model of mammalian prey and mammalian predator, and found that water resources could play a crucial role in shaping the dynamics between mammalian prey and mammalian predator. Researchers^[8] revealed the fact that some species in the ecosystem suddenly burst back many years after almost being extinct. The researchers in^[9] considered a predator-prey model with fear-induced group defense and Monod-Haldane functional response, and highlighted the complex interplay of fear effect, group defense, and anti-predator sensitivity in predator-prey dynamics. The researchers in^[10] raised a mathematical model with Holling type Ⅱ functional response and nonlinear harvesting, and elucidated the dual impact of harvesting and the presence of invasive species. The researchers in^[11] discussed the dynamics and optimal harvesting of a prey-predator fishery model by incorporating the nonlinear Michaelis-Menten type of harvesting in predator, and derived the optimal threshold for the predator harvesting, which could give maximum financial profit to sustain the fishery resources. The researchers in ^[12] explored two kinds of reaction-diffusion predator-prey systems with quadratic intra-predator interaction and linear prey harvesting, and disclosed that the intra-predator interaction and prey harvesting could have a significant effect on the spatiotemporal pattern formations. The researchers in^[13] constructed a cross-diffusive predator-prey model with the inclusion of prey refuge, and revealed that the interaction of both self- and cross-diffusion could play a significant role on the pattern formation.

However, departing from the Lotka-Volterra predator-prey model, forward-thinking mathematicians refined a predator-prey model, which can result in the enhanced Leslie-Gower ameliorated predator-prey model^[14,15]. The Leslie-Gower ameliorated predator-prey model typically takes the following form^[16]:

where $ f(x) $ is named a Leslie–Gower term. Clearly, various functional response functions $ f(x) $ and ecological factors exert distinct impacts, which can lead to diverse outcomes. Consequently, numerous scholars have explored different functional response functions and ecological factors through the Leslie-Gower predator-prey model, such as these papers ^{[17,18,19,20,21,22,23,24,25,26]}. The researchers in^[17] considered a predator-prey model with fear effect and inquired into the occurrence of Turing, Hopf and Turing-Hopf bifurcation. The researchers in^[18] formulated a three-species food chain model to investigate the impact of fear and discovered that the fear effect could transform the system from chaotic dynamics to a stable state. The researchers in^[19] constructed a slow-fast predator-prey system with group defense of the prey and revealed that some certain species in the ecosystem suddenly burst back many years after being about extinct. The researchers in^[20] discussed a predator-prey model with prey refuge and explored the local bifurcation and stability of the limit cycle. The researchers in^[21] described a prey-predator system with constant prey refuge and their objective was to maximize the monetary social benefit through protecting the predator species from extinction. The researchers in^[22] examined the influence of the Allee effect in a prey-predator interaction model with a generalist predator, and found that Allee effect could turn the system more structurally stable compared to prey-predator model with generalist predator. The researchers in^[23] investigated the local and global dynamics of the prey-predator model with emphasis on the impact of strong Allee effect. The researchers in^[24] investigated dynamics of non-autonomous and autonomous systems based on the Leslie–Gower predator-prey model using the Beddington-DeAngelis functional response. The researchers in ^[25] proposed a three-species food chain model to survey the impact of fear and found that fear effect could transform the system from chaotic dynamics to a stable state. The researchers in ^[26] constructed an aquatic ecological model to describe the aggregation effect of Microcystis aeruginosa.

Furthermore, in 1931, the researchers in ^[27] observed the fluctuations in complex populations and concluded that when population density fell below a certain threshold, the birth rate decreased while the mortality rate increased, which was known as the Allee effect. Some researchers ^{[28,29,30,31,32]} incorporated the Allee effect into the predator-prey model, explored the impact of Allee effect on the interaction between predator and prey, and achieved some excellent research results. The researchers in^[28] considered a Leslie-Gower predator-prey model with the Allee effect in prey and illustrated the impact in the stability of positive equilibrium point by adding an Allee effect. The researchers in^[29] proposed a Leslie-Gower predator-prey model with the Allee effect and revealed the influence of Allee effect on the dynamic behaviors. The researchers in^[30] established a phytoplankton-zooplankton model with a strong Allee effect, and pointed out that the Allee threshold for the phytoplankton population could significantly influence the overall dynamics. The researchers in^[31] dealt with an eco-epidemiological predator-prey model with the Allee effect and noted Allee effect had an important and fundamental aspect on population growth. The researchers in^[32] investigated dynamical behavior of a discrete logistic equation with the Allee effect, theoretically and numerically investigated some bifurcation dynamical behaviors, and provided some important dynamic results.

The Beddington-DeAngelis functional response was randomly disturbed by the well-known mean-reverting Ornstein-Uhlenbeck process^[33], and the main difference of this functional response from other functional responses was that it contained an extra term presenting mutual interference by predators, meaning that the predator population density seriously affected the predation dynamic mechanism. Thus, the Beddington-DeAngelis functional response could significantly affect the stability of the Leslie-Gower predator-prey model. Some researchers ^[34,35,36] introduced Beddington-DeAngelis functional response into the predator-prey model, explored its impact on dynamic behavior, and yielded some significant results. The researchers in ^[34] investigated the complex dynamics in a discrete-time predator-prey model with a Beddington–DeAngelis functional response, and determined that the model could exhibit rich complexity features such as stable, periodic, and chaotic dynamics. The researchers in^[35] discussed the dynamic complexities of a three-species food chain with Beddington-DeAngelis functional response and concluded that the model had dynamic properties. The researchers in^[36] developed a predator-prey model with a Beddington-DeAngelis functional response and indicated that the model could appear in a series of complex phenomenon, such as period-doubling, chaos attractor, and period-halfing. Based on the above research results, it can be concluded that Beddington-DeAngelis functional response can cause the predator-prey model to have more diverse dynamic behaviors; we apply the Beddington-DeAngelis functional response to describe the dynamic relationship between predator and prey with sufficient accuracy in this paper.

The focus on sustained harvesting effort was crucial in the study of the predator-prey model^[37]. Some researchers in^[38,39,40] investigated how harvesting factors influence the dynamic relationship between predator and prey, and achieved some important results. The researchers in^[38] explored a predator-prey model to evaluate the impacts of harvesting and summarized that the harvesting of predators was beneficial and could promote the coexistence of species only when their growth from other food sources was too much. The researchers in^[39] proposed a predator-prey model with constant-yield prey harvesting and confirmed that the constant-yield prey harvesting could drive both species to extinction suddenly. The researchers in^[40] constructed a predator-prey system with harvesting, and pointed out that harvesting efforts could generate a region of stability.

Moreover, specific dynamic behavior has always been one of the hot research topics in many fields, and some good results have been obtained in these papers ^{[41,42,43,44,45,46,47,48]}. The researchers in^[41] found that the nonlocal fear effect could enable the system to exhibit Hopf bifurcation and Turing-Hopf bifurcation. The researchers in^[42] provided some discussion of the persistence and extinction of the infective population and examined the global asymptotic stability of the equilibrium point. The researchers in ^[43] indicated that Turing instability could be induced by the negative diffusion coefficients. The researchers in ^[44] studied stability and local bifurcation of semi-trivial steady-state solutions. The researchers in ^[45] investigated global stability of the disease-free equilibrium point in a diffusion system. The researchers in ^[46] analyzed the existence of Hopf bifurcation by analyzing the distribution of the characteristic values. The researchers in ^[47] inquired into some threshold dynamical behaviors for extinction or continuous persistence of disease. The researchers in ^[48] discussed global stability of unique endemic equilibrium point by constructing suitable Lyapunov function.

In this paper, we explore a predator-prey model with a Beddington-DeAngelis functional response functions, the Allee effect, and harvesting effort, namely:

where $ \overline{x}(\overline{t}) $ and $ \overline{y}(\overline{t}) $ represent the population densities of prey and predator respectively, $ r $ and $ s $ represent the intrinsic growth rate of prey and predator respectively, $ K $ is maximum environmental capacity, $ M $ represents the Allee effect threshold ($ 0 < M < K $), $ \alpha $ stands for maximum predation rate, $ \overline{b} $ and $ \overline{c} $ are the half-saturation constant and the functional response constant respectively, $ q_{1} $ is the catchability co-efficient of prey, $ m_{1} $ represents the part of prey that can be harvested, $ e_{1} $ is the effort value for the harvest from prey, $ h $ is used to measure the food quality of prey in order to transform them into offspring of predator, $ q_{2} $ is the catchability co-efficient of predator, $ m_{2} $ represents the part of predator that can be harvested, $ e_{2} $ is the effort value for the harvest from predator. Moreover, it is worthy of our recognition that the main advantage of the model (1.2) is the introduction of the Allee effect and harvesting effort, which not only creates a critical threshold for the extinction and persistence of prey population, but also regulates the persistent survival mode between prey and predator. Furthermore, it is obvious to know that the unit growth function of the prey population is $ f(\overline{x})) = r(1-\frac{\overline{x}}{K})(\overline{x}-M) $, then we have $ \frac{df(\overline{x})}{d\overline{x}} = \frac{r(M+K)-2r\overline{x}}{K} $. Thus, we can obtain $ \frac{df(\overline{x})}{d\overline{x}}|_{\overline{x} = 0} = \frac{r(M+K)}{K} > 0 $, $ f(0) = -rM < 0 $ and $ f(\frac{M+K}{2}) = \frac{r(K-M)^{2}}{4K} > 0 $. According to the conditions satisfied by the strong Allee effect, it can be inferred that the Allee effect introduced in this model is a strong Allee effect.

By performing some straightforward conversions and simplifications, the following transformations were given:

Then we transform the model (1.2) into (1.3)

where $ b = \overline{b}K, c = \frac{\overline{c}rK}{\alpha}, \delta = \frac{s}{\alpha Kh}, \beta = \frac{\alpha h}{r}, \lambda_{1} = \frac{q_{1}m_{1}e_{1}}{rK}, \lambda_{2} = \frac{q_{2}m_{2}e_{2}}{rK} $ are positive constants.

The framework of the paper is organized as follows: In Section 1, we introduce the origin and theoretical basis. In Section 2, the boundedness of the model (1.3) is analyzed. In Sections 3 and 4, the existence and stability of the equilibrium points of the model (1.3) are discussed. In Section 5, the transcritical bifurcation, saddle-node bifurcation, Hopf bifurcation, and Bogdanov-Takens bifurcation in the model (1.3) are studied. In Section 6, numerical simulation experiments are conducted to explore the dynamic behaviors and expound the biological significance. In Section 7, based on the analysis and research of the previous six sections, a brief conclusion is given.

2.   Boundedness of the solutions

In this section, we first examine the limits of $ x(t) $ and $ y(t) $ in the model (1.3) to facilitate a subsequent dynamic analysis.

Theorem 2.1. Under the initial conditions, the solution for the model (1.3) remains positive at all times: $ (x(0), y(0))\in\Omega = \left\lbrace {(x, y)\in R^{2}\mid x > 0, y > 0}\right\rbrace $.

Proof. Based on the model's conditions, we can perceive the boundary using the equation below:

Therefore, the model (1.3) typically exhibits its most common boundary $ \left\lbrace {(x, y)\in R^{2}\mid x > 0, y > 0}\right\rbrace $. Next, we investigate the bounds of $ x(t) $ and $ y(t) $ through the two equations associated with the model (1.3), respectively. □

Theorem 2.2. As long as the model (1.3) satisfies $ \lambda_{2} < \delta \beta $, the range of $ x(t) $ and $ y(t) $ in the model (1.3) can be confined to a positive set:

Proof. We pay attention to the first equation of the model (1.3), and give the following scaling form:

Regarding this equation, we will analyze and discuss three scenarios to determine the approximate range of $ x(t) $:

1) If $ x(t) > 1 $, then $ \dot{x} < 0 $.

2) If $ 0 < x(t) < m $, then $ \dot{x} < 0 $.

3) If $ m < x(t) < 1 $, then $ x(t) < 1-\frac{1}{1+C_{1} e^{(1-m)t}} $, so $ \mathop{lim}\limits_{t \to +\infty} supx(t)\le1 $.

The first and second points are self-evident, let us scale it up and down

then

Simplify through integration on both sides, we can get

then

Obviously, if $ x(t) > 1 $, then $ \dot{x} < 0 $. If $ 0 < x(t) < m $, then $ \dot{x} > 0 $. If $ m < x(t) < 1 $, then $ x(t) < 1-\frac{1}{1+C_{1} e^{(1-m)t}} $, so $ 0 < x(t) < 1 $ when $ (x(t), y(t))\in R_{+}^{2} $. Then we pay attention to the second equation of the model (1.3), give the following scaling form:

Regarding this equation, we will analyze and discuss two scenarios to determine the approximate range of $ y(t) $:

1) If $ y\ge\beta-\frac{\lambda_{2}}{\delta} $, then $ \dot{y} < 0 $. This contradicts the positive solution of $ y(t) $ in Theorem 2.1.

2) If $ 0 < y < \beta-\frac{\lambda_{2}}{\delta} $, then $ y(t) < \beta-\frac{\lambda_{2}}{\delta}-\frac{\beta-\frac{\lambda_{2}}{\delta}}{1+C_{2} e^{\delta(\beta-\frac{\lambda_{2}}{\delta})t}} $, so $ \mathop{lim}\limits_{t \to +\infty} supy(t)\le\beta-\frac{\lambda_{2}}{\delta} $.

The first point is self-evident, so let's focus on proving the second one:

Simplify through integration on both sides, we can get

then, we can obtain

By calculation, we can clearly see $ \mathop{lim}\limits_{t \to +\infty} supy(t)\le\beta-\frac{\lambda_{2}}{\delta} $. Based on the prior discussions regarding $ x(t) $ and $ y(t) $, we can infer that the model (1.3) is subject to specific boundaries, and we encapsulate this conclusion within a set:

□

3.   The existence of all possible equilibrium points

The existence of all possible equilibrium points in the model (1.3) is particularly important, which is the foundation for bifurcation dynamical research and indicates that prey and predator can remain stable in a certain state. In this section, the existence of all possible equilibrium points in the model (1.3) is carefully studied.

Based on the prey population equation $ F(x) $ and the predator population equation $ G(x) $, we convert the model (1.3) into the equation system (3.1) in order to more effectively expose the dynamical behavior at the equilibrium point, the equation as following:

If $ (m+1)^{2}-4(m+\lambda_{1}) > 0 $ holds, then we can obtain that the model (1.3) has two boundary equilibrium points, a predator-free equilibrium point $ E_{1}(x_{1}, 0) $ and a predator-free equilibrium point $ E_{2}(x_{2}, 0) $, where $ x_{1} $ and $ x_{2} $ are the roots of the equation:

solving the above equation, we can obtain $ x_{1} $ and $ x_{2} $ as

It is obvious to find that there is only one boundary equilibrium point $ (\frac{m+1}{2}, 0) $ when $ (m+1)^{2}-4(m+\lambda_{1}) = 0 $ holds. However, at this juncture, the absence of an internal equilibrium point in the model (1.3) renders it unsuitable for our intended study on internal equilibrium points. Consequently, to ensure the existence of such a point, we must fulfill certain prerequisites which need to satisfy $ (m+1)^{2}-4(m+\lambda_{1}) > 0 $, where $ x^{*} $ and $ y^{*} $ are the roots of the equation:

From the second equation of the equation system (3.2), we can get $ y = (\beta -\frac{\lambda_{2}}{\delta})x $. From section two, we can get $ \beta-\frac{\lambda_{2}}{\delta} > 0 $. Integrate the first equation with the second equation, we can get the Eq (3.3):

Let

Theorem 3.1. For the number of positive internal equilibrium points, we have:

(1) If $ A = B = 0 $ holds, then the model (1.3) does not have any internal positive equilibrium point.

(2) If $ \varDelta > 0 $ holds, then the model (1.3) does not have any positive equilibrium point.

(3) If $ \varDelta = 0 $ holds, then the model (1.3) has a positive equilibrium point $ E_{1}^{*} $ or $ E_{2}^{*} $, where $ x_{1}^{*}, x_{2}^{*} $ are dual positive roots.

(4) If $ \varDelta < 0 $ holds, then the model (1.3) has two single positive equilibrium points $ E_{3}^{*} $ and $ E_{4}^{*} $ or $ E_{5}^{*} $ and $ E_{6}^{*} $.

Proof. For the number of positive internal equilibrium points, we have:

1) When $ A = B = 0 $ holds, according to Cardano formula, then Eq (3.3) has a triple real root, and according to Descartes sign rule, when $ 1-(m+1)\varphi\leqslant0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1)\leqslant0 $ hold, obtaining a triple negative root is not helpful for our model research, so it is omitted.

2) When $ \varDelta > 0 $ holds, according to Cardano formula, then Eq (3.3) has a real root and a pair of conjugate imaginary roots.

(ⅰ) When $ 1-(m+1)\varphi > 0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1) > 0 $ hold, according to Descartes sign rule, then Eq (3.3) has a negative root and not have positive root.

(ⅱ) When $ 1-(m+1)\varphi < 0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1) > 0 $ hold, according to Descartes sign rule, then Eq (3.3) does not have a positive root or has two negative roots, thus the model (1.3) does not have positive root.

(ⅲ) When $ 1-(m+1)\varphi > 0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1) < 0 $ hold, for the same reason (ii), Eq (3.3) does not have positive internal equilibrium point.

(ⅳ) When $ 1-(m+1)\varphi < 0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1) < 0 $ hold, for the same reason (i), Eq (3.3) does not have positive root. Thus, when $ \varDelta > 0 $ holds, Eq (3.3) does not have positive root, that is to say, the model (1.3) does not have any internal positive equilibrium point.

3) When $ \varDelta = 0 $ holds, according to Cardano formula, then Eq (3.3) has three real roots, including one double root.

(ⅰ) When $ 1-(m+1)\varphi > 0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1) > 0 $ hold, according to Descartes sign rule, then the equation (3.3) has three negative roots, including one double negative root.

(ⅱ) When $ 1-(m+1)\varphi < 0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1) > 0 $ hold, according to Descartes sign rule and Vieta theorem for univariate cubic equations, $ x_{1}+x_{2}+x_{3} < 0 $ and $ x_{1}x_{2}x_{3} < 0 $, thus Eq (3.3) has a double negative root and a single negative root.

(ⅲ) When $ 1-(m+1)\varphi > 0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1) < 0 $ hold, according to Descartes sign rule and Vieta theorem for univariate cubic equations, $ x_{1}+x_{2}+x_{3} > 0, x_{1}x_{2}x_{3} < 0 $, thus Eq (3.3) has a double positive root and a negative root, then the model (1.3) has a positive equilibrium point $ E_{1}^{*} = (x_{1}^{*}, y_{1}^{*}) $, where $ x_{1}^{*} $ is a dual positive root.

(ⅳ) When $ 1-(m+1)\varphi < 0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1) < 0 $ hold, according to Descartes sign rule and Vieta theorem for univariate cubic equations, $ x_{1}+x_{2}+x_{3} > 0, x_{1}x_{2}x_{3} < 0 $, thus Eq (3.3) has a double positive root and a negative root, then the model (1.3) has a positive equilibria point $ E_{2}^{*} = (x_{2}^{*}, y_{2}^{*}) $, where $ x_{2}^{*} $ is a dual positive root. Thus, when $ \varDelta = 0 $, the model (1.3) has a positive equilibrium points $ E_{1}^{*} $ or $ E_{2}^{*} $ under certain conditions.

4) When $ \varDelta < 0 $ holds, according to Cardano formula, then Eq (3.3) has two unequal real roots.

(ⅰ) When $ 1-(m+1)\varphi > 0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1) > 0 $ hold, according to Descartes sign rule and Vieta theorem for univariate cubic equations, $ x_{1}+x_{2}+x_{3} < 0, x_{1}x_{2}x_{3} < 0 $, thus Eq (3.3) has three single negative roots.

(ⅱ) When $ 1-(m+1)\varphi < 0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1) > 0 $ hold, for the same reason (i), Eq (3.3) does not have positive root.

(ⅲ) When $ 1-(m+1)\varphi > 0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1) < 0 $ hold, according to Descartes sign rule and Vieta theorem for univariate cubic equations, $ x_{1}+x_{2}+x_{3} < 0, x_{1}x_{2}x_{3} > 0 $, thus Eq (3.3) has two single positive root and a negative root, then the model (1.3) has two unequal positive equilibrium points $ E_{3}^{*} = (x_{3}^{*}, y_{3}^{*}) $ and $ E_{4}^{*} = (x_{4}^{*}, y_{4}^{*}) $, where $ x_{3}^{*}, x_{4}^{*} $ are all single positive roots and $ x_{3}^{*} < x_{4}^{*} $.

(ⅳ) When $ 1-(m+1)\varphi < 0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1) < 0 $ hold, according to Descartes sign rule and Vieta theorem for univariate cubic equations, $ x_{1}+x_{2}+x_{3} < 0, x_{1}x_{2}x_{3} > 0 $, thus Eq (3.3) has a negative root and two single positive root, then we can obtain two unequal positive equilibrium points $ E_{5}^{*} = (x_{5}^{*}, y_{5}^{*}), E_{6}^{*} = (x_{6}^{*}, y_{6}^{*}) $ for the model (1.3), where $ x_{5}^{*}, x_{6}^{*} $ are all single positive roots and $ x_{5}^{*} < x_{6}^{*} $. Thus, when $ \varDelta < 0 $ holds, according to Cardano formula, the model (1.3) has two single positive equilibrium points $ E_{3}^{*} $ and $ E_{4}^{*} $ or $ E_{5}^{*} $ and $ E_{6}^{*} $ under certain conditions. □

Theorem 3.2. Based on the equilibrium point derived from Theorem 3.1 $ x_{1}^{*}, x_{2}^{*}, x_{3}^{*}, x_{4}^{*}, x_{5}^{*}, x_{6}^{*} $, we can establish certain conditions that will facilitate our subsequent research endeavors: (a) $ g(x_{1}^{\ast}) = 0 $ or $ g(x_{2}^{\ast}) = 0 $; (b) $ g(x_{3}^{\ast}) < 0 $ or $ g(x_{5}^{\ast}) < 0 $; (c) $ g(x_{4}^{\ast}) > 0 $ or $ g(x_{6}^{\ast}) > 0 $.

4.   Stability of some equilibrium points

This section delves into the stability analysis of two boundary equilibrium points $ E_{1}, E_{2} $ and some internal equilibrium points. Typically, the stability of equilibrium point can be ascertained by examining the signs of the eigenvalues at that particular point. Consequently, we present the Jacobian matrix of the model (1.3) evaluated at any equilibrium point $ E(x, y) $:

utilizing the Jacobian matrix at any given point, we can formulate the following theorem.

4.1.   Stability of the boundary equilibrium point

Theorem 4.1. The stability of the boundary equilibrium point $ E_{2}(\frac{m+1+\sqrt{(m+1)^{2}-4(m+\lambda_{1})}}{2}, 0) $ is discussed as follows:

1) If $ \lambda_{2} > \delta\beta $ holds, then the equilibrium point $ E_{2} $ is a stable node.

2) If $ \lambda_{2} < \delta\beta $ holds, then the equilibrium point $ E_{2} $ is a saddle.

3) If $ \lambda_{2} = \delta\beta $ holds, then the equilibrium point $ E_{2} $ is a attracting saddle-node. In essence, a small enough area surrounding the equilibrium point $ E_{2} $ is partitioned into two sections by two dividing lines that traverse its top and bottom, converging towards $ E_{2} $ as the region diminishes. Furthermore, the left half plane comprises a parabolic sector, whereas the right half plane is comprised of two hyperbolic sectors.

Proof. We can obtain that the Jacobian matrix of the equilibrium point $ E_{2} $ is:

Apparently, $ J_{E_{2}} $ has two eigenvalues $ \mu_{1} = -3x_{2}^{2}+(2+2m)x_{2}-m-\lambda_{1} = -2x_{2}^{2}+(1+m)x_{2} = -2(\frac{m+1+\sqrt{(m+1)^{2}-4(m+\lambda_{1})}}{2})^{2}+(1+m)(\frac{m+1+\sqrt{(m+1)^{2}-4(m+\lambda_{1})}}{2}) = x_{2}(-\sqrt{(m+1)^{2}-4(m+\lambda_{1})}) < 0 $ and $ \mu_{2} = \delta\beta-\lambda_{2} $. Since $ \mu_{1} $ is consistently less than 0, it is imperative to discuss the sign of $ \mu_{2} $ in order to assess stability. We will approach this discussion from three distinct angles: (a) If $ \mu_{2} = \delta\beta-\lambda_{2} < 0 $, $ i.e. $, $ \lambda_{2} > \delta\beta $, then the boundary point $ E_{2} $ is a stable node. (b) If $ \mu_{2} = \delta\beta-\lambda_{2} > 0 $, $ i.e. $, $ \lambda_{2} < \delta\beta $, then the boundary point $ E_{2} $ is a saddle. (c) If $ \mu_{2} = \delta\beta-\lambda_{2} = 0 $, $ i.e. $, $ \lambda_{2} = \delta\beta $, then the model (1.3) has two eigenvalues are $ \mu_{1} = x_{2}(-\sqrt{(m+1)^{2}-4(m+\lambda_{1})}) $ and $ \mu_{2} = 0 $. Determining the stability of scenarios (a) and (b) is relatively straightforward. Subsequently, our focus will primarily be on scenario (c). We will shift $ E_{2} $ to the origin by $ (X, Y) = (x-x_{2}, y) $ and expand model (1.3) to the third-order using Taylor's series, obtaining:

where $ \alpha_{10} = -3{x_{2}}^{2}+2(1+m)x_{2}-(m+\lambda_{1}), \quad \alpha_{01} = -\frac{x_{2}(1+bx_{2})}{(1+bx_{2})^{2}}, \quad\alpha_{02} = \frac{cx_{2}}{(1+bx_{2})^{2}}, \quad\alpha_{11} = -\frac{1}{(1+bx_{2})^{2}}, $ $ \alpha_{20} = -3x_{2}+1+m, \quad\alpha_{30} = -1, \quad\alpha_{03} = -\frac{c^{2}x_{2}}{(1+bx_{2})^{3}}, \quad\alpha_{21} = \frac{b}{(1+bx_{2})^{3}}, \quad \alpha_{12} = -\frac{c(bx_{2}-1)}{(1+bx_{2})^{3}}, $ and $ M_{1}(X, Y) $, $ N_{1}(X, Y) $ are fourth-order infinitesimal quantity.

By the simplistic transformation

then

where $ \alpha_{10} = -3{x_{2}}^{2}+2(1+m)x_{2}-(m+\lambda_{1}), \quad \alpha_{01} = -\frac{x_{2}(1+bx_{2})}{(1+bx_{2})^{2}}. $

Thus, the model (4.1) becomes a standard form

where $ \alpha_{10} = -3{x_{2}}^{2}+2(1+m)x_{2}-(m+\lambda_{1}), \alpha_{01} = -\frac{x_{2}(1+bx_{2})}{(1+bx_{2})^{2}}, h_{1} = \alpha_{20}\frac{-2\alpha_{01}}{\alpha_{10}}+\alpha_{11}, h_{2} = \alpha_{20}(\frac{\alpha_{01}}{\alpha_{10}})^{2}-\frac{\alpha_{11} \alpha_{01}}{\alpha_{10}}+\alpha_{02} $, $ M_{2}(x, y) $ and $ N_{2}(x, y) $ are fourth-order infinitesimal quantity, and the remaining algorithms of $ h_{3}, h_{4}, h_{5}, h_{6} $ are the same, so we will not list them one by one here. Since the coefficient of $ y^2 $ for the second equation of the model $ (4.2) $ is $ -\delta < 0 $, the key internal point $ E_{2}(\frac{m+1+\sqrt{(m+1)^{2}-4(m+\lambda_{1})}}{2}, 0) $ is a attracting saddle-node if $ \lambda_{2} = \delta\beta $. Thus we can obtained this results from Theorem 7.1 in Chapter 2 in ^[49]. □

Furthermore, it is easy to obtain that the boundary equilibrium point $ E_{1}(\frac{m+1-\sqrt{(m+1)^{2}-4(m+\lambda_{1})}}{2}, 0) $ is a saddle if $ \lambda_{2} > \delta\beta $, is an unstable node if $ \lambda_{2} < \delta\beta $, and is a saddle-node if $ \lambda_{2} = \delta\beta $.

4.2.   Stability of some internal equilibrium points

We will delve into the stability of some internal equilibrium points, echoing the discussions presented in Section 4.1. Specifically, we will proceed to compute the Jacobian matrix for any given internal equilibrium point as follows:

then we get:

4.2.1.   Stability of the equilibrium points $ E_{1}^{*} $ and $ E_{2}^{*} $

Lemma 4.1. (^[49]). The model

where $ M_{1}(\alpha, \beta) $ and $ N_{1}(\alpha, \beta) $ are tired-order infinitesimal quantity, i.e., $ M_{1}(\alpha, \beta) = o(\left| \alpha, \beta\right| ^2) $, $ N_{1}(\alpha, \beta) = o(\left| \alpha, \beta\right| ^2) $, we can transform Eq (4.3) into (4.4)

by certain nonsingular transformations in the domain of $ (0, 0). $

Theorem 4.2. If $ \Delta = 0, 1-(m+1)\varphi > 0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1) < 0 $ hold, then the model (1.3) has an internal point $ E_{1}^{*} = (x_{1}^{*}, y_{1}^{*}) $, where $ x_{1}^{*} $ is a dual root, then:

1) If $ m\neq-3{x_{1}^{*}}^{2}+(2+2m)x_{1}^{*}-\frac{(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*}+c((\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{2}}{(1+bx_{1}^{*}+c(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{2}}-\lambda_{1}+\lambda_{2}-\delta\beta $ and $ m\neq3x_{1}^{*}-1+\frac{\beta-\frac{\lambda_{2}}{\delta}}{(1+bx_{1}^{*}+c(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{3}} $ hold, then the internal point $ E_{1}^{*} $ is a saddle-node.

2) If $ m = -3{x_{1}^{*}}^{2}+(2+2m)x_{1}^{*}-\frac{(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*}+c((\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{2}}{(1+bx_{1}^{*}+c(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{2}}-\lambda_{1}+\lambda_{2}-\delta\beta $ holds, the internal point $ E_{1}^{*} $ is a cusp. Further, if $ m\neq3x_{1}^{*}-1+\frac{\beta-\frac{\lambda_{2}}{\delta}}{(1+bx_{1}^{*}+c(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{3}} $ and $ m\neq 3x_{1}^{*}-1+\frac{(\beta-\frac{\lambda_{2}}{\delta})-(\beta-\frac{\lambda_{2}}{\delta})bx_{1}^{*}+(\beta-\frac{\lambda_{2}}{\delta})cy_{1}^{*}}{2(1+bx_{1}^{*}+c(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{3}} $ hold, then the internal point $ E_{1}^{*} $ is a cusp with codimension 2. If $ m = 3x_{1}^{*}-1+\frac{\beta-\frac{\lambda_{2}}{\delta}}{(1+bx_{1}^{*}+c(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{3}} $ or $ m = 3x_{1}^{*}-1+\frac{(\beta-\frac{\lambda_{2}}{\delta})-(\beta-\frac{\lambda_{2}}{\delta})bx_{1}^{*}+(\beta-\frac{\lambda_{2}}{\delta})cy_{1}^{*}}{2(1+bx_{1}^{*}+c(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{3}} $ hold, then the internal point $ E_{1}^{*} $ is a cusp with codimension at least 3.

Proof. Firstly, we utilize the approach outlined in Lemma 4.1 to shift the origin to $ E_{1}^{*} $ by setting $ (X, Y) = (x-x_{1}^{*}, y-y_{1}^{*}) $ and derive a new model (4.5) accordingly:

where

and $ M_{3}(X, Y) $, $ N_{3}(X, Y) $ are third-order infinitesimal quantity.

Case 1: $ m\neq-3{x_{1}^{*}}^{2}+(2+2m)x_{1}^{*}-\frac{(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*}+c((\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{2}}{(1+bx_{1}^{*}+c(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{2}}-\lambda_{1}+\lambda_{2}-\delta\beta $.

In this scenario, the Jacobian matrix of the model (4.5) is presented as follows:

then we can get that $ \mu_{1} = 0 $, $ \mu_{2} = q_{10}^{\prime}+p_{01}^{\prime} $ are two eigenvalues of $ J_{E_{1}^{*}} $. By a transformation, we can transform the model (4.5) into the model (4.6):

After that, the model (4.5) becomes

where

and $ \gamma = \beta-\frac{\lambda_{2}}{\delta} $, $ M_{4}(x, y) $, $ N_{4}(x, y) $ are third-order infinitesimal quantity.

We introduce a new transformation $ \iota $ to the model (4.7) by $ \iota = (q_{10}^{\prime}+\lambda_{2}-\delta\beta)t $, and continue to use $ t $ as a substitute for $ \iota $, and upon substitution, thus we can obtain the following model (4.7):

where $ r_{ij}^{\prime} = \frac{w_{ij}^{\prime}}{q_{10}^{\prime}+\lambda_{2}-\delta\beta} $, $ s_{ij}^{\prime} = \frac{z_{ij}^{\prime}}{q_{10}^{\prime}+\lambda_{2}-\delta\beta} $ $ (i+j = 2) $, $ M_{5}(x, y) $, $ N_{5}(x, y) $ are third-order infinitesimal quantity.

Then we can obtain

and

According to ^[49], we can determine that $ E_{1}^{*} $ is a saddle-node if $ z_{02}^{\prime}\neq0 $ and $ s_{02}^{\prime}\neq0 $. That is, if

i.e.,

and

i.e.,

Case 2: $ m = -3{x_{1}^{*}}^{2}+(2+2m)x_{1}^{*}-\frac{(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*}+c((\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{2}}{(1+bx_{1}^{*}+c(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{2}}-\lambda_{1}+\lambda_{2}-\delta\beta. $

A new Jacobi matrix of the model (4.5) is

then we can get that $ \mu_{1} = 0 $, $ \mu_{2} = 0 $ are two eigenvalues of $ J_{E_{1}^{*}} $. By a transformation, we can transform the model (4.5) into (4.8)

After that, the model (4.5) becomes

where

and $ \gamma = \beta-\frac{\lambda_{2}}{\delta} $, $ M_{6}(x, y) $, $ N_{6}(x, y) $ are third-order infinitesimal quantity.

We introduce a new transformation $ \iota $ to the model (4.9) by $ \iota = \delta t $, and continue to use $ t $ as a substitute for $ \iota $, hence we can obtain the following model (4.9):

where $ r_{ij} = \frac{w_{ij}}{\delta} $, $ s_{ij} = \frac{z_{ij}}{\delta} $ $ (i+j = 2) $, $ M_{7}(x, y) $, $ N_{7}(x, y) $ are third-order infinitesimal quantity.

According to ^[49], we can determine that $ E_{1}^{*} $ is a cusp. Let us make the next deffnitions

We can get $ y+A(x, y) = 0 $ and $ r_{20}\neq0 $, and also we can obtain

then we have

According to Lemma 4.1, we can transform the model (4.9) into (4.10)

where $ N_{8}(x, y) $ is third-order infinitesimal quantity.

Then we can obtain

where $ T_{3} = 1+bx_{1}^{*}+cy_{1}^{*} $. Therefore, according to ^[49], we can determine that $ E_{1}^{*} $ is a cusp when $ k = 2h, h = 1, q_{2m} = s_{20}, N = 1, B_{N} = 2r_{20}+s_{11} $. Furthermore, if $ s_{20}\neq0 $ and $ s_{11}+2r_{20}\neq 0 $, then the internal point $ E_{1}^{*} $ is a cusp with codimension 2. If $ s_{02} = 0 $ or $ s_{11}+2r_{20} = 0 $, then the internal point $ E_{1}^{*} $ is a cusp with codimension at least 3. That is

i.e.,

□

Otherwise, when $ \Delta = 0 $, $ 1-(m+1)\varphi < 0 $ and $ (m+\lambda_{1})\varphi+\gamma-(m+1) < 0 $ hold, the stability investigation of the internal point $ E_{2}^{*} $ is similar to the discussion of stability of the equilibrium point $ E_{1}^{*} $, so we simply ignore it.

4.2.2.   Stability of the equilibrium point $ E_{i}^{\ast} $

If the conditions for the existence of equilibrium points $ E_{i}^{\ast} $ ($ i = 3, 4, 5, 6, $) are satisfied, the values of $ Det(J_{E_{3}^{\ast}}) $ and $ Det(J_{E_{5}^{\ast}}) $ are consistently negative,

Therefore, as their determinants are consistently less than 0 by Theorem 3.2, the equilibrium points $ E_{3}^{\ast} $ and $ E_{5}^{\ast} $ are classified as saddle. Pursuant to Theorem 3.2, it is ascertainable that the values of $ Det(J_{E_{4}^{\ast}}) $ and $ Det(J_{E_{6}^{\ast}}) $ remain positive at all times. Subsequently, our discussion shall encompass three perspectives: (a) If $ Tr(J_{E_{i}^{\ast}}) > 0 $, it is a source. (b) If $ Tr(J_{E_{i}^{\ast}}) = 0 $, it is a center. (c) If $ Tr(J_{E_{i}^{\ast}}) < 0 $, it is a sink.

Hence, we can consolidate the aforementioned analysis and gain the following theorem.

Theorem 4.3. Pursuant to Theorem 3.2, it is ascertainable that the values of $ Det(J_{E_{4}^{\ast}}) $ and $ Det(J_{E_{6}^{\ast}}) $ remain positive at all times. Subsequently, our discussion shall encompass three perspectives: (a) If $ Tr(J_{E_{i}^{\ast}}) > 0 $, it is a source. (b) If $ Tr(J_{E_{i}^{\ast}}) = 0 $, it is a center. (c) If $ Tr(J_{E_{i}^{\ast}}) < 0 $, it is a sink.

Theorem 4.4. Therefore, as their determinants are consistently less than 0 by Theorem 3.2, the equilibrium points $ E_{3}^{\ast} $ and $ E_{5}^{\ast} $ are classified as saddle.

5.   Bifurcation analysis

To investigate the impact of Allee effect and harvesting effort on the dynamic behavior of the model (1.3), we chose $ \lambda_{2} $ and $ m $ as bifurcation control parameters and encompassed transcritical bifurcation, saddle-node bifurcation, Hopf bifurcation, and Bogdanov-Takens bifurcation of the model (1.3).

5.1.   Transcritical bifurcation

Theorem 5.1. The model (1.3) can undergo a transcritical bifurcation when $ \lambda_{2} = \lambda_{TC} = \beta\delta $.

Proof. When $ \lambda_{2} = \lambda_{TC} = \beta\delta $, we can get the Jacobian matrix from Theorem 4.1:

Next, we demonstrate the occurrence of transcritical bifurcation by the Sotomayor's theorem. Assuming that $ U $ represents the eigenvector of $ J_{E_{2}} $ pertaining to 0, and $ V $ corresponds to the eigenvector of $ J_{E_{2}}^T $ pertaining to 0, we present the following exposition:

Then we can get

Therefore, we can get

Therefore, the model (1.3) can undergo a transcritical bifurcation when $ \lambda_{2} = \lambda_{TC} = \beta\delta $. □

5.2.   Saddle-node bifurcation

According to the Theorem 3.1 Case 3, we can get a bifurcation surface for saddle-node:

where $ T_{1} = 1-(m+1)[b+c(\beta-\frac{\lambda_{2}}{\delta})] $ and $ T_{2} = (m+\lambda_{1})[b+c(\beta-\frac{\lambda_{2}}{\delta})]+\beta-\frac{\lambda_{2}}{\delta}-(m+1) $.

We can observe that the sign of $ \Delta $ can be altered by $ \lambda_{2} $, during which process the number of equilibrium points transforms from 0 to $ 1 $ and then to $ 2 $. Consequently, to ascertain whether the model (1.3) is capable of undergoing a saddle-node bifurcation, we proceed with the following derivation.

Theorem 5.2. Under the condition of:

1) $ \beta-\frac{\lambda_{2}}{\delta} > 0 $,

2) $ 1-(m+1)[b+c(\beta-\frac{\lambda_{2}}{\delta})] < 0 $,

3) $ (m+\lambda_{1})[b+c(\beta-\frac{\lambda_{2}}{\delta})]+\beta-\frac{\lambda_{2}}{\delta}-(m+1) > 0 $,

when $ \Delta = 0 $, i.e., $ \lambda_{2} = \lambda_{SN} $, the model (1.3) can undergo a saddle-node bifurcation.

Proof. Now, we demonstrate the occurrence of transcritical bifurcation by the Sotomayor's theorem, the Jacobian matrix at $ E_{1}^{*} $ is:

If $ \lambda_{2} = \lambda_{SN} $, the Jacobian matrix at $ E_{1}^{*} $ can be written in the following form:

where $ \gamma = \beta-\frac{\lambda_{SN}}{\delta} $, $ e_{12} = -\frac{x_{1}^{*}(1+bx_{1}^{*})}{(1+bx_{1}^{*}+c(\beta-\frac{\lambda_{2}}{\delta}))^{2}} $.

Zero is one of the eigenvalues, then we can assume that $ U $ represents the eigenvector of $ J_{E_{1}^{*}} $ pertaining to 0, and $ V $ corresponds to the eigenvector of $ J_{E_{1}^{*}}^T $ pertaining to 0, we present the following exposition:

Therefore, we can obtain

Finally, we can get

Therefore, the model (1.3) can undergo a saddle-node bifurcation when $ \lambda_{2} = \lambda_{SN} = \beta\delta $. □

5.3.   Hopf bifurcation

From Theorem 4.4, $ E_{3}^{\ast} $ and $ E_{5}^{\ast} $ are always saddle whenever they exist. From Theorem 4.3, $ E_{4}^{\ast} $ and $ E_{6}^{\ast} $ may be a source or a sink or a center. Therefore, only $ E_{4}^{\ast} $ and $ E_{6}^{\ast} $ are potentially susceptible to Hopf bifurcation. Given the similarity in properties between $ E_{6}^{\ast} $ and $ E_{4}^{\ast} $, we shall focus our discussion on the prototypical internal equilibrium point $ E_{4}^{\ast} $. We designate $ \lambda_{2} $ as the variable of interest, which is derived from the condition where the trace equals zero $ Tr(J_{E_{4}^{\ast}}) = 0 $. As $ \lambda_{2} $ varies and surpasses the threshold $ \lambda_{H} $, the stability of $ E_{4}^{\ast} $ is disrupted. Subsequently, we will furnish a rigorous proof to support this assertion.

Theorem 5.3. Unstable limit cycles will occur near $ E_{4}^{\ast} $ when the first Lyapunov coefficient $ l_1 > 0 $, and furthermore, the internal equilibrium point $ E_{4}^{\ast} $ will also lose its stability due to subcritical Hopf bifurcation when $ \lambda_{2} = \lambda_{H} $.

Proof. We also know $ Det(J_{E_{4}^{\ast}}) > 0 $ and $ Tr(J_{E_{4}^{\ast}}) = 0 $ when $ \lambda_{2} = \lambda_{H} $. Then,

then

The internal equilibrium point $ E_{4}^{\ast} $ will also lose its stability due to subcritical Hopf bifurcation when $ \lambda_{2} = \lambda_{H} $.

Furthermore, to assess the stability and direction of the limit cycle formed by this point $ E_{4}^{\ast} $, we need to calculate its first Lyapunov number. This can be achieved by employing a transformation, specifically, $ q = x-x_{4}^{*} $, $ w = y-y_{4}^{*} $, we can shift $ E_{4}^{\ast} $ to the origin, and gain:

where

and $ M_{1}(q, w) $, $ N_{1}(q, w) $ are fourth-order infinitesimal quantity.

The first Lyapunov coefficient $ l_{1} $ is

In ^[49], the dynamic relationship between Lyapunov coefficients and Hopf bifurcation was referred to. The literature indicates that stable limit cycle will emerge near $ E_4^\ast $ when the first Lyapunov coefficient $ l_1 < 0 $. Additionally, due to supercritical Hopf bifurcation, the internal equilibrium point $ E_4^\ast $ will lose its stability. Unstable limit cycles will occur near $ E_4^\ast $ when the first Lyapunov coefficient $ l_1 > 0 $, and the internal equilibrium point $ E_4^\ast $ will also lose its stability due to subcritical Hopf bifurcation. □

5.4.   Bogdanov-Takens bifurcation

In the previous three sections, we discussed the bifurcation of the codimension-one branch of the model (1.3). Next, we will prove the occurrence of the codimension-two Bogdanov-Takens bifurcation. According to Theorem 4.2, we conclude that $ E_{1}^{*} $ is a codimension-two cusp when the following conditions meet $ \Delta = 0, 1-(m+1)\varphi > 0, (m+\lambda_{1})\varphi+\gamma-(m+1) < 0, m = -3{x_{1}^{*}}^{2}+(2+2m)x_{1}^{*}-\frac{(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*}+c(\beta-\frac{\lambda_{2}}{\delta})^{2}{x_{1}^{*}}^{2}}{(1+bx_{1}^{*}+c(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{2}}-\lambda_{1}+\lambda_{2}-\delta\beta $ and $ Det(J_{E_{1}^{\ast}})\neq0 $. Next, we study the Bogdanov-Takens bifurcation with parameters $ \lambda_{2} $ and $ m $.

Theorem 5.4. If we choose $ \lambda_{2} $ and $ m $ as bifurcation parameters, then the model (1.3) can generate a Bogdanov-Takens bifurcation around $ E_{1}^{*} $ with changing parameters $ (\lambda_{2}, m) $ near $ (\lambda_{BT}, m_{BT}) $ for $ \Delta = 0, 1-(m+1)\varphi > 0, (m+\lambda_{1})\varphi+\gamma-(m+1) < 0, m = -3{x_{1}^{*}}^{2}+(2+2m)x_{1}^{*}-\frac{(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*}+c(\beta-\frac{\lambda_{2}}{\delta})^{2}{x_{1}^{*}}^{2}}{(1+bx_{1}^{*}+c(\beta-\frac{\lambda_{2}}{\delta})x_{1}^{*})^{2}}-\lambda_{1}+\lambda_{2}-\delta\beta $ and $ Det(J_{E_{1}^{\ast}})\neq0 $, where $ (\lambda_{BT}, m_{BT}) $ denotes the bifurcation threshold value i.e.,

Proof. To derive precise expressions for saddle points, Hopf, and homoclinic bifurcation curves within a small vicinity around the Bogdanov-Takens point, we convert the model (1.3) into the canonical form of Bogdanov-Takens bifurcation. Subsequently, we introduce a parameter vector $ (\epsilon_{1}, \epsilon_{2}) $ that is infinitely close to $ (0, 0) $. By applying a minor perturbation, we gradually bring $ \lambda_{2} $ and $ m $ closer to $ \lambda_{2} = \lambda_{BT}+\epsilon_{1} $ and $ m = m_{BT}+\epsilon_{2} $, respectively. Incorporating the perturbation arising from these new parameter variables into the model (1.3), we get

This can be achieved by employing a transformation, specifically, $ \zeta_1 = x-x_{1}^{*} $, $ \zeta_2 = y-y_{1}^{*} $, to shift $ E_{1}^{\ast} $ to the origin, and proceeding accordingly:

where

and $ M_{1}(\zeta_1, \zeta_2, \varepsilon) $, $ N_{1}(\zeta_1, \zeta_2, \epsilon) $ are third-order infinitesimal quantity.

Then we will perform the transformation

shift the model (5.2) to the model (5.3)

where

and $ M_{1}(X, Y, \epsilon) $ and $ N_{1}(X, Y, \epsilon) $ are third-order infinitesimal quantity.

So we can add the next change:

shift the model (5.3) to (5.4)

where

and $ N_{3}(h_1, h_2, \epsilon) $ is third-order infinitesimal quantity.

Employing a fresh variable $ \tau $ by $ dt = (1-f_{02}(\epsilon)h_{1})d\tau $, then we get

Let

then we can shift the model (5.5) to the model (5.6)

where

and $ N_{4}(v_{1}, v_{2}, \epsilon) $ is third-order infinitesimal quantity.

We can observe that $ h_{20}(\epsilon) $ is an extremely intricate number, rendering it difficult to ascertain the sign of $ h_{20}(\epsilon) $ when $ \epsilon_{1} $ and $ \epsilon_{2} $ are small enough. Consequently, to proceed with the subsequent transformation, it is imperative for us to delve into the following two scenarios.

Case 1: For $ \epsilon_{1} $ and $ \epsilon_{2} $ that are small enough, if $ k_{20}(\epsilon) $ is greater than 0, we proceed to the next transformation:

We can get

where

and $ Q_{5}(e_{1}, e_{2}, \epsilon) $ is third-order infinitesimal quantity.

Let

then we have

where

and $ Q_{6}(j_{1}, j_{2}, \epsilon) $ is third-order infinitesimal quantity.

In case of $ k_{11}(\epsilon)\neq0 $, then we have $ H_{11}(\epsilon) = R_{11}(\epsilon) = \frac{k_{11}(\epsilon)}{\sqrt{k_{20}(\epsilon)}}\neq0 $, and give the next transformation:

then we have

where

and $ Q_{7}(X, Y, \epsilon) $ is third-order infinitesimal quantity.

Case 2: For $ \epsilon_{1} $ and $ \epsilon_{2} $ that are small enough, if $ k_{20}(\epsilon) $ is smaller than 0, we proceed to the next transformation:

We can get

where

and $ Q_{5}^{\prime}(e_{1}^{\prime}, e_{2}^{\prime}, \epsilon) $ is third-order infinitesimal quantity.

Let

we have

where

and $ Q_{6}(j_{1}^{\prime}, j_{2}^{\prime}, \epsilon) $ is third-order infinitesimal quantity.

In case of $ k_{11}(\epsilon)\neq0 $, then we have $ H_{11}^{\prime}(\epsilon) = R_{11}^{\prime}(\epsilon) = \frac{k_{11}(\epsilon)}{\sqrt{-k_{20}(\epsilon)}}\neq0 $, and go on the next transformation:

we have

where

and $ Q_{7}^{\prime}(X^{\prime}, Y^{\prime}, \epsilon) $ is third-order infinitesimal quantity.

To reduce the number of cases to be taken into account, we will retain $ \xi_{1}(\epsilon) $ and $ \xi_{2}(\epsilon) $ to stand for $ \xi_{1}^{\prime}(\epsilon) $ and $ \xi_{2}^{\prime}(\epsilon) $ in $ (5.12) $. When the matrix $ \left|\frac{\partial (\xi_{1}, \xi_{2})}{\partial (\epsilon_{1}, \epsilon_{2})}\right| $ is nonsingular, then the transformation is a homeomorphism in a adequately small domain of the $ (0, 0) $. Moreover, based on the above conditions, it is evident that $ \xi_{1} $, $ \xi_{2} $ are two independent variables. From the conclusions in ^[49], it is obvious that B-T bifurcation is formed when $ \epsilon = (\epsilon_{1}, \epsilon_{2}) $ is in a fully small domain of the (0, 0). Accordingly, the local formulas near the origin of bifurcation curves can be written as ("+" expresses $ k_{20}(\epsilon) > 0 $ and "-" expresses $ k_{20}(\epsilon) < 0 $):

1) The saddle-node bifurcation curve can be written as

$ SN = \left\lbrace (\epsilon_{1}, \epsilon_{2}):\xi_{1}(\epsilon_{1}, \epsilon_{2}) = 0, \xi_{2}(\epsilon_{1}, \epsilon_{2})\neq0\right\rbrace $.

2) The Hopf bifurcation curve can be written as

$ H = \left\lbrace (\epsilon_{1}, \epsilon_{2}):\xi_{2}(\epsilon_{1}, \epsilon_{2}) = \pm\sqrt{-\xi_{1}(\epsilon_{1}, \epsilon_{2})}, \xi_{1}(\epsilon_{1}, \epsilon_{2}) < 0\right\rbrace $.

3) The homoclinic bifurcation curve can be written as

$ HL = \left\lbrace (\epsilon_{1}, \epsilon_{2}):\xi_{2}(\epsilon_{1}, \epsilon_{2}) = \pm\frac{5}{7}\sqrt{-\xi_{1}(\epsilon_{1}, \epsilon_{2})}, \xi_{1}(\epsilon_{1}, \epsilon_{2}) < 0 \right\rbrace $. □

Based on mathematical theory derivation, we obtained threshold conditions for inducing transcritical bifurcation, saddle-node bifurcation, Hopf bifurcation, and Bogdanov-Takens bifurcation in the model (1.3). These conditions can serve as the theoretical basis for subsequent numerical simulations, and directly indicate that the values of some key parameters can seriously affect the bifurcation dynamics evolution process of the model (1.3). Moreover, according to the theoretical derivation process, it is worth emphasizing that the size of the predator and prey harvesting behavior can alter the intrinsic dynamic characteristics of the model (1.3).

6.   Simulation analysis and results

To verify the effectiveness of theoretical derivation and explore the bifurcation dynamics evolution process of the model (1.3), we conduct relevant bifurcation dynamics numerical simulations on the model (1.3).

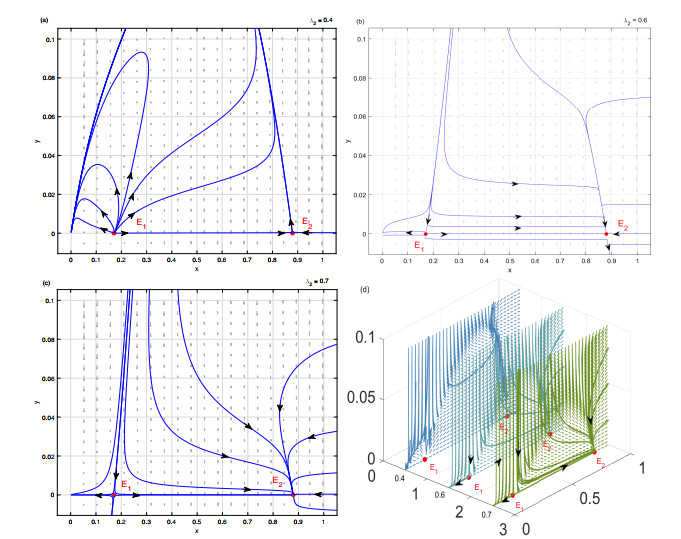
According to Theorem 5.1, we can choose $ m = 0.05, b = 0.2, c = 0.2, \beta = 2, s = 0.3, \lambda_{1} = 0.1 $, and we can directly calculate $ \lambda_{TC} = 0.6 $; thus, we can numerically simulate the dynamic evolution process of the model (1.3) undergoing transcritical bifurcation, and the detailed results can be seen in Figure 1. When the value of $ \lambda_{2} $ is 0.4, the model (1.3) has two boundary equilibrium points $ E_{1} $ and $ E_{2} $, the boundary equilibrium point $ E_{1} $ is an unstable node and the boundary equilibrium point $ E_{2} $ is a saddle (see Figure 1(a)). When the value of $ \lambda_{2} $ is equal to 0.6, the boundary equilibrium points $ E_{1} $ and $ E_{2} $ are saddle-node (see Figure 1(b)). When the value of $ \lambda_{2} $ is greater to 0.6, the model (1.3) has a saddle $ E_{1} $ and a stable node $ E_{2} $ (see Figure 1(c)). Therefore, this numerical simulation result not only points out the feasibility of Theorem 5.1, but also indicates that excessive harvesting of predator can lead to the extinction of predator population.

Based on the condition of Theorem 5.2, we can take $ m = 0.05, b = 0.2, c = 0.2, \beta = 0.3, \delta = 2, \lambda_{1} = 0.22 $ thus, we obtain $ \lambda_{SN} = 0.5761948068 $, which means that the model (1.3) will experience a saddle-node bifurcation as $ \lambda_{2} $ varies around $ \lambda_{SN} $. Furthermore, it is worth noting from Figure 2 that the model (1.3) has no internal equilibrium point when $ \lambda_{2} = 0.575 $, has an internal equilibrium point $ E_{1}^{\ast} $ when $ \lambda_{2} = 0.5761948068 $, and has two internal equilibrium points $ E_{3}^{\ast} $ and $ E_{4}^{\ast} $ when $ \lambda_{2} = 0.5781948068 $. Furthermore, it is worth emphasizing that the internal equilibrium point $ E_{3}^{\ast} $ is a saddle and the internal equilibrium point $ E_{4}^{\ast} $ is a stable node. Hence, it not only proves that Theorem 5.2 is valid, but also infers that prey and predator can form a constant steady state persistent survival mode, which implies that harvesting predator reasonably can be beneficial for the sustainable survival of prey and predator.

Based on Theorem 5.3, we take $ m = 0.05, b = 0.2, c = 0.2, \beta = 2, \delta = 0.3, \lambda_{1} = 0.16 $, then we can obtain $ \lambda_{H} = 0.55600668 $. It is obvious to find from Figure 3 that the model (1.3) has an unstable limit cycle when $ \lambda_{2} = 0.55575668 < 0.55600668 $. This is because the corresponding first Lyapunov number $ l_{1} = 669.843133 \pi > 0 $, which indicates that the limit cycle is unstable, then the unstable focus $ E_{4}^{\ast} $ transforms into the center when $ \lambda_{2} = 0.55600668 $, and the internal equilibrium point $ E_{4}^{\ast} $ turns into a stable focus from the center when $ \lambda_{2} = 0.556666668 > 0.55600668 $. Furthermore, it is worth pointing out from Figure 3(d) that the model (1.3) visually displays a Hopf bifurcation process as the parameter $ \lambda_{2} $ value increases, and if the parameter $ \lambda_{2} $ value increases, the amplitude of the limit cycle will also increase. Therefore, it is necessary to clarify that the model (1.3) has undergone a subcritical Hopf bifurcation, which can induce the formation of periodic oscillation persistent survival mode between prey and predator.

Based on Theorem 5.4, we take $ m = 0.050810774, b = 0.2, c = 0.2, \beta = 2, \delta = 0.3, \lambda_{1} = 0.16 $; hence, we can deduce $ m_{BT} = 0.050810774 $ and $ \lambda_{BT} = 0.5562939 $, and conduct relevant numerical simulations on Bogdanov-Takens bifurcation, the detailed numerical simulation results are shown in Figure 4. It is must be worth emphasizing from Figure 4 that if there are slight changes in the values of key parameters $ m $ and $ \lambda_{2} $ near the key values $ m_{BT} = 0.050810774 $ and $ \lambda_{BT} = 0.5562939 $, the dynamic behavior of the model (5.1) will undergo fundamental changes, which contains that the persistent survival model of prey and predators have undergone dynamic changes. Therefore, it is easy to see from Figure 4 that the persistent survival mode of prey and predator may exhibit constant steady state or periodic oscillation under the disturbance of key parameter $ m $ and $ \lambda_{2} $ values, which also directly indicates that the value of key parameters $ m $ and $ \lambda_{2} $ can synergistically affect the persistent survival mode of prey and predator.

To explore how the harvesting effort of prey affects the dynamic behavior of the model (1.3) and persistent survival mode between prey and predator, we will select parameter $ \lambda_{1} $ as a control parameter to simulate the relevant dynamic behavior, the detailed simulation results are shown in Figure 5. It is obvious to know that the model (1.3) has a stable internal equilibrium point when $ \lambda_{1} $ is $ 0, 0.05 $ and $ 0.1 $ respectively, which means that prey and predator can coexist in a constant steady state. Furthermore, it is worth pointing out that the model (1.3) has a limit cycle when $ \lambda_{1} $ is $ 0.15 $, which means that prey and predator can coexist in periodic oscillation. Moreover, it is easy to see that the model (1.3) has a chaotic attractor when $ \lambda_{1} $ is $ 0.160004 $, which means that prey and predator can coexist in an irregular state. However, it must also be emphasized that prey and predator will gradually become extinct when $ \lambda_{1} $ is $ 0.162 $. Therefore, it is worth summarizing that prey and predator are prone to persistent survival when the parameter $ \lambda_{1} $ values are relatively small, that si to say, if we want to maintain the sustainable survival of predatory ecosystems, we cannot over capture prey population.

The above numerical simulation results not only verify the feasibility and effectiveness of the theoretical derivation, but also dynamically display the specific dynamic evolution process of the model (1.3), and intuitively demonstrate the persistent survival mode of prey and predator, especially constant steady state mode and periodic oscillation mode, which are particularly beneficial for the long-term and sustainable cyclic development of predatory ecosystems.

7.   Conclusions

As is well known, the Allee effect and harvesting effort can seriously affect the dynamic behaviors of predator-prey model. Thus, we introduce the Allee effect and harvesting effort to construct a predator-prey model, the main purpose is to explore how they affect the bifurcation dynamics evolution process of the model (1.3), and reveal the persistent survival mode of prey and predator and its driving mechanisms. Mathematical theoretical work mainly investigate the existence and stability of some equilibrium points, as well as the triggering conditions of specific bifurcation dynamics, such as transcritical bifurcation, saddle-node bifurcation, Hopf bifurcation, and Bogdanov-Takens bifurcation, which can provide a theoretical basis for elucidating the driving mechanisms behind the formation of specific persistent survival mode between prey and predator. The numerical simulation work show the evolution process of the specific bifurcation dynamics behavior of the model (1.3), which can visualize the persistent survival mode and the dynamic variation characteristics of population density.

Based on mathematical theory and numerical simulation results, it is worth emphasizing that Allee effect and harvesting effort seriously affect the dynamic behavior of the model (1.3), especially bifurcation dynamics. Furthermore, it must be pointed out that the magnitude of harvesting efforts on predator can trigger the formation of transcritical bifurcation, saddle-node bifurcation and Hopf bifurcation. The saddle-node bifurcation can cause the model (1.3) to generate a stable internal equilibrium point, which can lead to the formation of a constant steady state persistent survival mode between prey and predator. The Hopf bifurcation can induce the occurrence of periodic solution in the model (1.3), which can result in the formation of a periodic oscillation persistent survival mode between prey and predator. Therefore, it is an important discovery that the saddle-node bifurcation and Hopf bifurcation are intrinsic driving force behind the formation of specific persistent survival mode between prey and predator. Moreover, it is worth clarifying that Allee effect in prey and harvesting effort in predator are able to collaboratively drive the model (1.3) through Bogdanov-Takens bifurcation, which implies that prey and predator can switch back and forth between constant steady state persistent survival mode and periodic oscillation persistent survival mode under small perturbations in key parameter values. Furthermore, it is necessary to emphasize that appropriate harvesting effort on the prey population can also enable prey and predator to coexist persistently in constant steady state, periodic oscillation, and irregularity state.

One innovation of this research is the introduction of harvesting effort for prey and predator in the ecological modeling process, which not only makes the ecological model (1.3) more controllable, but also enhances its applicability. Another innovation of this research is to reveal the persistent survival mode and underlying driving mechanism from the perspective of bifurcation dynamics evolution, which directly elucidates the impact mechanism of Allee effect and harvesting effort on the bifurcation dynamics of ecological model (1.3). Furthermore, it is worth comparing and explaining that the introduction of harvesting effort in the original model can form a periodic oscillation persistent survival mode between predator and prey, which directly indicates that regulatory measures can prevent the outbreak of algal bloom. Furthermore, it is worth noting that the introduction of Allee effect in the original model can synergistically enrich the dynamic behavior with other key parameters.

Although we obtained some theoretical and numerical results, there is much work to be studied, such as the spatial interaction characteristics between prey and predator, the prey substitutability in predator population, and the controllability problem based on state feedback. However, it is hoped that the research findings of this paper can contribute to the rapid development of predator-prey model dynamics research.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grants N0.31570364 and No.61871293), the Zhejiang Province College Student Science and Technology Innovation Activity Plan (New Talent Plan) (No.2024R429A010), and the National Key Research and Development Program of China (Grant No.2018YFE0103700).

Conflict of interest

The authors declare there is no conflicts of interest.