1. Introduction
Zebrafish (Danio rerio) has emerged as a model organism in drug discovery, disease studies and developmental biology [1,2]. An advantage of zebrafish as a model organism is that the embryos and larvae are small, transparent and undergo rapid development outside the mother’s body, allowing phenotypic analysis of embryogenesis and organogenesis in vivo [3,4,5]. The gonadal sex differentiation mechanism(s) in zebrafish is however an elusive phenomenon. Unraveling the molecular mechanisms could facilitate the use of zebrafish in exploring human reproductive diseases such as polycystic ovary syndrome (PCOS) and testicular dysgenesis syndrome (TDS) [6,7,8].
Sex differentiation is a process where two unique organs, testis and ovary, arise from a complex interaction between the bipotential primordial germ cells (PGC) and cells in the genital ridge [9], and where the sex determination mechanisms differ among species [10]. Some species have genetic sex determining systems (GSD) while others rely on environmental factors to control sex determination (ESD) [11,12]. GSD can be of two major forms: chromosomal sex determination (CSD) where a single chromosome determines the sex of an individual and polygenic sex determination (PSD) where multiple genes regulate sex differentiation [13]. It has been suggested that PSD includes species that have multiple loci on different sex chromosomes [13] such as in Lake Malawi cichlid species [14] or species with multiple loci on autosomal chromosomes such as European seabass lacking sex chromosome [15]. PSD and ESD can act together to influence the outcome of an individual’s sex e.g. zebrafish. In some species both GSD and ESD are involved in sex determination. In Japanese medaka (Oryzias latipes) the Y chromosome harboring Dmy gene determines the sex [16], however high temperature can alter the sex ratios [17,18,19].
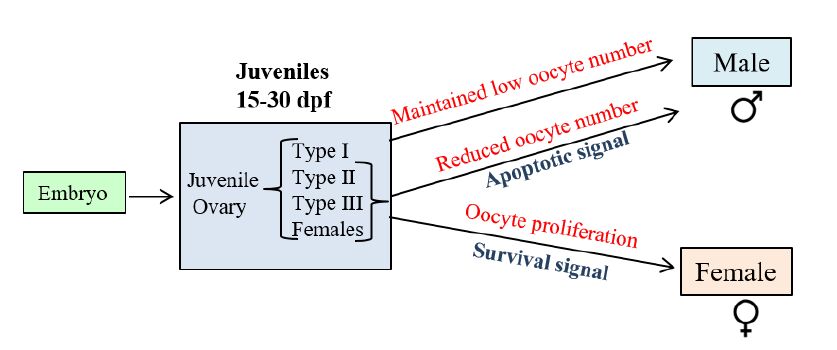
In juvenile zebrafish, gonadal development is initiated with oogenesis [20] and based on the oocyte number, the juveniles are grouped into type I, type II and type III males or females [21]. At 15 days post fertilization (dpf) type II males, type III males and females show a well-defined juvenile ovarian structure that either develop further to differentiate into proper ovaries or transform to testes [20,21,22]. However there are exceptions in some individuals that show a negligible amount of oocytes (type I males) during the juvenile ovary stage [21,23]. The transformation of dimorphic gonads from ovaries to testes is regulated by apoptosis [24,25]. The first sign of gonadal differentiation is evident at 10 dpf when the primordial germ cells show signs of oogenesis [20] and by 14-16 dpf oocytes are present in all juveniles [20,21]. Juveniles at 20-25 dpf that have well-defined ovarian structures may further increase in number and size to develop into mature ovaries [20,21,22], while some juveniles at around 23 dpf undergo transformation with progressive degeneration of oocytes to initiate testis differentiation [20,21](Figure 1).
2. Sex chromosome in zebrafish?
The sex determination process in humans is controlled by sex chromosomes (XY) where the master regulator gene “sex determining region Y” (SRY) on the Y chromosome drives the male differentiation pathway [9]. In zebrafish, the molecular mechanism of sex determination is unknown as neither cytogenetic studies [26,27,28,29], comparative analysis of recombination rates between the two sexes [30] nor breeding experiments [12] have led to the definite identification of sex chromosomes. However, one breeding experiment suggests the presence of zebrafish sex chromosomes with a heterogametic female indicating ZW/ZZ system [31]. A karyotype study with wild zebrafish obtained from Mansar Lake, Jammu, India, showed that female zebrafish are heterogametic [32]. This was recently confirmed, as zebrafish collected directly from nature (NA: Nadia, CB: Cooch Behar) and two wild strains (WIK, EKW) showed polymorphism in chromosome 4 with females being heterogametic, suggesting that zebrafish has a ZW/ZZ sex determination system [33]. However, the polymorphism was not detected in two inbred/laboratory strains (AB, TU) suggesting loss of the wild-type sex locus [33]. Studies on the inbred strains suggests that, like Sea bass, zebrafish also has a polygenic sex determination system, where multiple genes act in synchrony to control male and female differentiation pathways [12]. In addition to genetic regulation, zebrafish gonadal differentiation is also under environmental control, as hypoxia, temperature and variation in temperature cycles have been shown to influence the process [19,34,35,36].
A linkage map study demonstrated the presence of a sex associated region on chromosome 5 containing doublesex and mab-3 related transcription factor1 (dmrt1) and chromosome 16 containing cytochrome P450, family 21, subfamily A, polypeptide 2 (cyp21a2) that contribute to zebrafish sex determination [37]. Another study indicated the presence of sex associated regions on chromosome 3 containing hydroxysteroid (17-a) dehydrogenase-1 (hsd17b19) and chromosome 4 containing 5S rRNA genes, one spermatocyte specific gene patched domain containing 3 (ptchd3) and additional genes that are not specifically expressed in gonads [38]. However, chromosome 4 was suggested to be the candidate zebrafish sex chromosome as it showed suppressed recombination, a characteristic feature observed in sex chromosomes of other species. Additionally, chromosome 4 was also found to be late replicating, repeat rich and highly heterochromatic, which are also the characteristics of sex chromosomes [33,38]. Among the repetitive elements, a cluster of 55 members of the mir-430 gene family on chromosome 4, that plays a crucial role in regulating expression of Nanos1 and tudor domain containing 7a (Tdrd7a) in primordial germ cell (PGC) in zebrafish [39], was considered an important feature in characterization of chromosome 4 as a possible sex chromosome [38]. The microRNA mir-430 also regulates the expression of stromal cell-derived factor 1 alpha (Sdf1a) that is involved in defining the path of PGC migration [40]. While additional studies are needed to confirm the presence of sex chromosomes in zebrafish, several genes, including SRY-box containing gene 9 (sox9), anti-Müllerian hormone (amh), cytochrome P450, family 19, subfamily A, polypeptide 1a (cyp19a1a), nuclear receptor subfamily 5, group A, member 1 (nr5a1a & b), forkhead box protein L2 (foxl2), dead end (dnd), and factor in germ line alpha (fig alpha) have been linked to zebrafish sex differentiation [21,22,41,42,43].
A recent study by Luzio et al. [44] employed random amplified polymorphic DNA (RAPD) and identified three fragments in chromosome 2, 3 and 11 of the zebrafish AB strain. A fragment containing zinc-finger transcription factors in chromosome 2 and a fragment between latrophilin-2 and vitellogenin3 in chromosome 11 were enriched in females while the third fragment containing rhomboid 5 homolog 1 (Drosophila) in chromosome 3 was enriched in males. These fragments successfully identified 80% of males and 100% of females from zebrafish samples. Identification of all these genes in different chromosomes in different studies further confirms that zebrafish sex differentiation is polygenic.
Although studies indicate the presence of sex chromosome as well as polygenic system in zebrafish, a recent study by Wilson and coworkers [33] could help to explain this anomaly. It was observed that zebrafish in nature may be using a ZZ/ZW sex determination system while the laboratory strain has lost this mechanism and relies on interactions between different genes to control gonadal differentiation [33]. The present review focuses on the results obtained from laboratory zebrafish.
3. Male or female, fight for signaling pathways
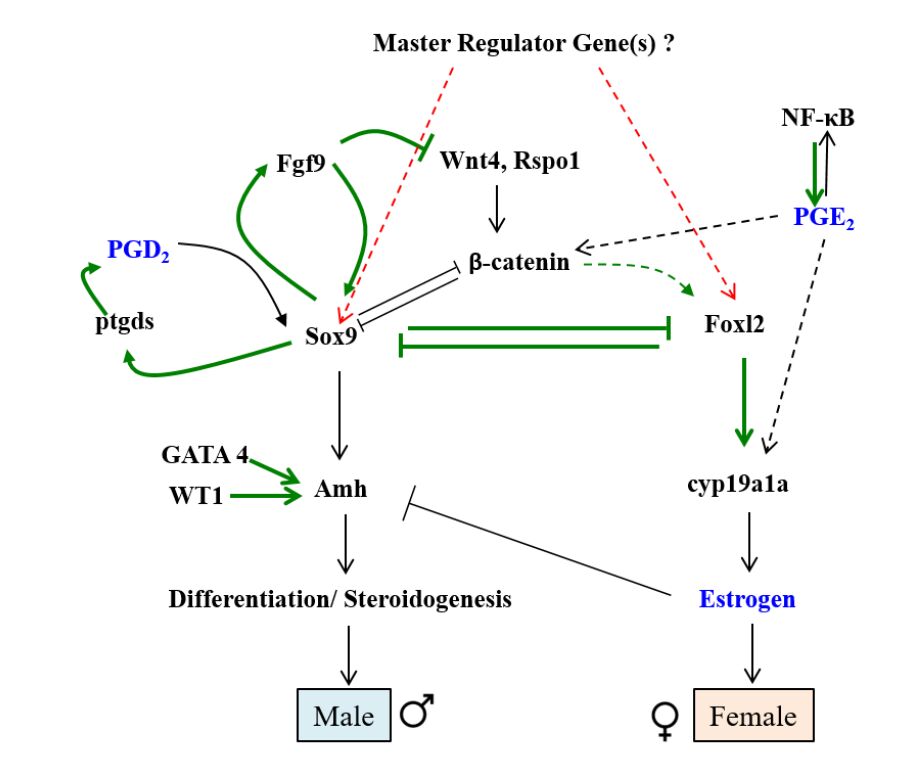
Sryexpression in mammalian XY gonads activates the sertoli cell specific marker Sox9, the initial signal for testis differentiation [9,45,46,47], while maintenance of male pathway and development into a proper testis is ensured by the expression of Sox9 together with other male specific genes including Ptgds, Amh and fibroblast growth factor 9 (Fgf9) [47,48,49,50,51]. In zebrafish, the master regulator gene for sex differentiation has been elusive [42,52], however sox9a, amh and cyp19a1a are early markers expressed in undifferentiated gonads and are likely to be the upstream regulator of sex differentiation [43]. Out of 6 sex related genes analyzed in RNA extracted from whole juvenile zebrafish, Jorgensen et al. [53] observed 3 male specific genes including sox9a, androgen receptor, and dmrt1a and 2 female specific genes cyp19a1a, and fig alpha to form two groups of high and low expressers. However, only 56% of the male and female showed the expected expressions for these 5 segregated genes [53]. This either suggests that there are other crucial genes that play an equally important role in sex differentiation or that the gene analysis was confounded by signals from other tissues.
The downstream sex related genes and the signaling pathways in zebrafish as summarized in Figure 2 share similar mechanisms to those of mammals. In zebrafish sox9 and foxl2 have been suggested as upstream regulators involved in the male and female differentiation pathway respectively [25,42,43].
In mammals, Sox9 also negatively regulates the female specific genes β-catenin and foxl2 [48,50] and Sox9 mediated up-regulation of the male specific gene Fgf9 further inhibits Wnt signaling to control the female differentiation pathway and sex reversal [54,55,56]. The mammalian AMH, apart from degenerating Müllerian ducts, also regulates gonadal steroidogenesis to drive male differentiation. The proximal region of the mammalian Amh promoter contains a number of cis-elements for Steroidogenic factor 1 (SF1), GATA4, Wilm’s tumor-associated protein 1 (WT1) and Sox9 to promote maximal activity [57,58,59].
Although, fish do not have Müllerian ducts, amh role in sex differentiation is well documented [22,42,43,60,61,62]. In Patagonian pejerrey (Odontesthes hatcheri) the duplicated copy of the amh, gene known as amhy, is the sex-determining gene present in a single metacentric/submetacentric of Y chromosome. In the early gonads, amhy expression occurs much before the autosomal amh and drives male differentiation, while amhy knockdown leads to ovary development due to upregulation of foxl2 and cyp19a1a genes [60]. amh and cyp19a1a shows reciprocal expression in zebrafish, with males that have high amh levels have lower levels of cyp19a1a and vice versa in females [61]. In the same study the expression of P450 11b-hydroxylase (cyp11b), enzyme responsible for 11-ketotestosterone (11-KT) synthesis was found to be reciprocal with that of cyp19a1a, however its expression was lower and did not precede amh expression indicating that Amh and Cyp19a1a are important gonadal regulators [61]. In fugu (Takifugu rubripes), the Amh type II receptor (Amhr2) is the sex-determining gene. A single amino acid change, His/Asp384 in the kinase domain regulates male differentiation. Males are heterozygous while females are homozygous (His/His384) [63].
The Wnt/β-catenin signaling pathway is known to promote ovarian differentiation in mammals [48,50] and has also been shown to influence zebrafish ovarian differentiation [64,65]
. R spondin 1 (Rspo1) that interacts with WNT4 and prostaglandin E2 (PGE2) regulate β-catenin activity [64,66,67,68,69,70,71,72]. Inhibition of β-catenin leads to sex reversal in mammals while in zebrafish male biased populations are observed [64]. In mammals, β-catenin impacts cell proliferation and differentiation, and has been suggested to be a positive regulator of the female specific gene Foxl2. Foxl2 activates aromatase (Cyp19a1) involved in estrogen synthesis to maintain ovarian differentiation [73,74]. In addition, β-catenin and Foxl2 have inhibitory effects on Sox9 to further suppress the testis differentiation pathway [75].
Aromatase has also been indicated as an important regulator in teleost ovarian differentiation [76].Estrogen synthesis inhibition using aromatase inhibitor in juvenile zebrafish has shown to induce masculinization [77]. Treatment with aromatase inhibitors in sexually adult female zebrafish leads to ovarian retraction followed by testis like organ formation with cyst structures containing spermatocyte-like cells [78]. This suggests that, like in other teleost species, estrogen not only induces ovarian differentiation in juvenile zebrafish but also maintains femaleness in adult zebrafish. Ethynylestradiol (EE2) exposure in juveniles leads to female biased population [79,80]. The mechanism driving EE2 mediated feminization is suggested to be the down regulation of male specific genes including amh and dmrt1 [81]. The disruption of male gonadal differentiation is also evident from the transcription analysis of testis samples from EE2 exposed males that show reduced expression of male specific genes including sox9a, amh, dmrt1 and nr5a1b [82]. Anti-androgen, vinclozolin, treatment also skews sex ratio to femaleness [83] while the synthetic androgen, trenbolone, leads to masculinization in zebrafish [80,84]. Apart from the sex hormones, thyroid hormones have also been shown to impact gonadal differentiation in zebrafish [85,86,87]. The skewed male sex ratios mediated by thyroid hormone was suggested to be due to inhibition of cyp19a1a and estrogen receptor genes and up regulation of male specific genes including amh and androgen receptor [86].
Although data clearly suggests that genes involved in zebrafish sex differentiation are similar to those of mammals, there are no studies that indicate the principal upstream regulator gene in zebrafish gonadal differentiation.
A recent study showed that wild zebrafish may have a chromosomal sex determination system while the inbred or laboratory strains have lost the polymorphism in the sex related locus [33]. As a consequence a multitude of genes control gonadal differentiation in inbred zebrafish. This indicates that identification of master regulator gene(s) in inbred species will be challenging. Analysis of signalling pathway in zebrafish collected from nature could help to better understand the regulation as well as the regulators involved in sex differentiation.
4. New regulators in zebrafish gonadal differentiation
4.1. NF-κB and gonadal differentiation
Nuclear factor kappa beta (NF-κB) is a nuclear transcription factor involved in many cellular activities including regulation of inflammation, apoptosis, cell growth and differentiation [88,89,90,91]. It can be activated by various physical and chemical factors [88,91]. NF-κB subunits are generally sequestered in the cytoplasm by the inhibitor protein “IκB”. The IκB consists of ankyrin repeats which interact with Rel homology domain (RHD) of the NF-κB and this interaction masks the nuclear localization signal (NLS), and blocks nuclear translocation [92,93]. Numerous factors, including UV irradiation, stress, cytokines and free radicals can induce IκB degradation through a chain of reactions starting with phosphorylation, ubiquitination and finally proteolysis by the proteasome complex allowing the translocation of NF-κB to the nucleus for transcription of target genes [93,94,95,96].
NF-κB activation blocks apoptotic processes and promotes cell survival by interacting with Inhibitor of apoptosis protein (IAP) family of genes [88,97]. NF-κB has also been reported to crosstalk with other nuclear receptors including the glucocorticoid receptor and the androgen receptor as well as with other proteins that regulate gene expression [98,99,100]. NF-κB is highly expressed in mammalian sertoli cells and assumed to be involved in regulation of spermatogenesis [101].However, it can also down-regulate AMH gene expression in mammalian testis [102]. This suggests that activation of NF-κB may hinder ovary to testis transition through anti-apoptotic signaling cascades, and that the AMH suppression by NF-κB could further support female sex differentiation. We have shown that activation of NF-κB by heat killed bacterial and sodium deoxycholate (DOC) can drive female differentiation pathway in zebrafish while NF-κB inhibition leads to male biased sex ratio [25]. NF-κB appears to be an important upstream regulator that can impact apoptosis and survival signaling. It remains to be determined if NF-κB expression is sexually dimorphic in the early gonads and what genes regulate NF-κB during gonadogenesis. Further analysis of NF-κB signaling in zebrafish will help identify key upstream and downstream regulators of zebrafish gonadal differentiation process.
4.2. Prostaglandins and gonadal differentiation
Arachidonic acid, a polyunsaturated fatty acid functions as a substrate for prostaglandin synthase (PTGS/COX) and is converted into prostaglandin H2 (PGH2), a common substrate for other prostanoids (PGD2, PGE2, PGI2, PGF2α, TXA2). The conversion is catalyzed by specific synthases, where prostaglandin D synthase (Ptgds) and prostaglandin E synthase (Ptges) catalyses PGD2 and PGE2 synthesis respectively [103,104,105,106]. Among the two COX isoforms (COX-1/PTGS1 and COX-2/PTGS2), COX-2 is the inducible form that is up-regulated during inflammatory conditions [103], probably through the NF-κB, NF-IL6 and Sp1 response elements in the COX-2 promoter region [105,107,108]. NF-κB is also linked to the cyclooxygenases, which are mediators of inflammation. NF-κB activation alleviates cox-2 transcript levels [109,110] and simultaneously PGE2 up-regulate NF-κB activity [111].
COX-2 is involved in zebrafish embryogenesis [112], has various physiological and pathological roles [93,95], and has an active role in the sex determination processes [97,98,99,100,101,102]. Among the different prostaglandins, “PGD2” and “PGE2” have been studied extensively to understand their role in the sex differentiation processes. Differential expression of Ptgds is reported in the mouse embryonic gonads with high expression in the sertoli cells and prospermatogonia [113]. A feedback loop has been proposed where PGD2 activates SOX9, which then binds to the ptgds promoter to enhance its expression, resulting in PGD2 up-regulation [114]. These results clearly link Ptgds to the testis differentiation pathway.
PGE2 is the major prostanoid synthesized by Ptges during COX-2 activation that acts through EP/PTGER receptors (EP1-4/PTGER1-4) [115]. The EP2 and EP4 receptors regulate cell proliferation through activation of the β-catenin pathway [103]. PGE2 is known to up-regulate NF-κB [111], β-catenin [71] and aromatase [116] activity. Ptges is differentially expressed in the mouse gonads with high expression in the ovary [117]. It is upregulated during ovulation in mice [118] and is linked with ovary development and maturation [119,120]. Thus, while Ptgds appears to be involved in testis development a multitude of data links Ptgesto ovarian functions.
In zebrafish, we have demonstrated that exposure of juveniles to PGD2 analog BW245C results in male biased population by upregulating Sox9 and other male specific genes. On the other hand, exposure to PGE2 results in female biased population by upregulating NF-κB and β-catenin pathway [63]. We provide strong evidence that prostaglandins, like in mammalian system, also plays a crucial role in zebrafish sex differentiation and both share highly similar signalling mechanisms to sculpture gonadal structures.
5. Involvement of primordial germ cells in gonad differentiation
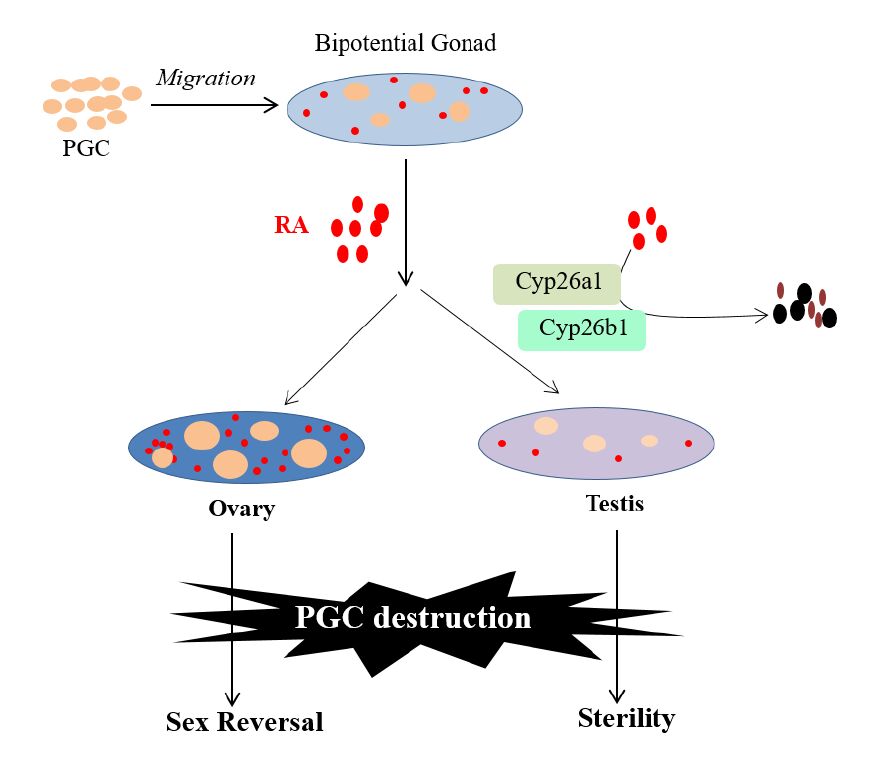
Sex determination in teleost is diverse with some relying on sex chromosomes whereas environmental factors play a crucial role in other species [121]. Apart from genetic and environmental cues gonadal sex differentiation also relies on germ cell status [22,122,123,124]. Germ cells are the progenitors of both oocytes and spermatozoa, and for the development of functional gonads, a proper interaction between germ cells and gonadal somatic cells are needed [125]. The contribution of germ cells to sex differentiation varies among vertebrates. In goldfish, loach and red-eared slider turtle, germ cell depletion does not alter gonadal fate [126,127,128] whereas germ cell loss in medaka [123], three-spined stickleback [129] and zebrafish [22,122,124] results in development of males. In zebrafish knockdown of germ cell markers dnd and nanos leads to development of sterile males [22,122]. Dranow and coworkers further showed that germ cells are not only important in early stages of gonadal development but also crucial for maintaining sexual phenotype of adult zebrafish. It was demonstrated that ablation of germ cells in adult female zebrafish results in sex reversal to sperm producing males [130]. It has been shown that zebrafish lacking germ cells can still initiate the expression of early sex related genes including cyp19a1a, amh, and foxl2 and later develop testis without any sperm [22,131] (Figure 3). This suggests that germ cells are not a prerequisite for early onset of somatic markers and testis development, but a complex interaction between germ cells and developing oocytes is necessary to maintain proper female development. However in mammals there are conflicting observations on germ cell status and the gonad differentiation [132]. Studies have indicated that germ cells are involved in differentiation of ovarian somatic cells and loss of germ cells can result in somatic trans-differentiation in ovaries [133,134]. At the same time a recent study shows that germ cells are not a prerequisite for ovarian differentiation [135].
Germ cells proliferate through mitotic divisions before migrating to the presumptive gonadal sites and under the influence of surrounding environment, program itself to further proliferate and enter meiotic divisions [136,137]. In mammals, germ cells enter meiosis I early in females while in males germ cells arrest in the G0/G1 phase of the mitotic cycle and delays meiosis until puberty [125].Studies using either XX or XY germ cells show that germ cells when placed in the developing ovary undergo meiosis while mitotic arrest is observed in the environment of developing testis [113]. This indicate that the chromosomal constituency is not a prerequisite for meiosis entry but that the surrounding environment is critical and the sex chromosomes only influences the meiosis progress and gametes formation. Retinoic acid (RA) and the RA degrading enzyme CYP26B1 are implicated to be important determining factors in regulating the germ cell meiosis pathway [138,139,140]. Apart from RA, PGD2 has also emerged as a potential male germ cell differentiating factor in mouse. PGD2 leads to mitotic arrest in male germ cells by repressing pluripotency markers, suggesting it to be an early regulator of germ cell [141]. Given the role of PGD2 in regulating the zebrafish male differentiation pathway [64], deciphering the role of prostaglandins in germ cell regulation could help in better understanding of signaling and regulation between germ cells and gonadal differentiation in zebrafish.
In testis the germ cells are blocked from entering meiosis until puberty by RA degrading enzyme cytochrome P450, family 26, subfamily b, polypeptide 1 (CYP26B1) [140] which is differentially expressed in the gonads with higher expression in the testis [139,142]. In mammals, SOX9 and steroidogenic factor 1 (SF1) are known to activate Cyp26b1 whereas, the female specific gene, “foxl2” is known to inhibit SOX9 and SF1 mediated up-regulation of Cyp26b1 [138].
The role and regulation of RA during zebrafish gonadal differentiation is not well documented but a recent study showed that inhibition of RA synthesis leads to decreased sperm count and egg number indicating a role for RA in maintenance of germ cells [143]. Dietary restriction of RA results in a reduction in egg number in zebrafish [144]. In contrast to the mammalian system, meiotic initiation in zebrafish was not dimorphic and cyp26a1 instead of cyp26b1 was indicated to be an important RA degrading enzyme when analysed in juvenile gonads [145]. In another study cyp26b1 was found to be dimorphic in adult zebrafish gonads while Cyp26a1 showed no difference [143]. This discrepancy could be due to gonadal sample analysis at different developmental or reproductive stages, as it is clear from Rodriguez-Mari and co-workers [145] that cyp26a1 expression although dimorphic, either becomes high in testis or in ovary depending on the different gonadal stages being analyzed. A gene expression study by Tzung and co-workers [124] on control and PGC depleted zebrafish juveniles demonstrated that at 14 dpf the gonads are in a meiotic stage and PGC depleted vs control samples showed clear difference in genes involved in meiosis, cell cycle regulation and immune response. Based on the gene expression it was suggested that meiosis entry is an important early step in ovarian differentiation. This clearly indicates that zebrafish PGC regulation in controlling gonadal differentiation could be similar to mammalian system.
Our recent findingsdemonstrate that RA is a determining factor in regulating sperm and egg number [143], which indicates that RA as reported in mammalian system could also be involved in zebrafish gonadal differentiation. Zebrafish ovarian differentiation is sensitive to PGC threshold number [124], however it is not clear what kind of signalling is relayed from PGC to soma and from soma to PGC for proper gonad formation. Future studies to unravel this signalling will further help in better understanding of zebrafish gonadal differentiation.
6. Conclusion and future perspectives
Gonadal sex differentiation in zebrafish remains elusive, partly due to the absence of sex chromosomes and presence of a polygenic sex differentiation system. In the wild, zebrafish seems to be employing sex chromosomes for regulating gonadal differentiation. Future studies with wild type strains hold promise in identifying specific sex differentiation pathways not prerequisite in domesticated strains. Identification of the zebrafish gonadal sex differentiation pathway will certainly help to fast track therapeutic research.
Teleosts have evolved environmental as well as XY and ZW sex determination systems, which makes them ideal for sex determination and sex related disease studies. Sex related diseases including polycystic ovary syndrome (PCOS), premature ovarian aging, testicular dysgenesis and germ cell cancer of testis and ovary are prevalent worldwide [146]. PCOS is the most common endocrine disorder that affects reproductive function in women [147] and till date the etiology remains elusive [148]. Along with reproductive functions, PCOS also affects metabolic, cardiovascular, inflammatory, oncological and sleep systems [148]. Future studies with zebrafish to understand this complex disease could help improve the etiology, diagnostic as well as therapeutic potential in humans. On the other hand TDS affects the male population and is a general term that represents different disorders, including reduced semen quality, testicular cancer, hypospadias, cryptorchidism, short anogenital distance and decreased testosterone production [149,150]. Zebrafish shows great promise as a model system to study these disorders as well.
Acknowledgments
The research was financed by the Swedish Research Council (to AP and PEO), the knowledge Foundation, Sweden (to PEO) and Örebro University (to PEO).
Conflict of Interest
Authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: