En recuerdo de Ireneo: ‘Sed breves con las malas noticias’
1.
Introduction and statement of the results
In the paper [8], Ireneo Peral and coauthors proved an existence and summability result on the solutions of the Dirichlet problem
Here Ω is a bounded open subset of RN, N>2, such that 0 belongs to Ω, M:Ω→RN2 is a measurable matrix such that
for almost every x in Ω and for every ξ in RN, with 0<α≤β, B>0 and f belongs to some Lebesgue space Lm(Ω).
If B=0, the summability results by G. Stampacchia (see [11]) state that the weak solutions u in W1,20(Ω) of (1.1) are bounded if m>N2; while they belong to Lm∗∗(Ω), with m∗∗=NmN−2m, when 2∗=2NN+2≤m<N2.
If B>0, the differential operator
may no longer be coercive, so that both existence and summability results for (1.1) may not be true. However, we recall the following result due to Hardy:
Proposition 1.1 (Hardy inequality). If v belongs to W1,20(Ω), then
Moreover H2=(N−22)2 is optimal and is not achieved (for the proof, see [10] or [9]).
Thanks to Hardy inequality, if 0<B<αH2, then the differential operator A(v) is coercive, so that existence and summability results for (1.1) can be proved. However, with respect to the case B=0, there is an important difference: the summability of the solution depends not only on the summability Lm(Ω) of the datum f, but also on the "size" of B. Indeed, in [8] it is proved that if 1<m<N2, and if
then there exists a (weak, or distributional, depending on whether m≥2∗ or m<2∗) solution u of (1.1), with u belonging to Lm∗∗(Ω). Note that if m tends to N2, or if m tends to 1, then B tends to zero, and that if m=2∗, then the condition on B becomes 0<B<αH2. In particular, observe that if f only belongs to L1(Ω), and B>0, neither existence nor summability results can be proved for Eq (1.1). Note also that, as it is proved in [8], if 0<B<αH2, and f belongs to Lm(Ω), with m>N2 (the classic threshold in order to have bounded solutions), then there exists a solution u in W1,20(Ω) of Eq (1.1), but such solution never belongs to L∞(Ω).
In some recent papers (see [2], as well as [3]), the problem
was studied when a(x)≥0 is a function in L1(Ω) such that there exists Q>0 such that
Under this assumption, the authors proved the existence of a weak solution u in W1,20(Ω) of (1.5), with the property that
so that u belongs to L∞(Ω), even though the datum f may only be a function in L1(Ω). This is clearly in sharp contrast with the existence results for the case a(x)≡0, where the solution u does not in general belong to W1,20(Ω), nor it is bounded.
The purpose of this paper is to prove existence and summability results for the boundary value problem
with B>0, and a(x) and f(x) such that (1.6) holds. In other words, we will study whether assumption (1.6) (which yields existence of bounded solutions if B=0) allows to improve the results of [8] as far as existence and summability of solutions is concerned. As we will see, if no further assumptions on a(x) with respect to the function B/|x|2 are made, then existence of solutions in W1,20(Ω) for (1.7) follows for every 0<B<αH2, with solutions that become more and more summable as B approaches zero.
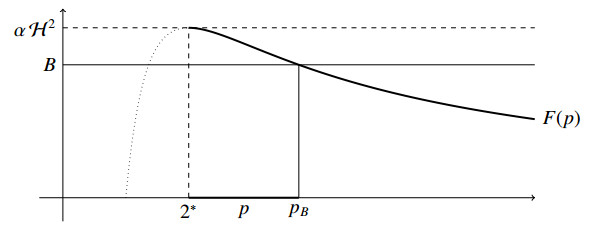
In order to state our first result, let us define 2∗=2NN−2 and the function F:[2∗,+∞)→R by
We remark that F(2∗)=αH2, that F is strictly decreasing (so that t=2∗ is a maximum for F on [2∗,+∞)), and that F(t) tends to zero as t tends to infinity (see Figure 1).
The following result will be proved in Section 2.
Theorem 1.2. Let a(x)≥0 and f(x) in L1(Ω) be such that (1.6) holds. IfB>0 is such that
then there exists a unique weak solution u of Eq (1.7), that is a function u in W1,20(Ω) such that a(x)u belongs to L1(Ω) and
for every φ in W1,20(Ω)∩L∞(Ω). Furthermore, if pB>2∗ is the unique solution of the equation F(pB)=B on (2∗,+∞), then u belongs to Lp(Ω) for every 2∗≤p<pB.
Remark 1.3 Observe that condition (1.6) allows the coefficient a(x) to vanish in a subset of Ω. The results of Theorem 1.2 can be compared with those of [1] and [4]. In [1] (dedicated to Ireneo Peral for his 70th birthday), existence and Lp-regularity of solutions for the equation
is proved for any B>0, under the assumption a>0 (so that a cannot vanish), and r>2∗: note that in this case the lower order term has a much stronger growth with respect to the one in Eq (1.7). These results were then generalized in [4,Theorem 2.1], where existence of solutions for the equation
is proved for B even larger than αH2 and, roughly speaking, the nonnegative coefficient a(x) can vanish in a set of positive measure in the interior of Ω, under the assumptions r>2 and a(x)|f(x)|rr−1 belongs to L1(Ω). Note that also in this case we have that the lower order term grows more than linearly, but that the datum f need not be "bounded" with respect to a(x).
Remark 1.4. Note that if B tends to αH2, then pB tends to 2∗, while if B tends to zero then pB tends to infinity. Note also that, in contrast with what happens in the case B=0, the value of the constant Q in (1.6) has no influence on the summability of the solution.
Remark 1.5. We remark the similarity between the summability result of Theorem 1.2, and the summability result of the paper [8] quoted before. In this latter paper, if m>2NN+2 and B>0 are such that (1.4) holds, then the weak solution u in W1,20(Ω) of Eq (1.1) belongs to Lm∗∗(Ω). In our Theorem 1.2, the weak solution u in W1,20(Ω) of Eq (1.7) belongs to Lp(Ω) for every p such that B<F(p) (this inequality is equivalent to inequality p<pB). If we choose p=m∗∗=NmN−2m, the condition B<F(p) means
which is exactly (1.4). Thus, the same assumption on B which yields solutions in Lm∗∗(Ω) for equation (1.1), yields solutions in Lm∗∗(Ω) for Eq (1.7): note however that in the case of Eq (1.7) the datum f only belongs to L1(Ω).
We now remark that the function a(x) belongs to L1(Ω), while the function B/|x|2 belongs to Lm(Ω), for every 1≤m<N2, so that it is more summable than a(x). This means that it may happen that the function a(x) dominates the function B/|x|2. In this case, for every B>0 we are going to prove that there exist weak solutions u of Eq (1.7), which belong to L∞(Ω). Our result is the following, and will be proved in Section 3.
Theorem 1.6. Let a(x)≥0 and f(x) in L1(Ω) be such that (1.6) holds. If B>0 and ρ>1 are such that
then there exists a unique weak solution u in W1,20(Ω)∩L∞(Ω) of (1.7).
Suppose now that a(x)=C/|x|2, with C>0. If C>B, the result of Theorem 1.6 states that there exist bounded weak solutions u of (1.7); if C=B then any weak solution u of (1.7) is also a solution of
with |f(x)|≤QB/|x|2: it is well known from the results of Stampacchia that in this case u may not be in L∞(Ω). This shows that condition (1.11) (with ρ>1) is somehow necessary in order to have bounded solutions.
If C<B<αH2 one can only apply Theorem 1.2 to deduce the existence of weak solutions u of Eq (1.7), with u in Lp(Ω) for every p<pB. In Section 4 we are going to prove that the result of Theorem 1.2 is in some sense sharp: for every p>pB there exists Cp<B, such that for a(x)=Cp/|x|2 (and a suitable function f(x) satisfying (1.6)) there exists a weak solution u of Eq (1.7) such that u does not belong to Lp(Ω).
In the final section of this paper, we will study the boundary value problem associated to a nonlinear quasilinear equation with a lower order term with quadratic growth with respect to the gradient, namely
where f(x) is a function in L1(Ω) and g:R→R is a continuous function such that g(0)=0 and g(t)t is increasing on (0,+∞) (and decreasing on (−∞,0)). Also in this case, as in the case of Theorem 1.6, we will prove that the lower order term g(u)|∇u|2 "dominates" the term Bu/|x|2, so that existence of solutions in W1,20(Ω) will follow for every B>0.
2.
Proof of Theorem 1.2
In what follows, we will denote by C any constant depending on the data of the problem (such as N, Ω, α, β, …) but never on the approximation parameter n.
Proof. Let n in N be fixed, and define
with Q>0 given by (1.6). Note that, since the function t↦t1+Qnt is increasing for t>0, from (1.6) it follows that
so that (1.6) is satisfied by fn(x) and an(x) for every n in N. A straightforward application of the Schauder theorem yields that for every n in N there exists a weak solution un in W1,20(Ω) of the equation
Furthermore, since the right hand side is bounded by Bn2+n, and since an(x)≥0, the function un belongs to L∞(Ω) thanks to the results by G. Stampacchia (see [11]).
We are going to prove that if B>0 satisfies assumption (1.9) then the sequence {un} is bounded in W1,20(Ω). In order to do that, we choose un as test function in the weak formulation for Eq (2.2) to deduce that
Using (1.2) and (1.6), we obtain from the previous identity that
which implies, thanks to Hardy inequality (1.3), that
We now observe that since t(t−Q)≥−Q2 for every 0≤t≤Q and that a(x)≥0, we have
Using this inequality in (2.4) we obtain that
Thanks to assumption (1.9), and to the fact that a(x) belongs to L1(Ω), from (2.5) we obtain that the sequence {un} is bounded in W1,20(Ω), as desired. Therefore, there exists a function u in W1,20(Ω) such that, up to subsequences, the sequence {un} converges to u weakly in W1,20(Ω), weakly in L2∗(Ω), and almost everywhere in Ω.
Thanks again to the boundedness of {un} in W1,20(Ω), and to Hardy inequality (1.3), the sequence {un2|x|2} is bounded in L1(Ω); therefore, from (2.3) (dropping the positive first term) and from Young inequality we have that there exists C>0 such that
Therefore, the sequence {an(x)un2} is bounded in L1(Ω). Let now E be a measurable subset of Ω. Then, for k>0 we have
where we have used the boundedness of {an(x)un2} in L1(Ω) in the last passage. Let now ε>0 be fixed, and choose k>0 large enough to have that Ck<ε. Once k>0 has been chosen, let meas(E) be small enough in order to have
Such a choice of E is possible since a(x) belongs to L1(Ω). We have thus proved that if meas(E) is small enough, then
that is, that the sequence {an(x)un} is uniformly equi-integrable. Since it is almost everywhere convergent to a(x)u, Vitali theorem implies that
This convergence, the convergences already proved on the sequence {un}, and the strong convergence of B|x|2+1n to B|x|2 in Ls(Ω), for every s<N2, imply that one can pass to the limit in the identities
for every φ in W1,20(Ω)∩L∞(Ω), to have (1.10) holds true.
Once existence of a weak solution has been proved, we turn now to uniqueness. Suppose that u and v are two weak solutions of (1.7), and define w=u−v. Since w belongs to W1,20(Ω), from Hardy inequality (1.3) it follows that w2|x|2 belongs to L1(Ω). For k>0, and t in R, let us define
and consider
Since we have that Sk tends to zero almost everywhere in Ω, and since
by Lebesgue theorem we have that the sequence {Sk} tends to zero strongly in L1(Ω). Observe now that w is a weak solution of
that is, we have
for every φ in W1,20(Ω)∩L∞(Ω). Choosing φ=Tk(w) we obtain, using (1.2), dropping a positive term, and recalling that w=Tk(w)+Gk(w), that
Recalling the definition of Sk, and using Hardy inequality (1.3), the previous inequality implies that
which yields that
Recalling that 0<B<αH2, and letting k tend to infinity, we obtain from the above inequality, using that the sequence {Sk} tends to zero in L1(Ω), that
which then implies that w=0, and so u=v.
We now turn to the second part of the result. Since we already know that there exists a solution u in W1,20(Ω), in order to show that u belongs to Lp(Ω), for every 2∗≤p<pB, it is enough to prove that the sequence {un} is bounded in Lp(Ω) for every 2∗≤p<pB. To this aim, let γ≥1, and choose |un|2γ−2un as test function in the weak formulation of Eq (2.2) (this can be done since un belongs to L∞(Ω) for every n in N). We have
Using (1.2) and (1.6) we obtain from the previous identity that
We now remark that
so that (2.7) can be rewritten as
Thus, using Hardy inequality (1.3), from (2.8) we deduce that
Since t2γ−1(t−Q)≥−Q2γ for every 0≤t≤Q, we have
so that from (2.9) we obtain that
If we now assume that γ≥1 is such that
from (2.10) it follows that the sequence {|un|γ} is bounded in W1,20(Ω). Thanks to Sobolev embedding, this implies that the sequence {|un|γ} is bounded in L2∗(Ω), so that the sequence {un} is bounded in L2∗γ(Ω).
Summing up, we have that if (2.11) holds, that is if
then the sequence {un} is bounded in L2∗γ(Ω). Setting p=2∗γ we have, after some straightforward simplifications, that
Recalling that by definition F(pB)=B, we have from (2.12) that the sequence {un} is bounded in Lp(Ω) for every p≥2∗ such that F(pB)<F(p); since F is decreasing on [2∗,+∞), we have that the sequence {un} is bounded in Lp(Ω) for every 2∗≤p<pB, as desired.
3.
Proof of Theorem 1.6
Proof. In this case, by assumption (1.11), for any n in N, we slightly modify the approximate problems (2.2) and we consider the solution un of
Observe that since the function t↦t1+Qnt is increasing, and since (1.11) holds, we have
so that
Let k>0 and choose Gk(un) as test function in the weak formulation of (3.1) (recall that the function Gk(t) is defined by (2.6)). We have
Using (1.2) and (1.6), as well as (3.2), from the above identity we obtain that
From the above inequality we obtain, dropping a positive term, that
Choosing k>0 such that (1−1ρ)k>Q, we therefore have that
from which it follows that Gk(un)=0; that is, |un|≤k almost everywhere in Ω, which implies that the sequence {un} is bounded in L∞(Ω). Once this boundedness has been proved, choosing un as test function in the weak formulation of Eq (3.1), and using (1.2), one has (dropping a positive term) that
so that the sequence {un} is bounded in W1,20(Ω). From these estimates, and reasoning as in the proof of Theorem 1.2, it follows that the weak limit u of the sequence {un} in W1,20(Ω) is a weak solution u of (4.1) that belongs to L∞(Ω). Uniqueness is then proved as in the proof of Theorem 1.2.
Remark 3.1. Note that any weak solution of (1.7) is also a weak solution of
where
Since under assumption (1.11) we have that
and since if |f(x)|≤Qa(x) one also has that |f(x)|≤QA(x), with
the boundedness result of Theorem 1.6 can also be obtained using the boundedness result of [2]. It is by the convenience of the reader that we have given a self contained proof of the above theorem.
4.
An example
As stated in the Introduction, we are going to prove that if α=1, then for every 0<B<H2, and for every p>pB there exist ap(x)≥0, with ap(x)≤B/|x|2, and fp(x), such that (1.6) holds, for which there exists a weak solution u in W1,20(Ω) of
with u that does not belong to Lp(Ω). Therefore, Theorem 1.2 is sharp since the summability of the solution u can be at most LpB(Ω), and not better.
In order to prove the result, let Ω=B1(0), let 0<B<H2, and let p>pB>2∗; since F(pB)=B, and F is decreasing, we have that B>F(p). Define
and observe that u is the weak solution in W1,20(Ω) of the equation
Define
Thanks to these definitions, we have that 0≤ap(x)≤B/|x|2, that |fp(x)|≤Qpap(x), and that u, which does not belong to Lp(Ω), is a weak solution of
Since such weak solution is unique by Theorem 1.2, we have proved that the result of that theorem is sharp.
5.
Lower order terms with quadratic growth with respect to the gradient
The result of Theorem 1.6 states that if the lower order term a(x) dominates the Hardy potential B/|x|2, then existence of bounded solutions follows for any B>0. The same result is true if one considers gradient dependent lower order terms having quadratic growth. Our result is the following.
Theorem 5.1. Let B>0, and let f(x) be a function in L1(Ω). Let g:R→R be a continuous functionsuch that g(0)=0 and that g(t)t is increasing on (0,+∞) and decreasing on (−∞,0). Then there exists a weak solution u in W1,20(Ω) of the boundary value problem (1.12), that is: g(u)|∇u|2 belongs to L1(Ω) and
for every φ in W1,20(Ω)∩L∞(Ω).
Proof. Let n in N, let fn(x)=Tn(f(x)), and let un in W1,20(Ω) be a solution of
The existence of un follows from the results of [7], where it is also proved that un belongs to L∞(Ω) for every n in N (note that the right hand side of the equation is bounded by Bn2+n).
We now follow [5] (see also [6]) and choose T1(un) as test function in the weak formulation of (5.2). We obtain, dropping a positive term and using (1.2),
From this inequality it follows, using that g(t)t is increasing on (0,+∞) and decreasing on (−∞,0), that
Defining μ=min(α,max{g(1),|g(−1)|}), from the above inequality it follows that
We now observe that by Hölder, Sobolev and Young inequalities we have
where in the second to last passage we have used that N>2 so that 1/|x|4NN+2 belongs to L1(Ω). Using this inequality in (5.3) we have that
from which it follows that
Passing to a subsequence if necessary, we may assume the sequence {un} converges to a function u weakly in W1,20(Ω), strongly in Lρ(Ω) for every ρ<2∗, and almost everywhere in Ω. From these convergences it follows that
In particular, it converges in L1(Ω), so that one can repeat the proof of [5] to have that
which in turn implies that
In order to pass to the limit in the weak formulation of (5.2), we need to deal with the lower order term with quadratic growth with respect to the gradient: we are going to prove that
Since we already know that g(un)|∇un|2 almost everywhere converges to g(u)|∇u|2 as a consequence of the almost everywhere convergence of un, of the continuity of g(t), and of (5.5), to prove (5.6), by Vitali theorem, it suffices to show the equi-integrability of the sequence {g(un)|∇un|2}. In order to do that, let h>0, k>0 and choose 1hTh[Gk(un)] as test function in the weak formulation of (5.2). Dropping the positive first term, and letting h tend to 0, we obtain (see [5])
Since |un|/|x|2 is compact in L1(Ω), and since meas({|un|>k}) tends to zero as k tends to infinity uniformly in n in N, from (5.7) we have that
Let now E be a measurable subset of Ω; for every k>0 we have
We now fix ε>0 and use (5.8) to choose k>0 large enough in order to have
Once k>0 has been chosen, we use (5.4) in order to choose meas(E) small enough to have
Therefore, for every ε>0 we have that if meas(E) is small enough, then
which proves the equi-integrability of the sequence {g(un)|∇un|2}, which implies that (5.6) holds true.
Having proved all these convergences, we can pass to the limit in the identities
which hold for every φ in W1,20(Ω)∩L∞(Ω), to have that u is such that (5.1) holds.
Acknowledgments
The first author is supported by FEDER-MINECO (Spain) grant PGC2018-096422-B-I00 and Junta de Andalucía (Spain) grant FQM-116.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad:



