Wannier functions and discrete NLS equations for nematicons

1.   Introduction

We study the derivation of nonlocal discrete nonlinear Schrödinger (DNLS) models for a system describing the propagation of a laser light in a nematic liquid crystal substrate with a periodic structure in the direction normal to the optical axis. This is the setup of laser light propagation in an effectively planar waveguide array in a nonlocal medium. Our work is motivated by the experimental work of ^[1,2,3] and some of the discrete NLS systems proposed to model the experiments. We are particularly interested in a DNLS model proposed by Fratalocchi and Assanto ^[4] that has a Hartree-type cubic nonlinearity. Recent theoretical and numerical studies have shown interesting departures from the dynamics of the cubic DNLS, specifically new non-monotonic amplitude profiles of breather solutions, additional internal modes in the linearization around breathers ^[5,6], and possibly enhanced mobility of traveling localized solutions ^[7]. The goal of our study is to derive and generalize the Fratalocchi-Assanto model.

The derivation of DNLS equations can be made systematic by the use of Wannier functions ^[8], and this formalism has been also used to show some rigorous justifications of the DNLS equations in a special limit referred to as the tight binding approximation ^[9,10].

The present work adapts this formalism to a nonlocal problem. A first step is to simplify the original equations describing the interaction of the laser field with the liquid crystal orientation field, deriving an NLS equation coupled to a linear elliptic equation with periodic coefficients, see Section 2. Wannier functions are constructed and computed using a periodic Schrödinger operator that appears naturally in the elliptic equation. We see that we can solve the elliptic equation using the Wannier basis and formally reduce the system to an evolution equation for the Wannier coefficients. The coefficients describing linear and nonlinear interactions between the Wannier modes involve integrals of Wannier functions and related functions and must be evaluated numerically. We examine a subset of these interactions with a first goal of obtaining the simplest extension of the Fratalocchi-Assanto model. We arrive at a system combining a nonlinear nonlocality of Hartree type similar to the one in the Fratalocchi-Assanto model with a linear nonlocality that is studied mathematically by several authors in systems with power law nonlinearity ^[11,12,13]. Some related nonlocal equations with periodic coefficients were studied in ^[14,15].

The computed coefficients suggest that nonlocal effects are more pronounced when the periodicity in the transverse direction has a smaller amplitude, and we also see parameter regimes where the nonlinear part dominates. For larger amplitude periodicity the standard cubic NLS seems to be an adequate model. The model we examine in more detail here is restricted to interactions among Wannier modes of the first energy band of the associated Schrödinger operator. Preliminary calculations suggest that other interactions within the first band and with other bands may also be important, see also ^[1] for experimental evidence. Extensions will be pursued in further work.

The paper is organized as follows. In Section 2 we derive a simplification of the physical model, and identify a periodic Schrödinger operator used to define the Wannier basis. In Section 3 we use the Wannier basis to arrive at a general evolution equation for the Wannier coefficients of the laser field amplitudes. In Section 4 we present numerical results on the coefficients for a small subset of the possible indices, considering only the lowest energy band. In Appendix A we present additional material on the numerical computation of the Wannier functions.

2.   Coupled NLS-elliptic system for optical solitons in liquid crystals

Optical beams in a nematic liquid crystal are described by the system

with $\gamma$ , $\nu$ positive constants, see ^[16,17], and $\Delta = \partial^2_x + \partial^2_y$ . The variable $z$ is analogous to time and we are interested in solutions to (2.1), (2.2) with $u$ , $\theta$ given at $z = 0$ . Physically $u$ represents the amplitude of the electric field of a laser beam that propagates along the $z-$ direction. The field $u$ is assumed to have only one component, along the (vertical) $x-$ axis. $\theta$ is the macroscopic field of angles describing the liquid crystal molecular orientation at each point, i.e., a macroscopic local average orientation of the liquid crystal molecules, assumed to be parallel to the $x$ , $z-$ plane. $\theta_0$ and $E_0$ are assumed to be known functions. $\theta_0$ represents an orientation field produced by an additional electric field $E_0$ applied to the sample. The field $E_0$ is assumed to have only an $x-$ component.

Equations (2.1), (2.2) follow from a Maxwell-Oseen-Frank system that couples the electric fields $E_0$ and $u$ and the director angle $\theta$ , see ^[18], Appendix. Intuitively, (2.2) describes the tendency of the molecular and electric field orientations to align, as well as an elastic resistance of the material to localized changes in orientation, while (2.1) describes the focusing effect of aligned molecular and electric field orientations.

To enhance this basic effect, it has been understood that the system must be "prepared" by first producing a nontrivial "pretilt" angle field $\theta_0$ in the sample. We are here considering an experimental setup where $\theta_0$ is produced by a known external field $E_0$ , e.g., placing the sample between two capacitor plates. Other experimental ways to produce $\theta_0$ are described in ^[19,20]. $\theta_0$ and $E_0$ are thus related, see below. The main point, however, is that these two functions can be used to introduce variable coefficients in the system, and we will consider the case where $\theta_0$ , $E_0$ are $b-$ periodic in the horizontal direction $y$ , and independent of the $z$ coordinate.

To describe the relation between $\theta_0$ and $E_0$ in the absence of the laser beam, we use (2.2) with $\theta = \theta_0$ , $u = 0$ ,

see ^[18] for the boundary conditions. In the presence of a laser beam, the laser field interaction changes the angle field to $\theta = \theta_0 + \psi$ , i.e., $\psi$ is the change from the pretilt angle $\theta_0$ observed in the absence of the beam. Letting $\theta = \theta_0 + \psi$ and substituting (2.3) into (2.2) we obtain the system

see ^[16]. The second equation has been examined in more detail in ^[18] for the case of $E_0$ , $\theta_0$ constants, with $\theta_0 \in ({\pi \over 4}, {\pi \over 2})$ . This assumption is important for solving (2.5) uniquely, see ^[18]. Here we are looking for an explicit expression of $\psi$ in terms of $u$ and we simplify the system first assuming $\psi$ small. Then system (2.4), (2.5) is, up to terms of $O(\psi^2)$ ,

see also ^[18].

Further analysis of the equations assumes that $E_0$ , $\theta_0$ are known. To simplify the problem we will choose $E_0$ , $\theta_0$ that are reasonably consistent with (2.3), i.e., avoiding solving (2.3) exactly. One way to do this is to assume $E_0$ , $\theta_0$ of the form

with $0 < \epsilon \leq \delta$ small parameters. The applied electric field $E_0$ is thus assumed to consist of two parts, a contribution $\sqrt{\epsilon}E_{0, V}$ that depends only on the vertical direction $x$ , and a smaller contribution $\delta E_{0, H}$ that will be assumed $b-$ periodic in the horizontal direction $y$ . $E_0$ models the electric field of a set of parallel metallic stripes that run along the $z-$ axis and are placed at the two planes bounding the experimental domain from above and below, at $x = \pm L$ respectively, see ^[1]. The lower and upper stripes have opposite charges, producing an electric field that is $b-$ periodic in the $y$ (transverse) direction.

Matching orders in (2.3) up to $O(\epsilon^{3/2} \delta)$ leads to

The first equation is similar to the one arising in the case of constant applied field, i.e., compare to (2.3) with $E_{0}$ constant, and is solved using boundary conditions for $\theta_0$ at the vertical boundaries $x = \pm L$ , see e.g., ^[17]. In the second equation $E_{0, H}(\sqrt{\epsilon}x, y)$ is assumed $b-$ periodic in $y$ , and the solution ${\theta}_{0, H}(\sqrt{\epsilon}x, y)$ can also be chosen $b-$ periodic in $y$ .

To use (2.8)–(2.11) in (2.6), (2.7), we note that since $E_0$ , $\theta_0$ vary slowly in the vertical direction $x$ , their value in the center of the sample can be approximated by constants. We therefore substitute (2.8)–(2.11) into (2.7), approximating first $E_{0, V}(\sqrt{\epsilon}x)$ by ${\overline E}_{0}$ , $E_{0, H}(\sqrt{\epsilon}x, y)$ by ${\widetilde E}_{0}(y)$ , and ${\theta}_{0, V}(\sqrt{\epsilon}x)$ by ${\overline \theta}_0 \in (\pi/4, \pi/2)$ , ${\theta}_{0, H}(\sqrt{\epsilon}x, y)$ by ${\widetilde \theta}_0(y)$ , to obtain

up to terms of $O(\delta^2)$ on the left hand side, and terms of $O(\delta^2 \epsilon)$ on the right hand side. Thus the terms omitted on each side can be considered of $O(\delta^2)$ .

Note that ${\widetilde E}_{0}(y)$ , ${\widetilde \theta}_0(y)$ are $b-$ periodic, and are related by

the simplification of (2.11). Thus ${\widetilde \theta}_0$ can be determined from ${\widetilde E}_0$ , moreover if ${\widetilde E}_0$ is $b-$ periodic, then ${\widetilde \theta}_0$ can be also chosen $b-$ periodic.

We further simplify the analysis by considering $u$ , $\psi$ independent of the vertical variable $x$ . Letting $\delta = \epsilon$ , and considering terms of up to $O(\epsilon^{3/2})$ in (2.12), system (2.6), (2.7) then becomes

The first equation follows from (2.6) using the expansion (2.9) for $\theta_0$ and the simplifications above, in particular ${\widetilde \beta} = |\sin 2 {\overline \theta}_0| + O(\epsilon^{3/2})$ , where the omitted $O(\epsilon^{3/2})$ terms are $b-$ periodic in $y$ . The second equation is (2.12) up to terms of $O(\epsilon^{2})$ , so that $g^2$ is a positive constant, and $\alpha$ , $V$ $b-$ periodic functions, defined implicitly by comparing the second equation to (2.12).

Since we are primarily interested in the inhomogeneity of the second equation and the inversion of the operator $- \partial_y^2 + V(y) + g^2$ , we will only consider the lowest order, constant parts of $\alpha$ , $\beta$ of the respective $\widetilde \alpha$ , $\widetilde \beta$ above, and consider the simplified system

where assuming ${\overline \theta}_0 \in ({\pi \over 4}, {\pi \over 2})$ ,

are positive constants, and

We can assume that $V$ has a negative minimum $- V_m$ that satisfies $V_m < g^2$ , with $g^2$ as in (2.18). We can then suitably redefine $g^2$ , and $V$ of (2.19) so that both are positive. These sign assumptions are valid also for the variable coefficients ${\widetilde \alpha}(y)$ , ${\widetilde \beta}(y)$ of the intermediate system above.

The goal of the paper is to write further explicit simplifications of system (2.16), (2.17) using the Wannier basis defined by the Schrödinger operator $- \partial^2_y + V(y)$ , with $V$ as in (2.19).

An alternative approach to simplifying the system is to write the inverse of the operator $- \partial_y^2 + g^2 + V$ in (2.17) as

and keep the lowest order terms in the expansion

Assuming $|V|$ bounded, both $A^{-1}$ , and $V$ are bounded operators in $L^2({\bf R}, {\bf C})$ , with norms $g^{-2}$ (by Plancherel's theorem), and $V_M = \max_{y \in {\bf R}} |V(y)|$ respectively. The $g^{-2} V_M < 1$ implies that $A + V$ has a bounded inverse given by the convergent series expansion (2.21). We can also use the explicit expression

where $f$ is a function and $K*f$ denotes the convolution

Then (2.16) becomes

The lowest order approximation that includes the effect of the periodic potential $V$ is

The fact that the variable coefficient equation has additional terms seems inconvenient for computations, and in the next section we describe a different approach to solving (2.17).

3.   Discrete nonlinear equations for laser-nematic liquid crystal system

3.1.   The discrete nonlinear equation for nematicons

We consider the system of periodic nematicon equations derived in the previous section

with $\alpha$ , $\beta$ , $g^2$ positive constants, and $V$ $b-$ periodic and positive.

We recall the definition of the Wannier functions associated to the operator $- \partial_y^2 + V(y)$ , $V$ $b$ -periodic, see ^[10,21] for the theory. Bounded solutions $\phi_{n, k}$ (Bloch functions) and eigenvalues $E_{n, k} \in \mathbb{R}$ of the periodic Schrödinger equation satisfy

where

for all $y \in \mathbb{R}$ , $n \in \mathbb{N}$ , $k \in \mathbb{R}$ . Furthermore,

for all $n \in \mathbb{N}$ , $k$ , $y \in \mathbb{R}$ . By the above we can consider $k$ in any interval of length $2\pi/b$ . The index $n$ is referred to as band index (or number). For any fixed $k$ in an interval of length $2\pi/b$ , $E_{n, k}$ is the $n-th$ largest eigenvalue of (3.2) with boundary conditions $\phi_{n, k}(y + b) = e^{i k b} \phi_{n, k}(y)$ , implied by (3.3).

For $n \in \mathbb{N}$ , $y \in \mathbb{R}$ , we consider the Fourier coefficients

of $\phi_{n, \cdot}(y)$ , and we also have the inversion formula

The set of functions $w_n^m:\mathbb{R} \rightarrow \mathbb{C}$ , $n \in \mathbb{N}$ , $m \in \mathbb{Z}$ defined by (3.5) are referred to as Wannier functions ^[21,22], They form an orthonormal set of $L^2(\mathbb{R}; \mathbb{C})$ , also by (3.5), (3.3),

Thus, fixing $n$ , the function $w^{m}_n$ is a translation of the function $w^{0}_n$ by $m b$ . The definition of $w^{0}_n$ and the regularity of the $\phi_{n, k}$ in $k$ also leads to strong localization of the $w^{0}_n$ in $y$ , see ^[10,23].

We use expansions $\psi$ and $u$ in Wannier functions $w_{n}^{m}$ as

We first consider the second nematicon equation (3.1b). We multiply (3.1b) by $\phi_{n', k'}^*(y)$ , integrate over $y \in \mathbb{R}$ , and use the Schrödinger equation (3.2) to obtain

hence

We then multiply (3.11) by $e^{imk'b}$ and integrate both sides over $k \in [-\pi/b, \pi/b]$ . Interchanging the order of integration in $k$ , $y$ , and using the definition of Wannier functions we obtain that $\psi$ is given by (3.8) with

where

To expand the first nematicon equation (3.1a) in coefficients of Wannier functions, we substitute the series expansions (3.8), (3.9) into (3.1a), multiply (3.1a) by $w_{n'}^{m'*}(y)$ , and integrate over $y \in \mathbb{R}$ . We obtain

where

Substitution of (3.12) into (3.14) leads to the system

where by (3.13), (3.15)

The above infinite system of ordinary differential equations for the Wannier coefficients is a spatial discretization of the original system of partial differential equations, and a first step to simplifying truncations leading to discrete NLS equations and systems ^[8]. In the present work, the main goal is a systematic derivation of nonlocal versions of DNLS equations and systems, motivated by the Fratalocchi-Assanto equation ^[4]. Important features of the Wannier functions $w_n^m$ include their spatial localization (^[10], see also Appendix), and the translation property (3.7). Truncations involving $m \in \mathbb{Z}$ , $n \in \{1, \ldots n_{\max}\}$ , are expected to preserve the translation symmetry of periodic systems, and we increase the spatial resolution by considering larger $n_{\max}$ .

3.2.   Comparison with the discrete model of Fratalocchi and Assanto

We now consider simplifications of (3.16), (3.17) leading to a DNLS model that is comparable to the equation

with $\Gamma(m-m') = e^{-\kappa |m-m'|}$ , $\kappa > 0$ , $C_1$ , $C_2 > 0$ , proposed by Fratalocchi and Assanto ^[4].

The first simplification of (3.16), (3.17) will be to consider only the first band, and interactions among of Wannier coefficients $w_{1}^m$ , $m \in \mathbb{Z}$ (setting $u_{n, m} = 0$ , $\forall n > 1$ ). Thus we only consider coefficients $D_{1, 1}^{m, m'}$ and $V_{1, 1, 1, 1}^{m_1, m_2, m_3, m'}$ .

The second simplification comes by approximating the Wannier coefficients $c_{1, m}$ of $\psi$ in (3.12) by

assuming that the coefficient $K_{1, 1, 1}^{m_1, m_2, m}$ of (3.13) vanishes if $m_1 \neq m_2$ . Equation (3.16) is therefore replaced by

The last step is to assume that $I_{1, 1, 1}^{m, m_3, m'}$ vanishes unless $m_3 = m'$ . Then we obtain the model equation

where

We now examine the symmetries of the linear and nonlinear coefficients of (3.21).

Considering the linear coefficients, by (3.15) we have

therefore $D_{n, n'}^{m, m'} = (D_{n', n}^{m', m})^*$ . Using the reality of the Wannier functions (see Appendix) we see that $D_{n, n}^{m, m'}$ depends on $|m-m'|$ . Also $D_{n, n}^{m, m} < 0$ . The above holds for all $n \in \mathbb{N}$ , $m \in \mathbb{Z}$ .

We also show that $V_1(m_1, m') = V_{1, 1, 1, 1}^{m_1, m_1, m', m'}$ of (3.22) is real and depends on $|m_1 - m'|$ . Combining (3.13), (3.15) with the inversion formula (3.6) for $\phi_{1, k}^*$ we have

By (3.7) and the variable changes $v = y-m_1 b$ and $u = y-m'b$ we then have

Letting $m_2 = m_0-m_1$ and $m_3 = m-m'$ we then have

showing that $V_1(m_1, m')$ depends on $m_1 - m'$ . We use the reality of the Wannier functions to see that

is even in $k$ . By (A.16), $E_{1, k}$ is also even in $k$ . Then (3.26) implies that $V_1(m_1, m')$ is real and depends on $|m_1 - m'|$ , as claimed.

The above properties of $D_{1, 1}^{m, m'}$ and $V_{1, 1, 1, 1}^{m_1, m_1, m', m'}$ also imply that (3.21) can be written as a Hamilton's equations

with Hamiltonian

The Hamiltonian structure of (3.21) is not surprising given that the continuous system (2.16), (2.17) we expanded in Wannier functions is also Hamiltonian. This follows from the fact that the operator $(A + V)^{-1}$ in (2.24) is symmetric, see e.g., ^[24]. A more systematic derivation of the Hamiltonian structure of the discrete system, considering first the Hamiltonian structure of (3.17), will be presented elsewhere. Note that system (2.4), (2.5) is also Hamiltonian in the sense described in ^[25], see also ^[18] for a similar system.

4.   Numerical evaluation of linear and nonlinear coefficients

To evaluate the linear and nonlinear coefficients of (3.21) we have used the Wannier functions of the periodic square-well potential of (A.2). Appendix A contains further details. We are interested in the dependence of the coefficients on the amplitude $V_0$ of the potential and consider values $V_0 \in [0.1, 10]$ . In all cases, the potential has period $b = 2 \pi$ .

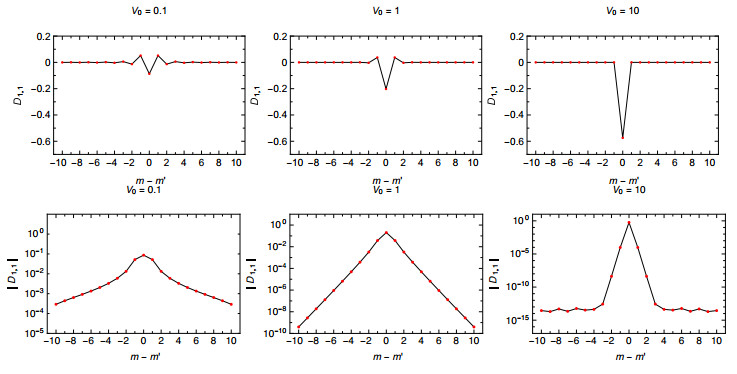
The linear coefficients $D_{1, 1 }^{m, m'} = D_{1, 1}(m-m')$ are plotted in Figure 1 for different potential amplitudes $V_0$ . Their values for nearest neighbors are shown in Table 1. The nonlinear coefficients $V_{1}(m_1, m')$ of (3.26) are shown in Figure 2. They depend on the potential amplitude $V_0$ and $g^2$ . Their values for nearest neighbors are shown in Table 2.

Figures 1 and 2 show clearly that both linear and nonlinear coefficients, $D_{1, 1 }^{m, m'}$ and $V_{1}(m_1, m')$ respectively, decay more slowly as the amplitude $V_0$ is decreased. The nonlinear coefficients also decrease with $g^2$ , Figure 2, as expected from their definition, e.g., (3.26).

We also fitted the linear and nonlinear coefficients $|D_{1, 1}|$ and $|V_1|$ to exponentials of the form $C e^{- \gamma |m-m'|}$ and $C e^{- \gamma |m-m'|^{\xi}}$ . These are typically good for some ranges of $|m-m|$ . Considering the linear coefficient $|D_{1, 1}|$ we see that for $V_0 = 0.1$ , $|D_{1, 1}| \sim 5.352 e^{-4.875|m-m'|^{0.3}}$ in the range $|m-m'|\ge 2$ ; for $V_0 = 1$ , $|D_{1, 1}| \sim 2.423 e^{-9.288|m-m'|}$ in the range $0\le|m-m'|\le10$ ; and for $V_0 = 10$ , $|D_{1, 1}| \sim 0.574e^{-8.700|m-m'|}$ in the range $|m-m'| \le 3$ . For $V_0 = 10$ , $|D_{1, 1}|$ vanishes up to double-precision error at larger distances. In the case of $V_0 = 0.1$ , we have a sub-exponential decay, with $\xi < 1$ .

Fits to nonlinear coefficient $|V_1|$ are according to $V_0$ and $g$ . For $V_0 = 0.1$ with $g = 0$ , and $0.1$ fits yield $|V_1| \sim 1.316 e^{-0.73|m-m'|^{1.17}}$ , and $1.145e^{-0.78|m-m'|^{1.17}}$ respectively, assuming $|m-m'|\le5$ in both cases, such decays are slightly super-exponential, and faster than the decay of the linear coefficient; for $g = 1$ and $10$ respective fits yield $|V_1| \sim 0.096 e^{-1.49|m-m'|}$ and $0.001e^{-1.64|m-m'|}$ assuming $|m-m'| \le3$ in both cases. For $V_0 = 1$ , and $|m-m'|\ge3$ we have $|V_1| \sim C e^{\gamma|m-m'|}$ , with $\gamma \in [1.93, 1.96]$ depending on $g$ , such exponential decays can be appreciated in the log-plots in Figure 2. For $V_0 = 10$ , and $|m-m'| \le 3$ we see $|V_1| \sim C e^{-\gamma|m-m'|^{\xi}}$ , with $\gamma \in [11, 14]$ and $\xi \in [0.72, 0.90]$ depending on $g$ . For $V_0 = 10$ , nonlinear coefficients show a sub-exponential decay. These results show that as we vary $V_0$ and $g$ we see a variety of long-range interactions. For moderate potentials $V_0\sim1$ we recover the nonlinear decay of model Eq. (3.18).

Figure 2 and Table 2, with $V_0 = 0.1$ , show evidence for a rapidly decaying nonlocal interaction that is similar to the one described by the model of (3.18).

Also, by Figures 1 and 2 case $V_0 = 0.1$ , the signs of the linear and nonlinear terms are compatible to the ones assumed in (3.18), and correspond to the focusing sign combination. The off-diagonal linear coefficients are also rather small ($\sim 0.05$ ) compared to the nonlinear coefficients ($\sim 1$ ), we are thus near the "anti-continuous" limit considered for the nonlocal problem in ^[5,6]. A similar observation applies to the larger potential amplitudes shown, $V_0 = 1$ , $10$ . (The diagonal linear coefficient $D_{1, 1}^{m, m}$ is independent of $m$ and can be eliminated by a phase change.) In those two cases the cubic power DNLS seems to be an adequate model. Figure 2 shows the decay of the nonlinear interaction is faster for larger $V_0$ .

5.   Discussion

We derived a model NLS-elliptic system for an optical waveguide array in a nonlocal medium, and used Wannier functions defined by an associated Schrödinger operator with periodic potential to write an infinite system for the interaction of the Wannier modes of the laser beam amplitude. We also discuss a simplified system that considers a subset of the interactions of Wannier modes whithin the first energy band of the periodic Schrödinger operator. We obtain a generalization of a nonlocal DNLS model derived by Fratalocchi-Assanto ^[4]. We see that nonlocal effects are more pronounced for small amplitude oscillations of the system coefficients across the waveguide array.

The NLS-elliptic model we use is a variant to the one considered by ^[4], where the authors use alternative perturbative arguments to solve approximately the equations for the pretilt angle $\theta_0$ and for an additional angle $\psi$ produced by the laser beam. In the present work we focus on the equation for the additional angle $\psi$ , and solve it by introducing expansions in Wannier functions. Another difference is in the treatment of the equation for the electric field, where ^[4] uses a coupled mode Ansatz, with mode couplings of a predetermined. The present paper considers a related but more general idea, expansion in a Wannier basis ^[8]. The computation of the Wannier functions is involved, but advantages include the fact that the Wannier mode interactions are determined by the continuous equation. Also the general discrete system that describes the interactions among all modes can be simplified by considering a finite (and small) number of Wannier modes per site, and a subset of the mode interactions. Calculations that will be reported elsewhere suggest that these simplifications can be also made at the level of the Hamiltonian, preserving the Hamiltonian structure of the continuous model.

The simplification leading to discrete equations with the structure of the Fratalocchi-Assanto model suggests nonlinear interactions that decay roughly in an exponential way, as in ^[4]. The construction of ^[4] considers only nearest-neighbor linear interactions. In cases of slower decay for the nonlinear coupling, i.e., more pronounced nonlocality, our results suggest that we could also consider nonlocal linear coupling terms. Even in these cases however, linear couplings decay faster that nonlinear couplings, justifying the simplification in ^[4], and also suggesting the relevance of the anti-continuous limit considered in ^[5,6].

In future work we plan to examine models describing a larger class of interactions within the first band, as well as interactions with the second band. Higher local modes may be especially relevant for higher nonlocality, and are also relevant to experimental observations ^[1,2,3]. It would be also of interest to construct discrete models with saturation effects ^[18], starting from (2.4), (2.5). The formalism described so far does not apply directly.

A.   Appendix. Computation of Wannier functions and energies

A.1.   Two linearly independent solutions $\psi_1(y)$ and $\psi_2(y)$ of the Schrödinger equation

We solve the Schrödinger equation (3.2)

for the $b$ -periodic square-well potential

where $V_0 > 0$ is the potential amplitude and $\vartheta$ its width. Results for some spacial cases are in ^[10,26].

Solutions of (A.1) have eigenenergies that belong to intervals called energy bands. $\Psi$ 's solutions may be expressed in terms of the so-called Bloch wave functions $u_{n, k}(y)$ , that have the same period as $V$ , as

$k$ is the parameter that allows to explore values within the energy bands

For the general solution of (A.1), we first find two linearly independent solutions $\psi_1(y)$ and $\psi_2(y)$ assuming the initial conditions

For $E_{n, k} > V_0$ , solutions are

and for $E_{n, k} < V_0$

with $\eta = \sqrt{E-V_0}$ , $\Gamma = \sqrt{E}$ , and $\zeta = \sqrt{V_0-E}$ .

A.2.   Bloch functions

The Schrödinger equation (A.1) is a second-order linear differential equation. The general solution $\Psi(y) = \Psi_{n, k}(y)$ may be computed as a linear combination of the independent solutions $\psi_1(y)$ and $\psi_2(y)$ . Such linearity also applies to the derivatives, leading to the system

By assuming the initial conditions $\Psi(y_0^+)$ and $\Psi'(y_0^+)$ , using $y_0^+ = 0^+$ , we eliminate the constants $A$ and $B$ . The resulting system of equations is written in matrix form following the procedure of Bruno and Nacbar ^[23]

where the $2\times2$ matrix in the right-hand side is known as the transfer matrix $T$ from $y_0^+$ to $y$ .

Eigenfunctions $\Psi(y)$ and $\Psi'(y)$ satisfy the Bloch theorem, i.e., $\Psi_{n, k}(y+b) = e^{ikb} \Psi_{n, k}(y)$ . Evaluation of (A.13) at $y = y_0^++b$ , and use of the Bloch theorem leads to

where $(M_{ij})$ $(i, j = 1, 2)$ are elements of the primitive matrix $M$ defined by

Initial conditions with non trivial $\Psi(y_0^+)$ and $\Psi'(y_0^+)$ to solve (A.14) lead to the secular equation

with

Substitution of $M_{11}$ and $M_{22}$ in the last expression yields the well-known transcendental equation for the eigenenergies $E_{n, k}$ as a function of $k$ , or equivalently $\eta$ and $\Gamma$ . For the square-well potential, for $E_{n, k} > V_0$ it is

and for $E_{n, k} < V_0$

Now, computation of $\Psi(y)$ in terms of the initial conditions is obtained from the first equation in (A.13), which is

$\Psi(y_0^+)$ and $\Psi'(y_0^+)$ may be related from (A.14) and (A.15) as

therefore substitution of one of them into (A.20) leads to $\Psi(y)$ known up to one constant. Substitution of (A.22) into (A.20), for $M_{12} \neq 0$ , leads to

The initial condition $\Psi(y_0^+)$ is chosen to normalize the $\Psi(y)$ function. Bruno and Nacbar started with the Schrödinger equation and used the derivative of the secular equation to find an analytical expression for the normalization constant $|\Psi(y_0^+)|$ , see Appendix B of ^[23]. The corresponding normalization constant for the Schrödinger equation in (3.2), is

assuming that $\mu'(E)\neq0$ . Bruno and Nacbar define positive-$\Psi$ Wannier functions if the initial condition $\Psi(y_0^+)$ is positive and such that

with $|\Psi(y_0^+)|$ given by (A.24). In what follows, we used a positive initial condition $\Psi(y_0^+)$ , as defined through (A.25) and (A.24) for Bloch functions given by (A.23).

$\Psi_{n, k}$ of (A.23) depends explicitly on $k$ through $\cos kb$ in the real part and $\sin kb$ in the imaginary part. $\Psi_{n, k}$ also depends implicitly on $k$ though $E_{n, k} = E_{n}(k)$ by $\Psi(y_0^+)$ , $M_{12}$ , $M_{11}$ , $\psi_1(y)$ and $\psi_2(y)$ . If $E_{n}(k)$ has even parity on $k$ then all terms implicitly depending on $k$ are also even by their definition. In such a case, $\Psi_{n, k}(y)$ obeys the inversion symmetry $\Psi_{n, -k}(y) = \Psi_{n, k}^*(y)$ and Wannier functions are real, according to (3.5)

A.3.   Eigenenergy spectrum and Wannier functions

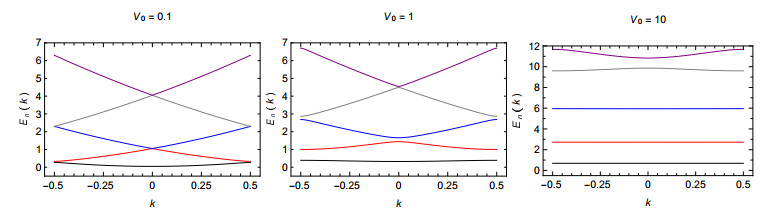
We numerically solve (A.18) and (A.19) to find $E_{n, k}$ as a function of $k$ , for the square-well potential of period $b = 2\pi$ and amplitude width $\vartheta = \pi$ . Solutions were computed using Newton's method. As potential amplitudes we chose $V_0 = 0.1, 1, \text{ and } 10$ . Figure 3 shows results of the lowest energy bands $E_{n}(k)$ in the range $k \in [-1/2, 1/2]$ . Results show even parity on $k$ .

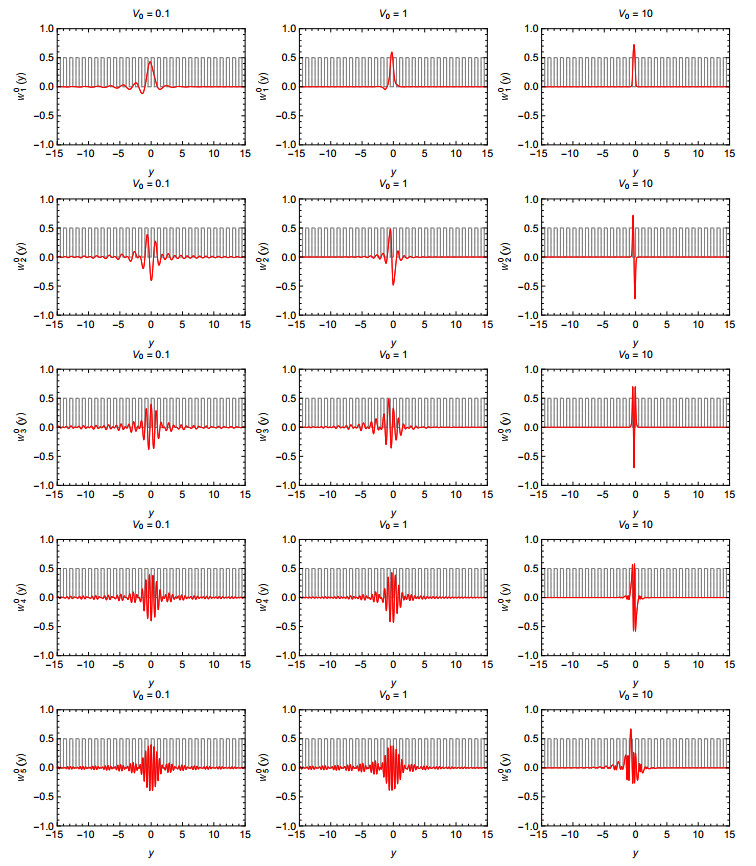
We used the eigenenergies to evaluate the real and imaginary parts of the Wannier functions from (3.5) using the Bloch functions (A.23). Wannier functions are real, in agreement with the inversion symmetry of Bloch functions ^[23]. The integral in (3.5) is computed by Simpson's rule using a grid with $10^3$ points. Figure 4 shows Wannier functions $w_n^0(y)$ of the first five energy bands (for $n = 1, \ldots, 5$ ) for potentials $V_0 = 0.1, 1, \text{ and } 10$ . Plots range from $y \in [-15 b, 15b]$ in lattice units. Wannier functions show oscillations that decay along the $y$ -coordinate. The number of oscillations increases with the band number $n$ , and decreases with the amplitude of the potential $V_0$ . Oscillations still persist after several periods from the origin, primarily for large energy bands.

Acknowledgments

The authors acknowledge partial support from grant PAPIIT112119. J. A. V.-P. also thanks Consejo Técnico de la Investigación Científica for a posdoctoral fellowship at IIMAS-UNAM. We also thank the anonymous referees for comments that led to significant improvements.

Conflict of interest

The authors declare no conflict of interest.