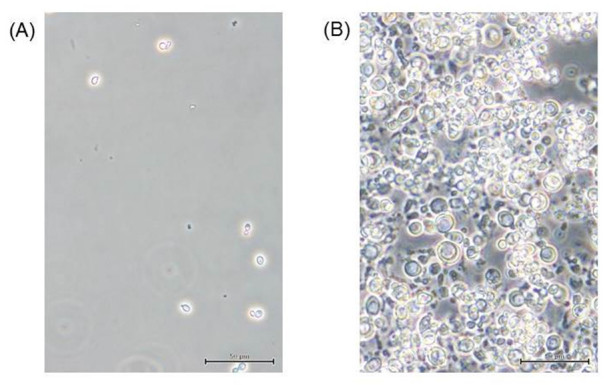
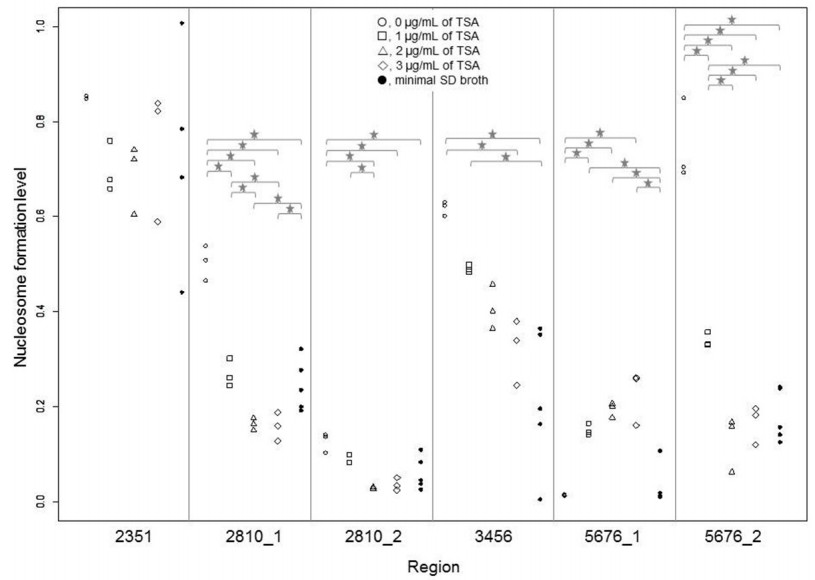
Changes in nucleosome formation at gene promoters in the archiascomycetous yeast Saitoella complicata

1.   Introduction

The fractional perimeter of a measurable set $E\subseteq {\mathbb R}^d$ is defined as follows:

After being first considered in the pivotal paper ^[4] (see also ^[15] where the definition was first given), this functional has inspired a variety of literature both in the community of pure mathematics, regarding for instance existence and regularity of fractional minimal surfaces, and in view of applications to phase transition problems and to several models with long range interactions. We refer to ^[17], and references therein, for an introductory review on this subject.

The limits as $s\to 0^+$ or $s\to 1^-$ are critical, in the sense that the fractional perimeter (1.1) diverges to $+\infty$. Nevertheless, when appropriately rescaled, such limits give meaningful information on the set.

The limit of the (rescaled) fractional perimeter when $s\to 0^+$ has been considered in ^[11], where the authors proved the pointwise convergence of $s \mathrm{P}_s(E)$ to the volume functional $d\omega_{d} |E|$, for sets $E$ of finite perimeter, where $\omega_d$ is the volume of the ball of radius $1$ in ${\mathbb R}^d$. The corresponding second-order expansion has been recently considered in ^[8]. In particular it is shown that

in the sense of $\Gamma$-convergence with respect to the $L^1$-topology of the corresponding characteristic functions, where the limit functional is independent of $R$, and it is called the $0$-fractional perimeter.

The limit of $\mathrm{P}_s(E)$ as $s\to 1^-$, in pointwise sense and in the sense of $\Gamma$-convergence, has been studied in ^[1,5], where it is proved that

where $\mathrm{P}(E)$ stands for the classical perimeter of $E$.

In this paper we are interested in the analysis of next order expansion. In particular we will prove in Theorem 2.1 that

in the sense of $\Gamma$-convergence with respect to the $L^1$-convergence, and the limit functional is defined as

for sets $E$ with finite perimeter, and $\mathcal{H}(E) = +\infty$ otherwise. Here we denote by $\partial^*E$ the reduced boundary of $E$, by $\nu(y)$ the outer normal to $E$ at $y\in \partial^* E$ and by $H^-(y)$ the hyperplane

We observe that, in dimension $d = 2$, the functional $\mathcal{H}(E)$ coincides with the $\Gamma$-limit as $\delta\to 0^+$ of the nonlocal energy

as recently proved by Muratov and Simon in [16,Theorem 2.3].

We also mention the recent work ^[6], where the authors establish the second-order expansion of appropriately rescaled nonlocal functionals approximating Sobolev seminorms, considered by Bourgain, Brezis and Mironescu ^[2].

As for the properties of the limit functional $\mathcal{H}$, first of all we observe that it is coercive in the sense that it provides a control on the perimeter of the set, see Proposition 3.1. Moreover it is bounded on $C^{1, \alpha}$ sets, for $\alpha > 0$, and on convex sets $C$ such that for some $s\in (0, 1)$ the boundary integral $\int_{\partial^* C} H_s(C, x)d\mathcal{H}^{d-1}(x)$ is finite, where $H_s(C, x)$ is the fractional mean curvature of $C$ at $x$, which is defined as

see Proposition 3.3. In particular when $E$ has boundary of class $C^2$, in Proposition 3.5 we show that the limit functional $\mathcal{H}(E)$ can be equivalently written as

where $H(E, x)$ denotes the (scalar) mean curvature at $x\in\partial E$, that is the sum of the principal curvatures divided by $d-1$. Notice that the first term in the expression above is the (squared) $L^2$-norm of a nonlocal second fundamental form of $\partial E$ (see e.g. [7,Appendix B]). We recall also that an analogous representation formula for the same functional in dimension $d = 2$ has been given in ^[16].

Some interesting issues about the limit functional remain open, for instance existence and rigidity (at least for small volumes) of minimizers of $\mathcal{H}$ among sets with fixed volume, see the discussion in Remark 2.7.

The paper is organized as follows. Section 2 is devoted to the proof of the main result, which is Theorem 2.1. The result is based on two main steps: the pointwise limit of $\frac{\omega_{d-1} \mathrm{P}(E)}{1-s} - \mathrm{P}_s(E)$ on smooth sets proved in Proposition 2.4, and the monotonicity of a related functional showed in Lemma 2.5. In Section 3 we analyze some properties of the limit functional $\mathcal{H}$.

2.   Second order asymptotics

We introduce the following functional on sets $E\subseteq {\mathbb R}^d$ of finite Lebesgue measure:

We now state the main result of the paper.

Theorem 2.1. There holds

in the sense of $\Gamma$-convergence with respect to the $L^1$-topology, where the functional $\mathcal{H}(E)$ is defined in (1.2).

Remark 2.2. Observe that $\mathcal{H}(E)$ can be also expressed as

Indeed by the divergence theorem and by the fact that $\mathrm{div}_y\left(\frac{y-x}{|y-x|^{d+1}}\right) = -\frac{1}{|y-x|^{d+1}}$ we get

First of all we recall some properties of the functional $\mathcal{P}_s$.

Proposition 2.3 (Coercivity and lower semicontinuity). Let $s\in (0, 1)$. If $E_n$ is a sequence of sets such that $|E_n|\leq m$ for some $m > 0$ and $\mathcal{P}_s(E_n)\leq C$ for some $C > 0$ independent of $n$, then $\mathrm{P}(E_n)\leq C'$ for some $C'$ depending on $C, s, d, m$.

In particular, the sequence $E_n$ converges in $L^1_{\rm loc}$, up to a subsequence, to a limit set $E$ of finite perimeter, with $|E|\leq m$.

Moreover, the functional $\mathcal{P}_s$ is lower semicontinuous with respect to the $L^1$-convergence.

Proof of Proposition 2.3. Let $E$ with $|E|\leq m$. By the interpolation inequality proved in [3,Lemma 4.4] we get

For a sequence $E_n$ as in the statement, this gives

From this we conclude that necessarily $\mathrm{P}(E_n)\leq C'$, where $C'$ is a constant which depends on $C, s, d, m$. As a consequence, by the local compactness in $L^1$ of sets of finite perimeter (see ^[14]) we obtain the local convergence of $E_n$, up to a subsequence, to a limit set $E$ of finite perimeter.

Now, assume that $E_n\to E$ in $L^1$ and that $\frac{c}{1- s} \mathrm{P}(E_n)- \mathrm{P}_{s}(E_n)\leq C$. By the previous argument, we get that $\mathrm{P}(E_n)\leq C'$, where $C'$ is a constant which depends on $C, s, d, |E|$. By the compact embedding of $BV$ in $H^{s/2}$, see ^[10,15], we get that $\lim_n \mathrm{P}_s(E_n) = \mathrm{P}_s(E)$, up to passing to a suitable subsequence. This, along with the lower semicontinuity of the perimeter with respect to local convergence in $L^1$ (see ^[14]) gives the conclusion.

The proof of Theorem 2.1 is based on some preliminary results. First of all we compute the pointwise limit, then we show that the functional $s\mathcal{P}_s(E)$ is given by the sum of the functional $\mathcal{F}_s(E)$, defined in (2.13), which is lower semicontinuous and monotone increasing in $s$, and of a continuous functional. This will permit to show that the pointwise limit coincides with the $\Gamma$-limit.

Proposition 2.4 (Pointwise limit). Let $E\subseteq {\mathbb R}^d$ be a measurable set such that $|E| < +\infty$ and $\mathrm{P}(E) < +\infty$. Then

where $\mathcal{H}(E)$ is defined in (1.2) and $H^-(y)$ in (1.3).

Proof. We can write $\mathrm{P}_s(E)$ as a boundary integral observing that for all $0 < s < 1$

So, by the divergence theorem, (1.1) reads

where $\nu(y)$ is the outer normal at $\partial^* E$ in $y$.

We fix now $y\in \partial^* E$ and we observe that

Now we compute, denoting by $B'_1$ the ball in ${\mathbb R}^{d-1}$ with radius $1$ (and center $0$),

If we substitute (2.8) in (2.7) we get

By (2.6) and (2.9) we obtain

Now we observe that, by Lebesgue's dominated convergence theorem, there holds

Moreover, by the monotone convergence theorem,

if $\frac{|(y-x)\cdot \nu(y)|}{|x-y|^{d+1} }\in L^1((E\Delta H^-(y))\cap B_1(y))$ and $\lim_{s\to 1^-} \int_{(E\Delta H^-(y))\cap B_1(y) } \frac{|(y-x)\cdot \nu(y)|}{|x-y|^{d+s} } dx = +\infty$ otherwise. The conclusion then follows from (2.10), (2.11), (2.12) sending $s\to 1^-$.

Lemma 2.5. For $s\in (0, 1)$ and $E\subseteq {\mathbb R}^d$ of finite measure, we define the functional

Then the following holds:

(1) The map $s\mapsto \mathcal{F}_s(E)$ is monotone increasing as $s\to 1^-$. Moreover, for every $E$ of finite perimeter

(2) For every family of sets $E_s$ such that $\mathcal{F}_s(E_s)\leq C$, for some $C > 0$ independent of $s$, and $E_s\to E$ in $L^1$, there holds

Proof. (1) Arguing as in (2.3) and using (2.5), we get

Therefore from (2.6), and (2.9), we get for $0 < \bar s < s < 1$

which gives the desired monotonicity.

Now we observe that by Lebesgue's dominated convergence for every $E$ with $|E| < +\infty$ and $\mathrm{P}(E) < +\infty$,

So, we conclude by Proposition 2.4.

(2) We fix a family of sets $E_s$ such that $\mathcal{F}_s(E_s)\leq C$ and $E_s\to E$ in $L^1$ as $s\to 1^-$. Fix $\bar s < 1$ and observe that by the monotonicity property proved in item (ⅰ), we get

where we used for the first limit the lower semicontinuity proved in Proposition 2.3, and Lebesgue's dominated convergence theorem for the second limit.

We conclude by item (1), observing that $\mathcal{F}_{\bar s}(E) < C$, and sending $\bar s\to 1^-$.

We are now ready to prove our main result.

Proof of Theorem 2.1. We start with the $\Gamma$-liminf inequality. Let $E_s$ be a sequence of sets such that $E_s\to E$ in $L^1$. We will prove that

which will give immediately the conclusion. Recalling the definition of $\mathcal{F}_s(E)$ given in (2.13), we have that

By Lemma 2.5, item (2) and by Fatou lemma, we get

where the last equality comes from (2.3).

The $\Gamma$-limsup is a consequence of the pointwise limit in Proposition 2.4.

We conclude this section with the equi-coercivity of the family of functionals $\mathcal{P}_s$, which is a consequence of the monotonicity property of $\mathcal{F}_s$ obtained in Lemma 2.5.

Proposition 2.6 (Equi-coercivity). Let $s_n$ be a sequence of positive numbers with $s_n\to 1^-$, let $m, \, C\in {\mathbb R}$ with $m > 0$, and let $E_n$ be a sequence of measurable sets such that $|E_n|\leq m$ and $\mathcal{P}_{s_n}(E_n)\leq C$ for all $n\in\mathbb N$.

Then $\mathrm{P}(E_n)\leq C'$ for some $C' > 0$ depending on $C, d, m$, and the sequence $E_n$ converges in $L^1_{\rm loc}$, up to a subsequence, to a limit set $E$ of finite perimeter, with $|E|\leq m$.

Proof. Reasoning as in Proposition 2.3, we get that $E_n$ has finite perimeter, for every $n\in \mathbb N$. Recalling (2.13), we get that

We fix now $\bar n$ such that $s_{\bar n} > \frac{1}{2}$ and we claim that there exists $C'$, depending on $m, d$ but independent of $n$, such that $\mathrm{P}(E_n)\leq C'$ for every $n\geq \bar n$. If the claim is true, then it is immediate to conclude that eventually enlarging $C'$, $\mathrm{P}(E_n)\leq C'$ for every $n$.

For every $n\geq \bar n$, we use the monotonicity of the map $s\mapsto \mathcal{F}_s(E_n)$ proved in Lemma 2.5, and the fact that $|E_n|\leq m$, to obtain that

This implies in particular that $\mathcal{P}_{s_{\bar n}}(E_n)\leq \frac{|C|}{s_{\bar n}}+ m^2\leq 2|C|+m^2$, and we conclude by Proposition 2.3.

Remark 2.7 (Isoperimetric problems). Let us consider the following isoperimetric-type problem for the functionals $\mathcal{P}_s$ and $\mathcal{H}$:

where $m > 0$ is a fixed constant. Observe that $\widetilde E$ is a minimizer of (2.14) if and only if the rescaled set $m^{-\frac{1}{d}}\widetilde E$ is a minimizer of

Note in particular that the functional $\mathcal{P}_s$ is given by the sum of an attractive term, which is the perimeter functional, and a repulsive term given by the fractional perimeter with a negative sign.

In general we cannot expect existence of solutions to these problems for every value of $m$. However, from [9,Thm 1.1,Thm 1.2] it follows that there exist $0 < m_2(s)\leq m_1(s)$ such that, for all $m < m_1(s)$, Problem (2.14) admits a solution and moreover, if $m < m_2(s)$, the unique solution (uo to translations) is the ball of volume $m$. Actually, the bounds $m_1(s), m_2(s)$ tend to $0$ as $s\to 1^-$, hence these results cannot be extended directly to Problem (2.15).

A weaker notion of solution, introduced in ^[13], are the so-called generalized minimizers, that is, minimizers of the functional $\sum_i \mathcal{P}_s(E_i)$ (resp. of $\sum_i \mathcal{H}(E_i)$), among sequences of sets $(E_i)_{i}$ such that $|E_i| > 0$ and $P(E_i) < +\infty$ for finitely many $i$'s, and $\sum_i |E_i| = m$. Note that, if $E_n$ is a minimizing sequence for (2.14) or (2.15), by reasoning as in Proposition 2.6, we get that there exists a constant $C = C(m) > 0$ such that $\mathrm{P}(E_n)\leq C$ for every $n$. Then, as it is proved in [12,Proposition 2.1], there exists $C' = C'(m) > 0$, depending on $C$ and $m$, such that $\sup_x|E_n\cap B_1(x)|\geq C'$. Using these facts, reasoning as in ^[13], it is possible to show existence of generalized minimizers both for (2.14) and (2.15), for every value of $m > 0$.

3.   Properties of the limit functional

In this section we analyze the main properties of the limit functional $\mathcal{H}$. Note that, since it is obtained as a $\Gamma$-limit, it is naturally lower semicontinuous with respect to $L^1$ convergence.

First of all we observe that by the representation of $\mathcal{H}$ in (2.2), for every $E$ with finite perimeter there holds

We start with a compactness property in $L^1$ for sublevel sets of $\mathcal{H}$, which follows from a lower bound on $\mathcal{H}$ in terms of the perimeter.

Proposition 3.1. Let $E\subseteq {\mathbb R}^d$ be such that $\mathcal{H}(E)\leq C$. Then there exists a constant $C'$ depending on $C, |E|, d$ such that $\mathrm{P}(E)\leq C'$.

In particular, if $E_n$ is a sequence of sets such that $\mathcal{H}(E_n)\leq C$, then there exists a limit set $E$ of finite perimeter such that $\mathcal{H}(E)\leq C$ and $E_n\to E$ in $L^1_{\rm loc}$ as $n\to +\infty$, up to a subsequence.

Proof. By Lemma 2.5, for $s\in (0, 1)$ there holds

The estimate on $P(E_n)$ then follows by Proposition 2.6.

The second statement is a direct consequence of the lower semicontinuity of $\mathcal{H}$, and of the local compactness in $L^1$ of sets of finite perimeter.

We point out the following rescaling property of the functional $\mathcal{H}$, the will allow us to consider only sets with diameter less than $1$.

Proposition 3.2. For every $\lambda > 0$ there holds

Proof. We observe that for every $R > 0$, with the same computation as in (2.8) we get

Therefore, arguing as in Proposition 2.4, we can show that $\mathcal{H}(E)$ can be equivalently defined as follows, for all $R > 0$

This formula immediately gives the desired rescaling property (3.2).

Now, we identify some classes of sets where $\mathcal{H}$ is bounded.

Proposition 3.3. Let $E$ be a measurable set with $|E| < +\infty$ and $P(E) < +\infty$.

1. If $\partial E$ is uniformly of class $C^{1, \alpha}$ for some $\alpha > 0$, then $\mathcal{H}(E) < +\infty$.

2. If $E$ is a convex set then, for every $s\in (0, 1)$, there holds

where $\mathrm{diam} E: = \sup_{x, y\in E} |x-y|$, and $H_s(E, y)$ is the fractional mean curvature of $E$ at $y$, which is defined as

in the principal value sense.

Proof. (1) If $\partial E$ is uniformly of class $C^{1, \alpha}$, then there exists $\eta > 0$ such that for all $y\in \partial E$, $\partial E \cap B_\eta(y)$ is a graph of a $C^{1, \alpha}$ function $h$, such that $\|\nabla h\|_{C^{0, \alpha}(B_\eta'(y))}\leq C$, for some $C$ independent of $y$. Up to a rotation and translation, we may assume that $y = 0$, $h(0) = 0$ and $\nabla h (0) = 0$ and moreover $-C|x'|^{1+\alpha} \leq h(x')\leq C|x'|^{1+\alpha}$ for all $x'\in B'_\eta$. Therefore recalling that $E\cap B_\eta = \{(x, x_d) \ |\ x_d\leq h(x') \}$ and that $H^-(0) = \{(x', x_d)\ |\ x_d\leq 0\}$, there holds

We compute

Then, recalling (3.1) we get that

(2) Let $R = \mathrm{diam} E$. Then by (3.3), we get

By convexity for every $y\in \partial^*E$, recalling that $E\subseteq B_R(y)$, there holds

Therefore, substituting this equality in the previous estimate, we get

Remark 3.4. Note that by Proposition 3.3, $\mathcal{H}(Q) < +\infty$ for every cube $Q = \Pi_{i = 1}^d [a_i, b_i]$.

Indeed for $y\in \partial^* Q$, there holds that $H_s(Q, y)\sim \frac{1}{(d(y, (\partial Q\setminus \partial^* Q)))^{s}}$ for $s\in (0, 1)$ and so $\int_{\partial^* Q}H_s(Q, y)d\mathcal{H}^{d-1}(y) < +\infty$.

Finally we provide some useful equivalent representations of the functional $\mathcal{H}$.

Proposition 3.5.

(i) Let $E$ be a set with finite perimeter such that $\mathcal{H}(E) < +\infty$. Then

(ii) Let $E$ be a compact set with boundary of class $C^2$. Then

Proof. $\rm(i)$ If the diameter of $E$ is less than $1$, then $E\setminus B_1(y) = \emptyset$ for all $y\in \partial E$, and so

Using that

we compute the second inner integral for $y\in \partial^* E$, recalling that $E\subset B_1(y)$,

Now we observe that

since, for $y\in\partial^* E$, there holds that $\frac{(E-y)}{\delta}\to H^-(y)$ locally in $L^1$ as $\delta\to 0$, see [14,Thm II.4.5]. We compute

and

Therefore

If $\partial E$ has diameter greater or equal to $1$, we obtain the formula by rescaling, using (3.2).

$\rm(ii)$ Let us fix $y\in \partial E$ and define for all $x\in \partial E$, $x\neq y$, the vector field

By the Gauss-Green Formula (see [14,I.11.8]), for $\delta > 0$ there holds

where $\mathrm{div}_\tau \eta(x)$ is the tangential divergence, that is $\mathrm{div}_\tau\eta(x) = \mathrm{div}\eta(x)- \nu(x)^T\nabla \eta(x)\nu(x)$. Therefore integrating the previous equality on $\partial E$, we get that

Now we compute

where we used the equality $rf'(r) = \frac{1}{r^{d-1}}-(d-1)f(r) = \frac{1-(d-1)\log r}{r^{d-1}}$.

If we substitute this expression in (3.4) we get

The conclusion then follows by substituting $\omega_{d-1}\log \delta \mathrm{P}(E)$ with the previous expression in the representation formula obtained in (i), and observing that $1-\nu(x)\nu(y) = (\nu(x)-\nu(y))^2/2$.

Aknowledgements

The authors are members and were supported by the INDAM/GNAMPA.

Conflict of interest

The authors declare no conflict of interest.