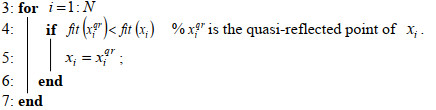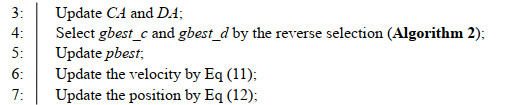Multi-objective particle swarm optimization with reverse multi-leaders

1.   Introduction

In most practical application problems, there are widely multiple conflicting objectives that need to be optimized simultaneously, such as job shop scheduling, wastewater treatment, path planning, etc., which are often called multi-objective optimization problems (MOPs) ^[1]. Due to the conflict between the objectives, the improvement of one objective may cause the degradation of other objectives. Therefore, a set of compromise solutions are usually obtained in MOPs, which are called Pareto optimal solutions ^[2]. The set of all Pareto optimal solutions is called a Pareto optimal set (PS). Their mapping in the objective space is called a Pareto front (PF) ^[3]. When solving MOPs, it is critical to obtain a set of solutions that are as close to the true PF as possible and well distributed on it.

In recent years, a variety of meta-heuristic algorithms inspired by natural and physical phenomena have vigorously developed, such as genetic algorithm (GA) ^[4], ant colony optimization (ACO) ^[5], differential evolution (DE) ^[6], firefly algorithm (FA) ^[7] and particle swarm optimization (PSO) ^[8]. Among them, PSO is a type of classical swarm intelligence algorithm, which was proposed by Kennedy and Eberhart in 1995. It is a bionic evolutionary swarm intelligence algorithm inspired by the foraging behavior of birds, and has been widely used to solve single objective optimization problems because of its simple mechanism and fast convergence speed. After some research, it was found that PSO had great potential to be extended to solve MOPs. Coello et al. ^[9] proposed a multi-objective particle swarm optimization (MOPSO) in 2002. In MOPSO, the optimal position of each particle during the historical search process is called the personal best (pbest), and the optimal position currently searched by the whole population is called the global best (gbest), which guide particles to fly towards the true PF. In addition, MOPSO introduced an external archive to store the non-dominated solutions found by the algorithm in the search process, which provided good candidate solutions for the selection of gbest. It can be seen that the maintenance of external archives and the selection of two optimal solutions are extremely important for the convergence and diversity of the algorithm. However, in the process of optimization, the global search ability of traditional MOPSO is still weak, which can easily lead to premature convergence of algorithm. Additionally, since different pbest and gbest will guide the particles to approach the true PF in different directions, it will have a certain impact on the balance between convergence and diversity.

In order to effectively balance convergence and diversity, researchers put forward many improvement strategies to improve the performance of MOPSO. Primarily, choosing different leaders will guide particles to fly in different directions. If properly selected, the convergence and diversity of the algorithm can be effectively improved. For example, Cui et al. ^[10] introduced a two-archive mechanism in MOPSO, using crossover and mutation operators for particles in the two archives to improve the quality of global leaders, which can take convergence and diversity into account. Li et al. ^[11] proposed a newly defined virtual generational distance indicator to select the appropriate gbest and designed an adaptive pbest selection strategy based on different evolutionary states to enhance the exploitation and exploration abilities of particles. Sharma et al. ^[12] assigned solutions with minimum penalized bounded intersection fitness as global leaders in each baseline based cluster after updating the external archive by a reference line-based diversity preference method. Second, maintaining an external archive is one of the most commonly used techniques. Hu et al. ^[13] proposed fuzzy crowding distance to update elite archives, and this method successfully extended traditional crowding distance to the fuzzy objective environment. Li et al. ^[14] used the method based on dominant difference and crowding density estimation to update external archives, and the experimental results showed that the algorithm had improved performance in terms of convergence and diversity. Yang et al. ^[15] designed a new external archive maintenance method based on vector angle, which effectively balanced the convergence and diversity of the algorithm, and the additional time cost was relatively low. Wu et al. ^[16] proposed an improved archive maintenance strategy based on predefined reference points, and in order to improve the diversity of solutions in the external archive, associated other solutions with some crowded reference points as a second criterion. In addition, many scholars also adjusted flight parameters to improve the overall performance of the algorithm. Han et al. ^[17] proposed an adaptive flight parameter adjustment mechanism, which used diversity information and population spacing information to obtain particle distribution with an appropriate diversity and convergence, so as to balance local exploitation ability and global exploration ability of the particles. The experimental results show that compared with some non-adaptive MOPSOs, the algorithm has certain improvements in balancing convergence and diversity. Huang et al. ^[18] also designed an adaptive strategy to adjust flight parameters, and used the increment of the ratio of dissipated energy to mass to detect evolution environment of the algorithm. The flight parameters could be dynamically adjusted according to the time-varying evolution environment, so as to effectively balance convergence and diversity. Generally speaking, the above-mentioned improved MOPSOs can improve convergence and diversity of the algorithm when solving most MOPs, but it still need to be further improved in terms of balancing convergence and diversity and improving overall performance of the algorithm.

Based on the above review and analysis, in order to further balance convergence and diversity and to improve the overall performance of the algorithm, a multi-objective particle swarm optimization with reverse multi-leaders (RMMOPSO) is proposed. The main contributions of the proposed RMMOPSO are as follows:

1) In RMMOPSO, the convergence strategy of global ranking and the diversity strategy of mean angular distance are proposed. It is used to update the convergence and diversity archives, respectively, to improve the convergence of solutions in the archive and select solutions with a better diversity. It improves the quality of candidate solutions of the global leader and enhances the convergence and diversity of the algorithm.

2) A reverse selection method is proposed to select the global best with a good convergence (gbest_c) and the global best with a good diversity (gbest_d). This method is beneficial to select the appropriate learning samples for each particle and lead particles to quickly fly to the true PF. In addition, an information fusion strategy is proposed to update pbest, which enhances the information interaction between particles in the population and improves convergence of the algorithm.

3) After redefining the selection of gbest_c and gbest_d in RMMOPSO, a new particle velocity updating method is proposed, in which the two global leaders selected are used to cooperatively guide the flight of particles in the population. In order to promote the exchange of social information, it is conducive to improving the quality of particles in the population and achieving a better balance between convergence and diversity.

The remainder of this paper is organized as follows. Some related work is described in Section 2. Section 3 introduces the details of the proposed RMMOPSO. In Section 4, the performance of RMMOPSO is verified by simulation experiments with existing MOPSOs and multi-objective evolutionary algorithms (MOEAs) on three suites of benchmark problems. Finally, the conclusion of the algorithm is given in Section 5.

2.   Related work

2.1.   Multi-objective optimization problem

The general multi-objective optimization problem ^[19] can be formulated as follows:

where $x = \left( {{x_1}, {x_2}, \cdots , {x_D}} \right)$ is a D-dimensional decision vector in decision space $X \subset {R^D}$, $F\left( x \right)$ represents the m-dimensional objective vector, ${f_i}\left( x \right)$ represents the objective function of the i-th dimension, ${g_i}\left( x \right) \geqslant 0\left( {i = 1, 2, \cdots , q} \right)$ is an inequality constraint, and ${h_j}\left( x \right) = 0\left( {j = 1, 2, \cdots , r} \right)$ is an equality constraint.

Because MOPs has multiple conflicting objectives, almost no absolute optimal solution can optimize them all at the same time. Therefore, the concept of Pareto dominance ^[20] can be used to evaluate the quality of solutions in MOPs. That is, a solution x dominates the other solution y, denoted as $x \prec y$, if and only if $\forall i \in \left\{ {1, 2, \cdots , m} \right\}:{f_i}\left( x \right) \leqslant {f_i}\left( y \right)$ and $\exists \;j \in \left\{ {1, 2, \cdots , m} \right\}:{f_j}\left( x \right) < {f_j}\left( y \right)$.

2.2.   Particle swarm optimization

PSO ^[8] is a traditional swarm intelligence algorithm. It is an optimization algorithm inspired by the foraging behavior of birds, which is easily implemented and has a fast convergence speed. In PSO, each particle updates its own velocity by learning the pbest and gbest. If the velocity vector of the i-th particle is ${V_i} = \left( {{v_{i, 1}}, {v_{i, 2}}, \cdots , {v_{i, D}}} \right)$, the position vector is ${X_i} = \left( {{x_{i, 1}}, {x_{i, 2}}, \cdots , {x_{i, D}}} \right)$, where $i = 1, 2, \cdots , N$, N is the population size, D is the dimension of the decision space. Then, the velocity and position of the i-th particle at the t+1-th iteration are updated as follows:

where t is the number of iterations, $\omega$ is the inertia weight, ${c_1}$ and ${c_2}$ are learning factors, and ${r_1}$ and ${r_2}$ are two random numbers uniformly generated in $\left[ {0, 1} \right]$.

The formula of particle velocity update is mainly composed of three parts. The first part is called the memory term, which represents the influence of magnitude and direction of previous velocity on the current velocity and is the inheritance of the previous velocity of the particle. The second part is called the self-cognition term, which means the particles learn from their previous experience. The third part is called the group cognition term, which represents the ability of particles to learn from the whole population and reflects knowledge sharing and cooperation between particles.

3.   The proposed RMMOPSO

In order to better balance the convergence and diversity of the algorithm and to improve the comprehensive performance of the algorithm, this paper proposed a MOPSO with reverse multi-leaders. The proposed RMMOPSO will be described in detail in this section. The algorithm consists of five parts, as shown in Figure 1. First, in order to improve the quality and diversity of the initial population, the quasi-reflection-based learning (QRBL) mechanism ^[21] is adopted to initialize the population. Second, the RMMOPSO proposed a convergence strategy of the global ranking and the diversity strategy of the mean angular distance and the convergence archive (CA) and the diversity archive (DA) are updated, respectively. Third, global leaders gbest_c and gbest_d are selected for each particle from CA and DA, respectively, through the reverse selection method. In this way, the selected leaders can lead particles to quickly fly to the true PF, and can better play the role of each non-dominated solution than the roulette wheel selection method. Meanwhile, an information fusion strategy is proposed to update pbest to improve the convergence of the algorithm. Finally, global leaders gbest_c and gbest_d cooperate to guide particles flight, which achieves a balance between the convergence and diversity and improves the overall performance of the algorithm.

3.1.   Population initialization strategy

At present, the initial population of most MOPSOs is generated by random distribution, which will lead to random errors in the optimization results, thus affecting the optimization accuracy and the speed of the algorithm to a certain extent. Ergezer et al. ^[21] proved that the quasi-reflected point is the candidate point that is most likely to approach optimal solutions, and some scholars have applied it to other algorithms and achieved good results.

Therefore, this paper introduces the QRBL mechanism into the initial population of MOPSO to generate a new quasi-reflected population. It not only ensures the randomness of the initial population of the algorithm, but also improves the operation efficiency and search speed of the algorithm. The specific details of the QRBL mechanism to initialize population are shown in Algorithm 1. After RMMOPSO randomly generates a population P in the decision space, it conducts the QRBL mechanism on population P to generate a new quasi-reflected population ${P^{qr}}$. Then, each particle is compared with the new particle obtained after quasi-reflected learning. Here, the sums of fitness values $fit\left( x \right)$ and $fit\left( {{x^{qr}}} \right)$ on all objectives of particles before and after learning are compared, which can roughly reflect the convergence information of particles ^[22]. Finally, the optimal particles are retained as the final initial population P.

3.2.   Update the archives

The external archive is an important feature of MOPSO, which is used to store all non-dominated solutions found by the algorithm during the search process to provide good candidate solutions for the selection of gbest. Therefore, the quality of non-dominated solutions in the archive is particularly important. However, with the increase of the number of iterations, the number of non-dominated solutions substantially increases, which leads to a gradual increase in computational complexity. Therefore, it is increasingly necessary to evaluate non-dominated solutions in an appropriate way. Therefore, in this study, the convergence strategy of global ranking (GR) and the diversity strategy of mean angular distance (MAD) are proposed to update the convergence archive CA and the diversity archive DA of a predefined size, respectively. In addition, the archive sizes of CA and DA are similar to those set in literature ^[23]. The CA and DA play important roles in their respective fields, storing non-dominated solutions of different properties. Updating CA by GR can guide the population to quickly converge to the true PF, and updating DA by MAD can improve the distribution of the population in the objective space. The proposed two strategies effectively improve the convergence and diversity of the algorithm, and the specific analysis is as follows.

GR can effectively select the non-dominated solutions with a good convergence, thus improving the convergence of the algorithm. The smaller the GR value, the better the convergence of the non-dominated solutions. The specific description is as follows:

where ${x_i}$ is the i-th non-dominated solution in the external archive, L is the number of non-dominated solutions in the external archive, M is the number of objectives, ${f_m}\left( \cdot \right)$ is the fitness function of the m-th objective, $Rank\left( \cdot \right)$ is the rank function, and ${f_{m, \max }}$ and ${f_{m, \min }}$ are the maximum and minimum values on the m-th objective, respectively. Here, using the maximum ranking (MR) ^[24] is preferred to select the solution with the best performance for some objectives, while the global detriment (GD) ^[25] is a method to consider how significant the differences between solutions are. The solution selected by GD is easy to eliminate the extreme value. Therefore, GR integrates the characteristics of MR and GD to evaluate the solutions in the archive. Here, we adopt the normalization method for formulas (5) and (6) to ensure the additivity of MR and GD.

MAD can better measure the similarity of solutions in the archive and effectively evaluate the diversity of non-dominated solutions, thereby increasing the diversity of the population. Additionally, the larger the value of MAD, the better the diversity of non-dominated solutions. Assuming that the two adjacent solutions of solution ${x_i}$ are ${x_{i - 1}}$ and ${x_{i + 1}}$, respectively, MAD can be described as:

where $d\left( {{x_i}, {x_j}} \right)$ is the Manhattan distance between non-dominated solutions ${x_i}$ and ${x_j}$, $angle\;\left( {{x_i}, {x_j}} \right)$ is the vector angle between the solutions ${x_i}$ and ${x_j}$, $F\left( {{x_i}} \right)$ and $F\left( {{x_j}} \right)$ represent the fitness values of solutions ${x_i}$ and ${x_j}$ respectively, $F\left( {{x_i}} \right) \cdot F\left( {{x_j}} \right)$ is the inner product of $F\left( {{x_i}} \right)$ and $F\left( {{x_j}} \right)$, and $norm\left( \cdot \right)$ is the norm function. The Manhattan distance and vector angle ^[26] are combined to ensure the distribution and uniformity of the final solution set, so that the solutions with good diversity are retained in DA.

3.3.   Gbest selection based on reverse selection

In most meta-heuristic algorithms, how to effectively balance convergence and diversity of algorithms is a crucial problem. In most MOPSOs, a particle chooses only one global leader in its social learning part. In this case, the particles cannot learn more useful experiences from various samples, thus reducing the diversity of the population. In fact, in human society, people always learn from multiple samples in the process of social learning. An individual will gain more experiences from multiple learning samples than from a single sample.

In RMMOPSO, each particle balances its convergence and diversity by selecting two global leaders. The two global leaders are selected one by one through the reverse selection method from archives CA and DA, respectively, denoted as gbest_c and gbest_d. In ^[27], researchers used a one-by-one selection strategy to select individuals, which can effectively improve the performance of the algorithm. In this paper, the reverse selection method proposed here can match the appropriate leader for each particle. The method guides particles to the nearest non-dominated solutions so that the particles can approach the PF in a few iterations. Additionally, every non-dominated solution is fully utilized to maximize the utilization of limited resources and to ensure a good distribution of the population. The method is specifically described as follows.

Assuming that the population size is N and the number of non-dominated solutions in the archive is N_A, the population is first randomly divided into h = ceil (N/N_A) groups, where the ceil function represents the integer in the direction of positive infinity. Then, the leaders are selected for particles of each group in turn. Primarily, for example, taking the particles in the k-th, the distance ${D_{k, 1}}$ between the first non-dominated solution $N{S_1}$ in the archive and all particles in this group is calculated in the objective space. Additionally, the shortest distance ${d_{k, 1}}$ in ${D_{k, 1}}$ and the corresponding particle ${x_{k, i}}$ are found. Then, the distance ${D_{k, 2}}$ between particle ${x_{k, i}}$ and the remaining non-dominated solutions in the archive is calculated, and the shortest distance ${d_{k, 2}}$ in ${D_{k, 2}}$ and the corresponding non-dominated solution $N{S_j}$ is found. Finally, the sizes of ${d_{k, 1}}$ and ${d_{k, 2}}$ are compared. If ${d_{k, 1}} \leqslant {d_{k, 2}}$, the non-dominated solution $N{S_1}$ is selected as the gbest of particle ${x_{k, i}}$. Otherwise, the non-dominated solution $N{S_j}$ is selected as the gbest of particle ${x_{k, i}}$. Additionally, the particles that have chosen leaders and the corresponding non-dominated solutions are emptied. In particular, when all the non-dominated solutions have been matched, it is necessary to reuse these solutions as candidate leaders of particles that have not yet chosen leaders. Algorithm 2 is the pseudo-code of taking CA as an example to select gbest_c by using the reverse selection. The pseudo-code for selecting gbest_d from DA by the reverse selection is similar to Algorithm 2.

Notably, the reverse selection method is similar to the matched pattern, in that the non-dominated solutions that have already been selected will not be used as candidate solutions when selecting leaders for the remaining particles in each group. In order to intuitively illustrate the process of selecting gbest by the reverse selection method, Figure 2 shows the process of selecting leaders for six particles from the six non-dominated solutions in a two-dimensional objective space.

3.4.   Information fusion for pbest

In RMMOPSO, in order to improve the convergence of the algorithm, an information fusion strategy is proposed to update pbest after selecting the global leaders for the particles, namely:

where ${r^d}$ is a random number uniformly distributed in $\left[ {0, 1} \right]$, and $gbest\_c_i^d$ is the d-th dimension of the global leader of particle i.

Figure 3 shows the details of the pbest update. During pbest updates, if the previous position is dominated by the current position, then the current position will replace the previous position. Otherwise, pbest will be updated using the information fusion strategy. In order to increase the diversity of the population, a random number r is first generated when updating each dimension of pbest. If the random number r is larger than the predefined parameter p, the corresponding dimension is updated by using Eq (10). Otherwise, a random number in the search range $\left[ {{L^d}, {U^d}} \right]$ is initialized. Here we simply set p to 1/N. This is because a relatively small p can protect the structure of pbest and gbest_c to a certain extent, and to make the particles learn more experiences from gbest_c and to jump out of the local optimum more easily.

3.5.   New speed update method

The RMMOPSO improves the updating method of particles, that is, when each particle in the population is updated, two global leaders gbest_c and gbest_d are selected for each particle from the archives CA and DA, respectively, by the reverse selection method, which are used to guide the particle flight in the population cooperatively, so as to promote the exchange of social information. This is beneficial to improve the quality of particles in the population and to better balance the convergence and diversity of the algorithm. The specific update method are as follows:

where t is the number of iterations, $\omega$ is the inertia weight, ${c_1}$ and ${c_2}$ are learning factors, and ${r_1}$ and ${r_2}$ are two random numbers uniformly generated in $\left[ {0, 1} \right]$.

3.6.   General framework of RMMOPSO

The main components of RMMOPSO are introduced in detail above, namely initialization by the quasi-reflection-based learning mechanism, the archives update, gbest selection based on reverse selection, information fusion for pbest, and a new speed update method. The pseudo-code of RMMOPSO is shown in Algorithm 3, where G and ${G_{\max }}$ represent the current iteration number and the maximum iteration number, respectively.

At first, RMMOPSO initializes the population in line 1 by introducing the QRBL mechanism, as described in Algorithm 1. After that, RMMOPSO starts the loop of the population search process in lines 2–8. The archives CA and DA are updated by the global ranking and mean angular distance, respectively (in line 3). Additionally, the global leaders gbest_c and gbest_d are selected from the archives CA and DA, respectively, by the reverse selection of Algorithm 2 (in line 4). At the same time, an information fusion on pbest is performed, as described in Section 3.4. Finally, the velocity and position of the particles are updated using Eqs (11) and (12) (in lines 6 and 7). The above evolution process is repeated until the maximum number of iterations is reached, and the final external archive A is output.

3.7.   Computational complexity of RMMOPSO

In order to analyze the computational complexity of RMMOPSO, the main components of the algorithm in a generation are considered. Algorithm 3 shows that the computational steps of RMMOPSO mainly include initialization by the quasi-reflection-based learning mechanism, an update of archives CA and DA, selection of gbest based on reverse selection, information fusion for pbest, and a new speed update method. Assuming that the population size is N, the sizes of CA and DA are both ${N \mathord{\left/ {\vphantom {N 2}} \right. } 2}$, the number of objectives is M, and the dimension of the decision variables is D. Then, the complexity of initialization by the quasi-reflection-based learning mechanism in Algorithm 1 is $O\left( {ND + N} \right)$. The computational complexity of the update of archives CA and DA includes two cases, and when the archives are not full, the computational complexity is $O\left( 1 \right)$. However, when CA and DA overflow, the particles in the archives need to first be sorted by non-dominated sorting. In the worst case, the computational complexity of non-dominated sorting is $O\left( {M{N^2}} \right)$. In addition, the worst-case complexity of updating CA with GR convergence strategy is $O\left( {N + {N^2}} \right)$, and the worst-case complexity of updating DA with MAD diversity strategy is $O\left( N \right)$. Therefore, in the worst case, the update of CA and DA costs $O\left( {M{N^2}} \right)$. After that, the computational complexity of selecting gbest_c and gbest_d by reverse selection is $O\left( N \right)$. Finally, in the update of pbest, the Pareto dominance relationship between the previous position and the current position should be judged first, and then pbest needs to be updated with an information fusion strategy. Therefore, in the worst case, updating pbest costs $O\left( {ND} \right)$ calculations. The computational complexity of the new speed update method is $O\left( 1 \right)$. Therefore, the total complexity of the proposed RMMOPSO in the worst case of a generation is $O\left( {M{N^2}} \right)$.

4.   Experimental studies

4.1.   Test problems

In order to evaluate the performance of RMMOPSO more objectively, a total of 22 test problems from three different benchmark suites, ZDT ^[28], UF ^[29], and DTLZ ^[30], are used to evaluate the performance of the algorithms. Among them, there are five two-objective test problems in ZDT benchmark suite, seven two-objective test problems and three three-objective test problems in UF benchmark suite, and seven three-objective test problems in DTLZ benchmark suite. These test problems have different characteristics and complex PFs, such as concavity and convexity, multi-modal, disconnected, irregular PF shape, etc., which can effectively verify the reliability and efficiency of the algorithms. For the two-objective test problems, the number of decision variables of ZDT1-ZDT3 and UF1-UF7 is set to 30, and the number of decision variables of ZDT4 and ZDT6 is set to 10. For the three-objective test problems, the number of decision variables of UF8~UF10 is set to 30, that of DTLZ1 is set to 7, that of DTLZ2~DTLZ6 is set to 12, and that of DTLZ7 is set to 22. The parameter settings for each test problem are shown in Table 1, where FEs represents the maximum number of evaluations.

4.2.   Performance indicators

This paper uses inverted generational distance (IGD) ^[31] and hypervolume (HV) ^[32] as the performance evaluation indicators of the algorithm. These two indicators are used to evaluate the performance of RMMOPSO with the selected MOPSOs and MOEAs.

The IGD indicator is a comprehensive performance indicator, which is used to measure the distance between the Pareto optimal solution set obtained by the algorithm and true PF. Additionally, it can effectively test the convergence and diversity of the algorithm; the smaller the IGD value of an algorithm, the better the convergence and diversity of the algorithm. The calculation formula of IGD is:

where S represents the Pareto optimal solution set obtained by the algorithm, ${P^ * }$ is the solution set uniformly distributed on PF, $dist\left( {{x^ * }, S} \right)$ is the shortest Euclidean distance between the solution ${x^ * }$ and S, and $f_i^{\min }$ and $f_i^{\max }$ represent the minimum value and maximum value of the i-th objective value, respectively, ($i = 1, 2, \cdots , k$, $k$ is the number of objectives), ${a_j} \in S$ and $j = 1, 2, \cdots , \left| S \right|$.

The HV indicator is also a comprehensive performance indicator, which refers to the volume of the region in the objective space enclosed by the Pareto optimal solution set obtained by the algorithm and the reference points. This indicator can estimate the convergence and diversity of the solution set obtained by the algorithm; the larger the HV value of an algorithm, the better the overall performance of the algorithm. Assuming ${Z^r} = \left( {Z_1^r, Z_2^r, \cdots , Z_m^r} \right)$ is a reference point dominated by all Pareto optimal solutions in the objective space, then HV can be calculated as follows, where $\delta$ denotes the Lebesgue measure.

4.3.   Experimental settings

In this section, in order to better verify the performance of RMMOPSO, eight algorithms are selected for performance comparison, including four MOPSOs (NMPSO ^[33], MPSOD ^[34], MMOPSO ^[35] and SMPSO ^[36]) and four MOEAs (DGEA ^[37], SPEAR ^[38], NSGAIII ^[39] and MOEAD ^[40]).

In order to ensure the fairness of the algorithm performance comparison, the relevant parameters set by all the comparison algorithms are consistent with the original references. The main parameter settings of each algorithm are shown in Table 2, where $\omega$, ${c_1}$ and ${c_2}$ are the parameters used for the update velocity in MOPSOs, and ${p_c}$ and ${p_m}$ represent crossover probability and mutation probability, respectively.${\eta _c}$ and ${\eta _m}$ are the distribution indexes of the simulated binary crossover (SBX) and the polynomial mutation (PM), respectively. In MPSOD, F and CR are set differential evolution parameters. In MMOPSO, $\delta$ is the probability that the controlling parent solutions are selected from the neighborhood of T. R is the number of direction vectors in DGEA. In MOEAD, T represents the size of the neighborhood between the weight coefficients. In addition, the population size of all algorithms is set to 200, and the maximum number of function evaluations is set to 10000. Each algorithm is independently run for 30 times on each test problem, and then the mean and standard deviation of IGD and HV values are recorded. Additionally, all experimental results of the algorithms are implemented by MATLAB R2021b under the Intel(R) Core(TM) i7-6700 CPU @ 3.40GHz 3.40GHz Windows 7 system. The source codes of all comparison algorithms are provided by PlatEMO ^[41].

4.4.   Comparisons of performance indicators

4.4.1.   Comparisons with four existing MOPSOs

Tables 3 and 4 show the mean and standard deviation of IGD and HV values of RMMOPSO and other four MOPSOs on 22 test problems, respectively, and the best IGD and HV values for each test problem are shown in bold. The Wilcoxon rank sum test ^[42] is adopted at the significance level of $\alpha = 0.05$ to show significant differences between test results. The symbols '+', '-', and '≈' in the tables indicate that the results of other algorithms are significantly better than, significantly worse than, and statistically similar to RMMOPSO, respectively. In addition, the two-tailed t-test ^[43] is carried out at the significance level of $\alpha = 0.05$, and the test results of the two-tailed t-test are also shown in the tables. The t values in the tables are presented in bold to indicate that RMMOPSO is significantly superior to other algorithms, and the symbol '^*' indicates that the performance of RMMOPSO is statistically similar to other algorithms. The '/' in Table 4 indicates that the standard deviations of the two compared arrays are 0, and the t values cannot be calculated.

It can be directly observed from Table 3 that the comprehensive performance of the proposed RMMOPSO is obviously better than the four compared MOPSOs among the 22 benchmark problems. According to the Wilcoxon rank sum test results, RMMOPSO and the comparison algorithms NMPSO, MPSOD, MMOPSO, and SMPSO perform significantly better in 14, 19, 9, and 18 of the 22 comparisons, respectively. Additionally, similar results are obtained in 2, 0, 5, and 1 of the comparisons, respectively. It can be seen from the best IGD values in the table that RMMOPSO obtains 13 best IGD values on 22 test problems, while the number of the best IGD values obtained by NMPSO, MPSOD, MMOPSO and SMPSO are 1, 0, 6, and 2, respectively. In addition, according to the statistical results of the t-test in the penultimate row of Table 3, the algorithm proposed in the paper is significantly superior to the comparison algorithms on most test problems. Therefore, we can conclude that when the IGD indicator is used to measure the comprehensive performance of the algorithm, RMMOPSO outperforms the other four algorithms. MPSOD does not perform best on any of the test problems, because based on the decomposition of the objective space, the strategy of MPSOD does not improve the performance of the algorithm to a large extent, which is slightly worse than other algorithms. However, MMOPSO has the best performance on test problems DTLZ1 and DTLZ4, because it adopted simulated binary crossover and polynomial mutation operators in addition to the original MOPSO update strategy. However, the results on ZDT benchmark suite are not very satisfactory. Therefore, from the overall analysis of IGD indicator, it can be found that the comprehensive performance of RMMOPSO on the 22 test problems is better than the other four comparison algorithms.

In addition to the IGD indicator, HV is also used to further evaluate the comprehensive performance of RMMOPSO. As can be seen from the best HV values in Table 4, RMMOPSO obtained 11 best HV values on 22 test problems, while the number of the best HV values obtained by NMPSO, MPSOD, MMOPSO, and SMPSO are 3, 0, 5, and 2, respectively. Moreover, according to the statistical results of Wilcoxon rank sum test and t-test in Table 4, RMMOPSO is significantly superior to the comparison algorithms on most test problems. Therefore, it can be seen from Table 4 that RMMOPSO and the selected MOPSOs still have a strong competitiveness when the HV indicator is used to measure comprehensive performance of the algorithms.

4.4.2.   Comparisons with four existing MOEAs

Tables 5 and 6 respectively show the mean and standard deviation of the IGD and HV values of RMMOPSO and four MOEAs on 22 test problems. Similarly, the Wilcoxon rank sum test and two-tailed t-test are used at the significance level of $\alpha = 0.05$ to test for significant differences between the results. Additionally, the best IGD and HV values for each test problem are shown in bold. The '/' in Table 6 indicates that the standard deviations of the two compared arrays are 0, and the t values cannot be calculated.

As can be seen from Table 5, the comprehensive performance of the proposed RMMOPSO is significantly better than the four compared MOEAs among the 22 test problems. According to the results of Wilcoxon rank sum test, RMMOPSO and comparison algorithms DGEA, SPEAR, NSGAIII, and MOEAD perform significantly better than these algorithms in 19, 12, 15, and 16 of the 22 comparisons, respectively, and obtained similar results in 1, 4, 3, and 0. Similarly, from the statistical results of t-test in the penultimate row of Table 5, RMMOPSO is significantly better than the comparison algorithms DGEA, SPEAR, NSGAIII, and MOEAD on 19, 12, 15, and 16 test problems, respectively. It can be seen from the best IGD values in the table that RMMOPSO obtains 14 best IGD values on 22 test problems, while the number of the best IGD values obtained by DGEA, SPEAR, NSGAIII, and MOEAD are 0, 2, 0, and 6 respectively. It can be observed that when the IGD indicator is used to measure the comprehensive performance of the algorithm, RMMOPSO outperforms the four comparison algorithms. NSGAIII and DGEA do not perform the best on any of the selected test problems, because the strategy of NSGAIII reference-based non-dominated ranking and the strategy of DGEA adaptive offspring generation cannot improve the performance of the algorithm to a great extent, which is slightly worse than other algorithms. Therefore, from the overall analysis of the IGD indicator, it can be found that the comprehensive performance of RMMOPSO on the 22 test problems is better than the other four comparison algorithms, because the reverse multi-leaders strategy proposed in this paper significantly improves the search ability of RMMOPSO and can effectively balance the convergence and diversity of the algorithm.

As shown in Table 6, the comparison results using the HV indicator are similar to those using the IGD indicator. RMMOPSO also obtains 14 best HV values on 22 test problems, while DGEA, SPEAR, NSGAIII, and MOEAD obtain 0, 1, 1, and 5 best HV values, respectively. Therefore, it can be seen from Table 6 that RMMOPSO has a better comprehensive performance than the other four MOEAs when the performance of the algorithm is measured by the HV indicator.

4.5.   Intuitive comparisons of graphics

4.5.1.   Comparisons with four existing MOPSOs

In order to visually compare the stability of each algorithm on three suites of benchmark problems, ZDT, UF, and DTLZ. Figure 4 shows the statistical box plots of the IGD values distribution obtained by the RMMOPSO and other four MOPSOs running independently for 30 times on some test problems, where 1, 2, 3, 4, and 5 on the horizontal coordinate of these box plots are successively represented as NMPSO, MPSOD, MMOPSO, SMPSO, and RMMOPSO, and the vertical coordinate represents the IGD value of each algorithm. The smaller the gap between the upper and lower quartiles of the box plot is, and the flatter the box is, indicating that the experimental data is more concentrated and the stability is better. The symbol "+" in the box plots represents the abnormal value in the data. As you can see from these figures, Figure 4 shows a comparison consistent with Table 3. Compared with other four comparison algorithms, there are fewer abnormal values in the experimental data of RMMOPSO, and the boxes of RMMOPSO in most of the test problems are flatter and the IGD values are smaller, which indicates that the performance of RMMOPSO is more remarkable than other four algorithms in terms of both the solution results and the stability of the algorithm.

In order to compare the convergence and distribution of the algorithms more intuitively and observe whether they really converge to the approximate PF. The Figures 5 and 6 show the distribution of the non-dominated solution sets of RMMOPSO and NMPSO, MPSOD, MMOPSO, and SMPSO on the two-objective test problem ZDT2 and the three-objective test problem UF9, respectively. As can be seen from Figure 5, on the two-objective test problem ZDT2, only NMPSO, MMOPSO, and RMMOPSO can fully converge to the true PF, but NMPSO and MMOPSO distribution is not very uniform, while other two algorithms have poor performance in convergence and distribution. It can be observed from Figure 6 that on the three-objective test problem UF9, several comparison algorithms have poor performance in convergence and distribution, and most of the non-dominated solutions obtained by RMMOPSO can fully converge to true PF. In conclusion, RMMOPSO has better performance in convergence and distribution than other algorithms.

Finally, the convergence speed is also an important indicator to compare the performance of algorithms. Figure 7 shows the IGD convergence trajectories obtained by RMMOPSO and the four MOPSOs on the two-objective test problems ZDT2, UF7, and the three-objective test problem UF9 evaluated for 10000 times. As can be seen from the figures that RMMOPSO has the fastest convergence speed and is significantly better than other four comparison algorithms.

4.5.2.   Comparisons with four existing MOEAs

Figure 8 shows the statistical box plots of the IGD value distributions obtained by RMMOPSO and the other four MOEAs running independently for 30 times on some test problems, which is used to visually compare the stability of each algorithm on these test problems, where 1, 2, 3, 4, and 5 on the abscissa of the box plots are successively represented as DGEA, SPEAR, NSGAIII, MOEAD, and RMMOPSO, and the ordinate represents the IGD value of each algorithm. As shown in Figure 8, the comparison results are consistent with Table 5. As can be seen from Figure 8, although the stability of RMMOPSO on UF4, UF5, UF8, and DTLZ2 are not as good as that of other algorithms, the IGD values of RMMOPSO are smaller than them. Furthermore, in most test problems, the experimental data of RMMOPSO has fewer abnormal values, its boxes are relatively flat, and the IGD values are smaller. It shows that the performance of RMMOPSO has obvious advantages over the other four MOEAs in both the solution results and the stability of the algorithm.

In the same way, in order to visually compare the convergence and diversity of each algorithm, Figures 9 and 10 show the approximate PFs of RMMOPSO, DGEA, SPEAR, NSGAIII, and MOEAD on the two-objective test problem ZDT2 and the three-objective test problem UF9, respectively. As can be seen from Figure 9, on two-objective test problem ZDT2, only RMMOPSO can fully converge to the true PF, while the other four algorithms performed poorly in both convergence and distribution. It can be observed from Figure 10 that on the three-objective test problem UF9, although some non-dominated solutions of the four comparison algorithms converge to the true PF, most of them fail to converge and have poor distribution; only RMMOPSO has a relatively good convergence and distribution. To sum up, RMMOPSO has advantages over other algorithms in terms of convergence and distribution.

Next, we compare the convergence speed between the proposed RMMOPSO and the other four MOEAs on the two-objective test problems ZDT2, UF7, and the three-objective test problem UF9. Figure 11 shows the IGD convergence trajectories obtained by evaluating each algorithm on ZDT2, UF7, and UF9 for 10000 times. As can be seen from the figures, RMMOPSO has the fastest convergence speed, which is significantly better than the other four comparison algorithms.

In summary, from the box plot, the PF diagram, and the convergence trajectory diagram, the proposed RMMOPSO had a better comprehensive performance compared with the selected competitive algorithms, especially on the benchmark suites ZDT and UF. Therefore, it has superior advantages than the other comparison algorithms in solving the most complex multi-objective optimization problems.

4.6.   Overall performance of RMMOPSO

As shown in Tables 7 and 8, in order to further compare the overall performance of RMMOPSO with all comparison algorithms, we also rank the average IGD and HV values of RMMOPSO and all comparison algorithms on the 22 test problems. Generally speaking, the smaller and more frequent ranking indicates the better overall performance of the algorithm. For instance, in Table 7, the rank 1 value of RMMOPSO is 11, which indicates that when RMMOPSO and all comparison algorithms are compared on 22 test problems, RMMOPSO achieves 11 best IGD values. In addition, we also use the Friedman test ^[44] to calculate the average ranking of all algorithms. The numbers with the most rank 1 and the best average ranking in the tables are shown in bold. It can be seen from Table 7 and Table 8 that the final ranking of the proposed RMMOPSO is the first in both the average IGD value and the HV value, and the number of rank 1 is also the most. This indicates that RMMOPSO can obtain a better convergence and diversity solutions when solving the most MOPs. Therefore, it has a better advantage than other algorithms in solving MOPs.

4.7.   Effectiveness of the QRBL mechanism

In order to verify the effectiveness of the proposed algorithm using the QRBL mechanism to initialize population, we set an experiment to compare RMMOPSO with its variant RMMOPSO_NQ, where RMMOPSO_NQ represents RMMOPSO without using the QRBL mechanism to initialize population. The parameter settings of this experiment are the same as the above experiments. RMMOPSO and RMMOPSO_NQ are independently run for 30 times on each of the three suits benchmark problems to obtain the statistical means and standard deviations (standard deviations in parentheses) of the IGD indicator. The comparison results are shown in Table 9, and the best IGD value on each test problem is shown in bold. As can be seen from Table 9, RMMOPSO significantly outperforms RMMOPSO_NQ on most test problems, and obtains 17 best IGD values on a total of 22 test problems. The above experiment verifies that the QRBL mechanism plays an important role in the initialization process of RMMOPSO. This is because the quasi-reflected point of a point is more likely to be close to the optimal solutions than the point itself. Introducing the QRBL mechanism into the initial population of MOPSO not only ensures randomness of the initial population of the algorithm, but also improves operation efficiency and optimization speed of the algorithm.

5.   Conclusions

In order to achieve a balance between convergence and diversity and to improve the overall performance of the algorithm, a multi-objective particle swarm optimization with reverse multi-leaders is proposed. The convergence strategy of the global ranking and the diversity strategy of the mean angular distance are put forward to update the convergence and diversity archives, respectively. Therefore, the convergence of the algorithm is improved, and the diversity of the population is maintained. At the same time, the global leaders are selected by the proposed reverse selection method, which can lead the particles to quickly fly to the true PF. In addition, the information fusion strategy is further applied to the update of pbest to improve the convergence of the algorithm. Finally, a new particle velocity updating method combines two global leaders to guide the flight of particles in the population. In this way, the performance of RMMOPSO is enhanced, and the balance between the convergence and diversity is effectively achieved.

In the simulation experiments, RMMOPSO is compared with selected advanced MOPSOs and competitive MOEAs on three suites of benchmark problems. The experimental results also verify that RMMOPSO has an improved comprehensive performance and can better balance the convergence and diversity.

Acknowledgments

This work was supported in part by Key Laboratory of Evolutionary Artificial Intelligence in Guizhou (Qian Jiaoji [2022] No. 059) and the Key Talens Program in digital economy of Guizhou Province.

Conflict of interest

The authors declare there is no conflict of interest.