1.
Introduction
Medical image registration is an important branch of computer vision [1,2]. It is a significant step in actualizing medical image analysis, completing auxiliary clinical diagnosis, and understanding medical images [3,4,5]. Registration is also the basis of fusion [6]. Medical image registration is a necessary step in image guidance, motion tracking, and image segmentation [7]. It is also widely used in the comparison of real medical images and atlases, surgical navigation, tumor parameter estimations, cardiac motion estimations, the creation of an average atlas, surgical location, and radiotherapy plan design [8,9,10].
In modern external beam image-guided radiation therapy (IGRT) [11], cone-beam computed tomography (CBCT) is commonly used to monitor daily anatomical changes [12]. The image quality of CBCT is inferior to that of computed tomography (CT) for soft tissues due to the presence of artifacts. Therefore, deformable registration (DR) of planning CT (pCT) to the daily anatomy of CBCT images has been proposed to correct CBCT imaging artifacts for adaptive radiation therapy [13,14,15]. CBCT can monitor the location of a tumor in real-time [16,17]. With the help of CBCT, the radiation dose of normal tissue can be reduced, and the radiation dose of the tumor area can be increased, which can improve the local control rate of the tumor and reduce radiotherapy complications [18].
How to improve the quality of CBCT images for registration is an important problem [19]. A number of scholars have proposed automatic registration methods, which have greatly improved the efficiency and accuracy of medical diagnosis and treatment [20]. However, image quality seriously affects readability because CBCT is greatly affected by scattered rays contains considerable noise, artifacts and blurry edges [21,22]. There remains a large difference between the low contrast areas of CBCT images and conventional pCT images. It is especially difficult to recognize and outline target areas.
Deep learning is involved in considerable image registration research [23,24]. Broadly speaking, two strategies are prevalent in the literature: 1) Wu et al. [25], Simonovsky et al. [26], and Cheng [27] used deep learning networks to estimate a similarity measure for two images to derive an iterative optimization strategy; and 2) Miao et al. [28] and Yang et al. [29] directly predicted transformation parameters using deep regression networks. Recently, DeTone [30] proposed a homography network, which is a supervised network similar to the visual geometry group [31]. The algorithm learns the advantages of the homography and the convolutional neural network model parameters in an end-to-end way. Krebs [32] used artificial agents to optimize the parameters of the deformation models, and good results were obtained in 2D/3D. Currently, compared to medical images with accurate annotations, medical image data without annotations are easier to obtain, and unsupervised learning has quickly become a hot research topic [33]. In an unsupervised registration network, registration pairs are imported into the network to obtain a deformation field, and the moving image is transformed by deformation interpolation to obtain the registered image. In an unsupervised registration network, the selection and usage of the similarity measure function is an important and difficult point to improve the registration accuracy.
In our proposed deformed image registration network, a total of five similarity functions are used, namely, the mean squared error (MSE), mutual information (MI), Pearson correlation coefficient (PCC), structural similarity index measurement (SSIM) and PCC + SSIM.
Here, we propose a deep learning deformed registration (DLDR) method using super-resolution preprocessing (SR-DLDR). The method uses a high precision super resolution (SR) approach based on a very deep super resolution (VDSR) network. Next, three traditional rigid registration methods (rigid, affine and similarity) prove that adding SR during image preprocessing can significantly improve the accuracy of rigid body registration. Finally, experimental comparisons between registration with and without SR are given. Furthermore, we also improved the similarity function for the DR by combining the PCC with SSIM as the similarity measure function of the model. The experimental results show that SR-DLDR is superior and more reliable than VoxelMorph (VM).
In short, using the nature of SR [34,35,36] image processing in the denoising stage of CBCT and using the VDSR model can improve the image quality and fill in the blank information of an image. The quantitative and qualitative indicators of CBCT images and pCT image registration after preprocessing are better.
2.
Methods
2.1. SR in CBCT image preprocessing
Nearly 400 sectioned images were used in this study. The image dataset of each patient was obtained before the radiotherapy fraction. Each patient's dataset contained a group of 120 slices of pCT images and one group of 90 slices of CBCT images. The pCT images had a matrix size of 512 by 512 on the axial plane with a pixel size of 1.171875 mm by 1.171875 mm. The CBCT images had a matrix size of 410 by 410 on the axial plane with a pixel size of 1 mm by 1 mm. The thicknesses of the CT and CBCT slices were both 3 mm. Among the images from the five patients, those from four patients were used to train the network, and those from the remaining patients were retained for testing. Using the leave-one-out cross validation method, four patients were randomly selected from the five patients datasets as the training set, and the rest were used as the test set. This process was repeated five times. The final result was the mean value of five verifications. To accelerate the model training time, we used paired data for modeling. We also clipped all image sizes down to 384 × 384 to minimize the anatomical region to accelerate the calculation time.
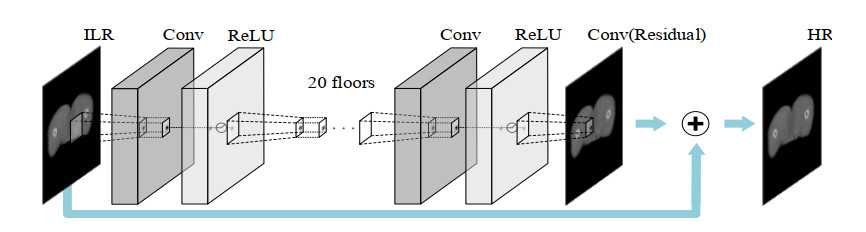
Figure 1 shows the SR model flow of CBCT enhancement processing [37]. It is a single image super-resolution processing model with a very high recovery rate. The model uses 20 weight layers to improve the accuracy and the network architecture is deepened significantly. And then by cascading small filters several times, the contextual information of large image regions is applied more comprehensively in the deep learning network. However, for such a deep network model, the training time is significantly longer and the training cost increases. In response, we propose a simple and effective training procedure to control the training time.
The SR system model was constructed by using a forward relation model [37]. The relationship between a low-resolution image and a high-resolution image is expressed as follows:
where p is the number of frames in the image sequence; xj, yk and nj are the high-resolution image of the j-th frame to be calculated, the low-resolution image observed in the k-th frame and the noise during image acquisition, respectively; D is the down-sampling matrix; Bj is the blur matrix; and Mk,j is the motion matrix composed of the motion vectors between the j-th and k-th frames.
This network was inspired by Simonyan and Zisserman [38]. Twenty weighted layers were utilized. The model has three layers: reconstruction, nonlinear mapping, and patch extraction/representation. The SR network predicts picture details from an interpolated low-resolution image as input. In SR approaches the technique modeling image details is frequently used. The SR model consists of 20 layers, all of which, with the exception of the first and last, are of the same type: a 3×3×64 filter that acts on the 3×3 spatial region using 64 channels. The input image is used by the first layer. The last layer is a single 3×3×64 filter that is used to recreate images. At the input of the model, the image size is processed by MATLAB. MATLAB processes the image size at the model's input. We uniformly reduced the low-resolution photos from an image block size of 384×384 down to 123×123 using bicubic interpolation, and then we fed the low-resolution images into the model to train and output the predicted image detail texture [39]. To draw conclusions using the SR approach, image center pixels need a large number of surrounding pixels. A broad surrounding area will result in poor inference accuracy for the center pixels; therefore, it should be kept to a minimum. A final image that has been cropped is too small to be aesthetically attractive. We make use of contextual data dispersed across very vast image regions. It frequently happens that a little patch of information is insufficient to recover details (ill-posed). A VDSR network with a wide receptive field takes into account a lot of the visual context.
2.2. Deformable registration
The moving image Im and the fixed image If in the model frame diagram are and respectively. To create a predictive registration domain using deep learning, the model is fed a pair of moving and stationary photos. To create the distorted moving image, the moving image is subjected to a registration field and B-spline space transformation. Calculating the difference between the fixed image and the distorted images allowed us to return the loss difference to the deformed image registration network, which we then used to retrain the deformed field until the loss difference was minimum and the network was at its best [40]. The loss function can be expressed mathematically as follows:
where 1sim is the image similarity measure and R denotes the regularization of ϕ. λ is a controllable weighting parameter that the user defines. The minimizer can then estimate the parameters θ that produce the ideal registration field [41].
The optimal ϕ is then given by:
2.3. SR-DLDR
The SR-DLDR process is shown in Figure 2. First, the CBCT image is processed using the SR processing algorithm described in the previous section, and the resulting high-quality CBCT image is used as moving image Im. After that, the pCT image is cropped to match the CBCT size and used as the fixed image If. The moving image Im and fixed image If are combined as a set of image pairs to be the input of the alignment network, and a spatial deformation field is generated by a U-shaped convolutional network to complete deformation of the moving image Im. A spatial transformer is used to distort the moving image Im according to the generated deformation field data to obtain the alignment image. The similarity measure between the aligned image and the fixed image is calculated as a loss and returned to the U-shaped convolutional network to update the network parameters to obtain the best aligned deformation field through continuous iteration.
2.3.1. ConvNet structure
The network structure of ConvNet is similar to that of U-Net [42]. The input size of the model is 384×384, and the output image size is the same. The network has a coding path to transform a single input image pair into a 2×M×M volume. The convolutional layer of each layer is followed by a rectified linear unit (ReLU), and the 2×2 maximum pooled downsampling method is adopted. In the decoding stage, the upsampling "up-convolution" calculation is used [42]. The output structure of this part is integrated with the output of the feature graph in the coding process by upsampling each feature graph. The output registration domain with 16 feature maps is then created by using 16 3×3 convolutions and two 1×1 convolutions. Figure 2 depicts the network architecture schematically.
2.3.2. B-spline spatial transformation
Nonlinear picture deformation is applied by using the B-spline function as the spatial transformer [41,43]. By combining the effects of the B-spline spatial converter and the deformation registration domain, the moving picture is used to calculate the loss error with the fixed reference image [44], as shown in Figure 3. The definition of the B-spline basis function is as follows:
Set u as a collection of m+1 nonrecurring subtractions, u0⩽u2⩽u3⩽u4⩽...⩽um, ui as the nodes, u as the node vector, and the semi-open interval [ui,ui+1) as node interval i. Note that some ui may be equal and some node intervals will not exist. If a node ui appears k times (i.e., ui=ui+1=...=ui+k−1), where k>1, ui is a multiple node with a repeatability of k, and it is written as ui(k). p represents the number of base functions.
The warp is determined by a flow field of displacement vectors ω that define the correspondences of pixel intensities in the output image to the pixel locations in the moving image. The intensity at each pixel location M in the output image Im∘ϕ(M) is defined by:
2.4. Similarity measure function
The similarity measure, which is used to evaluate the outcomes of each transformation and serve as the foundation for the following step in the search strategy, is a criterion for measuring the results of each transformation.
The feature space and search space are strongly related to similarity transformation, and various feature spaces frequently correlate to various similarity measures. The value of the similarity measure [45] will be used to choose the registration transformation and decide whether the image is appropriately matched with the present transformation model. The capacity of the registration method to resist jamming is often assessed using feature extraction and similarity measurement.
In our work, we applied five evaluation indices to verify the effect of image registration. They are the MSE, MI, PCC, SSIM and PCC+SSIM.
2.4.1. MSE
The MSE is the sum of the average values divided by the square of the difference between the actual value and the anticipated value. The square method is frequently employed as the loss function in linear regression since the calculation is straightforward to lead. A measurement of image fidelity that works for both fixed and moving images with a similar contrast and intensity distribution is the MSE. The MSE is calculated as
where Ω is the spatial domain Id and If represent the alignment image and the target image, respectively. In order to ensure the consistency of the loss function in the model output, the similarity function is defined as: 1sim(Im,If,ϕ;θ)=MSE(Id,If).
2.4.2. MI
In information theory, MI is a valuable information metric [46]. It can be thought of as the amount of knowledge that one random variable has about another, or as the uncertainty of one random variable being lessened by being aware of another. It is frequently important to compare the similarity of two photos when processing images. Consider two photos, A and B. Then, the calculation formula of their mutual information value is:
H(A,B) is the joint entropy of A and B. Let pIf(a) and pId(b) be the marginal probability distributions of the fixed and deformed moving images. MI can be defined as follows:
The joint distribution, pIfId(a,b), can be computed as follows
The loss function produced using MI as a similarity measure function cannot be back-propagated to the network because the Dirac delta function is not differentiable; thus, we use the differentiable Gaussian function to roughly substitute pIfId(a,b).
where σ is a user-defined parameter that can vary depending on the images of a certain application. The calculated MI value is negative, so the loss function is defined as: 1sim(Im,If,ϕ;θ)=−MI(Id,If).
2.4.3. PCC
The Pearson product-moment correlation coefficient, which has a value of [−1,1], is a statistical measure of the correlation (or linear correlation) between two variables x and y. The coefficient is frequently used in natural science to assess how closely two variables are correlated with one another. Its use in the registration of medical images has been discussed [47]. The PCC is defined as the covariance between images divided by the product of their standard deviations:
where ˉIf and ˉId represent the mean intensities, Ω is the total number of pixels in the image, and I∗(i) is the pixel value at the corresponding position in the image. In order to lose the consistency of the function, let 1sim(Im,If,ϕ;θ)=1−PCC(Id,If).
2.4.4. SSIM
Brightness, contrast, and structure are the three main characteristics that the structural similarity index may derive from an image [48]. From the standpoint of picture composition, distortion is characterized as a mix of brightness, contrast, and structure, whereas structural information is defined as a property independent of the brightness and contrast to reflect the structure of the objects in a scene. The standard deviation is used to evaluate contrast, the covariance is used to quantify structural similarity, and the mean is used to estimate brightness. The SSIM is a crucial metric for assessing the quality of medical image registration.
where C1 and C2 are small constants needed to avoid instability; μIf and μId, σIf and σId are the local standard deviations of images If and Id, respectively. Similarly, in order to ensure the consistency of the loss function, the loss function is defined as: 1sim(Im,If,ϕ;θ)=1−SSIM(Id,If).
2.4.5. PCC + SSIM
The PCC is more sensitive to robust image noise but less sensitive to fuzzy edges. Using the PCC as the loss function alone causes slow convergence, and the SSIM can model image details, including noise and artifacts, through the network. Therefore, we combine the PCC and SSIM to evaluate the image registration performance. Both the PCC and SSIM [40] are bounded within the range [−1,1]. The closer the value is to 1, the higher the similarity between the two images. Thus, we propose combining the SSIM and PCC using equal weights:
3.
Experiments and results
The goal of the work was to improve CBCT with pCT registration accuracy. We performed validation on pelvic data from clinical patients and selected a total of 400 pairs of section data from the corresponding sites. Of these, 350 slice pairs were selected as the training set and 50 slice pairs as the test set. The image size was based on the SR-processed CBCT, and all slices were processed to a 384 × 384 size. The range of selected pixel values was between [0-2000 HU]. The proposed method was implemented by using Keras with a TensorFlow backend on an NVIDIA 2080TI (11 GB). The platform environment of the experiment was unchanged, and the dataset used was that of the image after the SR process was performed. The registration results were compared with those of VoxelMorph (VM).
For the parameter setting of the network, due to the hardware device limitation of the training platform, we set the learning rate to 10−4 and the learning rate decay to 0.88. The input images were not sliced, the number of single batch inputs was set to 8 and the number of iterations was set at 4000. After extensive testing, we were able to basically determine that the alignment network will reach convergence at about 3920 iterations in the worst case.
3.1. SR + Rigid registration validation and evaluation
First, we looked at how SR pretreatment affected the stiff alignment of medical images. The studies showed that SR-treated samples performed better under rigid alignment. Figure 4 compares the three registration maps with CBCT preprocessing to the registration maps with affine transformation, comparable transformation, and stiff transformation. Table 1 lists five distinct quantitative evaluation indicators of the similarity measure function in addition to the qualitative analysis of the benefits and drawbacks of registration in Figure 4.
Through observation using human vision, the experimental results in this paper vaguely show that the effect of rigid registration of medical images is not good; therefore, it was gradually replaced by elastic registration. In the experiment, four image registration similarity indices (the MSE, MI, PCC and SSIM) were used to compare the rigid registration effect. "SR + Rigid" means rigid transformation registration based on SR, "SR + Affine" means affine transformation registration based on SR, and "SR + Similarity" means similarity transformation registration based on SR. The data in Table 1 show that the second method has higher accuracy in medical image registration.
As shown in the picture effect, the first line of Figure 4 starts from the third column, which is an affine transformation registration map, rigid transformation registration map, and similar transformation registration map, respectively. Combined with quantitative data comparison, it can be concluded that the similarity transformation of rigid registration is better than affine transformation and better than rigid transformation. The results of the comparison of experimental data with and without preprocessing show that the accuracy of adding the preprocessing method is higher than that of direct registration.
3.2. SR + DR validation and evaluation
3.2.1. DR comparison with and without SR
The registration examples of five different similarity measure loss functions are shown in Figure 5. The top row is the direct image registration results through the ConvNet under five loss functions, and the second row is the resulting images of CBCT registration with pCT after SR preprocessing. In addition, Table 2 shows the results.
In the experiment, "an iteration" represents the number of times the network is updated by back-propagation. It is also the number of registered domain updates. According to the experiments performed in this paper, the effect of the model is the best when the number of iterations is 4000.
In Table 2, "Iterations" denotes the number of times the parameters are updated by the registered network model. There are five types of loss functions. Table 2 lists the registration effects under different numbers of iterations (100, 500, 1000 and 4000) and different evaluation functions in detail. At 4000 iterations, the registration effect of SR-DLDR is better than that of DLDR under each evaluation index. In Table 2, bold fonts are used to express excellent effects.
In each iteration, by comparing the deformation of the moving image with the loss function of the fixed image, the corresponding difference will be obtained. In the experiment, the difference of each iteration was retained. To output the experimental results with high clarity and readability, the average loss functions of 500 iterations, 1000 iterations and 4000 iterations were taken as the experimental results. The advantage of the data is not obvious when the MSE and MI are used as evaluation indices. Only when the number of iterations was more than 1000 was the loss function of SR-DLDR slightly better numerically than common registration without SR processing. When the SSIM and PCC combination was used as a loss function, the image registration accuracy was better. As the evaluation index of structural similarity, the output result of SR-DLDR was better than that of common registration without SR processing from the beginning, and the effect was more significant when 1000 iterations were conducted. The best effect in the experiment was with 4000 iterations. The SSIM of DLDR was 0.9626334, while the SSIM of SR-DLDR was 0.9666951. When PCC + SSIM was used as the evaluation index, the DLDR achieved 0.9727479, and SR-DLDR achieved 0.9770569.
3.2.2. DR comparison between SR-DLDR and VM
In this part of the experimental results, regardless of whether the visual or experimental data are shown in Figure 6 and Table 3, we can see that the alignment results using the DLDR method were better than those of the VM, with an improvement of about 6%. And the SR+DLDR alignment method that uses SR samples had higher alignment accuracy. For more convenient statistical loss function output, the smaller all loss function output in the program design achieved higher image registration accuracy.
4.
Discussion
In this paper, we investigate the effect of super-resolution on the registration accuracy. The image quality of the input moving was improved by adding super-resolution before registration, and the registration effect of the image pair with SR processing is compared with that of the image pair without SR processing.
The comparison experiments used two types of mainstream registration methods, i.e., rigid registration, and elastic registration. We compared the registration accuracy of images processed without the SR technique and images processed with the SR technique under the conditions of three rigid registration methods, i.e., rigid transform [49], affine transform [50], and similar transform [51]. The data in Table 1 shows that all three registration accuracies had different degrees of improvement after using SR to preprocess the data, which proves that improving the quality of the input image is helpful to increase the registration accuracy.
For the mainstream registration methods using deep learning, the registration accuracy and generalizability of elastic registration exceed those of rigid registration. We also conducted experiments on elastic registration, because supervised registration requiring the SR processing of images and labeled data is not applicable, and we chose an unsupervised registration algorithm using deep learning methods [40] for testing. The same experimental procedure as the rigid registration method was tested with four loss functions, MSE, MI, PCC and SSIM. Table 2 demonstrates that the images processed with the SR technique are still effective in improving the registration accuracy by up to 4% (under the SSIM loss function). For the feature that images processed by the SR technique have more pixel information, we combined PCC and SSIM loss functions to construct a compound loss function of PCC + SSIM, which can utilize the rich pixel information of the input image while constraining the structure and similarity of the image. From the experimental data, it can be concluded that the newly proposed composite function can further improve the registration accuracy when the input SR-processed image is used, and the improvement reached 5% compared to the image without SR processing.
We demonstrate that the higher the quality of the input image, the higher the registration accuracy, which is applicable under both rigid and elastic registration. However, we have only validated this based on 2D data so far, and have not extended it to 3D data, which is incomplete. All of our experiments were based on clinical pelvic images and it is not possible to confirm whether the method is effective on other sites. In the future, we will further test whether the SR technique can improve the registration accuracy of data in a 3D data environment.
5.
Conclusions
In this paper, we have proposed a method to enhance the registered images using SR and demonstrated the use of a compound loss function PCC + SSIM to enhance the registration effect. We have demonstrated via our experiments that the higher the quality of the image the better the registration. It can also be seen in the results of the experiments that our proposed method can effectively improve the registration accuracy, and that the composite loss function PCC + SSIM used has better performance in registration compared to other loss functions. This method is important for improving the registration accuracy in IGRT and enhancing the treatment results.
Acknowledgments
This work is partially funded by the National Science Foundation for Young Scientists of China (Grant No. 61806060), China. We also acknowledge support from the Basic and Applied Basic Research Foundation of Guangdong Province (2021A1515220140) and the Youth Innovation Project of Sun Yat-sen University Cancer Center (QNYCPY32).
Conflict of interest
The authors declare that there is no conflict of interest.









 DownLoad:
DownLoad:








