Laboratory and numerical investigation of the 2-array submerged vanes in meandering open channel

1.   Introduction

In the meander section of the rivers, secondary flow develops when flow crosses the tip due to a combination of transverse pressure gradient and centrifugal force ^[1]. The outer meander of the river is subject to erosion due to the high flow velocity, while the low velocity of the flow near the bed towards the inner shore causes accumulation ^[2]. Also, induced velocity field variations are the reason for shear stress changes that cause erosion and sediment transport. ^[3]. In order to reduce these effects of erosion and sediment, studies with a submerged vane on meander curves by Odgaard and Kennedy ^[4,5] led to the introduction of submerged vane into the literature as a new method. Ghorbani and Kells ^[6] examined the effect of a submerged vane on local scour in a cylindrical leg. Davoodi and Bejestan ^[7] experimented with four different longitudinal distances between submerged vane, equal to 4, 6, 8, and 10 H, under four different flow conditions. Gemici ^[8] investigated the effects of different Froude numbers, vane arrangement, vane length/vane height, and approach angle combinations on flow velocity. Mohammadiun et al. ^[9] conducted their research to reduce sedimentation and erosion potential at the junction of curved and straight channels. Fathi and Zomorodian ^[10] presented the results of laboratory experiments investigating how submerged vanes affect scrubbing around a vertical wall and overflow abutments under clean water conditions. Kalathil et al. ^[11] used submerged vanes to control sediment entry into the inlet channel with a physical model. Zarei et al. ^[12] investigated the effects of submerged vanes around the bridge pier and on bed topography changes. Karami Moghadam ^[13] used a 55° intake channel branched from a rectangular channel for shear stress effect under submerged vanes. Azizi and Bajestan ^[14] investigated the rectangular vane and five other modified vanes with tapered leading edges with angles of θ = 30°, 45°, 60°, 70°, and 73.3°. Baltazar et al. ^[15] examined the effect of a submerged vane field on the flow pattern and bed morphology near and inside the entrance reach of a movable bed 90° lateral diversion. Lake et al. ^[16] investigated the effect of river-based, submerged vane structures in Australia. When the previous studies on the submerged vane are examined, especially the models made with computational fluid dynamics (CFD) are limited. It is difficult to analyze while the basic equations of fluid mechanics were applied to parameters such as complex geometries, viscosity, flow velocity, and temperature. CFD could be applied to the solution of problems in fluid mechanics ^[17]. In the past, some researchers have used 3D numerical models to determine flow characteristics ^{[18,19,20,21,22,23,24]}.

When the past studies were examined, it has been determined that there were very few or limited studies to reduce/prevent scours caused by high flow velocities in the meandering of the rivers. This study focuses on the effect of the submerged vane, which is accepted as a new method ^[25], on the meandering open channel. For this purpose, experiments were carried out where in the meandering part of the open channel which is of 2-array with 6 submerged vanes, and without a vane using a channel discharge of 20 L/s. The submerged vane experiments conducted in this study will contribute to the literature by researching the originality of the river meanders and the effect of the vane. In addition, flow velocities in the open channel were modeled with the CFD method and the cross-sectional flow velocity changes were investigated along the depth.

2.   Materials and methods

The performance of no vane (V₀ model) and 2-array with 6 submerged vanes (V₁) models in meandering open channel flows has been investigated by using a flow discharge of 20 L/s in this study. Detailed information about the experimental setup, experimental conditions, and mathematical model for the V₀ and V₁ experiments conducted in the open channel are given below.

2.1.   Experimental set-up

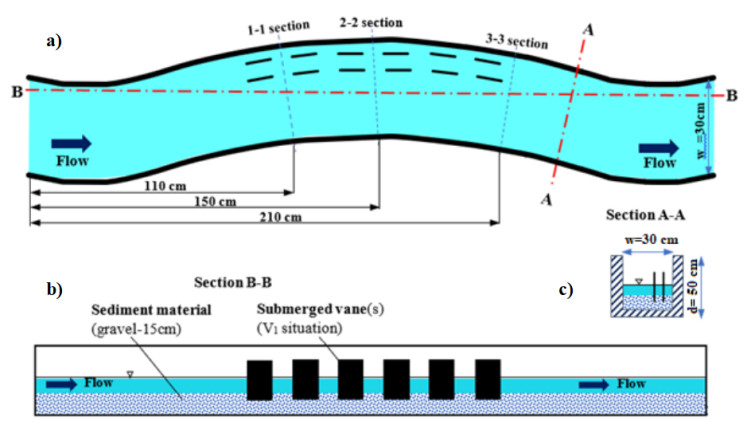
At Bartın University hydro-mechanic laboratory, a 30 cm wide curvilinear channel was built within a 50 cm wide rectangular channel inside the existing open channel system. The initial conditions for the experiment are given in Table 1. Q, B, d, A, T, R_h, Fr, and V_mean denote the discharge flow, channel width, depth of flow, wetted area, wetted perimeter, hydraulic radius, flow Froude number and inlet mean flow velocity in Table 1. The subcritical flow has occurred in the open channel where close to the energy-reducing tank and the upstream because the Froude number is less than 1.

In order to reduce the turbulence of the flow of water entering the channel with the pump, the entering water is taken to the settling tank and the energy of the entering water is reduced. The open channel assembly in which the submerged vane experiment was performed had a base slope of 0.0003. A meandering channel was constructed along the 50 × 50 cm sectioned rectangular channel with approximately 3 meters long and 30 cm wide. The curved 30° meander is connected between upstream and downstream rectangular channels. The meandering channel has a center radius R = 3.60 m. The submerged vane is constructed using 2 mm thick sheet metal. In order to determine the flow discharge, the flowmeter ultrasonic device was used at the entrance to the open channel system from the water tank. On the bottom of the submerged vane, 5 mm thick sheet of material was mounted in accordance with the slope/dimensions of the meandering channel and was removed and installed during each V₀, V₁ experiment. These dimensions have also been considered in the numerical simulations.

The flow discharges were measured by an Acoustic Doppler Velocimetry (ADV) flowmeter. Measurements were made at 60% of the depth (0.6 d). Discharge flow was recorded with an ultrasonic flow meter. The experimental setup and all sections were shown in Figure 1.

For the flow occurrence in river conditions, the bottom of the channel was laid with 15 cm of sediment (gravel) material and the base of the vane was placed on the sand of 5 cm. The experiment conditions prepared for the V₁ case were also provided for the V₀ case. With the start of the pump, the water drawn from the water tank passed through the gravel filters and reached the flow conditions to stabilize. It took approximately 15 minutes for the flow conditions to stabilize. After flow conditions were stabilized, flow discharges were recorded and flow discharge adjustments were made with an ultrasonic flow meter.

During the design phase, the boundary conditions and flow properties of the experiment were defined using the Gambit program. CFD was applied with the Fluent software after the design. Flow velocity simulations at the measurement points of the open channel were examined as experimental and CFD results separately. Finally, the experimental results of the V₁ case were analyzed based on hydraulic terminology and its comparative effect was investigated with the V₀ case.

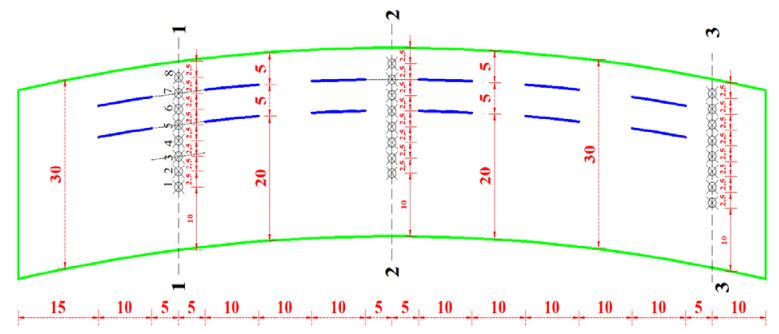
For the V₁ case, measurements were taken in the middle of the 10 cm gap after each vane (5 cm) (see Figure 2). Flow velocity measurements were taken perpendicular to the flow at 2.5 cm intervals at 8 post-vane measurement points. The section measured after the vane in the first row was called the 1-1 section. The section after the 6th vane was called the 3-3 section. For the V₁ case, the experimental measurement points are given in Figure 2. The velocity changes were investigated in 2.5 cm intervals in each section. Velocity variations are discussed in V₀ and V₁ cases.

2.2.   Numerical modeling

The flow conditions of modeling, are turbulent flow and free surface flow which is directed by gravity. According to the literature, this kind of free surface flow can be simulated by the volume of fluid (VOF) method as water-air 2 phase flow problems. The standard k-ε turbulence model was used in the three-dimensional numerical simulation of flow. The k-ε turbulence model was a possible method for the free surface flow simulations ^[26,27].

2.2.1.   Basic equations

The investigated open channel flow was a 3D, turbulent, unsteady free surface flow. For the k-ε turbulence model given by Launder and Spalding ^[28], the continuity equation, the momentum equation, and the equations for k-ε were given Eqs (1)–(6).

Continuity equation:

Momentum equation:

Turbulence kinetic energy (k) equation:

Turbulence dissipation rate energy (ε) equation:

where, t is the time; u_i is the velocity components; x_i is the coordinate components; ρ is the density; µ is the molecular viscosity coefficient; P is the correct pressure; µ_t is the turbulent viscosity coefficient, which can be derived from the turbulent kinetic energy k and turbulent dissipation rates:

σ_k and σ_ε are turbulence Prandtl numbers for k and ε equation respectively, σ_k = 1.0, σ_ε = 1.3, C_1ε and C_2ε are ε equation constants, C_1ε = 1.44, C_2ε = 1.92, C_μ = 0.09 is a constant, determined by experimentally.

VOF model

In this study, the VOF method was used to calculate the water-air interface. This method was used for 2-phase air-water flow simulation ^[29] and to compute the free surface of the flow ^[30]. The VOF method essentially determines whether the element volumes in the computational mesh are empty, partially filled, or completely filled with water. Representing the volumetric filling ratio of the mesh elements, the mesh element is fully filled for F = 1, empty (filled with air) for F = 0, and partially filled with water for 0 < F < 1 ^[31]. In this approach, the tracking interface between air and water is accomplished by the solution of a continuity equation for the volume fraction of water:

where, α_w is volume fraction of water. In each cell, the sum of the volume fractions of air and water is unity. Volume fractions of air denote α_a can be given as

2.2.2.   Boundary conditions

Flow field boundary conditions must be specified differently on walls, channel inlet, outlet and free surface; due to unsteady and channel flow. Since the boundary and inlet conditions are different for each variable, they must be selected separately. Velocities on free surfaces and at side-bottom channels, velocities on submerged vane faces were obtained using the standard wall function based on the recommendation of Launder and Spalding ^[28]. This wall function accepts a log-law velocity profile close to the wall and was determined as in Eq (9):

where, "u_p" is the average stream flow velocity at the "p" point; "K" von Karman constant (0.418); "y_p" is the distance from point p to the wall; empirical constant "E" has the value of 9.79; "u_*" is the friction velocity. The "u" uniform velocity distribution was given to the horizontal velocity component in the x-direction at the inflow boundary. The vertical velocity component "v" in the y-direction was set to zero. The inlet velocity field to the channel consists of a forward 'u' horizontal velocity and zero 'v' vertical velocities at all points except points close to the channel.

The wall y+ is a dimensionless distance similar to the local Reynolds number often used in CFD to indicate how the mesh is for a particular flow. It determines whether the effects in cells adjacent to the wall are laminar or turbulent ^[32].

where u_τ is the friction velocity, y is the height from the wall to the mid-point of the wall-adjacent cells, v is the kinematic viscosity, τ_w is the wall shear stress and ρ is the fluid density at the wall. Values of y⁺ close to the lower bound (y⁺ ≈ 30) are most desirable for wall functions, whereas values of y⁺ ≈ 1 are better for near-wall modelling ^[33].

2.2.3.   Meshing and grid detail

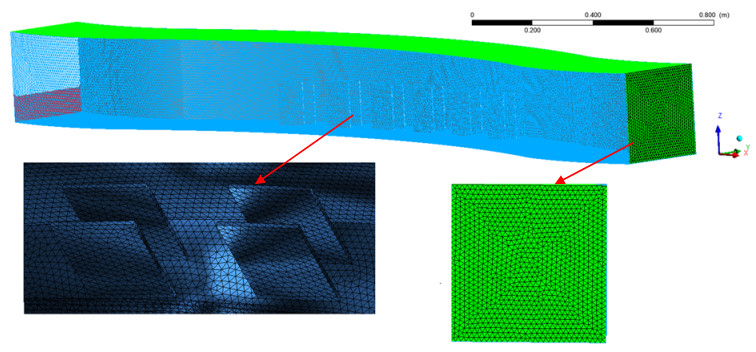
In this paper, the 3D analysis was built up for V0 and V1 structures. CFD model was created according to the open channel experiment (Figures 1 and 2). Inlet conditions and boundary layer conditions were established according to the experimental study. 1,280,602 meshes for V0 submerged vane case and for the V1 case, 1,293,691 meshes were assigned. Also, tetrahedron-type meshes were used in the design. The mesh for the design of V1 case is given in Figure 3.

The proposed model was used to simulate the variation of submerged vane open channel flow. The biggest problem during the implementation of the submerged vane in the Fluent model was the skewness error of the network grid. The mesh qualities were controlled with equiangular skewness, equisize skewness and aspect ratio in the Gambit program. Skewness and other problems were solved by getting a smaller mesh dimension grid line. Since the real shape of the vane was considered in the model, the skewness error was increased due to the shape of the open channel. Those errors were defined and corrected by increasing the amount of mesh with Gambit. However, when the mesh gets smaller, the number of mesh was increased. Furthermore, the computational domains for all cases were approximately divided 1,280,602–1,293,691 tetrahedral mesh volumes to obtain acceptable skewness coefficients, as seen in Figure 3. This represents approximately 235,000 nodes. In the meshing cases, the convergence criterion of flow parameters was taken at 0.01 for all runs.

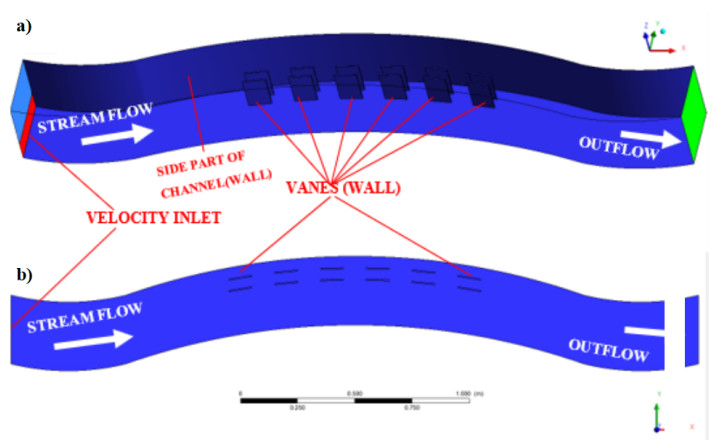
The 3D analysis was built up for V0 and V1 cases. The CFD model was created according to the open channel experiment setup consisting of 1 main meander channel (Figures 1 and 2). According to the experimental inlet measure (Table 1), inlet conditions and boundary layer conditions were established. The boundary conditions of the flow formed with V0 and V1 cases have been defined. Figure 4a), b) show the surfaces for the CFD model solution. According to Figure 4, the water inlet height = velocity inlet, submerged vane - open channel surfaces = wall and outlet section (in downstream) = outflow were accepted. Also, for the flow discharge of 20 L/s, the water inlet height was defined as 5.5 cm.

The mesh independence test was performed by doubling the mesh numbers in the lateral and vertical directions. However, no significant difference in flow velocity results was observed due to mesh improvement. This finding showed that the flow velocity results were independent of the mesh.

2.2.4.   Numerical solver

When the velocity fields into the open channel have complex flows such as circulation flow, turbulent flow and secondary flow problems arise because the open channel flows are nonlinear and velocity—the pressure field interdependent. These problems were solved using the "Coupled" procedure approach. This procedure was the iteration method and it was based on the prediction-corrector approach. Fluent provides the option to choose "Coupled" pressure-velocity coupling algorithms. The full implicit scheme was used in the model, since the flow was unstable and the analysis time is very long ^[19]. As an initial state, the inlet channel is first filled with air and water. Then, water at a certain height was released into the free flow at a certain rate from the inlet channel to the upstream end. The channel flow continues until it reaches the downstream limit. The calculation continued for about 600 seconds, at which point the front had already crossed the downstream boundary and any change in flow area was ignored. A time step of 1 second was chosen after preliminary trials to have the desired converged solution. Discretization methods and solver settings are presented in Table 2.

3.   Results and discussion

3.1.   Submerged vane experimental and CFD results

The flow velocities were measured in the open channel for the V₀ and V₁ cases and it was simulated CFD. Then, the experimental and numerical results were compared for V₀ and V₁ cases. In order to see the velocity change after the section, the measured and simulated flow velocity results were given as dimensionless based on the average velocity.

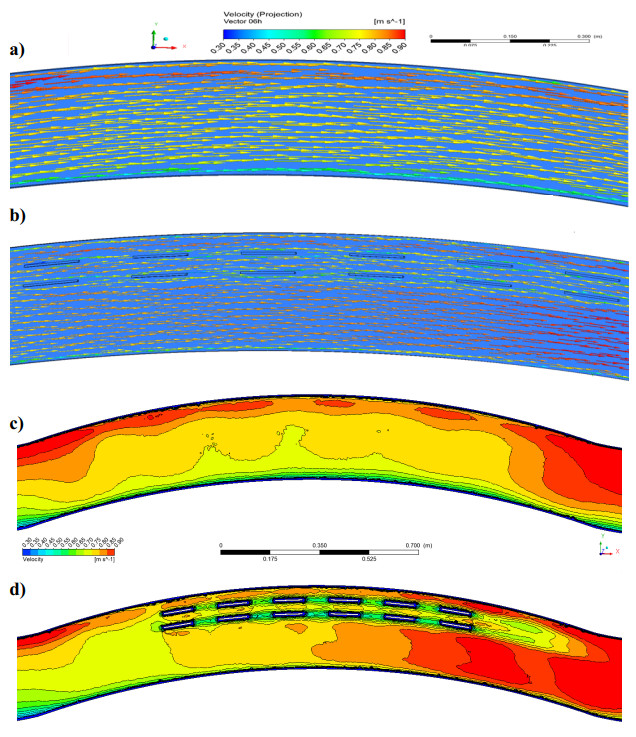
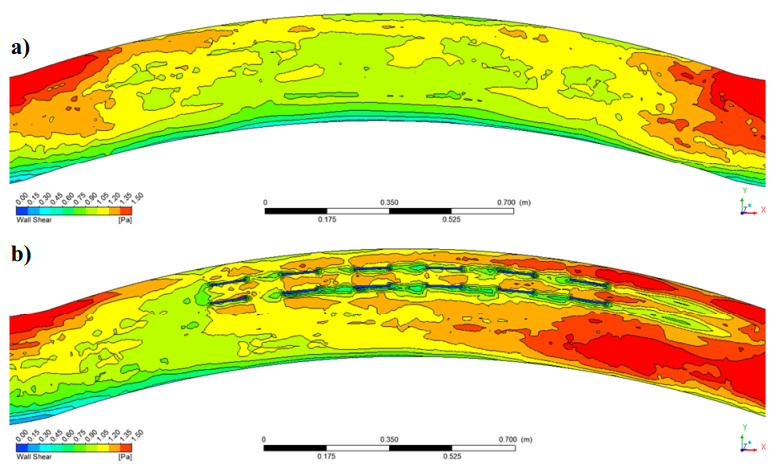
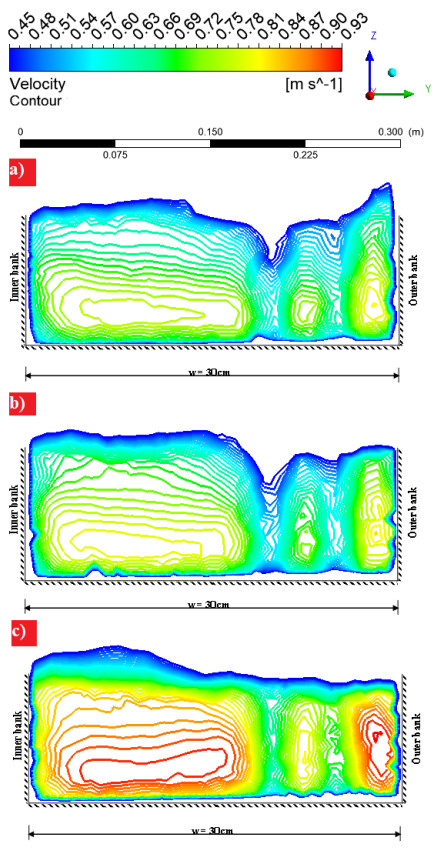
CFD results are given with the measured points according to the 1-1, 2-2, and 3-3 sections as seen in Table 3, Figures 5 and 6. It was observed that high flow velocities are seen at inner points where the channel meandering first starts (Figure 5a), b)). The flow velocity increased from the inner meander to the outer meander. In Figure 5a), b), it was observed that the flow velocity around the vane reduced and between the vanes it had a flow velocity of 0.50–0.75 m/s. It has been seen that flow has a velocity between 0.75–0.90 m/s, near the middle outer meander region and in channel parts without vane. In order to see the changes at the 0.6 d, it was given as a velocity contour in Figure 5c), d) with V₀ and V₁ cases. As it was presented in the figures, it was observed that the flow was directed around the vane and the flow velocity between the vanes decreased. It was seen that the vane structures were effective in directing the flow and reducing the flow velocity, and the flow reaches equilibrium in the inner meander and outer meander in the channel. Figure 6 shows the shear stress variation for V₀ and V₁. It has been determined that shear stress decreases behind and around the submerged vane.

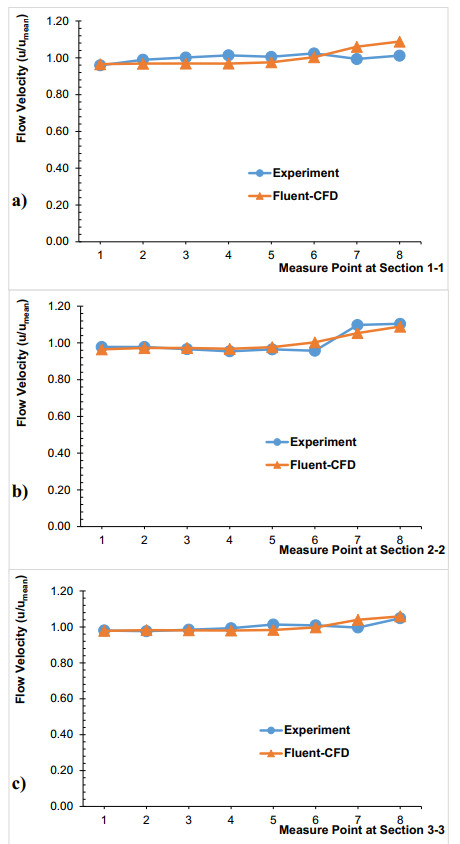
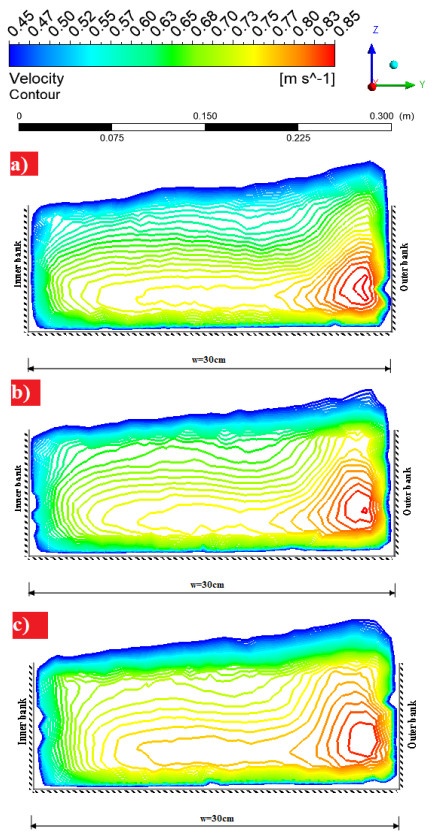
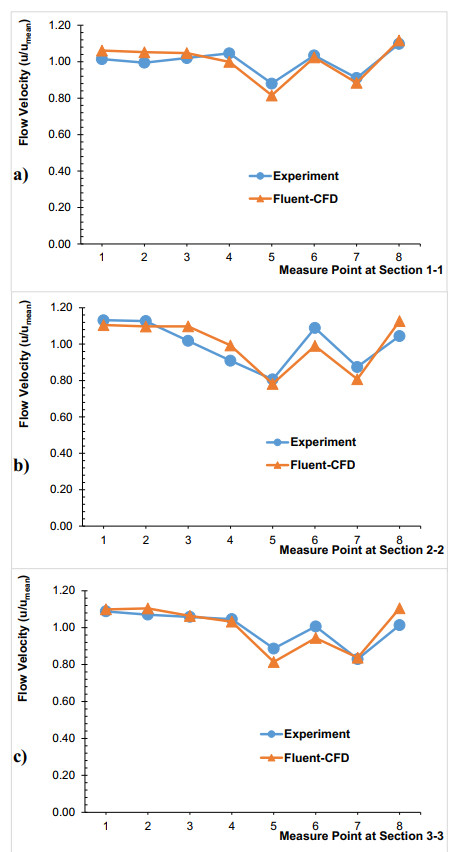
The flow velocity at sections was accepted as dimensionless velocity ^[34] "u/u_mean". The 1st point represents the point close to the inner meander, and the 8th point represents the point close to the outer meander. According to the velocity inlet; 1, 1 meters (x₁), 1, 5 meters (x₂) and 2, 1 meters (x₃) were accepted as a 1-1, 2-2 and 3-3 sections, respectively (see Figure 1). The experimental and numerical model dimensionless velocity values obtained in all sections were shown in Figure 7. Table 3 shows the errors by comparing the experimental and CFD analysis results. In Figure 8a)–c), velocity contours of the 1-1, 2-2 and 3-3 cross-sections for V₀ case were given, respectively. Table 3, Figures 7 and 8 were examined, and it was seen that the error percentage of the velocities was less at the midpoints than at the edges. Maximum error was observed in the outer meander (7–8th points) for V₀ case 1-1 section (6–8%). In general, it was found that the experiment and Fluent-CFD results were in good agreement. According to Figure 8a)–c), it was seen that the velocity increased in the outer meander and decreased in the inner meander. Also, as can be seen in Figure 8, the water depth decreased in the inner meander, while the water depth increases in the outer meander ^[34] (the water depth changes with the blue contour lines). For the V₀ case, it was seen that the experiment and CFD results were generally compatible and the errors were at a reasonable level (see Table 3). The experimental and numerical model (V₁ case) velocity values obtained in all sections were shown in Figure 9. Table 4 shows the errors by comparing the experimental and CFD analysis results. In Figure 10a)–c), velocity contours of the 1-1, 2-2 and 3-3 cross-sections (V₁ case) were given, respectively.

Table 4, Figures 9 and 10 were examined, it was seen that the error percentage of the velocities is less at the midpoints than at the edges. Maximum error was observed in 4th point) for V₁ case 2-2 section (9%). In general, it was found that the experiment and Fluent-CFD results are in good agreement.

According to Figures 9 and 10, decreases in flow velocities were seen behind the vane. Compared to the 1-1 section without the vane (Figures 7a) and 8a)), it was understood that the flow velocity decreased from 0.759 to 0.590 m/s (5. point). It has been determined that there was a nearly 26% decrease in flow velocity. Compared to the 2-2 section without the vane (Figures 7b) and 8b)), it was observed that the flow velocity decreased from 0.820 to 0.583 m/s (7. point). It has been extracted that there is a nearly 29% decreased in flow velocity. Compared to the 3-3 section without the vane (Figures 7c) and 8c)), it was observed that the flow velocity decreased from 0.829 to 0.697 m/s (7. point). It has been determined that there was a nearly 16% decreased in flow velocity. Also, as can be seen in Figure 10a)–c), the flow water depth in the inner meander and the water depth in the outer meander were balanced (the water depth changes with the up blue contour lines).

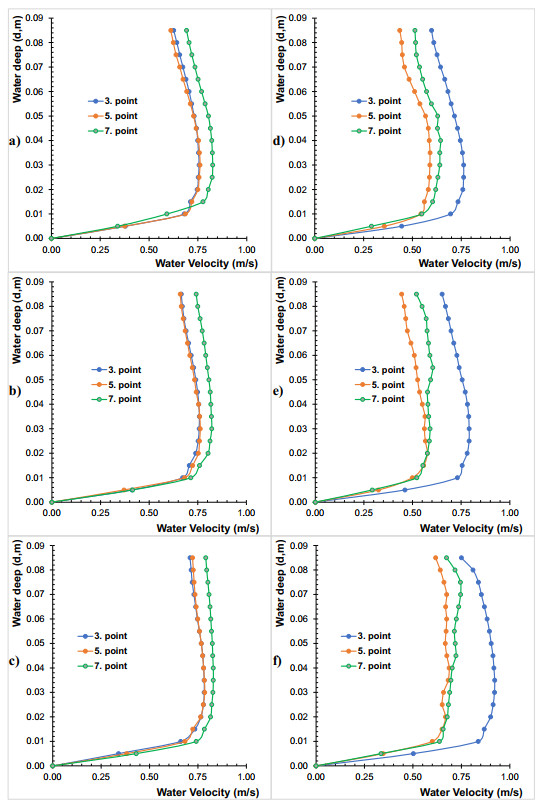
In Figure 11, CFD -velocity variations across water depth in V₀ and V₁ cases with different measuring points. Here, the 5th and 7th points represent the back of the vane, and the 3rd point represents the V₀ case inner meander. Figure 11a)–c) are the velocity changes depending on the depth at the 3rd, 5th and 7th points at 1.1, 1.5 and 2.1 meters for V₀ case. Figure 11d)–f) at the 3rd, 5th and 7th points at 1.1, 1.5 and 2.1 meters for V₁ case.

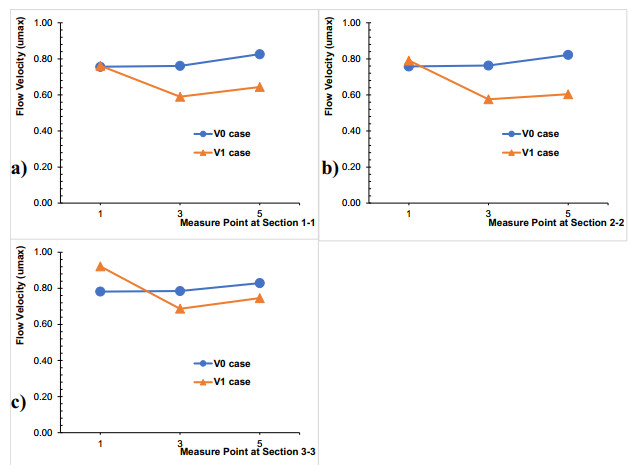
In Figure 11, it was observed that while the velocities were approximately 0.8 m/s in the vaneless outer meander, these velocities decreased to an average of 0.6 m/s in the vaneless outer meander. For case V₁, all sections were after the vane (5 cm) in the direction perpendicular to the flow. According to the after-vane structure's measurements, the submerged vanes reduced flow velocity by 30% in section 1-1, and decreased the flow velocity by 38% in sections 2-2 and 3-3.

According to the V₀ and V₁ case, while the velocity decreased on the inner meander, velocity increased on the outer meander. When the results of the experiments were examined in accordance with the CFD simulation results, a 12% error has been detected. Considering that most of the flows in the rivers are turbulent, an error of close to 10% is considered an acceptable error.

4.   Discussion

Flow velocity profiles made without a submerged vane are compatible with numerical model or experiment results ^[34,35]. Reported laboratory experiments show flow patterns of submerged vanes. Scour in the outer meander was caused by the increase in flow velocity and shear stress. The submerged vane cuts off secondary circulation or cross flow cuts off thereby reducing high velocities around the outer meander (Figures 10 and 12).

In the meander section of the open channel, velocity distribution diagrams of the submerged vaneless streamflow bed (Figures 7 and 8) show that it slides out of the meander and reaches the maximum level near the outer meander before the outlet of the meander. This experimental pattern was consistent with experimental measurements in the other channel meander ^[34]. The centrifugal force increases proportionally with the square of the flow velocity and the upper region with high flow velocity reaches more centrifugal force than the lower region ^[35]. Experimental flow velocity results measured at 0.6 d, modeled both with submerged vane and without submerged vane, showed that the model with submerged vane decreased the flow velocity by 26 and 29% and directed the flow (Figures 7–9). When the literature studies were examined, Gemici ^[8] experimentally found that submerged vane flow velocities were reduced by 7–19%. The flow models obtained with the 3D model were examined along with the depth (Figure 11), and it was observed that the maximum velocity was reduced by 22–27% (Figure 12). The result of this study will be useful for understanding the flow phenomenon, validation of numerical work and subsequent design of meander protection measures.

5.   Conclusions

In this study, the performance of V₀ and V₁ cases in open channel flows was investigated by using a flow discharge of 20 L/s. The effect of the vane structure on the flow velocity measured in the open channel was determined and the experiments performed were modeled by CFD. Dimensionless average velocity values were used to compare the measured and simulated velocity values. It was seen that the experimental and CFD flow velocity results were compatible in V₀ and V₁ cases, and the CFD model showed a low error for the dimensionless mean velocity. In addition, it is thought that this numerical model can be used in the next stages, in the future projection phase with simulation.

According to the flow velocity results, it was determined that the vanes significantly reduced the flow velocity, and the V₁ case affected the channel flow velocity by 26–29%. The flow results with the CFD were examined along the depth, it was seen that the maximum velocity decreased by 22–27%. Submerged vane structures balanced the water depth between the inner and outer meander open channel flows. The flow velocity was reduced by flow directed from the outer meander to the inner meander. Submerged vane structures were found to be effective in regulating flow. In future studies, the effect of straight/curve, angle and dimensions of the submerged vane can be investigated. The applicability of submerged vane structures in real river meanders and especially the submerged vane effect in flood situations can be investigated. It is also recommended that submerged vane structures can be applied as an effective method of reducing flow velocities and directing flows. It has been known that submerged vane contributes to the protection of the environment by regulating the flow in the inner and outer meanders.

Conflict of interest

The authors declare there is no conflict of interest.