A two-stage stochastic optimization model for the retail multiskilled personnel scheduling problem: a k-chaining policy with $k \ge 2$

1.   Introduction

Given the intensive use of human resources in the service industries, the personnel scheduling problem in these industries has been addressed by many researchers over the years ^[1]. In Pastor and Olivella ^[2], Kabak et al. ^[3], Henao et al. ^[4], and Chapados et al. ^[5], the authors indicated that the personnel scheduling problems in the service industries share characteristics that make them more difficult to solve than the analogous characteristics faced by manufacturing industries, such as: 1) regulatory constraints (e.g., minimum/maximum number of weekly working hours, minimum/maximum length of shift, maximum amount of consecutive working days, and minimum amount of resting days per week and per month), and 2) flexible employment contracts (e.g., contracts consider multiple feasible working day sequences, multiple feasible shifts per day, and multiple feasible positions of breaks into the shifts).

In addition, unlike other services industries (e.g., call centers, healthcare, cybersecurity, transportation), the personnel scheduling problem in the retail industry can be more difficult to solve because it must deal with predictable phenomena such as the demand seasonality, and unpredictable ones such as demand uncertainty and unscheduled staff absenteeism ^[4,6,7,8]. Particularly, Mac-Vicar et al. ^[9] and Cuevas et al. ^[10] explain that, in the retail industry, staff demand volumes may vary strongly over the weeks of the year, over the days of the week, and over the course of a single day. Consequently, these predictable and unpredictable phenomena hinder a perfect match between the supply and demand of personnel. Therefore, it is frequently observed that the number of employees assigned in a given store department could be below (i.e., understaffing) or above (i.e., overstaffing) than what is required. When personnel scheduling models do not efficiently solve the problems arising from overstaffing and understaffing, retail companies typically incur an increase in labor costs, a deterioration in the service levels offered to customers, and a loss in expected revenues ^[3,10].

Several pieces of research in the retail industry have shown that the use of multiskilled employees is an effective source of labor flexibility to minimize the levels of over/understaffing (e.g., ^[4,6,7,9,11]). In the context of a retail store, multiskilled employees are those who are trained to work in $k$ departments of the store (with $k\ge 2$). This labor flexibility allows moving multiskilled employees from overstaffed departments to understaffed ones. However, since multiskilling is not free, it is essential to answer two key questions: how much and how to add multiskilling. In the literature on the use of multiskilling, k-chaining has been reported as the most cost-effective policy for generating training plans that answer both questions (e.g., ^{[6,7,11,12,13,14,15,16,17,18,19,20,21]}).

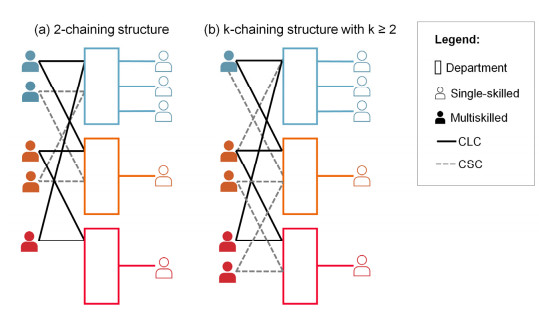
Under a k-chaining policy, training plans ensure that a set of employees will be trained to work in $k$ store departments with $k\ge 2$, such that the assignment decisions between employees and departments are represented through a bipartite graph involving the formation of closed chains. The constructed closed-chains can be closed short chains (CSC) and/or closed long chains (CLC). While in a CSC a subset of store departments is connected through a subset of multiskilled employees, in a CLC a subset of multiskilled employees connects all store departments. The literature shows that k-chaining provides greater flexibility in the personnel allocation to deal with scenarios of uncertain demand and/or unscheduled employee absenteeism. Within the k-chaining policies described in the literature, typically the 2-chaining policy has been identified as the most recommended and popular ^{[6,7,11,14,21,22,23]}. This policy requires all multiskilled employees to be trained in at most two departments, i.e., $k = 2$. Figure 1(a) shows an example of a 2-chaining structure, which includes one CLC (solid lines) with three multiskilled employees connecting all departments, and one CSC (dashed lines) with two multiskilled employees connecting two departments. Note that, in Figure 1(a), each multiskilled employee is trained in two departments (i.e., $k = 2$).

The literature also shows that fewer studies have evaluated the benefits associated with k-chaining policies with $k\ge 2$. Under the context of a retail store, Figure 1(b) shows an example of a k-chaining structure with $k\ge 2$, which includes one CLC (solid lines) and two CSCs (dashed lines). Note that, in Figure 1(b), there are two multiskilled employees trained in three departments (i.e., $k = 3$) and three multiskilled employees trained in two departments (i.e., $k = 2$). In the service sector Wallace and Whitt ^[12], Iravani et al. ^[13], and Abello et al. ^[19], studied k-chaining policies with $k\ge 2$. In manufacturing, k-chaining policies were evaluated by Muriel et al. ^[24], Yang ^[25], Parvin et al. ^[26], Deng and Shen ^[27], Simchi-Levi and Wei ^[28], and Wang and Zhang ^[29]. For example, Wang and Zhang ^[29] evaluated and compared the performance of CLCs using a 2-chaining policy versus a k-chaining policy with $k > 2$. They found that, at higher levels of demand variation (i.e., high coefficients of variation), lower were the returned benefits of the 2-chaining policy. However, k-chaining policies with $k > 2$ retained high levels of performance even with high levels of demand variation. This suggests that in the face of high levels of demand uncertainty it is more beneficial to have a higher degree of flexibility in chaining. In turn, the results of Wang and Zhang ^[29] also showed that for values of $k\ge 5$ the returned benefits were almost identical, indicating that decreasing returns to scale are present as $k$ increases. Therefore, high multiskilling levels may be unnecessary, and, consequently, it is relevant to determine the most cost-effective multiskilling levels.

Although the literature has focused on 2-chaining policies, we consider it interesting to discuss under which demand uncertainty scenarios a k-chaining policy with $k\ge 2$ can be more cost-effective than a strict policy with $k = 2$. Therefore, for the retail industry and considering uncertainty in personnel demand, this paper proposes a two-stage stochastic optimization (TSSO) model to determine the multiskilling levels that minimize the expected costs of over/understaffing through a k-chaining policy with $k\ge 2$. Then, the proposed methodology is tested for a case study associated with a Chilean retail store, which uses real and simulated data. The case study considers nine representative levels of demand variability to evaluate the impacts of uncertain demand on multiskilling decisions.

This article is an extended version of the conference paper Mercado and Henao ^[30]. We improve on our previous work through the following extensions. First, unlike previous papers, this paper provides an exhaustive literature review of papers that in the last 20 years have addressed personnel scheduling problems using multiskilled personnel. Second, we provide a detailed description of the simulated and real data used in the case study. Third, we considerably extend our case study. This latter extension allows us to: (ⅰ) Answer not only the question of how much multiskilling to add, but also the question of how to add it. (ⅱ) Compare the reliability of the TSSO approach solutions relative to two myopic approaches: zero multiskilling and total multiskilling. Note that, under a zero-multiskilling approach, all employees are single-skilled and can perform in a single store department. Under a total-multiskilling approach, each store employee is multiskilled and can perform in all departments of the store. (ⅲ) Measure the level of conservatism in the TSSO approach solutions by using two types of truncations in the probability density function (pdf) associated with the personnel demand.

2.   Literature review

The personnel scheduling problem with multiskilling has been studied by several authors in previous studies. A selection of these studies is presented in Table 1, together with brief indications from each of them on the elements presented below.

1) Decision level (DL): Abernathy et al. ^[31] and Henao et al. ^[4] state that the personnel scheduling problem can be analyzed under a hierarchical process that considers three decision levels: strategic, tactical, and operational. Strategic level, considers decisions such as: (a) Staffing (S), determining staffing by type of task (or department) and contract. Tactical level, considers decisions such as: (b) Shift scheduling (SS); (c) Days-off scheduling (DOS); and (d) Tour scheduling (TS). Such that, tour scheduling problem simultaneously assigns shifts and days-off. Operational level, considers decisions such as: (e) Assignment (A), assignment of employees to task types without considering the scheduling of shifts and rest days. We emphasize that this article addresses a personnel assignment problem.

2) Multiskilling (MS): Indicates whether multiskilling was modeled as a decision variable (Var), or parameter (Par).

3) Demand uncertainty (DU): Indicates whether the problem considered demand uncertainty.

4) Supply uncertainty (SU): Indicates whether the problem considered unscheduled staff absenteeism.

5) Chaining: Indicates whether the study used a k-chaining policy to evaluate the benefits of multiskilling. In case using this policy, it specifies whether the study used 2-chaining or k-chaining with $k\ge 2$.

6) Number of skills (NS): Indicates whether in the study the maximum number of skills in multiskilled employees is limited. The study can be: (a) restricted (R), each multiskilled employee can have only two skills in total, and (b) unrestricted (NR), each multiskilled employee can have more than two skills in total.

7) Solution Method (SM): It can be (a) heuristics (H); (b) simulation (S); (c) optimization (OPT); y (d) analytics (AN); y (e) markov processes (MP).

8) Uncertainty modeling (UM): Indicates the approach that was used to evaluate the uncertain parameters of the mathematical model. These approaches can be classified as follows: (1) In-optimization, approaches that incorporate uncertainty explicitly into the mathematical formulation, they can be (a) robust optimization (RO); (b) closed-form equation (CF); (c) stochastic programming (SP); and (d) distributionally robust optimization (DRO). Note that, CF and SP assume complete knowledge of the pdf of the uncertain parameter, DRO assumes only partial information of the pdf, while RO has no knowledge of the pdf. (2) Post-optimization, approaches that evaluate the impact of uncertainty once the deterministic solution of the problem is known, they can be (a) sensitivity analysis (SA), which measures how changes or perturbations in key model parameters impact the behavior of the deterministic optimal solution; and (b) multiple scenario evaluation (MSE), which uses a finite number of scenarios and solves each of them independently.

9) Application (AP): Economic sector or industry where the study was applied. It can be: (a) retail (RE); (b) manufacture (MA); (c) healthcare (HE); (d) cybersecurity (CS); (e) call-centers (CC); (f) technology (TE); (g) electric power plant (EPP); and (h) postal services (PS).

The 20 studies in Table 1 that evaluated the benefits of multiskilling through a k-chaining policy can be grouped and classified into four categories. In Subsections 2.1, 2.2, 2.3 and 2.4 some of the studies associated with each of these four categories are reviewed in more detail. Then, Subsection 2.5 presents the main contributions associated with our article, which respond to the main gaps identified from the literature review.

2.1.   Multiskilling as a parameter and 2-chaining

Table 1 shows that several studies modeled multiskilling as a parameter and used a k-chaining policy with $k = 2$ (i.e., Chou et al. ^[39]; Simchi-Levi and Wei ^[14]; Liu ^[44]). In Simchi-Levi and Wei ^[14], a paper associated with manufacturing, the authors studied the performance of flexibility designs in balanced systems with stochastic demand. A balanced system is one where the number of supply nodes is equal to the number of demand nodes. They proposed an analytical method to develop a theory that explained the effectiveness of flexible designs with CLC in finite-size systems. The authors discovered a fundamental property of closed long chains, which they called supermodularity. This property is used to show that the expected benefits from the use of flexibility increase as the size of the chain increases. They also indicated that the largest expected benefit is achieved when the long chain is constructed, and when this long chain is closed by adding the last arc to the system.

In Liu ^[44], the author proposed a two-stage stochastic optimization model and a simulation model for planning a multiskilled workforce in a system with two types of tasks. His main intention was to investigate the impact of the closed-chained multiskilling structures on the optimal number of personnel. In the first stage of the stochastic model, the staffing per task type was determined, while in the second stage, the personnel allocation to the two types of tasks was performed.

2.2.   Multiskilling as a parameter and k-chaining with $k\ge 2$

Table 1 shows that several studies modeled multiskilling as a parameter and used a k-chaining policy with $k\ge 2$ (i.e., ^{[13,24,25,26,27,28,29,37]}). In Iravani et al. ^[13] the authors developed a simulation model to evaluate the benefits of what they called structural flexibility. Which consists of using multipurpose resources such as: multiskilled personnel (in more than two task types), machines, and/or flexible factories. They explain that the use of these multipurpose resources allows reallocating productive resources and, in this way, responding to changes in demand or in installed capacity. They analyzed a case study in the call center industry. Their results showed that the use of multiskilled employees trained in more than two task types increased the system flexibility to respond to changes in demand and installed capacity. In addition, the authors indicated that a multiskilling structure with chaining provides higher expected benefits than those without chaining.

In Wang and Zhang ^[29] the authors evaluated and compared the performance of CLCs using a 2-chaining policy versus a k-chaining policy with $k > 2$. Their research considered a balanced and symmetric system. A symmetric system is one where all supply nodes have equal capacity and demand nodes are independent and identically distributed. They found two interesting results. First, they observed that, at higher levels of demand variation, the k-chaining policies with $k > 2$ retained high levels of performance while the 2-chaining policy's performance decreased. This result is interesting as it indicates that, at high levels of demand variability, k-chaining policies with $k > 2$ may be more beneficial than strict policies with $k = 2$. Second, they also showed that there are diminishing returns to scale as $k$ increases, i.e., the returns when $k = 5$ and $k = 6$ were almost identical. This last result is also interesting, as it reinforces the idea that total multiskilling is costly, impractical, and unnecessary.

2.3.   Multiskilling as a variable and 2-chaining

Table 1 shows that several studies modeled multiskilling as a decision variable and used a k-chaining policy with $k = 2$ (i.e., ^{[6,7,11,22,35,41,42]}). In Gnanlet and Gilland ^[42], considering a system with only two task types, the authors obtained closed-form equations to estimate the optimal number of multiskilled nurses. They reported a 1.2% improvement in expected profits when using a 2-chaining policy with closed chains versus a 2-chaining policy without closed chains.

In Porto et al. ^[11], for the retail industry, the authors developed a methodology to evaluate the potential benefits of incorporating a hybrid labor flexibility strategy: (ⅰ) flexible contracts and (ⅱ) multiskilled employees under a 2-chaining policy. They proposed a mixed-integer linear programming model to determine how many employees are required in each type of contract, how many of them will be multiskilled, and in which second department they will be trained. Their objective was to minimize the levels of overstaffing/understaffing caused by seasonality and variability in demand. Their results showed that as levels of demand variability increased, the requirement for multiskilled employees also increased, and that such increase was greater for multiskilled employees associated with short shifts. This showed that flexible contracts (i.e., those including shorter shift lengths) and multiskilling are complementary sources of labor flexibility.

In Henao et al. ^[6] and Henao et al. ^[7], for the retail industry, the authors proposed different methodologies to explicitly incorporate demand uncertainty into the mathematical formulation. Henao et al. ^[6] proposed a robust optimization approach, while Henao et al. ^[7] derived a closed-form equation. Both studies considered an already hired workforce and relied on a 2-chaining policy to determine how many employees should become multiskilled and in which second department each of them should be trained. Note also that, Porto et al. ^[11], Henao et al. ^[6], and Henao et al. ^[7] had applications associated with the retail industry. This implies that the personnel scheduling problems they studied modeled unbalanced systems. That is, systems where there are more supply nodes (i.e., employees) than demand nodes (i.e., departments). Finally, the studies of Henao et al. ^[6] and Henao et al. ^[7] reported an interesting conclusion. Their studies showed that, unlike applications in balanced systems where CLC is reported as the most cost-effective 2-chaining design, in unbalanced systems a combination of CLCs and CSCs of different lengths represents the best solution.

2.4.   Multiskilling as a variable and k-chaining with $k\ge 2$

In this category, we found the studies developed by Wallace and Whitt ^[12] and Abello et al. ^[19]. In Wallace and Whitt ^[12] the authors studied a call center environment with various types of calls where they considered that it is neither possible nor profitable to use employees under a total multiskilling approach. They proposed a simulation approach to determine the optimal number of multiskilled employees required. Their results showed that most of the benefits associated with multiskilling are achieved by adding the second skill (i.e., $k = 2$). They also indicated that only modest improvements are achieved when the number of additional skills is increased (i.e., $k > 2$). Although this result seems to indicate that training employees with more than one additional skill ($k > 2$) do not generate any value, it should be clarified that their study did not consider uncertainty in the personnel demand. In Bassamboo et al. ^[37] and Wang and Zhang ^[29], studies with applications in manufacturing, the authors already showed that for higher levels of demand variation, k-chaining policies with $k\ge 2$ reported higher benefits. Therefore, considering uncertain demand, similar results could be observed for applications in service sector industries, such as call centers and retail.

In Abello et al. ^[19] the authors solved a days-off scheduling problem considering uncertain demand. Similar to us, they also proposed a retail industry case to evaluate the benefits of a policy k-chaining with $k\ge 2$. Notably, their preliminary findings showed that as variability in demand increases, it was beneficial to have employees trained in two or three departments (i.e., $k = 2$ and $k = 3$). However, their study presents key differences compared to our study. First, they addressed a different personnel scheduling problem. We address an assignment problem whereas they addressed a days-off scheduling problem. Thus, in Abello et al. ^[19] the authors were focused on scheduling decisions (weekly schedules of working days and resting days), whereas our study is focused on multiskilling decisions. Consequently, unlike Abello et al. ^[19], our article is oriented to answer two key questions: how much multiskilling to add and how to add it. Second, the case study presented by Abello et al. ^[19] is limited. These limitations are: (ⅰ) Unlike our case study, they did not perform an out-of-sample analysis to validate the performance of the solutions reported by the TSSO model. (ⅱ) They considered only three levels of demand variability to assess the impacts of uncertain demand. (ⅲ) None of the extensions proposed by our study and described at the end of the Introduction section were considered by Abello et al. ^[19].

2.5.   Main gaps found

Table 1 demonstrates the considerable efforts that different authors have made to understand the benefits of multiskilling. However, it is possible to identify the following gaps.

First, Table 1 shows that most of the articles modeled multiskilling as an input, i.e., they did not include a decision variable to determine in which set of task types (or departments) an employee could be trained or not trained. This is not a minor limitation, as it restricts the possibilities of finding more cost-effective multiskilling structures. In addition, within the set of studies evaluating the benefits of multiskilling through a k-chaining policy, a smaller proportion of them incorporated multiskilling as a decision variable (i.e., ^{[6,7,11,12,19,22,35,41,42]}).

Second, Table 1 also reveals that few studies used an in-optimization approach to explicitly incorporate demand uncertainty into the mathematical formulation (i.e., ^{[6,7,14,18,19,28,29,39,42,47]}). Note that, under an in-optimization approach, the obtained multiskilling solutions are found to be good and robust under different levels of uncertainty. Whereas, under a post-optimization approach, the obtained multiskilling solutions cannot guarantee robustness or feasibility.

Third, Table 1 shows that most studies modeled multiskilling through a strict 2-chaining policy. That is, multiskilled employees can perform only in a maximum of two types of tasks (or departments). Moreover, except for Wallace and Whitt ^[12], Iravani et al. ^[13], and Abello et al. ^[19], studies implementing a k-chaining policy with $k\ge 2$ were focused mainly on the manufacturing industries.

In summary, our extensive literature review shows the following gaps for the retail industry: (ⅰ) Shortage of studies on personnel scheduling problems that simultaneously model multiskilling as a decision variable and use k-chaining policies with $k\ge 2$. (ⅱ) Few studies explicitly incorporate demand uncertainty into the mathematical formulation. This paper will simultaneously address both gaps.

3.   The problem

For a retail store with an initially single-skilled workforce and considering variability in personnel demand, our problem consists of designing a suitable training plan using a k-chaining policy with $k\ge 2$. This training plan should provide sufficient labor flexibility to minimize the mismatch between personnel supply and demand associated with the weekly personnel assignment problem under uncertain demand. Therefore, it is expected that the closed-chained multiskilling structures involving trained employees in two or more departments can be robust to different levels of demand variability and, consequently, these structures achieve the greatest savings in staff training costs and expected over/understaffing costs. In summary, the solution problem will simultaneously determine: (ⅰ) how many employees should be single-skilled and multiskilled; (ⅱ) in which and how many departments should multiskilled employees be trained; (ⅲ) what type of closed chains (CLC and/or CSC) are required; and (ⅳ) how working hours will be weekly assigned to single-skilled and multiskilled employees. Finally, it is expected to determine under what levels of demand uncertainty is more beneficial a k-chaining policy with $k\ge 2$ than a 2-chaining policy.

Table 2 shows the mathematical notation that will be used in the mathematical formulation of the recently described problem.

The mathematical formulation of our problem considers the following assumptions: (1) There is full knowledge of the probability distribution associated with the uncertain demand for each department (${r}_{l}\left(s\right)$). Independence among the demands per department is also assumed. (2) The personnel demand for each department can be partially satisfied. Therefore, a cost of understaffing (associated with expected lost sales) is included in the total cost function. (3) A cost of overstaffing is also included, which quantifies the opportunity cost incurred in paying for idle personnel who could be performing productive tasks. (4) Training costs are also included in the total cost function. (5) It is assumed that the costs of understaffing ($u$), overstaffing ($b$), and training ($c$) do not differ among store departments. (6) Unscheduled staff absenteeism is not considered. (7) We model a single full-time contract, whereby all employees are assigned to the same number of working hours per week ($h$). (8) At the beginning of the planning horizon, all employees are single-skilled. (9) Multiskilled employees can be trained to work in two or more departments. (10) Employees are modeled as a homogeneous workforce, meaning that the individual productivity of each employee is the same.

4.   Methodology

In this section, we present the proposed methodology to solve the problem presented above. First, in Subsection 4.1 we present a deterministic optimization model to solve the problem addressed. Then, to explicitly incorporate demand uncertainty, in Subsection 4.2 we reformulate the model presented in Subsection 4.1 by means of a two-stage stochastic optimization model.

4.1.   Deterministic optimization model using a k-chaining approach with $k\ge 2$

We present the deterministic Mixed-integer linear programming (MILP) model to solve the multiskilled personnel assignment problem using the k-chaining approach with $k\ge 2$. The deterministic MILP model can be formulated as follows:

In the objective function (1) the following weekly costs are minimized: (a) employee training in additional departments; (b) understaffing; and (c) overstaffing. Constraints (2) account for demand fulfillment and allow us to calculate the level of over/understaffing associated with each department. Constraints (3) ensure that each employee works exactly the number of hours per week stipulated by his/her contract. Constraints (4) impose that each employee can be assigned to work only in those departments in which he/she is trained. Constraints (5) indicate the department in which each employee is initially trained. Constraints (6) calculate the number of additional trained skills to each employee (i.e., ${v}_{i}$). Note that, if ${v}_{i}$ = 0 employee $i$ continues to be single-skilled, while ${v}_{i}\ge 1$ represents that employee $i$ is multiskilled. For each department $l$, constraints (7) guarantee an equality between, the number of additional trained skills for employees whose original department is $l$ (${\sum }_{i\in {I}_{l}}{v}_{i}$) and, the number of additional trained skills to work in department $l$ and which are associated with employees whose original department is different from $l$ $\left({\sum }_{i\in \{I-{I}_{l}\}}{x}_{il}\right)$. Therefore, constraints (7) ensure the implementation of a k-chaining policy with $k\ge 2$. Finally, constraints (8)–(11) define the domain of the decision variables.

4.2.   Stochastic optimization model using a k-chaining approach with $k\ge 2$

We reformulate the deterministic (DT) model into a TSSO model that considers stochastic demand. The TSSO model considers first-stage variables (known as "here-and-now" decisions) and second-stage variables (known as "wait-and-see" decisions). In our formulation, the first-stage variables, ${x}_{il}$ and ${v}_{i}$, are related to decisions about training employees in different departments. Such decisions are made before the random realizations of demand are known. The second-stage variables, ${\omega }_{il}\left(s\right), {\kappa }_{l}\left(s\right),$ and ${\delta }_{l}\left(s\right)$, are related to personnel allocation decisions. Such decisions are made once the uncertain demand in each department is observed. That is, once the demand realizations are known, overstaffing or understaffing may occur.

Below, we present the TSSO version of the formulation (1)–(11). To perform this reformulation, we use the method commonly known as Sample Average Approximation (SAA). For more details about the theory of TSSO and SAA, we refer readers to Birge and Louveaux ^[49].

The objective function (12) minimizes the training cost (first-stage decisions) and the expected cost of weekly over/understaffing (second-stage decisions). Note that, in the TSSO version, first-stage decisions (multiskilling decisions) will affect second-stage decisions (assignment personnel decisions). That is, decisions about which employees are trained in two or more departments will affect the levels of over/understaffing. Therefore, under a TSSO approach, the objective is to choose the first-stage variables that minimize the sum of the first-stage costs and the expected value of the second-stage costs. Now, let us analyze the reformulation of constraints (2)–(11). Regarding constraints (2)–(4) and (10)–(11) of the DT model, since they involve second-stage variables, they were modified to explicitly incorporate demand uncertainty. Regarding constraints (5)–(9), which are associated with first-stage variables, they did not receive any modification. Also, note that the interpretation of constraints (13)–(22) and constraints (2)–(11) is the same.

Finally, since formulation (12)–(22) explicitly incorporates multiple uncertainty scenarios, this allows us to obtain a training plan that is feasible and robust to disturbances in the personnel demand. However, this robustness cannot be guaranteed by formulation (1)–(11), which may lead to higher labor costs due to inadequate staff planning.

5.   Case study

5.1.   Performance metrics

To evaluate the performance of the TSSO approach, its solutions are compared with the solutions obtained by the myopic approaches: zero multiskilling (ZM) and total multiskilling (TM). These comparisons are performed using the following metrics:

1) Percentage of multiskilled employees. Calculates the percentage of multiskilled employees in relation to the total number of hired employees.

2) Percentage of total multiskilling. Calculates the percentage of additional trained skills in relation to the theoretical maximum amount possible.

3) Total weekly cost. Sum of costs incurred in training and over/understaffing associated with any approach.

4) Weekly over/understaffing cost. Sum of costs incurred in over/understaffing associated with any approach.

5) Percentage savings associated with the total weekly over/understaffing cost. While ${\psi }_{ZM}$ is the weekly over/understaffing cost incurred when all employees are single-skilled, ${\psi }_{TM}$ is the weekly over/understaffing cost incurred when all employees are multiskilled and they can work in all store departments. Therefore, (${\psi }_{ZM}–{\psi }_{TM})$ represents the maximum possible savings in this cost when there is total multiskilling. Therefore, the savings of any approach is represented by:

6) Conditional value at risk (CVaR-95) on the weekly over/understaffing cost: CVaR, also called mean excess loss or expected shortfall, is a modified form of the VaR metric. In our case study, VaR-95% represents the worst possible weekly over/understaffing cost for 95% of demand scenarios. Thus, CVaR-95% represents an expected average cost, which is calculated for those demand scenarios whose cost exceeds the calculated VaR-95.

Note that, %ME and %TM measure multiskilling requirements, φ and $\psi$ calculate weekly costs incurred, %SSS is a measure of reliability, and CVaR-95 measures the risk associated with the solutions delivered by each approach.

5.2.   Data requirements

For a retail store in the Chilean context, we tested the mathematical formulation presented in Section 4. The real and simulated data used in this case study are described below.

5.2.1.   Real data

Data include information on: (ⅰ) store size, i.e., number of employees and departments; (ⅱ) number of single-skilled employees initially hired in each store department; (ⅲ) department in which each employee is initially trained; (ⅳ) labor contract characteristics; (ⅴ) average weekly demand in each store department; and (ⅵ) cost parameters. Similar to Henao et al. ^[4,6,7,21] and Porto et al. ^[11,23,50] we also assume a minimum training cost. Table 3 shows the values associated with these sets and parameters. Finally, note that in our case study, we consider that the deterministic personnel assignment problem is fully well-balanced. That is, the working hours available for allocation in any department, ($\left|{I}_{l}\right|h$), are equal to the value in hours of the average demand in that department (${\overline {r}}_{l}$).

5.2.2.   Simulated data

Datasets include information on the uncertain parameter of weekly demand in each department of the store. Two types of simulated data are considered: (ⅰ) In-sample data and (ⅱ) Out-of-sample data. In-sample data represent the data used to find the optimal solution for the first-stage variables of the TSSO approach. Out-of-sample data represent the data reserved from the sample to validate the performance of the TSSO approach and compare its solutions with the solutions of the myopic approaches. For both simulated datasets, we consider nine levels of variability (coefficients of variation, CV) in personnel demand:$CV = 5, \;10, \;20, \;30, \;40, \;50, \;60, \;70, \; 80{\%}$. Additionally, for both datasets, the realizations of stochastic demand for each store department are considered to follow a normal probability distribution. Guaranteeing that, in both datasets, negative demand values are not allowed. We highlight that, Henao et al. ^[6,7,21] and Porto et al. ^[11,23], articles with retail case studies, also used this same probability density function to evaluate the benefits of multiskilling but using a 2-chaining policy.

On the one hand, for the in-sample data, we use Monte Carlo simulation to randomly generate 1000 demand scenarios (i.e., |S| = 1000) for each department and CV. We carry out a data sample evaluation to identify the sample size of |S|. Consequently, we choose |S| = 1000 since around that value the TSSO solutions stabilized. Additionally, we are interested in measuring the level of conservatism in the solutions reported by the TSSO approach. Therefore, for the in-sample data, we generate two datasets using different types of truncations in the pdf associated with the personnel demand. The first dataset considers a truncation type more conservative and, consequently, the pdf was truncated at zero. This implies that, for high CVs, extreme values of demand (in both tails) can be generated more frequently. The second dataset considers a truncation type less conservative and, therefore, the pdf was truncated at 5th and 95th percentiles. That is, we consider 90% of the central data of the distribution, thus avoiding extreme values. Note that, we consider that a truncation type is more conservative when it allows a wider range in the possible realizations of the uncertain demand.

On the other hand, in the out-of-sample data and to simplify the analyses, we used a single type of truncation instead of two of them. Thus, for a pdf truncated at zero, we use Monte Carlo simulation to randomly generate 10000 demand scenarios for each department and CV.

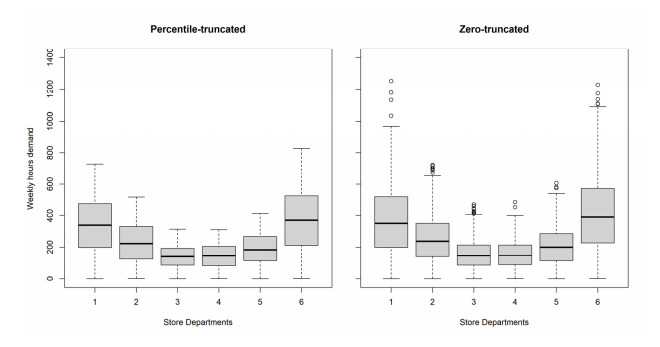
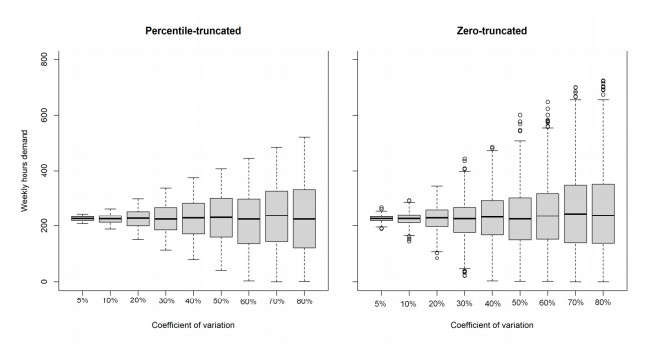
In Figures 2 and 3 we present boxplots to visualize the simulated data associated with the in-sample data.

For a CV = 80% across the six store departments, Figure 2 shows a comparison between the percentile-truncated and zero-truncated datasets. It is clearly observed that the values of the weekly demand realizations are more dispersed for the zero-truncated pdf. More specifically, the percentile-truncated pdf values range from 0 to 827 hours, while the zero-truncated pdf values range from 0 to 1252 hours. Also note that, the values of the average weekly demand in each department are those already reported in Table 3.

Additionally, Figure 3 shows for Department 2 and each CV, another comparison between the percentile-truncated and zero-truncated datasets. Recall that $\overline {{r}_{2}} = 225$ hours for Department 2. From the figure, it can be seen how as CV increases the range of weekly demand values expands. For example, for a percentile-truncated pdf, when CV = 5% the weekly demand values range from 207 to 243 hours, while when CV = 80% the weekly demand values range from 1 to 520 hours. It is also observed again how the values of the weekly demand realizations are more dispersed for the pdf truncated at zero. In fact, Figures 3 and 4 show the presence of outliers for the zero-truncated pdf. This is expected since the zero-truncated pdf considers a larger percentage of the data distribution.

6.   Results and discussion

In this section, we describe the computational experiments performed to evaluate the benefits of multiskilling under a k-chaining policy with $k\ge 2$. We also present the results obtained at different levels of demand variability along with some discussion of the case study. In Subsection 6.1, using the in-sample data, we present the multiskilling requirements reported by the TSSO approach. Recall that, the solution of the TSSO approach considers two in-sample datasets: Zero-truncated (TSSO-ZT) and Percentile-truncated (TSSO-PT). In Subsection 6.2, using the out-of-sample data, we analyze and compare in terms of cost, reliability, and risk, the solutions reported by the TSSO approach (TSSO-ZT and TSSO-PT) and the myopic approaches (ZM and TM).

6.1.   In-sample analysis

This section evaluates the performance of the TSSO approach proposed in Section 4.2. The model (12)–(22) was written in AMPL and run through Neos Server for 8 hours (restrictive) using the commercial software CPLEX. For all instances, we obtained optimality gaps of less than 0.05%. For the in-sample analysis, results and discussions are presented in the following three subsections: (ⅰ) Model characteristics, (ⅱ) How much multiskilling to add? and (ⅲ) How to add multiskilling?

6.1.1.   Model's characteristics

Table 4, for each CV, reports the characteristics of the TSSO-ZT, TSSO-PT, and Deterministic (DT) models. On the one hand, the computational times of the TSSO-ZT and TSSO-PT models (in hours) and the DT model (in seconds) are reported. On the other hand, the sizes of the models in terms of the number of constraints and variables are also reported. It is observed that, due to the difference in the size of the models, the solution times for the TSSO-ZT and TSSO-PT models are higher compared to the DT model. It is also noted that, given that personnel training decisions are considered tactical-strategic and made over medium and long-term planning horizons, the solution times for the TSSO-ZT and TSSO-PT models are acceptable.

6.1.2.   How much multiskilling to add?

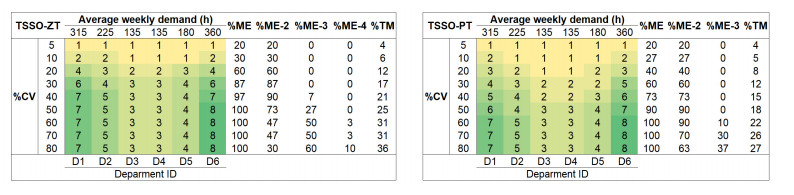
This subsection seeks an answer to the following tactical question: How many employees should be multiskilled and in how many additional departments? For the six departments and nine CVs, Figure 4 (in color) shows the optimal number of multiskilled employees required under the TSSO-ZT and TSSO-PT approaches. Metrics for the total percentage of multiskilled employees (%ME) and the percentage of total multiskilling (%TM) are also reported. Additionally, %ME-k metrics are reported. These metrics represent the percentage of multiskilled employees trained in ($k-1$) additional departments (in relation to the total number of hired employees), implying that they are employees trained in a total of $k$ departments. For example, the %ME-3 metric represents the percentage of multiskilled employees trained in two additional departments and, therefore, are employees trained in a total of three departments.

Figure 4 shows several noteworthy aspects. First, the number of multiskilled employees increases as the average demand for a department and its coefficient of variation increase. In turn, for the whole store, multiskilling requirements (%ME, %TM) are observed to increase as the %CV of demand also increases. Second, for both approaches (TSSO-ZT and TSSO-PT), if the level of demand variability is minimal (CV = 5%), only one multiskilled employee per department is required. This result can be interpreted as the minimum necessary investment in multiskilling (i.e., TM = 4% and ME = 20%). Third, for both approaches, if the level of demand variability is maximum (CV = 80%), all employees are required to be multiskilled (ME = 100%). In fact, for the TSSO-PT approach, if CV ≥ 60%, 100% of employees are required to be multiskilled. For its part, the TSSO-ZT approach requires 100% of employees to be multiskilled if CV ≥ 50%. This result is reasonable, as the TSSO-ZT approach considers a larger set of random realizations of demand. Consequently, the TSSO-ZT approach reports more conservative solutions than those reported by the TSSO-PT approach. In other words, the TSSO-ZT approach always reports the same or higher multiskilling requirements than the TSSO-PT approach.

Continuing with the analysis in Figure 4, a fourth noteworthy analysis is to determine for what levels of demand variability a k-chaining policy with $k\ge 2$ versus a 2-chaining policy is more cost-effective. On the one hand, for the TSSO-ZT approach it is observed that if CV ≤ 30%, multiskilled employees are trained in only one additional skill (i.e., a total of two departments). This indicates that for these levels of demand variability a 2-chaining policy is sufficient. For the TSSO-PT approach, it is observed that when CV ≤ 50% the 2-chaining policy is the most beneficial. On the other hand, under the TSSO-ZT approach, it is observed that for CV greater than 30%, multiskilled employees are required in one, two, and up to three additional departments. Similarly, under the TSSO-PT approach, CVs greater than 50% require multiskilled employees trained in one or up to two additional departments. These results show that for a high %CV in demand, a 2-chaining policy is not sufficient and, therefore, k-chaining policies with $k\ge 2$ are required to achieve the maximum benefit associated with multiskilling. A fifth noteworthy aspect is that, for both approaches, no CV required multiskilled employees trained in four or more additional departments (i.e., five or more departments in total). This indicates that k-chaining policies with $k = 2$, $k = 3$ and $k = 4$ values offer the most cost-effective results.

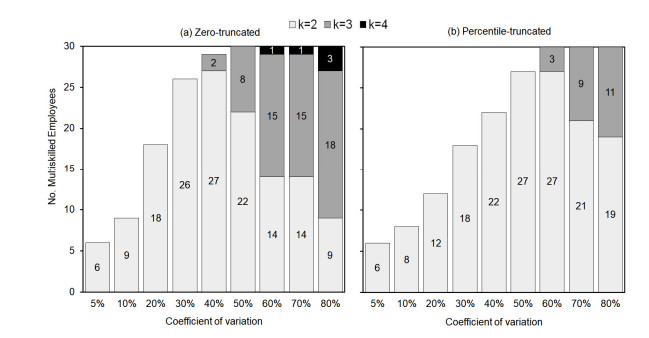
Finally, for both approaches and each CV, Figure 5 shows in detail the number of multiskilled employees in the store who are trained in a total of two, three, or four departments. Note that, under the TSSO-PT approach some employees were trained in a maximum of two additional departments, while under the TSSO-ZT approach some employees were trained in a maximum of three additional departments. Furthermore, in Figure 4 it was observed that under a TSSO-ZT approach, the benefits of using k-chaining policies with $k\ge 2$ are reflected earlier (i.e., in lower CVs) than observed under the TSSO-PT approach. This result is intuitive, since under the TSSO-PT approach extreme demand values are avoided and, therefore, its level of protection against demand uncertainty is lower than that provided by the TSSO-ZT approach.

6.1.3.   How to add multiskilling?

The objective of this subsection is to analyze the set of closed-chained multiskilling structures obtained using a TSSO approach and a k-chaining policy with $k\ge 2$. It seeks to answer the following two tactical questions: In which additional departments should each multiskilled employee be trained? and How many closed chains (CLC and/or CSC) will be formed and which departments should be linked in each of them?

As an example, Table 5 presents the set of closed-chained multiskilling structures obtained for a CV = 30% and the TSSO-ZT and TSSO-PT approaches. For each approach, the table shows the closed chains constructed, and what type they are (CLC or CSC).

In Table 5, under the TSSO-ZT approach, it is observed that six closed chains were constructed: two CLCs and four CSCs. For example, the closed short chain "D1-D6-D5-D1" means that an employee from Department 1 (D1) was trained in D6, an employee from D6 was trained in D5, and an employee from D5 was trained in D1. Under the TSSO-PT approach also six closed chains were built, in this case, one CLC and five CSCs. Although the number of chains constructed was the same, the TSSO-ZT approach required 26 additional trained skills, while the TSSO-PT approach required 18.

From Table 5, for the TSSO-ZT approach, it is also observed that the set of closed-chained multiskilling structures constructed, repeats training arcs such as: "D1-D2", "D1-D6", "D6-D5" and "D5-D1". Therefore, in light of a TSSO approach, it may be convenient to connect more than once, pairs of departments with large average demands. Recall that, in our case study (see Table 3), the departments with larger average demands are D1, D2, D5 and D6. This result is interesting, since in studies based on constructive heuristics to generate chaining such as those presented by Henao et al. ^[6] and Henao et al. ^[7], authors sought to maximize flexibility and, therefore, they recommended avoiding the repetition of training arcs.

6.2.   Out-of-sample analysis

This section evaluates and compares the performance of the training plans reported by the in-optimization approaches under uncertainty (TSSO-ZT and TSSO-PT) and myopic approaches (ZM and TM). Table 6, for each approach and %CV, shows performance metrics associated with in-sample and out-of-sample results. Columns 3, 4, 5, 6 and 7 show the multiskilling requirements reported in the in-sample analysis (i.e., %ME, %ME–2, %ME–3, %ME–4, %TM). Columns 8, 9, 10, and 11 report the metrics associated with the out-of-sample analysis. Note that these last metrics are calculated based on the 10000 random demand scenarios generated through Monte Carlo simulation. Column 8 reports the percentage savings in the average weekly cost of overstaffing/understaffing ($\%\overline {SSS}$). Column 9 presents the CVaR-95 risk metric. High values of this metric indicate that the reported multiskilling solution is weaker in the face of high-risk demand scenarios (i.e., scenarios associated with the 5% of the highest over/understaffing costs). Column 10 reports the average total weekly cost incurred ($\overline {\varphi }$). Column 11 presents the metric called Homogeneous Groups. This metric allows, using the Fisher's least significant difference (LSD) procedure, to compare and determine whether there are significant differences between the average total weekly costs incurred by the four approaches. With 95% confidence, approaches aligned with an "X" in the same subcolumn show no significant difference in the average total weekly cost, while those located in different subcolumns do differ significantly. In turn, those approaches aligned in subcolumn "1" are the least costly and, therefore, are the most cost-effective.

Table 6 shows several interesting results. First, for all CVs, the TSSO-ZT approach always delivers the lowest average total cost ($\overline {\varphi }$). Second, the ${\%}\overline{SSS}$ and CVaR-95 metrics allow us to evaluate and compare the reliability and risk of the solutions delivered by each approach. It is observed that, for each CV, the myopic approaches, ZM and TM, always deliver the minimum and maximum possible savings in the average weekly cost of over/understaffing (${\%}\overline{SSS}$), respectively. This result is intuitive, as TM represents the most reliable and conservative approach providing the maximum protection against uncertainty (i.e., %ME = %TM = ${\%}\overline{SSS}$ = 100%). While ZM represents the least reliable and conservative approach and, therefore, offers no protection against uncertain demand (i.e., %ME = %TM = ${\%}\overline{SSS}$ = 0%). This same result is also replicated by the CVar-95 metric for each CV, as the ZM and TM approaches always deliver the maximum and minimum value of that metric, respectively.

Third, for each CV the TSSO-ZT approach despite being less conservative than the TM approach, also obtains the maximum possible savings in the average weekly cost of over/understaffing (${\%}\overline{SSS}$ = 100). While the TSSO-PT approach obtains ${\%}\overline{SSS}$ values greater than or equal to 98%. In addition, note also that the TSSO-ZT and TSSO-PT approaches report CVaR values very close to those reported by the TM approach. These results show that, using the proposed TSSO approach under a k-chaining policy with $k\ge 2$, it is possible to reap 100% of the achievable potential benefits, but with a much lower investment in multiskilling than that required by a total-multiskilling policy. Fourth, for each CV, the metric called homogeneous groups shows that the TSSO-ZT and TSSO-PT approaches are the only ones that always belong to the least-cost group of approaches, which makes them the most cost-effective and attractive to decision-makers.

7.   Conclusions and future research

This study proposes to solve a personnel assignment problem with multiskilling and uncertain demand for the retail industry. Our work presents several contributions. First, to explicitly incorporate the uncertainty of personnel demand, we develop a two-stage stochastic optimization model to minimize the cost of training and the expected average cost of overstaffing/understaffing. Second, in a novel way, our mathematical formulation simultaneously models multiskilling as a decision variable and uses a k-chaining policy with $k\ge 2$. Third, through extensive computational analysis, we compare our TSSO approach with the myopic approaches ZM and TM, also, we evaluate the conservatism of the solutions reported by the TSSO approach using two types of truncations in the pdf associated with uncertain demand.

The methodology was applied for a retail store with multiple departments in a Chilean context. For the case study, using real and simulated data, we performed in-sample and out-of-sample analysis considering nine levels of demand variability. On the one hand, the in-sample analysis allowed us to answer two tactical questions associated with multiskilling: how much and how to add it? On the other hand, the out-of-sample analysis allowed us to evaluate and compare the reliability and level of risk associated with the solutions reported by the in-optimization approaches under uncertainty (TSSO-ZT and TSSO-PT) and the myopic approaches (ZM and TM).

Regarding the in-sample analysis, we highlight three interesting findings. First, the results showed that for low %CVs in demand a 2-chaining policy delivers the maximum benefit of multiskilling. However, for high %CVs in demand, a 2-chaining policy is not sufficient and, therefore, it is required to use k-chaining policies with $k\ge 2$ to achieve the maximum benefit. Additionally, it was evidenced that this threshold associated with %CV differs between the TSSO-ZT and TSSO-PT approaches. That is, for the TSSO-ZT approach a k-chaining policy with $k\ge 2$ is required when CV > 30%, while for the TSSO-PT approach this policy was required when CV > 50%. Second, for the TSSO-ZT and TSSO-PT approaches, the results showed that most of the multiskilled employees were trained in one or two additional departments, i.e., $k = 2$ and $k = 3$, respectively. Whereas, only for the TSSO-ZT approach, some multiskilled employees were trained in a maximum of three additional departments, i.e., $k = 4$. Considering that this study evaluated a store with 6 departments, this result shows that: (ⅰ) total multiskilling is unnecessary and (ⅱ) there are diminishing returns to scale when the number of additional trained skills increases. Third, it was observed that the sets of closed-chained multiskilling structures obtained showed a combination of CSCs of different lengths and CLCs. Furthermore, although it is desirable to have variety in the training arcs that make up the closed chains, we found that connecting pairs of departments with large average demands more than once is also cost-effective.

Regarding the out-of-sample analysis, the solutions of the myopic approaches, ZM and TM, represented respectively the minimum and maximum bound associated with the level of conservatism of the solutions. That is, theoretically, the TM approach represents the maximum protection against demand variability (i.e., total multiskilling), while the ZM approach offers no protection at all (i.e., zero multiskilling). However, with multiskilling investments much lower than those required by the TM approach, the TSSO-ZT and TSSO-PT approaches achieved respectively 100% and 98–100% of the feasible savings in the over/understaffing costs. In fact, for all %CV on demand, both approaches were always the most cost-effective and, therefore, the training plans built by those approaches represent the most attractive to implement for decision-makers.

As for future research, new studies could relax the following assumptions of our formulation: (1) Incorporate staffing decisions. (2) Model a heterogeneous workforce, such that the individual productivity of multiskilled employees may differ across departments where they are trained. (3) Evaluate a case study where the costs of overstaffing, understaffing, and training vary across store departments.

Acknowledgments

The authors thank Shift's colleagues for providing the real data used in this research. This research was supported by "Fundación para la Promoción de la Investigación y la Tecnología (FPIT)" under Grant 4.523.

Conflict of interest

The authors declare they have no financial interests. In addition, the authors have no conflicts of interest to declare that are relevant to the content of this article.