An OGI model for personalized estimation of glucose and insulin concentration in plasma

1.   Introduction

Type 1 diabetes is a chronic autoimmune disease that insulin production ceases because an autoimmune attack destroys the insulin-producing cells ($\beta$-cells) in the pancreas ^[1]. Insulin deficiency can induce high blood glucose (BG) and cause various complications (i.e., retinopathy, angiocardiopathy, and neuropathy). Generally, people with type 1 diabetes rely on exogenous insulin infusion to manage blood glucose levels. The time and amount of exogenous insulin infusion directly determine the controlling effectiveness of glucose level ^[2]. Given that the insulin demand always changes along with the changes of individual condition, it is difficult for patients to have appropriate and timely insulin infusion ^[3].

Recent technology advanced in the continuous glucose monitoring (CGM) ^[4,5] and insulin pump ^[6] has resulted in the development of artificial pancreas (AP) for diabetes care ^[7,8]. AP also refers to a closed-loop glucose regulation system that can offer glucose-responsive insulin delivery automatically, by integrating the CGM system and insulin pump ^[9,10].

At this stage, the most widely used CGMs are to measure interstitial glucose concentration ^[11]. It is worth noting that the decline of BG caused by insulin and the raise of BG caused by carbohydrate intake both occur in plasma. Obtaining the plasma glucose concentration (PGC) is helpful for AP to control glucose changes ^[12]. Similarly, given the safety and convenience, insulin pump normally infuses exogenous insulin in subcutaneous tissue ^[13]. Indeed, the infused insulin cannot be absorbed rapidly, remaining at the subcutaneous tissue before entering circulation ^[12], especially after insulin bolus. The amount of previously infused insulin that is present in plasma or the subcutaneous space, referred to as the insulin on board (IOB), must be quantified to prevent overdosing ^[14]. Therefore, it is necessary to estimate PIC and PGC from the sampled glucose and insulin infusion data in subcutaneous tissue ^[15].

Recognizing that (1) the inherent noise error of sensor and accuracy of mathematical models have a significant impact on the estimation accuracy, (2) the manual input of carbohydrate intake information can introduce another source of error from patient s inputs ^[16], filtering technology are adopted to estimate the hidden states ^[17] (i.e. the glucose and insulin concentration in plasma and the carbohydrate intake). For example, De Pereda et al. estimated the plasma insulin concentration by combining the classical Hovorka glucose-insulin dynamic model with extended Kalman filtering (EKF) ^[18]. Turksoy et al. detected the carbohydrate intake using unscented Kalman filtering (UKF), and the effectiveness was verified using the UVa/Padova simulation platform ^[19]. Charalampidis et al. introduced particle filter technology to the estimation of plasma glucose concentration for ICU subjects, overcoming the uncertainty from glucose measurement error ^[20]. Considering the individual variability, Hajizadeh et al. ^[21] estimated PIC by estimating the extended parameters related to insulin absorption based on UKF. While promising, the efforts reviewed above still face the challenges from the model parameter uncertainty due to the inter-individual variability. Specifically, since only part of the model parameters extendable to observable state variables can be identified dynamically ^[22], research to-date has mainly focused on personalizing part of the model parameters related to insulin absorption. The inter-individual variability presents in whole metabolism ^[23,24]. Although many models have been proposed and analyzed ^{[25,26,27,28]}, we contend that (1) there is a need to establish a glucose-insulin dynamic model of which the parameters and disturbances can be extended to observable variables; and (2) an appropriate Bayesian filtering estimator needs to be developed to personalize the parameters and disturbances.

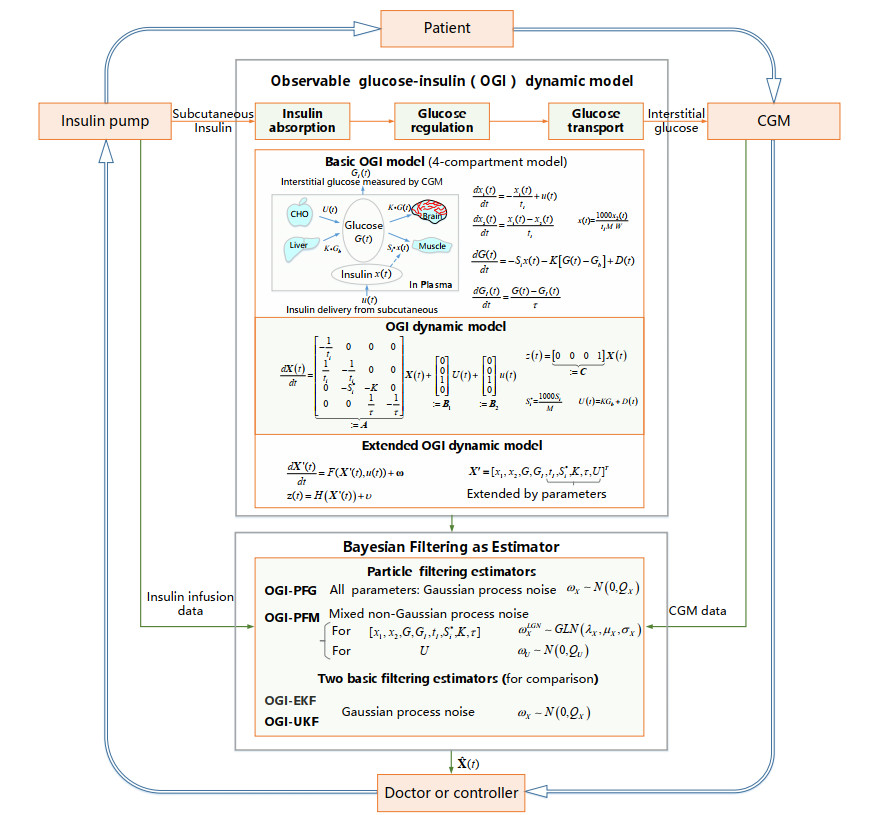
In this research, a new observable glucose-insulin (OGI) dynamic model is proposed. According to the physiological mechanism of glucose metabolism, the OGI model describes the integrated glycemic regulation with three processes: insulin absorption, glucose regulation and glucose transport. In the OGI model, the model parameters can be extended to the observable variables and mapped by CGM data. Next, the Bayesian filtering technology is implemented to personalize the model parameters and external disturbances for PIC and PGC estimation in real time. EKF and UKF are first explored. Since both the filtering techniques are built upon Gaussian propagation process ^[22], the applicability of these filters may be questionable given that some state variables are non-negative due to the physiological constraints. In view of this, an emerging filtering technology, particle filtering (PF) ^[29] is introduced. PF obtains numerical results by Monte Carlo simulation, having advantages in dealing with nonlinear engineering problems and non-Gaussian assumption ^[30,31]. In this study, the applicability of PF and its extensions to OGI is investigated comparing to EKF and UFK.

The rest of this paper is organized as follows. In Section 2, the observable glucose-insulin (OGI) dynamic model is developed and the observability of OGI dynamic model is verified. In section 3, four Bayesian filtering estimators, based on EKF, UKF, the PF with Gaussian noises (PFG), and the PF with mixed non-Gaussian noises (PFM), are designed to estimate the extended state variables (i.e. the model parameters and external disturbances) dynamically and to estimate the plasma glucose and insulin concentration in real time. Section 4 introduces the experiment for validation. The results and discussions are illustrated in section 5 and 6. The conclusion is drawn in section 7.

2.   Modelling

2.1.   Basic OGI model

As seen in Figure 1, basic OGI model considers three processes: (1) the insulin absorption from subcutaneous infusion to plasma, (2) the glucose regulation under the influence of PIC and external disturbance, and (3) the glucose transport from plasma to the subcutaneous interstitial, where the glucose concentration can be measured by CGM.

2.1.1.   Insulin absorption

The insulin absorption sub-model describes the insulin absorption process from subcutaneous infusion to plasma. As given by ^[23], a two-compartment model is established to describe this process:

where $u(t)$ represents the exogenous insulin delivery rate(U/min, 1U/min = 1/60 U/h) at time t (immediate insulin bolus is modeled as a short burst insulin infusion), ${{x}_{1}}(t)$ and ${{x}_{2}}(t)$ represent the amount of effective insulin in the first and second insulin absorption compartment respectively (U), $x(t)$ is the plasma insulin concentration (PIC) (mU/L), the number 1000 is derived from the unit conversion (1 U/L = 1000 mU/L), ${{t}_{I}}$ is the time-to-maximum of effective insulin concentration (min), $M$ is the metabolic clearance rate (L/kg/min) of effective insulin, and $W$ is the measured body weight (kg).

2.1.2.   Glucose regulation

The glucose regulation sub-model describes the kinetics of PGC regulation. Similar to the Bergman model ^[32,33], this regulation is described by a single-compartment model, where the rate of PGC changes equals the production of glucose minus the consumption of glucose. As shown in Figure 1, the glucose production involves the endogenous glucose production (by liver) and the digestion of carbohydrate. The glucose consumption involves the consumption independent of insulin (by brain), and the consumption stimulated by insulin (by the liver and muscles). Here, supported by ^[23,34,35], it is assumed that the insulin-dependent glucose utilization does not depend on PGC. That is

where $G(t)$ is the PGC (mmol/L), ${{S}_{i}}$ is the effect of insulin sensitivity (mmol/L/min per mU/L), ${{G}_{b}}$ is the basal glucose level (mmol/L) and $K$ is the glucose self-regulation fractional rate (min$^{-1}$) which has an effect of glucose self-regulation towards ${{G}_{b}}$. $D(t)$ is a lumped signal to describe the external disturbance to glucose changes, such as carbohydrate intake and exercise (mmol/L/min).

2.1.3.   Glucose transport

The CGM measures the glucose level in interstitial fluid. Lumping the dynamics introduced by the CGM systems, the plasma glucose converts into interstitial glucose across a concentration gradient with time lag $\tau$ (min). The interstitial glucose concentration is given as

where ${G_I}(t)$ is the interstitial glucose concentration which can be measured by CGM (mmol/L).

2.2.   Observable Glucose-insulin dynamic model

The inter-individual variability induces the variability of model parameters, named parameter uncertainty, which has a direct effect on PIG and PGC estimation. To identify parameters by filtering techniques, the model parameters should be are extendable to observable state variables, as discussed in ^[18].

It is the purpose of this study to achieve a deeper personalization, not limited to personalize the parameters related to insulin absorption. We merged and simplified the parameters to form an OGI dynamic model. To summarize, the OGI dynamic model can be expressed as

where $\mathit{\boldsymbol{X}} = [x_1, x_2, G, G_I]^T$. The $U(t)$ represents the compound uncertainty of the system, composed by ${K}, {G_b}$ and ${D(t)}$, $U(t) = {K}{G_b}+{D(t)}$. $S_i^* = \frac{1000S_i}{M}$ represents a parameter related to insulin sensitivity. $z(t)$ is the measurable output of system (interstitial glucose concentration $G_I(t)$).

On this basis, the parameters $[{{t}_{I}}$, ${{S}_{i}^*}$, $K$, $\tau]$ and compound uncertainty $U$ are generally regarded as the extended variables, $\frac{{d\theta}}{{dt}} = 0$, $\theta\in\mathit{\boldsymbol{\theta}}$, $\mathit{\boldsymbol{\theta = }}[{{t}_{I}}$, ${{S}_{i}^*}$, $K$, $\tau$, $U]$. Here, the extended OGI dynamic model can be formed as:

where $\mathit{\boldsymbol{X'}}$ is the vector of state variables, $\mathit{\boldsymbol{X'}}$ = [${x}_{1}$, ${{x}_{2}}$, $G$, ${G_I}$, ${{t}_{I}}$, ${{S}_{i}^*}$, $K$, $\tau$, $U$]$^T$.

To construct the estimator (observer), observability ensures that the state variable can be observed and estimated ^[22], i.e., the state variable $\mathit{\boldsymbol{X'}}(t)$ can be uniquely mapped to the output $z(t)$.

For a nonlinear system, the proof of observability is usually performed by calculating the observability matrix derived from the chain of Lie derivatives ^[36,37]. The observability matrix of nonlinear system is

where $n$ is the order of the system, $L_{{F}}^{k}[H\left(\mathit{\boldsymbol{X'}}(t)\right)] = \frac{\partial }{\partial \mathit{\boldsymbol{X'}}}$ $L_{{F}}^{k-1}[$ $H\left(\mathit{\boldsymbol{X'}}(t)\right)]F$, and $L_{{F}}^{0}\left[H\left(\mathit{\boldsymbol{X'}}(t)\right)\right] = H\left(\mathit{\boldsymbol{X'}}(t)\right)$. For the extended OGI dynamic model, the rank of observability matrix is $Rank(\mathit{\boldsymbol{\psi}}(t))$ $= 9$, and it is concluded that all the state variables are observable. That is, all the state variables [${{x}_{1}}$, ${{x}_{2}}$, $G$, ${G_I}$, ${{t}_{I}}$, ${{S}_{i}^*}$, $K$, $\tau$, $U$] can be estimated from glucose measurement.

Since the CGM data are sampled discretely, a discrete OGI dynamic model is rewritten using the first forward difference derivative approximation. To be consistent with practice, unmodeled dynamics is introduced (refer to process noise). Besides, considering the parameter uncertainty, the extended states are also incorporated in process noise ^[21]. To characterize the uncertainty of glucose measurement, the measurement noise is added. The discrete OGI dynamic model is

where $T$ is the sampling period. $\mathit{\boldsymbol{\omega}}$ represents the process noise vector, $\mathit{\boldsymbol{\omega}}$ = $[{\omega}_{x1}$, ${\omega}_{x2}$, ${\omega}_{G}$, ${\omega}_{G_I}$, ${\omega}_{t_I}$, ${{\omega}_{S_i^*}}$, ${{\omega}_{K}}$, ${\omega}_{\tau}$, ${\omega}_{U}]^{T}$, and $\upsilon$ represents the measurement noise.

3.   Bayesian filtering as estimator

Bayesian filtering technology incorporates the Bayesian inference with first-order hidden Markov process ^[38]. The posterior distributions of the state variables are recursively conditioned on sensor information collected up till the present moment. Based on the Bayesian inference, the posterior distribution ${{\mathit{\boldsymbol{X}}}_{k}}$ can be obtained by

where $p\left({{z}_{k}}|{{\mathit{\boldsymbol{X}}}_{k}} \right)$ is the likelihood probability at the $k^{th}$ sampling time, $p\left({{\mathit{\boldsymbol{X}}}_{k}}|{{z}_{1:k-1}} \right)$ represents the prediction-step probability determined by the previous results $p\left({{\mathit{\boldsymbol{X}}}_{k-1}}|{{z}_{1:k-1}} \right)$, that is

Differing in the specific way to update $p\left({{\mathit{\boldsymbol{X}}}_{k}}|{{z}_{1:k}} \right)$ and $p\left({{\mathit{\boldsymbol{X}}}_{k}}|{{z}_{1:k-1}} \right)$, four filtering estimators are designed in the following parts, including extended Kalman filtering (EKF), unscented Kalman filtering (UKF), particle filtering with Gaussian noises (PFG), and PF with mixed non-Gaussian noises (PFM). The EKF and UKF are developed for comparison with PF.

3.1.   EKF and UKF

EKF and UKF are based on the Kalman filtering principle. Both of them adopt the Gaussian propagation to obtain the posterior solution, i.e., the process noise and measurement noise are assumed to be Gaussian ^[22] ($\mathit{\boldsymbol{\omega}}\sim N\left(0, \mathit{\boldsymbol{Q}}\right)$ and $\upsilon \sim N\left(0, R \right)$). In EKF, the nonlinear model is approximated with first-order Taylor expansion at the last estimated point, then the standard Kalman filtering formulas are used to calculate the posterior distribution ^[18]. The details of the EKF algorithm are given in Appendix. In UKF, unscented transformation (UT) is adopted. It uses a deterministic sampling approach to estimate the mean and covariance of variables with a minimal set of sample points, also called sigma points ^[39]. These sigma points are propagated through the true nonlinear system, meanwhile the weighted mean and the covariance are calculated. The details of the UKF algorithm are given in Appendix. The determination of the noise covariance matrix in EKF and UKF is given in section 4.

3.2.   Particle filtering technology

3.2.1.   PFG-particle filtering for Gaussian noise

Particle filtering (PF) approximates the posterior distribution of state variables based on Monte Carlo statistical method ^[31]. For each $X\in\mathit{\boldsymbol{X}}$, the probability $p\left({{X}_{k}}|{{z}_{1:k}} \right)$ can be approximated by $N$ random particles $X_{k}^{\left(i\right)}$ and their associated weights ${{W}_{X}}_{k}^{\left(i\right)}$ in a weighted summation, such as

As the measured data are updated, the weights are adjusted in real time. In each update step, sequential importance sampling (SIS) is incorporated to achieve the iteration ^[31]. The weight of the $i^{th}$ particle at the $k^{th}$ step can be calculated by

where ${{W}_{X}}_{k-1}^{i}$ is the weight of the ${{i}^{th}}$ particle at the last step, $p\left({{z}_{k}}|X_{k}^{i} \right)$ is the likelihood probability related to the measurement function and measurement noise $\upsilon$, $p\left(X_{k}^{i}|X_{k-1}^{i} \right)$ is the prior probability related to the state transition function and process noise ${\omega}_{X}$, ${\omega }_{X}\in\mathit{\boldsymbol{\omega}}$, $q\left(X_{k}^{i}|X_{k-1}^{i}, {{z}_{k}}\right)$ is the sampling probability related to the distribution of particle samples. Generally, the particles are sampled from the prior distribution, and the weight of the ${{i}^{th}}$ sampled particle is

Nevertheless, the particles tend to degenerate in the recursive estimation, and few particles survive if the case comes to the worst. In view of this, a resampling procedure is conducted in regions of higher sampling importance ^[40]. In other words, particles with higher probabilities generate more new particles.

For a fair comparison, Gaussian noise is taken in PF, i.e., $\mathit{\boldsymbol{\omega}}\sim N\left(0, \mathit{\boldsymbol{Q}}\right)$ and $\upsilon \sim N\left(0, R \right)$. This filtering is termed PFG (the details of PFG algorithm is given in Appendix).

3.2.2.   PFM - particle filtering for mixed non-Gaussian noise

The state variables [${{x}_{1}}$, ${{x}_{2}}$, $G$, ${G_I}$, ${{t}_{I}}$, ${{S}_{i}^*}$, $K$, $\tau$, $U$] consist of (1) the state variables with non-negativity constraint, that is, $[{{x}_{1}}, {{x}_{2}}, G, {G_I}]$, which are transformed from glycemic model variables, and the state variables [${{t}_{I}}$, ${{S}_{i}^*}$, $K$, $\tau$], which are extended from model parameters with non-negative physiological meaning; (2) the compound uncertainty $U$ can be either positive or negative (specifically, positive $D$ indicates the glycemic effect induced by carbohydrate disturbance, while negative $D$ indicates the hypoglycemic effect induced by exercise disturbance).

As for the state variables with non-negativity constraint, [${{x}_{1}}$, ${{x}_{2}}$, $G$, ${G_I}$, ${{t}_{I}}$, ${{S}_{i}^*}$, $K$, $\tau$], the shifted log-normal distribution ^[41] with three parameters is introduced to model the process noise to ensure the non-negativity of state variables. For each process noise of the non-negative state variable $\omega _{X}^{GLN}$, it is assumed $\omega _{X}^{GLN}\sim GLN({{\lambda }_{X}}, {{\mu }_{X}}, {{\sigma }_{X}})$ with PDF

where ${{\lambda }_{X}}$ is the position parameter, ${{\mu }_{X}}$ is the shape parameter, and ${{\sigma }_{X}}$ is the scale parameter. The position parameter ${{\lambda }_{X}}$ shifts the log-normal distribution along X-axis to ensure that the expectation of process noise is 0. Thus, log-normal distribution is chosen as the prior distribution of each non-negativity parameter, just like the assumptions in ^[23]. Specifically, the hyper-parameters $\lambda _{X}^{k}$, $\mu _{X}^{k}$, $\sigma _{X}^{k}$ at the ${{k}^{th}}$ step can be derived as

As for the compound uncertainty $U$, without the limitation of non-negativity, its process noise is still set to Gaussian. This filtering mixed non-Gaussian noise is termed PFM (the details of PFM algorithm is given in Appendix).

4.   Experiments

The objective of this study is to develop an observable glucose-insulin model of which the parameters can be personalized, to estimate plasma glucose concentration (PGC) and plasma insulin concentration (PIC) dynamically. Taking a progressive research approach, three sets of experiments are conducted: (1) Experiment I is to prove that the proposed model has the ability to estimate PIC and PGC. (2) Built upon the success from the first experiment, Experiment II is to validate the capability of our model in identifying physiological parameters, in this study, 4 parameters, [${{t}_{I}}$, ${{S}_{i}^*}$, $K$, $\tau$]. Considering the difficulty to continuously monitor PIC and PGC values on human participants, 30 in-silico subjects with type 1 diabetes produced by UVa/Padova simulator ^[42] are used both in Experiment I and Experiment II. Other than the 4 physiological parameters, we have a compound uncertainty parameter $U$, related to the disturbance, in the OGI model. (3) Since $U$ is a time-varying parameter changed in responding to meal intakes, we design Experiment III to demonstrate that parameter $U$ is identifiable as an indicator for meal identification. Recognizing that the meal intake of in-silico subjects only have intra-day variability, not inter-day variability, we have extended Experiment III to include 10 human subjects.

The UVa/Padova simulator is a substitute for preclinical testing in diabetes care accepted by FDA (Food and Drug Administration) ^[43]. The model embedded in UVa/Padova simulator is different from the OGI model, which consists of 12 nonlinear differential equations, 18 algebraic equations and 35 parameters ^[42]. In general, this model is not usable for the quantification of specific metabolic relationships, but is suitable for system simulation ^[44,45]. It contains 30 in-silico subjects (10 adults, 10 adolescents, 10 children), having been widely used in glycemic modeling and simulation ^[46,47,48]. In the UVa/Padova simulator, a simulation scenario was developed. The experimental duration was set to one week (7 days), and the insulin injection rate of each subject was set to the default value, determined automatically by the simulator in terms of the subject's basal injection rate and the specific ratio of carbohydrate to insulin. The schedule of daily carbohydrate intake is given in Table 1. In total, 1050 meals were produced in the experiment.

This study was approved by the institutional review boards (IRB), and all the participants signed informed consent forms prior to participation. The study was based on the group of 10 participants with type 1 diabetes (see Table 2 for details). This dataset was used in ^[24]. The insulin and glucose data of each participant were monitored over one week. All the participants used insulin pumps (MiniMed 712, Medtronic) for insulin Lispro infusion, and they did not take any drugs other than exogenous insulin infusion. The experiment of human subjects is an ambulatory study where subjects who are already insulin pump users participated, came in to get a CGM, then went home to carry on with their life. The daily routines and carbohydrate intakes of subjects are online reported to respective physicians in real time via the Internet. Taking meal intake as an example, the types, weights, and cooking methods of the ingredients for each meal were reported to their physicians, and then carbohydrate intake was calculated by the hospital's nutritionist. A total of 206 meals were recorded, and the glucose data were sampled every 15 min by the glucose sensor, FreeStyle Libre CGM system (Abbott Diabetes Care). The injection time and doses of insulin were recorded by the insulin pump. The timestep of updating model is 15 min ($T$ = 15min).

In this study, the variances of state variables were heuristically adopted to $\mathit{\boldsymbol{Q}}$ = $diag[10^{-2}, 10^{-2}$, $1$, $1$, $10^{-6}$, $10^{-6}$, $10^{-6}$, $1$, $1]$. The variance of measurement noise was set to $R = 0.45$ ^[18]. The initial state variables $[x_1, x_2, G, G_I]$ were set $[u_1\cdot{t_I}, u_1\cdot{t_I}, {z_1}, {z_1}]$, where ${{u}_{1}}$ was the first value of insulin delivery rate (IDR) data and ${{z}_{1}}$ was the first value of CGM data. The initial values of $[{{t}_{I}}$, $K]$, were set as $[42$, $0.004]$ according to the population values in ^[23]. The initial values of ${{S}_{i}^*}$ is 294, calculated by $S_i^* = \frac{1000S_i}{M}$, where initial value of $S_i$ is 0.005 ^[23]. The initial value of $\tau$ was set to 16 min ^[17]. The number of particles in PFG and PFM was set to 1000 after balancing the relationship between the accuracy and the amount of calculation (details please see appendix). It is worth noting that the sensor noise produced by UVa/Padova simulator is close to that in real CGM (FreeStyle Libre, Abbott Diabetes Care), which is complex ^[49]. For simplicity, this noise is usually considered to be Gaussian approximately, such as in ^[39] and ^[46].

To evaluate the performances of OGI model on estimating PGC and PIC, root mean square error (RMSE) is used to measure the accuracy:

One of the outputs is the estimated $U$, which can be used to identify the state of carbohydrate disturbances ^[46,47]. Similar to ^[16], the CGM data, the forward difference of disturbance ${{D}_{U}}(k)$, and previous identification results are used to identify a new carbohydrate intake. Specifically, an active identification of new carbohydrate intake, three conditions must be met at the same time: (1) ${{D}_{U}}(k)$ exceeds the threshold two times successively; (2) measured CGM data goes beyond a threshold (5.56 mmol/L ^[47]); (3) it has been more than 120 minutes since the last active identification. The indicator 'Flag' takes 1 when carbohydrate intake is identified, otherwise it takes 0. The specific formula of 'Flag' can be given as:

Here the ability to identify carbohydrate disturbance within two hours is also evaluated.

For each carbohydrate disturbance, the 120 min counted from the beginning of the meal is defined as an identification test window $T_{carbo}$, as defined in literature ^[16,47]. The definitions of true-positive (TP) event, false-negative (FN), false-positive (FP) event, and true-negative (TN) event are given below.

On this basis, four metrics: accuracy rate (AR), precision rate (PR), false-positive rate (FPR) and recall rate (RR) are derived as:

5.   Results

The performances of OGI model on estimating PGC, PIC and physiological states are evaluated with four Bayesian filtering estimators: EKF, UKF, PFG, and PFM.

5.1.   Experiment I: PIC and PGC estimation

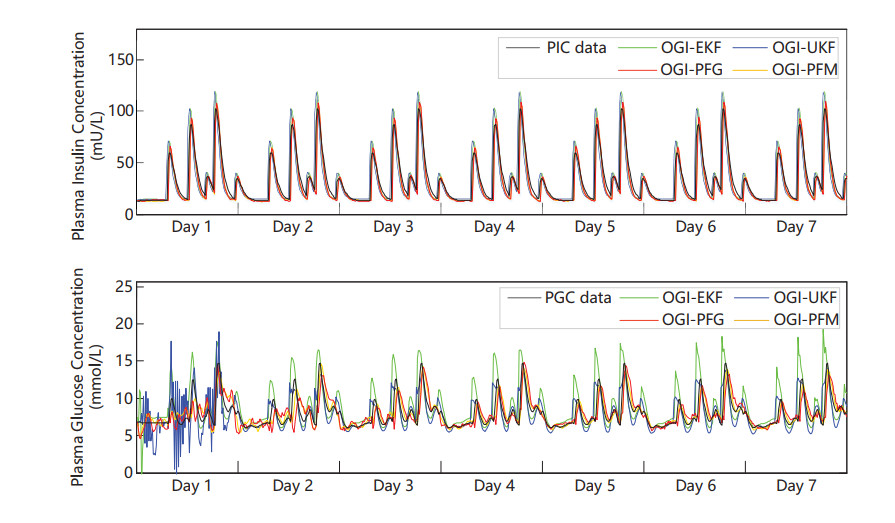
Figure 2 shows an example of PIC and PGC estimation for an in-silico subject based on OGI-EKF, OGI-UKF, OGI-PFG, and OGI-PGM respectively. As seen, the results show that the OGI model can estimate the insulin and glucose concentration in plasma with any one type of Bayesian filtering estimator.

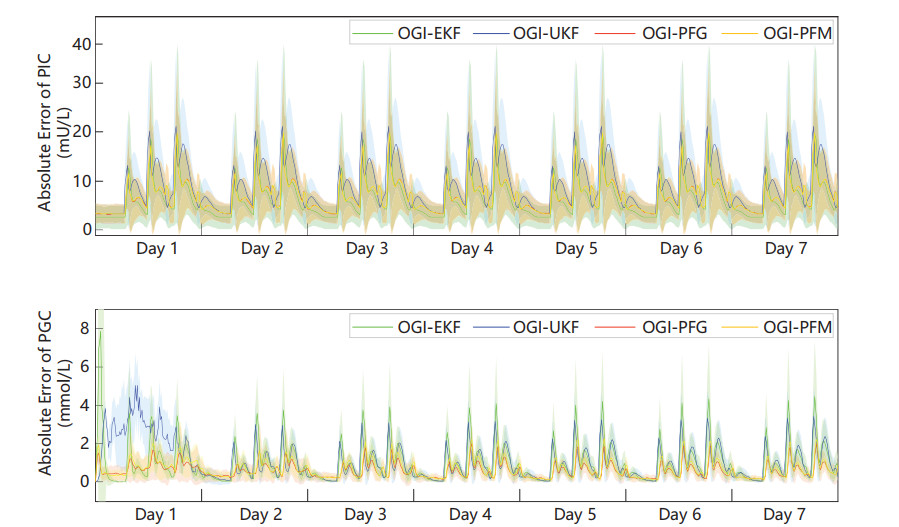
To quantify the performances, Figure 3 illustrates the absolute errors of different Bayesian filtering estimators on PGC and PIG estimation for all in-silico subjects. The top figure shows the absolute errors of PIC estimation. It is observed that the absolute errors of OGI model stay lower than 20 mU/L for all four estimators. The error profiles of OGI-PFG and OGI-PFM are fairly close to each other, and both are under OGI-EKF and OGI-UKF. The bottom figure illustrates the estimation results of PGC. It is worth noting that similar to the results in ^[50], the absolute errors in the first few days are larger than those of the other days, especially for OGI-EKF and OGI-UKF. This is because the state variables require a period of training time to converge. Besides, the errors of estimated PIC and PGC appear periodic changes. For PGC estimation, OGI-EKF and OGI-UKF have larger absolute errors than OGI-PFG and OGI-PFM. The results confirm the advantages of PF technology (PFG and PFM) for PIC and PGC estimation.

For different groups of in-silico subjects (adults, adolescents, and children), the RMSEs of estimated PGC and PIC on each age group are given in Table 3. The results of each group are not only confirmed the advantages of PFG and PFM for the estimation again, but also interestingly found that OGI model performs better for the adult group.

5.2.   Experiment II: Identifying physiological parameters

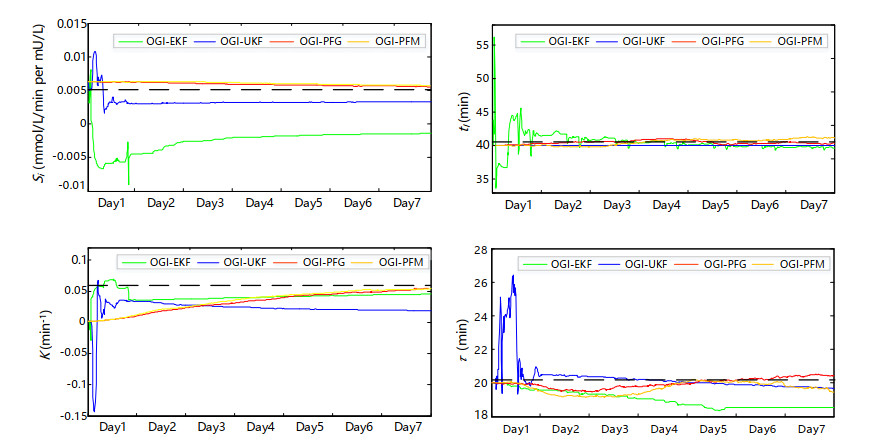
Due to the difference in model structure, the parameters in UVa/Padova simulator are different from those in OGI model. As human subject based study, obtaining the ground truth from in-silico subjects is challenging. Instead of providing ground truth as a prior, we decide to take a sensitivity analysis approach, that is, we interrogate the model performances on the data generated by giving parameter settings. A glucose dataset is generated by giving model parameters, meal intake and insulin delivery data. Glucose data and insulin delivery data, as the input, are used to estimate parameters. An example of parameter evolution over 7 days is shown in Figure 4. The black dashed line is the true value of the parameter.

It can be seen that the estimated values converge to the true values, especially after the warm-up period. Although the changes of all parameters estimations under the four filters are smoothed over time, it is observed that the results from OGI-UKF and OGI-EKF fluctuate greatly in the early stage, especially on the first day due to the warm-up period. This phenomenon is consistent with the results in ^[50]. In contrast, the performance of OGI-PFG and OGI-PFM in this warm-up period is more stable.

The parameter estimations for in-silico subjects with mean and standard deviation are shown in Table 4. The results are average estimation across 30 in-silico subjects throughout 7 days.

The parameter estimations for in-silico subjects with population mean and standard deviation are shown in Table 4. It is worth noting that the in-silico subject are closer to the real environment, the nonlinearity and uncertainty are stronger, and the performances of different filters have remarkable differences. This further reflects the advantages of the designed particle filter.

5.3.   Experiment III: Identifying carbohydrate disturbance

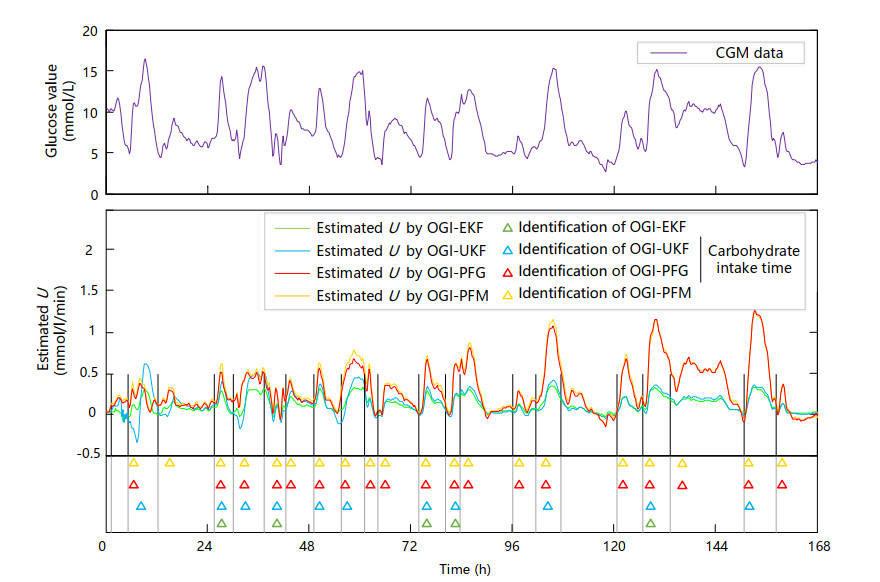
In this experiment, given that meal intake can be known as a ground truth, we decide to use this information to demonstrate that the parameter $U$ can be identified and has potential in real-world application such as meal identification. As for the performances of OGI model with different estimators on identifying compound uncertainty $U$, an example of meal identification from a human subject is illustrated in Table 5 and Figure 5 (the meal times and sizes of the subject are summarized in the table and identification results are shown in the figure). The top figure shows the glucose level given by CGM, while the bottom figure illustrates the estimated $U$ and the identification results of carbohydrate disturbances.

As seen, OGI-PFG and OGI-PFM are able to identify most of the carbohydrate disturbances. The performances on meal identification for all the subjects, including the in-silico and human participants, are shown in Table 6 (with the threshold heuristically set to 0.1 mmol/L/min). It shows that the performances from OGI-PFG and OGI-PFM are similar which outperform OGI-EFK and OGI-UKF. The OGI-PFM shows the daily ability with AR $95.46\%\pm0.65\%$, PR $68.89\%\pm3.57\%$, FPR $31.11\%\pm3.57\%$, and RR $71.90\%\pm3.72\%$.

6.   Discussion

It is a benefit for a fully automatic AP system to estimate the PGC and PIC based on the collected CGM and IDR data. However, the inter-individual variability limits the accuracy of estimation, because they increase the uncertainty of model parameters from the mathematical perspective. To solve this problem, it is feasible to extend the uncertainty parameters into state variables and estimate them based on Bayesian filtering estimator. But this method can be adopted only if the extended variables are completely observable. This research proposes an observable glucose-insulin (OGI) model in which the model parameters and environment disturbance can be extended to state variables and the observability of the extended system is proved. On this basis, four Bayesian filtering estimators (EKF, UKF, PFG, and PFM) are designed to estimate all the state variables and the PGC and PIC.

It is observed from the experiment of in-silico subjects that the proposed model has high accuracy in PIC and PGC estimation (Figure 2 and Figure 3), and the OGI-PFM outperforms other estimators in most cases. According to the results of different groups, it is found that the OGI model tends to perform better for the older subjects (Table 3). Based on the estimation of physiological states, the OGI model has the potential in identifying parameters and disturbance (Figure 4, Figure 5, Table 4 and Table 6).

In looking at the estimators, the EKF is less effective than the UKF in PIC estimation, which is consistent with the results in ^[21]. An interesting observation is that PF (PFG, PFM) has better performances than EKF and UKF indicating the promises of PF based estimator, which is not consistent with the conclusion drawn from ^[39]. This may be because when more model parameters are extended to state variables, the nonlinearity of the model is further enhanced. In this case, the advantages of PF in dealing with nonlinear systems are fully utilized. Comparing PFG vs. PFM, while PFM has the best performance among the four, it is surprising that the outperformance of PFM over PFG is marginal. It is contended that this may be due to the limited dataset where the mixed noises are not apparent. This discovery indeed points out the immediate future effort which is to collect PIC and PGC data from human participants, to conduct the validation on the larger dataset, and to explore the influence of other noise distributions on the estimation.

Although PFG and PFM have better performance in estimating PIC and PGC, PFG and PFM rely on powerful computing power. The simulation is implemented in the computer (Intel(R) Core i9-9900 K 2-Core 3.60 GHz processor). It is worth noting that in real application scenarios, these are not high-performance computation devices but embedded devices with significant constraints in processing power, memory, and power usage. Therefore, it is essential to develop a low-computational and low-power mode in future work, as discussed in ^[51]. For example, if the computational cost needs to be reduced due to the limitation of computing power and a little accuracy is allowed to be sacrificed, some parameters with low sensitivity can be fixed.

To the best of our knowledge, research to date has mainly focused on PIC estimation, in which the variability of insulin absorption parameters was focused. Few works of literature discussed the estimation accuracy of PGC. Thus, OGI is compared with the models from the literature on PIC estimations only. Since the objective of the study in ^[21] aligns with our study, the comparison of our proposed OGI model with the methods in ^[21] is conducted using our dataset. As seen in Table 7, using the method mentioned in ^[21], the RMSEs of PIC estimation enhanced by EKF and UKF are 16.64 mU/L and 13.28 mU/L respectively, which is larger than that conducted by OGI-PFM 9.49 mU/L. It can be concluded that OGI-PFM has better performances on our dataset.

In parameter identification, two types of parameters are involved in the model, physiological parameters [$t_I$, $S_i^*$, $K$, $\tau$] and parameter of compound uncertainty $U$. Given that (1) in the experiment on in-silico subjects produced by the UVa/Padova simulator, physiological parameters are fixed as in ^[16,46]; (2) in human subjects, although the physiological parameters changes all the time, the specific changes of these parameters cannot be continuously monitored, the ability to dynamically identify variable parameters needs to be verified in future work. Nevertheless, since (1) meal intake can induce the $U$ changes; (2) the time and size of meal intake can be set in UVa/Padova Simulator and are also recorded in the experiment of human subject, meal identification is developed to be an application to show the ability to dynamically identify the parameter $U$. Please note that the focus of this study is to develop a complete observable model. Meal identification is just a preliminary attempt to show the potential of identifying the parameter impacted by external disturbance (carbohydrate intake). It is the author's future work to improve meal identification based on estimated $U$, such as adding post-processing and choosing an appropriate threshold. Developing a fast and effective way to detect meal intake is worthy of further research.

When the cannula site is no longer absorbing the insulin effectively or even occlusion, the insulin delivery rate displayed in the insulin pump cannot achieve the desired hypoglycemic effect. It is guessed that the parameters which have positive effects on rising glucose level may be overestimated, such as $[t_I, U]$, while the parameters which have negative effects may be underestimated, such as $S_i$. This may also bring new challenges to meal identification. Exploring the performance of the proposed method in facing such faults is very valuable. Taking fault diagnosis as an example, it may be warning that the cannula site is no longer absorbing the insulin effectively or even occlusion, when the parameter $t_I$ is overestimated (exceeding a certain threshold). In addition, it is also worth exploring how to ensure the robustness of the system in the case of sensor data loss.

7.   Conclusion

In this study, an OGI dynamic model is proposed for personalized estimation of PIC and PGC based on CGM and IDR data. The OGI model, which describes the dynamics of glucose and insulin changes, takes full account of the parameter uncertainty caused by inter-individual variability. To deal with the uncertainty, the OGI model is extended to a non-parametric dynamic model, of which all the state variables, including the original ones and those extended from the model parameters, are observable. On this basis, four types of Bayesian filtering estimators are designed to estimate the state variables, including EKF, UKF, PFG, and PFM. For EKF, UKF and PFG, the Gaussian assumption is adopted, but considering the non-negativity of some state variables, PFM explores the non-Gaussian characteristic of process noise and assuming it to be subjected to a distribution mixed of Gaussian and shifted log-normal distribution. Tested by the in-silico experiment, OGI-PFG and OGI-PFM show better abilities to estimate PIC and PGC than OGI-EKF and OGI-UKF. Especially, the OGI-PFM has a particularly promising performance (RMSE of PIC estimation: $9.49\pm3.81$ mU/L, RMSE of PGC estimation: $0.89\pm0.19$ mmol/L). It also indicates that particle filter has advantages in personalizing the parameters and disturbances. It is also found that compared with the influence from filtering types, the distribution of noise has much less influence on the estimation performances. Moreover, the personalized estimations of PIC and PGC for clinic application remains to be verified.

Acknowledgments

The authors acknowledge funding support from Beijing Advanced Innovation Center for Big Data-based Precision Medicine. Authors also recognize support by Department of Endocrinology, Xuanwu Hospital Capital Medical University, China, for clinical suggestions, and efforts by Department of Endocrinology, The First Peoples Hospital of Yangquan City, China for recruitment of subjects and collection of physiological data.

Conflict of interest

The authors declare no conflict of interest.

Appendix

Algorithm of EKF

The pseudocode of the EKF algorithm is presented in Algorithm 1.

Algorithm of PFG

The pseudocode of the PFG algorithm is presented in Algorithm 3.

Algorithm of PFM

The pseudocode of the PFM algorithm is presented in Algorithm 4.

RMSEs of PGC and PIC estimation with various particle numbers

We have presented the RMSEs of PGC and PIC estimation with various particle numbers in the Table 8 and added explanation on it.

As expected, we can see that as the number of particles increases, the accuracy gradually increases. Nevertheless, when the number of particles exceeds 1000, the increase of particles has less and less influence on the improvement of estimation accuracy, and the corresponding calculation cost is heavier and heavier. Considering the limited computing power of the artificial pancreas, we balanced the relationship between the accuracy and the amount of calculation. For this reason, we set the number of particles to 1000.