1. Introduction
Behind the formation of an ultrasound image are complicated physical phenomena. When propagating inside a medium, ultrasound waves are subjected to non linear attenuation and scattering by the medium's micro-structures. In fact, scattering is caused by small inhomogeneities in the acoustic impedance, which are randomly distributed in the three dimensional space of the medium. As a consequence, emitted waves which were traveling in phase on their way to the scatterers are no longer in phase after being back scattered. Due to the phase-sensitive detection of back scattered waves interfering in the resolution cell of the transducer, an ultrasound image is characterized by a granular pattern of white and dark spots. This phenomenon is denoted speckle and is considered as a process which tends to degrade the resolution and contrast of ultrasound images [1].
The speckle noise is assumed to have a multiplicative model and in most applications it needs to be effectively reduced in order to have a successful automatic image segmentation which is our case. Note, however, that it is not always desired to remove speckle as its presence is critical to the success of some techniques such as speckle tracking [2,3] and for many methods of ultrasound tissue characterization [4,5]. The objectives of this paper are to explain the origin of the speckle, to review the models for intensity levels distribution (commonly referred to as speckle pattern) in ultrasound images, to propose and investigate an empirical model for speckle in data measured using the Sampling Phase Array technique (also known as Full Matrix Capture).
The modeling of the statistical properties of the speckle was a main query for many scientific works. From a methodological point of view, either parametric or nonparametric estimation strategies can be employed for this purpose [6]. Specifically, our focus will be on the parametric modeling approach. Here, the principle idea is to postulate a given mathematical distribution for the statistical modeling of ultrasound images. Afterward, parameter estimation for the distribution is performed in order to determine the statistical properties of speckle in images. The modeling process forms a crucial task for specific image analysis purposes, for instance characterization [7,8] or classification [9,10] of image regions. Parametric models can be organized into two classes: theoretical and empirical models. The theoretical parametric models are derived using a scattering model of waves. On the opposite, empirical models are obtained by directly fitting a model to the experimental values, without any assumption of physical concepts.
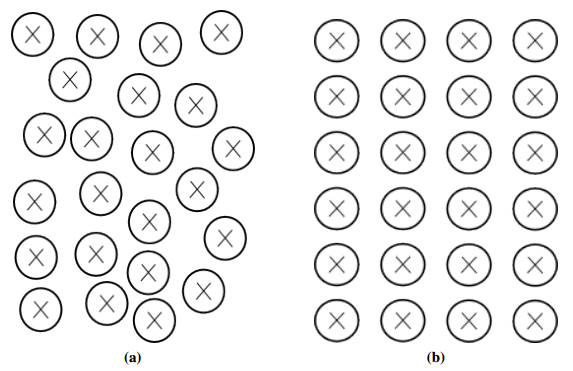
Moreover, it is useful to note that similarities exist between the images obtained by Synthetic Aperture Radar (SAR) and ultrasound techniques where their main characteristic is the appearance of speckle grains giving them a noisy appearance. This explains the reason why established speckle models in SAR are as well applied for speckle modeling in ultrasound images (see Figure 1).
On another hand, the speckle problem is well investigated in the medical field (on radio frequency signal and image levels). However, much less work has been done to characterize the speckle in industrial data. Indeed, the micro-structures are completely different between a CFRP, a fiber glass and a human carotid arteries or liver for example. A question poses itself: are speckle models proposed for medical ultrasound data valid for industrial data as well?
Thus, and independently of the application's type, the next section is devoted to present a review of theoretical parametric models of speckle.
2. Materials and Methods
2.1. Theoretical Parametric Models of Speckle
Let a resolution cell (also called range cell) of a transducer correspond to the smallest resolvable detail [11]. Moreover, consider a scatterer i which is randomly located inside the waves propagation medium. The back scattered echo Λi from the scatterer i is characterized by an amplitude αi≥0 and a phase ϕi. It can be expressed as:
|
Λi=αi⋅exp(j(ω0(t)+ϕi(t)))
|
(1)
|
where ω0≥0 is the angular frequency of excitation and j=√−1 is the imaginary number.
In the case when Ns scatterers, Ns∈N, interfere in the same resolution cell, the back scattered echoes in the cell can be expressed as [12,13]:
|
Λ=Ns∑i=1αi⋅exp(j(ω0(t)+ϕi(t)))=ℜ(Λ)+j⋅ℑ(Λ)
|
(2)
|
where ℜ(Λ) is the real part and ℑ(Λ) is the imaginary part of the complex back scattered echo Λ.
Consequently, the interference of the back scattered echoes can be constructive or destructive according to each particular repartition of scatterers. If interference is mainly constructive then the intensity in the resolution cell will be high. In case of mainly destructive interference, the intensity will be low.
The envelope of the back scattered echo EΛ is given by:
Speckle is explained as an interference phenomenon between all the back scattered echoes interfering in the same resolution cell. Therefore the size of speckle granules is about the same as the resolution of the transducer both in longitudinal and lateral direction [11]. Additionally, note that the speckle size is not only dependent on the transducer's characteristics, but varies with the scatterers density as well [14].
In the modeling process, the following hypotheses are usually considered to be fulfilled [15,16,17]:
• The amplitude of the back scattered echo from each scatterer is considered to be deterministic and the phase is considered to be uniformly distributed in [0,2π].
• The number of scatterers is large enough so that each resolution cell contains sufficient scatterers (Ns≥10 [18]).
• The scatterers are independent and there is no single scatterer dominating inside the resolution cell.
Under the above cited hypotheses and according to the central limit theorem [19], in case of a large number of randomly located scatterers (Figure 2a), the scatter is fully developed. In this case, the real and imaginary parts of Λ are Gaussian, thus, EΛ follows a Rayleigh distribution [11,20,21]. The probability density function (pdf) of Rayleigh distribution is given by:
|
PR(s,β)=sβ2⋅exp(−s22β2)
|
(4)
|
where s≥0 is the intensity value in the range cell of the transducer (also called local brightness in [22]) and β>0 is the scale parameter.
Nowadays, with the advent transducers emitting high frequency waves, it is possible to obtain high resolution ultrasound images. Due to the increased resolution, the number of reflectors per cell is reduced. Note that the back scattering characteristics of a scatterer are depending on its dimensions relatively to the wavelength of the ultrasound [23,24]. Hence, the fundamental assumption of fully developed speckle is no longer valid. Consequently, the Rayleigh distribution tends to fail in modeling the speckle distribution in ultrasound data.
As alternative, in case of non-fully developed scatter*, Shankar [13] proved that the envelope EΛ will be Rician distributed. This model is considered to be appropriate in case of regular repartition of scatterers that might, for instance, account for regular structures or quasi periodic scatterers in the medium (Figure 2b). The pdf of Rician distribution is given by:
|
PRician(s,β,ν)=sβ2⋅exp(−s2+ν22β2)⋅I0(sνβ2)
|
(5)
|
*Case of few scatterers.
I0(⋅) is the modified Bessel function of the first kind of order zero defined as:
|
I0(sνβ2)=1π∫π0exp(sνβ2cosα)dα
|
(6)
|
where s⩾0, β>0 and α∈[0,π].
The parameter ν⩾0 is considered as specular component which is added to the Rayleigh pdf. Thus, when ν is null, the Rician distribution is reduced to a Rayleigh distribution.
Jakeman et al. [25] proposed to use K-distribution as a model for a weak scattering condition which corresponds to a small number of scatterers. The pdf of the K-distribution is given by:
|
PK(s,β,Ns)=2βΓ(Ns+1)⋅(βs2)Ns+1⋅KNs(βs)
|
(7)
|
In this equation, β>0 is a scaling factor, Ns>−1 is the number of scatterers in the resolution cell and KNs(⋅) represents the modified Bessel function of second kind and order Ns:
|
KNs(βs)=∫∞0cosh(Nst)exp(−βscosht)dt
|
(8)
|
where t∈[0,∞) and s≥0.
The function Γ(.), known as gamma function, is a generalization of factorial function to non integer values n and defined by:
where t∈[0,∞). In case of integer values, Γ(n) is reduced to be n!.
In [13], the author proposed a simpler model called the Nakagami distribution in order to model the speckle in ultrasound data. This distribution is derived from the basic assumption of a Gaussian model for the back scattering phenomena. According to the study done by Shankar et al. [13], Nakagami distribution is claimed to be suitable for modeling almost all scattering conditions. The pdf of the Nakagami distribution is defined as:
|
PN(s,ν,Ω)=2ννs2ν−1Γ(ν)Ων⋅exp(−νs2Ω)
|
(10)
|
where ν≥12 is the Nakagami shape parameter and Ω>0 is a scaling factor. When ν=1, the Nakagami pdf is equivalent to a Rayleigh pdf: PN(s,Ω)=sΩ⋅exp(−s2Ω), where Ω=2β2. Nakagami pdf becomes Rician for ν>1.
Further investigations on modeling the statistical properties of the received echo signal and more complex models have been proposed to take into account different scatterer conditions. Among these models are the generalized K-distribution [26], the homodyned K-distribution [27] and the Rician inverse of Gaussian distribution [28].
Anastassopoulos et al. [29] proposed the generalized Gamma distribution (GΓD) [30,31] to model the characteristics of radar clutter. In their study [29], the authors proved and validated that the pdf of GΓD distribution performs better than K-pdf and can model the speckle and the modulation component of the radar clutter (speckle) in case of a high resolution radar. The GΓD pdf is given by:
|
PGΓD(s,β,ξ,ν)=ξβΓ(ν)⋅(sβ)ξν−1⋅exp(−(sβ)ξ)
|
(11)
|
In this equation, β>0 is the scale parameter, ν>0 is the shape parameter and ξ>0 is the power of GΓD [29]. GΓD forms a general model. Standard models commonly used in modeling SAR data, like exponential (ξ=1, ν=1), Rayleigh (ξ=2, ν=1), Nakagami (ξ=2), Weibull (ν=1), and gamma pdf (ξ=1) are special cases of the GΓD.
Assuming that the real and imaginary parts of the back scattered signal are independent zero-mean generalized Gaussian, Moser et al. [12] introduced the Generalized Gaussian Rayleigh distribution (GGR) with a pdf given by:
|
PGGR(s,β,ν,α)=β2ν2sΓ(1ν)2⋅∫π20exp[−(βs)ν⋅(|cosα|ν+|sinα|ν)]dα
|
(12)
|
where β>0 is a scaling factor, ν>0 is a shape factor dealing with the sharpness of the pdf and α∈[0,π/2].
The effectiveness of the proposed GGR model was validated on SAR images [12]. The pdf of GGR gave a higher correlation value with the histogram of the SAR images compared to other probability density functions (pdfs) of: the Nakagami, Skewed α Stable (SαS) generalized Rayleigh [32,33,34] and K-distributions. Note that SαS statistical model was applied by Kappor [35] to describe woodland regions in ultra-wideband synthetic aperture radar images, where it was shown that it provides a better fit to the tails of the clutter amplitude distribution than the Gaussian or K distribution. Similar work was done by Banerhee [36] where the authors proved that SαS statistical model provides better segmentation and detection results when compared to Gaussian models.
To summarize, theoretical models are usually derived from the analysis of the acoustic physics and the information available of the ultrasound transducer [37]. However, as stated by Tao et al. [10], these models only give the speckle probability density at the transducer. The density has to be transformed into speckle density in the image. This task is complicated for two reasons. First, the transducer signal passes through different signal processing stages such as amplification and interpolation etc. before its presentation as an image. Propagating the density through the complex signal processing chain is difficult [10]. A second reason is that the complete information during the acquisition process is not always available. A common method to avoid these difficulties is to use empirical pdfs which can be accurately fitted to the speckle in the image.
2.2. Empirical Models of Speckle
For P, S, T∈N, let ΩP,S,T⊂N3 be a set of coordinates defined as:
|
ΩP,S,T={(x,y,z)∈N3: 1⩽x⩽P; 1⩽y⩽S; 1⩽z⩽T}
|
(13)
|
where P, S and T are respectively the dimension of the volume's grid.
Let u denote a ultrasound noisy volume† defined as a mapping from ΩP,S,T to R+:
|
u:ΩP,S,T⟶R+(x,y,z)⟼u(x,y,z)
|
(14)
|
†An array or an image are special cases of a volume.
where u(x,y,z)∈R+ is the noisy intensity observed at coordinates (x,y,z). For simplicity reasons, u(x,y,z) will be only written as u in the pdfs of Table 1.
Table 1. Probability density functions used in modeling speckle in SAR and ultrasound images. Note that u is used as abbreviation (to simplify the pdf formulas) for the intensity at voxel (x,y,z) in the volume u and u(x,y,z)≥0.
| Model | Probability density function | Parameters |
| Weibull | p(u)=νβuν−1exp(−uνβ) | ν: shape |
|
| α,β>0 | β: scale |
| Normal | p(u)=1β√2πexp(−(u−μ)22β2) | μ: location |
|
| μ∈R, β>0 | β: scale |
| Lognormal | p(u)=1uβ√2πexp(−(ln(u)−μ)22β2) | μ: location |
|
| μ∈R, β>0 | β: scale |
| Gamma | p(u)=1Γ(ν)βνuν−1⋅exp(−uβ) | ν: shape |
|
| ν,β>0 | β: scale |
| Fisher-Tippett | Y=ln(X), PX(u)=uβ2exp(−u22β2) | β: scale |
|
| PY(ρ)=2exp([2ρ−ln(2β2)]−exp([2ρ−ln(2β2)])) | |
|
X: magnitude image, Y: log of X | ρ∈R, β>0 | |
Several empirical models have been reported for modeling the speckle in ultrasound images. These models are validated on the actual ultrasound images by measuring the goodness of fit of the model to the actual data distribution. Thus, results are completely data-dependent and cannot be considered as general models valid for other types of data.
In general, many applied models in ultrasound speckle characterization are taken from SAR speckle studies. These models include Gamma [15,38], Weibull [15,39,40] and Lognormal [41,42] distributions (see Table 1).
Vegas-Sanchez-Ferrero et al. [37] studied the distribution of fully developed speckle noise by comparing the goodness of fit of ten families proposed in the literature. The work was done on 120 clinical cardiac ultrasound images. The compared pdfs were for: Gamma, Lognormal, Rayleigh, Normal, Nakagami, Beta, Rician Inverse Gaussian [28], Rice, Exponential and K-distribution. The authors used χ2 goodness of fit test and concluded that the pdf of Gamma distribution fits at best the speckle noise.
Tao et al. [10] compared the validity of four families of distribution of the speckle noise on clinical cardiac ultrasound images: Gamma, Weibull, Normal and Lognormal [43,44]. The pdf of the Gamma distribution was found to have the best fit to the data and classified blood and tissue at a low misclassification rate. The authors used Rao-Robson [45] statistic to measure the goodness of fit and the generalized likelihood ratio test to classify regions into tissue and blood.
The pdf of Fisher-Tippett distribution was proposed by [18,46] as a model for fully formed speckle in log-compressed ultrasound images. In fact, in ultrasound imaging log-compression is often applied to the amplitude of the received echoes in order to adjust their values to fit in the 8 bits digitization dynamic range [23].
In their recent contribution, Li et al. [47] proposed to use the pdf of the Generalized Gamma distribution GΓD to empirically model SAR images data distribution. The authors compared the pdf of GΓD distribution with Weibull, Nakagami, K, Fisher [48], GGR [12] and Generalized Gamma Rayleigh GΓR [49] pdfs. The obtained qualitative (visual comparison) and quantitative results proved that, in most cases, the pdf of GΓD provided better performance in fitting SAR image data histograms than the majority of the previously developed parametric models.
Although empirical models are used in many segmentation approaches, c.f. [4,22] for extensive surveys, authors often assume that speckle is Rayleigh, Gamma [38,50,51,52] or Fisher-Tippett [53] etc. distributed, without proving the validity of this assumption.
In the next section, the focus will be on finding the model which fits the speckle in SPA volumetric data.
2.3. Speckle Distribution in 3D Ultrasound Data
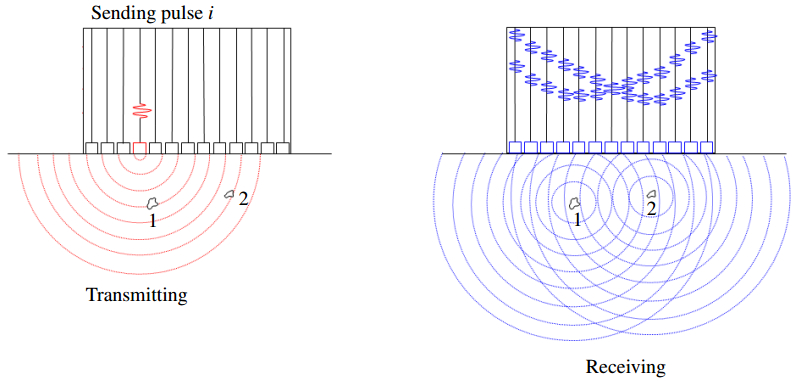
The ultrasound data considered in this study were obtained using a 5 MHz linear array transducer incorporating 16 elementary transducers. The array was triggerd using the concept of Sampling Phased Array (SPA, also known as full matrix capture) [54,55] where per position, the first element of the array sends and all other elements receive (SPA 1 × 16 mode, see Figure 3). The received signals were reconstructed using the well established algorithm Syntethic Aperture Focusing Technique [56].
The speckle degrades the quality of the reconstructed SPA volumes and it is important to study it in order to have more knowledge about its statistics. The aim is to find the model that fits at best the speckle affecting the data measured with the SPA technique.
2.3.1. Proposed Model
From a methodological point of view, the parametric approach for noise distribution statistical analysis will be followed. Here, the Four-Parameters Generalized Gamma (4P-GΓD) distribution is proposed to model speckle in SPA data. Its pdf is defined as:
|
PGΓD(u(x,y,z),β,ξ,ν,γ)=ξβΓ(ν)⋅(u(x,y,z)−γβ)ξν−1⋅exp(−(u(x,y,z)−γβ)ξ)
|
(15)
|
where u(x,y,z)∈[γ,+∞] is the intensity value, β>0 is the scale parameter, ν is non null and represents the shape parameter, ξ>0 is the power of GΓD and the new parameter γ∈R is the translation parameter. This paramter is introduced in order to improve the flexibility of the pdf thus potentially improving its capability to model speckle noise. Note that for γ=0 the model is reduced to the original model of the GΓD [30,31].
The proposed 4P-GΓD model is compared with the following commonly used pdfs to model speckle in ultrasound images: Gamma, Lognormal, Inverse Gaussian, Weibull, Rayleigh, Rice, Nakagami and Normal. In addition, the translation parameter γ was introduced into each of the previously cited pdfs. For instance when introducing a translation parameter to the original Gamma distribution, the newly obtained distribution will be:
|
p(u(x,y,z))=(u(x,y,z)−γ)ν−1Γ(ν)βν⋅exp(−u(x,y,z)−γβ)
|
(16)
|
In order to apply the 4P-GΓD (also applies for the other pdfs) as a model for SPA data, it is mandatory to estimate the pdf parameters β, ξ, ν and γ from the experimental data. In fact, in parametric modeling, the pdf estimation problem can be formulated as a pdf parameters estimation problem [12]. Several strategies have been presented in the literature to solve parameters estimation. The standard methods include the maximum likelihood (ML) [6,15] and the method of moments (MoM) [57]. More explanation about different parameters estimation methods of pdfs can be found in [58]. As for the estimation of pdfs used in this study, robust parameter estimation using ML estimate is obtained by using EasyFit tool provided by MathWave [59].
Quantitative measure of the goodness of fit is obtained using the Kolmogorov-Smirnov (K-S) statistic. The K-S statistic is a well known distance measure commonly adopted for the study of goodness of fit [29,60,61]. It is a simple measure based on the largest vertical difference D between the empirical (i.e., experimental) cumulative distribution function (ecdf) SQ(s) of a dataset and the known cumulative distribution function (cdf) F(s).
|
D=max−∞<s<+∞|SQ(s)−F(s)|
|
(17)
|
Remind that the cdf of a real random variable λ, with a given pdf pλ, is the probability that λ takes a value less than or equal to s: F(s)=pλ(λ⩽s). Moreover, the ecdf can be defined as follows: let λ1,⋯,λQ be Q data points from a common distribution with cdf S(s), the ecdf is defined as: SQ(s)=1Q∑Qi=1I(λi⩽s) where I is the indicator function (I=1 if λi⩽s and I=0 if λi>s). Small K-S distance D indicates a better fit of the particular pdf to the experimental data.
3. Results
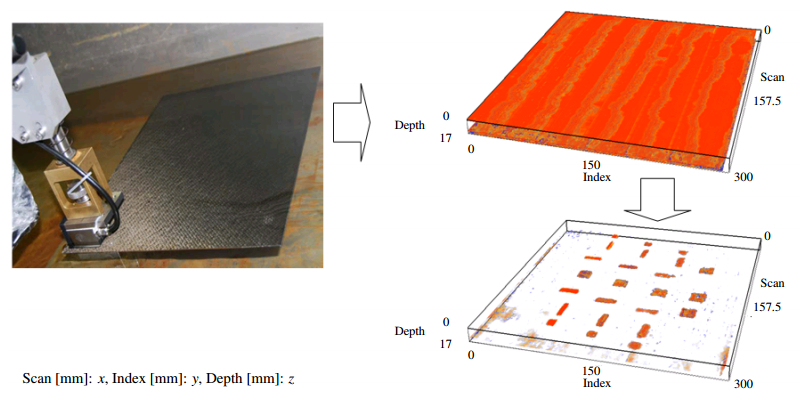
Experiments are reported on three reference volumes, without defects, extracted from original volumes which contain defects. The considered original volumes are: a CFRP volume (see Figure 4), an aluminum volume and a ceramic volume (see Table 2). Intensity values in the three volumes are encoded on unsigned 16 bits.
Table 2. Inspection of a CFRP specimen using SPA 1 × 16 mode and the obtained 3D reconstruction (upper right image) revealing the presence of defects inside the structure (lower right image).
| Type |
Original volume dimensions [x,y,z] |
Extracted volume dimensions [x,y,z] |
Voxel size [mm3] |
| CFRP |
[316, 301, 341] |
[100, 113, 92] |
[1, 1, 0.05] |
| Aluminum |
[841, 171, 951] |
[761, 133, 101] |
[1, 1, 0.05] |
| Ceramic |
[379, 95, 301] |
[291, 81, 41] |
[1, 1, 0.05] |
Figure 5a illustrates (on a layer) the selection of the reference volume (without defects) from the original volume. The obtained reference volume is presented in Figure 5b and its dimensions are reported in Table 2.
For visual comparison of speckle in the considered materials, one layer of respectively, CFRP, aluminum and ceramic reference volumes is presented in Figure 6.
In order to assess the effectiveness of the proposed parametric pdf, the different pdfs for each reference volumes are estimated. Evaluation of the estimation results are presented both: qualitatively by means of a visual comparison between the top ranked estimated pdfs and the data distributions (reference volume intensity levels histograms) and quantitatively by the K-S goodness of fit values between fitted distributions and the experimental data.
3.1. Speckle in CFRP Material
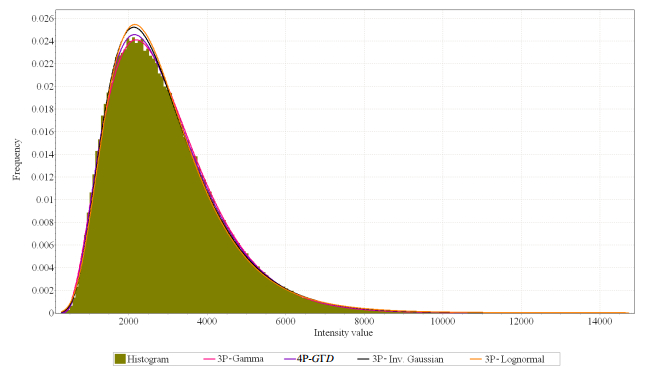
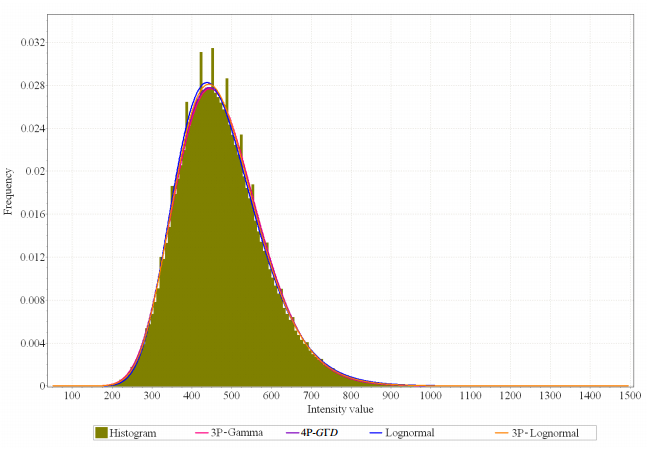
In case of CFRP material, the quantitative measure K-S suggests that the best fit for the intensity values distribution in the reference volume is given by the pdf of the 4P-GΓD distribution with a K-S value of 0.003 (see Table 3). Moreover, a visual comparison in Figure 7 between the normalized histogram and the plots of the top four best estimated pdfs illustrates the result obtained based on the quantitative measure.
Table 3. Values of the K-S distance obtained using the different pdfs to model speckle in the CFRP reference volume.
| Parametric model |
K-S distance |
Rank |
| 4P-GΓD |
0.003 |
1 |
| 3P-Gamma |
0.006 |
2 |
| 3P-Inv.Gaussian |
0.008 |
3 |
| 3P-Lognormal |
0.01 |
4 |
| Gamma |
0.0138 |
5 |
| GΓD |
0.0157 |
6 |
| Lognormal |
0.0188 |
7 |
| Inv.Gaussian |
0.022 |
8 |
| 2P-Rayleigh |
0.0313 |
9 |
| 3P-Weibull |
0.032 |
10 |
| Weibull |
0.042 |
11 |
| Rice |
0.065 |
12 |
| Rayleigh |
0.066 |
13 |
| Normal |
0.073 |
14 |
| Nakagami |
0.079 |
15 |
3.2. Speckle in Aluminum Material
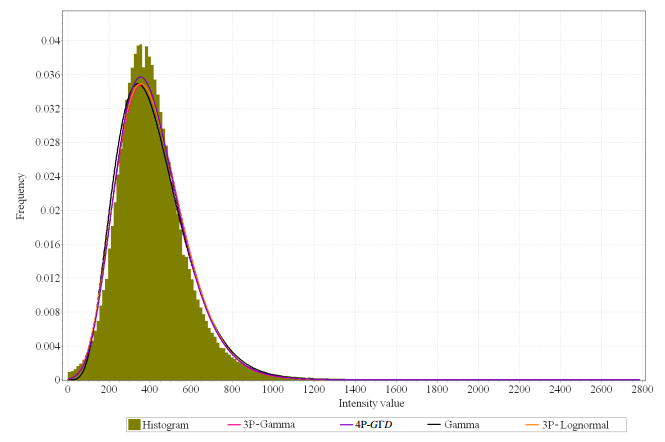
The analysis of the speckle in the aluminum reference volume reveals that the pdf of 3P-Lognormal fits at best the intensity values distribution in the volume. In the second rank comes the 4P-GΓD. Table 4 resumes the complete quantitative results obtained for all the considered pdfs. For a visual comparison see Figure 8.
Table 4. Values of the K-S distance obtained using the different pdfs to model speckle in the aluminum reference volume.
| Parametric model |
K-S distance |
Rank |
| 3P-Lognormal |
0.005 |
1 |
| 4P-GΓD |
0.007 |
2 |
| Lognormal |
0.008 |
3 |
| 3P-Gamma |
0.01 |
4 |
| GΓD |
0.0137 |
5 |
| Gamma |
0.0141 |
6 |
| Nakagami |
0.0305 |
7 |
| Normal |
0.0434 |
8 |
| 3P-Inv.Gaussian |
0.0436 |
9 |
| Inv.Gaussian |
0.0439 |
10 |
| Rice |
0.0505 |
11 |
| 3P-Weibull |
0.055 |
12 |
| Weibull |
0.06 |
13 |
| Rayleigh |
0.248 |
14 |
| 2P-Rayleigh |
0.267 |
15 |
3.3. Speckle in Ceramic Material
Lastly, the speckle in the ceramic reference volume is investigated. Table 5 reports the K-S distances measured between the experimental data and the pdfs. As it can be noticed, the K-S distance obtained for the fitted pdf of the 4P-GΓD distribution is the smallest. In the second rank comes the pdf of the 3P-Lognormal distribution. This is also visible in Figure 9, it can be seen that the pdf of the 4P-GΓD distribution tracks the evolution of the intensity values histogram better than other pdfs. However, it can be noticed that the histogram is not very well fitted by none of the pdfs.
Table 5. Values of the K-S distance obtained using the different pdfs to model speckle in the ceramic reference volume.
| Parametric model |
K-S distance |
Rank |
| 4P-GΓD |
0.0214 |
1 |
| 3P-Lognormal |
0.0264 |
2 |
| 3P-Gamma |
0.0273 |
3 |
| Gamma |
0.0317 |
4 |
| GΓD |
0.034 |
5 |
| Inv.Gaussian |
0.036 |
6 |
| 3P-Weibull |
0.055 |
7 |
| Weibull |
0.055 |
8 |
| Lognormal |
0.0623 |
9 |
| Normal |
0.066 |
10 |
| Rice |
0.068 |
11 |
| 3P-Inv.Gaussian |
0.101 |
12 |
| Nakagami |
0.109 |
13 |
| Rayleigh |
0.111 |
14 |
| 2P-Rayleigh |
0.128 |
15 |
4. Discussion
Different conclusions can be drawn from the obtained results. Based on the qualitative and quantitative measures, there is a clear evidence that the speckle in high resolution SPA data exhibit a non-Rayleigh behavior. The reason is that, with the increase of resolution, the hypothesis that each resolution cell contains a sufficient number of scatterers is not satisfied, therefore the central limit theorem cannot be invoked. The same remark applies for the Nakagami models which could not be the best fit to the SPA data. It was noticed that the pdf of the Rician distribution gave a better performance than the original Rayleigh's pdf (without the translation parameter). A possible explanation is that the Rician model was initially proposed for the case of non-fully developed scatterers. Nevertheless, it was not top ranked. Other models including Weibull/3P-Weibull, Inv.Gaussian and Normal models could not successfully provide the best fit to the speckle in SPA data. On the contrary, the proposed 4P-GΓD performed best for the CFRP and ceramic volumes, although it was slightly inferior to the 3P-Lognormal model for the aluminum volume. Thus, it can be seen that the speckle distribution depends on the material type, since the obtained best fitting model for CFRP and aluminum are not the same. Indeed, the visual appearance of the speckle in the layers at Figure 6 is different from one material to another. The reason is because each material has a specific internal micro-structure.
To sum up, the 4P-GΓD could, in all cases, successfully track the statistical properties of the SPA volumetric data. Visual and quantitative results proved that, in case of CFRP and ceramic volumes, the 4P-GΓD provided better performance than all other parametric models. Although, in case of the aluminum SPA volume, it was not the best, it had still achieved the second rank after the 3P-Lognormal.
5. Conclusion
In this paper, a review concerning the speckle noise in ultrasound data was presented. First, an examination of different theoretical and empirical techniques for speckle modeling in SAR and ultrasound images was conducted. Then, the speckle noise in SPA data was investigated. An extension of the original pdf of the GΓD distribution was proposed to model speckle in SPA data. Experimental results were reported for three different materials: CFRP, ceramic and aluminum.
Although the 4P-GΓD model is in most cases the best fit to the experimental data, nevertheless it was shown (for the aluminum specimen) that the fitting model is not always the same for the different material types. Thus, the model is dependent on the material's micro-structure.
Conflict of Interest
The authors declare no conflicts of interest in this paper.










 DownLoad:
DownLoad: