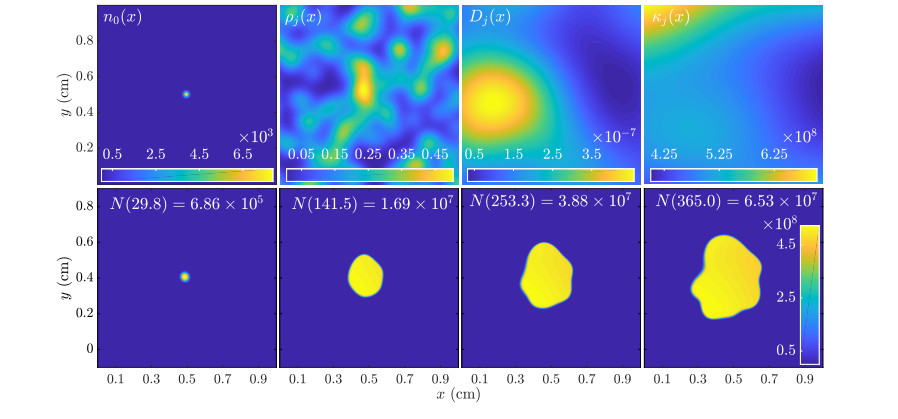
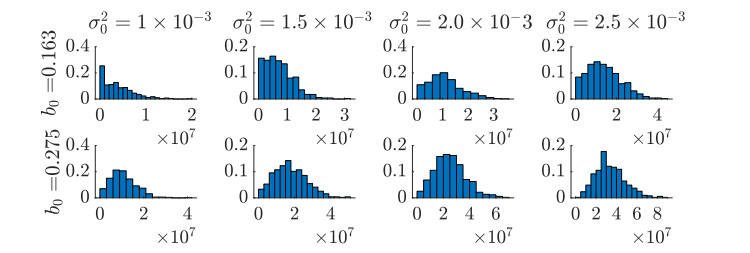
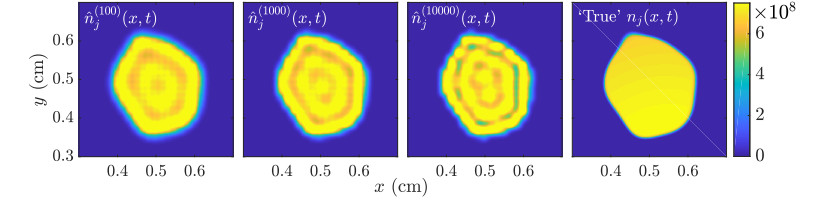
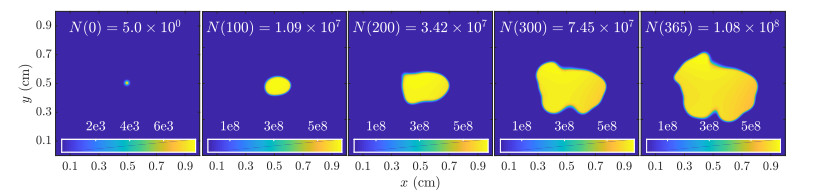
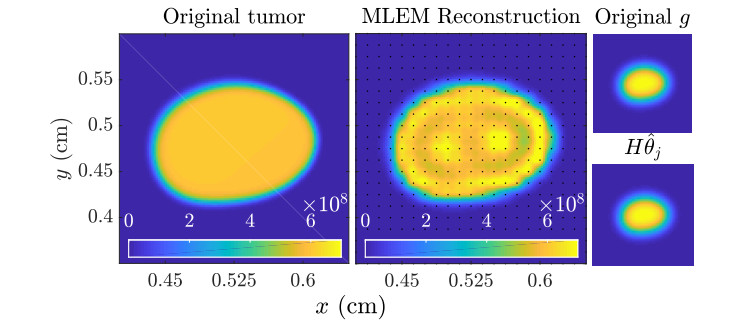
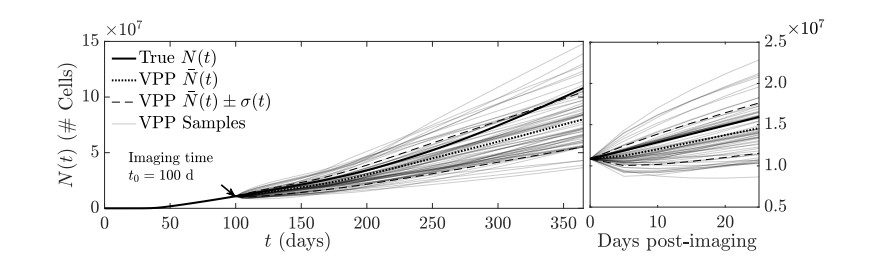
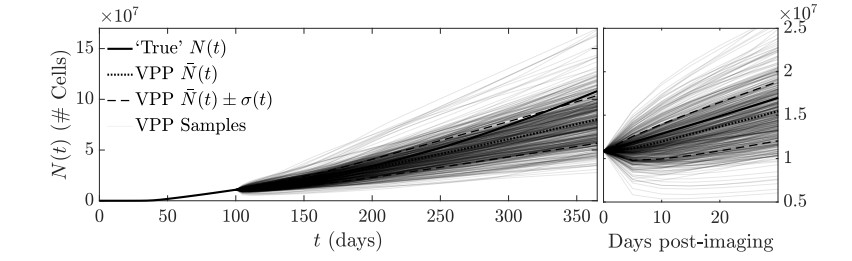
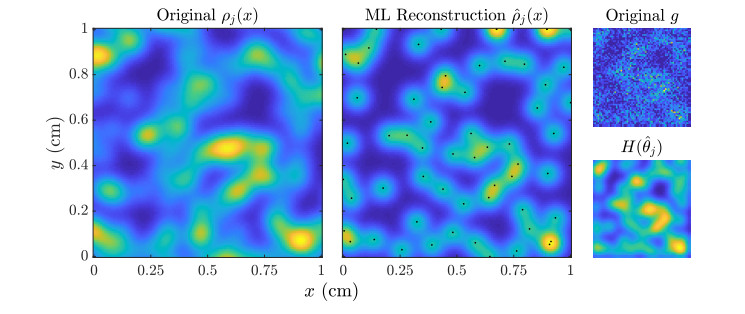
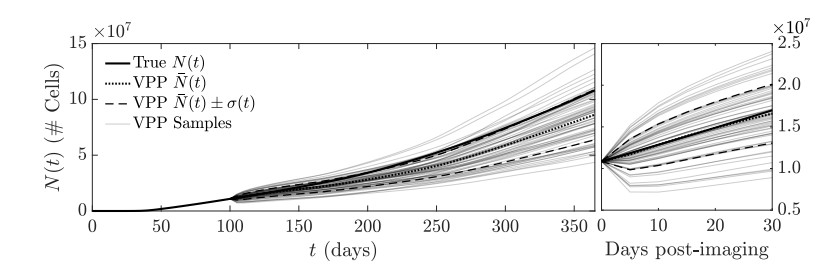
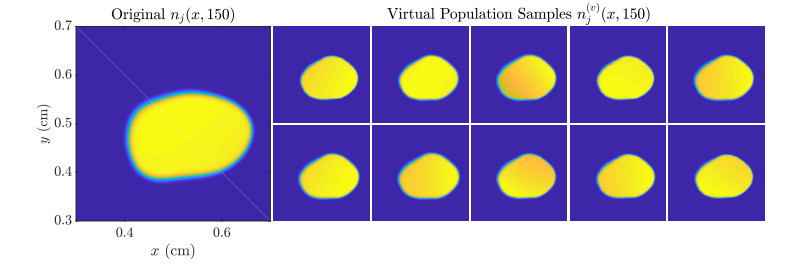
The use of mathematical tumor growth models coupled to noisy imaging data has been suggested as a possible component in the push towards precision medicine. We discuss the generation of population and patient-specific virtual populations in this context, providing in silico experiments to demonstrate how intra- and inter-patient heterogeneity can be estimated by applying rigorous statistical procedures to noisy molecular imaging data, and how the noise properties of such data can be analyzed to estimate uncertainties in predicted patient outcomes.
1.
Introduction
Macrofaunal bioturbation profoundly influences the mineralization of carbon in seafloor sediment by displacing particles and solutes [1,2,3,4]. Persistent sediment disturbances by, for example, bottom trawling or deposition of organic fish farm waste, can alter the composition of the resident macrofaunal assemblage and therefore affect carbon remineralization rates and the associated sediment–seawater exchange of dissolved carbon and nitrogen. Because this exchange links seafloor with pelagic ecosystem functions, changes in sediment bioturbation can have far-reaching consequences for coastal primary and secondary production [5,6,7].
Heart urchins of the genus Echinocardium Gray, 1825 have a disproportionally large influence on sedimentary transport and reaction processes [6,8,9,10]. They are globally widespread through soft sediment environments, inhabiting intertidal mud or sand flats to abyssal plains, and can form up to 60% of the macrobenthic biomass in some ecosystems [11,12]. Functioning as key bioturbators, they alter the physical and biological structure of their surrounding sediment both directly, by mixing sediment particles and porewater [4,6,9], and indirectly, by suppressing the presence of tube building polychaetes and small bivalve species (authors unpublished observation).
One well-studied species of the genus Echinocardium, E. cordatum (Pennant, 1777), forages by burying itself at depths of up to 20 cm in sandy sediment and up to 6 cm in muddy (silt and clay) cohesive sediment [12,13,14]. Once buried, E. cordatum ploughs the sediment horizontally at speeds ranging from 1–8 cm h−1 [9,13,15], selectively consuming microalgae and organic detritus [16,17,18]. When foraging, E. cordatum can displace and mix 60–150 times more sediment particles than the amount it ingests [9,19].
To meet its respiratory requirements while buried, E. cordatum maintains a current that irrigates the restructured sediment with oxygenated seawater, thereby enhancing the oxidation of reduced solutes and particulates, a process that would otherwise be constrained by the slow molecular diffusion of oxygen through cohesive sediment. Using dorsal spines and tube feet, the urchin constructs and sustains a vertical funnel, connecting the ambulacrum with the sediment surface [13,16]. The cilia of the ambulacral groove move oxygenated seawater down this funnel, facilitating gas exchange over respiratory tube feet [12,13]. To prevent suffocation due to the collapse of the respiratory funnel, the funnel-building tube feet excrete and apply mucus to the wall of the funnel [12,20]. Once the urchin has abandoned the funnel, microbial activity degrades this mucus, causing the funnel to eventually collapse [14]. Individuals dwelling in shallow cohesive sediment often maintain a second, larger funnel that connects the sediment surface in front of the urchin with the urchin's mouth [15]. Furthermore, subanal spines and tube feet construct and sustain a sanitary drain, extending laterally behind the urchin to accommodate excrements [12].
The displacement of particles and porewater by E. cordatum may create effects that last beyond the duration of the displacement event. For example, the tracks of E. cordatum contribute to the small-scale roughness of the sediment surface, potentially influencing the solute transport across the sediment–seawater interface [13,15]. Furthermore, particle mixing can stimulate sedimentary remineralization and oxidation processes by, respectively, introducing fresh organic matter into subsurface sediment layers either in the form of excrements or by displacement from the surface, and displacing reduced particles at depth to the surface, where they are exposed to oxygenated seawater [6,15,21,22,23]. These effects can collectively enhance the remineralization of labile and refractory organic carbon, potentially altering the rates of the sediment–seawater exchange of dissolved carbon and nitrogen.
Here, we asked if the previously demonstrated influence of moving E. cordatum on sedimentary solute transport and reaction processes extends beyond the sediment immediately next to the urchin. In other words, we asked if moving E. cordatum cause a 'legacy effect' that sustains a sediment–seawater solute exchange different from the exchange across a similar but never disturbed sediment? If so, then removing E. cordatum from the seafloor ecosystem should result in measurable difference between the solute exchange across the now undisturbed surface sediment and the surface of the repeatedly reworked sediment.
We experimentally tested this prediction by removing urchins from eight plots of the 10-m deep seafloor of Man O'War Bay, Hauraki Gulf, New Zealand, and then preventing recolonization and thus sediment reworking for about two months. Following this manipulation, we measured the sediment–seawater exchange of O2, NO3−, NO2−, NH4+, and N2 within and outside the exclusion areas. Because this exchange may be influenced by the activity of benthic algae and cyanobacteria, we conducted these measurements under conditions of light and darkness.
2.
Materials and methods
2.1. Study site
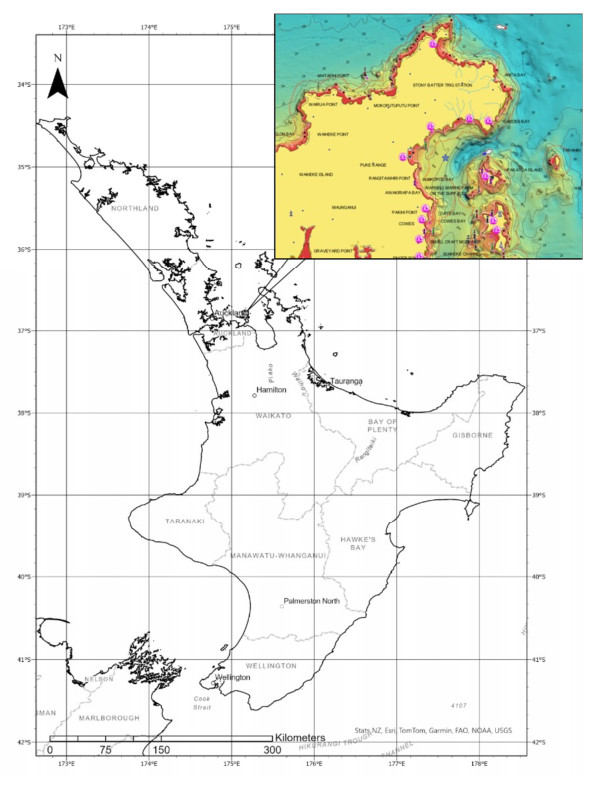
Man O'War Bay is situated on the east coast of Waiheke Island in the Hauraki Gulf, New Zealand (S 36° 47' 38", E 175° 10' 14", Figure 1). The Hauraki Gulf covers nearly 4,000 km2, with water depths up to 50 m and provides sheltered conditions that facilitate particle settling. The sediment in Man O'War Bay, which consists of terrigenous silt and clay with a small proportion of sand, is iron-rich, resulting in a dark grey-to-black subsurface layer due to an abundance of iron sulfides. Organic matter accounts for > 6% of the sediment dry weight, but the pore water of the top 20 cm of the sediment remains free of dissolved sulfides [24]. In May 2022, the salinity and temperature of the bottom seawater in Man O'War Bay were 34.5 and ~15 ℃, respectively.
The seafloor at our 10-m deep site in Man O'War Bay is devoid of macroalgae and sessile epifauna, with golden-brown diatom patches that accentuate the centimeter-scale surface topography shaped by two bioturbators: a burrowing mud shrimp of the genus Upogebia, and the ploughing heart urchin Echinocardium cordatum (Figure 2A). Other macroinfauna consists of small polychaetes (Prionospio, Sthenelais, and Cossura), an amphipod species (Paraphoxus), and a bivalve species (Theora lubrica) [25].
To describe the resident population of E. cordatum, a seafloor survey was conducted two weeks before the exclusion experiment. SCUBA divers used a GoPro Hero 4 camera to capture a still images of a 0.5 × 0.5-meter quadrate placed on the surface of the seafloor at 40 locations randomly distributed within a 1260 m2 area. At 10 locations, time-lapse photography was used to estimate the speed at which individuals ploughed the sediment. The frame that held the underwater camera (Figure 2A) was positioned within the camera's field of view, providing a reference for measuring distance.
2.2. Experimental procedures
On 3 May 2022, two SCUBA divers buried nine plastic rings (1 m diameter, 28 cm wide) within a ~700 m2 circular area. The placement of each ring was carried out with a 30-m guide rope anchored in the sediment and nine pre-determined compass/distance coordinates (i.e., 0–360 degrees, 1–30 m away from the anchor). The divers pushed each ring ~25 cm deep into the sediment, leaving about 3 cm exposed above the sediment surface. Subsequently, they carefully removed all urchins (10–20 individuals per ring) from the area within the rings. The rings remained free of E. cordatum and in place for 56 days, effectively isolating the enclosed sediment from further sediment restructuring by the urchins.
On 27 June 2022, the divers returned to collect one intact sediment core from within (Treatment) and outside (Control) each of nine rings, at least 20 cm away from the edge of a ring, avoiding the sediment around openings of shrimp burrows shown in Figure 2A. To do so, they placed an acrylic tube (height: 300 mm, internal diameter: 90 mm) perpendicular to the seafloor and pushed 200 mm of the tube into the sediment until two-thirds were filled. They then inserted a lid with an open valve into the protruding end of the tube. This was done slowly, to avoid creating pressure inside the tube that would otherwise resuspend the silt sediment. Following this, the divers inserted a lid in the buried end of the tube pushing the sediment core inside the tube upwards by about one centimeter. They then closed the valve in the top lid and lifted the core out of the sediment. The sediment cores were stored upright in two large 50 L boxes containing ice and transported to the laboratory within two hours.
2.3. Laboratory setup
In the laboratory, we removed the top lids of the acrylic tubes, and then submerged the sediment cores in the recirculating seawater (salinity = 34.5) of two 450-L holding tanks for a 3-day acclimatization. A third and identical tank (measurement tank) was set up to which sets of four or five cores were transferred for sediment–seawater solute flux measurements (see below).
Each tank was fitted with a pump (3260, Eheim) that moved ~9 L seawater per minute through a chiller unit (HC Chiller 300A, Hailea) and a UV sterilizer (Pond One UV-C 9W, ClearTec) to a 200 L header tank from which the seawater returned to the tank by gravity. The chiller maintained the seawater temperature close to the in-situ seawater temperature (15 ± 0.5 ℃). An additional pump pushed seawater through a UV particle filter (Aqua One Ocellaris 1400 UVC). A wave maker (SW, Jebao) attached to the inner wall of each tank, along with two jets of returning seawater from the UV particle filter and the header tank, ensured that advection was sufficient to prevent the seawater overlying the submerged sediment cores from becoming stagnant. Each tank had a Kessil A160WE Tuna Blue LED mounted above it, gradually increasing the intensity of photosynthetically active radiation (PAR) from 06:00 h to a midday maximum of ~120 µmol quanta m−2 s−1 and then gradually decreased this intensity until 18:00 h, when the LED was turned off. To account for evaporation, we monitored and adjusted the salinity of tank water each morning using reverse osmosis water.
2.4. Solute flux measurements
We transferred four or five cores at a time from the holding tanks into the measurement tank to determine the sediment–seawater solute flux under conditions of light and darkness. The light and dark solute flux was derived from the difference in the solute concentration in seawater collected ~10 mm above the sediment surface before and after a 4-h incubation period. This seawater was withdrawn slowly, using a tube connected to a syringe, avoiding particle resuspension. During the 4-h incubation period, the acrylic tube holding the sediment core and its overlying seawater was closed with a valved O-ring sealed lid. A peristaltic pump recirculated the enclosed seawater through Teflon tubes at a flow rate of 135 mL min−1 to prevent stagnation. The seawater O2 concentration was measured at the beginning and the end of each incubation with a dipping probe (DP-PSt3, Presens GmbH) connected to a portable fiber optic oxygen meter (Microx 4, Presens GmbH). The O2 concentration in the enclosed seawater never decreased below 86% saturation.
2.5. Sample analyses
For analyses of nitrite-N, nitrate + nitrite-N, and ammonia-N we collected, filtered (Sartorius CA 0.45 μm filter), and froze 10 mL of the seawater from each core, at the beginning and the end of each incubation. These samples were kept frozen until analyses. Seawater aliquots collected for N2 analyses (2 × 12 mL exetainers) were poisoned with 0.01 mL of a saturated mercuric chloride solution. Following the seawater sampling, we decanted the seawater above the sediment cores, extruded the cores, and extracted the top 2 cm of sediment for granulometric analyses.
We determined the sediment granulometric indices by laser particle size analyses (Mastersizer 2000, Malvern Instruments Ltd.) of 10 homogenized samples, one taken from the top 2 cm of each of 5 Control and 5 Treatment cores. The sediment water content was determined as the loss of weight after 24 h drying at 90 ℃. The seawater N2 content was measured with a Pfeiffer Prismaplus QME mass spectrometer and a Bay Instruments S-25-75D membrane inlet, and the seawater concentrations of nitrite-N, nitrate + nitrite-N, and ammonia-N were determined with an Astoria Pacific 2 micro-segmented flow analyzer (https://astoria-pacific.com/) following the Astoria protocols A182-A00 (range: 0.02–2.0 μmol L−1), A177-A00 (range: 0.05–7.5 μmol L−1) and A027-A00 (range: 0.05–5 μmol L−1) for operating their respective individual nutrient channels [26].
2.6. Solute flux estimates
We determined the sediment–seawater solute flux (μmol m–2 h–1) multiplying the start–end difference in solute concentrations (μmol L–1) by the volume of enclosed seawater (L) and dividing this by the surface area of the sediment core (m2) and the duration of the incubation (h). Since previous measurements revealed that the consumption/production of solutes in the seawater is negligible, this was not considered in our flux calculation. Note that a positive flux indicates sediment consumption whilst a negative flux is interpreted as solute release from the sediment.
2.7. Statistical analysis
All statistical data analyses were completed with R-4.4.0 [27]. For each solute we used Shapiro-Wilks test to confirm a normal distribution of the continuous variable. We then performed a two-way analysis of variance (ANOVA) investigating the effects of light (light versus dark conditions), experimental treatment (cores from within the exclusion rings versus cores from outside the rings), and the interaction between these discrete predictors, on the direction and magnitude of each solute flux. Visual analysis of the diagnostic plots for each of the five solutes confirmed that they met the assumptions of an ANOVA, including homogeneity of variance. When a significant result was found (alpha threshold = 0.05), we followed with post-hoc TukeyHSD analyses to further investigate significant individual effects.
3.
Results
3.1. Habitat
The sediment in the sheltered Man O'War Bay consisted of ~74% silt, 17% sand, and ~9% clay. The laser particle size analyses returned the following granulometric indices: Median = 30 μm (silt), Lower Quartile Q1 = 63 μm, Upper Quartile Q3 = 10 μm, Inclusive Sorting Coefficient QD1 = 1.95 (poorly sorted), and Inclusive Graphic Skewness Sk1 = 0.07. The water content of the sediment decreased from 75% in the top 2 cm to 65% at 9 cm depth.
Analyses of 100 photographs of the sediment surface revealed ~18.2 ± 6.7 (mean ± SD, n = 100) Echinocardium cordatum individuals per square meter. Time-lapse videos showed that urchins moved at ~45 ± 12 cm per day (mean ± SD, n = 6).
3.2. Experimental control
The sediment outside the exclusion rings, between foraging E. cordatum, and away from the immediate surrounding of the urchin, consumed O2 at similar rates under conditions of darkness and light (Table 1, Figures 2B and 3). In light, this sediment took up on average ~39% more N2 from the overlying seawater then under conditions of darkness (Table 1, Figures 2B and 3). The average sediment–seawater fluxes of nitrate and nitrite were an order of magnitude lower than that of N2; on average nitrate was released (negative flux in Table 1, Figures 2B and 3) while nitrite was taken up by the sediment, at similar rates under conditions of light and darkness (Figures 2B and 3).
The flux of ammonium in light differed significantly from that measured in darkness (p < 0.025, Tables 1 and 2). In light, the sediment released ammonium into the overlying seawater (negative flux in Table 1), while the average of fluxes measured in darkness indicated a small uptake (Table 1, Figures 2B and 3).
3.3. Sea urchin exclusion–experimental treatment
The solute fluxes (O2, N2, NO3−, NO2−, NH4+) across the surface of the sediment collected within the exclusion rings (Treatment) did not significantly differ from the fluxes measured across the surface of the sediment collected outside the exclusion rings (Control), under conditions of both light and darkness (Tables 1 and 2, Figure 3).
4.
Discussion
We expected that the exchange of dissolved oxygen and nitrogen across the surface of the sediment that lies beyond the immediate surrounding of foraging E. cordatum individuals would reflect a history of repeated reworking, so that after a 56-day cessation of this reworking the solute fluxes measured inside (Treatment) and outside (Control) the urchin exclusion rings would differ in their magnitude and/or direction. Our measurements, however, did not reveal any statistically significant differences between Treatment and Control. We considered the potential influence of E. cordatum on sedimentary solute reaction processes; repeated particle mixing and porewater oxygenation should have altered remineralization rates and thus modified the associated sediment–seawater solute exchange. Apparently, the rate at which the sediment was mixed and oxygenated by the resident E. cordatum population did not cause the expected influence; thus, the removal of urchins did not make a difference.
Besides the potential direct effects of sediment mixing on microbial reaction processes, we expected indirect effects, which can result from the influence of E. cordatum on cohabiting biota, most importantly, benthic microphytes. Photosynthesis of microphytes can cause dark/light differences in the total sediment–seawater O2 exchange as measured by core incubations, and an influence of E. cordatum on the abundance and activity of microphytes would then be evident from either an increase or decrease of these differences. Our sediment core incubations revealed, however, that the Control removed as much O2 from the bottom seawater in darkness than it did in light (Table 1). Assuming that the O2 demand of the sediment in light did not differ from that in darkness, this suggests that benthic photosynthetic O2 production must have been negligible. If this was the result of heart urchin predation limiting the growth of microphytes, then we would expect algae growth and photosynthesis to increase following the exclusion of the heart urchins. However, there was no evidence of such increase; apparently, benthic primary production in the Control sediment was not limited by predation, so the removal of predation as a potential factor made no difference.
Other studies reported a positive correlation between the abundance of E. cordatum (consuming microphytobenthos) and the chlorophyll-a content of its surrounding sediment [6,9,10,28]. In habitats where photosynthetically active radiation (PAR) is not limiting microphytobenthic production, this may follow from a stimulation of bacterial mineralization processes, increasing the porewater concentrations of inorganic nitrogen, so that algal growth outweighs consumption. Such gardening effect will be subject to seasonal variations in environmental conditions and heart urchin abundance and activity. Lower PAR and temperature in winter, for example, can hamper benthic primary production and slow urchin movement, respectively [29]. A repeat of our study in November/December may reveal if the influence of E. cordatum on the sediment–seawater solute exchange at our site in fact depends on seasonal changes in conditions for growth and production of microphytes or if what we have observed in May/June generally applies throughout the year.
Interestingly, both sediments, Control and Treatment, served as a sink for N2. Others have reported nitrogen fixation in ammonium-rich sediments, like those found in seagrass beds [30] or subtidal coastal sediments [31,32], and such fixation may be limited to microenvironments in which nitrogen becomes limiting [33]. As Bertics et al. [34] pointed out, however, sediments rich in organic matter and reduced substrates provide an unusual conundrum for anaerobic organisms—the excess electrons can damage cells and there is a need to regenerate electron carriers. Nitrogen fixation may be a mechanism for dissipating reducing power and maintaining an ideal intracellular redox state [35,36], so that nitrogen fixation is observed despite high ammonium concentrations.
The significant light–dark difference in the ammonium exchange of the Control sediment—a small uptake under conditions of darkness, but release in light—suggests an influence of photosynthesis on nitrogen cycling. This is in contrast to the interpretation of our light/dark O2 exchange data (negligible benthic photosynthesis, see above), and raises the question if our assumption of similar sediment O2 demand in light and darkness was valid. If the sediment O2 demand in light was greater than in darkness, then benthic photosynthesis may have played a role without leaving a measurable signature in the total sediment–seawater O2 exchange. Assuming that the ammonium and N2 concentrations in the sediment overlying seawater remained stable and independent of light, then the difference in the derived sediment–seawater flux must have resulted from changes in the sediment porewater solute concentrations. Phototrophs assimilating ammonium in darkness, but not in light, would then cause a light/darkness difference in the sediment–seawater ammonium exchange. Similarly, if more porewater N2 was to be consumed by diazotrophs in light than in darkness (energy limited N2 fixation [37]), then this would explain why the sediment uptake was greater in light than in darkness. Alternatively, a production of N2 via anammox in darkness would increase the porewater N2 concentration and so lower the rate at which the sediment removes N2 from the bottom seawater. Since this process also lowers the porewater ammonium concentration, it can explain both observations, a lower release or even uptake of ammonium, and lower uptake of N2 under conditions of darkness.
In conclusion, although foraging E. cordatum enhance the sediment–seawater solute exchange where and when they displace sediment particles, this effect does not necessarily outlast the disturbance event. At our subtidal site, at least in May/June, removal of the heart urchins did not alter the solute exchange across the surface of the sediment area that is not actively disturbed. This underlines the importance of evaluating the influence of bioturbators on ecosystem processes in the context of local environmental conditions, seasonal changes in these conditions and biological activity, urchin behavior, and population characteristics.
Author contributions
Evan Brown assisted in the field. K.V. designed the experiment, R.M. and M.S. with the assistance of Mohammad H. A. Usmani completed the laboratory sediment incubations. M.S. measured the inorganic nitrogen content of seawater samples, and R.M. and K.V. analyzed the data and wrote the manuscript.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The authors declare that the research has no financial or personal relationship with other people or organizations that can interfere with it.









 DownLoad:
DownLoad: