Critical analysis of electrohysterographic methods for continuous monitoring of intrauterine pressure

1.   Introduction

Preterm birth is a major problem in obstetrics, associated with a great majority of perinatal mortality and over half of perinatal and long-term morbidity ^[1,2]. Additionally, over the last couple of decades a significant increase in the worldwide preterm birth rate is visible ^[3,4]. Early prediction of the onset of preterm delivery by accurate pregnancy monitoring is crucial for prevention of preterm birth ^[5]. Early notification of problems allows physicians to intervene in a timely manner by prescribing rest, progesterone supplements, or tocolytic drugs. These treatments can in turn result in a significant reduction of preterm birth rates ^[5,6].

Insight into the time to delivery could be obtained by tracking the progression of uterine activity during pregnancy, by determining the frequency, duration, and amplitude of uterine contractions ^[7]. Accurate monitoring of the intrauterine pressure (IUP), which increases as a result of increased uterine activity, is a prerequisite for reliable contraction detection and analysis of additional parameters extracted from the EHG. When continuously measured over a prolonged period of time, the frequency, duration, and amplitude of uterine contractions can be used to reliably predict preterm delivery and prevent preterm birth throughout the last months of pregnancy; to this end ambulatory monitoring is required ^[8,9,10,11].

In clinical practice, the IUP is generally monitored by either indirect or direct measurement. The most widely used indirect method is external tocography, which measures the deformation of the abdominal surface using a tocodynamometer, a strain gauge transducer placed on the abdomen. External tocography can be used throughout pregnancy and delivery, as it is non-invasive. Deriving the IUP estimate from an indirect mechanical measure, however, is unreliable in obese patients and very susceptible to movement artifacts ^[12,13]. Patients must therefore remain steady during measurements, as movements affect the accuracy of the estimated amplitude, duration, and frequency of contractions. Movement artifacts can result in a low sensitivity and specificity, hampering accurate estimation of the uterine activity and the progression of pregnancy, and therefore making tocodynamometry unsuitable for long-term and ambulatory measurements.

A direct, quantitative measurement of the IUP can be obtained by placing an IUP catheter (IUPC) in direct contact with the amniotic fluid. The obtained IUP signal is accurate and currently serves as the gold-standard measurement. However, IUPC measurement requires rupture of the amniotic membranes and is thus performed only during delivery. Additionally, the use of an IUPC increases the risk of infections and can damage the uterus or the fetus ^[14,15]. Therefore, an IUPC should only be employed during delivery in complicated deliveries that require labor induction or augmentation ^[16].

Alternative methods for non-invasive uterine activity monitoring based on the electrohysterogram (EHG) are being developed for clinical use ^[17]. These EHG-based methods use the bio-electrical signals generated during contraction in the uterine muscle, or myometrium ^[18]. Myometrial cells can generate action potentials or can be excited by action potentials generated by a neighboring cell, resulting in propagation of action potentials through the myometrium. Propagation of action potentials through an adequate number of cells causes contraction of the uterine muscle and, consequently, an increase in IUP. The propagation of action potentials is reflected in the spectral properties of the EHG signal, whereas the number of cells involved in the contraction is proportional to the amplitude of the EHG signal ^[19]. Therefore, the EHG can be used to estimate the IUP increase associated with each contraction, providing essential information on uterine activity ^[20,21]. Additionally, the EHG can potentially indicate time to delivery, since the electrical resistance between the myometrial cells is relatively high during pregnancy, while at term low-resistance paths form, leading to effective contractions ^[10,22]. The use of abdominal electrodes makes the EHG technique non-invasive and, therefore, suitable for long-term uterine observation throughout pregnancy; it allows reliable measurements in obese patients and is less susceptible to movement artifacts than external tocography ^[23,24].

Various EHG based methods have been proposed to analyze the relation between electrical and mechanical activity of the uterus, comprising statistical approaches ^[25], filtering techniques ^{[26,27,28,29,30,31,32]}, fast Fourier transform, and wavelet transform-based methods ^{[23,33,34,35,36]}, as well as evaluation of nonlinear connectivity ^[9]. However, only recent studies have focused on EHG analysis as an alternative method for quantitative IUP estimation ^{[28,29,32,35]}.

Jezewski et al. used the root mean square (RMS) value of the EHG to estimate the uterine contraction pattern and compared it to a simultaneously recorded external tocogram ^[27,28]. A high correlation between the two signals was obtained, showing that the EHG could provide a reliable estimator for the the frequency of contractions. Skowronski et al. proposed an optimal linear filtering method using the EHG signal magnitude after low-pass filtering, followed by a Wiener filter, which showed a good resemblance to the simultaneously measured IUPC signal ^[29]. However, the method is unsuitable for long-term ambulatory measurements, because the Wiener filter requires a reference IUPC signal recorded during a 10 minute initialization period. Rabotti et al. used a spectrogram-based technique to obtain an IUP estimate that showed a high correlation with the simultaneously measured IUPC signal ^[35]. The method mimics the physiologic phenomena underlying the generation and propagation of action potentials, applying frequency compensation by scaling all spectrogram frequency bands relative to their central frequency. In addition, a second-order model was used to compensate for the influence of muscle fatigue and differences in electrical conductivity and contractile efficiency between individuals. Rooijakkers et al. proposed the use of the Teager energy (TE) operator after band-pass filtering to estimate the IUP using frequency compensation ^[32], retaining the original units of measurement in accordance with standard EMG force estimation ^[37]. This resulted in a higher correlation with the simultaneously measured IUPC signal compared to other algorithms from the literature, at a reduced computational complexity.

The aim of this paper is to determine the best composite method for EHG-based IUP estimation in an ambulatory setting by exploring the full design-parameter space defined by state-of-the-art algorithms from the literature. To this end, the defining parameters of all the algorithms are identified and, after determining the influence of these parameters, an optimal combination is selected for improved IUP estimation accuracy and reduced computational complexity, respectively.

The paper is structured as follows. Section 2 describes the recently published IUP estimation algorithms that allow for quantitative IUP estimation and describes their most defining parameters. In section 3, a set of quality measures is defined to determine both the estimation accuracy and computational complexity. Various techniques used to optimize each method for long-term EHG-based IUP estimation are provided in section 4. Section 5 presents the dataset of abdominal EHG measurements with simultaneous IUPC recordings that was used for validation. Section 6 shows the influence of the various defining parameters and compares the accuracy and complexity results for all algorithms before and after optimization. Finally, section 7 and section 8 contain the discussion and conclusion based on the obtained results.

2.   Methods from the literature

2.1.   TE-based IUP estimation

Rooijakkers et al. proposed the use of the TE operator to calculate a frequency-weighed EHG-based estimate of the IUP ^[32]. As a first step, the input signal is downsampled to 4 Hz after applying an anti-aliasing filter at 2 Hz to reduce the algorithm's computational complexity. Before IUP estimation, the influence of respiration artifacts and morphological changes of the ECG is reduced by band-pass filtering to obtain a clean EHG signal. The low and high cut-off frequencies of this filter were defined at $f_{\min} = 0.3\; \operatorname{Hz}$ and $f_{\max} = 0.8\; \operatorname{Hz}$ ^[32,38], respectively, providing the filtered EHG signal $x_f[n]$, where $n$ indicates the sample index. The instantaneous energy of the EHG signal $\Phi\left[n\right]$ uses the TE operator in its most basic form in the discrete time domain ^[39,40] and is defined as

The resulting signal $\Phi\left[n\right]$ spans only three consecutive samples of $x_f$ to calculate the instantaneous energy of the EHG signal, providing an excellent time resolution. The TE is proportional to both the square of the signal amplitude and the square of its frequency, and hence calculates the frequency-weighted energy of the EHG signal. Finally, the moving average of $\Phi\left[n\right]$ is calculated over a 30-second interval, after which the square root is taken to obtain the TE-based IUP estimate ($\operatorname{IUP}_{TE}$), defined as

with, $M \equiv 30\;$s, where the actual number of samples $M$ depends on the used sampling frequency ${fs}$. The resulting $\operatorname{IUP}_{TE}$ provides a physiology-based frequency-weighed energy estimate while retaining the original units of measurement in line with standard EMG force estimation ^[32,37].

2.2.   Spectrogram-based IUP estimation

Rabotti et al. proposed the use of the spectrogram to calculate the frequency-weighed energy of the EHG signal as an estimate of the IUP ^[35]. First, the time-frequency representation of the EHG signal $\rho[n, f]$ is calculated based on the squared magnitude of the short-time Fourier transform (STFT) with a Hamming window $w[m]$ of 70-second length defined as

The unnormalized first statistical moment $\Psi[n]$ is calculated by scaling $\rho[n, f]$ for each frequency interval in the range $\left[f_{\min} = 0.3\; \operatorname{Hz}, \; f_{\max} = 0.8\; \operatorname{Hz}\right]$ by its mean frequency $f$, as described by

By multiplying the in-band frequency intervals, which results in a band-pass filtering effect, $\Psi \left[n\right]$ uses the simultaneous change of both the frequency- and amplitude-related features of the EHG signal to determine the IUP wave estimate. Finally, a second-order polynomial model is used to improve the similarity between the between the first statistical moment of the EHG and the IUP reference.

2.3.   RMS-based IUP estimation

Jezewski et al. proposed a RMS-based IUP estimation algorithm, in which the EHG is first band-pass filtered between $f_{\min} = 0.05\;$Hz and $f_{\max} = 5\;$Hz, resulting in the filtered signal $x_f[n]$ ^[27,28]. Next, an initial IUP estimate $\widehat{ \operatorname{IUP}}_{RMS}$ is calculated as

where $w[m]$ is a Hamming window, which is used to smooth the estimate and reduce edge effects; $M \equiv 60\;$s is the length of the Hamming window dependent on ${fs}$; and $n$ is incremented in 3-second steps. Therefore, the resulting signal $\widehat{ \operatorname{IUP}}_{RMS}[n]$ has a sampling frequency of $1/3\;$Hz. Finally, $\widehat{ \operatorname{IUP}}_{RMS}[n]$ is resampled to the original sampling frequency, yielding the RMS IUP estimate $\operatorname{IUP}_{RMS}[n]$.

2.4.   Absolute-value-based IUP estimation

Skowronski et al. proposed a method for IUP estimation based on rectification of the EHG signal ^[29], in which the EHG signal is first normalized to have zero mean and unity variance. Next, the EHG signal is low-pass-filtered with cut-off frequency $f_{\max} = 2\;$Hz, down-sampled to a sampling frequency of 4 Hz, and rectified to obtain a first approximation of the energy in the EHG signal. After low-pass filtering with a cut-off frequency of $0.1\;$Hz to smooth the EHG energy signal, the signal is further downsampled to $0.2\;$Hz, resulting in the absolute-value-based IUP estimate $\operatorname{IUP}_{ABS}$. Finally, a Wiener filter $W(n)$ is used to better predict the IUP from the EHG signal. The Wiener filter coefficients are obtained by reducing the error signal $e(n) = d(n) - \operatorname{IUP}_{ABS}(n)*W(n)$ in 10-minute signal segments for each patient in a mean-squared sense. Here, $d(n)$ is the reference IUPC signal, and $*$ is the convolution operator.

3.   Quality measures

Quality measures need to be defined to allow comparison of the performance of the various algorithms and to determine the optimization options for each one.

3.1.   Accuracy measures

Two different measures are used to determine the accuracy of estimating the IUP for the various algorithms. Pearson's correlation coefficient $r$ gives a measure of similarity in shape between the estimated and reference IUP waveforms. It is defined as

with $x$ being the IUP estimate, $y$ the IUPC signal, $\overline{x}$ and $\overline{y}$ their respective means, and $N$ the total number of samples in the signal. The correlation coefficient $r$ is in the range $-1 \leq r \leq 1$, where a higher value defines a better similarity in shape between the two waveforms. The root-mean-square error ($\operatorname{RMSE}$), which is defined as

depends not only on similarity in shape but is also influenced by scaling factors and baseline offset. Before comparison, the basal tone of the IUP estimates are removed using the method described in ^[28], and their amplitudes are scaled to best match the IUPC signal. Additionally, the IUP estimate for each patient is shifted by a delay $\tau$ to compensate for the delay between the increase in bioelectrical activity and the resulting pressure increase in the uterus ^[18]. For each recording, the delay $\tau$ is obtained by maximizing $r$ between $x$ and $\bar{x}$, where $\tau$ is in the range of 0 s to 15 s.

3.2.   Complexity measure

The average number of multiplications per sample (MPS) is used as a measure of computational complexity. All operations that are more complex than a multiplication, such as division or square root, can be represented by a number of multiplications. Both division and square root have a complexity in the order of $O\left[n\right]$, where $n$ is the accuracy of a value in number of bits. Assuming an accuracy of 16 bits for both numerator and denominator, a division and square root are substituted by 9 and 17 multiplications, respectively ^[41]. All simple operations, such as addition, subtraction, or bit-shift, are estimated but not used in the analysis. The STFT can be represented as a sliding fixed-length window for which at each position a fast Fourier transform (FFT) is calculated. When the length of the STFT window $N$ is restricted to powers of 2, the number of multiplications of an FFT is in the order of $O\left[(N/2) \log_2(N)\right]$ ^[42,49]. With a window length $N = 2048$ samples, as required for the 70 s window defined by Rabotti et al., 8194 multiplications are needed to obtain the STFT for a single position of the sliding window ^[43].

4.   Optimization methods

4.1.   Optimization of IUP estimation accuracy

In an effort to determine the optimal method for EHG-based IUP estimation in an ambulatory setting, each of the algorithms presented in the previous section was implemented and optimized for improved IUP estimation accuracy and reduced computational complexity. To this end, the design parameters of each algorithm were selected, as presented in Table 1. Their influence on each algorithm was determined based on the definition of each parameter as given below. Finally, each algorithm was optimized for improved IUP estimation accuracy by maximizing the correlation coefficient $r$ between the estimated IUP and the IUPC signal, as described in section 3.

4.1.1.   Preprocessing

Only Skowronski et al. propose a preprocessing step other than filtering, which consists in normalization of the signal. However, it should be noted that this step assumes the entire signal segment to be available before analysis, which is not feasible in a real-time ambulatory setting. Therefore, normalization was omitted from the analysis performed in this paper.

4.1.2.   Filtering interval

Only part of the frequency spectrum of abdominally recorded biopotential measurements contains information pertaining to EHG signals. In these measurements, neither the upper nor the lower limit of EHG signals is exactly defined, and it can vary with the measurement method and electrode placement ^[33,44,45]. Furthermore, various additional signals and artifacts interfering with the EHG signal might negatively influence the accuracy of IUP estimation. These factors have resulted in filters with cut-off frequencies ranging from $f_{min} = 0-0.5$ Hz and $f_{max} = 0.8-5$ Hz ^{[18,28,29,35,38,44,45,46]} for a high-pass and low-pass filter, respectively. Optimizing the cut-off frequencies of the band-pass filter used for preprocessing was therefore performed in the 0 Hz to 5 Hz frequency range. Additionally, the influence of both the filter type and order on the optimal location of the cut-off frequencies was investigated.

4.1.3.   Frequency compensation

The methods of Jezewski et al. and Skowronski et al. have a flat frequency response, whereas the methods of Rabotti et al. and Rooijakkers et al. use frequency compensation to mimic the physiological frequency dependence of the EHG signal, to obtain a more accurate IUP estimate. All methods were tested with and without frequency compensation to determine its influence.

A differentiator can be used to implement a frequency corrective filter for both the RMS- and modulus-based methods, as it introduces a frequency dependence defined by $\dot{y}(t) = f\cdot y(t)$ ^[26,35]. This ideal differentiator can be closely approximated using alternative digital differentiation techniques ^[47]. The spectrogram-based method already contains frequency compensation, which is easily removed by omitting the multiplication with $f$ in (2.4) to obtain a result with a flat frequency response. Due to the intrinsic frequency weighing of the TE operator, no IUP estimate without frequency compensation can be computed for the method proposed by Rooijakkers et al.

4.1.4.   IUP smoothing

The presented IUP estimation methods either use a low-pass filter or apply a convolution with a window to smooth the final IUP estimate. For each method, we optimized the low-pass cut-off frequency as well as the shape (square or Hamming window) and length $M$ of the averaging window. The spectrogram-based method of Rabotti et al. intrinsically contains a smoothing window as part of the STFT operation and, low-pass filtering was therefore omitted.

4.1.5.   Postprocessing

Both Jezewski et al. and Rooijakkers et al. apply a first-order model to linearly scale the IUP estimate amplitude. Rabotti et al. applies a second-order model that allows for non-linear amplitude scaling. Skowronski et al. propose the use of a Wiener filter to create an improved IUP estimate. It should be noted that, as no IUPC reference signal is available in ambulatory measurements, the latter postprocessing method is not directly applicable on a per-patient basis in a long-term ambulatory setting.

4.2.   Optimization of computational complexity

For a fair comparison of the computational complexity of the algorithms presented in section 2, all algorithms were optimized for reduced computational complexity using a few basic methods. This reduction of the complexity was performed with minimal impact on the obtained estimation accuracy by limiting any single optimization to a maximum relative decrease in IUP estimation accuracy of 1%. As some of the optimizations are algorithm-specific, not all of them were applied in all cases.

The most straight-forward method to reduce the computational complexity of the algorithms is sample-rate reduction, or decimation, which utilizes a low-pass filter before downsampling to avoid aliasing. The complexity of all operations is reduced after decimation, but an overhead is introduced due to the required filtering step. Polyphase filters can be used to combine downsampling and filtering during decimation. This solution results in a reduction in filter complexity up to the decimation factor with respect to straight-forward decimation^[48,49].

The complexity of all the filters can be reduced by lowering the filter order, i.e. support width, or filter type. Changing the filter order affects the amount of retained out-of-band energy, which has a direct impact on the optimal cut-off frequencies. Therefore, the cut-off frequencies are adjusted to keep an optimal IUP estimation accuracy. IIR filters can be used instead of FIR filters to reduce the computational complexity at the cost of possible instability and non-linear phase distortion. Additionally, staged FIR filters can be used with a downsampling step in between to reduce complexity. A significant reduction in support width of the frequency compensation filter can be obtained without negative effects by reducing the relative magnitude error within the frequency band of interest only ^[47,50].

Various optimizations can be applied to the STFT calculation used in the spectrogram-based method. The overlap of consecutive STFT windows can be reduced from a maximum overlap of $N-1$ samples, as proposed by Rabotti et al., to $N/2$ samples, reducing the number of multiplications by a factor of $\frac{N-1}{N/2}$ ^[35]. This results in an implicit downsampling of the signal dependent on both overlap factor and window length, and might reduce the estimation accuracy. Additionally, using a rectangular window in the STFT of the spectrogram-based IUP estimation reduces the STFT to an FFT, with a complexity of $O\left[N\right]$, as described in ^[42].

Finally, various low-level optimizations can be applied to reduce the algorithm complexity. Sliding windows were implemented such that all multiplications by a single value are performed only once. In case of a symmetrical window, this reduces the number of multiplications by a factor of 2. For a square window or moving average, the computational load is reduced to a single addition, subtraction, and multiplication for each sample. Also, all multiplications and divisions by a power of 2 are replaced by a bit-shift operation. Finally, all divisions by a constant $K$ are replaced by a multiplication with a precalculated value $\widehat{K} = 1/K$.

Both the complexity measure in section 3.2 and the foregoing optimization steps assume integer calculations with a reduced word-length of 16 bits. Such calculations slightly influence the algorithm output accuracy due to (1) feature truncation and (2) variable truncation ^[51]. These effects, in addition to the high-level optimizations for reduced computational complexity may reduce the IUP estimation accuracy.

5.   Validation dataset

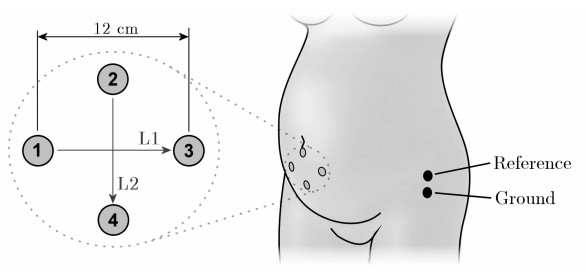
The same dataset as described by Rabotti et al. ^[35] was used for validation of the proposed algorithms. This dataset contains 21 measurements taken on nine women during labor at full gestation. All women signed an informed consent form. Recordings were made using four active unipolar electrodes configured as a diamond on the abdomen, with a ground and reference electrode placed on one side, as shown in Figure 1 ^[35]. The measured signals were bipolarized to eliminate a large portion of the noise affecting the EHG, the most important of which are maternal ECG, some movement artifacts, and electromagnetic noise ^[52]. Two bipolar leads $L1$ and $L2$ were obtained from the recorded signals in a horizontal and vertical direction, respectively. All electrodes, which were contact Ag-AgCl electrodes, were placed on the abdomen after skin preparation with a mildly abrasive paste to reduce skin impedance. The IUP was simultaneously measured by a Koala M1333A IUPC (Philips Medical Systems, Best, The Netherlands), which had been medically prescribed for insertion in the patient's uterine cavity. The EHG and IUP were both recorded at 1 kHz with a 20-bit discretization resolution using an M-PAQ (Maastricht Instruments B.V., The Netherlands). A subset of 17 recordings from seven patients was selected based on the requirements that the reference IUPC recorded a clear IUP waveform and that the EHG signal should not contain any significant measurement artifacts, e.g., due to broken wires or poor contacts. All recordings from a single patient were considered as one measurement, resulting in seven measurements ranging from 26 to 138 minutes with a total length of approximately 8 hours and 42 min.

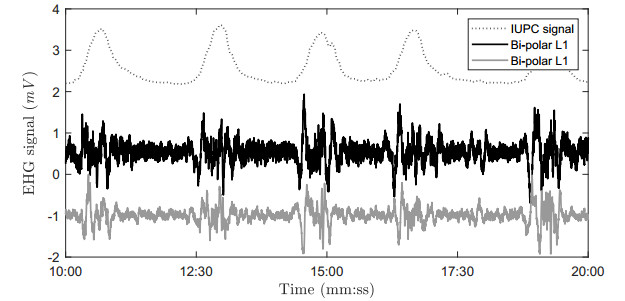
Both the EHG and IUPC signal were preprocessed prior to comparative analysis. The IUPC signal, which is adopted as the gold standard reference, was cleaned to minimize spikes caused by movement artifacts, using a non-causal centered median filter with a length of 5 s ^[28]. Both bipolar EHG signals as well as the IUPC signal were downsampled to 20 Hz using a Kaiser anti-aliasing filter at 8 Hz with a support width of 1 s. This is possible because all EHG signals are present in the 0.1 Hz to 5.0 Hz frequency band ^{[18,38,44,45]}. The peak spectral energy of the EHG occurs in the 0.42 Hz to 0.78 Hz range, depending on gestational age ^[33]. Figure 2 shows a recording segment with the reference IUPC signal as well as the recorded EHG signal.

6.   Results

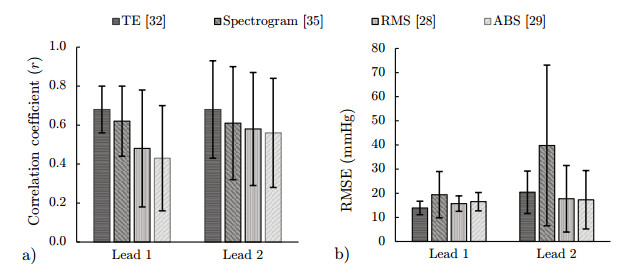
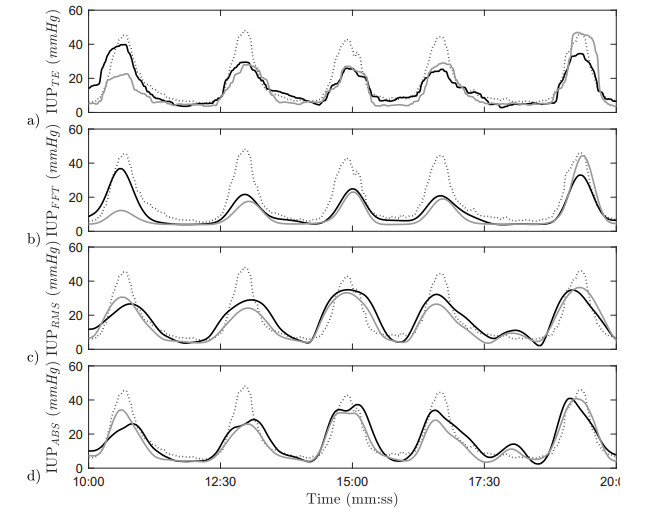
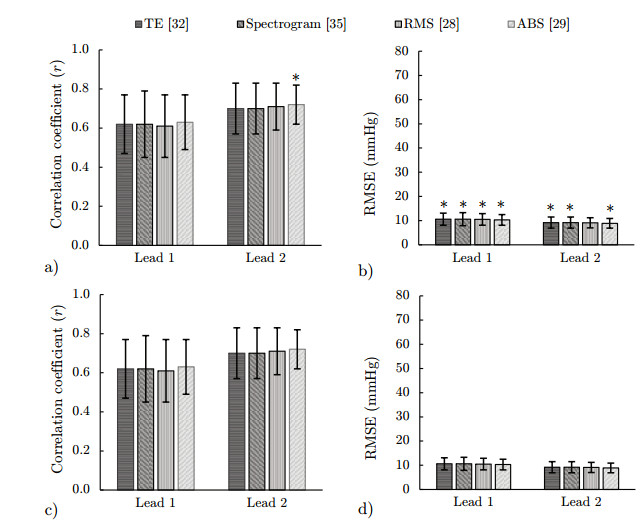
The algorithms from the literature were first compared prior to optimization for IUP estimation accuracy. The correlation coefficient $r$ and RMSE as well as their standard deviations are given in Figure 3 for the horizontal (L1) and vertical (L2) channels, respectively. Figure 4 shows an example of the IUP estimation results for each of the compared algorithms and a reference IUPC signal.

After optimization, the algorithms were again compared on IUP estimation accuracy, the results of which are shown in Figure 5. Fractional results for the number of multiplications are possible due to changes in the sampling rate as part of the algorithms.

Table 2 shows the computational complexity of the various algorithms at different stages. Because the optimizations for improved accuracy result in different parameter settings for each lead, the resulting computational complexity of an algorithm might differ between leads. The subsequent results were obtained using the absolute-value-based method, as it slightly outperforms the other methods after optimization.

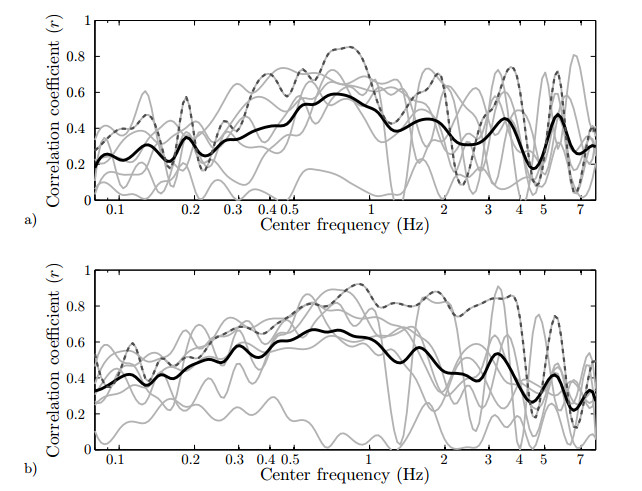
Figure 6 shows the correlation coefficient $r$ of the estimated IUP with the IUPC as a function of the frequency, where the frequency indicates the center of the band-pass filter used. The cut-off frequencies of the band-pass filter are set at $\pm 20\%$ of the center frequency, which is selected as a trade-off between filter support width and frequency specificity to evaluate the effect of the local frequency content on the IUP estimate. This allows for an analysis of the optimal filtering frequencies that takes into account the influence of both the EHG signal and that of noise and artifacts. It is clear from Figure 6 that the signal quality of L2 is better than that of L1 for all patients. Therefore, all further results are given for L2 only.

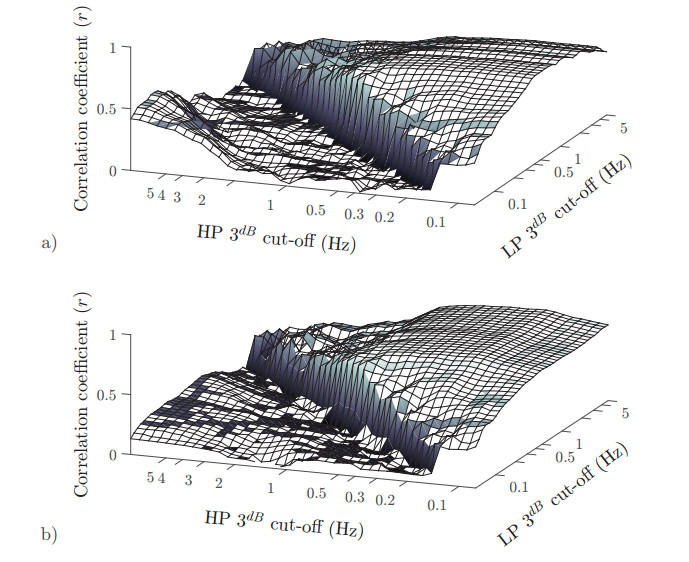
Figure 7 shows the influence of applying frequency compensation to the IUP estimation quality as a function of the low- and high-pass filter cut-off frequencies. The effect of the frequency compensation is clearly observable, as the IUP estimation quality is no longer affected by low-frequency noise, while the high-frequency noise of the ECG and other sources has a larger impact.

Figure 8 shows the influence of the choice of smoothing function on the IUP estimation quality. It can be observed that a smooth window allows for a slightly better IUP estimation than a square window or a low-order IIR filter.

Table 3 shows the parameters used for each of the algorithms after optimization for maximum IUP estimation accuracy and reduced computational complexity, respectively. The parameters shown for all algorithms are for lead L2, as it has proven to provide a significantly more accurate IUP estimation at a comparable complexity compared to L1.

7.   Discussion

Accurate continuous monitoring of the uterine activity is crucial for early prediction of the onset of preterm labor and prevention of preterm birth. Various non-invasive EHG-based IUP estimators have previously been presented allowing for contraction detection and analysis of additional parameters extracted from the EHG.

Four state-of-the-art methods for EHG-based IUP estimation are discussed in this paper and compared on IUP estimation accuracy and computational complexity to determine their applicability in a truly continuous ambulatory monitoring setting. We have defined the characteristic parameters of all methods and determined their influence on IUP estimation accuracy and computational complexity. All methods were optimized within their design space to improve their accuracy with respect to the simultaneously recorded IUPC signal and reduce their complexity.

To optimize the filter parameters, the influence of each frequency component in the EHG on the IUP estimation accuracy was determined. As previously reported, the EHG signal is present from 0.05 Hz to beyond 5 Hz with a varying signal-to-noise ratio (SNR) ^[18]. However, the signal above 1.2 Hz is typically strongly distorted due to the presence of the maternal ECG modulated by maternal breathing. This modulation is visible as amplitude and shape changes in the maternal ECG in phase with maternal breathing. Especially in a horizontal bipolar lead, in which the maternal ECG is most prominent ^[32], the effect of the first few harmonics of the ECG are clearly visible as dips in the IUP estimation accuracy in Figure 6. The accuracy of all signals below 0.3 Hz drops due to the presence of non-stationary noise sources, like maternal breathing, electrical activity of other smooth muscles, fetal activity, and baseline wander. For most patients, a spectral region is visible between 0.3 Hz and 1.2 Hz allowing for accurate IUP estimation. However, since no clear general filtering boundary can be defined, a 3rd order IIR filter was sufficient for all methods as both high- and low-pass filter. Because of the smaller contribution of the breathing artifacts and maternal ECG in the vertical measurement channel, and possibly due to a more prominent downward propagation direction of action potentials through the myometrium during delivery ^[53,54], the vertical bipolar lead in general allows for a more accurate IUP estimation.

The influence of applying frequency compensation to mimic the physiological phenomena underling the generation and propagation of action potentials was also investigated ^[35,32]. It reduces the influence of low-frequency noise in favor of higher frequencies, which in the presence of a prominent maternal ECG results in a strong reduction in IUP estimation accuracy above 1.2 Hz. For all base methods, applying frequency compensation resulted in a small increase of $r$ ($\pm$ 1%) while reducing the optimal cut-off frequencies of the band-pass filter. This has the added advantage that the sample rate can be further decreased, reducing the computational complexity.

We obtained the best IUP estimation accuracy using a smoothing window, although the difference is not statistically significant compared to the other smoothing methods proposed in the literature. The length of the applied window or the order and cut-off frequency of the applied window, however, clearly affect the accuracy and complexity of the IUP estimate. In a low-complexity algorithm it is therefore beneficial to apply a square window or low-order low-pass filter, significantly reducing the computational complexity. Finally, the choice of a simple postprocessing method can significantly influence the accuracy of the IUP estimate without adding much complexity; for instance, simple non-linear scaling can improve the correlation coefficient with the IUPC signal by as much as 10%.

The choice of sampling frequency has no significant impact on IUP estimation quality. However, it has a big impact on the computational complexity, because the complexity of various parts of the IUP estimation algorithms are $O\left[N^2\right]$. Therefore, reducing the sampling frequency at every point during IUP estimation is paramount, and can be done without significant negative effects on estimation accuracy. Reducing the sample rate is the largest contributor to reduction of complexity for all algorithms, especially when applying polyphase filters for downsampling, reducing the complexity by a factor 4 to 8 depending on the base method.

After our reduction of the computational complexity of each algorithm with a minimal loss of accuracy, the absolute-value-based method was found to provide both the highest IUP estimation accuracy and the lowest computational complexity. However, the difference with the other algorithms under evaluation is not significant in either accuracy or complexity. We can therefore conclude that the choice of a base method for IUP estimation is not as important as a correct choice of the filter cut-off frequencies, which strongly depend on the types of noise and artifacts present in the recordings. Additional parameters which can markedly improve the estimation accuracy are the order of the applied smoothing method, and non-linear postprocessing.

All of the analyzes performed in this paper envision a long-term continuous ambulatory monitoring environment, which in many cases will consist in measuring many days or weeks before delivery. Therefore, only single channel bi-polar EHG derivations were used to limit the computational complexity in estimating the IUP. Even so, as mentioned previously, only recordings made during delivery were used, because this is the only period in which a gold standard reference signal can be obtained. The signals which we would observe in an ambulatory setting might, therefore, be different in a number of ways compared to those in the used dataset. The EHG signal amplitude would be lower, with active bursts of uterine activity spaced further apart, shorter, less periodic, and with lower-frequency content ^[22,38]. Additionally, movement artifacts would play a more prominent role as patients are not limited in their movement. Any algorithm used earlier during pregnancy should therefore account for the changes in signal characteristics by adjusting the parameters of filtering interval, smoothing filter and postprocessing accordingly.

Apart from optimizations for use earlier during pregnancy, which would require acquisition of additional annotated data earlier in pregnancy, further improvement of the IUP estimation quality can possibly be obtained. This can consist in dynamic removal or suppression of the maternal ECG or its first harmonics, which would allow for use of a wider frequency band in estimating the IUP and is applicable throughout pregnancy. However, additional processing can possibly increase the computational complexity, and care should be taken to keep the overall complexity as low as possible to allow for long-term continuous monitoring.

8.   Conclusion

Accurate IUP estimation and reliable contraction detection are possible using abdominal EHG recordings. When continuously measured throughout the last months of pregnancy, EHG recordings can be used to predict preterm delivery in an effort to prevent preterm birth. Based on state-of-the-art methods from the literature, a design space exploration was performed to evaluate these methods on their suitability for continuous IUP monitoring. This resulted in an improved set of methods with a higher correlation with the simultaneously measured IUPC signal at a reduced computational complexity. We can conclude from the obtained results that a correct choice of the filter cut-off frequencies, the order of the applied smoothing, and the postprocessing method, based on the signal characteristics, is more important than the base energy estimation method. Although only by a small margin, the optimized absolute-value-based method was found to provide both the highest IUP estimation accuracy ($r = 0.72$) and lowest computational complexity (112.1 MPS). Because of its low computational complexity, it would be possible to obtain a continuous IUP estimate over a prolonged period of time in an ambulatory setting using this method. We can therefore conclude that long-term ambulatory monitoring of the uterine activity is possible using EHG-based methods.

Acknowledgments

This work was supported by the Dutch technology foundation STW and the NWO(TTW) HTSM grant 14663 (EWAM).

Conflict of Interest

The authors declare that there is no conflict of interest.