Experimental study on flexural behavior of concrete T-beams strengthened with externally prestressed tendons

1.   Introduction

External prestressing is defined as a prestress introduced by tendons located outside a section of a structural member, only connected to the member through deviators and end-anchorages. The first use with external steel tendons was in the 1950s, but after that it lay dormant for some time. Now external prestressing techniques with steel tendons have been widely used with success to improve existing structures in the world ^[1]. The main advantages using this technique are: higher utilization of small sectional areas, ease in inspection of the tendons and in their replacement and low friction losses ^[2]. Thus, this type of prestressing is becoming popular not only in new bridge construction but also as a strengthening method for existing concrete structures ^[3,4,5]. In recent years, some different strengthening techniques have been proposed. For instance, Hawileh et al. have studied the behavior of reinforced concrete beams strengthened with externally bonded hybrid fiber reinforced polymers ^[6], short-length CFRP plates ^[7] and hardwire steel-fiber sheets ^[8]. Externally strengthening method becomes more and more popular to retrofit the damaged structures.

To date, several investigators have reported about the theoretical and numerical method to calculate the flexural behaviour of reinforced concrete (RC) beam strengthened by external prestressing ^{[9,10,11,12,13,14,15,16]}, but limit experimental studies have be done. Among them, Tan and Ng ^[17] conducted tests on six identical RC T-beams strengthened in flexure using external prestressing tendons to study the effects of deviators and tendon configuration on the behavior of externally prestressed beam. Harajli et al. ^[18] performed several tests of external prestressed specimens without deviatiors, with one deviator and with two deviators to study the influence of deviators. Matupayont et al. ^[19] carried out tests on beams with different arrangements of deviators to demonstrate how large beam deflections cause secondary effects. Mutsuyoshi et al. ^[20] observed from test results of beams with two deviators provided at different spacings that the reduction in flexural resistance could be as high as 16 percent. Trinh ^[21] further observed the ultimate ductility of externally prestressed beams decreased with an increase in the amount of external tendons relative to the amount of internal tendons. Kwon et al. ^[22] examined the flexural behavior of externally post-tensioned lightweight agammaegate concrete (LWAC) beams under symmetrical top one-point, two third-point, and analogous uniform loading systems.

From the literature review, it can be seen that many studies have been done, but it is still not adequate. For instance, reference ^[17] studied the effects of deviators and tendon configuration on the behavior of externally prestressed beam, but only straight line tendon with two deviators were included. The effect of U shape line tendon with two deviators and different tensioning method on the behavior of externally prestressed beam were not studied. So, this paper will do such work to enrich the experimental results of different parameters on the effect of external strengthening method and give some advice on how to choose reasonable design parameters.

In this paper, an experimental study is carried out to evaluate the flexural response of RC T-beam strengthened with externally prestressed tendons, including the failure modes, load-deflection characteristics, load-strain curves, load carrying capacity, and ductility. The main parameters considered include the amount of deviators, the profile of external tendons, and the tension method. Some conclusions are drawn based on the results obtained from the experiment and can be used to guide the design and application.

2.   General description of the experiment

2.1.   Design of specimens

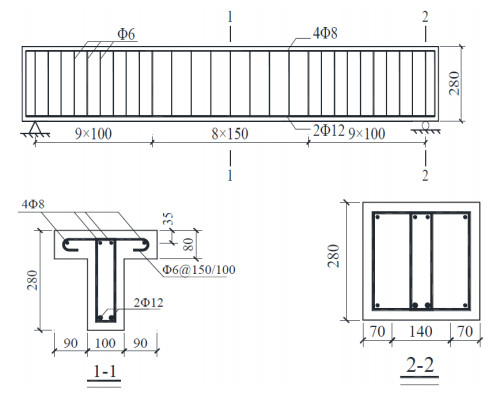
A total of six T-section RC beams strengthened with external tendons and one contrastive RC beam without external tendons were tested under four-point loading. All of the specimens are simply supported with total length of 3.2 m and calculated span of 3.0 m. The flange width and height of the section are 280 mm and 80 mm, respectively. The web width and height of the section are 100 mm and 200 mm, respectively. Figure 1 shows the geometric details of the testing beams. In all beams, the internal longitudinal reinforcement consisted of two 12-mm-diameter steel bars (Φ12 HRB335) at the bottom and four 8-mm-diameter steel bars (Φ8 HRB335) at the top. All the specimens were designed according to the principle of "strong shear capacity and weak bending capacity" to ensure flexure failure occurred before shear failure. The stirrups use Φ6 rebars with spacing of 100 mm in the bending-shear region near the support (from 0–1/3 L and 2/3 L–1L) and spacing of 150 mm in the pure bending region (from 1/3L–2/3L). The thicknesses of the protective layers of the concrete at the bottom and the top are 30 mm and 25 mm, respectively. The reinforcement details of the T-beam are shown in Figure 2.

Figure 1.  Basic dimensions of a T-beam specimen.

DownLoad: Full-Size Img PowerPoint

Figure 2.  Reinforcement details of the T-beam (unit: mm).

DownLoad: Full-Size Img PowerPoint

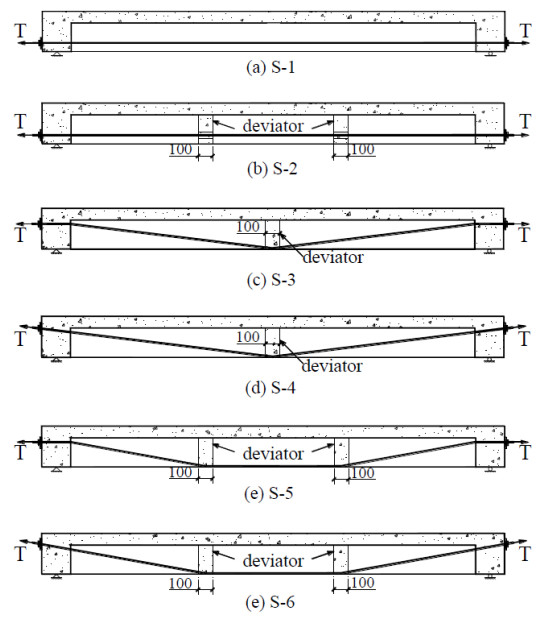
Two 9.5-mm-diameter prestressed steel strands with tensile strength of 1860 MPa were placed symmetrically with respect to the web, serving as the external tendons. Deviators are used to change the profile of the external tendons. According to the number of deviators, there are three types of tendon profile, namely, straight line along the beam, V shape line with one inflection point at the center of the beam, and U shape line with two inflection points at the load points. As respect to different profiles of tendons, there are two tension method: tilting tension and horizontal tension. The profiles and tension methods of external tendons are shown in Figure 3.

Figure 3.  Basic dimensions of a T-beam specimen.

DownLoad: Full-Size Img PowerPoint

The designed strength grade of the concrete is C40. In each cubic metre of concrete, the weight of the water, cement, fine agammaegate and coarse agammaegate are 200 kg, 571 kg, 520 kg and 1159 kg, respectively. When pouring the concrete beam, six 150 × 150 × 150 mm standard cubic specimens were also poured simultaneously. Standard test results showed that after curing for 28 days, the average cubic strength of the concrete is 53.4 MPa.

The major varying parameters of the specimen include the tendon profile, the tension method and the number of deviator. The experimental parameters are summarized in Table 1. Note that, the location of the deviators vary as the amount, when there is one deviator, it is located at the mid-span of the beam; when there are two deviators, they are placed at the two loading points of the beam.

Table 1.  Experimental parameters of specimens.

Group	Specimen No.	Prestress/MPa	Number of deviator	Tension method	Profile of tendon
G1	S-0	-	-	-	-
G2	S-1	930	0	Horizontal tension	Straight line
	S-2	930	2	Horizontal tension	Straight line
G3	S-3	930	1	Horizontal tension	V shape line
	S-4	930	1	Tilting tension	V shape line
G4	S-5	930	2	Horizontal tension	U shape line
	S-6	930	2	Tilting tension	U shape line

---

 | Show Table

DownLoad: CSV

All seven specimens were divided into four groups. The first group G1 includes one RC T-beam without external tendon which was designed as a contrastive specimen. The second group G2 includes two specimens with straight line external tendons, the variable parameter of this group is the number of the deviator. The third group G3 includes two specimens with V shape external tendons and the variable parameter of this group is the tension method. The fourth group G4 includes two specimens with U shape external tendons and the variable parameter of this group is also the tension method.

2.2.   Loading method

After 28 days curing of the specimen, the external tendons were installed through the pre-buried pipes, the profile of the tendon is shown in Figure 4. Then, the pretension force were applied at both beam ends as shown in Figure 5 with control prestress of 0.5 fu, where fu is the tensile strength of the external tendon which is 1860 MPa. During the tensioning, the tendon elongation and the concrete strain at the top of the beam are measured simultaneously to prevent concrete crack.

Figure 4.  Profile of the external tendon.

DownLoad: Full-Size Img PowerPoint

Figure 5.  Tensioning of the external tendon.

DownLoad: Full-Size Img PowerPoint

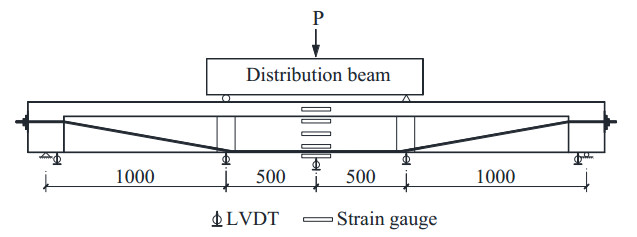
The load was provided by a 100 tons hydraulic testing machine and transferred to the specimen at two points by a distribution beam as shown in Figure 6. The magnitude of the load was recorded by a load cell attached to the testing machine. The load was applied monotonically at an increment of 5 kN before concrete cracking and maintained for 5 minutes to record the testing results. Force control method was adopt before the load reaches 80% of the calculated ultimate load, while displacement control method was adopt after the load reaches 80% of the calculated ultimate load.

Figure 6.  Loading device.

DownLoad: Full-Size Img PowerPoint

2.3.   Test points arrangement

Five linear variable differential transformers (LVDTs) were used to measure deflections at the mid-span, loading points, and two supports of the specimen (Figure 7). Ten BX120-100AA strain gauges were attached on the surface of the concrete at the central section as show in Figure 7. All of the strain and displacement results were recorded by a TDS 530 data logger (Tokyo Measuring Instruments Lab.). For each static load step, the concrete strain, deflection and crack width were measured.

Figure 7.  Schematic diagram of test points.

DownLoad: Full-Size Img PowerPoint

3.   Experimental results and discussions

3.1.   Failure mode

All seven specimens show approximately similar failure behaviour, so only the failure modes of specimens S-0 and S-1 are described hereinafter.

For specimen S-0, when the load reached 15.77 kN, an initial micro crack perpendicular to the bottom of the beam was observed in the pure bending region, and this load is termed as cracking load. As the load increased further, the deflection and concrete strain of the specimen increased continuously, the number of cracks in the pure bending region were also increased and the cracking region expanded from the pure bending region to the bending-shear region. When load reached approximately 34.73 kN, the stress of the steel reinforcement in the tensile region of the beam reached its yield strength, and this load is termed as yield load. After that, the steel reinforcement could not carry load anymore and the strain of the reinforcement increased significantly leading to the width and length of the cracks increased rapidly. In the last, when the load reached 48.66 kN which is termed as ultimate load (load carrying capacity), the cracks expanded through the section's tensile part to the compressive part and the specimen failed in a typical flexural failure with large deflection. The maximum crack width was up to 3.50 mm and the crack spacing was approximately 150 mm when the specimen failed. The failure mode of S-0 specimen is shown in Figure 8.

Figure 8.  Failure mode of S-0 beam.

DownLoad: Full-Size Img PowerPoint

Generally, the failure process of the specimens strengthened with external tendons are similar to that of the un-strengthened RC beam S-0. All of the strengthened specimens undergone the following steps: (1) formation of micro flexural cracks; (2) propagation of cracks; (3) yield of tensile steel reinforcement and widen of cracks; (4) beam failure due to large deflections. The cracking, yield and ultimate loads of the strengthened RC beams were larger than that of the un-strengthened RC beam due to the effect of the external prestressing. Taking specimen S-1 as an example, when the load increased to 40.64 kN, the first micro crack appeared at the midspan. As loading increased, the number of cracks at the midspan in the pure bending region increased continuously. When the load reached 72.24 kN, the longitudinal reinforcements in the tensile part began to yield, and the deflection of the specimen and stress of the external tendon increased rapidly, so the increased load was primarily carried by the external tendons. When the load reached 103.97 kN, the crack and deflection of the specimen became very large, and the specimen failed as shown in Figure 9. At last, the maximum deflection at the midspan was 33.76 mm. Compared with specimen S-0, the cracking and ultimate loads of specimen S-1 increased by 157.7% and 113.6%, respectively. Experimental observations and failure modes of other specimens strengthened by prestressed external tendons were similar to those of the specimen S-1 and are therefore not elaborated. The test results, such as cracking and ultimate loads, stresses of concrete, ultimate deflections at the midspan are summarized in Table 2.

Figure 9.  Failure mode of S-1 beam.

DownLoad: Full-Size Img PowerPoint

Table 2.  Summary of the test results.

Specimen No.	Cracking state			Ultimate state
	Cracking load/kN	Deflection at midspan/mm	Maximum tensile strain of concrete/10-6	Ultimate load/kN	Deflection at midspan/mm	Maximum tensile strain of concrete/10-6
S-0	15.77	1.30	158	48.66	38.66	1307
S-1	40.64	1.68	106	103.97	33.60	2208
S-2	45.42	2.92	254	112.35	37.44	2357
S-3	41.22	2.94	120	95.31	25.24	1774
S-4	40.19	3.12	268	93.75	22.78	2761
S-5	38.79	2.12	255	100.79	26.06	2113
S-6	40.75	2.56	219	107.79	24.26	2133

---

 | Show Table

DownLoad: CSV

3.2.   Load–deflection curves

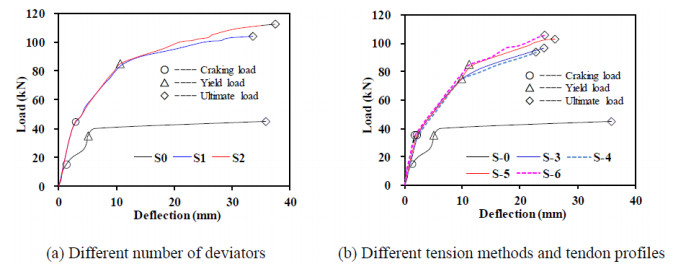
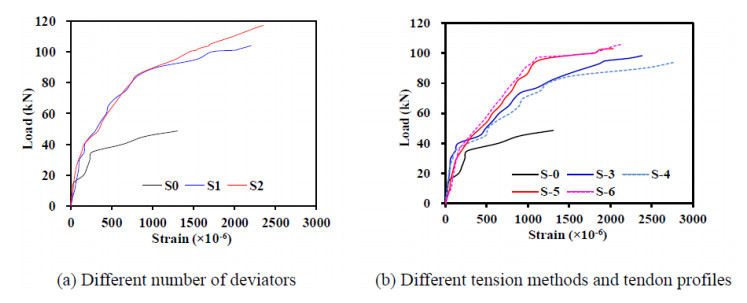
Load (P)–deflection (Δ) curves for various number of deviators, tension methods and tendon profiles are shown in Figure 10. Before the concrete cracks, the load-deflection curves for the reinforced RC beams with external tendons are essentially identical. Due to the strengthen effect of the external prestressing, the deflections of beams strengthened with external tendons were increased slower than that of the un-strengthened beam. For un-strengthened beam, the deflection increased rapidly after reinforcement yield and the specimen failed quickly.

Figure 10.  Load-deflection curves.

DownLoad: Full-Size Img PowerPoint

The effects of tendon profile are examined by comparing the test results of beams S-1 and S-2 as shown in Figure 10a. It can be seen that when the load is less than yield load, the deflection-load curves of S-1 and S-2 are consistent with each other. And when the load is larger than the yield load, the differences between the deflection-load curves of S-1 and S-2 increase as the load increases. The reason is that when the load was less than the yield load, the deflection of the beam was very small, so the external tendons and the deviators in S-2 were separated. However, when the load was larger than the yield load, the deflection of the beam increased rapidly and led to the external tendons attach to the deviators, so the deviators in S-2 began to take effect. The ultimate load of specimen S-2 is 112.35 kN which is increased by 8.1% compared to that of the specimen S-1. So, deviator has certain effect on the ultimate load of strengthened RC beam.

The effects of tension methods are examined by comparing the test results of beams S-3 and S-4, S-5 and S-6 as shown in Figure 10b. It can be seen that, the differences between the load-deflection curves of S-3 and S-4, S-5 and S-6 are very small, which indicate that the tension method of external tendons have little effect on the mechanical behaviour of the strengthened RC beams. By comparing S-3 and S-5, S-4 and S-6, it also can be seen that the number of deviators have significant effect on the ultimate load of strengthened RC beam. The ultimate loads of specimens S-5 and S-6 with two deviators are 100.79 kN and 107.79 kN which are increased by 5.7% and 15.0% as respect to the counterparts of specimens S3 and S4 with one deviator.

3.3.   Load–strain curves

Figure 11 shows the maximum tensile strain at the bottom of the beam versus the applied load. In the initial stage of loading, i.e., before the cracking load has been reached, the concrete strains of the un-strengthened and strengthened beams increase linearly as the load increases. After the cracking load has been reached, the concrete strain increases nonlinearly as the load increases. The maximum strain of an un-strengthened beam is significantly less than that of a strengthened beam.

Figure 11.  Load-strain curves.

DownLoad: Full-Size Img PowerPoint

By comparing Figure 11 and Figure 10, it can be seen that the strain-load curves are similar to the deflection-load curves. The tendon profile has limit influence on the cracking and yield load, but have significant effect on the ultimate load of the strengthened beam.

3.4.   Load carrying capacity

The tested cracking, yield and ultimate loads of specimens are listed in Table 3. From the table, it can be seen that the strengthening method with externally prestressed tendons can effectively increase the crackling, yield and ultimate loads of the RC beams. The cracking, yield and ultimate loads of strengthened beams increased approximately by 146%–188%, 108%–147% and 93%–131%, respectively. Among the specimens, the RC beam strengthened with straight line tendons and two deviators (i.e. beam S-2) has the maximum ultimate load, while the RC beam strengthened with V-shape tendons and one deviator (i.e. beam S-4) has the minimum ultimate load. It also can be seen that RC beams strengthened with U-shape tendons have better flexural bearing capacity than the beams strengthened with V-shape tendons.

Table 3.  Test results of load carrying capacity.

Specimen No.	Cracking load/kN	Percentage increase of cracking load	Yield load/kN	Percentage increase of yield load	Ultimate load/kN	Percentage increase of ultimate load
S-0	15.77	-	34.73	-	48.66	-
S-1	40.64	158%	72.24	108%	103.97	114%
S-2	45.42	188%	75.28	117%	112.35	131%
S-3	41.22	161%	77.25	122%	95.31	96%
S-4	40.19	155%	75.19	116%	93.75	93%
S-5	38.79	146%	80.34	131%	100.79	107%
S-6	40.75	158%	85.68	147%	107.79	122%

---

 | Show Table

DownLoad: CSV

3.5.   Ductility analysis

Throughout the test, the prestressed external tendon demonstrates the mechanical property of linear elasticity. The ductility of the structure is normally represented via a displacement ductility coefficient denoted by μ_Δ = Δu/Δy. Where Δy is the yield displacement of the beam defined as the deflection when the ordinary tensile reinforcement reaches its yield strength. Δu is the deflection at the midspan when the load reaches the ultimate load of the beam. The calculated displacement ductility coefficients of the specimens are listed in Table 4.

Table 4.  Displacement ductility coefficient calculation results.

Specimen No.	Profile of tendon	Δy/mm	Δu/mm	Δu/Δy	Percentage decrease of ductility
S-0	-	5.07	38.66	7.63	-
S-1	Straight line	7.66	33.60	4.39	42%
S-2		8.54	37.44	4.38	43%
S-3	V shape line	10.7	25.24	2.36	69%
S-4		9.86	22.78	2.31	70%
S-5	U shape line	11.02	26.06	2.37	69%
S-6		11.18	24.26	2.17	72%

---

 | Show Table

DownLoad: CSV

From the table, it can be seen that the strengthened beams are less ductile than un-strengthened beam. Compared with the un-strengthened beam (S-0), the ductility of the strengthened beams are decreased from 42% to 72%. It also can be seen that the profile of tendon has the most significant impact on the displacement ductility coefficient, the coefficients of strengthened beams with U shape and V shape external tendons decreased by approximately 70% compared with the un-strengthened beams, while the percentage decrease of ductility for the beams with straight line external tendon are approximately 40%. In addition, tension method of external tendon nearly has no effect on the displacement ductility coefficient.

4.   Conclusions

From the experimental study carried out on simply supported externally prestressed RC beams, the following conclusions can be drawn:

(1) Compared with the un-strengthened RC beam, the cracking load, yield load and ultimate load of beams strengthened with external tendons increased by about 146%–188%, 108–147% and 93%–131%, which shows that strengthening with externally prestressed tendons is a very effective method to improve the ultimate bearing capacity and mechanical behaviour of the RC beam.

(2) Deviator and tendon profile have a certain effect on the bearing capacity and ductility of the beam. For the specimens strengthened with straight line external tendons (group G1), the ultimate loads of the specimen with two deviators is 8.1% larger than that of the specimen with one deviator. The average ultimate loads of specimens with U shape line tendon (i.e. two deviators) are 10.3% larger than that of the specimens with V shape line tendon (i.e. one deviator). And the ductility of both the specimens strengthened with V shape line and U shape line tendons are 47.4% lesser than that of the specimens strengthened with straight line tendons. Among the six strengthened beams, S-2 has the maximum ultimate load and good ductility, so the strengthen parameters with straight line external tendon and two deviators are recommended. Such results have given some guidelines of how to choose the amount of deviators and the profile of the tendons.

(3) Tension method of the external tendon nearly has no effect on the bearing capacity and mechanical behaviour of the RC beams. So both tilting tension method and horizontal tension method can be used in engineering application.

(4) Further investigations need to be carried out to acquire a simplified method for predicting the load carrying capacity of the concrete beams strengthened with externally prestressed tendons based on the experimental study and detailed FE analysis.

Acknowledgments

The research described in this paper was financially supported by the National Natural Science Foundation of China (No. 51608135), the Science and Technology Program of Guangdong Province (Grant No. 2010A040308005), and the Natural Science Foundation of Guangdong Province (Grant No. S2012010009615).

Conflict of interest

All authors declare no conflict of interest in this paper.