Damping force and energy recovery analysis of regenerative hydraulic electric suspension system under road excitation: modelling and numerical simulation

1.   Introduction

Driving on the road, vehicles will generate vibrations under the different disturbances, such as the road roughness, braking force and acceleration etc. for commercial vehicles, only 10%-16% of fuel energy is used for driving, most of the energy is wasted on the thermal exhaust. Among them, the kinetic energy loss by the shock absorber is the main energy dissipation ^[1]. If the dissipated vibration energy is about 400 watts in a passenger car and the energy harvesting efficiency is about 60%, the fuel efficiency improvement can reach 2.5% ^[2], which is very considerable. In the past several decades, researchers have made lots of investigations about the power dissipated of suspension system.

Segel and Lu ^[3] analysed the influence of the road surface act on the vehicle's driving resistance when the car is driving on road. It is concluded that when the car is driven at a speed of 48 km/h, the suspension system dissipates approximately 200 W of energy for 4 wheels. Browne and Hamburg ^[2] studied on the energy dissipation in automotive shock absorbers of a running vehicle on urban road. It is found that each hydraulic shock absorber dissipates approximately 40-60 Watts. Hsu ^[4] discussed the application of electric motors which were used as the main actuators of active suspension systems for road vehicles. The results show that the active system on a midsize car can recover about 100 W of power per wheel on motorway. Yu et al. ^[5,6] simulated and analysed the performance of a car. When the car is driven by a speed of 72 km/h on the Class C road, it is found that the energy dissipated by the suspension is about 651 kJ. Zhang ^[7] built a dynamic simulation model of the suspension system to test the average recoverable energy. According to the ISO8608, when the vehicle speed is 30 km/h at the Class A, B, C, D and E roads, the recoverable power are 2.08 W, 8.33 W, 33.34 W, 133.37 W, and 533.21 W, respectively. Khoshnoud et al. ^[8] estimated the power dissipated in a 2 degrees of freedom (DOF) vehicle suspension model, which shows the regeneration potential of per damper is around 280 W. The results indicate that suspension energy recovery technique has great potential to convert vehicle vibration which normally wasted as heat into electricity.

According to the discovery of the enormous potential for vibration energy recovery in automotive vehicles, researchers propose sorts of regenerative shock absorbers, such as the linear electromagnetic type ^[9,10], the ball-screw type ^[11,12], the rack-pinion type ^[13,14] and hydraulic electric type ^[15,16]. However, Gupta et al. ^[17] studied that the power density of the electromagnetic coil shock absorber is insufficient for vehicles, which means that it cannot provide enough damping for a vehicle. In addition, the small magnetic pole gap may cause system damage ^[18]. As for the ball screw type, the rotational friction caused by the positive and negative rotation of the motor will reduce the durability of the entire system ^[19]. Although the rack-pinion type has a good fitting relationship and high regenerative efficiency, the rack and pinion will fail to response the excitation from road when the road surface excitation is too large ^[20].

Therefore, the hydraulic regenerative shock absorber has attracted widely attention due to its stable work and compact structure ^[21,22]. Fang et al. ^[23,24,25] developed a kind of hydraulic electric shock absorber, which can rectify the fluid flow by using accumulator and check valves. In this system, the damper force is modelled, which caused by pressure drops in rectifier and accumulator. The deviation between simulation results and test results cannot be ignored when the excitation is large. Therefore, the fluid losses in cylinder should be considered in their studies. Li et al. ^[26] optimized the flow oscillation in cylinder by modelling the parameters of check valves, flow rate and pressure. This model can be used to analyse the performance of power regeneration. However, they did not consider the effects of accumulator and the regeneration efficiency of this test is only about 30%. More comprehensive model needs to be built to optimize the regeneration performance. Wang et al. ^[27] designed a novel regenerative hydraulic shock absorber system. A model which takes into account the impacts of the dynamics of hydraulic flow, rotational motion and power regeneration is developed. It can be found that this system achieves recoverable power of 260 W with an efficiency of around 40% under sinusoidal excitation of 1 Hz and 25 mm amplitude when the accumulator capacity is set 0.32 L with the load resistance 20 Ω. In order to obtain a better damper performance in the hydraulic regenerative system, Ahmad and Alam ^[28] analysed the influences of applied components used in the system such as hydraulic cylinder, hydraulic motor and hydraulic accumulator. Zhang et al. ^[29] proposed a semi-active regenerative suspension system. This model takes into account the hydraulic losses in hydraulic system such as throttle resistance of valves, frictional resistance of pipe lines and resistance of motor. Zheng et al. ^[30] analysed a kind of regenerative hydraulic electric shock absorber. Key parameters of this system are optimised based on orthogonal method and the recoverable power can achieve average power of 331 W at 1 Hz-25 mm sinusoidal excitation in the system, which is approximately 65% efficiency. Zou et al. ^[31] mainly focused on the modelling and ride analysis of a 7-DOF full vehicle suspension model integrated with the energy regenerative shock absorber. And the characterization of system is given based on a parametrical analysis under a sinusoidal excitation. Abdelkareem et al. ^[32] analytically discussed the potential power content of a class-6 heavy-duty truck with respect to different driving circumstances. Given the results, a potential power content of 71-434 W and 287-1733 are available for ISO road grades of C and D, respectively, for a fully loaded truck.

In previous researches and studies, the vehicle suspension travel is defined as a variety of amplitudes and trends, such as step, ramp, sinusoidal, triangular, and periodic waves. As a basis for comparison, the predefined excitation using one of the mentioned waveforms with a given frequency and amplitude are sufficient for evaluating the performance of a given suspension system or shock absorber system but the realistic excitation conditions are insufficiently considered in the study of vehicle suspension system or regenerative shock absorber system. In addition, it is worth noting that damping characteristic is also important for the study of comfort and hand stability. So, the damping force of system needs to be effectively analysed to satisfy the requirement of vehicles to the suspension system. Therefore, this paper addresses a more comprehensive dynamic model of a RHES system. In Section 2, the system design and structure layout are proposed. Then, the system model is built in Section 3, which includes road profiles model, quarter car model and power regeneration model. Based on the proposed system model, key parameters of RHES system are analysed in Section 4, including motor displacement, accumulator capacity and electrical load, which mainly focus on the suspension behaviour, damping force and power regeneration. Finally, the discussion and change laws of RHES performance are concluded in Section 5 and Section 6.

2.   System design

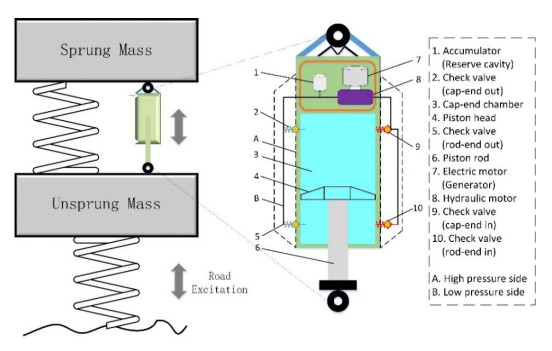
As shown in Figure 1, a RHES system is designed including suspension, hydraulic cylinder, check valves, accumulator, hydraulic motor, generator and suspension system. This system is used to represents the traditional suspension damper. With the excitation of road up and down, the fluid in the tank is forced to flow into the cylinder. The fluid only flow into the pipelines in one direction due to the adjustment of check valves. The accumulator can make the oscillating flow steady to provide a stable work condition for the motor. At the same time, the generator can output electric power with the rotation motion of hydraulic motor.

3.   Modelling of RHES system

The road surface roughness is the key source of vibration for the RHES system when vehicle is travelling on real roads, and the shock absorber experienced vibration is extremely dependent on the road conditions and vehicle driving speeds. The following sections detail the modelling method applied for RHES system, which includes the random wave spectra road profiles model, the quarter car model and the power regeneration model.

3.1.   Road profiles model

In 1995, the contemporary international standard, ISO 8608 was standardised as a road roughness assumption for the measured vertical road profile data from various roads and highways, due to classification of roads into eight classes as stated by their unevenness, equal intensity of road unevenness in the whole mathematical problems in Engineering range of wavelengths, and a general form of the fitted PSD was given. Road roughness can be classified from A to H. By comparing the PSDs associated with the classes, roads in smoother highways with a minimal degree are defined as high quality (very good or good) in Class A and B whereas in Class H roads with larger degrees of roughness state as extremely poor condition. Based on ISO 8608, the complete statistical description of road profiles is sufficient to specify its second order moments. Here, this requirement is satisfied by assuming that the road irregularities possess a known single-sided power spectral density, and can be approximated in form of:

Where Ω is the angular spatial frequency (cycles per meter), L_w is the wavelength, varying from a few metres to thousands of metres, and Ω = 2π/L_w, w denotes as waviness, and the undulation exponents (waviness index) are set in the range from 1.8 to 3.3, and w = 2 is set for most of the road surface at constant velocity. Φ(Ω₀) (m²/(rad/m)) provides a measure for the roughness of the road at the reference wave number Ω₀ = 1 rad/m, and n = Ω/2π is the spatial frequency with n₀ = 0.1cycle/m.

From Eq 1, it indicates that the increase of waviness w helps the longer wavelengths to become more observable while it suppresses the roughness at the shorter wavelengths. For this reason, a three-division method fits much better to the simpler single sided spectrum which can be considered to provide an opportunity for approximating and making an initial judgement of the road surface roughness. It adopts the following standard formulation to describe road roughness PSD, more involved function:

In Eq 2, Φ(Ω) is the discrete PSD in spatial domain at the reference angular spatial frequency, Ω₁ and Ω_N are the limit of the angular spatial frequency. The ISO suggested Ω₁ = 0.02π (rad/m) and Ω_N = 6π (rad/m) and other presented parameters keep the same definition in this Equation. Typically for modelling Eq 2 w₁ and w₂ are set as the values of 2 and 1.5 respectively. A large range of power spectral densities can be generated by using Eq 2. Throughout a large number of measurements, ISO 8608 standard lists a classification of road roughness in term of angular spatial frequency Ω, as shown in Table 1.

In order to simulate the effect of road roughness (PSD values), the geometric mean values in Table 1 are used for the performance evaluations of RHES system.

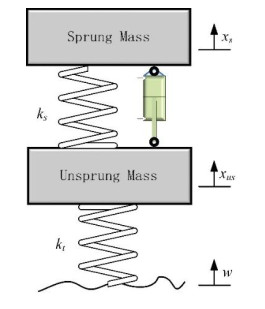
3.2.   Quarter car model

It consists of a single sprung mass (vehicle body, m_s), unsprung mass (tyre & wheel mass, m_us), the spring/tyre stiffness (k_s/k_t), and damping (c) in suspension system. w defines as the road disturbance. The values of these parameters are shown in Table 2:

3.3.   Power regeneration model

3.3.1.   Hydraulic flows

The suspension travel is the relative deflection between sprung mass x_s and unsprung mass x_us. Therefore, the movement of piston is expressed by:

When the shaft moves up and down, the volume change of cap-end chamber V_A and rod-end chamber V_B can be calculated by:

Where, X₀ refers to the starting level of the piston. A_A and A_B are the areas of cap-end and rod-end on both sides of piston, which can be calculated by:

Where, D and d are the diameter of piston and rod, respectively.

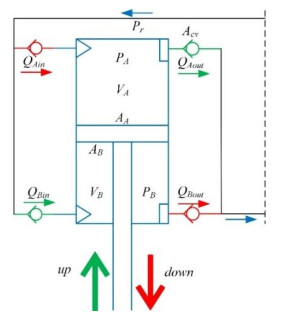
The processes of fluid flows in designed hydraulic system is shown in Figure 3. According to the Bernoulli's principle:

Where P is the pressure, ρ is the fluid density, v_f is the flow speed, h is the elevation of the point above a reference plane. The flow in cylinder and check valves can be expressed by:

Where, C_cv and A_cv are the flow coefficient and the area of inline check valve port. P_A, P_B and P_m represent the pressures at the cap-end chamber, the rod-end chamber and the motor inlet respectively. P_r is pressure in return pipeline.

Considering the fluid compressibility in hydraulic elements, the pressure out of the cylinder during the piston motion can be simultaneously expressed:

Where, β_A and β_B are the effective bulk modulus in cap-end and rod-end chambers. In general, there are many empirical formulas for the effective bulk modulus. According to the RHES is designed as low-pressure system (under 100 bar), Boes's model ^[33] is applied to determine the bulk modulus of the fluid in the cylinder and motor:

Where, reference bulk modulus β_ref and reference pressure P_ref is constant, whose value are chosen by the modelling principle of low pressure ^[34].

3.3.2.   Gas-charged accumulator flow

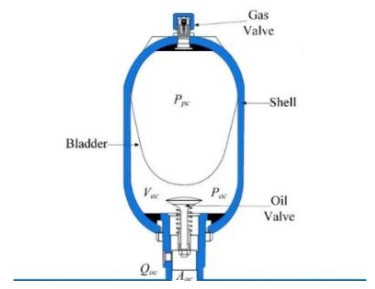
The flow rate and pressure in can significantly oscillate due to the differences of the piston area and annulus area in cylinder chambers, and then cause the different fluid flows.

As shown in Figure 4, a hydraulic accumulator is mounted on the inlet of the motor to adjust the pulsation of the fluid flow and explore its effect on the hydraulic behaviours and power regeneration. The pressure and volume variation of accumulator fluid can be written as:

Where V_ac0 is the volume of accumulator, P_pc is pre-charged pressure to accumulator, k_ac is the gas specific heat ratio of gas-charged accumulator, P_ac is the fluid pressure of the accumulator, and the fluid flow of accumulator can be written as:

The variation of total volume in accumulator is:

Fluid flow to accumulator:

Where C_ac is the accumulator flow coefficient, A_ac is the area of the accumulator inlet port.

3.3.3.   Hydraulic pipeline flows

Hydraulic pipeline is the necessary component to link the whole hydraulic system. According to the Darcy-Weisbach formula, the head loss along the pipeline is as follows:

Where L is the length of pipeline, D_pl is the diameter of pipe, λ is the loss coefficient, when the fluid flows in a circular pipe, it can be expressed by:

Where σ is the kinematic viscosity of the hydraulic oil, and the pipeline loss is:

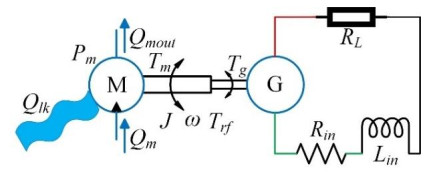
3.3.4.   Hydraulic motor and generator

As shown in Figure 5, considering the shaft friction between motor and generator, the rotational friction torque T_rf can be simplified as follows:

Where C_v is the viscous friction coefficient, and ω is the shaft speed. Based on Newton's second law of motion, the rotary motion can be written as:

The driving torque of motor T_m can also be expressed by:

Where D_m is the displacement of motor, η_m is the mechanical efficiency of motor. Considering the leakage of internal motor, the leakage flow is:

Where K_lk is the leakage coefficient, which can be expressed by Hagen-Poiseuille coefficient K_hp ^[35]:

Where σ_nom, ω_nom and P_nom are expressed as the nominal kinematic viscosity of the hydraulic oil, the nominal motor angular velocity the nominal motor pressure, respectively. and then their parameter settings ^[36] are shown in Table 3.

The outflow of motor with the rotation of shaft Q_mout is:

Where η_v is the volumetric efficiency of motor and the inflow of motor Q_m is:

A more accurate hydraulic motor pressure can be obtained for the modelling with considering the smoothing effect of the accumulator, the internal leakage of the hydraulic motor and the loss in the pipeline, and therefore the motor inlet pressure can be reconstructed as follows:

Where β_m is the effective bulk modulus in hydraulic motor and the variety of flow through motor V_m is:

The volume of pipeline V_pl is:

As for the generator, the electromagnetic torque T_g can be expressed based on the torque constant coefficient K_T and the electric current I as follow:

The electromotive force (EMF) E is given by ^[37]:

The dynamic model for the equivalent permanent magnetic DC generator depends on Kirchhoff's voltage law ^[38]. Assuming that the susceptibility at any temperature and the flux that is established by the PM poles is constant, it can be expressed as:

Where L_in is the internal inductance, R_in is the inner resistance, R_L is the electrical load. The instantaneous voltage U is given by:

The most intuitive means of quantifying the power regeneration is from the instantaneous power output and the power efficiency. In the modelling system, the regenerated power output P_reg can be calculated from the I²R_L. From the view of measurement, the instantaneous voltage U at terminals of the electrical load can be used to estimate the power potential output, and hence an equivalent expression for P_reg can be:

The model-related component parameters in the RHES are shown in Table 3.

4.   Sensitivity Analysis of energy recovery performance

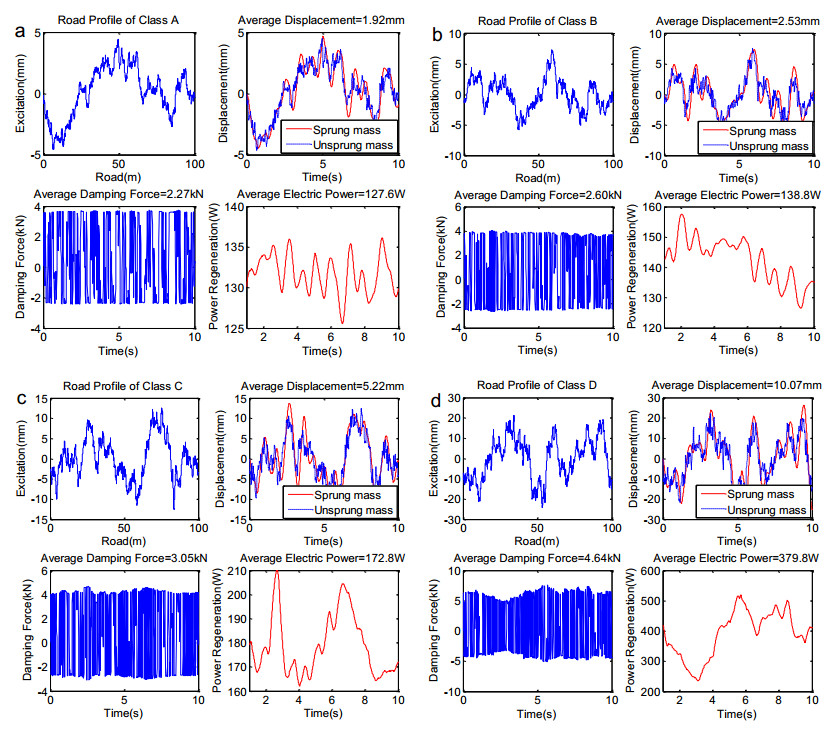
According to the Section 3, the random road excitation can be simulated. It is assumed to be a constant driving speed (10 m/s) and road distance (100 m) for each prediction to drive the proposed RHES system. Four types of roads are created: Class A, "very good"; Class B, "good"; Class C, "average" or Class D, "poor".

According to the key parameters in Table 3, the performance of RHES can be simulated by MATLAB based on the above built model. When a car travelling on road surface at a speed of 10 m/s. In the following study, numerical simulations are conducted in a variety of factors, which are shown as follow:

(1) Road roughness (ISO 8608 standard): Class A, Class B, Class C and Class D (Motor displacement 5.7 cc, accumulator capacity: 0.63 L and electrical load: 20 Ω).

(2) Motor displacement: Class C road 8 cc, 10 cc and 12 cc displacement (accumulator capacity: 0.63 L and electrical load: 20 Ω).

(3) Accumulator capacity: Class C road 0.40 L, 0.63 L and 1 L accumulator capacity (Motor displacement 8 cc and electrical load: 20 Ω).

(4) Electrical load: Class C road on 20 and 50 Ω electrical load, (Accumulator capacity: 0.63 L).

4.1.   Energy harvesting on different road roughness

To approach initially the evaluation of the RHES in irregular waves, different road profiles at 10m/s are applied to get the system behaviours and power regeneration.A large number of incident waves causes the large vertical displacements, and thus to increase the system performances and power regeneration in values.

As shown in Figure 6, the peak value of road excitation is about 5 mm of Class A, 10 mm of Class B, 15 mm of Class C and 20 mm of Class D, respectively. Responding to the road excitation, the suspension occurs the vertical displacements. And the sprung mass has similar average displacement behaviour with the unsprung mass, which increases from 1.92 mm to 10.07 mm when the road excitation changes from Class A to Class D. It shows that the response of suspension to the different road excitations determines the RHES behaviours. In addition, different average damping forces also show that RHES system needs adjust its damper characteristic to satisfy the requirement of soft and handling. The higher of road class is, the larger damping force is needed. Figure 6 shows that the average damping force is about 2.27-4.64 kN under the road excitation.

Power regeneration has an average value of 127.6 W with the peak of approximate 136.1 W on Class A road, and has an average value of 138.8 W with the peak of about 157.6 W on Class B road. Furthermore, the increase of road roughness provides the larger power regeneration, an average value of 172.8 W with the peak of approximate 209.9 W on Class C road and an average value of 379.8 W with the peak of about 519.8 W on Class D. It seems that the higher rough road is beneficial to the capability of the power regeneration in the RHES.

By comparing the effects of the road roughness, the RHES is influenced a lot by the sharp varies of wave amplitude and frequency, and remains relative stable during the smaller and very gradual waves. The higher class of the road surface causes the larger suspension displacement, damping force and power regeneration. It shows that the RHES can recovery about 100-400 W power from the dissipated heat and vibration energy. Meanwhile, system behaviours and power regeneration are highly dependent on the change of road excitation, which is proportional to the excitation frequency and amplitude.

4.2.   Effects of motor displacement

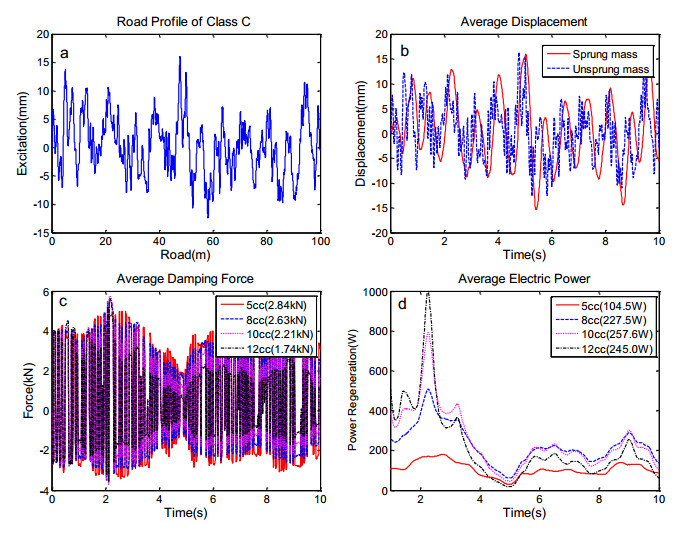
Analysing the effect of the hydraulic motor displacement, the accumulator capacity is set to 0.63 L and the electrical load is 20 Ω and the pre-charged pressure of 0.63 L accumulator is set to 20bar. In order to determine if the system outputs can be influenced by motor displacement, the test will be run with the same random road profile on Class C at 10 m/s vehicle. The hydraulic motor displacement is set to 5 cc for the modelling and numerical simulation, which is raised to 8 cc, 10 cc and 12 cc under the same road excitation.

As shown in Figure 7a, the random road profile is set to Class C, and the suspension displacement response is shown in Figure 7b. Under the same road excitation, four different behaviors and energy recovery are shown in Figure 7c and Figure 7d at the motor displacement of 5 cc, 8 cc, 10 cc and 12 cc, respectively. It is obvious that larger motor displacement can dramatically reduce the average damping force (decrease from 2.84 kN to 1.74 kN). Differently, results of power regeneration show that the highest average electric power is at the displacement of 10 cc. The power output reaches from 104.5 W to 257.6 W when the displacement varies from 5 cc to 10 cc, but it reduces slightly to 245.0 W at 12 cc. This law of change contributes to the design of a suitable suspension, which is sufficient to meet the demands of damping force with high energy recovery. Therefore, an appropriate motor displacement is helpful to obtain the acceptable damping force with higher power efficiency in different design criteria.

4.3.   Effects of accumulator capacity

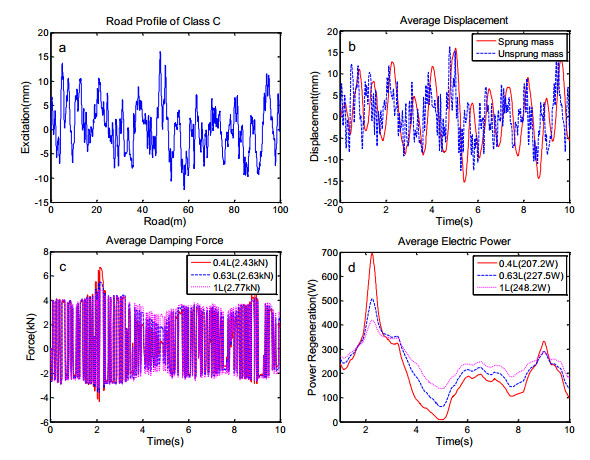
To confirm the effects of accumulator capacity on RHES, the system behaviours and power regeneration are evaluated under road excitation. In this work 0.40 L, 0.63 L and 1 L with 20 bar pre-charged pressure will be applied in sensitivity analysis. In addition, to determine if the system outputs can be smoothed by accumulator capacity, the test will be run with the same random road profile on Class C at 10 m/s vehicle. It is known that the instantaneous pressure and the change of volume in accumulator are dependent on the incident wave variations. However, varying the accumulator capacity will alter the volume in hydraulic circuit whilst changing the level of the hydraulic pressure and fluid flow, and hence to adjust the waveforms of power.

As shown in Figure 8d, Class C road at 10 m/s is used as the input wave, and three different accumulators are applied to evaluate the effects of the accumulator capacity. The power smoothing effect of the accumulator is presented, and the average power outputs at 0.40 L, 0.63 L and 1 L accumulators are 207.2 W, 227.5 W and 248.2 W with the peaks of 694.9 W, 507.7 W and 420 W, respectively. Compared to the nadir of three waves (8.9 W, 62.9 W and 136.1 W), it is obvious that the power output is steadier with the larger accumulator capacity. Although the peak power of smaller capacity can reach 694.9 W, there is no obvious contribution for bottom value. Furthermore, much more average power is generated at large accumulator capacity at the same incident waves.

In addition, the large accumulator capacity is able to provide sufficient smoothing for high damping force at high wave velocity. As shown in Figure 8c, the average hydraulic damping force increase from 2.43 kN to 2.77 kN with the larger accumulator capacity. Meanwhile, the wave of high capacity is more stable. Consequently, the damping force can be adjusted by the accumulator capacity to overcome continuously varying road surface profiles which can achieve the purpose of semi-active control in regenerative suspension system and obtain relatively good ride comfort and road safety.

4.4.   Effects of electrical load

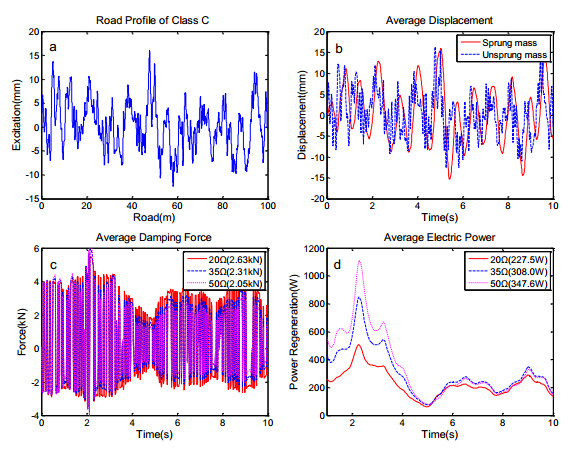
The external load is used to adjust the performance and power output in RHES. To maximise the power regeneration and investigate the system behaviours in irregular wave (random road surface), the electrical load is exhibited with comparison between 20 Ω, 35 Ω and 50 Ω on Class C road at 10 m/s.

As shown in Figure 9, the damping force and regenerative power are directly influenced by the applied external electrical load. It illustrates that the analysis of the RHES at resistance of 20 Ω, 35 Ω and 50 Ω. The larger resistance can reduce the average damping force from 2.63 kN to 2.05 kN. It can be found that varying the resistance can change the hydraulic damping in the RHES, and hence to change the power output (increase from 227.5 W to 347.6 W). The reduction of motor pressure and piston force using larger resistance reveals that the wide range of damping force can be produced by adjusting the electrical load, which could be available for semi-active control in practice application. However, the smaller electrical load seems to mean the steadier output. Therefore, adjusting external electrical load is an effective method to obtain the expected system behaviours which is particularly for damping force whilst recovering power in regular or irregular waves.

5.   Discussion

The proposed RHES system is used to replace the traditional vehicles suspension, which can recover the vibration energy of suspension dissipated in the form of thermal energy. It is intended to get higher power output while remaining a suitable system damping. In order to understand the system behaviors and power regeneration, all simulation results take into account the same road excitation based on ISO8608. For a light-duty truck of a total of 1612 kg unsprung mass, the predicted average electrical power is about 100-400W, which is obvious higher than previous literature study for recovering energy from suspension. For instance, Zhang ^[7] built a dynamic simulation model of the suspension system to test the average recoverable energy. According to the ISO8608, when the vehicle speed is 30 km/h at the Class A, B, C and D roads, the recoverable power is 2.08 W, 8.33 W, 33.34 W and 133.37 W, respectively. Khoshnoud et al. ^[8] estimated the power dissipated in a 2-DOF vehicle suspension model, which showed the regeneration potential of per damper is around 280 W. It can be found that the predicted power output from RHES system is about 200 W higher than these existing studies. In addition, some of these researches may not focus on the damping behaviors, which is also significant for the vehicle comfortable and handling. The simulation results also show that the change laws of damping force in hydraulic cylinder, which can provide good literature contribution.

6.   Conclusions

This paper proposed a RHES system, which is a redesign of vehicle suspension. By combining the hydraulic cylinder, check valves, accumulator, hydraulic motor and generator, the RHES system can act as the main damping mechanism while recovering the dissipated vibration energy. This paper built the numerical model of RHES and conducted the simulation by MATLAB. Main conclusions of simulation results are as follows:

(1) System damping behaviors and power regeneration are highly dependent on the change of road excitation, which is proportional to the road class (excitation frequency and amplitude).

(2) Larger motor displacement can dramatically reduce the average damping force (decrease from 2.84 kN to 1.74 kN). Particularly, average power regeneration is highest at the displacement of 10 cc (257.6 W) when the electrical load is 20 Ω and the pre-charged pressure of 0.63 L accumulator is set to 20 bar.

(3) The average hydraulic damping force is larger with the larger accumulator capacity and the power output is steadier, which is benefit to stable system.

(4) Increasing the electrical load can reduce the hydraulic damping in the RHES but get higher power regeneration. Hence, adjusting the electrical load is an effective method to obtain the expected system behaviors to achieve the purpose of control.

To enhance the travel comfort and road handing of the present systems, future research should pay more attention to design semi-active or active controllers and experimental verification. The key roles of a controller are to provide better performance while maintaining the regeneration capability at a high level.

Acknowledgments

This study was funded by: National Key Research and Development Program of China (grant number 2017YFB1300900); Science Foundation of National University of Defense Technology (grant number ZK17-03-02); Science Foundation of National University of Defense Technology (grant number ZK16-03-14); Chinese National Natural Science Foundation (grant number 51605483).

Conflicts of interest

The authors declare no conflict of interest in this paper.