Kinetic growth model for hairy root cultures

1.   Introduction

A gram negative soil dwelling bacterium Agrobacterium rhizogenes, infects a wide range of plants and induce hairy roots disease at the site of infection ^[4,5,14]. These transformed roots have several advantages over field culture as they (a) exhibit faster growth rates with profuse lateral branching, (b) have almost same characteristics as parent plant, (c) can be grown in hormone free media, (d) have high degree of genetic as well as biochemical stability and (e) contain valuable secondary metabolites either in comparable level or in higher than field production ^[7,23,29,32]. These secondary metabolites are used in commercial production of pharmaceuticals, bio-chemicals, agrochemicals, proteins, dyes and food additives ^{[6,11,15,16,18]}. At present, field cultivation is the major source for metabolites but its production is limited by several external factors like time duration, climate and pesticides ^[20]. In this scenario, in vitro cultivation of hairy roots emerged as a promising alternative.

Bioreactor is used for in vitro cultivation of hairy roots as they offer stable and controlled gas and liquid nutrient environment. An efficient and economic bioreactor design for large scale production of hairy root cultures is challenging due to the generation of dense root network and hence emerged as a growing area of research. The bioreactors for hairy root cultures are classified into liquid phase reactors in which liquid nutrient is in continuous phase and gas nutrient is in discrete phase and gas phase reactors in which gas nutrient is in continuous phase and liquid nutrient is in discrete phase. The liquid phase reactors are stirred tank reactor, bubble column reactor, rotating drum reactor, etc. and the gas phase reactors are spray reactor, trickle bed reactor, air lift reactor and nutrient mist reactor (NMR), etc. ^{[1,10,15,19,21,27,30,31]}. Whether grown in liquid phase or gas phase reactor, hairy roots form a dense matrix of root biomass and exhibits resistance to nutrient and oxygen transport due to profuse branching. Thus, it becomes very difficult for the nutrients to penetrate deep into the core of the root clump ^{[18,20,23,26]}. This hampers the total biomass production and secondary metabolites productivity. Development of a suitable bioreactor for the cultivation of hairy roots at commercial scale requires information such as growth characteristics of hairy roots and interaction between root culture system and nutrient medium.

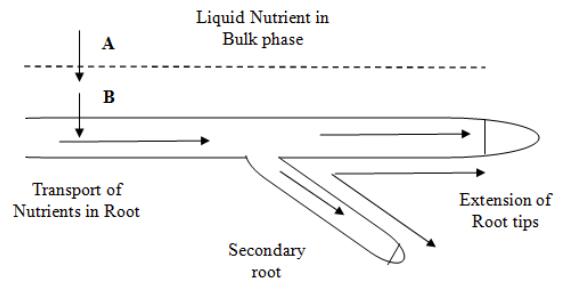
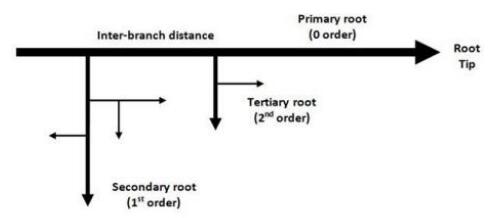
Liquid and gas phase nutrients are essential for sustained growth of hairy root cultures ^[13]. As the roots absorb nutrients through its surface, nutrient concentration in the liquid medium changes which is in contact with the roots. This process establishes a nutrient concentration gradient between the rhizosphere and the bulk liquid medium which drives nutrient transport through root surface. Thin hairy roots absorb more nutrients due to enormous surface area per unit volume but they also retain less water in relation to their thick hairy roots. The growth of hairy roots occurs due to the formation of younger lateral branches (secondary roots) on older parent roots (primary roots). The branching rules for hairy roots are quite complex in comparison to normal roots ^[25]. It is important to understand the branching phenomena and the root growth phases to model the growth kinetics of hairy root cultures. Root growth occurs in three distinct phases namely (a) elongation phase (first phase), (b) elongation and branching phase (second phase), and (c) maturity phase (third phase) ^[2,4,12,24]. In the first phase, primary root only elongates and no branching takes place, but the primary root doesn't grow indefinitely ^[2]. During the second phase, primary root elongates and new branches (tips) are produced. Apical meristem is the most active part of primary root where cell division takes place and as a result of it new laterals or secondary roots are formed ^[24]. In the third phase, primary root neither elongates nor branches but still nutrients are required for its maintenance ^[4,24]. The branching phenomena are shown in Figure 1.

Figure 1.  Branching phenomena of hairy root cultures.

DownLoad: Full-Size Img PowerPoint

Models have become important tools for characterizing the growth of untransformed and transformed roots. Models for normal root growth were first proposed in early 1970 ^[8,9], but the results of untransformed roots cannot be used directly in case of hairy roots as the latter is characterized by fast and profuse branching ^[25]. Kinetic expressions for hairy root growth have not been reported until 1989. Though numerous models have been developed to describe the growth of microbial cell cultures, very few models are available to describe the growth of hairy root cultures. Linear growth models have been proposed to explain the growth by considering lateral branching of the growing points at the tip with and without treating 1-napthaleneacetic acid ^[22]. Very few models have been proposed to describe the growth of hairy roots and are in terms of mass, length and number of branches. However, these models were not successful to explain the growth in terms of nutrient flow from bulk medium and internal flow of nutrients, growth of all individual secondary roots over same parent root and maturity phenomena mathematically.

Though hairy root culture system was developed several decades ago, commercial production of hairy root cultures at large scale has not yet been developed. Many attempts have been made to develop economical bioreactors but they could not resolve the contradiction between investment and consumption, which made them impractical for commercial use. The major bottleneck in the commercial exploitation of hairy roots remains its successful scale-up due to gas and liquid mass transfer limitation in three dimensionally growing hairy root mass. Further, it is essential to predict the concentration profile of nutrient throughout the growing hairy root bed to avoid nutrient depletion condition for sustained growth of hairy roots. The local concentration of nutrient mainly controlled by the local packing fraction of the roots. Hence, it is paramount to estimate the growth of hairy roots ranging from primary root to all individual secondary roots in terms of length. The present kinetic growth model can describe growth of hairy roots in terms of primary root length and total root length through modeling. In the present modeling approach, the effect of branching phenomena, internal flow of nutrients from primary root to secondary roots, external transport of nutrients from medium to rhizosphere and nutrient consumption for maintenance of roots taken into consideration.

2.   Problem formulation

Nutrient transport from medium to culture is a dominating phenomenon in growth processes. The nutrient absorption by the roots directly related to its surface area, through which interphase mss transfer of limiting nutrient from nutrient medium to root cells takes place. Thus longer and thinner roots with more root hairs are essential for increasing the contact surface to improve nutrient absorption capacity. The nutrient absorption process is directly dependent on the nutrient concentration gradient between the rhizosphere and the root xylem. This nutrient concentration gradient remains constant when the nutrients are continuously replenished in the bioreactor system. The nutrients in the xylem flows in bidirectional between parent root and its branch root as well as throughout the individual root element. Continuous consumption of nutrients by the roots takes place for its maintenance and internal metabolic activities. As thin secondary roots grow much faster, they require more nutrients. The nutrients absorbed through external transport from the medium reservoir like primary root and the deficit nutrients are balanced by the internal flow of nutrients from primary root to secondary roots. Mathematically, it is modeled as the rate if internal sharing of nutrients between primary and secondary roots is proportional to the surface area fraction of secondary roots over primary root. The following assumptions made to simplify the modeling process.

2.1.   Assumptions

The model is developed with the following assumptions:(ⅰ)Root elements are cylindrical in shape, (ⅱ) Radius of elements remains constant, (ⅲ) Nutrient consumption is proportional to surface area of roots, (ⅳ) Root growth is assumed to be homogeneous, (ⅴ)Not more than one branch is produced at one nodal point, (ⅵ) Inter node distance remains constant, (ⅶ) Higher order (second order or higher) branching does not takes place, (ⅷ) Nutrients consumption for maintenance is directly proportional to mass of the roots, (ⅸ) Internal flow of nutrients from primary root to its secondary roots is proportional to the fraction of surface area of secondary roots over primary root, and (x) External nutrients are an infinite reservoir or present in abundance.

2.2.   Model development

Nutrient medium consists many required organic and inorganic substances. Glucose is taken as the limiting nutrient. The nutrient transport from the bulk medium to root tissues occurs in three sequential steps (Figure 2): (ⅰ) transport of nutrient from bulk medium to the edge of boundary layer over root element, (ⅱ) transport of nutrient through the concentration boundary layer in which concentration gradient set up due to continuous absorption of nutrient at root surface, (ⅲ) internal transport of nutrient through root tissues. When the concentration of nutrient in the medium is uniform the step (ⅰ) can be safely ignored. However, the step (ⅲ) is flow characterization inside root element is out of present study. The present study focused on the transport of nutrients across root surface. Continuous absorption of nutrients at the surface of root due to the concentration difference across root surface. Availability of nutrients throughout the culture period is necessary for the sustained growth of hairy roots.

Figure 2.  External and internal flow of nutrients. (A). Flow of nutrients across edge of concentration boundary layer, and (B). Flow of nutrients through root surface.

DownLoad: Full-Size Img PowerPoint

Nutrient consumption from medium is necessary for the purpose of maintenance of root metabolic activities and growth process. The primary roots and its higher order roots get enough nutrients from the medium through external transport. Both primary root and secondary roots absorb nutrients based on individual root surface area. During elongation only phase, the nutrient uptake by external transport take place for primary roots only. During elongation and branching phase, both primary root and all secondary roots able to get nutrients from the medium through external transport. However, when primary root reaches maturity phase, no significant change in its surface area and hence the rate of consumption of nutrients from medium remains unchanged whereas, the secondary roots keep growing and absorb more amounts of nutrients with time.

Model equations developed for both primary root and individual secondary roots based on limiting nutrient material balance as follows. Nutrients absorbed by primary root are used for the following purposes: (a). Nutrients used up roots for the maintenance of their metabolic activities, (b). Nutrients are used for the growth of roots, and (c). the excess nutrients flows to its secondary roots internally in proportional to the surface area fraction of secondary roots present over primary root. The secondary roots get nutrients from medium through external transport and from its primary root through internal transport. Nutrients available to secondary roots are utilized for the purpose of growth and maintenance. For the both primary root and its secondary roots, the growth is directly related to consumption rate of nutrients from the medium and hence the growth equations have been developed as function of nutrient consumption in this section.

The nutrient mass balance for primary root is

Rate of nutrient uptake from external medium is defined as the product of mass transfer flux of limiting nutrients and root surface area (2πR_pL_p). The mass transfer flux is the product of mass transfer coefficient (K_m) and limiting nutrient concentration difference across root surface (ΔC). The consumption of nutrients for maintenance changes with mass of roots and is defined as the product of maintenance coefficient (M_p) and mass of root. Further, the mass of roots defined as the product of density of root and volume of root. As primary root growing, the secondary roots are produced based on inter node distance. The excess nutrients flows internally primary root to its secondary roots based on their surface area fraction. Equation 1 is written as,

Where K_m is the mass transfer coefficient across root surface (cm.s⁻¹), ΔC is the concentration difference across root surface (g.cc⁻¹), R_p is the radius of primary root (cm), L_p is the length of primary root (cm), M_p is the maintenance coefficient of primary root (g.g⁻¹.s⁻¹), ρ_p is the density of primary root (g.cc⁻¹), f_nb is the nutrient to biomass ratio (g.g⁻¹), S_s is the surface area fraction of all secondary roots over primary root.

Therefore, the growth equation for primary root is

Where, S_p is the surface area fraction of primary root, is equal to (1−S_s). The ratios K_1p and K_2p are defined as

The number of secondary roots(N_s) produced is given by

Where, L_b is the branching length of primary root (cm), where first lateral branch generates, L_m is the length of maturity length of primary root (cm) and nd is inter node distance (cm), i.e., distance between two successive secondary roots over primary root.

The nutrient mass balance for a secondary root 'i' is

Where, R_s is the radius of secondary root (cm) assumed constant for all secondary roots, L_si is the length of i^th secondary root (cm), S_si is the surface area fraction of i^th secondary root over primary root, M_s is the maintenance coefficient of secondary root (s⁻¹), ρ_s is the density of secondary root (g.cc⁻¹).

Therefore, the growth of i^th secondary root over primary root in terms of length is given by

Where ${K_{1s}} = \frac{{2\Delta C{K_m}}}{{{R_s}{\rho _s}{f_{nb}}}}$; ${K_{2s}} = \frac{{{M_s}}}{{{f_{nb}}}}$ and ${K_3} = \frac{{{M_p}R_p^2{\rho _p}}}{{{f_{nb}}R_s^2{\rho _s}}}$

In a simplified form,

The surface area fraction of all secondary roots and single secondary root 'i' defined using Eqs 9 and 10 respectively.

Length of primary root L_p is given by Eq 3 and for all individual secondary roots Eq 8 is applicable. The model can be extended to tertiary root level also by treating secondary root as a primary root for tertiary branches. Based on inter node distance over secondary roots, number of tertiary roots will be produced. Further, the growth equations can be extended to tertiary roots also. In this scenario, the total number of roots is the sum of primary roots, secondary roots and tertiary roots. However, the tertiary roots are very thin compared to primary and secondary roots and hence the biomass contribution is small. Hence, the model is limited to secondary root level growth. The governing equations for three distinct growth phases are as follows.

2.2.1.   Elongation only phase

At the initial stage, when branching has not taken place, the nutrients are utilized only for the growth and maintenance of the primary root. Thus, there will be no sharing of nutrients with the secondary root and S_s become zero. During this phase, total nutrient uptake is always greater than nutrients required for maintenance and used for elongation of primary root. The increase in the biomass is due to the elongation of the primary root only and therefore, Eq 3 is modified and is given by,

Where k_p defined as growth reaction constant of primary root (d⁻¹) and is equal to (K_1p−K_2p).

The value of k_p can be estimated by fitting the length versus time data of primary root during elongation only phase using the equation,

Where L_p0 is initial length of primary root (cm).

The constant molar flux of nutrient across root surface assumed and is estimated using the equation,

The estimated mass transfer flux is assumed constant throughout all the growth phases of hairy roots.

2.2.2.   Elongation and branching phase

During this phase, the branching process initiated as the primary root reaches branching length. During this second phase, primary root utilizes nutrients for its growth and maintenance. However, the newly born secondary root elements receive nutrients from the external medium as well as from its parent root through internal sharing. As the internal flow of nutrients from parent root to secondary root controlled by surface area fraction of secondary roots, the fraction S_s is in the range of 0 < S_s < 1.0. The total biomass is the sum of the biomass of primary root and all secondary roots over primary root. Hence, for N_s number of secondary root elements, Eq 3 must be coupled with N_s number of Eq 8. Therefore, Eqs 3 and 8 can be used to estimate the growth of all primary root elements and all secondary root elements over each primary root element, respectively. For large number of secondary root elements, the value of area fraction reaches at 1.0 and therefore internal flow of nutrients from primary root to secondary root ceases. Hence, the absorbed nutrients are used only for the maintenance of primary root whereas the secondary roots will continue the nutrient absorption from the external medium.

2.2.3.   Maturity phase

In this last phase of growth, the available nutrients are utilized for the maintenance of the primary root element and this root element will reach its maturity phase when the surface area fraction of primary root becomes zero. Mathematically the transition from branching phase to maturity phase can be seen clearly as the surface area fraction of secondary roots reaches 1.0. The growth reaction constant k_p which is the ratio of amount of nutrients in excess of maintenance to amount of nutrients per unit biomass production reaches zero as the no excess nutrients available for growth and sharing. Hence from the Eq 3, there is no change in length of primary root during this phase as nutrients consumption only limited for roots maintenance.

Using Eqs 3 and 8, we will get

The above analysis clearly states that the growth reaction rate constant for primary root and secondary roots is not constant throughout the culture time. However, a preliminary growth model has been proposed and published by the authors by taking fixed growth constants during different growth phases of primary root as well as secondary roots ^[24]. In our previous model, the growth coefficients of primary and secondary roots during three growth phases are fitted through simulation and maturity length of primary root taken as an input parameter. The present model needs growth constant of primary root during elongation phase only and is estimated using Eq 12. The growth coefficients of primary root during branching phase and maturity phase, the growth coefficients of secondary roots during branching phase and maturity phase of primary root are estimated and fixed automatically using Eqs 3 and 8 respectively. It is important to note that the maturity of primary root is observed without using maturity length and maturity age data as input parameters. With discrete growth model, a sharp change in growth observed during growth phase transition whereas in the present model the growth curve is smooth and continuous. The growth reaction constants for primary and secondary roots during three distinct growth phases from previous work (Eqs 16 and 17) and present work (Eqs 18 and 19) shown below.

Growth rate constant of primary root, with discrete growth phases is defined as

Growth rate constant of secondary root, with discrete growth phases is defined as

Growth rate constant of primary root, with continuous growth is defined as

Growth rate constant of secondary root, with continuous growth is defined as

Where, K₀, K_p1, and K_pm are the growth rate constant (s⁻¹) of primary root during elongation only phase, elongation and branching phase and after maturity phase respectively. K_b1 and K_bm are the growth rate constants (s⁻¹) of secondary roots during elongation and branching phase and after maturity phase respectively.

From Eqs 16–19, it is clear that the maturity length data is essential for discrete model whereas, the maturity length is not an input parameter for simulation as the surface area fraction S_p or S_s will alters the growth reaction constant with culture time. This major simplification act as a strong basis for wide applicability of the present model with minimum growth related parameters. Therefore, the present model is superior to the existing growth models for hairy root cultures as it provides growth in terms of length for all primary and all individual secondary roots with culture time which enables us to estimate local packing fraction of growing root bed in order to understand the nutrient concentration profile in a dense hairy root bed.

3.   Results and discussion

The developed kinetic growth model equations are simultaneous first order non-linear ordinary differential equations. During elongation only phase, primary root growth Eq 3 alone integrated, during elongation and branching phase primary root growth Eq 3 and N_S number of secondary root growth Eq 8 integrated and during maturity phase N_S number of secondary root growth Eq 8 are integrated. Equation 3 for primary root growth and Eq 8 for all individual secondary roots were simulated using NAG FORTRAN library subroutine D02CJF. The subroutine D02CJF is a variable order and variable time step method which applies the ADAMS algorithm to integrate the ordinary differential equations until solution is zero for user specified function of the solution and returns the solution at user specified position. The simulations have been carried out in FORTRAN 90 on a LINUX platform.

3.1.   Model validation

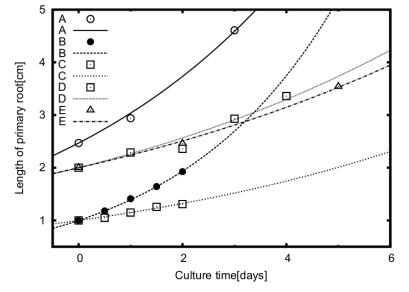
As the validation step is important in the process of modeling, published experiments data collected from the literature for four different species namely Atropa belladonna (A) ^[28], Hyoscyamus niger (B) ^[26], Hyoscyamus muticus (C, D) ^[22], and Solanum aviculare (E) ^[17]. The morphological properties of hairy roots and nutrient medium-growth related parameters are used for validation of the model. As stated earlier, growth reaction constant of primary root during elongation only phase is enough to describe growth of different orders hairy roots during different growth phases. This growth reaction constant is estimated by fitting the experimental data with the Eq 12 and taken as input parameter for estimation of other growth constants during integration of system of model equations. The elongation phase growth reaction rate constant estimation shown in Figure 3 for the four species hairy roots and the value is in the range of 0.1 to 0.4 d⁻¹. Further, the biomass data in terms of length with culture time is fitted with the simulation result using length of primary root at the beginning and at branching point, inter-node distance, maintenance coefficients, nutrient to biomass ratio, radii of primary and secondary roots and initial length of secondary roots as an input parameters and fitted parameters data listed in Table 1 for all four species.

Figure 3.  Estimation of k_p through fitting primary root length during elongation only phase for species Atropa belladonna (A), Hyoscyamus niger (B), Hyoscyamus muticus (C, D) and Solanum aviculare (E) for shake flask culture experiments. Solid and dotted lines represent simulation results.

DownLoad: Full-Size Img PowerPoint

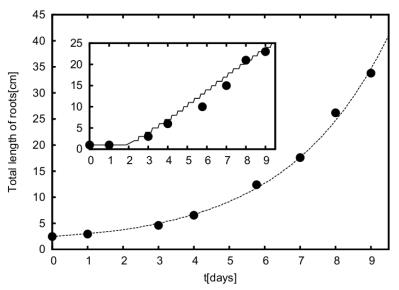
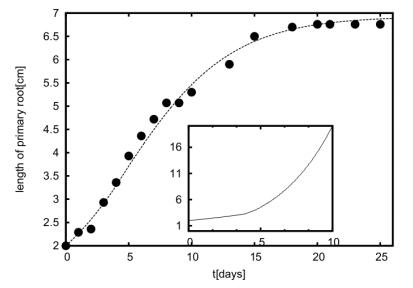
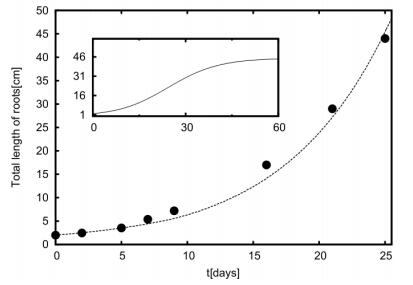
A transformed root of A. belladonna ^[28] maintained in MS medium with antibiotic containing 3% sucrose at 25 ℃ having root clump diameter viz. 3.5cm, 4 cm, and 5 cm. The growth of biomass is reported in terms of length and number of secondary roots produced from 9 days observation. The primary root branches on third day and the length data during this elongation phase used for estimation of growth reaction rate constant and it is found to be 0.2064 d⁻¹. Figure 4 shows the fitting of total length data which includes lengths of both primary and its secondary roots with culture time and number of secondary roots produced with culture time. A good agreement between the model result and experiment data has been observed for the fitted parameter values shown in Table 1 for A.belldonna species. The confidence limits of parameters fixed by performing millions of simulations for various combinations of parameters values against the experimental data. Minimum root mean square error (RMSE) observed for the parameter values shown in Table 1. Further, the most probable value for each parameter is identified using frequency plots for 1%, 5%, 10% and 20% error of minimum RMSE. The most probable fitted parameter value for 10% error of minimum RMSE shown within a bracket in Table 1. The minimum RMSE estimated for H.muticus, H.niger and S.aviculare by following same frequency plots analysis.

Figure 4.  Total length of roots as function of culture time for Atropa belladonna hairy roots grown in shake flask. The subplot represents total number of tips as function of culture time. The dotted line represents simulation results and filled circles represent experimental data.

DownLoad: Full-Size Img PowerPoint

Table 1.  Fitted growth coefficient and other parameters for validation.

Species	kp (d−1)	nd (cm)	fnb	Lso (cm)	Rp (cm)	Rs (cm)	M (s−1)	RSME (cm)
Range used		0.05–0.7	1.1–8.0	0.005–0.25	0.01–0.15	0.005–0.15	0.01–0.15
A.belladonna [28]	0.2064	0.31 (0.31)	2.5 (5.5)	0.11 (0.11)	0.03 (0.04)	0.02 (0.03)	0.025 (0.05)	0.57 (0.627)
H.muticus [22]	0.3302	0.10 (0.10)	1.5 (4.0)	0.19 (0.19)	0.06 (0.06)	0.05 (0.05)	0.13 (0.03)	0.09 (0.099)
S.aviculare [17]	0.1134	0.51 (0.51)	5.5 (5.5)	0.10 (0.09)	0.15 (0.14)	0.14 (0.13)	0.01 (0.01)	1.5 (1.65)
H.niger [26]	0.1249	0.09 (0.09)	1.3 (2.5)	0.15 (0.15)	0.03 (0.07)	0.02 (0.04)	0.15 (0.05)	0.14 (0.154)

---

 | Show Table

DownLoad: CSV

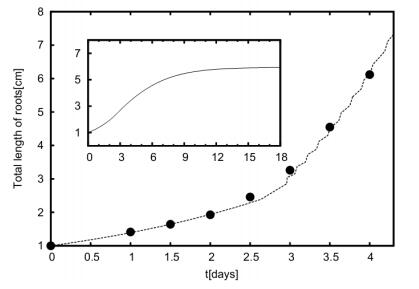
H.muticus hairy roots ^[22] of initial length 2.5 cm are taken in a 125 mL shake flask containing 50 mL of B5 medium, incubated at 25 ℃ at 120 rpm for 2 weeks. The simulated results predicted by model are compared with experimental results in Figure 5. It is clear from experimental results that total length is increasing exponentially with time and the simulated result predicted by model was also found to be showing approximately the same kind of behavior. Hence, a good agreement had been found between the experimental results and simulated results for H.muticus hairy roots cultivated in shake flask. The inside Figure shows the variation of primary root length with culture time for H.muticus hairy roots in shake flask. As the primary root grows, it attains maturity after a particular interval of time. This maturity period is different for different species. Once it attains maturity, it does not grow further and hence length also does not increase further. The fitted k_p values were found to be 0.1394 d⁻¹ for air only and 0.3302 d⁻¹ for air with 40% oxygen, respectively.

Figure 5.  Total length of roots as function of culture time for Hysis muticus. The subplot represents length of primary root as function of culture time. The dotted line represents simulation results and filled circles represent experimental data.

DownLoad: Full-Size Img PowerPoint

In another experiment ^[26], H.niger hairy roots of initial length of 1.7 cm has been cultivated in two different mediums. In an Erlenmeyer flask (5 mL of liquid medium), root tips are cultured for 10 days while in a petri dish (25 mL of medium with 0.8% agar) and these were cultivated for 25 days. Total length and number of secondary branches produced with time were compared. The experimental data for primary root length variation with time for first 6 days is used for fitting and the primary root growth constant found to be 0.1249 d⁻¹. From this model, it is observed by fitting that the primary root can grow up to 18 cm with the same growth constants but the experimental results show that primary root can elongate up to 6.7 cm only. The reason for this behavior is that the primary root shares nutrients with its subsequent branches and formation of new branches decreases gradually throughout the culture period. Thus, primary root grows with a slower growth rate and its growth stops once it gets matured. The comparison between the simulated results and experimental results has been performed to study the effect of the variation of primary root length with time for H.niger hairy roots (Figure 6).

Figure 6.  Primary root length as function of culture time for Hysis niger. The subplot represents total root length as function of culture time. The dotted line represents simulation results and filled circles represent experimental data.

DownLoad: Full-Size Img PowerPoint

S.aviculare hairy roots ^[17] grown in 36 shake flasks (250 mL volume, each) containing 6% sucrose in 100 mL MS medium with initial root tip length ranging between 2.3–2.5 cm were maintained at room temperature and 110 rpm for 54 days. Dry weight (DW), fresh weight (FW), branching kinetics, and metabolite content were analyzed for shake flask experiments. Bioreactor study for the same species was done in an airlift reactor (3L) and air supply rate was maintained at 60 mL per min containing 3% sucrose in MS medium with initial inoculum of 5.6 g FW. Figure 7 represents the comparison of simulated results against experimental results for total root length (shake flask). Experimental results show that total root length is increasing exponentially with time and the present model has a good agreement with the experimental results except at few points. Hence, the proposed model has good validation with the experimental data for different species.

Figure 7.  Total length of roots as function of culture time for S.aviculare. The subplot represents length of primary root as function of culture time. The dotted line represents simulation results and filled circles represent experimental data.

DownLoad: Full-Size Img PowerPoint

3.2.   Parameter study

Simulation studies for various parameters revealed the growth behavior of hairy root cultures under different growth conditions. The growth reaction constant of primary root directly alters the growth of primary roots and indirectly alters the growth of secondary roots. The inter-node distance parameter indirectly effects the growth of both primary and secondary root and it does not appear in the model equations. However, the number of secondary roots produced is controlled by the inter-node distance only. Nutrient medium concentration changes the gradient across root surface and influences the mass transfer rate of limiting nutrient. The amount of nutrient consumed per unit biomass produced is considered as it tells about the relation of growth and medium requirement. Finally, the radius of primary and secondary roots taken as radius ratio which definitely change growth phenomena, because of thinner roots growth characteristics and nutrient absorption rates are different than primary roots.

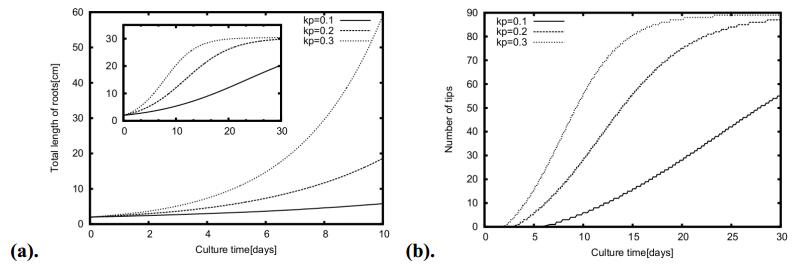
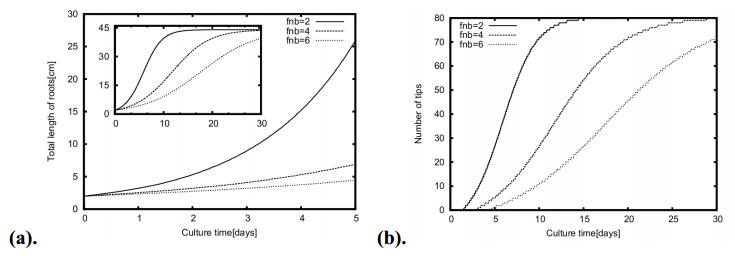
Figure 8a, b show the variation of the total length, primary root element length and number of tips with culture time, respectively for different values of growth reaction rate constant of primary root, k_p. It is evident from the Figure 8a, that higher value of k_p favors the increase in the mass transfer coefficients (K_m). The estimated value of k_p (from fitting of experimental data) has been used to calculate K_m. The higher value of mass transfer coefficient helps in yielding higher nutrient flux for the same value of ∆C. Therefore root elements will reach the maturity phase faster for large k_p values because of higher rate of nutrient transport. Further, we can see from Figures 8b, higher value of k_p will favor in the increase in primary root length which will favor in producing large number of root tips for the same inter node distance. The growth of the individual secondary root element is exponential. Therefore, the overall growth of all elements including primary root and its branches is highly exponential as depicted from these results.

Figure 8.  (a). Effect of primary root growth coefficient on total length of as a function of culture time. The initial length of roots is 2.0 cm and branching length 3.5 cm. The maturity of primary root shown in subplot. (b). Effect of primary root growth coefficient on number of tips as a function of culture time. The initial length of roots is 2.0 cm and branching length 3.5 cm.

DownLoad: Full-Size Img PowerPoint

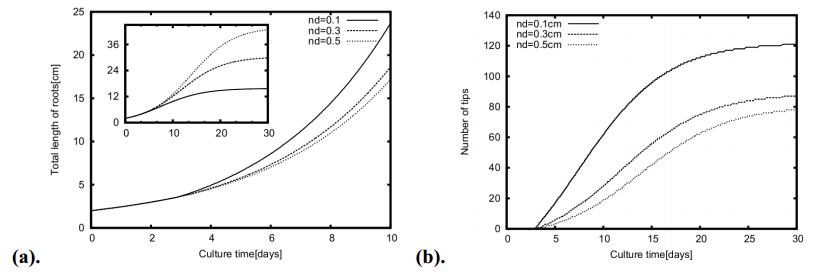
Figures 9a, b show the variation of the primary root element length, number of tips and total length of elements with culture time, respectively for different values of nodal distance. It is clear from the Figure 9a that the primary root length increases with the nodal distance. This happens because less number of branches is produced per unit length of primary root when the nodal distance is increased. Hence, more nutrients are available with the primary root for consumption. Also, more branches are produced per unit length of primary root when nodal distance is decreased. During exponential phase, primary root length decreases with a decrease in nodal distance but numbers of root tips are produced exponentially (Figure 9b). Number of branches produced per unit length of primary root is also increased. The contribution of secondary root tips in increasing the total length of the root is more as compared to primary root. Hence, the overall effect of the decrease in the nodal distance is reflected in the increment in the total length of the root.

Figure 9.  (a). Effect of inter-node distance on total length of roots as function of culture time. The initial length of roots is 2.0 cm and branching length 3.5 cm. The maturity of primary root shown in subplot. (b). Effect of inter-node distance on number of tips as function of culture time. The initial length of roots is 2.0 cm and branching length 3.5 cm.

DownLoad: Full-Size Img PowerPoint

Figures 10a, b show the variation of the primary root element length and total length of elements with culture time, respectively for different values of f_nb. It has been found that availability of nutrient is sufficient for small values of f_nb, hence the primary root element reaches maturity at faster rate. Also higher value of f_nb increases the total length of primary root because more nutrients have been used for the growth. No significant effect of this ratio on primary root length has been noticed during elongation and elongation and branching phases (Figure 10a). Further minimum consumption of nutrients is required for maintenance during maturity phase. Higher value of f_nb supports the increase in the growth rate during the initial stage of maturity phase because the nutrients requirement for maintenance remains same during all three growth phases. Therefore, more number of branches are produced per unit length for higher value of f_nb. These branches grow at an exponential growth rate and therefore, the overall growth of primary and all secondary root elements is exponential (Figure 10b).

Figure 10.  (a). Effect of nutrient to biomass ratio on total length of roots as a function of culture time. The initial length of roots is 2.0 cm and branching length 3.5 cm. The maturity of primary root shown in subplot. (b). Effect of nutrient to biomass ratio on number of tips as a function of culture time. The initial length of roots is 2.0 cm and branching length 3.5 cm.

DownLoad: Full-Size Img PowerPoint

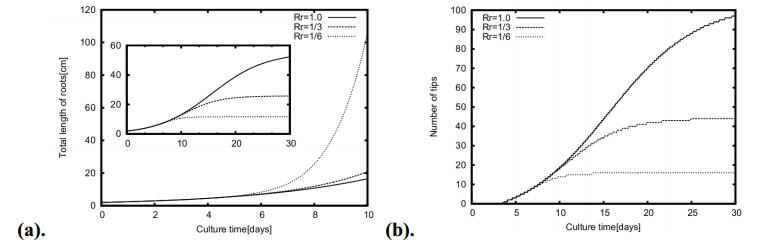
The morphological property radius of primary and secondary roots plays dominant role in the nutrient uptake rate as thin roots offer more surface area per unit volume. The ratio of radius of secondary to primary roots (R_r) varied and the total length of roots, length of primary root and number of tips produced with culture time shown in Figure 11a, b. Figure 11a shows the early maturity of primary root when thin roots produced as they offer enormous surface area which affects the absorption of nutrients as well as internal sharing of nutrients between primary and its secondary roots. However, the total length of roots significantly rises for thin roots due to excellent mass transfer rates as they offer more surface area per unit volume.

Figure 11.  (a). Effect of secondary root radius to primary root radius ratio on total length of roots as a function of culture time. The initial length of roots is 2.0 cm and branching length 3.5 cm. The maturity of primary root shown in subplot. (b). Effect of secondary root radius to primary root radius ratio on number of tips as a function of culture time. The initial length of roots is 2.0 cm and branching length 3.5 cm.

DownLoad: Full-Size Img PowerPoint

4.   Conclusions

The scenario of a growth reaction of hairy root cultures limited by transport of nutrients from the medium to roots is well explained with the present intrinsic growth model. The net growth rate depends upon the nutrient transport across the root surface, inter-node distance, nutrient consumption rates for maintenance and internal transport phenomena between primary and its secondary roots as the root matrix formed during growth process shows tremendous resistance to the nutrient transport and oxygen transport to the inner core of the root culture bed.

Growth kinetics of hairy roots has been studied with the help of a kinetic growth model which is developed for the liquid phase limiting nutrient. Growth coefficients are calculated during elongation only phase through fitting experimental data and further the mass transfer coefficient is estimated using these growth coefficient values and other parameter values. The sharing of nutrients between primary and its branches is dependent on the available area fraction of branches. The maintenance coefficient for maintenance of these root elements have also been discussed in this present work.

The maturity of the primary root is another important parameter which has been highlighted in this model. Also, minimum number of parameters has been used for simulation which makes this model more simple and feasible. The model is validated against published experimental results for four different species and growth characteristics are discussed based on simulations results. The primary root element reaches maturity when the area fraction of primary root reaches zero value where as no change in area fraction of primary root during elongation only growth phase. The growth is more favored for higher values of concentration difference, specific growth coefficient and smaller maintenance coefficient of primary root. The total mass of hairy roots increases for short inters node distance due to increased branches production rate. This model results the length of primary root as well as all secondary root elements with culture time. In addition to length data, one can obtain the area fraction of primary as well as secondary elements. This data will be a crucial input in determining the packing fraction of a growing root bed. Integration of this kinetic growth model with root bed model and reactor model enables us to find the optimum operating conditions of a bioreactor for the sustained growth of hairy root cultures.

Conflict of interest

The authors declare there is no conflict of interest.