1. Introduction

Some of the most significant developments in the field of Mathematical Epidemiology of infectious diseases concern the role of the feedback enacted onto an epidemic by the available information and rumors concerning the spread of an infectious disease. This requires to introduce into epidemic models new components modeling the 'human factor'. From this it follows a radically new viewpoint since in the classical approach to epidemic modeling the individuals are represented as interacting particles, and the infection process is modeled by means of the mass-action law of statistical physics [2,6,28,31,33]. However, this kind of approximation cannot adequately represent modern vaccination scenarios where conflicting instances determine private choices.

The scenario we are interested in is the vaccinal response of a population to an infectious disease in the increasingly important case where the vaccination is not mandatory. This means that, the vaccine being no more mandatory, the spread of a large number of non-vaccinator groups is observed [26,27,41,46]. Indeed, in such a case we observe the spread of 'pseudo-rational' behaviors towards vaccination: parents will tend to relate the decision to vaccinate their children to the available information on the state of the disease. Thus the propensity to vaccinate follows the incidence or prevalence of the disease targeted by the vaccine [7,19,30]. This behavior is in reality myopic because the low prevalences of some childhood diseases are caused by large level of vaccination [1,5], which allowed to hugely decrease the number of cases. Compare for example, the pre-and post-vaccine introduction time series of notified cases of measles in UK reported in figure 1.1 of [1].

In [19,20], a simple SIR-like vaccination model has been introduced, where the vaccination rate is a function of the available information on the disease state. The proposed model predicts that the elimination of the disease is an unfeasible task, and 'pseudo-rational' exemption may produce very large sustained recurrent (periodic) epidemics if the decision to vaccinate also depends on the past history of the disease.

The modeling approach adopted in [19,20] do not take into the account two important observed phenomena, widely investigated in the public health and epidemiology literature. The first one is that the vaccination propensity is the trade off of two opposite tendencies. On the one hand the information and rumors on the spread of the diseases increase the propensity to vaccinate. See for example the data concerning the rise of pertussis vaccine uptake in England and Wales following some large epidemic peaks [32,4], or the classical paper by Philipson [37] showing that in USA, between 1984 and 1990, the age in months of first dose of anti-measles vaccine was a decreasing function of the measles prevalence. On the other hand, the information and rumors on the vaccine side effects, which produces a propensity reduction. This effect has, for example, widely been observed during the (not yet fully ended) years of the MMR vaccine scare [21], when the vaccination uptake was as low as $87\%$ in Scotland and $80\%$ in England and Wales [35]. The second phenomena is that the mechanism that induces changes in human behavior is extremely complex and its non-instantaneous dynamics has to be explicitly taken into account. This implies, from the mathematical standpoint, that the propensity to vaccinate has to be a state variable.

A classical game-theoretic model of behavioral change in a given population is the imitation game. It has been adopted in [4] to model (in synergy with a SIR epidemic model) non-mandatory vaccinations under the hypothesis that the 'force' against the propensity to vaccinate is irrespective of any information on vaccine side-effects. In [17], an imitation game-based model has been proposed where the above mentioned 'force' depends on the information available on the vaccine-induced side effects. Differently from [4], in [17] it has been shown that a huge disproportion between the perceived risk of disease and vaccination is necessary in order to achieve high coverages. Furthermore, it has been confirmed that voluntary vaccination can never induce the elimination of the target disease.

In the follow up paper [18] the authors assume that even in a scenario where vaccinations are not mandatory the Public Health Systems (PHS) may enact strategies of persuasion to positively impact on the dynamics of the fraction of vaccinated subjects. This is a rather realistic scenario, see for example the IMI-funded project aimed at raising the awareness about Ebola experimental vaccine [25]. As a consequence, the imitation-game model proposed in [17] has been modified in order to include a term representing the efforts provided by a PHS to increase the propensity to vaccinate.

The above investigations concerning the interplay between private vaccine choices and public health interventions suffer of two major issues. The first is that they are aimed at being applied to childhood diseases and yet a SIR model approach is used, which fails into exploring some important dynamics of childhood diseases. The other piece missing is the assumption of seasonal fluctuations in the transmission rate. This component is very important in determining the population dynamics of infections, especially for childhood diseases [23].

The role of periodic changes of the transmission rates is a major and old issue. Indeed, early studies by H. E. Soper on measles time-series from Glasgow showed that seasonal variations occur in measles transmission rate [39]. He suggested that one of main driver of these fluctuation was the congregation of children during school terms. This hypothesis was also suggested in [29], where annual trends in the contact rate of measles, chickenpox and mumps were analyzed. Finally, from recent monthly data collected by WHO, it can be seen that number of cases is much higher during school terms, while there is a sort of decline in the transmission rate of measles during school holidays [42].

Probably, the most important effect of seasonal variations of disease transmission is the onset of nonlinear resonances [38], among which there are biennial periodic epidemics and chaos [36]. All these investigations suggest that the choice of a constant transmission rate may be too unrealistic for certain diseases. For this reason, we will consider a periodic contact rate and will study its impact on the spread of childhood diseases.

A difficulty that arises from considering a time-varying contact rate is that the resulting model is non-autonomous. Therefore some well established methods that work for autonomous models cannot be used any longer. In particular, the explicit expression of the basic reproduction number (from now on, BRN) cannot be computed by applying sic et simpliciter the well known next-generation approach (see e.g. [6,14,40]). On the other hand, it is also well known that the BRN computed by assuming the average value of the oscillating rates fails in predicting stability/instability [12,15]. Recently, an effective numerical algorithms for computing the BRN as well as an approximated formula for the case of sinusoidally varying contact rates has been provided by N. Bacaër [3]. Based on the early works of Bacaër, the BRN and its computation is also given for a large class of epidemic models in periodic environment in [44].

The aim of the present work is to investigate the possible interplays between seasonal variations of the transmission rates in childhood diseases and the actions of PHS to favor vaccination described in [18] in the framework of the SEIR epidemic model. Our basic questions are the following: Does the presence of seasonal fluctuations negatively interfere with the action of PHS? Or is there any form of synergy? Given the complexity of dealing with non-autonomous nonlinear dynamical systems, even in finite dimensions, our study was done by adopting analytical, approximate-analytical and numerical tools.

The paper is organized as follows: in Section 2 after concisely summarizing some key properties of the SEIR epidemic model, we introduce the SEIRp model. Note that the modeling approach we used to build the new model is radically different from the one used to infer the SIRp model in [18]. Here we adopt a statistical-mechanics/sociophysics based approach to infer the game-theoretical approach, whereas the SIRp model in [18] was built through a pay-off based economic interpretation of the game theory. In Section 3 we provide a qualitative analysis of the SEIRp model which includes equilibria and their stability and the uniform persistence analysis. The effective BRN at the mixed-state equilibrium is studied in Section 4 in both cases of periodic and piecewise constant fluctuations of the transmission rate. The analytical results are then supported by numerical simulations, in Section 5. Concluding remarks, in Section 6, close the paper.

---

2. From the SEIR to the SEIRp model

---

2.1. Key facts on the SEIR model with time-periodic contact rate

When modeling a disease spreading in a population, the disease transmission rate may be seen as the product of the per capita contact rate of infectious individuals (say, $\hat c$) and the probability that a contact between a susceptible individual and an infectious individual results in transmission (say, $\hat p$) [31]. Here we represent the fluctuation of the transmission rate as the result of fluctuations in one or both the terms $\hat c$ and $\hat p$. Therefore, we describe the transmission term as

$\beta(t)=\beta\,c(t)$

where $\beta$ is the (positive constant) baseline transmission rate and $c(t)$ is a positive time periodic fluctuation function such that $\langle c(t) \rangle =1$.

For the sake of precision, we assume that the force of infection is of the standard mass-action type [9]:

$F = \beta c(t) \frac{Y(t)}{N(t)},$

where $N$ represents the size of the target population at time $t$ and $Y(t)$ represents the size of the infectious sub-population at time $t$.

Let us now consider the following SEIR (Susceptibles - Exposed - Infectious - Removed) model:

$\label{SEIR} \begin{array}{ll} \dot{S}&= \mu (1 - S) - \beta c(t)SI \\ \dot{E}& = \beta c(t)SI - (\mu + \rho)E \\ \dot{I}& = \rho E - (\mu + \nu)I, \end{array}$

(1)

where the parameters $\mu$, $\rho$ and $\nu$ are positive constants and represent, respectively, the life expectancy at birth, the latency rate and the rate of recovery from the disease. The state variables $(S(t),E(t),I(t))$ denote the fractions at time $t$ of: susceptible subjects ($S$), of latent subjects that have been infected but that are not yet infectious ($E$), and, finally, the fraction of infectious subjects ($I$). The dynamics of the fraction $R(t)$ of removed individuals (i.e. subjects that, after having been infectious, can no more transmit the disease) is governed by the linear ODE: $\dot R= \nu I - \mu R$.

We remark that if we had assumed a full mass action-type force of infection $F = \beta c(t) Y$, the model with fraction state variable would have a contagion rate given by $N \beta c(t) S I$. However, since we are considering a disease that does not induce disease-specific deaths, the analysis we are going to illustrate would be unchanged (apart, of course, a numerical scaling for the constant $\beta$).

It can be easily checked that model (1) admits the disease-free equilibrium:

$DFE = (1,0,0).$

According to the Floquet theory [10,11], this equilibrium will be locally stable or unstable depending on the position in the complex plane of the Floquet eigenvalues (i.e. the characteristic multipliers of the periodic system (1)) associated with the matrix:

$\label{floquetM} A(\beta,c(\cdot)) = \left(\begin{array}{cc} -(\mu+\rho)&\beta c(t)\\ \rho&-(\mu+\nu) \end{array}\right).$

(2)

If the eigenvalues fall into the unit circle of the complex plane, then the linearized system is locally asymptotically stable, if they fall outside of it, then the linearized system is unstable.

If the DFE is locally stable, then there is self-limitation of the epidemics and a public health control is only useful to accelerate this process. Note that the most extreme case of local stability is the one where $\beta=0$ (i.e. suppressed transmission of the disease).

Thus here we will consider the more interesting case of unstable DFE, i.e. we suppose that the function $\beta c(t)$ is such that at least one of the two eigenvalues of the above Floquet matrix is external to the unit circle.

We will investigate the free vaccination scenario, where the public health authorities enact a strategy that favor the propensity to vaccinate. The more traditional case concerning the implementation of mandatory vaccination of newborns will be also mentioned.

---

2.2. The SEIRp model

We consider a population where it is possible to distinguish among parents who are pro-vaccine, and vaccinate their children, and parents that are against vaccination. We assume that the population of parents is proportional to the total (constant) population. We denote the fractions of the two groups at time $t$ as $p(t)$ and $A(t)$, respectively, and $p(t)+A(t)=1$ for all $t$.

The imitation game, following the key idea on which this important concept is based, is a double contagion of ideas process [16,43]:

$\label{mechPA0} \begin{array}{ll} \dot p= - \alpha^* A p + \theta^* p A\\ \dot A= \alpha^* A p- \theta^* p A, \end{array}$

(3)

In practice, the opinions of the anti-vaccination group have a force of infection of the type

$F_A = \alpha^* A,$

and those of the pro-vaccination group have a force of infection of the type:

$F_P = \theta^* p .$

In the seminal papers by Bauch [4], who directly writes an imitation game equation, it is implicitly assumed that the transmission rate of the group A is amplified by the perception of the disease-related adverse events, which results in the assumption that $\theta^*$ is in reality an increasing function of the prevalence of the disease. In [4] the rate $\alpha^*$ is constant. In [17], d'Onofrio and co-workers go a step beyond by assuming that the exchange of group from $p$ to $A$ is helped by the information on vaccine-related side-effects, thus leading to assume that $\alpha$ is not constant, but an increasing function of $p$. With our notation this means that the system (3) has to be rewritten as follows:

$\label{mechPA} \begin{array}{ll} \dot p= - \alpha(p) p A + \theta(I) p A\\ \dot A= \alpha(p) p A - \theta(I) p A. \end{array}$

(4)

Both the functions $\alpha(p)$ and $\theta(I)$ are, in general, assumed to be increasing and positive functions [18] although later we will limit ourselves to the linear case.

Remark 1. Assuming a linear form for $\theta$ one formally obtains a term of the type $const \times I \times p \times A$, which resembles a triple mass action. In reality it is only a formal 'side-effect' of the assumption of linear dependence of $\theta$ on the state variable $I$. Similarly, assuming $\alpha$ as a linear function of $p$ leads to a term of the form $const \times p^2 \times A$, which could be formally read as a nonstandard contagion (of ideas!) rate. Again, this is simply a formal effect of the assumption of linear dependence of $\alpha$ on $p$.

The action of Public Health (PH) authorities can be modeled as convincing people in the anti-vaccine subset to get vaccinate, and it can in first approximation be modeled as an additional transfer rate from the group that has no propensity to vaccinate to the group that has propensity to vaccinate, yielding:

$\label{mechNHS} \begin{array}{ll} \dot p&= - \alpha(p) p A + \theta(I) p A + \gamma(t) A\\ \dot A&= \alpha(p) p A - \theta(I) p A - \gamma(t) A. \end{array}$

(5)

where $\gamma(t)$ is a positive function that, generally speaking, captures the effectiveness of actions enacted by the PH agencies (as information, education, availability of vaccination infrastructures...) in influencing the perceptions regarding both vaccination and disease consequences. These various actions enacted by the PHS induce a flux (from the group $A$ to the group $p$) which is different from the one generated by the exchange of ideas typical of the imitation-games.

Since $A=1-p$, one can write down the following extension of an imitation-game equation:

$\dot p = p(1-p)(\theta(I)-\alpha(p)) +\gamma(t)(1-p),$

(6)

which had been qualitatively proposed (without our inference based on the mutual influence of two groups, one in favor and one contrary to vaccination) in [18]. Namely, in [18] the imitation-game based model introduced in [17]

$\dot p = p(1-p)(\theta(I)-\alpha(p))$

was extended by the heuristic addition of the new term $+\gamma(t)(1-p)$ based on the actions of PHS in favor of vaccination propensity. These actions were considered modulated: more intense when $p \approx 0$, less intense if $p \approx 1$.

We now couple the equations (5) with the SEIR epidemic model (1) and assume that

$\theta(I)=k_0 \theta\,I,\;\;\;\;\;\;\alpha(p)=k_0 \alpha\,p,$

where $\theta$ and $\alpha$ are positive constant, $k_0$ is a positive scale factor (useful in the practice, and to compare with [18], but not strictly necessary from the mathematical viewpoint) and

$\gamma(t)=k_0 \gamma,$

where $\gamma$ is a positive constant (the case of a time-varying function $\gamma(t)$ is considered in [8], where this function is obtained as output of an optimal control problem, in the case of constant transmission rate). We obtain:

$\label{SEIp} \begin{array}{ll} \dot{S} &= \mu (1 - p) - \beta c(t)SI - \mu S \\ \dot{E} &= \beta c(t)SI - (\mu + \rho)E \\ \dot{I} &= \rho E - (\mu + \nu)I \\ \dot{p} &= k_0(1 - p)((\theta\,I - \alpha\,p)p + \gamma). \end{array}$

(7)

Remark 2. Note that vaccine-related side-effects, although rare, do exist, thus the case $\alpha=0$ is purely hypothetical. Indeed, as it is immediate to verify, it would lead to a purely hypothetical scenario where $p(t)$ is an increasing function that tends to the equilibrium value with $100\%$ vaccination propensity. Similarly the case $\theta =0$ is equally unrealistic because there is always perception of the fact that disease have serious consequences for the health. Note that in the case $\alpha>0$, $\theta=0$ and $\gamma =0$ would lead to a state with no vaccinations at all ($p(t)\rightarrow 0$).

---

3. Qualitative analysis of the SEIRp model

---

3.1. Pure-vaccinator equilibrium (PVE)

Let

$\label{omega} \Omega = \{(S,E,I,p)\in \mathbf{R}_{+}^{4} : 0\le S + E + I \le 1 , 0\le p \le 1 \}.$

(8)

It is easy to check that any solution of (7) starting in $\Omega$ does not leave it by crossing one of its faces. Therefore $\Omega$ is a positively invariant region. It is also easy to check that model (7) admits a pure-vaccinator, disease-free equilibrium (PVE), given by

$E_1 = (0,0,0,1)$

(9)

The following stability result holds for the PVE:

Theorem 3.1. If $\gamma \ge \alpha$, then the PVE, $E_1$, is globally asymptotically stable in $\Omega$. If $\gamma<\alpha$, then it is unstable.

Proof. Since $\gamma \ge \alpha$, the following differential estimates hold:

$\begin{array}{ll} \dot{p} &= k_0(1 - p)((\theta I - \alpha p)p + \gamma) \ge k_0(1 - p)((\theta I - \alpha p)p + \alpha) \\ &\ge k_0(1 - p)( - \alpha p + \alpha) \notag = k_0\alpha(1 - p)^{2}. \end{array}$

On the other hand, it is easy to check that the solution of the differential equation:

$\dot{q}(t) = k_0\,\alpha(1 - q)^{2},$

is given by the family

$q(t) = 1 - \frac{1}{ k_0\alpha t + C},$

where $C$ is a real valued constant. Since $q(t) \to 1$ when $t \to +\infty$, from the comparison principle it follows:

$\liminf\limits_{t \to +\infty}p(t) \ge 1.$

Moreover, being $0\le p(t) \le 1$, we get $p(t) \to 1$ when $t \to +\infty$. As a consequence, since for all $\epsilon>0$ it exists a $t_{\epsilon}$ such that $p(t)<1-\epsilon$ for $t>t_{\epsilon}$, and being

$\dot{S} < \mu (\epsilon - S),$

it follows that for $t>t_{\epsilon}$, we get $0<S(t)<\epsilon$, i.e. $S(t) \to 0$ when $t \to +\infty$. In view of the differential inequality:

$\dot{E} \le \beta c(t) \epsilon - (\mu+\rho) E$

we easily infer that also $E(t)$ tends to zero, and the same holds for $I(t)$.

This prove the global stability of $E_1$ in $\Omega$.

Finally, linearizing around $E_1$:

$(S,E,I,p)=E_1+(s,e,i,y)$

one gets the following equation for the linear dynamics of $p$: $y^{\prime}=k_0(\alpha -\gamma)y$. Hence if $\gamma<\alpha$, then $E_1$ is unstable.

The condition $\gamma> \alpha$ has a simple epidemiological interpretation: it implies that the flux induced from group $A$ to group $p$ by the PHS actions is able to over-compensate the flux from group $p$ to group $A$. This can be seen by rewriting the imitation-game equation as follows:

$\dot p = \theta I p(1-p) + (\gamma - \alpha p)(1-p).$

(10)

We have:

$\gamma>\alpha \Rightarrow \gamma -\alpha p > 0,$

implying that both addenda at the r.h.s. of (10) are positive, and in turn that $p(t) \rightarrow 1$.

---

3.2. The mixed state equilibrium (MSE)

Model (7) may also admit another disease-free equilibrium, the mixed-state equilibrium (MSE), given by

$E_2 = (1-p_2,0,0,p_2),$

where

$p_2 = \sqrt{\frac{\gamma}{\alpha}}.$

(11)

Clearly, the MSE exists only if $\gamma < \alpha$.

Note that for all $p_2 \le p \le 1$ it follows:

$\dot{S} + \dot{E} + \dot{I} < \mu ( 1 - p_2) - \mu (S + E + I ).$

On the other hand, we know that the PVE equilibrium $E_1$ is unstable if $\gamma < \alpha$. It is easy to check that the plane $p(t)=1$ is a stable manifold for $E_1$. Therefore, for any $x_0=(S_0,E_0,I_0,p_0)$ in the interior of $\Omega$, it is not possible that $p(t,x_0)\rightarrow 1$ for $t\rightarrow\infty$. Therefore, there exists a time $\tilde t>0$ such that any solution of (7) starting in the interior of $\Omega$ will be confined in the region

$\label{omegatilde} \Omega_2 = \{(S,E,I,p)\in \mathbf{R}_{+}^{4} : 0\le S + E + I \leq 1-p_2 , p_2\le p \le \tilde p \}.$

(12)

where

$\tilde p = \sup\limits_{(t,x_0)\in (\tilde t,+\infty)\times {\mathring{\Omega}}} p(t,x_0) < 1.$

In the following we will obtain sufficient conditions, expressed in terms of the function $c(t)$ guaranteeing that the MSE is globally attractive. Before stating this result, it is useful to recall an important property of linear cooperative system.

Consider the following linear system:

$\label{linear1} y^{\prime}(t)= \left(\begin{array}{cc} -(\mu+\rho)&\beta c(t)\psi\\ \rho&-(\mu+\nu) \end{array}\right)\,y(t);\;\;\;\;y(0)=y_0$

(13)

where $y=\left(y_1,y_2\right)^{Tr}$ and $y_1(0)\geq 0$, $y_2(0)\geq 0$, $\psi \in [0,1]$ (for $\psi=1$ the matrix reduces to (2)). System (13) is cooperative [13,24], since

$\partial_{y_2} y_1^{\prime}(t) = \beta c(t) \psi > 0;\;\;\; \partial_{y_1} y_2^{\prime}(t) = \rho > 0$

Using the Kamke's theorem [13] it follows the following property:

$\label{propertyA} \psi_1<\psi_2 \Rightarrow y_j^{\psi_1}(t,y_0)\le y_j^{\psi_2}(t,y_0), \;\; j=1,2$

(14)

More compactly: $y^{\psi_1}(t,y_0)<y^{\psi_2}(t,y_0)$, where we have used the notation: $y^{\psi}(t;y_0)$ $= y(t; y_0, \psi)$.

The property (14) implies that if $\psi$ increases then the eigenvalues cannot go back inside the unit circle. This can be easily checked. Indeed, assume that one of the eigenvalues is on the unit circle in correspondence of $\psi=\psi_1$ and the eigenvalues are both inner to the unit circle for $\psi=\psi_2$, with $\psi_2>\psi_1$. Then $y^{\psi_2}(t) \rightarrow (0^+,0^+)$. However this implies a contradiction since on the one hand $y^{\psi_1}(t)$ does not tend to zero and in the other hand $y^{\psi_1}(t)<y^{\psi_2}(t)$.

Finally, the eigenvalues of the Floquet matrix associated to (13) are inside the unit circle for $\psi=0$, whereas at least one of the two eigenvalues is outside the unit circle for $\psi=1$. Due to the continuity of the eigenvalues with respect to continuous parameters of the Floquet matrix, from the above analysis it follows that it exists a threshold value $\psi_{cr}(c(\cdot)) \in (0,1)$, which depends on the function $c(\cdot)$, and which is such that for $\psi<\psi_{cr}(c(\cdot))$ the eigenvalues are internal to the unit circle.

Remark 3. In order to simplify the notation, from now on we will omit all dependencies on $c(\cdot)$.

Now, set $p_{cr} = 1-\psi_{cr}$, where $\psi_{cr}$ is the above mentioned threshold value for $\psi$. We are in position to state the following result:

Theorem 3.2. If $\alpha (1-\psi_{cr})^2< \gamma < \alpha$, i.e. if $p_2>p_{cr}$, then the MSE, $E_2$, is globally asymptotically stable in $\Omega_2$.

Moreover, if $\gamma < \alpha (1-\psi_{cr})^2$, i.e. if $p_2 < p_{cr}$, then the MSE, $E_2$, is unstable.

Proof. Consider the following differential inequality:

$\dot{p} = k_0(1 - p)((\theta I - \alpha p)p + \gamma) > k_0(1 - p)(- \alpha p^2 + \gamma).$

This implies that

$\label{p2} \liminf\limits_{t \rightarrow +\infty} p(t) = p_2,$

(15)

and, in turn,

$\limsup\limits_{t \rightarrow +\infty} S(t) = 1-p_2.$

since $\dot S \leq \mu(1-p_2)-\mu S$. This last limit means that for all $\epsilon>0$ it exist a $t_{\epsilon}$ such that for $t> t_{\epsilon}$ it is

$\dot{E} < -(\mu+\rho) E + \beta c(t) (1-p_2 +\epsilon),$

implying that for $t>t_{\epsilon}$

$(E,I) < y^{1-p_2 +\epsilon}(t,y_{\epsilon}),$

where

$y_{\epsilon}=(E,I)(t_{\epsilon}).$

Therefore it can be chosen $\epsilon$ small enough to have $\epsilon < p_2-p_{cr}$, which implies that

$\lim\limits_{t \rightarrow +\infty}(E(t),I(t))= (0,0),$

and in turn:

$\liminf\limits_{t \rightarrow +\infty} S(t) = 1-p_2.$

As a consequence, $E_2$ is GAS in $\Omega_2$, as in the first claim.

Linearizing at MSE by setting

$(S,E,I,p)=(1-p_2+y_S,y_E,y_I,p_2+y_p)$

one easily obtains that the behaviour of the linearized system is determined by the linear equations for $(y_E,y_I)$, which have the same matrix of system (13). Thus, by the above illustrated analysis of system (13) it immediately follows the second claim.

Summarizing the above theorems, it exists a threshold value

$\gamma_{cr} = \alpha (1-\psi_{cr})^2,$

such that: ⅰ) if $\gamma < \gamma_{cr}$ then $E_2$ is unstable; ⅱ) if $\gamma_{cr}< \gamma < \alpha$ then $E_2$ is GAS in $\Omega_2$; ⅲ) if $\gamma \ge \alpha$ then $E_1$ is GAS in $\Omega_2$.

Remark 4. We stress here that the above mentioned threshold values for the parameters $\psi$, $\gamma$ and $p$ depends on the whole periodic function $c(t)$, since they are related to the Floquet analysis of the linearization matrix at $E_2$.

---

3.3. Uniform persistence

The SEIp model (7) admits a globally asymptotically stable equilibrium, the MSE, when $\gamma > \gamma_{cr}$, where $\gamma_{cr}=\alpha(1-\psi_{cr})^2$ (Theorem 3.2). In this section we will show that system (7) is uniformly persistent when $\gamma < \gamma_{cr}$, according to the definition given in [48], for $T$-periodic semiflow. More precisely, let $X_0$ and $\partial X_0$ be open and closed subsets of a complete metric space $X$ with metric $d$, and let $T>0$. Assume also that $X_0$ is positively invariant. An $T$-periodic semiflow $Q(t)$ is said to be uniformly persistent with respect to $(X_0, \partial X_0)$ if there exists $\eta>0$ such that for any $x\in X_0$, $\liminf_{t\to +\infty} d(Q(t)(x_0),\partial X_0 ) \ge \eta$.

In our case, we begin by taking

$X = \{(S,E,I,p) \in \mathbf{R}^{3}_{+} \times [0,\tilde p]\},\;\;\; X_0 =\{(S,E,I,p) \in X : E > 0 , I > 0\},$

and denote

$\label{partialX0} \partial X_0 := X / X_0= \{(S,E,I,p)\in X: E=0\,{\rm and}\,I\geq 0\,{\rm or}\,I = 0\,{\rm and}\,E\geq 0 \}.$

(16)

Then, we introduce the Poincaré map:

$P\colon x_0 \in X \to u(T,x_0) \in X,$

where $u(t,x_0)$ is the unique solution of system (7) corresponding to initial data $x_0 = (S_0,I_0,E_0,p_0) \in X$.

Denote with $\parallel\cdot\parallel$ a norm in $\mathbf{R}^4$. We need to prove the following result:

Lemma 3.3. If $\gamma < \gamma_{cr}$, then there exists $\delta^{*}> 0$ such that $\forall x_0 \in X_0$,

$\lim\limits_{n\to +\infty} \sup\limits_{k\ge n} \parallel P^{k}(x_0) - E_2 \parallel \ge \delta^{*}.$

Proof. When $\gamma < \gamma_{cr}$, it can be seen ([44], Theorem 2.2) that $r\bigl(\Phi_{F - V}(T)\bigr) > 1$, where the matrices $F$ and $V$ are given in the appendix A, the matrix $\Phi_{F - V}(T)$ is the fundamental solution matrix of the linear ordinary differential system $x'= \left(F(t) - V(t)\right)x$, and $r\bigl(\Phi_{F - V}(T)\bigr)$ is the spectral radius of $\Phi_{F - V}(T)$. Set $V_{\varepsilon} = V - M_{\varepsilon}$, where the matrix $M_{\varepsilon}$ is the perturbation matrix

$M_{\varepsilon} (t)= \begin{pmatrix} 0&\varepsilon \beta c(t) \\ 0& 0 \end{pmatrix}$

for all $\varepsilon >0$. From Lemma 2.1 in [44] it follows that

$\lim\limits_{\varepsilon \to 0} r \bigl( \Phi_{F - V_{\varepsilon} } (T) \bigr) = r\bigl(\Phi_{F - V} (T)\bigr).$

Therefore, we can choose $\overline{\varepsilon}$ small enough to have :

$\label{39} i)\ \ \ r\bigl(\Phi_{F - V_{\overline{\varepsilon}}}(T)\bigr) > 1,$

(17)

and

$ii)\ \ \ \overline{\varepsilon} < 1 - p_2.$

Now, let $\delta < \overline{\varepsilon}$. For the continuity from the initial conditions there exists $\delta^{*}:$ $=\delta^{*}(\delta)> 0$ such that for all $x_0 \in X_0$ with $\parallel x_0 - E_2\parallel \le \delta^{*}$, it follows

$\parallel u(t,x_0) - u(t,E_2) \parallel = \parallel u(t,x_0) - E_2 \parallel < \delta, \ \ \ \ \forall t\ge0.$

Assume for contradiction that there exists $x_0 \in X_0$ such that:

$\lim\limits_{n\to +\infty} \sup\limits_{k\ge n} \parallel P^{k}(x_0) - E_2 \parallel \le \delta^{*}.$

Without loss of generality, we assume that $\parallel P^{n}(x_0) - E_2 \parallel < \delta^{*}$ for all $n \ge 0$. By the propriety of composition of semiflows it follows:

$u(t + nT , x_0) = Q(t + n T)(x_0) = Q(t) Q(n T)(x_0) = Q(t)(P^{n}(x_0)),$

and therefore

$u(t + nT , x_0) = u(t,P^{n}(x_0)).$

Furthermore, for all $t \ge 0$ we can write $t =nT + t'$ with $n = \bigl[\frac{t}{T}\bigr]$ and $t' \in [0,T]$.

It follows:

$\parallel u(t,x_0) - E_2\parallel = \parallel u(t',P^{n}(x_0)) - E_2 \parallel , \ \ \ \forall t \ge 0.$

For this reason, from $\parallel P^{n}(x_0) - E_2 \parallel < \delta^{*}$ it follows :

$\label{44} \parallel u(t,x_0) - E_2\parallel =\parallel u(t',P^{n}(x_0)) - E_2 \parallel < \delta <\overline{\varepsilon} , \ \ \ \forall t \ge 0.$

(18)

Recall that for all $t\ge0$, $u(t,x_0)$ is the solution $(S(t),E(t),I(t),p(t))$ of (7) with initial condition $x_0$. Therefore from (18), it follows:

$|S(t) - (1 - p_2)| < \overline{\varepsilon} \Longrightarrow S(t) > 1 - p_2 -\overline{\varepsilon}, \ \ \ \forall t\ge 0.$

This last condition implies the following differential inequality:

$\dot{E} > \beta c(t) (1 - p_2 - \overline{\varepsilon})I - (\mu + \rho)E,$

which allows to consider the comparison system:

$\begin{array}{ll} \dot{\overline{E}} &= \beta c(t)(1 - p_2 - \overline{\varepsilon})\overline{I} - (\mu + \rho)\overline{E}\\ \dot{\overline{I}} &= \rho \overline{E} - (\mu + \nu)\overline{I}, \end{array}$

which can be expressed in matrix form as:

$\label{Zlinear} \frac{dz}{dt} = ( F(t) - V_{\overline{\varepsilon}}(t))\; z(t),$

(19)

where $z = (\overline{E},\overline{I})^{Tr}$. Now, setting :

$q = \frac{1}{T} \ln \,{ r \bigl( \Phi_{F - V_{\overline{\varepsilon}} } (T) \bigr) },$

from Lemma B.1, it follows that the existence of a $T$-periodic non negative function $v(t)$ such that $J(t) = v(t) e^{qt}$, is a solution of system (19).

In view of (17), it follows $q>0$, and hence $J(t) \to +\infty$ when $t \to +\infty$. Therefore, from the comparison principle it follows that $I(t)$ and $E(t)$ are not bounded and this is a contradiction.

Now we can state the uniform persistence result.

Theorem 3.4. If $\gamma < \gamma_{cr}$, then there exists $\eta > 0$ such that every solution $x(t)=(S(t),E(t),I(t),p(t))$ of model (7) with initial condition $x_0 = (S_0,E_0,I_0,p_0)\in X_0$ satisfies:

$\liminf\limits_{t\to +\infty}(I(t),E(t)) \ge (\eta,\eta).$

Proof. The proof is based on checking that all the requirements of the strong repellers theorem (Theorem 1.3.1 in [48]) are satisfied. We begin by proving that the Poincaré map is uniformly persistent with respect to $(X_0,\partial X_0)$. Following [34], we consider the set:

$M_{\partial} = \{ x_0 \in \partial X_0 : P^{n}(x_0) \in \partial X_0 , \forall n \in \mathbf{N} \}.$

From (16) we have that: $\{(S,0,0,p)$ : $S\ge 0$, $0\le p \le \tilde p \} \subset M_{\partial}$. Then, any solution starting in $\partial X_0$ satisfies $S(t)>0$, $E(t)=0$, $I(t)=0$, $0\leq p \leq \tilde p$, for all $t>\tilde t$. This implies that

$M_{\partial} = \{(S,0,0,p) : \ \ \ S\ge 0, \ \ \ 0\le p \le \tilde p\}.$

Now, clearly $E_2$ is a fixed point of $P$ and $\{E_2\}$ is an invariant set and isolated. Recalling that:

$W^{S}(E_2) = \{x_0\in X : \; \lim\limits_{n \to +\infty} \parallel P^{n}(x_0) - E_2 \parallel = 0 \},$

from Lemma 3.3 it follows:

$W^{S}(E_2) \cap X_0 = \emptyset.$

Furthermore, it is easy to check that the orbits in $M_{\partial}$ approaches $E_2$. Finally, the existence of the region (8) ensures that $P$ has a global attractor, i.e. a positively invariant set which attracts all the positive orbits in $X$. This proves that if $\gamma < \gamma_{cr}$, all the conditions required by Theorem 1.3.1 (and Remark 1.3.1) in [48] are satisfied. Therefore we deduce that $P$ is uniformly persistent respect to $(X_0,\partial X_0)$.

Finally, being $P$ compact and point dissipative, from Theorem 3.1.1 in [48] it follows that there exists $\eta > 0$ such that :

$\liminf\limits_{t\to +\infty} d(Q(t)(x_0),\partial X_0 ) \ge \eta , \ \ \ \forall x_0 \in X_0,$

which means

$\liminf\limits_{t\to +\infty}(E(t),I(t)) \ge (\eta,\eta) , \ \ \ \forall x_0 \in X_0.$

---

4. The effective basic reproduction number (BRN) at MSE

---

4.1. Periodic fluctuation function $c(t)$

The aim of this section is to compare the impact of the periodic fluctuation on the condition $p_2>p_{cr}$ implying the GAS of $E_2$ (see Theorem 3.2).

It is well known that the classical threshold condition for the disease elimination, $\mathcal{R}_0<1$, becomes $\mathcal{R}_0 (1-\pi) <1$ for SIR model with mandatory vaccination of newborns, where $\pi$ denotes the fraction of vaccinated newborns [6]. In other words, one can define an 'effective' BRN, say $\mathcal{R}_{eff} = \mathcal{R}_0(1-\pi)$, smaller than the original one. Note also that the elimination condition for the SIR model can be read as follows: $\pi> \pi_{*} := 1-1/\mathcal{R}_0$. Similarly, for the SEIR model with constant contact rate, where the BRN is:

$\mathcal{R}_{SEIR}= \frac{\beta}{\mu+\nu}\frac{\rho}{\mu+\rho},$

in case of constant mandatory vaccination the elimination condition reads as follows $\mathcal{R}_{eff}<1$ i.e.

$\label{pstar} \pi> p_{*} := 1- \frac{1}{\mathcal{R}_{SEIR}}$

(20)

For the SEIR model, in the case of constant contact rate (i.e. absence of oscillations) the GAS condition for $E_2$ can be written as follows:

$\mathcal{R}_{SEIR} (1-p_2) <1,$

that is: $p_2 > p_*$.

In the case of periodically varying transmission rate, the effective BRN of the SIR epidemic model is

$\mathcal{R}_{eff} = \frac{\langle \beta(t) \rangle}{\mu+\nu}(1-\pi),$

thus the elimination solely depends on the average value of the transmission rate. However, if the transmission rate is time-periodic then the computation of the BRN is much more complex for both the SEIR model (with or without vaccination) and the SEIRp model, since it depends on the 'shape' of $c(t)$.

Here we will consider a classical idealized period waveform for $c(t)$:

$\label{c(t)} c(t) = 1 + \sigma cos(\omega t + \chi).$

(21)

In order to estimate the BRN we need the following result:

Proposition 1. ([3], par. 5.1.2) If the contact rate is given in the form (21) and the model consists of two infected compartments $x_1$ and $x_2$, whose equations linearized at DFE are expressed as¹

$\label{cyclic} \begin{array}{ll} \dot{x_1} &= a_2\left(1 + \sigma cos(\omega t + \chi)\right)x_2 - b_1x_1\\ \dot{x_2} &= a_1x_1 - b_2x_2, \end{array}$

(22)

¹A model taking the form (22) is a special case of 'cyclic' model, see [3].

where $a_i$, $b_i$, $i=1,2$ are positive constant, then the following estimate of the BRN holds:

$\label{Roapprox} \mathcal{R}_0 \approx \frac{a_1a_2}{b_1b_2}\biggl(1 - \frac{b_1b_2}{\omega^{2} + (b_1 + b_2)^{2}}\frac{\sigma^{2}}{2}\biggr).$

(23)

Now, let us consider the Jacobian matrix of the system (7) evaluated at $E_2$:

$J(E_2 ) = \begin{pmatrix} -\mu&0&-\beta c(t)(1 - p_2)&-\mu \\ 0&-( \mu + \rho)&\beta c(t)(1 - p_2)&0 \\ 0&\rho&-(\mu + \nu)&0 \\ 0&0&k_0\theta ( 1 - p_2)p_2&-2k_0\alpha p_2(1 - p_2) \end{pmatrix}.$

Therefore, the linearized equations corresponding to the 'infected' compartments at $E_2$ are:

$\begin{array}{ll} \dot{E} &= \beta (1 - p_2)c(t) I - (\mu + \rho)E \\ \dot{I} &= \rho E - (\mu + \nu)I \end{array}$

Being in the form (22) we can use (23) to obtain:

$\label{Roptilde} \mathcal{R}_{eff} \approx \mathcal{R}_{SEIR} \phi(\sigma) (1-p_2),$

(24)

where

$\phi(\sigma) = 1 - \xi \sigma^{2},$

and

$\xi = \frac{1}{2}\frac{(\rho + \mu) (\mu + \nu)}{\omega^{2} + ( (\rho + \mu) + (\mu + \nu ))^{2}}.$

Note that: ⅰ) The effective BRN $\mathcal{R}_{eff}$ depends on the 'shape' of $c(t)$ via the function $\phi$, as well as on $\gamma$, of course. The knowledge of the average value $\beta$ is not sufficient to assess the stability/instability; ⅱ) $\phi$ is smaller than one; ⅲ) $\phi$ is a decreasing function of $\sigma$.

This last point has an interesting implication: compared to the case of constant transmission rate, the elimination threshold is smaller in case of fluctuating transmission rate, i.e.:

$p_{cr}(\sigma) = 1-\frac{1}{\mathcal{R}_{SEIR} \phi(\sigma)}<p_{*},$

where $p_*$ is given in (20).

Summarizing, since:

$p_{cr}(\sigma)< p_*$

it follows that the role of $\sigma$ in determining the behavior of MSE is as follows:

• If $\gamma \ge \alpha$ then the pure vaccinator equilibrium, PVE, is GAS.

• If $1>p_2>p_*$ (or equivalently: $\alpha>\gamma>\gamma_*=\alpha p_*^2$) then the MSE is GAS, independently from the oscillations of the transmission rate. Indeed, since $p_2>p_*$ and $\phi(\sigma)<1$ it follows that

$\mathcal{R}_{eff} \approx \mathcal{R}_{SEIR} \phi(\sigma) (1-p_2) <\mathcal{R}_{SEIR} (1-p_2) <1.$

• If $p_{cr}(\sigma)<p_2< p_*$ (equivalently: $\gamma_{cr}(\sigma)<\gamma<\gamma_*$, with $\gamma_{cr}(\sigma) = \alpha p_{cr}^2(\sigma)$) then the MSE is GAS, and in this case the GAS does depend on $\sigma$.

• If $p_2< p_{cr}(\sigma)$ then the MSE is unstable and the disease is persistent.

Remark 5. The above considerations are only valid, of course, for those $\sigma \in (0,1)$ such that the approximation (24) is valid (see [3]).

It is of some interest to study the somewhat reverse case where $\gamma$ (and, as a consequence, $p_2$) is given. In such a case the following question arises: which is the impact on the stability of the MSE of the oscillation amplitude $\sigma$? Of course, first of all we must assume that $\gamma<\gamma_{*}$ (i.e. $p_2 < p_*$), otherwise the dynamics of $I(t)$ is determined: $I(t) \rightarrow 0^+$ independently from the initial conditions and from $\sigma$.

From the GAS condition:

$\label{Gascondition} \mathcal{R}_{SEIR} \phi(\sigma) (1-p_2) < 1,$

(25)

one obtains

$\label{sigmac} \sigma > \sigma_c = \sqrt{\frac{1}{\xi}\left(1-\frac{1}{\mathcal{R}_{SEIR}(1-p_2)}\right)},$

(26)

Condition (25) can be also written $\mathcal{R}_{SEIR} (1-p_2) < 1/(1-\xi \sigma^2)$ and, since $\sigma \in (0,1)$, it follows:

$\mathcal{R}_{SEIR} (1-p_2) < \frac{1}{1-\xi }.$

Again from $\sigma \in (0,1)$, we get that if

$\label{gcr1} \gamma<\gamma_{cr}(1) = \alpha \left(1- \frac{\mathcal{R}_{\xi}}{\mathcal{R}_{SEIR}}\right)^2,$

(27)

where $\mathcal{R}_{\xi}=1/(1-\xi)$, then the disease is persistent.

Remark 6. (Comparison with the SIR model). One could wonder whether seasonal fluctuations of the transmission rate have some relevant dynamical effects also in case of SIR modeling approach. The answer is negative. In fact, in case of a SIRp model (see equations (4)-(6) in [18]) it can be proved, by following the same reasoning of the previous sections, that if $\gamma > \alpha$, then the PVE is globally asymptotically stable. On the other hand, if $\gamma < \alpha$, and $\mathcal{R}_{SIR}(1-p_2)<1$, i.e. if $p_2 > 1-1/\mathcal{R}_{SIR}$, then the MSE is GAS. Indeed, we observe that also in the SIR case we get $S(t) \le (1-p_2)$, which implies the inequality $\dot{I}(t) \le I(\beta c(t) (1-p_2) -(\mu+\nu))$, from which, remembering that $\langle c(t)\rangle =1$, the claim easily follows.

Remark 7. (Mandatory vaccination scenario). Assume that a fraction $\pi$ of the newborns are vaccinated on mandatory-basis. Then the first equation in (7) changes in the following: $\dot{S} = \mu (1 - \pi - S) - \beta c(t)SI$. Reasoning as in the proof of theorem 3.2, it is easy to show that if $\pi>p_{cr} = 1-\psi_{cr}$, then the elimination equilibrium point $EEP=(1-\pi,0,0)$ is globally asymptotically stable in $\Omega$.

---

4.2. Piecewise constant fluctuation function $c(t)$

As remarked above, the investigation on the BRN given in the previous subsection is only an approximate investigation, and the result is valid only for small-medium values of $\sigma$. Nevertheless, the result is stimulating: even in some cases when $p_2<p_{*}$ (i.e. when stable elimination is not possible in the case of constant transmission rate) the presence of oscillations in the contact rate is able to stabilize the MSE, through the threshold condition (26). This behavior could also led to think to a paradoxically beneficial effect of the increase of $\beta(t)$.

As a matter of fact, no stabilizing effects can be observed in the time interval when the instantaneous effective BRN,

$\mathcal{R}_{eff}(t)= \mathcal{R}_{SEIR}(1-p_2)c(t),$

is larger than one. Indeed, it is evident that the beneficial stabilizing effect of the oscillations can take place only in the phase when

$\mathcal{R}_{eff}(t)= \mathcal{R}_{SEIR}(1-p_2)c(t)<\mathcal{R}_{SEIR}(1-p_{*}),$

and

$c(t)<\frac{1-p_{*}}{1-p_2}.$

(28)

This reasoning is very heuristic, but it can be made more rigorous by considering another important model of transmission rate, the piecewise constant transmission rate, which mimics the effects of the alternation of large vs. low average contacts during, respectively, the working periods vs. the holidays.

Although such a representation is considered to be more realistic than the sinusoidally oscillating contact rate, its waveform must also be considered an idealization [22]. Indeed, on the one hand it is discontinuous, thus mimicking the decrease of contacts during holiday terms, but, on the other hand, it does not take into account the time-varying factors that contribute to the transmission but are not only related to the average number of contacts. This is confirmed by the fitting of transmission rate of measles to data from England and Wales [22], which suggests that this rate is a time-continuous function although there are remarkable fluctuations between holidays and School terms (see also Figure 1 in [23] and the related discussion).

Here, we consider a simplified model where there is a unique period of holidays, yielding:

$c(t) = \begin{cases} c_L &\mbox{if } (t ; mod: T) \in (0, f T) \\ c_H&\mbox{if } (t ; mod: T) \in (f T,T), \end{cases}$

with $c_L<c_H$. We can consider that the period $[0,T]$ is split in two phases. The second phase is such that the effective BRN is constant and larger than one. On the contrary, in the first phase the effective BRN, although constant, can be less than one provided that (28) holds, i.e. it must be:

$c_L<\frac{1-p_{*}}{1-p_2}.$

(29)

For example, if we very roughly approximate our sinusoid with a square-wave (where $f=1/2$) of amplitude $\sigma$, this would implies $c_L=1-\sigma$ (and $c_H=1+\sigma$) leading to the following necessary condition for stable elimination:

$\sigma > 1- \frac{1-p_{*}}{1-p_2} ,$

i.e. a threshold effect on the amplitude of the oscillations.

In the general case, applying the constraint $\langle c(t) \rangle =1$ yields: $f c_L + (1-f) c_H = 1$. Let us now introduce the new parameter $\eta$ such that $c_L = \eta c_H$. Hence $\eta$ is a measure of how much the contact rate reduces during the holidays with respect to the working period. Then one gets

$c_L=\frac{\eta}{\eta f + (1-f)},$

and

$c_H=\frac{1}{\eta f + (1-f)}.$

Thus, the piecewise contact rate will depend (apart of the period $T$, which however is set to be one year) on two parameters, $\eta$ and $f$, both varying in $(0,1)$. Therefore, the necessary condition (29) becomes

$\eta < \frac{1-f}{\frac{1-p_2}{1-p_{*}}-f}.$

(30)

Of course (30) is only a necessary condition, and the specturm of the Floquet matrix associated to the linearized system for $(E,I)$ at the disease elimination equilibrium MSE has to be computed.

Defining the matrix:

$A(U) =\begin{bmatrix} -(\mu+\rho)&\beta \psi U\\ \rho&-(\mu+\nu) \end{bmatrix} ,$

where $\psi = 1-\sqrt{\gamma/\alpha}$, the Floquet matrix is given by:

$F = e^{ (1-f) T A(c_H) } \times e^{ f T A(c_L) } ,$

(31)

which can be analytically computed together with its eigenvalues. However the symbolical computations leads to very complex formula for the spectrum of $F$ that does not yield insights on the impact of the various parameters on the stability, although it allows precise numerical computations.

---

5. Numerical simulations

In this section, we support the analytical results obtained in the previous sections by providing numerical simulations in the noteworthy case $\gamma < \alpha$.

---

5.1. Periodic fluctuation function $c(t)$

We consider the fluctuation function (21). Choosing one year as time unit, it follows that the period is $T=1$ and the pulsation $\omega = 2 \pi$. In order to represent a maximum value in correspondence of school term and a minimum value for school holidays, we set $\chi = -0.8$.

The numerical simulation of model (7) are then performed by using the following values for the parameters: $\mu^{-1} = 78\,years$, $\rho^{-1} = 10\,days$, $\nu^{-1} = 7\,days$, $\mathcal{R}_{SEIR}=10$. As in [18], for convenience of simulations we define $\bar{\gamma}:= \gamma/\theta$, $\bar{\alpha}=\alpha/\theta$, $\bar{k}=k_0 \theta$ and we set $\bar{\alpha}= 1.6382 \times 10 ^{-4}$, $\bar{k} = 5 \times 10 ^{7}$.

As shown in subsection 4.1, the quantity $\gamma_{cr}(1)$ in (27) is useful to discriminate the dynamical behavior of the SEIRp system (7) when the approximation (23) is valid. More precisely, for $\gamma < \gamma_{cr}(1)$ the system is persistent, whereas the behavior for $\gamma \in (\gamma_{cr}(1),\gamma_*)$ is strongly dependent on $\sigma$.

However, just due to the approximation, the usefulness of these predictions is limited. Therefore, it is important to evaluate the actual behavior of the system around the MSE by computing the effective BRN, say $\mathcal{R}(p_2,\sigma)$, where $p_2$ is given in (11).

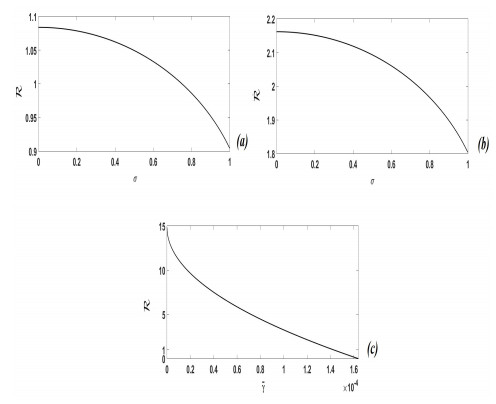
We computed this important parameter by employing the numerical algorithm proposed by N. Bacaer in [3]. Figure 1 shows the relation between $\mathcal{R}(p_2,\sigma)$ and $\sigma$ (given the value of $\bar{\gamma}$) or $\bar{\gamma}$ (given the value of $\sigma$).

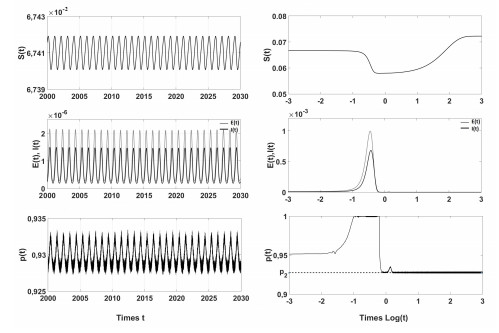
We see in panels (a) and (b) of Figure 1 that the BRN decreases as $\sigma$ increases.

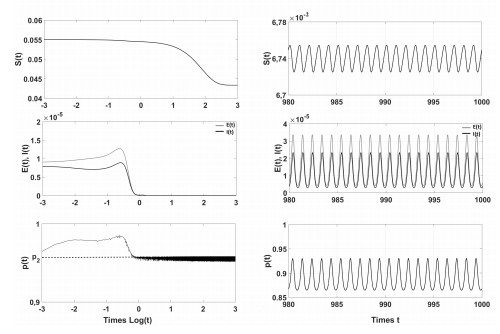
In Figure 1(a), we assumed $\gamma > \gamma_{cr}(1)$ and we obtained that effectively there is a threshold value $\widehat{\sigma}$ for which the BRN is one and such that for $\sigma> \widehat{\sigma}$ the MSE is GAS (see right panel of Figure 2), whereas for $\sigma< \widehat{\sigma}$ MSE is unstable and there is the onset of oscillations (see left panel of Figure 2). However, when $\gamma < \gamma_{cr}(1)$, (Figure 1(b)), the seasonal variation is not enough to reduce the effective reproduction number under one. All this suggests that the approximate formula (23) gives useful -albeit qualitative-indications about the stability threshold.

In Figure 1(c) the relation between the effective BRN and $\bar{\gamma}$ is shown (for $\sigma= 0.3$). We see that $\mathcal{R}(p_2,\sigma=0.3)$ is greater than one for values of $\bar{\gamma}$ lower than the threshold $\gamma_{cr}(1) \approx 1.45 \cdot 10^{-4}$.

In Figure 3, left panel, $\bar{\gamma}$ is assumed to be over the threshold, so that the MSE is GAS. In Figure 3, right panel, the value of $\bar{\gamma}$ is under the threshold and the system is oscillating (see also the above mentioned right panel of Figure 2).

---

5.2. Piecewise constant fluctuation function $c(t)$

As we have mentioned in subsection 5.1, for the specific piecewise constant fluctuation function $c(t)$ the Floquet matrix and its eigenvalues can be analytically computed leading to formulas that, although too complex to disentangle the weight of key parameters, yet allow 'exact' numerical analysis without having to simulate differential equation.

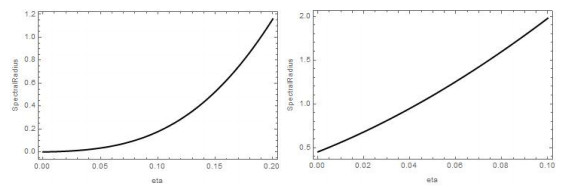
We have found that the stabilization can be obtained only for values of $p_2$ very close to the threshold $p_*$ defined in (20), even when considering the square-wave approximation of the sinusoidal transmission rate, which corresponds to the case $f=1/2$. For example, assuming $p_2=0.99 p_{*}$ we obtained that although the necessary threshold was $\eta<0.63$ about (i.e. $\sigma > 0.22$), the actual condition leading to the stabilization of the MSE is much sharper: $\eta<0.18$ about (i.e. $\sigma >0.69$ about). A more realistic representation of school holidays can be obtained taking $f=1/4$ (for example, this is the case of Italy, where until the seventies of the past century, the school holidays term were from mid June to the beginning of October). In this case the threshold for $\eta$ is approximately $0.04$, whereas the threshold of the necessary condition is much larger (approx. $0.84$).

In Figure 4, we plot the spectral radius of the Floquet matrix $F$ defined in (31) for $f=1/2$ (left panel) and $f=1/4$ (right panel).

---

6. Concluding remarks

In this work we have faced the task of a more realistic modeling of a public health campaign aimed at convincing parents to vaccinate their children against a childhood infectious disease. This problem has been originally considered in [18] for SIR type diseases with constant contact rate. Here we have reconsidered the problem and have proposed two important, epidemiology-motivated, changes.

The first is the description of the dynamics of the disease spread by including a compartment of latent individuals, who are infected but not infectious yet. The second key point is that we take into account of the impact of regular fluctuations of the transmission rate.

First, we have obtained the conditions ensuring the global stability of a pure-vaccinator equilibrium, where all the individuals are vaccinated and, as a consequence, there are no more susceptibles in the population. Then, we have studied the existence and the global stability of a mixed state equilibrium, which is a disease-free equilibrium where, differently from the PVE, the equilibrium value of the vaccinating fraction (or 'propensity') is less than $1$. This implies a residual 'reservoir' of susceptible individuals that could be infected. In the case where the conditions ensuring the global stability of the MSE are not satisfied, we have shown that the disease remains permanent in the population.

Particularly interesting is the case where the MSE is globally stable. Indeed, in such a case for sinusoidally varying transmission rates the approximate expression (23) of the BRN suggests an apparent paradox: given a value of $\gamma$ insufficient to guarantee the GAS of the MSE in absence of oscillations, there may be a minimum amplitude of the sinusoidal oscillations such that the MSE is GAS.

We have explained this apparent paradox heuristically. To this aim, we have considered another important fluctuation function to describe the time-dependence of the transmission rate: a piecewise constant function oscillating between two constant levels. The phase of increase of the transmission rate does not favor stabilization. In other words, seasons with an increased number of contacts, and/or an increased probability of transmission per contact, do not favor disease elimination. On the contrary, they favor instability. The stabilization is evidently obtained thanks to the phase where the number of contacts, and/or the probability of infection per contact, is decreased. This phase can be able sometime to -roughly speaking -'over-compensate' the destabilizing effects of the complementary phase. The analysis of the piecewise constant varying transmission rate case allowed us to find a necessary condition for the fluctuation-induced disease elimination.

The actual threshold values can be exactly computed since the Floquet matrix is analytical. In the case of sinusoidal fluctuations, the Floquet Matrix, as well as its spectrum, may be computed numerically. We have found that the predictions obtained by means of the approximate expression of the BRN (see (23)) are qualitatively valid, at least in the range of parameters we considered.

As remarked in section 4.1 we have shown that adding fluctuations to the transmission rate in the SIRp model, as considered in [18], no fluctuations-induced stabilization of the MSE is observed. In other words, the stabilization occurs due to the combined presence of the fluctuations and of the latency phase in the disease transmission.

The interest of showing that the elimination threshold in the case of oscillating transmission rate is lower than the one obtained for the static case of constant transmission rate goes beyond its mathematical interest. Indeed, a lower elimination threshold for $\gamma$ means a lower expenditure, so that the saved money could be devoted to other Public Health activities.

It is of interest to summarize the above analytical and numerical findings by noting that, in presence of latent compartment, in no cases the scenarios were ruled by the average transmission rate. In all cases, indeed, the results depended of the whole 'waveform' of the periodic function $c(t)$. Thus it is fundamental to infer from epidemiological data the full time variation of the transmission rate, and not only its average value.

Finally, we briefly mention that in no cases we found chaotic or even period-doubling solutions. This might be linked with the fact that the vaccination with dynamic rate $p(t)$, whose dynamics is such that $\partial_I (\dot p) >0$, can 'read' as a feedback control. And this involuntary 'control' is able to suppress chaos.

We are planning to follow this research along two lines of investigation. The first is to assess the impact of time changes in the public health effort to increase the vaccine propensity, i.e. $\gamma(t)$. Could fluctuations in $\gamma(t)$ allow a further stabilization? Moreover, could such oscillations induce nonlinear resonances in the system?

The second line joins the present study with our work concerning the optimal control of the SIRp model [8]. It would be worth investigating the economic impact of the SEIR structure and of the oscillations in the transmission rate. A major issue will be to find the optimal time-profile of the function $\gamma(t)$ ensuring the minimization of the global expenditure by the PHS.

---

Acknowledgments

We want to thank three anonymous referees, whose suggestions helped us to greatly improve this work. The work of B. B. has been performed under the auspices of the Italian National Group for the Mathematical Physics (GNFM) of National Institute for Advanced Mathematics (INdAM).

---

Appendix A. Useful matrices

In the framework of the next-generation approach (see e.g. [6,14,40]) the transmission vector $\mathcal{F}$ and in-out vector $\mathcal{V}$ of (7) are defined as follows:

$\mathcal{F}(t,S,E,I,p) = \begin{pmatrix} \beta c(t)SI \\ 0 \end{pmatrix}; \;\;\;\;\; \mathcal{V}(t,S,E,I,p) = \begin{pmatrix} (\mu + \rho)E \\ -\rho E + (\mu + \nu)I \end{pmatrix}.$

From these we can compute:

$F(t)=\biggl( \frac{\partial \mathcal{F}_i(E_2)}{\partial x_j} \biggr)_{i,j = 1,2} = \begin{pmatrix} 0&\beta c(t)(1 - p_2)\\ 0&0 \end{pmatrix}$

$V(t)=\biggl( \frac{\partial \mathcal{V}_i(E_2)}{\partial x_j} \biggr)_{i,j = 1,2} = \begin{pmatrix} 0&\mu + \rho\\ -\rho&\mu + \nu \end{pmatrix}$

Setting $x = (E,I)^{Tr}$, linearized equations of $E$ and $I$ can be expressed as follows:

$\frac{dx}{dt} = (F(t) - V(t))\,x.$

(32)

---

Appendix B. Solutions of linear $T$-periodic ordinary differential systems

Lemma B.1. [47] Let $A(t)$ be a continuous, cooperative, irreducible, and $T$-periodic k $\times$ k matrix function, $\Phi_{A(\cdot)}(t)$ be the fundamental solution matrix of the linear ordinary differential system $x'= A(t)x$, and $r\bigl(\Phi_{A(\cdot)}(T)\bigr)$ be the spectral radius of $\Phi_{A(\cdot)}(T)$. Denote:

$q = \frac{1}{T} \ln\,{ r \bigl( \Phi_{A(\cdot)} (T) \bigr) }$

Then, there exists a positive, $T$-periodic function $v(t)$ such that $e^{qt}v(t)$ is a solution of $x' = A(t)x$.

---