1. Introduction

Infectious diseases of humans may be transmitted via several modes, such as direct (e.g., influenza, measles, HIV/AIDS), indirect (e.g., gastrointestinal diseases such as cholera, rotavirus infection, cryptosporidiosis), vertical (e.g., HIV/AIDS, HSV-2), vector-borne (e.g., malaria, Zika virus (ZIKV), dengue fever). Multiple modes of transmission have been ascertained for some of those: for instance Toxoplasma gondii can be transmitted through the environment or sexual contacts [15]; hepatitis A can be transmitted through contaminated food or water, or direct contacts including sexual contacts [4]. While the actual occurrence of a particular transmission mode can be ascertained by isolating active virions (or more generally pathogen agents) in a specific site, or occasionally by case reports that unequivocally establish the path through which an individual has become infected, it may be difficult to recognize the relative importance of different transmission modes in sustaining an epidemic.

The transmission of the flavivirus Zika (ZIKV) was initially described as occurring solely through the bite of infected adult female mosquitoes of the genus Aedes. From its discovery in 1952 and the first confirmed human case in 1954 [19] until 2007, confirmed cases of ZIKV infection from Africa and Southeast Asia have been rare [12]. The first widespread epidemic was in 2007 in the Micronesian island of Yap, and there was no evidence of direct human-to-human transmission during this outbreak [8].

However, data collected during the 2015 ZIKV outbreaks in South America (the largest in history) shows the presence of Zika virions in the semen of some infected males, even several weeks after the likely time of disease exposure [17]. Moreover, several cases of ZIKV infections were documented outside the epidemic area, especially in the United States, that could be explained only through sexual contacts with partners that had travelled to Zika-infected areas [10]. Male-to-female sexual transmission of ZIKV has been clearly established, even when the ZIKV-infected male is asymptomatic [3], and there was a (single) well-documented case of female-to-male sexual transmission in the USA [6].

Still, the general understanding in the epidemiological community is that transmission through infected mosquitoes is dominant in sustaining the Zika epidemic [1, 20]. Correspondingly, mathematical models being proposed for the Zika epidemics (see, for instance, [9, 14, 22]) generally do not incorporate sexual transmission, mostly for mathematical tractability and lack of reliable data (see however [18]).

However, recently, Coelho et al. [5] suggested instead that sexual transmission may have a much greater role than previously envisaged. Their argument is based on the much larger number of cases of ZIKV reported among women than among men, even after correcting for the bias due to the systematic screening of pregnant women. They argue that the disproportionately large number of infected women can be explained by the fact that male-to-female ZIKV transmission is much larger than the female-to-male transmission in sexual contacts (thereby implying that sexual transmission has, all along, been an important factor in the spread of the Zika flavivirus).

It is quite possible that the significant gender disparity in reported cases is due to a higher attention (of the public health agencies, and of the general public) to ZIKV infection in women, including those that are not pregnant but of child-bearing age. We do not intend to discuss this specific issue, as we have no data or direct information source to assess it. Rather, we ask the question of what can be theoretically inferred about the relevance of different transmission modes on unequal prevalence amongst the sexes and how such relevance can be determined from epidemic data, assuming that they have been collected without bias (or that existing biases have been removed).

In the next section, we examine a simple Kermack-McKendrick type [13] deterministic model for ZIKV dynamics that only accounts for heterosexual transmission. In this simple context, we are able to derive a relation between sex-biased transmission of the infection and sex-biased incidence. This model is further extended to also allow for direct transmission of ZIKV (as a proxy for vector-borne transmission), to study how sex-biased incidence depends both on sex-biased infectiousness and on the relative importance of heterosexual transmission. Finally, we consider a model with vector transmission. Although this final model represents a major simplification of the reality of vector-based transmission of ZIKV, it still poses major challenges in deriving analytical expressions for theoretically measuring the impact of such transmission mode. Thus, we perform some numerical simulations to see whether the conclusions obtained in the case of direct transmission also hold in that case.

---

2. The model with heterosexual transmission only

The simplest model for heterosexual transmission of a disease takes the form of an SIR (susceptible-exposed-infected) Kermack-McKendrick formulation [13]. As we are interested in the epidemic development over a short time-course, we neglect human demography.

It is assumed, for the sake of simplicity, that males and females have the same population size $N_f = N_m = N$, and we neglect heterogeneities in sexual behavior. Thus, any individual has, on average, $c$ new sexual partners per unit time. On the other hand, we assume that the probability of ZIKV transmission from an infected female to a susceptible male, denoted by $\psi_m$, may be different from $\psi_f$, the probability of ZIKV transmission from an infected male to a susceptible female. It should be noted that for many infectious diseases, it has been estimated that $\psi_m < \psi_f$ [2].

Furthermore, we assume that the average duration of the infection may differ between males and females. In other words, the recovery rates — $\gamma _m$ for males and $\gamma _f$ for females — are not necessarily equal. This leads to the following model, where $S_f$ and $I_f$ denote the density of susceptible and infected females (and similarly for males), and the dot above a state variable denotes its derivative with respect to time. It is worth mentioning that the equations for removed individuals, $R_f$ and $R_m$, are not written explicitly because $S_f + I_f + R_f \equiv N \equiv S_m + I_m + R_m$ is assumed constant:

$\label{main_model} \left\{ \begin{array}{lcl} \dot S_f &= &- \beta _f S_f \displaystyle\frac{I_m}{ N}, \\ \dot I_f &= & \beta _f S_f\displaystyle \frac{I_m}{ N} - \gamma _f I_f, \\ \dot S_m &= &- \beta _m S_m\displaystyle\frac{I_f}{ N}, \\ \dot I_m &= & \beta _m S_m\displaystyle\frac{I_f}{ N} - \gamma _m I_m, \end{array} \right.$

(1)

where, and $\beta _f = \psi_f c$ and $\beta _m = \psi_m c$ are, respectively, the male-to-female and female-to-male transmission rates.

To analyze the model (1), it is convenient to use a minor modification of the conservation method used for the standard Kermack-McKendrick model, as follows

$\label{cons}\left\{\begin{array}{ll} \displaystyle\frac{d}{dt}\left[ \gamma _m \log(S_f) -\frac{\beta _f}{N }(S_m+I_m) \right] &= 0, \\\\ \displaystyle\frac{d}{dt}\left[ \gamma _f \log(S_m) -\frac{\beta _m}{ N}(S_f+I_f) \right] &= 0. \end{array}\right.$

(2)

It can be shown, following the same argument as for the standard model (see, e.g., [7]), that $\displaystyle\lim_{t \to \infty} I_f(t) = \lim_{t \to \infty} I_m(t) = 0$. Furthermore, letting $S_f^\infty = \displaystyle\lim_{t \to \infty} S_f(t)$ and $S_m^\infty=\displaystyle\lim_{t \to \infty} S_m(t)$ (it is obvious that these limits exist and are positive), and applying the conservation equations (2), it follows that

$\label{final_eqs1} \left\{ \begin{array}{ll} \log\left(\displaystyle\frac{S_f^\infty}{ S_f^0}\right) &= \displaystyle\frac{\beta _f}{\gamma _m N }\left(S_m^\infty - S_m^0 - I_m^0\right), \\\\ \log\left(\displaystyle\frac{S_m^\infty}{ S_m^0}\right) &= \displaystyle\frac{\beta _m}{\gamma _f N}\left(S_f^\infty - S_f^0 - I_f^0\right). \end{array} \right.$

(3)

We now analyze Equation (3) under the assumption that no individuals were already removed at time $t=0$, and that only a small fraction were already infected. That is $S_m^0+I_m^0 = S_f^0+I_f^0 = N$ and $I_m^0/N = \varepsilon _m \ll 1$, $I_f^0/N = \varepsilon _f \ll 1$. Finally, letting $z_m = 1 -\displaystyle \frac{S_m^\infty}{ S_m^0}$ and $z_f = 1 -\displaystyle \frac{S_f^\infty}{ S_f^0}$ denote the final attack ratios for males and females, respectively, Equation (3) gives

$\label{final_eqs2} \left\{ \begin{array}{ll} \log\left(1 - z_f\right) &= \displaystyle\frac{\beta _f}{\gamma _m }[(1-z_m)(1-\varepsilon _m) -1 ], \\\\ \log\left(1 - z_m\right) &= \displaystyle\frac{\beta _m}{\gamma _f }[(1-z_f)(1-\varepsilon _f) - 1 ]. \end{array} \right.$

(4)

By eliminating one unknown at a time in Equation (4), it can be shown that the system has a unique solution $z=(z_f, z_m) \in (0, 1)^2$ for each value of $\varepsilon _m$ and $\varepsilon _f$ in $(0, 1)$.

If we consider the limit of $z$ as $\varepsilon _m$ and $\varepsilon _f$ tend to 0, we see that it has to be solution of $H(z)=(H_1(z), H_2(z)) = 0$, where

$\label{H}\left\{ \begin{array}{ll} H_1(z) &= \log\left(1 - z_2\right) + \displaystyle \frac{\beta _m}{\gamma _f }z_1, \\ H_2(z)&= \log\left(1 - z_1\right) + \displaystyle\frac{\beta _f}{\gamma _m }z_2. \end{array}\right.$

(5)

Concerning Equation (5), we have the following

Theorem 2.1. $(0, 0)$ is a solution of $H(z)=0$ for all parameter values. The equation $H(z) = 0$ has also exactly one positive solution if, and only if, $\mathcal{R}_0^s >1$ where

$\label{R0s} \mathcal{R}_0^s = \sqrt{\frac{\beta _m \beta _f}{\gamma _m \gamma _f }}.$

(6)

Proof.Consider Equation (5); clearly, $(0, 0)$ is a solution of $H(z) = 0$ for any parameter values. Further, any other solution must lie at the intersection of the curves $z_2 = g_1(z_1)$ and $z_2 = g_2(z_1)$, where

$\left\{ \begin{array}{ll} g_1(x) &= 1 - e^{-\beta _m x/\gamma _f}, \\\\ g_2(x) &= - \frac{\gamma _m}{\beta _f }\log(1-x). \end{array}\right.$

Both $g_1$ and $g_2$ are increasing functions, with $g_1''(x) < 0 < g_2''(x)$ for $x\in(0, 1)$, and $g_1(1) < 1$, while $\underset{z\to {{1}^{-}}}{\mathop{\text{lim}}}\, {{g}_{2}}(z)=+\infty$. Hence, there exists a unique solution $\bar{z}=(\bar{z}_1, \bar{z}_2)$ of $H(z) = 0$ if, and only if, $g_1'(0) > g_2'(0)$. Computing $g_1'(x)$ and $g_2'(x)$, one sees this is equivalent to $\mathcal{R}_0^s >1$.

The threshold quantity $\mathcal{R}_0^s$ is the basic reproduction number for this model, and can be obtained using the method of next-generation matrix [7]. The superscript $s$ on $\mathcal{R}_0^s$ is used to indicate that it corresponds to (hetero)sexual transmission. We shall use other superscripts later to indicate other modes of transmission.

The parameter $z_f$ [$z_m$] represents the fraction of females [males] that has been infected by the end of the epidemic; in epidemiology, this quantity is often termed attack rate (see. e.g., [11]), but we shall use the name attack ratio, as it is a ratio rather than a rate. The focus of our work will actually be $z_f/z_m$, i.e. the sex ratio of attack ratios.

We claim the following result

Theorem 2.2. Assume $\mathcal{R}_0^s > 1$ and $\beta _f/\gamma _m > \beta _m/\gamma _f$; then, the positive solution of the system (5) satisfies $\bar{z}_1 >\bar{z}_2$. Conversely, if $\beta _f/\gamma _m < \beta _m/\gamma _f$, then the positive solution of the system (5) satisfies $\bar{z}_2 >\bar{z}_1$.

Proof.Obviously, we need only to prove the first assertion. Suppose, by contradiction, that $\bar{z}_1 \le \bar{z}_2$. Then,

$\displaystyle\frac{\beta _m}{\gamma _f }\bar{z}_1 < \displaystyle\frac{\beta _f}{\gamma _m }\bar{z}_2 \ \ \mbox{ and }\ \ \log\left(1 - \bar{z}_2\right) \le \log\left(1 - \bar{z}_1\right).$

Hence,

$H_1(\bar{z}) = \log\left(1 - \bar{z}_2\right) + \frac{\beta _m}{\gamma _f }\bar{z}_1 < \log\left(1 - \bar{z}_1\right) + \frac{\beta _f}{\gamma _m }\bar{z}_2 = H_2(\bar{z}) = 0,$

contradicting the assumption that $H(\bar{z}) = 0$.

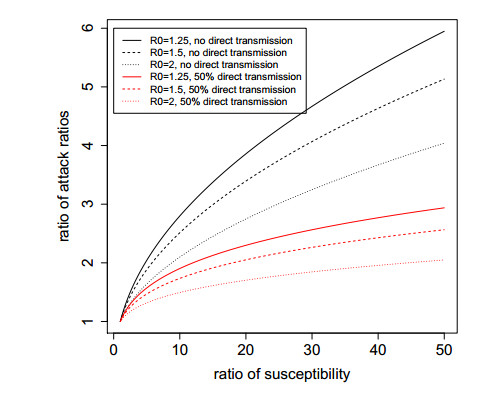
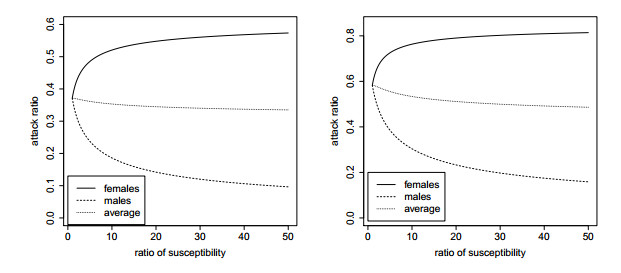
In order to quantify the relative sizes of the attack ratios $\bar{z}_1$ and $\bar{z}_2$, we find numerical solutions of $H(z) = 0$. We fix a value for $\mathcal{R}_0^s$ and vary the ratio of susceptibilities of females to males, $(\beta _f \gamma _f)/(\beta _m \gamma _m)$, between 1 and 100 to see the effect on $\bar{z}_1$ and $\bar{z}_2$. The results are shown in Fig. 1 for $\mathcal{R}_0 = 1.25$ on the left and for $\mathcal{R}_0^s=1.5$ on the right. We note that, indeed, increasing the susceptibility of females relative to that of males increases the attack ratio in females and decreases the rate in males, with an overall modest decrease.

---

3. Model with heterosexual and direct contact transmission

In this section, we model the scenario where the disease can be transmitted both heterosexually and through other direct modes. Although this is probably not realistic for ZIKV, it may be of interest in other contexts, and is also useful as an approximation for models with vector-borne transmission (see next Section). We further assume that such contacts are independent of the individuals' sex, and that the probability of getting infected per contact is the same for all individuals. Specifically, we assume that each susceptible individual can be infected through such contacts at a rate $\tilde\beta _d (I_f + I_m)/(2N)$, where $\tilde\beta _d$ is an aggregate parameter depending on the number of such contacts per unit time and on the probability of getting infected per contact. The denominator is equal to $2N$ as this is the total population density, including females and males. Based on the above assumptions, we obtain the following system:

$\label{model_w_direct} \left\{ \begin{array}{lcl} \dot S_f &= &- \beta _f S_f \displaystyle\frac{I_m}{ N} - \tilde\beta _d S_f \displaystyle \frac{(I_f + I_m)}{2N }, \\\\ \dot I_f &= & \beta _f S_f \displaystyle\frac{I_m}{ N} + \tilde\beta _d S_f \displaystyle\frac{(I_f + I_m)}{2N } - \gamma _f I_f, \\\\ \dot S_m &= &- \beta _m S_m\displaystyle\frac{I_f}{ N} -\tilde \beta _d S_m \displaystyle\frac{(I_f + I_m)}{2N }, \\\\ \dot I_m &= & \beta _m S_m\displaystyle\frac{I_f}{ N}+\tilde\beta _d S_m \displaystyle\frac{(I_f + I_m)}{2N } - \gamma _m I_m. \end{array} \right.$

(7)

It follows, by modifying the conservation equations (2), that

$\label{conserve}\left\{ \begin{split} &\frac{d}{dt}\left[ \log(S_f) -\frac{(\beta _f + \beta _d)}{\gamma _m N }(S_m+I_m) - \frac{ \beta _d}{\gamma _f N }(S_f+I_f) \right], \\ = &\frac{d}{dt}\left[ \log(S_m) -\frac{(\beta _m+\beta _d)}{ \gamma _f N}(S_f+I_f) - \frac{ \beta _d}{\gamma _m N }(S_m+I_m)\right] = 0, \end{split}\right.$

(8)

having introduced, for ease of notation, the constant $\beta_d = \tilde \beta _d/2$.

Integrating (8) for $t$ from $0$ to $\infty$, and using the same notation as in the previous section, gives

$\label{final_eqs_w_d}\left\{ \begin{split} \log\left(1 - z_f\right) &= \frac{\beta _f + \beta _d }{\gamma _m }[(1-z_m)(1-\varepsilon _m) -1] + \frac{ \beta _d}{\gamma _f }[(1-z_f)(1-\varepsilon _f) - 1], \\ \log\left(1 - z_m\right) &= \frac{\beta _m + \beta _d}{\gamma _f }[(1-z_f)(1-\varepsilon _f) - 1] + \frac{ \beta _d}{\gamma _m }[(1-z_m)(1-\varepsilon _m) - 1]. \end{split}\right.$

(9)

By taking the limit as $\varepsilon _m$ and $\varepsilon _f$ tend to 0, it follows that of $z=(z_f, z_m)$ has to be solution of $H(z) =(H_1(z), H_2(z))= 0$, where, now,

$\label{H2}\left\{ \begin{split} H_1(z) &= \log\left(1 - z_2\right) + \frac{\beta _m + \beta _d}{\gamma _f }z_1 + \frac{\beta _d}{\gamma _m } z_2, \\ H_2(z)&= \log\left(1 - z_1\right) + \frac{\beta _f + \beta _d}{\gamma _m }z_2 + \frac{\beta _d}{\gamma _f } z_1. \end{split}\right.$

(10)

Clearly, $z=(0, 0)$ is a solution of $H(z) = 0$. In order to look for other solutions, the first equation of (10) is solved for $z_1$ to get

$\label{z1_2} z_1 = g_1(z_2) = -\frac{\gamma _f}{ \beta _m + \beta _d}\left(\log\left(1 - z_2\right) + \frac{ \beta _d}{\gamma _m } \right),$

(11)

while solving the second equation for $z_2$ gives

$\label{z2_2} z_2 = h_2(z_1) = -\frac{\gamma _m}{ \beta _f + \beta _d}\left(\log\left(1 - z_1\right) + \frac{ \beta _d}{\gamma _f } \right).$

(12)

Both $g_1$ and $h_2$ are convex functions on $[0, 1)$ satisfying $g_1(0) = h_2(0) = 0$ and

$\lim\limits_{x \to 1^-} g_1(x) = \lim\limits_{x \to 1^-} h_2(x) = + \infty.$

Thus, if $g_1'(0) \ge 0$, $g_1$ is invertible as a function from $[0, 1)$ onto $[0, + \infty)$. Moreover, if $g_1'(0) < 0$, then there exists $z_m > 0$ such that $g_1(z_m) = 0$ and $g_1$ is invertible as a function from $(z_m, +\infty)$ onto $(0, +\infty)$. In both cases, we can define an inverse function of $g_1$, $h_1: (0, \infty) \to (0, 1)$ say, which is increasing, concave and satisfies $\displaystyle\lim_{x \to \infty} h_1(x) = 1$. Furthermore, if $g_1'(0) \ge 0$, then $\displaystyle\lim_{x \to 0^+} h_1(x) = 0$ and, conversely, if $g_1'(0) < 0$, then $\displaystyle\lim_{x \to 0^+} h_1(x) = z_m > 0$.

Note that positive solutions of $H(z) = 0$ correspond to points $(z_1, z_2)$ such that

$\label{sols_w_d} z_2 = h_1(z_1) = h_2(z_1).$

(13)

It follows, from the properties of the functions $h_1$ and $h_2$, that (13) has a unique solution, unless $\displaystyle\lim_{x \to 0^+} h_1(x) = 0$ and $h_1'(0) \le h_2'(0)$. Because $\displaystyle\lim_{x \to 0^+} h_1(x) = 0$ implies that $h_1^\prime(0)=1/g_1^\prime(0)$, these conditions are equivalent to $g_1'(0) \ge 0$ and $h_2'(0) g_1'(0) \ge 1$, that can be rewritten as

$\label{R0m1_w_d} \frac{\beta _d}{\gamma _m } \le 1, \frac{\beta _d}{\gamma _f } \le 1,$

(14)

$\label{R0m2_w_d} \frac{\beta _d-\gamma _f}{ \beta _d-\gamma _m}\frac{\gamma _m^2(\beta _m+\beta _d)}{\ g_f^2 (\beta _f + \beta _d)} \ge 1.$

(15)

Inequality (15) can be further simplified to give

$\beta_d\left(\displaystyle\frac1{\gamma_f}+\displaystyle\frac1{\gamma_m}\right)+\displaystyle\frac{\beta_d(\beta_m+\beta_f)+\beta_m\beta_f}{\gamma_m\gamma_f}\le1.$

(16)

Since it is obvious that inequality (16) implies those in (14), the latter are superfluous and we only need to avoid (16) in order to have a unique solution. Therefore, we have proved the following result.

Theorem 3.1. The system $H(z) = 0$, defined by (10), admits a unique solution if, and only if,

$\beta_d\left(\displaystyle\frac1{\gamma_f}+\displaystyle\frac1{\gamma_m}\right)+\displaystyle\frac{\beta_d(\beta_m+\beta_f)+\beta_m\beta_f}{\gamma_m\gamma_f}>1.$

(17)

We shall see that inequality (17) is equivalent to $\mathcal{R}_0^{sn}>1$, where $\mathcal{R}_0^{sn}$, defined below, is the reproduction number corresponding to both sexual and non-sexual modes of transmission.

Theorem 3.2. The system $H(z) = 0$, defined by (10), admits a unique solution if, and only if, $\mathcal{R}_0^{sn}>1$.

Proof. We shall use the approach of the next-generation matrix. The next-generation matrix associated with model (7) is given by

$\label{ngm} K = \begin{pmatrix} \dfrac{\beta _d}{\gamma _f }&\dfrac{\beta _f + \beta _d}{\gamma _m } \\ \dfrac{\beta _m + \beta _d}{\gamma _f }&\dfrac{\beta _d}{\gamma _m } \end{pmatrix}.$

(18)

Indeed, one can easily see that $k_{i1}=(K)_{i1}$ represents the expected number of secondary infections produced in class $i=1$ (females) or $i=2$ (males) by an average infected female over her infectious period, assuming that the whole population is suceptible, and similarly for $k_{i2}$.

Then,

$\label{R0} \mathcal{R}_0 ^{sn}= \rho(K) = \frac{\beta _d}{2 }\left(\frac{1}{\gamma _f } + \frac{1}{\gamma _m }\right) + \sqrt{ \frac{\beta _d^2}{4 }\left(\frac{1}{\gamma _f } + \frac{1}{\gamma _m }\right)^2 +\frac{\beta _d(\beta _m+\beta _f)+\beta _m\beta _f}{\gamma _m \gamma _f } }.$

(19)

It follows that

$\mathcal{R}_0^{sn} < 1 \iff \sqrt{ \frac{\beta _d^2}{4 }\left(\frac{1}{\gamma _f } + \frac{1}{\gamma _m }\right)^2 +\frac{\beta _d(\beta _m+\beta _f)+\beta _m\beta _f}{\gamma _m \gamma _f } } < 1 - \frac{\beta _d}{2 }\left(\frac{1}{\gamma _f } + \frac{1}{\gamma _m }\right),$

which is equivalent to

$\label{R0ngm_m1} \left\{ \begin{array}{l} \dfrac{\beta _d}{2 }\left(\frac{1}{\gamma _f } + \dfrac{1}{\gamma _m }\right) < 1, \\ \dfrac{\beta _d^2}{4 }\left(\frac{1}{\gamma _f } + \dfrac{1}{\gamma _m }\right)^2 +\dfrac{\beta _d(\beta _m+\beta _f)+\beta _m\beta _f}{\gamma _m \gamma _f } < \left(1 - \dfrac{\beta _d}{2 }\left(\dfrac{1}{\gamma _f } + \dfrac{1}{\gamma _m }\right)\right)^2. \end{array} \right.$

(20)

It should now be noted that the inequalities in (14) imply the first inequality in (20). Expanding the second inequality in (20), it can be seen that it is equivalent to (16). This implies (14), as we have already seen. Hence, (20) is equivalent to (16), so that we can say that a unique solution of $H(z) = 0$ (corresponding to an epidemic outbreak) exists if, and only if, $\mathcal{R}_0^{sn} > 1$.

Finally, as in the case of Theorem 2.2, the following result can be proven.

Theorem 3.3. Assume $\mathcal{R}_0^{sn} > 1$ and $\beta _f/\gamma _m > \beta _m/\gamma _f$; then, the positive solution of the system (10) satisfies $\bar{z}_1 >\bar{z}_2$. Conversely, if $\beta _f/\gamma _m < \beta _m/\gamma _f$, then the positive solution of the system (10) satisfies $\bar{z}_2 >\bar{z}_1$.

Proof. We prove the first assertion. Assume, by contradiction, that $\bar{z}_1 \le \bar{z}_2$. Then,

$\displaystyle\frac{\beta _m}{\gamma _f }\bar{z}_1 < \displaystyle\frac{\beta _f}{\gamma _m }\bar{z}_2 \ \ \mbox{ and }\ \ \log\left(1 - \bar{z}_2\right) \le \log\left(1 - \bar{z}_1\right).$

Hence,

$H_1(\bar{z}) = \log\left(1 - \bar{z}_2\right) + \frac{\beta _m}{\gamma _f }\bar{z}_1 +\beta _d\left(\frac{1}{\gamma _f }+ \frac{1}{\gamma _m }\right) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ <\log\left(1 - \bar{z}_1\right) + \frac{\beta _f}{\gamma _m }\bar{z}_2 +\beta _d\left(\frac{1}{\gamma _f }+ \frac{1}{\gamma _m }\right) = H_2(\bar{z}),$

contradicting the assumption that $H(\bar{z}) = 0$.

This Theorem states that if there exists a bias in heterosexual transmission, such bias is always reflected in the expression for the final attack ratio, even when there is another form of direct transmission that is independent of sex. However, we wish to understand how the ratio of final attack ratios $z_f/z_m$ changes, depending on the relative importance of non-sexual (direct) vs. (hetero)sexual disease transmission. The relative weight of direct transmission is henceforth defined as

$\label{rel_w} \rho = \frac{\mathcal{R}_0^n}{ \mathcal{R}_0^n + \mathcal{R}_0^s}\ \ \ \ \mbox{with } \mathcal{R}_0^n = \frac{\tilde \beta _d}{ 2}\left(\frac{1}{\gamma _f } + \frac{1}{\gamma _m }\right) =\beta _d \left(\frac{1}{\gamma _f } + \frac{1}{\gamma _m }\right).$

(21)

It can be seen that $\mathcal{R}_0^{sn} > \mathcal{R}_0^n + \mathcal{R}_0^s$. Thus, $\rho$ cannot be exactly considered as the contribution of direct transmission to the overall $\mathcal{R}_0^{sn}$, but is simply based on the proportions of reproduction numbers relative to the two modes.

Fig. 2 shows the effect of the differences in male-female susceptibility in heterosexual transmission on the ratio of the sex-specific attack ratios, depending on whether direct transmission also occurs. It can be seen from this figure that with only heterosexual transmission, the final attack ratios can be rather different for the two sexes, although not as much as the differences in susceptibility. For instance, if females were 10 times more susceptible than males, the final attack ratio in females would less than 3 times higher than the final attack ratio in males. If the direct transmission route is responsible for a sizeable portion of all transmission, then the difference becomes quite smaller. For instance, if direct and heterosexual transmission are equal in transmission potential, the ratio of final attack ratios is always smaller than 3, even assuming a 50-fold difference in susceptibility.

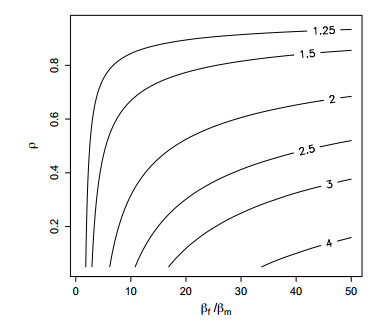
An alternative way to assess the joint impact of $\rho$ (relative importance of direct transmission) and $\beta_f/\beta_m$ (ratio of susceptibilities) can be seen in Fig. 3, where a contour plot of the ratio $\bar{z}_f/\bar{z}_m$, as a function of $\rho$ and $\beta_f/\beta_m$, is depicted.

In summary, the analyses in this section show that the final attack ratios can be obtained as the unique solution of $H(z) = 0$, when the reproduction number $\mathcal{R}_0^{sn}$, defined in (19), exceeds unity. The ratio between female and male attack ratios always exceeds 1 when male-to-female transmission is higher than female-to-male transmission. Its numerical value depends, as illustrated in Figures 2 and 3, on three parameters: $q$ (the ratio between female and male susceptiblity), $\mathcal{R}_0$ (the basic reproduction number) and $\rho$ (the relative importance of direct vs. heterosexual transmission). In principle, this allows for a retrospective estimate of $\rho$ from the sex-ratio of reported cases, if $q$ and $\rho$ are known, assuming that the model is approximately correct, and that there is no bias in reporting.

---

4. The model including vector-borne transmission

We assume now that infection can also be transmitted by effective contact with the disease vector (adult female Aedes mosquitoes in the case of ZIKV). We modify the system (1) by adding terms corresponding to infection from mosquito bites, as well as an equation for the dynamics of the infected mosquito population whose size we shall denote by $V_I=V_I(t)$. For mathematical tractability, we shall consider a constant total mosquito population of size $V$; we are implicitly assuming a source of mosquitoes to balance the loss due to natural mortality. We shall not model that source explicitly, since it is not needed here.

The mortality rate of adult mosquitos is denoted by $\mu_V$; the effective transmission rate of infection per human from mosquito to human, $\beta_V$, is the product of the average number of bites a human receives per unit time and the probability that the bite from an infected mosquito results in the infection of the susceptible human. Similarly, the effective transmission rate of infection per mosquito from an infected human, $\beta_H$, is the product of the average number of bites a mosquito makes per unit time and the probability that the bite from an uninfected mosquito to an infected human actually infects the mosquito.

$\label{main_vector} \left\{ \begin{array}{lcl} \dot S_f &= &- \beta _f S_f \displaystyle\frac{I_m}{ N} -\beta _V S_f \displaystyle\frac{V_I}{2N}, \\ \dot I_f &= & \beta _f S_f\displaystyle \frac{I_m}{ N}+\beta _V S_f \displaystyle\frac{V_I}{2N} - \gamma _f I_f, \\ \dot S_m &= &- \beta _m S_m\displaystyle\frac{I_f}{ N}-\beta _V S_m \displaystyle\frac{V_I}{2N}, \\ \dot I_m &= & \beta _m S_m\displaystyle\frac{I_f}{ N} +\beta _V S_m \displaystyle\frac{V_I}{2N}- \gamma _m I_m, \\ \dot V_I&=&\beta _H(V-V_I)\displaystyle\frac{I_f+I_m}{2N}-\mu_V V_I. \end{array} \right.$

(22)

For the model (22), it is not possible to obtain analytical expressions for the final attack ratios (similar to those obtained for the previous models). Hence, we resort to estimating the attack ratios numerically. The following parameter values, reported in the ZIKV study in Latin America by Ferguson et al. [9], are used: $\beta_H=0.035$, $\beta_V=0.05$, $\gamma _f = \gamma _m = 1/6$ and $\mu_V=0.2$ using 1 day as the time unit. It is worth mentioning that Ferguson et al. [9] also give estimates for $\mathcal{R}_0$ varying in time, but with an average slightly above 2. Furthermore, their model does not consider sexual transmission, so that $\mathcal{R}_0$ can be obtained (as in Ross-Mac Donald [16, 21]) as

$\label{R0v} \mathcal{R}_0^v=\sqrt{\displaystyle{\frac{\beta_H\beta_VV}{2\gamma\mu_VN}}}.$

(23)

Model (22) includes infection transmission both through mosquito bites and heterosexual contacts. To obtain the associated reproduction number, the infected compartments in the Equation (22) (that is, the second, fourth and fifth equations), will be used. At the disease-free equilibrium, $(0, 0, 0)$, the Jacobian of the aforementioned system, containing just the infected compartments, is

$\begin{pmatrix} -\gamma _f&\beta _f&\beta _V/2 \\ \beta _m&- \gamma _m&\beta _V/2 \\ \frac{\beta _H V}{2N }&\frac{\beta _H V}{2N }&- \mu_V \end{pmatrix},$

where we have used $S_f=S_m=N$. The associated next generation matrix is given by

$K = \begin{pmatrix} 0&\frac{\beta _f}{\gamma _m }&\frac{\beta _V}{2 \mu_V } \\ \frac{\beta _m}{ \gamma _f}&0& \frac{\beta _V}{2 \mu_V } \\ \frac{\beta _H V}{2\gamma _f N }&\frac{\beta _H V}{2\gamma _m N }&0 \end{pmatrix} = \begin{pmatrix} 0&b&a \\ c&0&a \\ d &d &0 \end{pmatrix},$

with $b= \beta _f/\gamma$, $a =\beta _V/(2 \mu_V)$, $c= \beta _m/ \gamma$, $d = \beta _H V/(2\gamma N)$, also having assumed, for the sake of simplicity, $\gamma _m = \gamma _f$.

Hence, it follows that, the basic reproduction number, $\mathcal{R}_0^{sv}$, is the spectral radius of $K$. Computing the determinant of $K - \lambda I$, one sees that

$(\mathcal{R}_0^{sv})^3 = \mathcal{R}_0^{sv} (2 ad + bc) + ad (b+c).$

(24)

An analytical solution to this equation is very cumbersome, so that $\mathcal{R}_0^{sv}$ has to be computed numerically. Moreover, the relation between $\mathcal{R}_0$ and the final attack ratios is different for models (22) and (7).

Thus, in order to compare the results obtained using model 7 (and illustrated in Figures 2 and 3) to those obtained with model (22), we concentrated on final attack ratios rather than on $\mathcal{R}_0$ (given by either (19) or (24)). Model (22) was simulated, choosing as initial values $I_m(0)/N = I_f (0)/N = \varepsilon \ll 1$, $S_f(0)/N = S_m(0)/N = 1 - \varepsilon$, $V_I(0) = 0$; the final attack ratios were computed as $z_f = 1 - S_f(T)/S_f(0)$ (in females) and $z_m = 1 - S_m(T)/S_m(0)$ (in males) where $T$ is a large enough value so that $I_m(t)$ and $I_f (t) \approx 0$ for $t > T$.

In Fig. 4 we show how the sex-ratio $z_f/z_m$ of final attack ratios changes with average final attack ratio $(\bar{z}_f + \bar{z}_m)/2$, for fixed

$q = \dfrac{\beta _f}{\beta _m }\ \ \ \mbox{ and }\ \ \ \rho = \dfrac{\mathcal{R}_0^v}{ \mathcal{R}_0^v + \mathcal{R}_0^s}.$

More specifically, we varied $\beta _m$ and adjusted the other parameters so as to keep $q$ and $\rho$ at the set values. This is compared to what is obtained by solving (10) for the same values of $q$ and $\rho$ (given by (21) in that case).

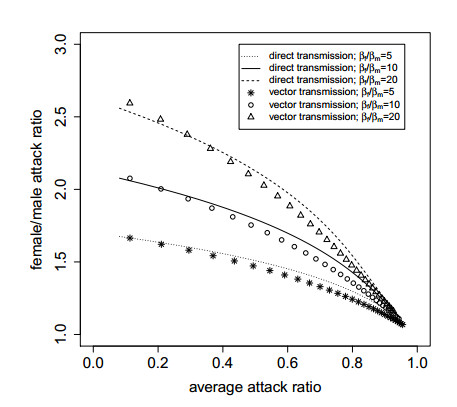
We remark that the ratio of final attack ratios obtained by simulating (22) depend on the values chosen for $b= \beta _f/\gamma$, $c= \beta _m/\gamma$ and $ad = \left(\mathcal{R}_0^v\right)^2$, but do not depend on individual parameters while keeping those quantities fixed. It should be noted that the results from model (22) show a very similar pattern to those obtained from model (7) for each value of $q$, both qualitatively and quantitatively. Thus, the results obtained in the analysis of the model with direct transmission are quite useful also in providing insight into the model with vector-based transmission.

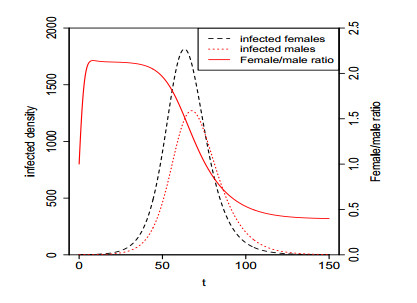
Finally, we note that examining the transient phase of the epidemic may yield a different picture. Indeed, initially, the sex-ratio in new cases is closer to the value $q$ representing the ratio of susceptibilities, but then drops because fewer susceptibles are left in that class. In Fig. 5, we show one simulation in time, illustrating this phenomenon. Even if the sex-ratio of final attack ratios is 1.25, the sex-ratio in new cases during the growing phase of the epidemic is around 2.

---

5. Conclusions

Three Kermack-Mckendrick type deterministic models have been developed and used to gain insight into the transmission dynamics of a disease within a two-sex closed population. The first model, which considers heterosexual contact as the sole mode of transmission, enables us to theoretically assess whether the frequently observed disparity in transmission rates per contact between male-to-female and female-to-male (usually the former being quite larger than the latter) necessarily leads to similar differences in the final attack ratios between the genders. The attack ratios can be obtained as solutions of a system of two nonlinear equations; we proved that the system has a unique solution if the net reproduction number exceeds unity, extending the classical result by Kermack and McKendrick [13] for an SIR model in a closed homogeneous popualtion. It is further shown, as intuitively expected, that the gender-specific final attack-ratios are biased in the same direction as the gender-specific susceptibilities. We have also shown that the ratio of attack ratios depends solely on the ratio of gender-specific susceptibilities and on the basic reproductive number of the epidemic, $\mathcal{R}_0$.

The second model extends the first by also allowing for infection transmission through direct contact in a gender-independent way. Here, too, we derived analytical expressions to obtain those attack ratios and proved that the attack ratios are non-zero if the net reproduction number exceeds unity; furthermore, the gender specific final attack ratios in that case are biased in the same direction as the gender-specific susceptibilities. Through some numerical examples, we show how the ratio of the gender-specific final attack ratios varies, depending on the relative importance of the two transmission pathways and on $\mathcal{R}_0$ (Figure 2). In principle, the relative importance $\rho$ of the two transmission pathways could be ascertained retrospectively, if we knew the ratio of gender-specific susceptibilities, the ratio of final attack ratios and the value of $\mathcal{R}_0$ (see Figure 3) and, of course, if this simple model were correct. Qualitatively, one can say that the ratio of final attack ratios will not exceed 1.5 if non-sexual transmission accounts for most transmission events ($\rho \ge 0.6$) and the ratio of gender-specific susceptibilities is not too large (say, 5 at most).

The third model, which also has two modes of transmission (namely, heterosexual contact and through a vector (mosquito bites)), can be considered a model for ZIKV that is very simplified in several respects; for instance, we assumed that the total vector population is constant, which implicitly requires a source for new unifected mosquitos to replace the ones that die. We derived, following standard methods [7], an expression for the net reproduction number as solution of a cubic equation, but were not able to find a simple equation that allows to obtain the final attack ratios. We showed, via numerical simulations, that results are quite similar to those obtained with second model, that allows for heterosexual and direct transmission. Thus, it seems that Figure 3 can be used to estimate the sex-ratio of final attack ratios for a given value of $q$ (ratio of male-to-female vs. female-to-male transmission probability) and $\rho$ (relative weight of vector-borne vs. heterosexual transmission).

It should, finally, be remarked that transient patterns can differ from final attack ratios. Indeed, it is quite intuitive that, if one sex succumbs to most of the infections during the early stages (as perhaps [5] was the case with females during the 2015 ZIKV outbreaks in the Americas) due to their larger susceptibility, there will be fewer susceptibles of that sex later in the epidemic and this will bias new infections towards the opposite sex. Clearly, this effect is partiuclarly strong when final attack ratios are relatively large, so that depletion of susceptibles is relevant. An example of such a pattern is provided by the simulation shown in Fig. 5. Thus, data showing no gender-bias in final attack ratios (as in the analysis of Zika epidemics in Zap island [8]) are not necessarily in contradiction with gender-bias in reported new cases during the expanding phase of an epidemic (as suspected by some for Brazil [5]), even without assuming virus evolution, or behavioral differences in the populations.

We think that these models, while certainly overly simplistic, can help in assessing the potential role of gender-specific transmission in infections with multiple modes of transmission, by gauging what can be expected to be seen from reports of new cases, or seroprevalence surveys. Certainly, investigations of specific cases of sexual transmission remain essential for obtaining empirical information about the role of sexual transmission for Zika [1].

---