Parameters identification for a model of T cell homeostasis

1.   Introduction

The use of mathematical models to study the interaction between different biological elements is an important area in ecosystems. The main purpose of the model is to explore the dynamical behaviors between them, such as predation, symbiosis, parasitism, competition, and so on ^[1,2,3]. Since Lotka ^[4] and Volterra ^[5] separately proposed the Lotka–Volterra model to describe the ecological interaction by differential equation model, many mathematicians and biologists have been deeply interested in studying such models, especially the predator–prey models. In biology and biomathematics, the predation model is one of the important research topics, and it is also an important model of ecosystems ^[6]. There is a large amount of literature on predator–prey models with different types of functional responses. Holling ^[7,8,9] came up with three types of functional response functions to describe the relationship between the quantity of prey captured by predators and the density of prey. Taking into account the living environment and situation of prey and predators in reality, the dwellings of many prey have a certain protective effect, and their ability to resist natural enemies will be enhanced with the increase of the density of prey, or prey will learn to hide themselves under the pursuit of natural enemies, which will reduce the predation ability of natural enemies. Therefore, Andrews ^[10] proposed the Holling–IV functional response function in 1968. Besides, Ajraldi ^[11] proposed a square–root functional response to explain the aggregation behavior that plankton exhibit.

Recently, the discrete population models depicted by differential equations have been extensively studied ^[12,13,14]. Discrete-time systems, compared with continuous–time versions, have obvious advantages. On one side, data collection for biological samples is often on discrete time scales in reality (either in a week, a month, or another certain time period) rather than on a day. On the other side, assume that the population quantity of species does not overlap between successive generations; these could offer more efficient calculation results for numerical simulations ^[15,16]. Therefore, a lot of mathematicians have studied the dynamical behaviors of the discrete-time model corresponding to the continuous–time one. For instance, Agarwal ^[17] formulated bifurcation analysis of a discrete predator–prey model incorporating prey refuge. Ahmed et al. ^[18] explored a class of discrete prey predation models with fast–slow effects. Khan et al. ^[19] studied a class of discrete Rosenzweig–Macarthur predator–prey models and analysed their chaos.

Since the fear effect was first put forward by Wang et al. ^[20], the research of models with the fear effect has been paid more attention by many scholars ^[21,22,23]. The fear effect mainly refers to the mutual relationship between prey and predators, which makes prey populations instinctively fear predators, thereby reducing the birth rate of prey and thus achieving the purpose of reducing prey capture. It is obvious that this is a kind of anti–predation behavior. In ^[20], the expression for the fear effect is $ F(x, y) = 1/(1+ky) $, where the parameter $ k $ represents the level of the fear effect, and the prey population decreases as $ k $ goes up. Compared with the fear effect, the refuge effect is also an anti–predation behavior. It is important to note that the prey cost most of their lives nearby or hiding in shelters for avoiding predation, such as caves, crevices, dense vegetation, shells, or pipes. The notion of prey sanctuary has caught ecologists and mathematicians' attention since Gause et al. ^[24] and Smith ^[25] brought in the parameter refer to refuge. In the ecology, prey refuge could reduce the predation of the prey by the predator, thereby refraining from extinction of the prey population due to the predation factor; see ^{[26,27,28,29,30]} in detail. Many scholars studied a type of continuous predator–prey model with the fear effect or refuge effect ^{[31,32,33,34,35,36]}. For example, Pal et al. ^[32] added the fear effect, the Allee effect, and the influence of external disturbances such as refuges into a continuous predator–prey model. At the same time, the positivity, boundedness, stability of the equilibrium points, and bifurcation phenomena of the continuous predator–prey model were analyzed. Wang et al. ^[34] mainly considered the role of the fear effect and discussed the difference in stability with and without the fear effect; besides, they also studied some bifurcation phenomena. Consider that some populations without overlapping generations are not suitable for continuous models, so we can establish a type of discrete predator–prey model with a fear effect and a prey refuge effect. First of all, a continuous version is put forward as follows:

The discretization system (1.1) is obtained

Where $ x_n $ and $ y_n $ are the population densities at $ n $th generation of prey and predator, respectively. $ r, k, K, c, d, e $ and $ R $ severally stand for the growth rate of prey, the level of the fear effect, the carrying capacity of prey, the capture efficiency of the predator of prey, the natural mortality rate of the predator, the rate of conversion of energy, and the quantity of prey using refuge. All of the above parameters are strictly positive.

The dramatic increase in people's demand for resources has led to biological resources being over-exploited. It needs us to maintain sustainable development and maximize economic benefits for the exploitation of ecological resources. Current research refers to the effect of harvesting and mainly focuses on constant harvesting ^[37], proportional harvesting ^[38], and nonlinear harvesting ^[39]. We introduce the type of proportional harvesting of prey and predator. Our system takes the following form:

Here $ q_1, q_2 $ represent the catchability coefficients of the prey and predator, and $ E_1, E_2 $ mean the harvesting efforts of the prey and predator, respectively.

The outline of the rest of this paper is in the following manner: Sections 2 and 3 explore the existence and stability of all possible fixed points of system (1.3), respectively. In Sections 4 and 5, we investigate in detail two types of bifurcation analysis (Flip bifurcation and Neimark–Sacker bifurcation) at the interior fixed point of system (1.3). Also, the optimal harvesting strategy is analysed in Section 6. Numerical simulations are applied in Section 7 to illustrate our theoretical results analysed above. Finally, Section 8 contains the conclusion and discussion of our manuscript.

2.   The existence of fixed points

In this section, we are about to study the existence of possible fixed points, by solving the nonlinear system given by

Theorem 2.1. Fixed points obtained are as follows:

(1) $ A_1(0, 0) $ always exists.

(2) $ A_2(W, 0) $ is feasible if $ r > q_1E_1 $, where $ W = \frac{K(r-q_1E_1)}{r} $.

(3) $ A_3(Q, P) $ exists if $ S < 0 $ is satisfied, where $ Q = \frac{d+q_2E_2+eR}{e} $, $ P = \frac{-V+\sqrt{V^2-4ZS}}{Z} $ and $ Z = ckQ-ckR $, $ V = cQ-cR+q_1E_1kQ $, $ S = q_1E_1Q-rQ(1-\frac{Q}{K}) $.

Proof. Obviously, $ A_1(0, 0) $ always holds true. For $ A_2(W, 0) $, we just need to consider that $ W $ is positive (i.e., $ r > q_1E_1 $). For interior fixed point $ A_3 $, through simple calculation for system (2.1), we obtain Eq (2.2)

Appropriate transformation of the first term in Eq (2.2) yields

Let's define

And $ Z = ckQ-ckR $, $ V = cQ-cR+q_1E_1kQ $, and $ S = q_1E_1Q-rQ(1-\frac{Q}{K}) $, notice that

(ⅰ) $ V^2-4ZS > 0 $ implies that there exist two roots for $ F(y) = 0 $;

(ⅱ) Since $ Q = \frac{d+q_2E_2+eR}{e} > R $, $ V = c(Q-R)+q_1E_1kQ > 0 $ and $ Z = ck(Q-R) > 0 $ are valid, it indicates the axis of symmetry $ \overline{y} = -\frac{V}{2Z} < 0 $.

Now we only need to judge the constant term of $ F(y) $ to know whether $ F(y) $ has positive roots. When $ S > 0 $, there are two negative roots, whereas when $ S < 0 $, there is a unique positive root

At this point, we have completed the proof of Theorem 2.1.

3.   Stability analysis

We investigate the local stability of the above fixed points of system (1.3). The Jacobian matrix of (2.1) at $ (x, y) $ is given by

where

The characteristic equation of this Jacobian matrix (3.1) is

where

So as to the properties of fixed points of system (1.3), we provide the following lemma.

Lemma 3.1. Assume that $ F(1) > 0 $. Then

(ⅰ) $ |\lambda_1| < 1 $ and $ |\lambda_2| < 1 $ if and only if $ F(-1) > 0 $ and $ Det(J) < 1 $;

(ⅱ) $ |\lambda_1| > 1 $ and $ |\lambda_2| > 1 $ if and only if $ F(-1) > 0 $ and $ Det(J) > 1 $;

(ⅲ) $ (|\lambda_1| > 1 $ and $ |\lambda_2| < 1) $ or $ (|\lambda_1| < 1 $ and $ |\lambda_2| > 1) $ if and only if $ F(-1) < 0 $;

(ⅳ) $ |\lambda_1| = 1 $ and $ |\lambda_2|\neq1 $ if and only if $ F(-1) = 0 $ and $ Tr(J)\neq0, 2 $;

(ⅴ) $ \lambda_1 $ and $ \lambda_2 $ are conjugate complex roots, and $ |\lambda_1| = |\lambda_2| = 1 $ if and only if $ Tr(J)^2-4Det(J) < 0 $ and $ Det(J) = 1 $.

Proposition 3.1. The conclusions of fixed point $ A_1(0, 0) $ are as follows:

(ⅰ) $ A_1(0, 0) $ is sink if $ -2 < r-q_1E_1 < 0 $ and $ 0 < d+eR+q_2E_2 < 2 $;

(ⅱ) $ A_1(0, 0) $ is source (unstable) if $ r-q_1E_1 < -2 $ and $ d+eR+q_2E_2 > 2 $;

(ⅲ) $ A_1(0, 0) $ is saddle if $ r-q_1E_1 < -2 $, $ d+eR+q_2E_2 < 2 $ or $ -2 < r-q_1E_1 < 0 $ and $ d+eR+q_2E_2 > 2 $;

(ⅳ) $ A_1(0, 0) $ is non–hyperbolic if $ r-q_1E_1 = -2 $ and $ d+eR+q_2E_2\neq0\ {\rm, }\ 2 $.

Proof. At fixed point $ A_1(0, 0) $, the Jacobian matrix is

From the above matrix, we can calculate $ Tr(J_1) $ and $ Det(J_1) $ as follows:

At the same time, we can derive the eigenvalues

By Lemma 3.1, $ A_1(0, 0) $ is sink if $ \mid \lambda_{1J_1, 2J2} \mid < $1 ($ -2 < r-q_1E_1 < 0 $ and $ 0 < d+eR+q_2E_2 < 2 $). Similarly, $ A_1(0, 0) $ is source if $ r-q_1E_1 < -2 $ and $ d+eR+q_2E_2 > 2 $, saddle if $ r-q_1E_1 < -2 $, $ d+eR+q_2E_2 < 2 $ or $ -2 < r-q_1E_1 < 0 $ and $ d+eR+q_2E_2 > 2 $ and non–hyperbolic if $ r-q_1E_1 = -2 $ and $ d+eR+q_2E_2\neq0{\rm, }2 $.

Proposition 3.2. The conclusions of fixed point $ A_2(W, 0) $ are as follows:

(ⅰ) $ A_2(W, 0) $ is sink if $ -2 < q_1E_1-r < 0 $ and $ -2+d+eR+q_2E_2 < \frac{eK(r-q_1E_1)}{r} < d+eR+q_2E_2 $;

(ⅱ) $ A_2(W, 0) $ is source (unstable) if $ q_1E_1-r < -2 $ and $ \frac{eK(r-q_1E_1)}{r} < -2+d+eR+q_2E_2 $ (or $ \frac{eK(r-q_1E_1)}{r} > d+eR+q_2E_2 $);

(ⅲ) $ A_2(W, 0) $ is saddle if $ q_1E_1-r < -2 $ and $ -2+d+eR+q_2E_2 < \frac{eK(r-q_1E_1)}{r} < d+eR+q_2E_2 $ or $ -2 < q_1E_1-r < 0 $ and $ \frac{eK(r-q_1E_1)}{r} > d+eR+q_2E_2 $ or $ \frac{eK(r-q_1E_1)}{r} < -2+d+eR+q_2E_2 $;

(ⅳ) $ A_2(W, 0) $ is non–hyperbolic if $ q_1E_1-r = -2 $ and $ \frac{eK(r-q_1E_1)}{r}\neq -2+d+eR+q_2E_2 $ and $ \frac{eK(r-q_1E_1)}{r}\neq d+eR+q_2E_2 $.

Proof. Bring $ A_2(\frac{K(r-q_1E_1)}{r}, 0) $ into (3.1), then we obtain

At the same time, we can derive the eigenvalues $ \lambda_{1J_2} $ and $ \lambda_{2J_2} $ from the above matrix

By Lemma 3.1, if $ \lambda_{1J_2} $ = $ \mid1-r+q_1E_1\mid < 1 $ and $ \lambda_{2J_2} $ = $ \mid1+\frac{eK(r-q_1E_1)}{r}-d-eR-q_2E_2\mid < 1 $, i.e., $ -2 < q_1E_1-r < 0 $ and $ -2+d+eR+q_2E_2 < \frac{eK(r-q_1E_1)}{r} < d+eR+q_2E_2 $, then $ A_2(W, 0) $ is sink. Analogously, $ A_2(W, 0) $ is source if $ q_1E_1-r < -2 $ and $ \frac{eK(r-q_1E_1)}{r} < -2+d+eR+q_2E_2 $ (or $ \frac{eK(r-q_1E_1)}{r} > d+eR+q_2E_2 $), saddle if $ q_1E_1-r < -2 $ and $ -2+d+eR+q_2E_2 < \frac{eK(r-q_1E_1)}{r} < d+eR+q_2E_2 $ or $ -2 < q_1E_1-r < 0 $ and $ \frac{eK(r-q_1E_1)}{r} > d+eR+q_2E_2 $ or $ \frac{eK(r-q_1E_1)}{r} < -2+d+eR+q_2E_2 $ and non–hyperbolic if $ q_1E_1-r = -2 $ and $ \frac{eK(r-q_1E_1)}{r}\neq -2+d+eR+q_2E_2 $ and $ \frac{eK(r-q_1E_1)}{r}\neq d+eR+q_2E_2 $.

Proposition 3.3. The conclusions of fixed point $ A_3(Q, P) $ are as follows:

(ⅰ) $ A_3(Q, P) $ is sink if $ 1+Tr(J_3)+Det(J_3) > 0 $ and $ Det(J_3) < 1 $;

(ⅱ) $ A_3(Q, P) $ is source (unstable) if $ 1+Tr(J_3)+Det(J_3) > 0 $ and $ Det(J_3) > 1 $;

(ⅲ) $ A_3(Q, P) $ is saddle if $ 1+Tr(J_3)+Det(J_3) < 0 $;

(ⅳ) $ A_3(Q, P) $ is non–hyperbolic if $ 1+Tr(J_3)+Det(J_3) = 0 $ and $ Tr(J_3)\neq0, 2 $ (or $ Det(J_3) = 1 $ and $ |Tr(J_3)| < 2 $).

Proof. We put $ A_3(\frac{d+q_2E_2+eR}{e}, \frac{-(cx-cR+q_1E_1kx)+\sqrt{(cx-cR+q_1E_1kx)^2-4ck(x-R)[q_1E_1x-rx(1-\frac{x}{R})]}}{2ck(x-R)}) $ into (3.1), and if $ q_1E_1Q-rQ(1-\frac{Q}{K}) < 0 $ and $ 4ac < 0 $ are satisfied, then it yields that

From the above matrix, we can calculate its $ Tr(J_3) $ and $ Det(J_3) $:

The characteristic equation can be written as follows:

By Lemma 3.1, $ A_3(Q, P) $ is sink if $ F(-1) = 1+Tr(J_3)+Det(J_3) > 0 $ and $ Det(J_3) < 0 $. In the same way, $ A_3(Q, P) $ is source if $ 1+Tr(J_3)+Det(J_3) > 0 $ and $ Det(J_3) > 1 $, saddle if $ 1+Tr(J_3)+Det(J_3) < 0 $ and non–hyperbolic if $ 1+Tr(J_3)+Det(J_3) = 0 $ and $ Tr(J_3)\neq0, 2 $ (or $ Det(J_3) = 1 $ and $ |Tr(J_3)| < 2 $).

4.   Flip bifurcation

It is well known that flip bifurcation may occur when $ A_3(Q, P) $ is non–hyperbolic. If $ (r, k, K, c, R, q_1, E_1, d, q_2, E_2, e)\in FB $, where $ FB = \bigg\{r, k, K, c, R, q_1, E_1, d, q_2, E_2, e > 0; 4+\frac{kreQP}{(1+kP)^2}(1-\frac{Q}{K})+\frac{2r(K-Q)}{K(1+kP)}+cP(d+q_2E_2)$ = $[2-q_1E_1-\frac{r(2Q-K)}{K(1+kP)}][d+q_2E_2-e(Q-R)]; \frac{r(K-2Q)}{K(1+kP)}\neq(cP+q_1E_1)+[d+q_2E_2-e(Q-R)]$, $ (cP+q_1E_1)+[d+q_2E_2-e(Q-R)]-2\bigg\}. $

In this section we consider the bifurcation case at $ A_3 $. It is not difficult to find that system (1.3) experiences flip bifurcation at $ A_3 $ if $ e $ changes in a small range of $ e = \widehat{e} $. Giving $ \overline{e}^* $ $ (where \ \overline{e}^*\ll 1) $ of the parameter $ e $ in a small range of $ e = \widehat{e} $ to system (1.3), it yields that

In order to translate $ A_3 $ to the origin, we take the transformation $ u = x-Q $ and $ v = y-P $, then the system (4.1) transforms into the following form:

Taylor expansion of system (4.2) at $ (u, v, \overline{e}^*) = (0, 0, 0) $

Further, we can obtain

Subsequently, give an invertible matrix $ T $ as follows:

Then using the following conversion

system (4.3) becomes

where

According to the theoretical knowledge related to the center manifold theorem ^[40,41], in a small range $ \overline{e}^* = 0 $, it exists a center manifold $ W^c(0, 0) $ at the fixed point $ (0, 0) $ of system $ (1.3) $ of the form

With some simple transformations, we obtain

with $ uv = -a_{12}(1+a_{11})x^2+a_{12}(\lambda_2-2a_{11}-1)xy+a_{12}(\lambda_2-a_{11})y^2 $ and $ u^2 = a_{12}^2(x^2+2xy+y^2) $. By combining the above (4.5) and (4.6), we can get the corresponding coefficients of (4.5)

Limiting the center manifold $ W^c(0, 0) $ to the map $ G^* $

The coefficients of the above system are as follows:

In order to make system (1.3) generate flip bifurcation, it is sufficient to ensure that both discriminatory quantities $ \Upsilon_1 $ and $ \Upsilon_2 $ are not equal to $ 0 $, i.e.,

Theorem 4.1. System $ (1.3) $ exists flip bifurcation at $ A_3 $ when $ e $ changes in a small range of $ \widehat{e} $ and $ \Upsilon_1 \neq 0 $ and $ \Upsilon_2 \neq 0 $ are satisfied. Moreover, if $ \Upsilon_2 > 0 $ (or $ \Upsilon_2 < 0 $), then the period–2 point of the bifurcation from $ A_3 $ is stable (or unstable).

By a similar method as above, $ k $ can be selected as the bifurcation parameter, and we can limit the system (1.3) to

Similarly, to ensure that flip bifurcation occurs in system (1.3), we set the two discriminants $ \Psi_1 $ and $ \Psi_2 $ to be non-zero

The computational processes of $ \Psi_1 $ and $ \Psi_1 $ are shown in Appendix A.

5.   Neimark–Sacker bifurcation

Here we focus on the Neimark–Sacker bifurcation of system (1.3) at $ A_3 $. System (1.3) exists Neimark–Sacker bifurcation at $ A_3 $ if and only if all parameters belong to the set $ NSB = \bigg\{r, k, K, c, R, q_1, E_1, d, q_2, E_2$, $e > 0\ | \ e = \frac{\big(\frac{r(2Q-K)}{K(1+kP)}+q_1E_1-1\big)(d+q_1E_1)-(cP+q_1E_1)+\frac{r(K-2Q)}{K(1+kP)}+cP(d+q_2E_2)}{(Q-R)\big(\frac{r(2Q-K)}{K(1+kP)}+q_1E_1-1\big)-\frac{krQP}{(1+kP)^2}(1-\frac{Q}{K})}$, $ |2+\frac{r}{1+kP}-\frac{2rQ}{K(1+kP)}-cP-q_1E_1-d-q_2E_2+e(Q-R)| < 2$; $q_1E_1-r(1-\frac{Q}{k}) < 0 \mbox{ and } r, k, K, c, R, q_1, E_1, d, q_2, E_2 > 0\bigg\} $.

The characteristic equation (3.3) associated with (3.1) at $ A_3 $ is given by

There exists a pair of conjugate complex roots $ \lambda_1, \lambda_2 $ of the above characteristic equation at $ A_3 $, i.e.,

Given a parameter $ e^* $ (where $ e^*\ll 1 $) and $ e $ is located in a range of $ e = \overline{e} $ in (3.1), we have

Moving $ A_3 $ to the original point, we take the transformations $ \gamma = x-Q $ and $ \delta = y-P $, system (5.1) transforms into the following form:

Taylor expansion of the above system (5.2)

Parameters of (5.3) are as follows:

When $ (\gamma, \delta) = (0, 0) $, the characteristic roots of (5.3) above are as follows:

So we have $ |\lambda_{1, 2}(e^*)| = [DetJ(e^*)]^\frac{1}{2} $. When $ e^* = 0 $, then

Set $ \alpha_1 = Re(\lambda_{1, 2}) $ and $ \beta_1 = Im(\lambda_{1, 2}) $. We obtain an invertible matrix $ N $

Then use the following conversion:

System (5.3) becomes

where

We can know from the transformation (5.5) that $ \gamma = c_{12}x $ and $ \delta = (\alpha_1-c_{11})x-\beta_1y $, therefore

The Neimark–Sacker bifurcation occurs on system (1.3) if the following condition is met:

where

By calculation we have

Theorem 5.1. If $ l_1 $ defined is nonzero, then system (1.3) exists Neimark–Sacker bifurcation at $ A_3 $ provided that $ e $ changes in a small range of $ e = e^* $. Moreover, if $ l_1 < 1 $ (or $ l_1 > 1 $), then an attractively invariant closed curve bifurcates at $ A_3 $.

Similarly, consider $ k $ as a bifurcation parameter, it can be obtained that

Neimark–Sacker bifurcation occurs in system (1.3). The detailed calculation process of $ \tau_1 $ is shown in Appendix B.

6.   Optimal harvesting policy

Our aim is to maximize net returns and maintain ecological balance. Assign the net income function as $ M = \sum\exp(-\delta t)\{(p_1q_1x-h_1)E_1(t)+(p_2q_2x-h_2)E_2(t)\} $, where $ \delta $ expresses the discount rate. Thus

such that

The Hamiltonian function could be written in the following form:

According to the Pontryagin maximum principle, we have

Further we can obtain

By combining the above equations that

7.   Numerical simulations

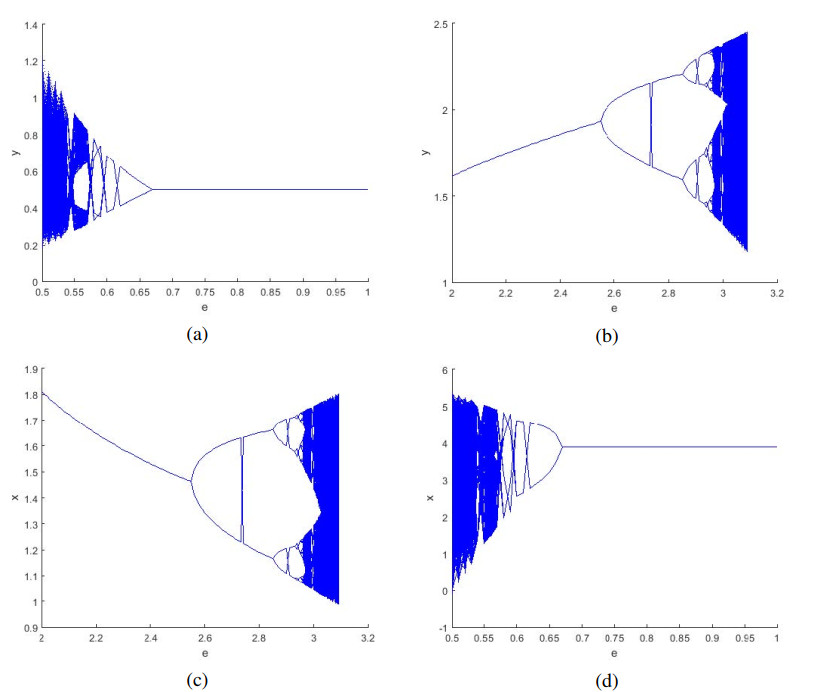
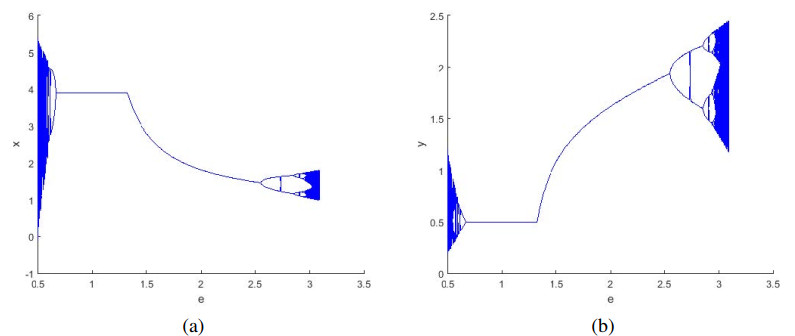
Example 7.1. To verify the theoretical results numerically. First, we value all parameters in turn $ r = 2.001 $, $ k = 0.57 $, $ K = 4.078 $, $ c = 0.743 $, $ R = 0.829 $, $ d = 0.8 $, $ q_1 = 0.467 $, $ E_1 = 0.201 $, $ q_2 = 0.42 $, $ E_2 = 0.435 $, and $ e\subset(0, 3.5) $ with initial conditions $ (x_0, y_0) = (1, 1.5) $. By simple calculation, we can know that $ \mid \lambda_{1, 2}\mid = 1 $, Neimark–Sacker bifurcation may appear at (2.29572, 1.65075). We can see from Figure 1 that Neimark–Sacker bifurcation occurs when $ e = 0.67 $. It follows that $ \mid \lambda_1\mid = 1 $ and $ \mid \lambda_2\mid \neq 1 $, flip bifurcation may appear at (1.214, 1.8965). We can see from Figure 1 that flip bifurcation occurs when $ e = 2.55 $.

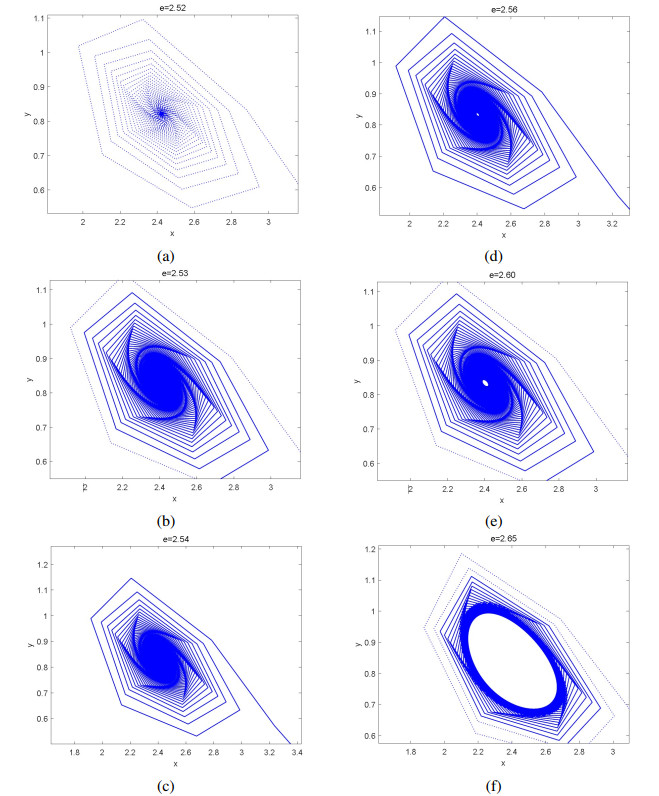
From Figure 2(a) and (d), we can know that Neimark–Sacker bifurcation will appear when $ e = 0.67 $, and when $ e $ belongs to (0, 1) and is greater than 0.67, system (1.3) is stable at the internal fixed point $ (2.29572, 1.65075) $, whereas when the bifurcation parameter $ e $ is less than 0.67, the system will lose stability at the internal fixed point $ (2.29572, 1.65075) $. In view of the ecological perspective, when $ e < 0.67 $, a fluctuation will occur, which means that the number of prey and predator populations will continue to fluctuate periodically around a central value, rather than reaching a fixed point. Such fluctuation may reflect seasonal changes in resources or other cyclical environmental factors in the ecosystem. According to Figure 2(b) and (c), with the change of bifurcation parameters $ e $, flip bifurcation will be generated in system (1.3) when its value reaches 2.55. When the bifurcation parameter $ e $ belongs to (1, 3.5) and is less than 2.55, system $ (1.3) $ is stable; conversely, when $ e $ is greater than 2.55, the system will lose stability. Biologically speaking, when $ e > 2.55 $, the number of prey and predators is no longer maintained at a constant level, whereas it presents a state of periodic fluctuation. Such fluctuation could have an impact on the stability of ecosystems and lead to a large fluctuation in the number of prey and predator populations, which can affect the overall ecosystem's sustainability.

In the process from Figure 3(a) to (f), it is clearly shown that the stability of the system (1.3) varies with the bifurcation parameter $ e $ when it belongs to the range of $ (1, 3.5) $.

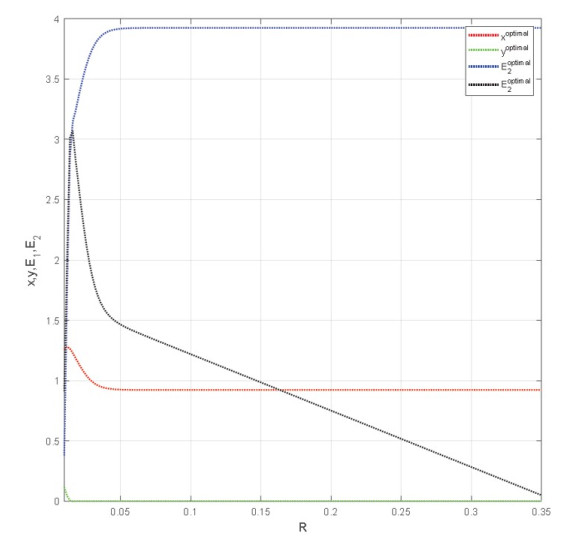
Example 7.2. We take the parameters $ r = 3.5, K = 8$, $c = 0.69, k = 3.9, d = 3.6, e = 0.77, q_1 = 0.36, q_2 = 0.21$, $p_1 = 0.75, p_2 = 3, h_1 = 1.41, h_2 = 1.8 $, and assign the initial value $ (x_0, y_0, E_{10}, E_{20}) $ = (1.32, 3, 0.05, 0.37). Through Figure 4, with the increase of the refuge coefficient $ R $, harvesting effort $ E_1 $ for prey will increase rapidly, when the refuge coefficient $ R = 0.03 $, the harvesting of the prey will tend to a stable state. Due to the value of $ E_1 $ for the prey population changing too rapidly, as the refuge coefficient $ R $ increases, the prey population will show a downward trend; until $ R = 0.03 $, the number of the prey population will tend to a stable state. For the predator population, the harvesting $ E_2 $ will also increase rapidly with increasing $ R $. Compared with the prey population, the number of predator populations is inherently smaller. Due to the rapid increase in the refuge coefficient $ R $ and the harvesting $ E_2 $, the predator population will be in a state of extinction. In general, whether it is for predators or prey, the harvesting of both of them should be moderate, so as to better promote the harmonious coexistence between humans and nature and ensure the maximum harvesting.

8.   Conclusions and discussion

In this article, we mainly study the bifurcation behavior and optimal harvesting strategy of a discrete predator–prey model in possession of fear and refuge effects. Firstly, the existence and stability of three fixed points of system (1.3) are researched, respectively. At the same time, the flip bifurcation and Neimark–Sacker bifurcation are analysed at the internal fixed point in detail. Together with Example 7.1, when the bifurcation parameter $ e = 0.67 $, Neimark–Sacker bifurcation will occur, and when $ e = 2.55 $, flip bifurcation will appear. It is easy to observe that relying on the increasing conversion rate of $ e $, the unstable system turns stable, and then it becomes unstable again. Besides, the predator populations gradually accumulate for the value of the conversion rate at a high level. Finally, we analyze an optimal harvesting problem and theoretically get the value of the optimal harvesting effort, which implies there exists a value of the harvesting effort guaranteeing maximization of the net revenue. From Example 7.2, with the increase of the refuge coefficient $ R $, $ x^{optimal}, y^{optimal}, E_1^{optimal} $ and $ E_2^{optimal} $ change in the range.

Generally speaking, comparing the continuous–time predator–prey models with the corresponding discrete versions, the conclusions on the existence and stability of equilibrium points (or fixed points) can be studied. Also, bifurcation analysis of the models can be discussed. Relative to bifurcation analysis, several bifurcation phenomena, such as Hopf bifurcation, saddle–node bifurcation, and transcritical bifurcation, are mainly investigated in the continuous system. Otherwise, fold bifurcation, flip bifurcation, and Neimark–Sacker bifurcation can be discussed in the discrete system. All in all, whether discrete or continuous system, by studying these characteristics for the system, we can better understand external disturbances, thereby achieving a better role in maintaining ecological balance.

Author contributions

Jie Liu: Conceptualization, Investigation, Methodology, Validation, Writing-original draft, Formal analysis, Software; Qinglong Wang: Conceptualization, Methodology, Formal analysis, Writing-review and editing, Supervision; Xuyang Cao: Validation, Visualization, Data curation; Ting Yu: Validation, Visualisation, Inspection.

Acknowledgments

The authors thank the editor and referees for their careful reading and valuable comments.

The work is supported by the Natural Science Foundation of Hubei Province (No.2023AFB1095) and the National Natural Science Foundation of China (No.12101211) and the Program for Innovative Research Team of the Higher Education Institution of Hubei Province (No.T201812) and the Teaching Research Project of Education Department of Hubei Province (No.2022367) and the Graduate Education Innovation Project of Hubei Minzu University (Nos.MYK2024071, MYK2023042).

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.