Shear-thinning effects of hemodynamics in patient-specific cerebral aneurysms

1.   Introduction

Coronavirus disease 2019 (COVID-19) is a fatal emerging illness caused by a novel coronavirus named severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) ^[1]. Since the first case appeared in Wuhan of China at the end of 2019, the disease has spread quickly from country to country, provoking enormous economic damage and lot of deaths worldwide. According to the World Health Organization (WHO) report of $ 7 $ June $ 2020 $ ^[2], SARS-CoV-2 infected $ 6 799 713 $ people worldwide and caused $ 397 388 $ deaths.

Recently, several mathematical models have been proposed and developed to understand the dynamics of SARS-CoV-2. However, most of these models described the propagation of the virus in human population. Therefore, the main objective of this study is to develop a within-host model that describes the interactions between SARS-CoV-2, host pulmonary epithelial cells and cytotoxic T lymphocyte (CTL) cells. This model is governed by the following nonlinear system:

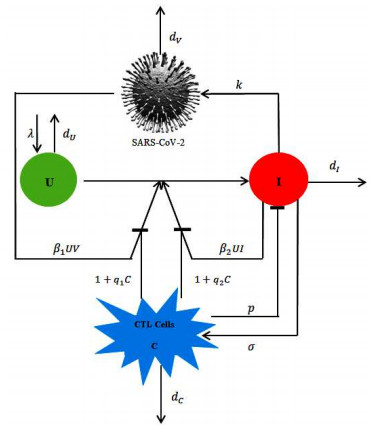
where $ U(t) $, $ I(t) $, $ V(t) $ and $ C(t) $ respectively indicate the concentration of uninfected pulmonary epithelial cells, infected pulmonary epithelial cells, free virus particles of SARS-CoV-2 and CTL cells at time $ t $. Uninfected pulmonary epithelial cells are generated at a constant rate $ \lambda $, die at rate $ d_{U}U $ and become infected either by free virus particles at rate $ \beta_{1} UV $ or by direct contact with infected pulmonary epithelial cells at rate $ \beta_{2}UI $. Both modes of infection are inhibited by nonlytic immune response at rates $ 1+q_{1}C $ and $ 1+q_{2}C $, respectively. Infected pulmonary epithelial cells die at rate $ d_{I}I $ and are killed by lytic immune response at rate $ pIC $. The biological meanings of the remaining parameters $ k $, $ d_{V} $, $ \sigma $ and $ d_{C} $ are respectively the production rate of virus from infected pulmonary epithelial cells, the clearance rate of virus, the immune responsiveness rate, and the death rate of CTL cells. The schematic illustration of model component interactions is given in Figure 1.

In absence of immune response, model (1.1) is reduced to

which is a special case of the model presented in ^[3]. Additionally, system (1.2) covers the within-host model used by Li et al. in ^[4] in order to estimate the parameters of SARS-CoV-2, it suffices to take $ \beta_{2} = 0 $ and $ \lambda = d_{U}U(0) $, where $ U(0) $ is the number of uninfected epithelial cells without virus.

In presence of immune response, model (1.1) includes the following models:

● Model of Nowak and Bangham ^[5], when both cell-to-cell mode and nonlytic immune response are ignored, i.e., $ \beta_{2} = 0 $ and $ q_{1} = 0 $.

● Model of Dhar et al. ^[6], when the classical virus-to-cell mode is only considered.

The rest of this paper is organized in the following manner. In the next section, we establish some preliminary results about the well-posedness of the model, the existence of feasible biological equilibria and the uniform persistence of infection. In Section $ 3 $, we analyze the local and global asymptotic stability of equilibria by means of characteristic equation and Lyapunov functionals. Based on morphometric lungs data and virus environmental stability, the parameters estimation of the model is presented in Section $ 4 $. It is followed by numerical simulations in Section $ 5 $ to illustrate the obtained analytical results. The last section is devoted to the mathematical and biological conclusions drawn from this study.

2.   Preliminary results

In this section, we determine some preliminary results such as the nonnegativity and boundedness of solutions in order to prove that our model (1.1) is biologically well-posed. Additionally, we establish the threshold parameters for the existence of feasible biological equilibria and we also discuss the uniform persistence of the proposed model.

Theorem 2.1. All solutions of model (1.1) with initial conditions in $ \boldsymbol{R}_{+}^{4} $ are nonnegative and bounded.

Proof. We have

This proves that $ {\bf{R}}_{+}^{4} $ is positively invariant with regard to (1.1). Next, we establish the boundedness of solutions by considering the following function

Hence,

where $ d = \min\{d_{U}, \dfrac{d_{I}}{2}, d_{V}, d_{C}\} $. Thus,

Then $ U(t) $, $ I(t) $, $ V(t) $ and $ C(t) $ are bounded.

Let $ U_{0} = \dfrac{\lambda}{d_{U}} $. Obviously, the point $ P_{0}(U_{0}, 0, 0, 0) $ is the unique infection-free equilibrium (1.1). Then we define the first threshold parameter which represents the basic reproduction number of model (1.1) as follows:

where $ \mathcal{R}_{01} = \dfrac{\lambda k\beta_{1}}{d_{U}d_{I}d_{V}} $ is the basic reproduction number of the classical virus-to-cell mode, while $ \mathcal{R}_{02} = \dfrac{\lambda\beta_{1}}{d_{U}d_{I}} $ represents the basic reproduction number of the direct cell-to-cell mode.

In absence of immune response and $ \mathcal{R}_{0} > 1 $, model (1.1) has another biological equilibrium called the infection equilibrium without cellular immunity labeled by $ P_{1}(U_{1}, I_{1}, V_{1}, 0) $, where

In presence of immune response, the remaining biological equilibrium of (1.1) satisfies the following equations:

Since $ C\geq0 $, we have $ U\leq\dfrac{\lambda}{d_{U}}-\dfrac{d_{I}d_{C}}{\sigma d_{U}} $. This indicates that there is no biological equilibrium when $ U > \dfrac{\lambda}{d_{U}}-\dfrac{d_{I}d_{C}}{\sigma d_{U}} $ or $ \dfrac{\lambda}{d_{U}}-\dfrac{d_{I}d_{C}}{\sigma d_{U}}\leq 0 $. Let $ Y $ be a function defined on the closed interval $ [0, \dfrac{\lambda}{d_{U}}-\dfrac{d_{I}d_{C}}{\sigma d_{U}}] $ as follows

where $ Z(U) = \dfrac{\sigma(\lambda-d_{U}U)-d_{I}d_{C}}{pd_{C}} $. We have $ Y(0) = -\dfrac{\sigma\lambda}{d_{C}} < 0 $ and

Since $ Z'(U) = -\dfrac{\sigma d_{U}}{pd_{C}} < 0 $, we have $ Y'(U) > 0 $.

When the immune response has not been established, we have from the last equation of model (1.1) that $ \sigma I_{1}-d_{C}\leq 0 $. Then we define the second threshold parameter which denotes the reproduction number for cellular immunity as follows

The biological meaning of this number is given in ^[7]. When $ \mathcal{R}_{1}^{C} < 1 $, we have $ I_{1} < \dfrac{d_{C}}{\sigma} $, $ U_{1} > \dfrac{\lambda}{d_{U}}-\dfrac{d_{I}d_{C}}{\sigma d_{U}} $ and $ Y(\dfrac{\lambda}{d_{U}}-\dfrac{d_{I}d_{C}}{\sigma d_{U}}) < \dfrac{k\beta_{1}U_{1}}{d_{V}}+\beta_{2}U_{1}-d_{I} = 0 $. Then there is no equilibrium when $ \mathcal{R}_{1}^{C} < 1 $.

When $ \mathcal{R}_{1}^{C} > 1 $, $ I_{1} > \dfrac{d_{C}}{\sigma} $, $ U_{1} < \dfrac{\lambda}{d_{U}}-\dfrac{d_{I}d_{C}}{\sigma d_{U}} $ and $ Y(\dfrac{\lambda}{d_{U}}-\dfrac{d_{I}d_{C}}{\sigma d_{U}}) > 0 $.

Therefore, model (1.1) has a unique infection equilibrium with cellular immunity $ P_{2}(U_{2}, I_{2}, V_{2}, C_{2}) $, where $ U_{2}\in(0, \dfrac{\lambda}{d_{U}}-\dfrac{d_{I}d_{C}}{\sigma d_{U}}) $, $ I_{2} = \dfrac{d_{C}}{\sigma} $, $ V_{2} = \dfrac{kd_{C}}{\sigma d_{V}} $ and $ C_{2} = \dfrac{\sigma(\lambda-d_{U}U_{2})-d_{I}d_{C}}{pd_{C}} $.

By applying Theorem 4.6 in ^[8], we can easily obtain the following result.

Theorem 2.2. If $ \mathcal{R}_{0} > 1 $, then model (1.1) is uniformly persistent, i.e., there exists a positive constant $ \varepsilon $, independent of initial conditions, such that

3.   Stability analysis

This section focuses on the stability analysis of the three equilibria $ P_{0} $, $ P_{1} $ and $ P_{2} $. The local stability is established by analyzing the characteristic equation. Whereas, the global stability is obtained by constructing favorable Lyapunov functionals.

Theorem 3.1. The infection-free equilibrium $ P_{0} $ is globally asymptotically stable if $ \mathcal{R}_{0}\leq 1 $ and unstable if $ \mathcal{R}_{0} > 1 $.

Proof. Consider the following Lyapunov functional

where $ \Psi(x) = x-1-\ln x $, for $ x > 0 $. It is obvious that $ \Psi(x)\geq0 $ for all $ x > 0 $, and $ \Psi(x) = 0 $ if and only if $ x = 1 $. Thus, $ L_{0}(U, I, V, C) > 0 $ for all $ U, I, V, C > 0 $ and $ L_{0}(U_{0}, 0, 0, 0) = 0 $. Further, we have

If $ \mathcal{R}_{0}\leq 1 $, then $ \dfrac{dL_{0}}{dt}\leq 0 $ with equality if and only if $ U = U_{0} $, $ I = 0 $, $ V = 0 $ and $ C = 0 $. By applying LaSalle's invariance principle ^[9], we deduce that $ P_{0} $ is globally asymptotically stable when $ \mathcal{R}_{0}\leq 1 $.

If $ \mathcal{R}_{0} > 1 $, then the characteristic equation of model (1.1) at $ P_{0} $ is given by

where

We have $ { \lim_{\xi\rightarrow +\infty}}f_{0}(\xi) = +\infty $ and $ f_{0}(0) = d_{I}d_{V}(1-\mathcal{R}_{0}) < 0 $ if $ \mathcal{R}_{0} > 1 $. Thus, the characteristic equation (3.1) has at least one positive eigenvalue when $ \mathcal{R}_0 > 1 $. Then $ P_0 $ is unstable if $ \mathcal{R}_0 > 1 $.

Next, we analyze the asymptotic stability of the two infection equilibria $ P_{1} $ and $ P_{2} $ by assuming that $ \mathcal{R}_{0} > 1 $ and the following hypothesis

where $ I_{i} $, $ V_{i} $ and $ C_{i} $ are infected pulmonary epithelial cell, virus and CTL cell components of the infection equilibrium $ P_{i} $ for $ i = 1, 2 $.

Theorem 3.2. Suppose that (H) holds for $ P_{1} $. Then the infection equilibrium without cellular immunity $ P_{1} $ is globally asymptotically stable if $ \mathcal{R}_{1}^{C}\leq 1 < \mathcal{R}_{0} $ and unstable if $ \mathcal{R}_{1}^{C} > 1 $.

Proof. Consider the following Lyapunov functional

The function $ \Psi $ was used by many authors (see for example ^[10,11,12]). By a simple computation, we find

Since $ \lambda = d_{U}U_{1}+\beta_{1}U_{1}V_{1}+\beta_{2}U_{1}I_{1} = d_{U}U_{1}+d_{I}I_{1} $ and $ kI_{1} = d_{V}V_{1} $, we have

Hence,

From $(H)$, we have

Since the arithmetic means (AM) is greater than or equal to the geometric mean (GM), we have

and

Then if $ \mathcal{R}_{1}^{C}\leq 1 $, we have $ \dfrac{dL_{1}}{dt}\leq 0 $ with equality if and only if $ U = U_{1} $, $ I = I_{1} $, $ V = V_{1} $ and $ C = 0 $. It follows from LaSalle's invariance principle that $ P_{1} $ is globally asymptotically stable when $ \mathcal{R}_{1}^{C}\leq 1 $.

It remains to show the instability of $ P_{1} $ when $ \mathcal{R}_{1}^{C} > 1 $. The characteristic equation at this equilibrium is as follows

where

Then $ \xi_{1} = \sigma I_{1}-d_{C} $ is a root of the characteristic equation (3.3). Since $ \mathcal{R}_{1}^{C} = \frac{\sigma I_{1}}{d_{C}} > 1 $, we get $ \xi_{1} > 0 $ which implies that the characteristic equation (3.3) has a positive root when $ \mathcal{R}_{1}^{C} > 1 $. Thus, $ P_{1} $ becomes unstable for $ \mathcal{R}_{1}^{C} > 1 $. This completes the proof.

Theorem 3.3. Suppose that (H) holds for $ P_{2} $. Then the infection equilibrium with cellular immunity $ P_{2} $ is globally asymptotically stable if $ \mathcal{R}_{1}^{C} > 1 $.

Proof. Construct a Lyapunov functional as follows

By using $ \lambda = d_{U}U_{2}+\frac{\beta_{1}U_{2}V_{2}}{1+q_{1}C_{2}}+\frac{\beta_{2}U_{2}I_{2}}{1+q_{2}C_{2}} = d_{U} U_{2}+d_{I}I_{2}+pI_{2}C_{2} $, $ I_{2} = \dfrac{d_{C}}{\sigma} $ and $ kI_{2} = d_{V}V_{2} $, we easily get

Thus,

Since AM is greater than or equal to GM, we have

By the above and (3.2), we deduce that $ \dfrac{dL_{2}}{dt}\leq 0 $ if $ \mathcal{R}_{1}^{C} > 1 $. It is obvious to show that $ \dfrac{dL_{2}}{dt} = 0 $ if and only if $ U = U_{2} $, $ I = I_{2} $, $ V = V_{2} $ and $ C = C_{2} $. Consequently, $ \{P_{2}\} $ is the largest invariant subset of $ \{(U, I, V, C)|\dfrac{dL_{2}}{dt} = 0\} $. From LaSalle's invariance principle, the steady state $ P_{2} $ is globally asymptotically stable if $ \mathcal{R}_{1}^{C} > 1 $.

When we ignore the nonlytic immune response, we have $ q_{1} = q_{2} = 0 $ and model (1.1) becomes

In this case, $(H)$ holds. By applying Theorems 3.2 and 3.3, we have the following result.

Corollary 3.4. Assume that $ \mathcal{R}_{0} > 1 $.

(ⅰ) If $ \mathcal{R}_{1}^{C}\leq 1 $, then $ P_{1} $ of model (3.4) is globally asymptotically stable.

(ⅱ) If $ \mathcal{R}_{1}^{C} > 1 $, then $ P_{1} $ becomes unstable and $ P_{2} $ of model (3.4) is globally asymptotically stable.

4.   Parameters estimation

According to our above analytical results, model (1.1) has an unique infection-free equilibrium of the form $ P_{0}(U_{0}, 0, 0, 0) $ which biologically represents the healthy state of patient without virus. Then $ U_{0} = \dfrac{\lambda}{d_{U}} $ is the total number of healthy pulmonary epithelial cells. In six adult human lungs, the mean alveolar number was $ 480 $ million with range $ 274 $–$ 790 $ million, and the range of volume lungs was $ 2062 $–$ 4744 $ mL ^[13]. For eight normal lungs ^[14,15], the mean lung volume was $ 4341 $ mL with range $ 3500 $–$ 5950 $ mL and the mean number of alveolar type II cells was $ 37\pm5 $ billion. Further, the mean lung volume was estimated to be $ 4340 \pm 285 $ mL in ^[16]. Based of the these morphometric data, we estimate $ \dfrac{\lambda}{d_{U}} $ to be between $ 5.7757\times10^{4} $ and $ 1.2\times10^{7} $ cells/mL. However, the death rate of uninfected epithelial cells was estimated by Lee et al. ^[17] to be $ 10^{-3} $ day$ ^{-1} $. Therefore, we get $ \lambda $ between $ 57.757 $ and $ 1.2\times10^{4} $ cells mL$ ^{-1} $ day$ ^{-1} $.

The median half-life of SARS-CoV-2 in aerosols was estimated to be between $ 1.1 $ and $ 1.2 $ hours with 95% credible interval $ [0.64, 2.64] $, it was approximately $ 5.6 $ hours on stainless steel and $ 6.8 $ hours on plastic ^[18]. Then we can estimate the clearance rate $ d_{V} $ of SARS-CoV-2 to be between $ 2.4464 $ and $ 15.1232 $ day$ ^{-1} $. It is important to note the values for $ d_{V} $ used in ^[4,19] are included in our estimated range. For example, $ d_{V} = 10 $ day$ ^{-1} $ in ^[19].

Based on the estimations in ^[4,19,20], we assume that the death rate of infected cells to be between $ 0.088 $ and $ 0.58 $ day$ ^{-1} $. We recall that the burst size is the mean number of virions produced by an infected cell during its lifespan. In the case of SARS-CoV-2, the burst size is unknown and was approximately estimated to be $ 10^{3} $ virions ^[21]. Thus, we obtain $ k $ between $ 88 $ and $ 580 $ virions cell$ ^{-1} $ day$ ^{-1} $. The estimation of other parameters are summarized in Table 1.

5.   Numerical simulations

In this section, we numerically discuss the dynamics of model (1.1) according to different parameter values.

Based on Table 1, we choose $ \lambda = 500 $, $ d_{U} = 0.001 $, $ \beta_{1} = 1.12\times10^{-7} $, $ \beta_{2} = 1.1\times10^{-7} $, $ q_{1} = 0.3 $, $ q_{2} = 0.6 $, $ d_{I} = 0.56 $, $ p = 0.06 $, $ d_{V} = 10 $, $ d_{C} = 0.85 $ and the other parameters $ \sigma $ and $ k $ are considered as free.

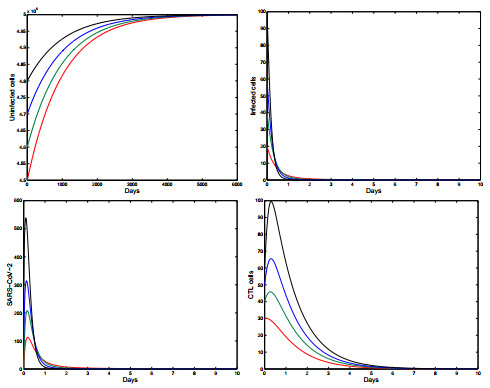
Case 1: When we take $ \sigma = 0.05 $ and $ k = 88 $, we have $ \mathcal{R}_{0} = 0.9782\leq 1 $. It follows from Theorem 3.1 that the infection-free equilibrium $ P_{0}(5\times10^{5}, 0, 0, 0) $ is globally asymptotically stable. This theoretical result is illustrated by Figure 2 which shows the solutions of model (1.1) with different initial values tend to $ P_{0} $.

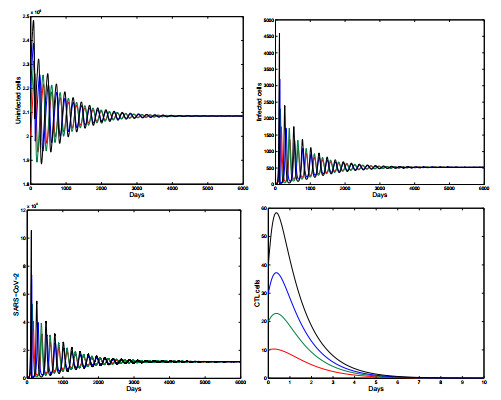
Case 2: If $ \sigma = 1.1\times10^{-3} $ and $ k = 230 $, then $ \mathcal{R}_{0} = 2.3982 > 1 $ and $ \mathcal{R}_{1}^{C} = 0.6737\leq1 $. Figure 3 displays that the trajectories of model (1.1) with different initial values converge towards the infection equilibrium without cellular immunity $ P_{1}(2.0850\times10^{5}, 520.5563, 1.1973\times10^{4}, 0) $. This confirms that $ P_{1} $ is globally asymptotically stable and thus illustrates the analytical result obtained in Theorem 3.2.

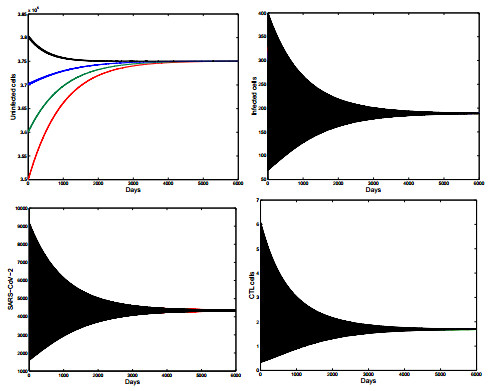
Case 3: When $ \sigma = 4.5\times10^{-3} $ and $ k = 230 $, we get $ \mathcal{R}_{0} = 2.3982 > 1 $ and $ \mathcal{R}_{1}^{C} = 2.7559 > 1 $. In Figure 4, we observe that the trajectories of model (1.1) starting from different initial conditions tend to the infection equilibrium with cellular immunity $ P_{2}(3.7506\times10^{5}, 188.2088, 4.3292\times10^{3}, 1.6977) $. This validates the global asymptotic stable of $ P_{2} $ given in Theorem 3.3.

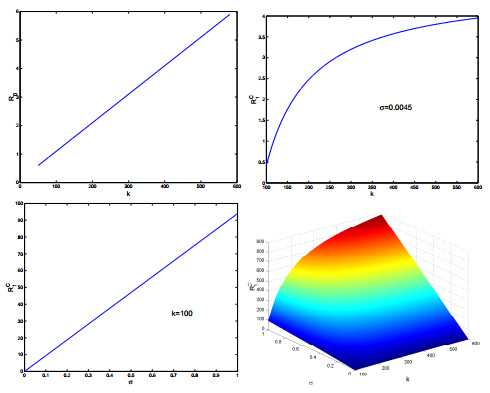
From the explicit formula of the basic reproduction number of $ \mathcal{R}_{0} $ given in (2.1), we see that $ \mathcal{R}_{0} $ is an increasing function with respect to $ k $ and it does not depend on $ \sigma $. Also, the second threshold parameter $ \mathcal{R}_{1}^{C} $ is a increasing function with respect to $ k $ and $ \sigma $ (see, Figure 5).

6.   Discussion and conclusion

In this article, we have proposed a new mathematical model to better describe the dynamics of COVID-19 in human body with virus-to-cell infection, cell-to-cell transmission, lytic and nonlytic immune responses. We have first provided the result regarding the well-posedness of the proposed model in terms of nonnegativity and boundedness of the solutions. Investigating for the biologically feasible equilibria of this SARS-CoV-2 infection model, we have obtained two threshold parameters which completely determine the dynamics of the model. The first threshold parameter called the basic reproduction number labeled by $ \mathcal{R}_{0} $ and the second is the reproduction number for cellular immunity denoted by $ \mathcal{R}_{1}^{C} $. We have proved in Theorem 2.2 that the proposed model is uniformly persistent when $ \mathcal{R}_{0} > 1 $, which biologically means that the SARS-CoV-2 persists in the host when $ \mathcal{R}_{0} > 1 $. Further, our analytical results suggest that the infection-free equilibrium $ P_{0} $ is globally asymptotically stable whenever $ \mathcal{R}_{0}\leq 1 $ (see, Theorem 3.1). This means the complete eradication of SARS-CoV-2 in human lungs. From our numerical results, this eradication of the virus and the extinction of the infection can be done after five days (see, Figure 2). However, $ P_{0} $ becomes unstable when $ \mathcal{R}_{0} > 1 $ and two scenarios arise depending on the value of the reproduction number for cellular immunity $ \mathcal{R}_{1}^{C} $. When $ \mathcal{R}_{1}^{C}\leq 1 $, the infection equilibrium without cellular immunity $ P_{1} $ is globally asymptotically stable (see, Theorem 3.2). This indicates that the immune response has not been established, which causes persistence of SARS-CoV-2 in human lungs. When $ \mathcal{R}_{1}^{C} > 1 $, $ P_{1} $ becomes unstable and the infection equilibrium with cellular immunity $ P_{2} $ is globally asymptotically stable (see, Theorem 3.3). In this case, the virus is also persisted in the lungs because of the weak response of cellular immunity (see, Figure 4). Furthermore, we have estimated some parameters of the model based on morphometric data and virus environmental stability.

Currently, there is no licensed drug or vaccine against COVID-19. The results of this study establish new within-host properties of SARS-CoV-2 and they can help the biologists and pharmaceutical companies to develop an effective treatment for COVID-19 that makes the patient's basic reproduction number $ \mathcal{R}_{0} $ less than or equal to one, which automatically lead to the eradication of SARS-CoV-2 from the patient's lungs. Since $ \mathcal{R}_{0} $ is the sum of the basic reproduction numbers for the virus-to-cell and cell-to-cell transmission modes, the last direct mode of transmission should not be ignored in the dynamics of SARS-CoV-2 infection so as not to underestimate the value of the basic reproduction number.

Acknowledgements

We would like to thank the editor and anonymous reviewers for their constructive comments and suggestions, which have improved the quality of the manuscript.

Conflict of interest

There is no conflicts of interest.