A new approach to solving local fractional Riccati differential equations using the Adomian-Elzaki method

1.   Introduction

In recent years, fractional differential equations (FDEs) have garnered substantial attention for their capacity to simulate intricate phenomena in a variety of disciplines, including finance, engineering, biology, and physics. These equations, which generalize classical differential equations to fractional-order derivatives, enable more precise description of heritable properties and memory in a variety of natural and man-made systems. Among these, local fractional differential equations (LFDEs) have emerged as a potent instrument for documenting the dynamical behavior of fractal and disordered domains. Nevertheless, the nonlinearity of these equations and the intricate interaction between fractional derivatives and stochastic components present substantial challenges when dealing with randomness or uncertainty. The individuals who have been gathered will be displayed using software.

A nonlinear differential equation with extensive applications in control theory, fluid mechanics, population dynamics, and quantum mechanics, the Riccati differential equation is a well-known equation. Fractional Riccati differential equations play an important role in modeling nonlinear systems that occur in physical and engineering applications. Fractional Riccati differential equations play an important role in modeling nonlinear systems that occur in physical and engineering applications. Adomian decomposition method, He's homotopy approximation, variational iteration method, and various numerical methods have been used in solving these equations. Momani and Shawagfeh ^[1] obtained accurate and convergent results using the decomposition method for solving fractional Riccati differential equations. Merdan ^[2] investigated solutions to the fractional Riccati differential equation using modified Riemann-Liouville derivatives. Abbasbandy ^[3] successfully applied the iterated He's homotopy perturbation method to the quadratic Riccati differential equation. He ^[4] introduced an approximate analytical method for fractional seepage flow, laying the groundwork for later applications. Jafari and Tajadodi ^[5] utilized the variational iteration method for solving fractional Riccati equations effectively. Khader ^[6] provided a numerical approach to solve these equations, while Khader, Mahdy, and Mohamed ^[7] worked on approximate solutions. Additionally, Khader ^[8] extended the numerical treatment to fractional diffusion equations. Finally, Khaniyev and Merdan ^[9] analyzed the fractional Riccati equation in detail and proposed further improvements.

The local fractional Riccati differential equation (LFRDE), its fractional counterpart, provides sophisticated modeling capabilities for systems with fractal-like structures. The applicability of these equations to problems where uncertainty or noise is a critical factor, such as stochastic processes or chaotic systems, is further enhanced by the inclusion of randomness. Nevertheless, the process of obtaining exact or approximate solutions to random local fractional Riccati differential equations (RLFRDEs) is a multifaceted endeavor that necessitates the use of efficient and robust solution techniques.

The Adomian decomposition method (ADM) ^{[10,11,12,13]} and the Elzaki transform method (ETM) are among the numerous methods that have been devised in recent years to solve fractional differential equations. The Elzaki transform technique was designed as a powerful tool for solving differential and integro-differential problems. Elzaki and Ezaki ^[14] provided a fundamental method for solving integro-differential equations with the Elzaki transform. In the same year, they expanded the method's scope by describing its applicability to higher order ordinary differential equations ^[15] and variable coefficient differential equations ^[16]. Mahgob and Elzaki ^[17,18,19] used the Elzaki transform to solve Volterra type integral equations and partial integro-differential equations using various special functions (e.g., the Bulge function). Bhadane et al. ^[20] used this approach to solve one-dimensional groundwater recharge issues in hydrogeology and showed that it is useful in engineering. Hilal and Elzaki ^[21] provided an analytical solution for the telegraph equation by demonstrating that the Elzaki transform is a modified version of the Sumudu transform. Elzaki and Ezaki ^[22] adapted the Elzaki transform to systems of partial differential equations and shown that the approach is also applicable to system solutions. Ziane and Cherif ^[23] provided an enhanced version of the approach that solves nonlinear partial differential equations using the Elzaki transform decomposition method. Finally, Shah et al. ^[24] successfully implemented the Elzaki transform to fractional multidimensional telegraph equations, achieving remarkably accurate results by combining the approach with the Adomian decomposition methodology.

The ETM offers an efficient framework for systematically transforming and solving differential equations, while the ADM is renowned for its capacity to decompose nonlinear problems into a set of simpler components. The Elzaki-Adomian decomposition method (EADM) is a prospective hybrid technique that capitalizes on the assets of both methods by combining these two approaches. The EADM has not yet been extensively investigated in the context of arbitrary local fractional differential equations, despite its potential.

This paper presents the EADM ^{[25,26,27,28,29,30]} as a novel technique for solving random local fractional Riccati differential equations. The suggested approach adeptly integrates the decomposition features of ADM with the transformation attributes of ETM, offering a robust instrument to tackle the difficulties presented by nonlinearity, unpredictability, and fractional order derivatives. The primary aims of this study are to establish a systematic framework for implementing EADM in RLFRDEs, to showcase its efficacy and precision via illustrative cases, and to evaluate its performance against existing methodologies. This work aims to introduce a novel analytical method for solving the fractional-time Riccati problem through the use of the local derivative. The suggested method employs the Elzaki transform and fractional local derivative in conjunction with Adomian polynomials to get the approximate analytical solution of the fractional time Riccati problem. Three numerical implementations are provided to illustrate the proposed approach for exponential, uniform, and normal random variables, with initial conditions selected from perfectly continuous distributions for the nonlinear Riccati equation. The alteration in the solution due to the fractional parameter is examined by numerical and graphical analyses.

The subsequent sections of this work are structured as follows: Section 2 provides the mathematical foundation and terminology pertinent to fractional calculus, local fractional derivatives, and stochastic differential equations. Section 3 delineates the Adomian-Elzaki method and its use in RLFRDEs. Section 4 provides numerical examples to substantiate the proposed method and emphasizes its benefits compared to conventional approaches. Section 5 ultimately finishes the report by discussing the research findings and prospective future directions in this field.

2.   Preliminaries

Here, we present some basic definitions of local fractional derivative that are important to our research.

Definition 2.1. Local fractional derivative of $𝒻\left(x\right)$ of order σ at $x = {x}_{0}, 0 < \sigma \le 1$:

Here, ${𝒻}^{\left(\sigma \right)}\left(x\right)\cong \underset{x\to {x}_{0}}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{Г(1+\sigma)\left[𝒻\left(x\right)-𝒻\left({x}_{0}\right)\right]}{{(x-{x}_{0})}^{\sigma }}$.

The local fractional partial differential operator of order σ is given by Kolwankar and Gangal ^[31,32],

Here, ${\Delta }^{\sigma }\left(\mathrm{U}\left({x}_{0}, t\right)-U({x}_{0}-{t}_{0})\right)\cong Г\left(1+\sigma \right)\left[\mathrm{U}\left({x}_{0}, t\right)-U\left({x}_{0}-{t}_{0}\right)\right]$.

Definition 2.2. Let $\mathcal{F}\left(t\right)$ be a function that is defined for $t$ greater than 0. The Elzaki transform of $\mathcal{F}\left(t\right)$ is defined as follows:

2.1.   Local fractional Elzaki transform method (LKED)

New transformation operatör ^[33] $LF{E}_{\sigma }:𝒻\left(x\right)\to {T}_{\sigma }\left(v\right)$:

For example,

and if $𝒻\left(x\right) = \frac{{x}^{\sigma }}{Г(1+\sigma)}$,

Definition.2.3. ^[33] Local fractional Elzaki transform of the function $𝒻\left(x\right)$ of order $\sigma$:

The inverse transformation may be derived as follows:

Teorem 2.1. ^[33] Elzaki transform of local fractional derivative:

If $LF{E}_{\sigma }\left\{𝒻\left(x\right)\right\} = {T}_{\sigma }\left(v\right)$,

and

Teorem 2.2. ^[33] Elzaki transform of local fractional integral

therefore,

Teorem 2.3. ^[34] Local fractional Elzaki transformations of various special functions are presented below:

ⅰ) $𝒻\left(x\right) = 1$, ${E}_{\sigma }\left(x\right) = \sum _{k = 0}^{\infty }\frac{{x}^{k\sigma }}{Г(1+k\sigma)}$,

ⅱ) $LF{E}_{\sigma }\left\{{x}^{\sigma }\right\} = Г(1+\sigma){v}^{3\sigma }$, $LF{E}_{\sigma }\left\{\frac{{x}^{\sigma }}{Г(1+\sigma)}\right\} = {v}^{3\sigma }$,

ⅲ) $𝒻\left(x\right) = {E}_{\sigma }\left({\left(ax\right)}^{\sigma }\right)$,

ⅳ) $𝒻\left(x\right) = \frac{{x}^{\sigma }}{Г(1+\sigma)}{E}_{\sigma }\left({\left(ax\right)}^{\sigma }\right)$,

2.2.   Elzaki Adomian decomposition method

This section presents the Elzaki-Adomian decomposition method ^[35] for the solution of fractional ordinary differential equations and equation systems when the fractional Riccati differential equation is expressed as

and let $y\left(0\right) = B$ be the initial condition, then the solution of the equation is $y\left(t\right)$, and ${D}_{t}^{\alpha }\equiv {}^{C}{D}_{t}^{\alpha }$ is a Caputo fractional derivative operator with $0 < \alpha \le 1$. The real-valued functions $p\left(t\right), q\left(t\right)$, and $r\left(t\right)$ are well-known. Using the Elzaki transform in Eq (2.3),

is obtained. Then, if the inverse Elzaki transform of the expression (13) is taken,

The Adomian decomposition approach posits that the function y may be expressed as an infinite series ^[36,37].

where ${y}_{n}$ can be defined recursively. This approach also presupposes that the nonlinear operator $Ny$ may be expressed as an infinite polynomial series.

where ${A}_{n} = {A}_{n}\left({y}_{0}, {y}_{1}, {y}_{2}, \dots, {y}_{n}\right)$ is an Adomian polynomial defined,

where $\lambda$ is a parameter. The Adomian polynomial ${A}_{n}$ can be defined as follows:

If we substitute (2.15) and (2.16) into (2.14),

If the terms of the same order in Eq (2.17) are equated,

Consequently, the Elzaki-Adomian decomposition approach yields the recursive relation for the solution of the ordinary differential equation (2.18) as follows:

3.   Convergence analysis

Define the Banach space $C[0, T]$ consisting of all continuous functions on the interval $[0, T]$ with a supremum norm. In this part, we examine the functions $y\left(t\right)$ and ${y}_{n}\left(t\right)\in C[0, T].$

Theorem 3.1. (Theorem of uniqueness ^[38,39]) The unique solution for the nonlinear fractional differential Eq (2.12) derived by Elzaki-Adomian is valid for $0 < \gamma < 1$.

Proof. The resolution of nonlinear FODEs in Eq (2.12) is delineated as follows:

Assuming that $y$ and $z$ are two distinct solutions of Eq (3.2), we may derive the following using the previously described equation:

Utilizing the convolution theory for the Elzaki transform, it is derived as

Subsequently, applying the integral mean-value theorem, it results in

Therefore, $\left|y–z\right| = 0$, as $0 < \gamma < 1$. Consequently, $y = z$. This demonstrates the solution's distinctiveness.

Theorem 3.2. (Convergence teorem ^[40,41]) Let X be a Banach space and $H:X\to X$ be a nonlinear mapping. Should the inequality

If it exists, then $H$ possesses a fixed point according to Banach's fixed point theorem ^[41]. Moreover, for the arbitrary selection of ${y}_{0}$ and ${y}_{1}$ in $X$, the sequence generated by the Elzaki-ADM converges to a fixed point of $H$.

Proof. Consider a Banach space $\left(C\right[J], \mathrm{ }\Vert.\mathrm{ }\Vert)$ comprising all continuous functions on J, with the norm defined as $‖h\left(\xi \right)‖ = {\mathrm{max}}_{\xi \in J}\left|h\right(\xi \left)\right|.$

We now illustrate that the sequence $\left\{{y}_{n}\right\}$ constitutes a Cauchy sequence within the Banach space:

Currently, the convolution theorem for Laplace transform is employed to provide the following:

Next, we obtain the result by employing the integral mean value theorem ^[41].

Let $m = n+1$, then we have

Utilizing the triangular inequality, it generates the following:

Because $\gamma \in \left(\mathrm{0, 1}\right)$, so $1-{\gamma }^{m-n-1} < 1$, then we have

Although $‖{y}_{1}–{y}_{0}‖ < \mathrm{\infty }$, as m approaches infinity, $‖{y}_{m}–{y}_{n}‖$ approaches zero.

Consequently, the sequence $\left\{{y}_{n}\right\}$ is a Cauchy sequence in $C\left[J\right]$ and is therefore convergent.

Example 1.

in this context, where B denotes a random variable with a uniform distribution, solve the local fractional order Riccati differential equation given the initial condition using the Elzaki-Adomian decomposition method and examine the probabilistic characteristics.

Solution:

Once the Elzaki-Adomian decomposition method was used on Eq (3.7), the following results were obtained:

For $n = 0$,

For $n = 1$,

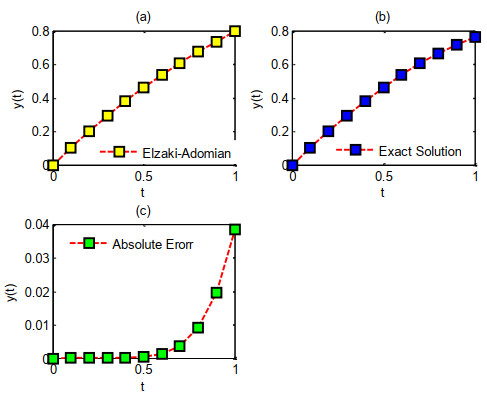
A solution is achieved. In particular, the absolute error diagrams and the comparison of the exact solution with the Elzaki-Adomian solution for $B = 0$ and $\alpha = 1$ are provided below.

The characteristics of the random variable $X$ follow a uniform distribution, denoted as $X~U(\xi, \eta).$ Employing the moment generating function of the uniform distribution

the first moment and variance of the random variable $B~U(\xi, \eta)$ are

is found ^[42,43]. Let us find the expected value and variance of the expression (3.8).

Expected value for special values $\xi = 2$ and $\eta = 4$,

For special values of $\xi = 2\mathrm{a}\mathrm{n}\mathrm{d}\eta = 4,$ the variance is

Example 2.

In this context, where B denotes a random variable with an exponential distribution, solve the local fractional order Riccati differential equation given the initial condition by utilizing the Elzaki-Adomian decomposition method and examine the probabilistic features.

Solution:

Should the Elzaki-Adomian decomposition technique be employed on Eq (3.9),

For $n = 0$,

For $n = 1$,

For $n = 2$,

solution is obtained.$X~Exp\left(\lambda \right)$ is a random variable with exponential distribution, the moment generating function ^[42,43].

The expected value and variance of the random variable $B~Exp\left(\lambda \right)$,

were obtained with the help of the moment generating function.

From the equation $Var\left(X\right) = E\left({X}^{2}\right)-{\left[E\left(X\right)\right]}^{2}$,

is found ^[42,43]. Let us find the expected value and variance of the expression (3.10).

The expected value for the special value $\lambda = 3$ is

For the special value $\lambda = 3,$ the variance is

Example 3.

In this context, where $C$ is a random variable following a normal distribution, solve the local fractional order Riccati differential equation given the initial condition by utilizing the Elzaki-Adomian decomposition method and examine the probabilistic characteristics.

Solution:

The Elzaki-Adomian decomposition method is used to Eq (3.11).

For $n = 0$,

For $n = 1$,

The characteristics of the random variable $X$ follow a normal distribution, denoted as $X~N(\mu, {\sigma }^{2}).$ Utilizing the moment generating function of the normal distribution

The first and second moments of the random variable $C~N(\mu, {\sigma }^{2})$ are $E\left[C\right] = \mu$,

and its variance,

is found ^[42,43]. Let us find the expected value and variance of the expression (3.12).

For special values of $\mu = 5, {\sigma }^{2} = 1,$ the expected value is

For special values of $\mu = 5, {\sigma }^{2} = 1,$ the variance is

4.   Results and discussions

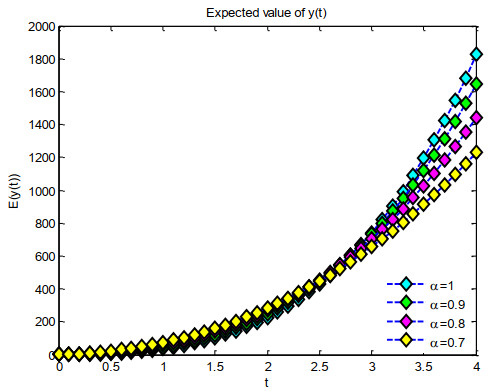
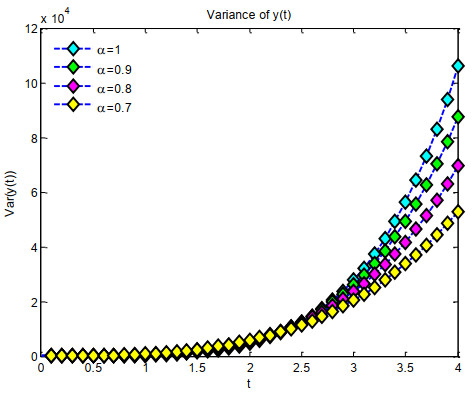
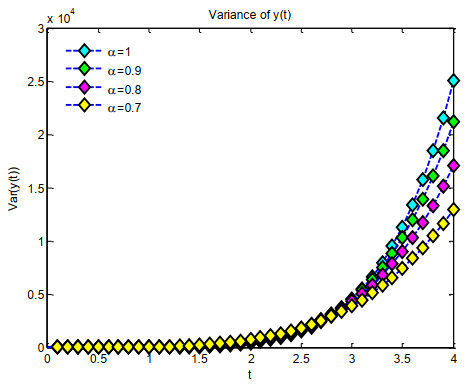
In Example 1, the graphs of the Elzaki-Adomian method, the precise answer, and the absolute error are illustrated in Figure 1. Figure 2 illustrates the binned expected value through 2D graphical representations within the interval $\alpha = 0.7, 0.8, 0.9,$ with 1 and $t\in \left[\mathrm{0, 4}\right].$ Figure 3 depicts consistently organized variance using 2D graphical representations throughout the interval $\alpha = 0.7, 0.8, 0.9,$ with 1 and $t\in \left[\mathrm{0, 4}\right]$.

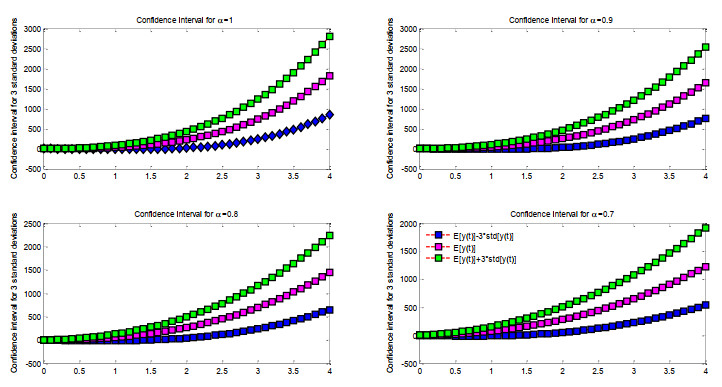
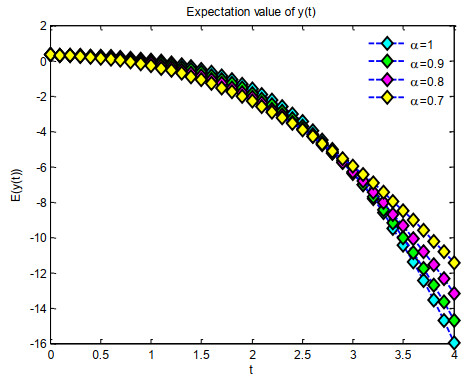
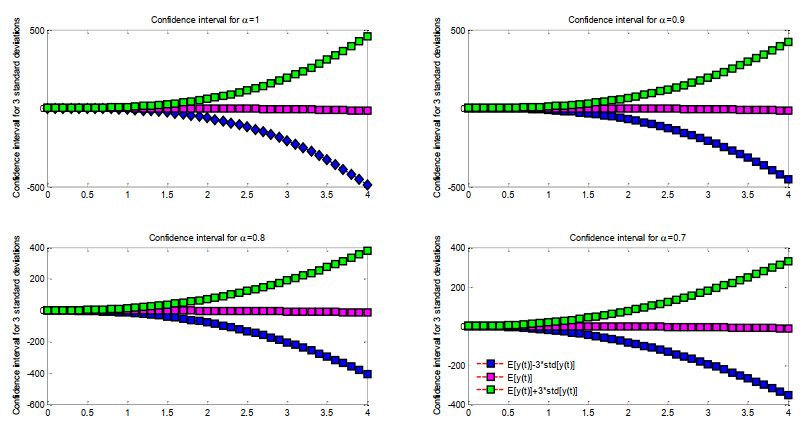
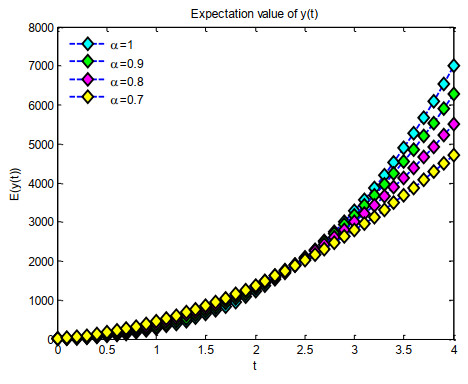
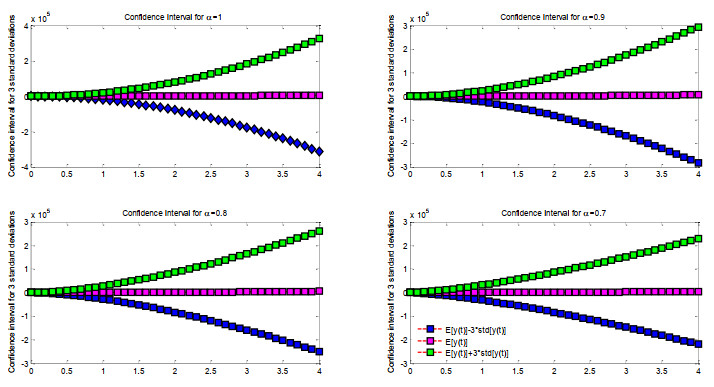
Figure 4 illustrates 2D graphs of confidence intervals for the lower confidence area, expected value, and higher confidence region for the intervals $\alpha = 0.7, 0.8, \mathrm{a}\mathrm{n}\mathrm{d}0.9$ with 1 and $t\in \left[\mathrm{0, 4}\right].$ In Example 2, the anticipated value depicted in Figure 5 is illustrated by 2D graphical plots within the interval $\alpha = \mathrm{0.7, 0.8, 0.9}$ for 1 and $t\in \left[\mathrm{0, 4}\right]$.

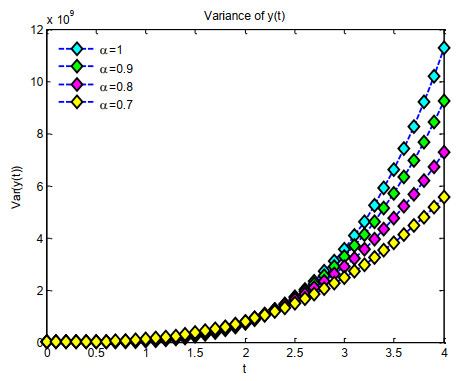
Figure 6 illustrates the two-dimensional graphs of the systematically organized variance for $\alpha$ values of $0.7, 0.8, 0.9$, and 1 with t ranging from 0 to 4. Figure 7 illustrates the two-dimensional graphs of the confidence intervals for the lower confidence bound, the anticipated value, and the upper confidence area for the intervals $\alpha = 0.7, 0.8, 0.9,$ and 1, with $t\in [\mathrm{0, 4}$] in Example 3. Figure 8 illustrates the two-dimensional graphs of the systematically organized variance for $\alpha$ values of $0.7, 0.8, 0.9,$ and 1, across the interval $t\in \left[\mathrm{0, 4}\right].$

Figure 9 illustrates the two-dimensional graphs of the systematically organized variance for $\alpha$ values of $0.7, 0.8, 0.9$, and 1, across the interval $t\in \left[\mathrm{0, 4}\right].$ Figure 10 illustrates two-dimensional plots of confidence intervals for the lower confidence, expected value, and higher confidence regions for the intervals $\alpha = 0.7, 0.8, 0.9$, and 1, with $t\in \left[\mathrm{0, 4}\right]$.

5.   Conclusions

In Example 1, the graphs of the Elzaki-Adomian method, the precise answer, and the absolute error are illustrated in Figure 1. The binned anticipated value in Figure 2 is depicted using a two-dimensional graphic. This study presents the Adomian-Elzaki method (AEM) as a novel hybrid approach for addressing random local fractional Riccati differential equations (RLFRDEs). The suggested technique effectively tackled the issues of nonlinearity, unpredictability, and fractional-order derivatives by integrating the strengths of the Adomian decomposition method (ADM) and the Elzaki transform method (ETM). The theoretical framework and numerical findings indicated that AEM is efficient and dependable in solving RLFRDEs, yielding precise approximations with low computing effort. AEM has several benefits over current methodologies, such as ease of implementation, accelerated convergence, and proficiency in managing nonlinearity and unpredictability. These attributes render it a viable contender for extensive applications in engineering, physics, and other fields where fractional modeling is significant.

Future study may concentrate on expanding AEM to encompass systems of stochastic fractional differential equations, investigating its relevance to practical issues in engineering and the physical sciences. Moreover, the integration of AEM with machine learning methodologies or sophisticated computational instruments might enhance its scalability and efficiency, rendering it a more adaptable approach for addressing progressively intricate challenges.

In summary, the Adomian-Elzaki Method is a notable advancement in the numerical resolution of stochastic local fractional differential equations. Its capacity to tackle complex issues with precision and computing efficiency facilitates its use across several scientific and technical domains.

Author contributions

Ph.D. Aydemir contributed to the article in the areas of Conceptualization, Formal Analysis, Methodology, Software; Ph.D. Merdan contributed to the article in the areas of Funding acquisition, Investigation, Supervision, Validation, Writing–review & editing; Ph.D. Demir contributed to the article in the areas of Resources, Visualization, Writing–original draft. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that they have no conflicts of interest.