An efficient and energy-stable scheme for the modified phase-field crystal equation with a strong nonlinear vacancy potential

1.   Introduction

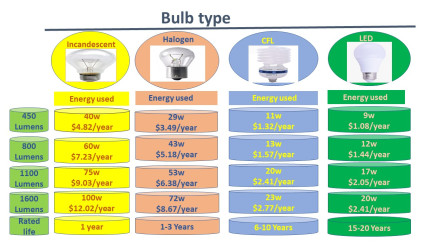
Over the last decade, electric power generation has increased dramatically worldwide. In 2012, the annual electricity production was estimated to be approximately 22,200 TWh. Moreover, in 2020 in the United States, about 4,010 billion KWh (i.e., 4.01 trillion KWh) of power was generated in utility-scale power generation offices; approximately 70% of this power was generated from fossil fuels such as coal, petroleum, and natural and other gasses. The stability of the power network, maintenance of load balance, and management of increasing demand is controlled by many power plants ^[1]. In addition, the increased use of fossil fuels from these power plants is depleting energy resources and raising a large portion of ${\rm CO_{2}}$ emissions. As a result, the Earth's average temperature increases, the climate and ecosystem change, and global warming occur. Several researchers investigated technologies for reducing energy consumption (EC) and controlling $CO_2$ emissions. Nosratabadi et al. ^[2] discussed the concepts of microgrids and virtual power plants to distribute energy resources in power systems. Yang et al. ^[3] investigated the current deployment strategies and the technological solutions of government in terms of security and privacy in a smart city environment, but they did not reduce EC. Kim et al. ^[4] investigated the research themes on smart homes and cities through a quantitative review. They proposed the bottom-up approach for energy conservation systems in smart cities, but did not focus on ${\rm CO_{2}}$ emissions reduction. Both of these factors are considered in the present model. Williams et al. ^[5] constructed a green SCM model to control greenhouse gas emissions. Their model proved how doubling the fuel efficiency of cars decreased emissions by $46\%$ compared to the baseline scenario. Lebrouhi et al. ^[6] reviewed the current bottlenecks and key barriers to the large-scale development of electric vehicles to achieve carbon targets and decarbonize transport while improving their electricity mixes. An integrated BWM and MARCOS model for air quality assessment of 22 European countries using six indicators were developed by Torkayesh et al. ^[7]. Their model's main intention was to reduce air pollution, including greenhouse gas emissions from the extensive use of fossil fuels. Several researchers adopted different technologies to control EC and ${\rm CO_{2}}$ emissions, but they did not consider the concept of smart LED production to save energy costs and lessen global emissions. The proposed study focuses on smart manufacturing technology in an energy supply chain management (ESCM) model to produce smart LEDs for high-level energy-saving and ${\rm CO_{2}}$ emissions control. Figures 1 and 2 demonstrate why LEDs are better for lighting.

Although smart energy products help save electricity costs, their market value is slightly higher than that of normal products, which causes demand uncertainty and affects the total system. The newsvendor problem is beneficial to handle this situation and determine the optimal inventory levels. Lariviere and Porteus ^[8] designated a newsvendor problem under a price-only contract. In their model, the manufacturer's profit and sales volume depended on the market's size and the wholesale price depending on the market's growth. To motivate customers, increase sales, and discover new customers, the manufacturer employs a credit payment strategy, which has not yet been investigated in any ESCM model. This credit payment contract offers the retailer a delayed purchase period ^[9]. The manufacturer does not charge any interest if the retailer pays the amount within the deferred period. Shaikh et al. ^[10] applied a credit payment strategy to an inventory model under variable demand and shortages. In the proposed ESCM, this payment strategy is based on two conditions: initial payment (fixed and not dependent on order volume, but only considered as the assurance cost) and delayed payment (dependent on order volume and committed to being paid within the delayed period).

Even though granting a delayed period increases sales, it can lead to default risk related to the credit status of the retailer ^[11]. The default risk rate is generally considered to be an exponential expression of the supplier's credit period (CP). The default risk rate becomes zero when CP is zero, and if CP tends to infinity, the default risk rate becomes $1$, adversely affecting the business industry. This study introduces an ESCM model with CP and default risk.

Other important factors, such as the variable production rate to cope with the stochastic demand and marginal reduction of ${\rm CO_{2}}$ emissions (due to production and inventory), are discussed here. Several researchers have incorporated variable production in inventory models with constant demand. Vandana et al. ^[12] managed waste and ${\rm CO_{2}}$ emissions in a supply chain management (SCM) model considering sales price-related demand and variable production. Still, they did not consider energy-efficient products and stochastic demand. To reduce EC and ${\rm CO_{2}}$ emissions, a multi-type biofuel production model under flexible production was developed by Sarkar et al. ^[13]. Still, they did not appraise CP, stochastic demand, and quality improvement policy. To reach maximum profit and reduce EC and ${\rm CO_{2}}$ emissions, a sustainable ESCM model of energy-efficient products is proposed in this study. Considering a credit payment strategy increases sales and maximizes the overall profitability of the system. Again, due to stochastic demand, overstock and understock situations may appear; this study considers flexible production to handle both situations and reach the desired profit level. In addition, the consideration of marginal reduction technology to control ${\rm CO_{2}}$ emissions (due to production and inventory) makes the model more eco-friendly. Furthermore, a certain investment is made in this work to improve product quality, enhance market size, and maintain the brand reputation. Finally, the total profit is calculated and optimized concerning the CP, product quality improvement, and flexible production.

1.1.   Research gaps

Numerous authors considered energy-efficient products in different SCMs for maintaining energy efficiencies and reducing ${\rm CO_{2}}$ emissions. Some researchers introduced the CP strategy in their SCMs with stochastic demand and ensured through statistical data that credit payment contract is an effective approach to increase sales, discover new customers, and maximize profits. Few researchers adopted flexible production to manage the demand uncertainty and run the SCMs smoothly. Several SCMs were studied under flexible production and quality improvement policies. Some significant gaps have been noticed in the past literature; these are itemized below.

1. Several SCMs considered smart LED bulbs for lower EC and ${\rm CO_{2}}$ emissions ^[14,15], which leads to uncertain demand. However, approving a CP contract with only a few guaranteed costs to address the stochastic demand for the products is a big gap in the literature.

2. Numerous SCMs were generated under the discretion of stochastic demand and fixed production rate ^[16,17]. However, an ESCM under stochastic demand, flexible production, and CP contract is still a research gap.

3. Several researchers estimated CP-dependent orders in their SCMs ^[18,19]. However, a significant research gap in the literature is a smart ESCM with CP-dependent orders, stochastic demand, flexible production, and ${\rm CO_{2}}$ emission reduction.

1.2.   Objective and contribution

Excessive use of power plants to meet daily electricity needs reduces the amount of stored fossil fuels, increases carbon emissions, and destroys the environmental balance. Then, what kind of products should be considered to control EC and reduce ${\rm CO_{2}}$ emissions and what strategies can be focused on to maximize profits has become a major concern for every industry and SCM manager. This study proposes a sustainable ESCM model of energy-efficient products under credit sales, flexible production, and stochastic demand to overcome this difficulty. The main objectives of this study are to reduce EC, increase sales, manage stochastic demand, maintain ecological balance and find maximum profits.

The proposed study contributes significantly to bridging the gaps in previous research and developing knowledge in this field.

● The proposed model promotes the credit payment strategy in an ESCM of energy-efficient products to maximize sales growth, profitability, and EC and ${\rm CO_{2}}$ emissions control.

● The current study considers flexible production to meet the uncertain demand and reassure customers about the product availability. Many works have been studied based on credit payment contracts, fixed production rates, and stochastic demand. In this work, an ESCM model with stochastic demand, credit payment contracts, and flexible production has been created to fulfill unpredictable customer demand and achieve the desired profits.

● The demand for any product depends on its quality. So, it is very important to improve the quality of the product to increase the demand and maintain the brand reputation of the product. The proposed ESCM considers some investment for product quality enhancement, thus making a substantial contribution to the literature.

● To reach the maximum profit level and make the environment more eco-friendly, this study adopts marginal reduction technology to limit the volume of ${\rm CO_{2}}$ emissions (which occurs due to production and inventory).

Thus, this study considers an ESCM model with stochastic demand, credit payment contract, flexible production, quality improvement, and marginal reduction technology to achieve the sustainable goal.

1.3.   Orientation of the paper

The remainder of this paper is organized as follows. Section 2 presents the literature review. Section 3 discusses the assumptions, problem definition, and notations used in this study. Section 4 offers the solution procedure for the mathematical model. Numerical examples and sensitivity analyses of different input cost parameters are discussed individually in Sections 5 and 6, respectively. Section 7 provides managerial insights and comparative studies. Finally, Section 8 presents the conclusions of this study.

2.   Literature Review

This section presents a keyword-based literature review along with the research gap (see Table 1).

2.1.   Energy-efficient products with a credit sales strategy

The energy sector is undergoing transformation planning, resulting from different technological and financial developments for electricity power stability and load balance. Energy-efficient products are smart consumer products like LEDs and power strips that improve energy efficiency and enable individual households to reduce energy costs. Research trends in the technological innovations related to LED bulbs with white lighting and the resulting energy conservation were discussed by ^[14]; this model also reviewed the issue of how energy conservation reduces ${\rm CO_{2}}$ emissions but did not consider CP and stochastic demand. Lazarov et al. ^[20] discussed the worldwide adoption of LED lamps for industrial and residential lighting but did not consider CP, stochastic demand, and marginal reduction technology. All of these factors are considered in the present work. Gorgulu and Kocabey ^[21] explored the potential for energy saving and environmental impacts of outdoor (including roads, gardens, and footpaths) lighting LED bulbs. Zarindast et al. ^[22] focused on smart dimmable LED panel bulbs, which are more beneficial for saving electrical energy. The proposed study also concentrates on smart LED production to reduce EC and ${\rm CO_{2}}$ emissions.

Again, the price of these products is higher than ordinary products. It poses a significant challenge for industries that want to increase the sales of these products and maximize their profits. This ESCM solves the issue easily.

The newsvendor problem in inventory management is generally applied to ensure an optimal inventory level for a single-type item with stochastic demand ^[23]. In the classical newsvendor model, the manufacturer and retailer can encounter both overstock and understock situations due to uncertain demand. However, it is difficult for the business supervisor to fix the order quantity at the beginning of a business. Zhan et al. ^[24] studied an SCM in which a capital-abundant manufacturer offered a consolidated deal to a capital-limited retailer, including the trade credit, minimum order, and price discount contract, but did not consider energy-efficient products, CP-dependent order, and shortages. Vandana et al. ^[12] introduced a two-tier trade credit policy in a sustainable SCM with credit period and sales price-based demand. In their model, they controlled EC and ${\rm CO_{2}}$ emissions and obtained the optimum solution of the decision variables in quasi-closed form. However, their model did not consider energy-efficient products and CP-dependent order. Jani et al. ^[25] demonstrated a perishable item-based model under variable demand and shortages. They examined the trade credit strategy by acclimatizing these varieties under the presumption of time-dependent holding expenditure, but did not consider CP-dependent order and controllable ${\rm CO_{2}}$ emissions. Kishore et al. ^[26] developed a three-layer SCM model under two-stage credit financing and CP-dependent demand. In this model, the manufacturer grants a credit payment contract for energy-efficient products to avoid overstock, obtain more orders, and cope with random demand.

From the previous research, it is known that several authors have discussed the concept of CP agreement, where the appearance of default risk is a very realistic scenario that was not yet been considered in their models. This research gap is discussed in the next section.

2.2.   Default risk and CP-dependent order

The manufacturer can grant a delayed payment option without any inquiries about the actual credit status of the retailer. Moreover, the retailer may default to paying an outstanding amount in the deferred period. Teng et al. ^[9] presented an economic production quantity model under a CP considering the default risk, but did not consider CP-dependent order, flexible production and quality improvement policy. Wu et al. ^[27] proposed an EOQ model in which the retailer allows a downstream CP to the buyer, which increases sales and revenue along with the opportunity cost and default risk. Wang et al. ^[28] designed an SCM based on two-tier trade credit, asymmetric information, and default risk. Still, they did not consider CP-dependent orders, flexible production, and marginal reduction technology. A two-echelon-integrated SCM with two-tier trade credit and default risk under uncertain demand and shortages was elaborated by Kaur ^[29]. Tsao et al. ^[30] developed a stochastic newsvendor model that considered the CP and defaulted risk of generating renewable energy. Still, they did not consider CP-dependent orders, quality improvement policy, and flexible production. In the case of default risk, the manufacturer charges interest for non-payment in full within the delayed period ^[19].

By granting a CP, the manufacturer indirectly enables interest-free loans for the retailer to alleviate capital constraints. Thus, the order volume must correspond to the CP offered by the manufacturer. In this case, it is practical to consider CP-dependent order volume. Several researchers, such as Chen and Teng ^[31] and Li et al. ^[18], considered the order volume an exponential expression of the CP. Shaikh and Cárdenas-Barrón ^[32] studied an EOQ model of deteriorating items under CP-dependent order and price as well as advertise-based demand. Still, they did not consider stochastic demand, flexible production, and quality improvement policy. Wang et al. ^[19] proposed a logistic service SCM model with random demand and CP-dependent order volume but did not consider flexible production and marginal reduction technology.

From the past research, it is clear that several researchers consider different SCMs under stochastic demand, CP, and default risk. However, the consideration of flexible production to meet stochastic demand and certain investments to improve product quality is a very realistic scenario which was not yet been considered in any ESCM model. This research gap is discussed in the next section.

2.3.   Variable production with quality enhancement policy

Because energy-efficient products cost slightly more than ordinary products, stochastic demand is possible. In such cases, a variable production rate should be considered for surviving among competitors, satisfying customer demand, avoiding shortages, and reaching maximum profit. Sarkar et al. ^[33] studied a smart production model under flexible production and selling price-dependent demand. They made some investments to reduce the setup cost of the system, but they did not consider CP and quality improvement policies. Again, the success of any business company depends on product quality. Therefore, numerous companies make continuous investments to improve their product quality; various researchers have examined the desirable profit of such models after considering some investments for product quality improvement. Sepehri et al. ^[34] discussed a production model considering some investments for ${\rm CO_{2}}$ emissions reduction and product quality enhancement. An imperfect production model with a quality improvement policy, lead time reduction, and safety stock was investigated by Choi et al. ^[35]. In their study, demand was dependent on selling price and service, and they considered an online-to-offline retailing strategy for selling products. Mondal et al. ^[17] discussed a hybrid manufacturing-remanufacturing SCM with demand uncertainty and a quality enhancement policy. They considered the CAPT strategy to reduce ${\rm CO_{2}}$ emissions and the Stackelberg game strategy to solve the model. Habib et al. ^[36] improved production process quality, reduced vendor setup cost, and verified the optimal global solution numerically and analytically in a biodiesel SCM model. A smart manufacturing system under variable production rate and demand was exhibited by Sarkar et al. ^[37]. Their model adopted an autonomation policy to detect defective products and deliver perfect quality products to customers. Still, they did not consider CP, default risk, and marginal reduction technology. Sarkar et al. ^[38] discussed the distribution-free approach to random demand and returned for the green products innovation under different production strategies but did not consider CP and marginal reduction technology. A flexible production model under imprecise market conditions with partial backlogging and rework was investigated by Yadav et al. ^[39]. They controlled waste and pollution in their model with some pollutant control costs.

In this sense, how the energy-efficient products and quality improvement flexible production are connected with stochastic demand, EC, and ${\rm CO_{2}}$ emission control in a sustainable ESCM are discussed in detail in the next section.

2.4.   Environmental effect

Climate change has become an increasingly critical issue. Many researchers have proved that efficient energy utilization is an effective approach for reducing ${\rm CO_{2}}$ emissions. Households are generally responsible for 15–20% of the total electricity consumption, which can be saved by promoting smart energy-based products and services. An LED bulb is a smart energy-saving product for lighting loads and ${\rm CO_{2}}$ emission reduction. Sarkar et al. ^[40] developed a sustainable SCM model considering waste recycling and controlled ${\rm CO_{2}}$ emissions. However, they did not consider energy-efficient products, flexible production, and quality improvement policy. Vandana et al. ^[12] managed waste, controlled ${\rm CO_{2}}$ emissions, and saved EC using an SCM model but did not consider quality improvement policy. A multi-stage biodiesel production SCM to control the growing energy demand and rapid depletion of fossil fuels was initiated by Habib et al. ^[41]. Their study also included ${\rm CO_{2}}$ emissions reduction in carbon tax to clean the production and distribution environment. Under advertisements, Kumar et al. ^[42] managed waste and reduced ${\rm CO_{2}}$ emissions in a sustainable SCM.

A sustainable manufacturing process under a basic economic-production paradigm, flexible production, and controllable ${\rm CO_{2}}$ emission was developed by Moon et al. ^[43]. A geometric programming procedure was employed to obtain their model's quasi-closed form of the optimal solution. A smart, reliable production system with low setup cost and controllable ${\rm CO_{2}}$ emissions was designated by Kugele et al. ^[44]. They also adopted a geometric programming approach with a degree of difficulty two in finding the optimal solution. Hota et al. ^[45] controlled ${\rm CO_{2}}$ emissions in a sustainable SCM under flexible production and selling price-based demand. Pal et al. ^[46] developed a dual-channel green SCM under promotional effort but did not consider stochastic demand, CP, and quality improvement policy. This ESCM paid special attention to EC and ${\rm CO_{2}}$ emissions reduction for environmental protection.

2.5.   Energy storage system

The power industries are facing major challenges in producing a large fraction of the total EC to meet the huge electricity demand. Thus, their interest in developing new energy-saving technologies to meet the growing demand is increasing. An energy storage system is a device that transforms electrical energy from a power system and stores energy safely, conveniently, and efficiently to supply when needed. Several authors have widely studied the energy storage system. Elsarrag ^[47] investigated how a small amount of home-made low-pressure hydrogen energy can power LED lamps for several hours and reduce EC. In addition, they provided important pointers on how the technology can be used safely at home, together with other energy-efficient technologies. Arce et al. ^[48] discussed how the thermal energy storage systems balance electricity loads and reduce EC and $CO2$ emissions in the buildings and the industrial sector. Navarro et al. ^[49] described the inclusion of thermal energy storage systems in the residential and commercial building sectors constructively and functionally. A smart LED outdoor lighting system based on the level of energy stored in the battery was designed by Kiwan et al. ^[50]. A review of thermal energy storage for storing cold energy with various solid-liquid low-temperature phase change materials was performed by Nie et al. ^[51]. Zhang et al. ^[52] developed a multi-functional power system with the integration of liquefied natural gas and compressed wind energy storage subsystems. Thus, several production systems considered smart energy-efficient products to reduce EC and ${\rm CO_{2}}$ emissions. However, to the best of our knowledge, previous researchers did not consider energy-efficient products, variable production rate, CP, default risk, carbon emission reduction, and quality enhancement policy in the same frame to save EC, meet uncertain demand, increase sales, maintain environmental sustainability, and improve product quality. Therefore, the model is more profitable and acceptable than the others.

3.   Problem Definition, Notation, and Assumptions

This section discusses the problem description, notations, and hypotheses. First, the problem definition is described in detail, followed by a brief discussion on the notations and assumptions used in this study.

3.1.   Problem definition

The proposed model involves ESCM for energy-efficient production, including a manufacturer and retailer under the credit payment and quality enhancement strategy, wherein a random variable represents the customer demand. The manufacturer first selects a credit payment strategy comprising two factors: an initial charge for order assurance and delayed payment on the order quantity; then, they motivate the retailer to sign the credit contract and receive products from them. The order quantity also depends on the CP, which is considered in this study. Moreover, a flexible production rate is applied because random demand increases the possibility of variable production. In this study, the manufacturer makes certain investments to improve product quality, and both manufacturer and retailer consider marginal reduction technology to maintain the environmental sustainability. It is common for retailers to purchase some products from a marketplace for their office staff or other requirements. This idea is considered in this model. A distribution-free strategy is introduced here to determine the upper bound of shortage and overstock quantities and evaluate the model.

3.2.   Notation

All symbols pertaining to this model are described in Table 2.

3.3.   Assumptions

The hypotheses related to the proposed model are provided below:

1. In this study, a single-stage inventory model is proposed for energy-efficient products (LED bulbs), where a constant (i.e., initial payment I for product assurance) and delayed payment strategy are used for the retailer. The delayed payment should be paid in credit time m (Wang et al.^[11]), and the considerable demand is random (Sarkar et al. ^[54]).

2. The order size $q$ is assumed to be $q = B e^{sm}$ where $B$ denotes the basic order quantity, and $s$ is the scaling parameter for credit sales. When the manufacturer grants a long CP, credit default risk is more likely to occur (Wang et al. ^[19]). This model assumes the coefficient of default risk as $\theta_l$, where $\theta _l$ is a non-negative constant. Again, the manufacturer demands a compound interest at the rate $\alpha_m$ for that default period.

3. Owing to variable production rate $P$ (Sarkar and Bhuniya ^[55]), the unit production cost is expected to be $u(P)$ = $B^P_{rm}+L_{i}/P +\alpha_{i} P^\rho$, where $B^P_{rm}$ denotes the unit raw material price for the manufacturer for manufacturing, $L_{i}$ is the development cost for each cycle of the production process (proportional to the production rate), and $\alpha_{i} P^\rho$ is the die/tool cost. The preparative expenditure function of $P$ is convex; it is minimized at $P = \sqrt{L_{i}/\alpha_{i}}$.

4. The initial carbon emission for every product for the manufacturer and retailer is $I_{cm}$ and $I_{cr}$, respectively. The emissions goals for each product are established by both the manufacturer and retailer ($I_{gm}$ and $I_{gr}$, respectively). This assumption proves that ESCM members are cautious about reducing carbon emissions. It is also assumed that the manufacturer and retailer have different operational costs for the reduction task, and the amount of reduction is quadratic in $(I_{cm}-I_{gm}), (I_{cr}-I_{gr})$ (Ghosh et al. ^[56]).

5. It is assumed that the price of products purchased by the retailer for their employees is equal to the selling price of $q_0$ units by the retailer. This model considers uncertain demand, $x$, and order size, $q$. The players have to pay the shortage cost if the customer demand $x > q$; moreover, if $x < q$, i.e., if there are some unsold items, the players hold them at a certain holding cost.

4.   Model Formulation

This section describes the formulation of the proposed ESCM model under the settings of the newsvendor model.

The manufacturer is responsible for credit payment planning, production, product quality enhancement investment, reducing the cost to control carbon emissions, and purchasing raw materials. In this ESCM, the manufacturer offers a CP contract (to encourage more orders) to the retailer; the retailer initially pays a certain cost, $I$, for the required items and the remaining amount in delay for the CP $m$. By signing the credit payment contract, the retailer orders $q$ products; then, the manufacturer constructs an infrastructure to produce $q$ items considering some investment to upgrade the product quality. Here, the production rate, $P$, is variable. The manufacturer pays a certain reduction cost to control the number of carbon emissions caused by the production of $q$ products; after production completion, the manufacturer delivers the products to the retailer. In this model, the manufacturer does not know the credit status of the retailer; regardless, they offer a delayed payment strategy. In such a case, there is a possibility of credit default risk. Therefore, the manufacturer charges compound interest to the retailer for the default period.

Furthermore, the retailer pays the purchase price of the finished product, carbon emission expenditure linked to inventory, and carbon emission reduction cost to control the volume of ${\rm CO_{2}}$ emissions. In addition, the retailer buys some products for their employees, whose value is the price of $q_0$ unit products. The demand, $x$, is stochastic, for which a shortage occurs if $x > q$, and if $x < q$, the players hold the unsold products.

4.1.   Manufacturer's model

The manufacturer is the most important player in any SCM. In this model, the manufacturer produces energy-efficient products with variable production rates and offers a CP to the retailer to get bulk orders and increase sales. Initial costs, such as ordering and setup costs, are included with the manufacturer's relevant cost. All costs associated with the manufacturer are discussed as follows:

4.1.1.   Ordering cost (OM)

Ordering cost is one of the important costs of the SCM to purchase raw materials for production. In this model, the manufacturer places an order for raw materials at a specific ordering cost:

4.1.2.   Setup cost (SM)

Setup cost is one of the primary costs for starting and running a business smoothly. In this model, the manufacturer sets up an infrastructure to run the production process with a usual setup cost:

4.1.3.   Variable production cost (VPM)

The demand for any product fluctuates according to its standing in the global market. Variable production rate helps the manufacturer in a competitive market to manage the unpredictable demand. In this case, the per-unit production cost is considered an expression of raw material cost, production rate, development cost, and too/die cost. If a manufacturing industry wants to launch smart products, they need to focus on smart technologies to develop the process and maximize profits. For this purpose, the company invests some development costs. Again, management needs to fix their machines and regularly check their equipment to keep production smooth and avoid machinery problems. All these types of expenditures are considered tool/die costs. The manufacturer produces $q$ products at a variable production rate in this study. Therefore, by Assumption of $3$, the production cost of $q$ products of the manufacturer is as follows:

4.1.4.   Quality enhancement cost (QEM)

The demand for any product depends on the quality. Accordingly, the manufacturer makes some investments to enhance the quality level of the finished products up to $q_u$, which is expressed as follows:

4.1.5.   Goodwill lost cost (GLM)

The quality of all products is not always $100\%$ perfect. Moreover, the product quality is often affected by some impurities $(1-q_u)$, which affects the brand image and goodwill of the manufacturer. Therefore, the goodwill lost expense borne by the manufacturer is expressed as follows:

4.1.6.   ${\rm CO_{2}}$ emission cost (CEM)

During the production process, a large amount of ${\rm CO_{2}}$ is emitted, disrupting environmental sustainability and affecting human health. In this study, the manufacturer sets an emission goal of $I_{gm}$ units for each product to control the amount of ${\rm CO_{2}}$ emission caused by the production of $q$ products. Thus, the ${\rm CO_{2}}$ emission cost paid to the manufacturer is expressed as follows:

4.1.7.   ${\rm CO_{2}}$ emission reduction cost (CERM)

In this study, the manufacturer pays special attention to ${\rm CO_{2}}$ emission reduction for environmental issues with a certain marginal reduction cost of $b$ per unit. Initially, the ${\rm CO_{2}}$ emission of each product is assumed as $I_{cm}$. Therefore, by Assumption $4$, the ${\rm CO_{2}}$ emission reduction cost of $q$ products of the manufacturer is as follows:

4.1.8.   Shortage cost (SPM)

Shortage cost is incurred by an industry/organization when it has no stock. These costs include business losses for consumers who go elsewhere to shop. In this model, when the demand $x \geq q$ shortage appears and then the shortage penalty cost paid by the manufacturer is expressed as follows:

4.1.9.   Holding cost (HM)

The holding cost is the amount that must be paid to save the excess inventory. In this ESCM, when the demand $x < q$, the manufacturer retains the unsold products at holding cost, $C_{hmn}$ per unit. Thus, the total holding cost paid by the manufacturer for saving the remaining inventory is expressed as follows:

4.1.10.   Revenue (RVM)

Revenue is the total income of a company from which all expenses are deducted to get net income or desired profit. Here, the manufacturer receives initial payment $I$ and delayed payment $wq e^{-(\theta_l+ \alpha_m) m}$ when $x \geq q$ and $w x e^{-(\theta_l+ \alpha_m) m}$ when $x < q$ from the retailer. Thus, the manufacturer's revenue under the two conditions is:

4.1.11.   Aggregate profit

The aggregate profit of the manufacturer under the two conditions can be obtained by subtracting all costs from the revenue; thus, the total profit of the manufacturer is

Now, the manufacturer's expected profit is

4.2.   Retailer's model

In the proposed work, the retailer pays some costs such as ordering cost, ${\rm CO_{2}}$ emission cost, ${\rm CO_{2}}$ emission reduction cost, shortage cost, and holding cost. After signing the CP contract, the retailer orders $q$ products from the manufacturer at an ordering cost of $A_0$. All costs associated with the ESCM retailer are discussed as follows:

4.2.1.   Ordering cost (OR)

Ordering cost is the most significant cost associated with ESCM, with which ESCM players are connected. The retailer pays the ordering cost to purchase the finished products from the manufacturer. In this work, the retailer places an order for the finished products at a specific ordering cost:

4.2.2.   ${\rm CO_{2}}$ emission cost (CER)

Due to the retailer's inventory, some amount of ${\rm CO_{2}}$ is emitted, which affects the environment. The retailer also sets an emission goal of $I_{gr}$ units for each product to control ${\rm CO_{2}}$ emission due to $q$ product inventory. Thus, the ${\rm CO_{2}}$ emission cost paid by the retailer is expressed as follows:

4.2.3.   ${\rm CO_{2}}$ emission reduction cost (CERR)

In this work, the retailer focuses on ${\rm CO_{2}}$ emission reduction with a certain marginal cost of $a$ per unit. Initially, the ${\rm CO_{2}}$ emission of each product is treated as $I_{cr}$ units. Therefore, by Assumption$4$, the ${\rm CO_{2}}$ emission reduction cost of $q$ products of the retailer is as follows:

4.2.4.   Shortage cost (SPR)

In this model, for the stochastic demand $x$, if $x \geq q$, a shortage occurs from the retailer's side. Now since $s_2$ is the retailer's per-unit shortage penalty cost; the total shortage penalty cost paid by the retailer is expressed as:

4.2.5.   Holding cost (HR)

After receiving the $q$ products from the manufacturer, if the customer demands $x < q$, the retailer holds the excess inventory at $C_{hrb}$ per unit. Thus, the total holding cost paid by the retailer for preserving the remaining stock is expressed as follows:

4.2.6.   Purchasing price for employees (PPR)

It is a very realistic scenario for the retailer to purchase certain products for their employees. In this ESCM, the retailer buys certain products for their employees, which is equal to the value of the $q_0$ products sold by the retailer. Thus, the purchasing price for retailer employees is expressed as follows:

4.2.7.   Revenue (RVR)

Due to the stochastic demand $x$, two possibilities arise; $x \geq q$ and $x < q$. Here, the per unit selling price of the retailer is assumed to be $p$. Then the retailer's revenue under two conditions is expressed as follows:

4.2.8.   Aggregate profit

The aggregate profit of the retailer under two conditions can be obtained by subtracting all costs from the revenue; thus, the total profit of the retailer is expressed as:

Now, the retailer's expected profit is

4.3.   Joint profit of the manufacturer and retailer

Using Equations (4.12) and (4.21), the combined profit expressions of the retailer and manufacturer can be given by:

[For reference, see Sarkar et al. ^[54]].

4.4.   Solution methodology

The classical optimization technique is used to solve the mathematical model. The total profit is optimized along with the decision variables $m$, $P$, and $q_u$. To prove the sufficient part, the Hessian matrix is calculated. First, the total profit is partially differentiated by the decision variables. Then by equating the aforementioned partial differentials to zero, the stationary points $m^*$, $P^*$, and $q_u^*$ can be derived as follows:

Where, the expressions of $G_1 (P), G_2(m)$ are shown in Appendix B, and the first-order partial derivatives are shown in Appendix C.

Some propositions are provided here to ensure the global optimality of the profit function and prove sufficient conditions. The propositions are as follows:

Proposition 1. The 1st order principal minor of the Hessian matrix for the joint profit function is less than zero at the optimum results of the decision variables $m^*, P^*, q_u^*$ if $G_3 (m, P) < 0$.

Proof: For proof see Appendix D and E.

Proposition 2. The 2nd order principal minor of the Hessian matrix for the joint profit function is greater than zero at the optimum results of the decision variables $m^*, P^*, q_u^*$ if $G_3 (m, P) G_4 (m, P)+ \left\lbrace G_6 (m, P) \right\rbrace ^2 < 0$.

Proof: For proof see Appendix D and 63141592631415927.

Proposition 3. The 3rd order principal minor of the Hessian matrix for the joint profit function is less than zero at the optimum results of the decision variables $m^*, P^*, q_u^*$ if $G_5 (q_u) \big[G_3 (m, P) G_4 (m, P)+ \left\lbrace G_6 (m, P) \right\rbrace ^2 \big] < 0$.

Proof: For proof see Appendix D and 73141592631415927.

Proposition 4. The joint profit function is concave at the optimum findings of the decision variables $m^*, P^*, q_u^*$ if $G_3 (m, P) < 0$, $G_3 (m, P) G_4 (m, P)+ \left\lbrace G_6 (m, P) \right\rbrace ^2 < 0$ and $G_5 (q_u) > 0$.

Proof: For proof see Appendix D and Appendix E - 73141592631415927.

5.   Numerical Experiment

The stabilization of EC and reduction of ${\rm CO_{2}}$ emissions have become a major challenge for industries worldwide. This study presents a smart ESCM model considering credit sales and default risk, wherein LED bulbs are produced at a flexible rate to meet unexpected demand and maximize the overall profit of the system.

To determine the maximum total profit with respect to the optimal CP, variable production rate, quality improvement, and CP-dependent order quantity, the parametric data are taken from Wang et al. ^[28], Sepehri et al. ^[34], Wang et al. ^[19] at their best fit. All the input parameters are demonstrated in Table 3.

The optimal consequences of the corresponding decision variables are obtained using MATLAB R2015a. Table 4 presents the output data set relative to the input data set.

Table 4 displays the optimal results for ${m}^*$, ${P}^*$, ${q_u}^*$, and ${q}^*$ as follows: the manufacturer provides a CP of $m^* =$ 0.37 years to the retailer, the variable production rate of the manufacturer is $P^* =$ 612.55 units, and the improvement of quality is $q_u^* =$ 0.91; then, the optimum order amount is $q^* =$ 791.9 units. Thereafter, using Equation (4.22), the joint total profit of the model is obtained to be $J_p^{MRC}(m^*, P^*, q_u^*) = ＄$2417.98.

The most important part of this study is that the delayed period, variable production, quality improvement, and CE are neglected; this study is similar to that by Sardar and Sarkar ^[16], wherein the total joint profit of the SCM under consignment policy was ＄1253.106. So the current model doubles the profit of the previous model. Thus, the proposed study is advantageous for the business industry.

5.1.   Proof of optimality (numerically)

The eigenvalues of the Hessian matrix are $-7371.8, -0.01, and -549.62$, which are negative. Thus, the Hessian indicates a negative definite status. This proves that the profit function is maximum at point $\left(0.37,612.55, 0.91\right)$; hence, $\left(0.37,612.55, 0.91\right)$ is a point of maximization of the profit function.

5.2.   Case study

In this model, an ESCM is discussed for two players, wherein the manufacturer produces smart LED bulbs to save electricity costs and protect the environment from ${\rm CO_{2}}$ emissions. However, because LED bulbs are costlier than incandescent, halogen, and CFL bulbs, the manufacturer offers a CP as an incentive to the retailer to motivate and sell more LED bulbs (which balance the electrical load and maintain electrical energy stability) and achieve the desired profit. Again, marginal reduction technology has been adopted here to reduce the amount of ${\rm CO_{2}}$ emissions due to production and inventory. Now, to ensure the proposed model is advantageous for the business industry, a scenario is considered in which CP and marginal reduction technology are ignored, and traditional bulbs, such as incandescent, halogen, and CFL, are produced. In this scenario, the CP $m$ is assumed to be $0$, and the manufacturer and retailer settle no emission goal. Table 5 presents the correct answer.

It is clear from Table 5 that if the manufacturer produces traditional bulbs and does not offer extra time or CP to the retailer, the order quantity and profit change to a significant extent. Ignoring the CP, the retailer's order quantity decreases from $791.9$ units to $600$ units, and the total system profit falls from $2417.98 ＄$ to $1964.13 ＄$, which is disadvantageous for the industry. It is also notable that without CP and marginal reduction technology, the amount of ${\rm CO_{2}}$ emissions increases from $633.52$ units to $660$ units.Therefore, implementing smart LED bulbs in households, offices, roads, and other sectors is essential to obtain large profits and maintain a healthy and safe economy and atmosphere. In addition, the CP offered by the manufacturer ensures profits for industries while maintaining their brand value. Hence, the consideration of CP is beneficial, and manufacturers are advised to produce LEDs and grant CPs to retailers to obtain more orders and increase the total profit of ESCM.

6.   Sensitivity Analysis

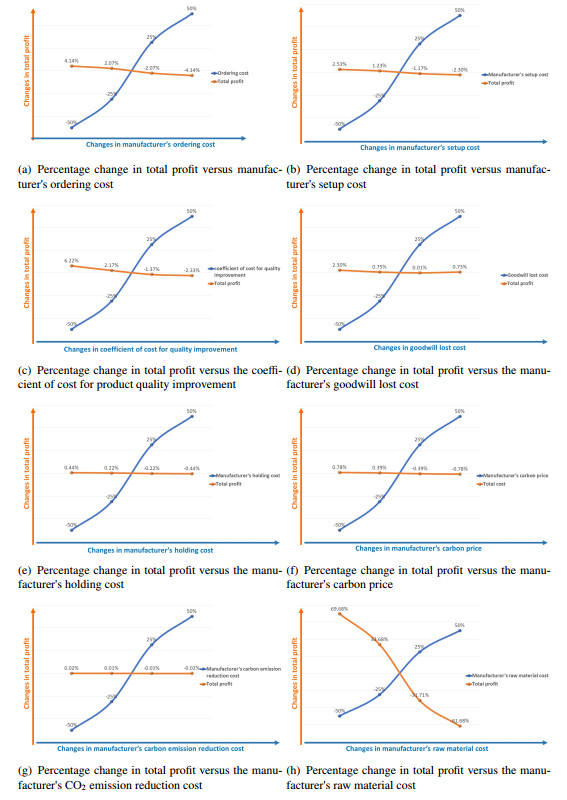
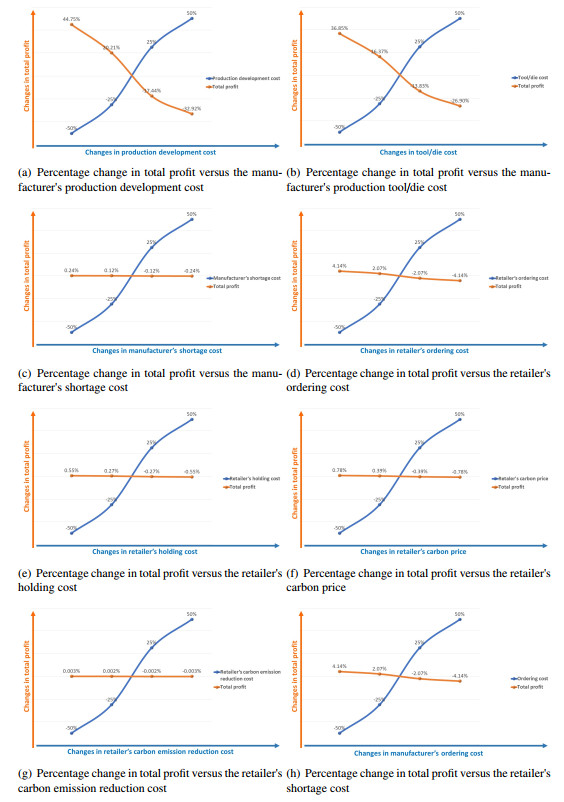
Table 6 summarizes the observations regarding the changes in profit corresponding to those in input cost parameters by -50%, -25%, +25%, and +50%.

It is evident from Table 6 that the total profit increases or decreases according to all cost parameters (except $g$) decreases or increases. The observations also indicate that the total profit of the ESCM model is not significantly sensitive to the per-unit holding costs, $C_{hmn}$ and $C_{hrb}$, per unit C.E. costs, $C_1$ and $C_2$, per unit C.E. reduction costs, $a$ and $b$, and shortage costs, $s_1$ and $s_2$, of the manufacturer and retailer, respectively. The setup cost, $C_{om}$, of the manufacturer; ordering costs, $C_{sm}$ and $A_0$, of the manufacturer and retailer, respectively; and coefficient of cost, $\alpha_3$, for product quality improvement obsess the ESCM profit moderately. The most sensitive parameters that affect the ESCM yield at the most level include the production process tool/die cost ($\alpha_3$), development cost ($L_i$) for the manufacturer, and purchase cost of raw material ($B^P_{rm}$) for the manufacturer.

Figures 4(a)-5(h) illustrate the change in total profit in each cost parameter involved in the model.

7.   Managerial Insights

When starting and developing a business, every industry must focus on scientific observations and statistical information. Business supervisors can achieve maximum profit by implementing various research ideas and technologies. The recommendations from this study are stated and discussed in this section.

1. The production of smart products is a significant issue for every industry. Smart LED bulbs can reduce electricity consumption and carbon emissions. Smart products can help companies maintain their brand image globally, survive in a competitive market, make customers aware of their energy-saving standards, reassure them about product quality, and maximize profits. Therefore, business supervisors should focus on producing and distributing smart products. A credit payment contract can help companies increase sales, expand their customer base, and determine the buyer's credibility.

2. In this study, the credit payment contract is considered, which is another important factor. It should be noted that the CP is the time limit offered by the company to customers to pay a certain amount (it does not represent the time taken by a customer to make payment for the purchased products). Thus, business supervisors should consider offering this policy.

3. Flexible production rate is an emergent issue in every business industry. In this study, the per-unit manufacturing cost is considered an expression of the development expenditure, tool/die expenditure, and production rate. Flexible production can help uplift industries in a competitive market considering unpredictable demand, improve the brand reputation, ensure customers about product availability, and avoid overstock and understock situations. Hence, every production company should concentrate on flexible production to handle such situations and meet expected profits.

4. The improvement of product quality is another important objective of every industry. In this study, certain investments are made by the production manager to enhance the product quality of the ESCM. Through these investments, companies can maintain their product quality, increase sales, and sustain a global reputation. Therefore, industries are advised to invest in improving product quality.

5. Carbon emission is a crucial and extensively analyzed issue that significantly impacts the ecosystem and environment of the earth. Due to production and inventory, large amounts of ${\rm CO_{2}}$ are released. In this study, energy-efficient LED bulbs are manufactured to save energy and reduce ${\rm CO_{2}}$ emissions. Including carbon emission expenditure with marginal reduction makes the model more eco-friendly. Accordingly, business supervisors can control ${\rm CO_{2}}$ emissions and produce eco-friendly products to satisfy conscious customers, save energy, and increase profits.

Thus, the results obtained through this study can be used by the business supervisors of any industry to make important decisions regarding smart energy products, credit sales, production rate, product quality improvement, and ${\rm CO_{2}}$ emission reduction, which can directly improve the overall profitability of the system.

8.   Conclusion

Nowadays, not a single day cannot run without electricity in any sector, starting from industries, offices, houses, and roads. Thus, plenty of energy is essential to meet all these requirements. Again this huge amount of energy comes from fossil fuels in power plants, which reduces fossil fuel reserves and disrupts the ecological balance due to ${\rm CO_{2}}$ emissions. Then, how to control EC, reduce ${\rm CO_{2}}$, and increase profits has become a significant global challenge. Several researchers have explored strategies to reduce EC, ${\rm CO_{2}}$ emissions, and reach the maximum profit levels. Khorasanizadeh et al. ^[15] described how the annual electricity consumption, electric bills, and emissions types were reduced by using smart LEDs for lighting. In order to maximize profits, Kaur ^[29] studied a two-echelon SCM with random demand, two-tier trade credit, and shortages, but they did not pay attention to sustainability. A logistic service SCM with random demand and CP-dependent order volume was proposed by Wang et al. ^[19]. Recently, a sustainable manufacturing process under a basic economic-production paradigm, flexible production, and controllable ${\rm CO_{2}}$ emission was developed by Moon et al. ^[43], but they did not consider a credit payment strategy to increase sales and discover new customers. Padiyar et al. ^[57] improved product quality and controlled vendor setup expenditure in an SCM model with constant and fuzzy demand. Still, they did not consider CP and flexible production to handle overstock and understock situations.

However, the proposed model investigated an ESCM for EC and ${\rm CO_{2}}$ emissions reduction and profit maximization under credit payment strategy and stochastic demand. This model proved that considering energy-efficient products like LEDs and credit period, the order volume and total profit for every industry can be improved. This model of variable production helps the industry meet unpredictable demand and manage overstock and understock situations. In this model, the upper bound of excess and shortage quantities were ascertained through a distribution-free strategy, and both players reduced ${\rm CO_{2}}$ emissions for environmental protection. Also, the manufacturer made certain investments to upgrade product quality during production. Finally, the total profit was optimized for the CP, product quality improvement, and variable production. MATLAB 2015a was used to obtain numerical results and ensure the global optimality of the profit function. From the proposed research, it may be concluded that if the demand is stochastic and the production rate is variable rather than constant, the total profit is increased by $28.64\%$. However, using the distribution-free approach in an SCM with stochastic demand, the total profit is increased by $11.36\%$. Moreover, the significant observation in the proposed research is CP, variable production rate, and stochastic demand. These concepts increase the total profit up to $92.96\%$.

The main limitations of this study are excess products, fixed setup costs, and fixed ordering costs. Here, the retailer and manufacturer stored the surplus product, which is disadvantageous for any industry. Therefore, the extension can be made by introducing the concept of a barter platform where retailers can exchange their surplus products with the required products through a broker (Hua et al. ^[58]). This concept can help retailers avoid overstock situations and achieve maximum profit. For further investigation, the manufacturer considered variable production rates to meet unpredictable demand. In this case, the system cost indirectly increased, which can be minimized by introducing investments for setup expenditure reduction and ordering policy for the manufacturer and retailer. The proposed model was validated using a distribution-free approach for random demand, which can be further analyzed by considering a particular type of random demand distribution function (Ullah et al. ^[59]). In this study, the remanufacturing strategy for LED bulbs was not considered; however, business industries can gain more profit by considering this strategy. Thus, this work can be extended by considering the remanufacturing strategy for energy-efficient LEDs (Rahman et al.^[60]). Next, the current two-echelon SCM involving a single manufacturer and retailer can be converted to a single manufacturer multi-retailer SCM (Hota et al. ^[61]). Furthermore, the proposed work can be extended by considering partial outsourcing to avoid the delay-in-delivery of products to the customers (Bachar et al. ^[62]). Exploring the Stackelberg game strategy to solve the model would be an interesting research aspect (Zhang et al. ^[63]). The proposed study can be developed by considering the idea of a circular economy to nullify waste and reduce ${\rm CO_{2}}$ emissions (Sarkar et al. ^[40]). Moreover, using an autonomation inspection policy to ensure error-free products during production and utilization of renewable resources for EC reduction (Sarkar and Bhuniya ^[55]) can be an exciting future extension of this study.

Conflict of interest

All authors declare no conflicts of interest in this study.

Appendix

A.  

Abbreviations

The following abbreviations are used in this manuscript:

B.  

$E (q-x)^+ \leq \frac{1}{2} \big[\sqrt{\varphi^2+ (q-l)^2}- (l-q)\big]$,

$E (x-q)^+ \leq \frac{1}{2} \big[\sqrt{\varphi^2+ (q-l)^2}- (q-l)\big]$,

$G_1 (P) = - \left\lbrace C_1 I_{gm}+ C_2 I_{gr}+ b (I_{cm}- I_{gm})^2+ a (I_{cr}- I_{gr})^2+ B^P_{rm}+L_{i}/P +\alpha_{i} P^ \rho \right\rbrace$ $+\frac{C_{hmn}+ C_{hrb}- p- s_1- s_2}{2}$,

$G_2 (m) = \frac{p+ s_1+ s_2 + C_{hmn}+ C_{hrb}}{2 \sqrt{\varphi^2+ (B e^{sm}-l)^2}}$

C.  

By differentiating Equation (4.22) with respect to the decision variables, $m$, $P$, and $q_u$, one can acquire:

D.  

Partial derivatives of the second order

The second-order partial derivatives of the profit function are given below:

Where, $G_3 (m, P) = B s^2 e^{sm} \left\lbrace G_1 (P) - G_2 (m)(B e^{sm}-1) \right\rbrace - G_2 (m) \left[ \frac{\left(B \varphi s e^{sm}\right)^2}{\varphi^2+ (B e^{sm}-l)^2}\right]$

$G_4 (m, P) = B e^{sm} \left[\frac{2 L_i}{P^3} + \alpha_i \rho \left(\rho - 1\right) P^{\rho-2}\right]$

$G_5 (q_u) = \frac{\alpha_3 \theta_1 \left(\theta_1 - 1\right)}{2} q_u ^{\theta_1 - 2}$

$G_6 (m, P) = B s e^{sm} \left\lbrace -\frac{L_i}{P^2} + \alpha_i \rho P^{\rho-1} \right\rbrace$

Different principal minors

At the optimum points, the Hessian matrix can be given by:

E.  

The first order principal minor is

F.  

The second order principal minor is

G.  

The third order principal minor is