1.
Introduction
Let B be a Banach space and A a nonempty closed convex subset of B. Let F:A→A be a mapping. A member m∗∈A is called a fixed points of F if Fm∗=m∗. We denote the set of all fixed point of F by F(F).
In [6], Berinde introduced a new class of mappings statisfying
for all m,q∈A, γ∈(0,1) and L≥0.
The author established that the class of mappings satisfying (1.1) is larger than the class of mappings introduced and studied by Zamfirescu in [41].
In [15], Imoru and Olantiwo gave a definition of a mapping considered to be generalization of the classes of mappings considered by Berinde [6], Osilike et al. [33] and some other existing contraction-type mappings as follows:
Definition 1.1. [15] A mapping F:A→A is called contractive-like if there exists a constant γ∈[0,1) and a strictly increasing continuous function ψ:[0,∞)→[0,∞) with ψ(0)=0 such that
for all m,q∈A.
Remark 1.1. If ψ(m)=Lm, then (1.2) reduces to (1.1).
Problems in so many fields of mathematics and other subjects in sciences can be transformed into an equation for a suitable operator. Furthermore, the existence of a solution to this equation is tantamount to the existence of a fixed point of the suitable operator. Basically, fixed point theory is a nice mixture of functional analysis, topology and geometry. Translating the real-life or theoretical problem into the fixed point problem is a good approach to find the corresponding solution. In general, fixed point theory plays a vital role in almost all areas of applied sciences and engineering such as: economics, game theory, theoretical computer science, biology, chemistry, physics and many more, see e.g. [8,19,20,24,25,26,27,28,29,30,31].
Proving the existence of a fixed point is an important step in finding a solution of a given problem, but it is also necessary to find the solution of a given problem when it exists. One valuable way of finding the desired fixed point is to utilize iterative method. For this reason, so many iterative methods for approximating the fixed points of different classes of operators have been introduced and studied by so many authors for the past two decades. Some widely used iterative methods in the literature are: Mann [21], Ishikawa [16], Noor [23], S [2], Abbas and Nazir [1], Tharkur [36] and many more.
Throughout this paper, the set of all natural numbers is denoted by N and the set of real numbers is donted by R. For the sequences {ϑn},{ϖn} and {ϱn} in [0, 1], the following iterative methods are known as Noor, S and M, respectively:
Very recently, Akutsah et al. [4] introduced the following three steps iterative method:
where {ϑn} and {ϖn} are sequences in [0, 1]. The authors analytically and numerically showed that the iterative method (1.6) converges faster than those of Ullah and Arshad [39], Karakaya et al. [18] and Thakur et al. [37], respectively for contractive-like mappings.
The preference of an iterative method over another is based on some crucial criteria such as fastness, stability and dependence. Data dependency of fixed points iterative methods has become an area that has attracted many researchers for several decades now. There exists several recent results on data dependency of fixed point, see e.g. [3,5,10,11,14,22,25,32].
Due to the importance of data dependency in fixed point theory, Akutsah et al. [4] raised the following question:
Open Question: Is it possible to obtain the data dependence result of the iterative method (1.6) for contractive-like mappings?
On other hand, a fixed point iterative method is said to be numerically stable if small modifications in the initial data involved in a computation process will produce a small impact on the computed value of the fixed point. The concept of stability was first considered by Ostrowski [34] for Banach contraction mappings. In 1988, Harder and Hicks [12,13] illustrated the importance of studying the stability of various iterative methods.
Definition 1.2. [12,13] Let {tn} be any sequence in A. Then, an iterative method tn+1=f(F,tn), which converges to fixed point m∗, is said to be F-stable or stable with respect to F, if for εn=‖tn+1−f(F,tn)‖, ∀n∈N, we have
In the last few years, many authors have studied the stability of several iterative methods for different classes of operators (see e.g. [11,17,22,25] and the references in them). Very recently, Akutsah et al. [4] established the following convergence and stability results for contractive-like mapping in Banach spaces.
Theorem 1.1. [4] Let A be a nonempty closed convex subset of a uniformly convex Banach space B. Let F be a mapping satisfying (1.2). Let {mn} be the iterative method defined in (1.6) with sequences {ϑn}, {ϖn}∈[0,1] such that ∞∑n=0ϖn=∞. Then, {mn} converges strongly to a unique fixed point of F.
Theorem 1.2. [4] Let A be a nonempty closed convex subset of a uniformly convex Banach space B. Let F be a mapping satisfying (1.2). Let {mn} be the iterative method defined by (1.6) with sequences {ϑn} and {ϖn} in [0, 1] such that ∞∑n=0ϖn=∞. Then, {mn} is F-stable.
In 2007, Berinde [8] showed throughout an example that taking an arbitrary sequence {tn} in Definition 1.2 led to an inconsistency. For this reason, Berinde [8] redefined the Definition 1.2 and gave a weaker, but more natural notion of stability known as weak stability. According the author, an approximate sequence of {mn} instead of arbitrary sequence {tn} in Definition 1.2 should be taken.
In 2012, Timi [38] introduced a wider concept of stability known as weak w2-stability by adopting equivalent sequences instead of arbitrary sequences in Definition 1.2.
Definition 1.3. [38] Let {mn} be an iterative sequence given by mn+1=f(F,mn). Assume that {mn} converges to an m∗∈F(F). Set
If for any equivalent sequence {tn}⊂A of {mn},
then the iterative sequence {mn} is said to be weak w2-stable with respect to F.
Motivated by the above results, we prove the strong convergence theorem of the iterative method (1.6) for contractive-like mappings without the necessity of the assumption: ∑∞n=0ϖn=∞ as considered in [4]. Also, we demonstrate the numerical convergence of (1.6) using a nontrivial example in higher dimensional space. Further, we prove analytically that the iterative method (1.6) is w2-stable and the analytical proof is supported with some illustrative examples. Also, we give an affirmative answer to the open question above which was raised in [4] by showing that the iterative method (1.6) is data dependent for contractive-like mappings. Furthermore, by applying our main results, we establish the existence, uniqueness and approximation results for the solutions of a nonlinear Volterra integral equation with delay. We also provide an example which supports the application of our results.
This paper is organized as follows: In Section 2, we list some definitions and lemmmas which will be used for further proof. In Section 3, we establish the convergence result of the iterative method (1.6) for contractive-like mappings. A supporting example is also provided. In Section 4, we show that the iterative algorithm (1.6) is weak w2-stable with respect to contractive-like mappings. The analytic result is supported with a numerical example. In Section 5, we prove the data dependence result of the iterative algorithm (1.6). In Section 6, we apply our main results to solve a nonlinear Volterra integral equation with delay and Section 7 gives the conclusion of our artilce.
2.
Preliminaries
In this section, we give some definitions and lemmas that will be useful in proving our main results.
Definition 2.1. [8] Let {mn} and {tn} be sequences in A. We say that {tn} is an approximate sequence of {mn}, if for any r∈N, there exists ε(r) such that
Definition 2.2. [7] Let F, ˜F:A→A be two operators. We say that ˜F is an approximate operator for F if for some ε>0, we have
Definition 2.3. [9] Let {mn} and {tn} be sequences in A. We say that these sequences are equivalent if
Lemma 2.1. [40] Let {θn} and {λn} be nonnegative real sequences satisfying the following inequalities:
where σn∈(0,1) for all n∈N, ∞∑n=0σn=∞ and limn→∞λnσn=0, then limn→∞θn=0.
Lemma 2.2. [35] Let {θn} be a nonnegative real sequence such that for all n≥n0∈N, the following condition holds:
where σn∈(0,1) for all n∈N, ∞∑n=0σn=∞ and λn≥0 for all n∈N, then
3.
Convergence result
In this section, we will prove a strong convergence result of the iterative method (1.6) for contractive-like mapping by weakening some conditions imposed on the control parameters by Akutsah et al. [4]. We also provide an example in three dimensional space to compare the convergence of various iterative methods.
Theorem 3.1. Let F be a mapping satisfying (1.2) defined on a nonempty closed convex subset A of a Banach space B with F(F)≠∅. Let {mn} be the iterative sequence defined by (1.6), then {mn} converges strongly to the unique fixed point of F.
Proof. From (1.6), for any m∗∈F(F), we have
Since {ϑn}, {ϖn}∈[0,1] and γ∈[0,1), then it follows that (1−(1−γ)ϑn)<1 and (1−(1−γ)ϖn)<1. Hence, (3.3) yields
Taking limit on both sides of the above inequality (3.4), we get limn→∞‖mn−m∗‖=0. Indeed, γ∈[0,1) and so limn→∞γ2n=0.
Remark 3.1. Clearly, the condition ∞∑n=0ϖn=∞ on the sequence {ϖn}∈(0,1) in Theorem 1.1 is superfluous.
Now we give the following example to validate the analytical proof in Theorem 6.1 and also carry out a numerical experiment to test the efficiency of the iterative method (1.6).
Example 3.1. Let A=[0,8]×[0,8]×[0,8] be the subset of a Banach space B=R3 with the texicap norm. Let F:A→A be defined by
Clearly, the only fixed point of F is (0,0,0). We will now show that F is a contraction-like mapping. To see this, we define a function ψ:R+→R+ by ψ(m)=m12. Clearly, ψ is a strictly increasing and continuous function satisfying ψ(0)=0. We show that
for all p,q∈A and γ∈[0,1). It will be useful to note the following. If m=(m1,m2,m3)∈[0,4)×[0,4)×[0,4), then
and
Similarly, if m=(m1,m2,m3)∈[4,8]×[4,8]×[4,8], we have
and
Next, we consider the following cases:
Case Ⅰ: If m=(m1,m2,m3),q=(q1,q2,q3)∈[0,4)×[0,4)×[0,4), then using (3.6), we have
Case Ⅱ: If m=(m1,m2,m3),q=(q1,q2,q3)∈[4,8]×[4,8]×[4,8], then using (3.7), we get
Case Ⅲ: If m=(m1,m2,m3)∈[0,4)×[0,4)×[0,4) and q=(q1,q2,q3)∈[4,8]×[4,8]×[4,8], then using (3.6), we have
Case Ⅳ: If m=(m1,m2,m3)∈[4,8]×[4,8]×[4,8] and q=(q1,q2,q3)∈[0,4)×[0,4)×[0,4), then using (3.6), we get
So, (3.5) is fulfilled with γ=17. Thus, F is a contractive-like mapping.
It is worthy mentioning that the above example is more interesting and not as simple as that of Akutsah et al. [4].
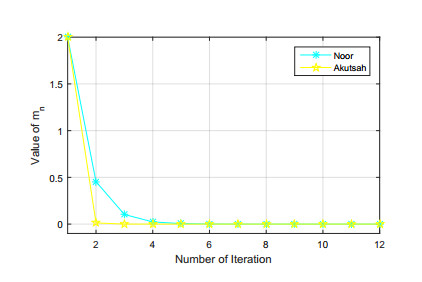
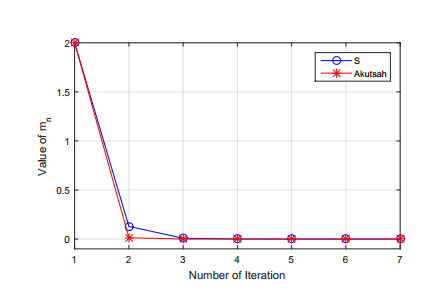
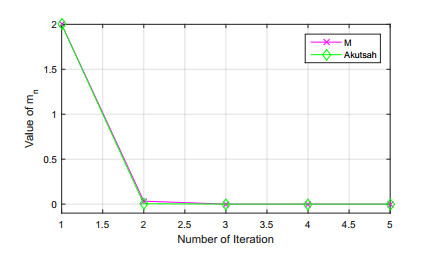
Using MATLAB R2015a, we obtain the following Tables 1–3 and Figures 1–3. Clearly, for control sequences ϖn=ϑn=ϱn=0.8 and starting value m0=(2,2.5,3.5), the iterative method (1.6) converges faster than a number of iterative methods. We also notice that M, Thakur and Karakaya iterative methods converge almost at the same rate.
4.
Stability result
In this section, we prove a stability result and provide some numerical examples to support our analytical proof.
Theorem 4.1. Let F be a mapping satisfying (1.2) defined on a nonempty closed convex subset A of a Banach space B with F(F)≠0. Let {mn} be the iterative sequence defined by (1.6), then {mn} is weak w2-stable with respect to F.
Proof. Let {tn}∈A be an equivalent sequence of {mn}. Define a sequence {ϵn} in R+ by
where {ϑn} and {ϖn} are sequences in [0, 1]. Let limn→∞ϵn=0, then from (1.2), (1.6) and (4.1), we have
Using (4.2)–(4.4), we have
Since {tn}∈A and its equivalence to {mn} yields limn→∞‖mn−tn‖=0. We have shown in Theorem 3.1 that ‖mn−m∗‖=0, consequently limn→∞‖mn+1−m∗‖=0. This implies that
Following similar argument as above, we have that
Since limn→∞‖mn−Fmn‖=ψ(limn→∞‖mn−Fmn‖)=0. It follows that
Also,
Therefore, from (4.8), we have
Thus, taking the limit on both sides of (4.5), we get
Hence, {mn} is weak w2-stable with respect to F.
Now, we furnish the following examples in support of the above claim.
Example 4.1. Let B=R with the usual norm and A=[0,1] be a subset of B. Define a mapping F:A→A by
Clearly, zero is the fixed point of F. Now we show that F is a weak contractive-like mapping satisfying (1.2). For this, let γ=12 and given as increasing function ψ:[0,∞)→[0,∞) with ψ(0)=0, then we obtain
The iterative method (1.6) corresponding to the operator F in (4.11) is defined as follows:
where {ϑn} and {ϖn} are sequences in [0, 1].
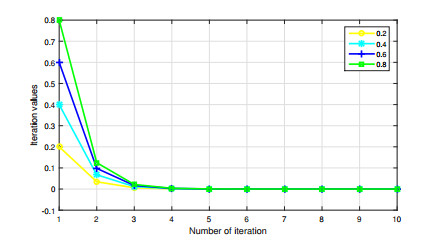
Let ϑn=ϖn=1n+2. Using MATLAB R2015a, the following Table 4 and Figure 4 are obtained. They show that the iterative method {mn} in (4.12) converges to m∗=0 for different choices of starting point m1∈[0,1].
From the above table and graph, it is evident that limn→∞mn=0=m∗∈F(F). On the other hand, we obtain limn→∞‖mn‖=‖limn→∞mn‖=0. If we take the sequence {tn} as tn=1n+3 for all n∈N, then we have
which yields limn→∞‖mn−tn‖=0. This implies that the sequences {mn} and {tn} are equivalent.
Now, we show that (1.6) is weak w2-stable with respect to F.
Clearly, limn→∞ϵn=0. Therefore, the iterative method {mn} is weak w2-stable with respect to F.
Example 4.2. Let B=R with the usual norm and A=[0,1] be a subset of B. Define a mapping F:A→A by
Apparently, zero is the fixed point of F and F satisfies (1.2) with γ=15.
Now, we show that the iterative sequence {mn}∞n=0 in (1.6) converges to p=0∈F(F) for different choices of real sequences in {ϖn},{ϑn} in [0, 1]. Let {m(1)n}∞n=0,{m(2)n}∞n=0,{m(3)n}∞n=0 be the iterative method (1.6) with control parameters (ϖn=ϑn=1n+1), (ϖn=ϑn=12n+1) and (ϖn=1n+2,ϑn=n+12n+1) for all n∈N, respectively.
For arbitrary x1∈[0,1], it follows that
Also,
Finally,
From (4.14)–(4.16), set
Then clearly, σ(i)n∈(0,1) for each i∈{1,2,3} and ∞∑nσ(i)n=∞ for each i∈{1,2,3}. Thus, by Lemma 2.1, we have that limn→∞m(i)n=p=0∈F(F) for each i∈{1,2,3}.
On the other hand, we have limn→∞‖m(i)‖=‖limn→∞m(i)‖=0 for each i∈{1,2,3}. Taking the sequence {tn}∞n=0 to be tn=1n+4 for all n∈N, then we get
which shows that limn→∞‖m(i)−tn‖=0 for each i∈{1,2,3}, in other words, each of {m(i)n}∞n=0, i∈{1,2,3} and {tn}∞n=0={1n+4}∞n=0 are equivalent sequences.
Let ϵ(1)n, ϵ(2)n and ϵ(3)n be the corresponding sequences to the iterative algorithms {m(1)n}∞n=0, {m(2)n}∞n=0 and {m(3)n}∞n=0, respectively. Then we have
Obviously, limn→∞ϵ(i)n=0 for each i∈{1,2,3}. Hence, all the iterative sequences {m(i)n}∞n=0, i∈{1,2,3} are w2-stable with respect to F.
5.
Data dependence result
In this section, the data dependence result of (1.6) for contractive-like mapping is obtained, hence, giving an affirmative answer to the above open question raised by Akutsah et al. [4].
Theorem 5.1. Let ˜F be an approximate operator of a mapping F satisfying (1.2). Let {mn} be an iterative method generated by (1.6) for F and define an iterative method as follows:
where {ϑn} and {ϖn} are sequences in [0,1] satisfying the following conditions:
(i) 12≤ϖn,∀n∈N,
(ii) ∞∑n=0ϖn=∞.
If Fm∗=m∗ and ˜F~m∗=~m∗ such that limn→∞˜mn=~m∗, we have
where ϵ>0 is a fixed number.
Proof. Using (1.2), (1.6) and (5.1), we obtain
Using (5.3) and (5.4),
Putting (5.5) into (5.6), we obtain
Since ϖn, ϑn ∈[0,1] and γ∈[0,1), it follows that
From (5.7) and (5.8), we have
By our assumption (ⅰ), we have
This yields
Set
From Theorem 3.1, we know that limn→∞mm=m∗ and since Fm∗=m∗, then from (4.7), (4.9) and Lemma 2.2, we obtain
Since by Theorem 3.1, we have that limn→∞mn=m∗ and using the hypothesis limn→∞˜mn=~m∗, it follows from (5.11) that
6.
Application
In this section, we discuss an application to nonlinear Volterra integral equation with delay. Consider the integral equation
with initial function
where ϕ∈C[a−τ,a],R), a,b∈R and τ>0.
Let C[a,b] denote the set all of continuous functions defined on [a,b] endowed with infinity norm ‖m−p‖∞=maxa≤t≤b‖m(t)−p(t)‖. It is well known that (C[a,b],R),‖⋅‖∞) is a Banach space.
Theorem 6.1. Let K be a nonempty closed convex subset of a Banach space M=(C([a,b],R),‖⋅‖∞). Let {mn} be the iterative method (1.6) with ϖn,ϑn∈[0,1]. Let F:K→K be the operator defined by
Suppose the following assumptions hold:
(a) g:I→R is continuous;
(b) f:I×I×R×R→R is continuous in the sense that there exists a constant Lf>0 such that
for all t,s∈I, ui,vi∈R(i=1,2);
(d) 2λLf(b−a)<1.
Then, the problem (6.1) with (6.2) has a unique solution, say m∗∈C[a,b]. Moreover, if F is a mapping satisfying (1.2). Then, {mn} converges strongly to m∗.
Proof. Now, using the contraction principle, we show that F has a fixed point. Note that
Next, for any t∈I, we have
therefore,
From condition (d), the operator F is a contraction and using the contraction principle we deduce that the operator F has a unique fixed point, F(F)={m∗}, i.e. the problem (6.1) with (6.2) has a unique solution m∗∈C[a,b].
Next, we show that {mn} converges strongly to m∗. For m,p∈A, we have
therefore,
From (6.4), it is clear that F is a mapping satisfying (1.1). Set γ=2λLf(b−a), and by assumption (d), we have γ<1. Thus, the operator F is a contractive-like mapping satisfying (1.2) on K with L=1 since for ψ(m)=Lm, (1.2) reduces to (1.1). Taking A=K and B=M, then all the assumptions of Theorem 4.2 are satisfied. Therefore, the sequence {mn} defined by the iterative algorithm (1.6) converges strongly to the unique solution of the problem (6.1) with (6.2).
7.
Conclusions
In this study, we have proved the strong convergence results of the iterative scheme (1.6) for fixed points of contractive-like mapping under mild conditions. We have presented some interesting and nontrivial examples in three dimensional space to compare the efficiency of the iterative method (1.6) with some existing iterative methods. Also, we have shown analytically and numerically that the iterative method (1.6) is w2-stable for different choices of parameters and initial guesses. Again, our data dependence result gives an affirmative answer to the open question raised by Akutsah et al [4]. As an application of our results, we have established the existence, uniqueness and approximation results for the solutions of a nonlinear Volterra integral equation with delay (6.1) with (6.2).
Acknowledgements
The work was supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project (No. PNURSP2022R14). The authors A. Khan and T. Abdeljawad would like to thank Prince Sultan University for paying the APC and for the support through the TAS research lab.
Conflict of interest
The authors declare no conflicts of interest.









 DownLoad:
DownLoad: