Modeling and analysis of Cystic Echinococcosis epidemic model with health education

1.   Introduction

Chaotic systems, which are a form of dynamic system, are extremely sensitive to initial conditions. Despite their natural predictability, chaotic systems are distinguished by their unpredictability and the perception of randomness. However, they have a broader range of applications in a variety of natural and artificial systems, including pattern recognition, biological systems, and secure communication. It should be emphasized that synchronization is a critical issue of study in all these systems. In the last two decades, a large number of works on the synchronization of chaotic systems have been published (for example, see ^{[1,2,3,4,5,6]}). The majority of these works describe chaotic systems in the Lur'e form, which includes both a linear and a nonlinear term that meets the sector-bound constraint. Such systems are frequently referred to as chaotic Lur'e systems. It should be pointed out that the master-slave paradigm is commonly used to synchronize chaotic Lur'e systems, with the goal of designing an adequate controller so that the slave system's output follows the master system's output ^{[7,8,9,10,11,12]}. Despite substantial research on the subject, strengthening the synchronization criterion by increasing the sampling period or time delay bound in the control design remains a point of contention, indicating that more research is needed.

To address the synchronization issues of chaotic Lur'e systems, numerous control techniques have been presented in the literature. One of the most difficult aspects of designing a synchronization controller is delivering signals over input channels with limited capacity, which is especially prevalent in digital computer control systems that apply finite-precision arithmetic. To overcome this issue, signal quantization has been implemented ^[13,14]; nevertheless, this cannot be directly addressed by classical control theory, as the signal transmission is accomplished with infinite precision. So research communities utilized the sector-bound approach ^[15,16], which is now widely employed to attenuate quantization effects by interpreting quantization error as nonlinearity or uncertainty and bounding it. Following these pioneering research, some significant challenges on synchronization of chaotic Lur'e systems with quantized feedback control techniques have been reported ^{[17,18,19,20,21]}. Interestingly, in ^[19], a quantized sampled-data controller design for delayed chaotic Lur'e systems has been proposed by presenting the extended Wirtinger-inequality-based Lyapunov approach, which results in a longer sampling period than some previous ones; and in ^[20], some improved synchronization conditions for delayed chaotic Lur'e systems with a quantized sampled-data controller have been obtained by developing a novel Lyapunov functional based on the auxiliary function-based integral inequality. As a result, considering the influence of quantization in controller design for achieving synchronization in chaotic Lur'e systems is practical and broadens the spectrum of applications.

One of the most important research areas in the field of systems and control theory in recent years has been the development of improved synchronization criteria for chaotic Lur'e systems. In order to achieve this goal, researchers developed and used a number of methodologies in addition to the Lyapunov stability theory. As a result, over the last decade, literature has seen an explosion of intriguing works on this subject (for example, see ^{[22,23,24,25,26,27]}). In ^[23], some improved sampled-data synchronization criteria for two identical chaotic Lur'e systems subject to aperiodic samplings have been derived by proposing an improved fragmentation strategy and employing the looped-functional technique. In ^[25], improved synchronization criteria for uncertain chaotic Lur'e systems with time-varying delay have been obtained by developing an appropriate Lyapunov-Krasovskii functional with triple and quadruple integral terms. By introducing the integral-term-related free-weighting-matrices approach and using the Bessel-Legendre inequality, improved and less conservative synchronization conditions for chaotic Lur'e systems have been provided in ^[27]. On the other hand, the delay-product-type Lyapunov functional technique, which is one of the important methods for improving the stability of time-varying delayed systems with delay rate information ^[28,29], has been widely used in recent years to support the goal of solving problems in a variety of time-varying delayed systems. A few significant works on this subject can be found in ^{[30,31,32,33]}. As a result, researchers have expressed an interest in applying this technique to improve synchronization criterion for chaotic Lur'e systems ^[34,35,36]. However, there is potential for future exploration in order to reduce conservatism in these works, which is the objective for conducting this research.

Motivated by the preceding descriptions, the goal of this research is to provide improved synchronization conditions for chaotic Lur'e systems with a quantized time-varying delay feedback controller. To summarize, the contributions of this paper to the achievement of this goal are as follows:

● A feedback controller that takes into account time-varying delay and quantization is designed to achieve synchronization in chaotic Lur'e systems, guaranteeing that the control system responds predictably and dependably.

● To reduce the conservatism of synchronization criteria for the considered system, an augmented Lyapunov-Krasovskii functional with quadratic, integral, and delay-product terms is employed in conjunction with a generalized free-weighting-matrix technique, an augmented zero equality, and a convex combination strategy.

● Chua's circuit model is utilized to demonstrate the relationship between quantization density and time-varying delay, as well as the superiority of the established synchronization criteria, implying that the results of this paper provide a larger delay bound than those reported previously, such as in ^{[26,27,34,36]}.

This paper is briefly described as follows: The description of chaotic Lur'e systems and the design of quantized time-varying delay feedback controller is covered in Section 2. The asymptotic synchronization conditions for the addressed system are presented in Section 3. The validation of theoretical findings and the overall conclusion of this work are provided in Sections 4 and 5, respectively. Table 1 lists the notations used in this work together with their meanings for the sake of brevity.

2.   Problem formulation and preliminaries

This paper investigates a class of chaotic Lur'e systems, the dynamics of which are defined in the master-slave paradigm as follows:

where $\{x(t), \hat{x}(t)\}\in \mathbb{R}^{n}$ denote the state vectors of the master and slave systems; $f(\cdot): \mathbb{R}^{m}\rightarrow \mathbb{R}^{m}$ is a diagonal nonlinearity vector in the feedback path of subsystems; $u(t)\in \mathbb{R}^{n}$ is the control input vector susceptible to the quantization effect; $\{y(t), \hat{y}(t)\}\in \mathbb{R}^{p}$ are the output vectors of the master and slave systems; $A\in \mathbb{R}^{n\times n}$, $B\in \mathbb{R}^{n\times m}$, $G\in \mathbb{R}^{m\times n}$, and $C\in \mathbb{R}^{p\times n}$ are given matrices.

In this paper, it is assumed that $G = \mathtt{col}\{g_{1}^T, g_{2}^T, \ldots, g_{m}^T\}$, where $g_{l}\in \mathbb{R}^{n}$ $(l = 1, 2, \ldots, m)$ and $f(\cdot)$ meets the following sector-bound condition:

where $k_{l}^{-}, k_{l}^{+}\in \mathbb{R}$.

Remark 1. The arbitrary scalars $k_{l}^{-}$ and $k_{l}^{+}$ $(l = 1, 2, \ldots, m)$ in the nonlinear bound condition (2.2) can have any positive, negative, or zero value. The nonlinear bound conditions in ^{[4,8,9,10,12,17,18,23,24]} are achieved if the values of $k_{l}^{-}$ $(l = 1, 2, \ldots, m)$ are considered to be zero. As a result, the condition (2.2) is clearly more generic than certain existing ones, which is preferable for minimizing the conservatism of the proposed results.

We now provide a time-varying delay feedback controller design that guarantees the asymptotic synchronization of the system under consideration (2.1). It should be mentioned that inaccurate signal transmission is an unavoidable technological challenge in information interchange, owing to practical constraints on the control channel's transmission capacity. As a result, signal quantization is important to consider while designing a controller. The design goal of a quantized controller is to simplify the control system by limiting the controller output to a finite set of discrete values. While this technique has benefits such as simplicity and robustness, it does have precision limitations that must be carefully examined during the design phase. In light of this, the following controller, which considers the influence of quantization, is utilized for (2.1):

where $\mathtt{Q}(\cdot) = [\mathtt{Q}_{1}(\cdot), \mathtt{Q}_{2}(\cdot), \ldots, \mathtt{Q}_{p}(\cdot)]^T$ is the logarithmic quantizer; $K\in \mathbb{R}^{n\times p}$ is the control gain to be determined and $h(t)$ is a time-varying delay that is assumed to satisfy $0\leq h(t)\leq h_{M}$ and $\mu_{1}\leq \dot{h}(t)\leq \mu_{2} < 1$, where $h_{M}$ and $\mu_{a}$ $(a = 1, 2)$ are given scalars.

The logarithmic quantizer $\mathtt{Q}(\cdot)$ is assumed to be symmetric with $\mathtt{Q}_{j}(\varpi) = -\mathtt{Q}_{j}(-\varpi)$ $(j = 1, 2, \ldots, p)$ throughout this paper, and the quantization levels are explored for each logarithmic quantizer as: ${\bf Q}^{j} = \{\pm\lambda_{q}^{j} : \lambda_{q}^{j} = (\sigma^{j})^{q}\lambda_{0}^{j}, \ q = 0, \pm 1, \pm 2, \ldots\}\cup \{0\}$, where $\lambda_{0}^{j} > 0$ and $\sigma^{j}\in (0, 1)$ $(j = 1, 2, \ldots, p)$ are the scaling parameter and quantization density of the $j$-th quantizer, respectively. The corresponding $j$-th quantizer $\mathtt{Q}_{j}(\varpi)$ is defined as follows:

where $\rho_{j} = \frac{1-\sigma^{j}}{1+\sigma^{j}}\in (0, 1)$. As a result, the following conclusion is straightforward:

Using the sector bound approach in ^[15] and the above constraints, the $j$-th quantizer is represented as $\mathtt{Q}_{j}(\varpi) = (1+\Delta_{j})\varpi$, where $\Delta_{j}\in [-\rho_{j}, \rho_{j}]$. Furthermore, by defining $\tilde{\Delta} = \mathtt{diag}\{\Delta_{1}, \Delta_{2}, \ldots, \Delta_{p}\}$, the controller (2.3) is rewritten as

By considering the synchronization error vector as $e(t) = x(t)-\hat{x}(t)$, the following error dynamics can be obtained:

where $\varphi(Ge(t)) = f(Gx(t))-f(G\hat{x}(t))$.

Let $g_{l}^T$ represent the $l$-th row vector of the matrix $G$. The following is then derived from (2.2):

To accomplish the goal of this study, the following section uses the Lyapunov-Krasovskii stability theory and the lemma given below.

Lemma 1. ^[37] For any matrices $\{X, Y\}$ of appropriate dimensions and $Q\in \mathbb{S}_{+}^{n}$, the following inequality holds for all continuously differentiable function $\{x(t)\in \mathbb{R}^{n}: t\in [a_{1}, a_{2}]\}$:

where $\eta_{0}$ is any vector, $\theta_{1} = {\int}_{a_{1}}^{a_{2}}x(v)\mathrm{d}v$ and $\theta_{2} = -\theta_{1}+\frac{2}{a_{2}-a_{1}} {\int}_{a_{1}}^{a_{2}} {\int}_{w}^{a_{2}}x(v)\mathrm{d}v\mathrm{d}w$.

3.   Main results

The required synchronization criteria are developed and stated as linear matrix inequalities in this section. Consider the augmented vector and notations listed below for ease of representation:

Furthermore, the desired synchronization analysis is divided into two portions based on the proposed control law (2.4): (ⅰ) Without quantization effect and (ⅱ) with quantization effect. To begin, consider the following error system derived from (2.5) by ignoring the quantization impact:

Let us establish the asymptotic stability criterion for (3.1) in the following theorem, which assures the desired synchronization of (2.1) via the proposed controller (2.4) without the quantization influence.

Theorem 1. Given scalars $\gamma > 0$, $h_{M} > 0$, and $\mu_{1}\leq \mu_{2} < 1$, the error system (3.1) is asymptotically stable if there are matrices $P\in \mathbb{S}_{+}^{7n}$, $Q_{a}\in \mathbb{S}_{+}^{6n}$, $Q_{3}\in \mathbb{S}_{+}^{3n}$, $R_{a}\in \mathbb{S}_{+}^{4n}$, $H_{1} = \mathtt{diag}\{\alpha_{1}, \alpha_{2}, \ldots, \alpha_{m}\}\in \mathbb{D}_{+}^{m}$, $H_{2} = \mathtt{diag}\{\beta_{1}, \beta_{2}, \ldots, \beta_{m}\}\in \mathbb{D}_{+}^{m}$, $H_{3}\in \mathbb{D}_{+}^{m}$, $N_{a}\in \mathbb{S}^{2n}$, $\{X_{a}, Y_{a}\}\in \mathbb{R}^{(12n+m)\times 3n}$, $L\in \mathbb{R}^{n\times n}$, $U\in \mathbb{R}^{n\times m}$, and $W\in \mathbb{R}^{(12n+m)\times 2n}$ $(a = 1, 2)$ such that the requirements listed below hold for $\dot{h}(t)\in \{\mu_{1}, \mu_{2}\}$:

where

Based on the foregoing results, the proposed control gain is calculated using the equation $K = L^{-1}U$.

Proof. Select an augmented Lyapunov-Krasovskii functional candidate with delay-product terms for the error system (3.1), as indicated below:

where

with

Then, the results of $\dot{V}_{\tau}(e(t))$ $(\tau = 1, 2, 3, 4, 5)$ are presented below:

In addition, a zero equality is added to $\dot{V}_{3}(e(t))$, as shown below:

where $N_{a}\in \mathbb{S}^{2n}$ $(a = 1, 2)$. As a result, $\dot{V}_{3}(e(t))$ is written as follows:

The integral terms involving $Q_{N_a}$ $(a = 1, 2)$ in (3.11) are bounded using Lemma 1 as follows:

where $X_{a}$, $Y_{a}$, $\Theta_{a}(h(t))$ $(a = 1, 2)$, and $\eta_{0}$ are defined in the theorem statement.

Consider the following inequality, which is obtained from (2.6), for any $H_{3}\in \mathbb{D}_{+}^{m}$:

On the other hand, a zero equation based on (3.1) is taken into consideration as follows:

where $L\in \mathbb{R}^{n\times n}$, $U = LK$, and $\gamma > 0$ is a given scalar. Furthermore, a zero equality is considered using the elements of the augmented vector $\xi(t)$ as follows:

where $W\in \mathbb{R}^{(12n+m)\times 2n}$.

Using (3.4)–(3.16), the following bound is obtained:

where

Following that, $\bar{\Phi}(h(t), \dot{h}(t))$ can be expressed as matrices in (3.2) and (3.3) using the Schur complement and convex combination approach for $h(t)\in [0, h_{M}]$ and $\dot{h}(t)\in [\mu_{1}, \mu_{2}]$. Then, the system (3.1) can be guaranteed to be asymptotically stable as a result of the inequalities (3.2) and (3.3). □

The following theorem extends Theorem 1 by including the quantization influence in the proposed control law.

Theorem 2. Given scalars $\gamma > 0$, $h_{M} > 0$, and $\mu_{1}\leq \mu_{2} < 1$, the error system :(2.5): is asymptotically stable if there are matrices $P\in \mathbb{S}_{+}^{7n}$, $Q_{a}\in \mathbb{S}_{+}^{6n}$, $Q_{3}\in \mathbb{S}_{+}^{3n}$, $R_{a}\in \mathbb{S}_{+}^{4n}$, $H_{1} = \mathtt{diag}\{\alpha_{1}, \alpha_{2}, \ldots, \alpha_{m}\}\in \mathbb{D}_{+}^{m}$, $H_{2} = \mathtt{diag}\{\beta_{1}, \beta_{2}, \ldots, \beta_{m}\}\in \mathbb{D}_{+}^{m}$, $H_{3}\in \mathbb{D}_{+}^{m}$, $N_{a}\in \mathbb{S}^{2n}$, $\{X_{a}, Y_{a}\}\in \mathbb{R}^{(12n+m)\times 3n}$, $L\in \mathbb{R}^{n\times n}$, $U\in \mathbb{R}^{n\times m}$, $W\in \mathbb{R}^{(12n+m)\times 2n}$ $(a = 1, 2)$ and scalar $\varepsilon > 0$ such that the requirements listed below hold for $\dot{h}(t)\in \{\mu_{1}, \mu_{2}\}$:

where $\hat{\Phi}(h(t), \dot{h}(t)) = \Phi(h(t), \dot{h}(t))+\varepsilon\vartheta_{2}C^T\tilde{\Omega}C\vartheta_{2}^T$ with $\tilde{\Omega} = \mathtt{diag}\{\rho_{1}^{2}, \rho_{2}^{2}, \ldots, \rho_{p}^{2}\}$, and the definition of $\Phi(h(t), \dot{h}(t))$ is the same as in Theorem 1. Furthermore, the proposed control gain is calculated using the equation $K = L^{-1}U$.

Proof. The outcomes of this Theorem ((3.18) and (3.19)) are clearly an extended version of the results of Theorem 1. To complete the proof, consider the steps from (3.4)–(3.16) but use the following zero equation instead of (3.15):

Using the knowledge that $\pm2\psi_{1}^T\psi_{2}\leq \delta^{-1}\psi_{1}^T\psi_{1}+\delta\psi_{2}^T\psi_{2}$, where $\psi_{a}\in \mathbb{R}^{n}$ $(a = 1, 2)$ and $\delta > 0$, the following term has a bound as

where $\varepsilon > 0$ and $\tilde{\Omega}$ is defined in the theorem statement.

As a result, the new bound for $\dot{V}(e(t))$ is given by (3.20) and (3.21) as follows:

where $\bar{\Phi}(h(t), \dot{h}(t))$ is specified in (3.17). The matrices (3.18) and (3.19) are then obtained by applying the Schur complement and convex combination technique to (3.22), as in the prior theorem proof. □

Remark 2. This paper uses the delay-product-type Lyapunov-Krasovskii functional (3.4), which consists of several augmented vectors in the quadratic, integral, and delay-product terms, to establish the desired synchronization criteria for chaotic Lur'e systems (2.1). When compared to the works ^[34] and ^[36], the novelty of (3.4) can be stated as follows: The integral terms in this paper include augmented vectors like ${\int}_{s}^{t}\zeta(v)\mathrm{d}v$, ${\int}_{t-h(t)}^{s}\zeta(v)\mathrm{d}v$, ${\int}_{s}^{t-h(t)}\zeta(v)\mathrm{d}v$, ${\int}_{t-h_{M}}^{s}\zeta(v)\mathrm{d}v$, where $\zeta(v) = \mathtt{col}\{e(v), \dot{e}(v)\}$, whereas the integral terms in ^[34] and ^[36] contained vectors like ${\int}_{s}^{t}\dot{e}(v)\mathrm{d}v$, ${\int}_{t-h(t)}^{s}\dot{e}(v)\mathrm{d}v$, ${\int}_{s}^{t-h(t)}\dot{e}(v)\mathrm{d}v$, ${\int}_{t-h_{M}}^{s}\dot{e}(v)\mathrm{d}v$ and ${\int}_{s}^{t}e(v)\mathrm{d}v$, ${\int}_{t-h(t)}^{s}e(v)\mathrm{d}v$, ${\int}_{s}^{t-h(t)}e(v)\mathrm{d}v$, ${\int}_{t-h_{M}}^{s}e(v)\mathrm{d}v$, respectively. To summarize, certain cross-terms exist in the obtained findings as a result of the augmented vectors in the integral terms, which leads to a reduction in the conservatism of the proposed synchronization criteria.

Remark 3. It should be noted that Lemma 1 proposed in ^[37] is used in Theorems 1 and 2 to achieve the required synchronization criteria. Despite the fact that this lemma increases computing complexity, it is possible to lower it without sacrificing actual results by suitably modifying any vector $\eta_{0}$ based on the system parameter values chosen for the feasibility test. Given this, a suitable vector $\eta_{0}$, as opposed to $\eta_{0} = [\vartheta_{1}, \vartheta_{2}, \ldots, \vartheta_{13}]$ in the results of Theorems 1 and 2, is explored for the numerical example in the next section.

4.   A numerical example

The theoretical findings from the previous section are effectively validated in this section using a numerical example with simulation results.

Consider the well-known Chua's circuit model, the dynamics of which are shown below ^{[3,25,26,27,34,36,38]}:

with $\phi(x_{1}(t)) = m_{1}x_{1}(t)+0.5(m_{0}-m_{1})(|x_{1}(t)+1|-|x_{1}(t)-1|)$, where $\alpha = 9$, $\beta = 14.28$, $m_{0} = -1/7$, and $m_{1} = 2/7$. The preceding dynamics can be represented as (2.1) with the following parameters:

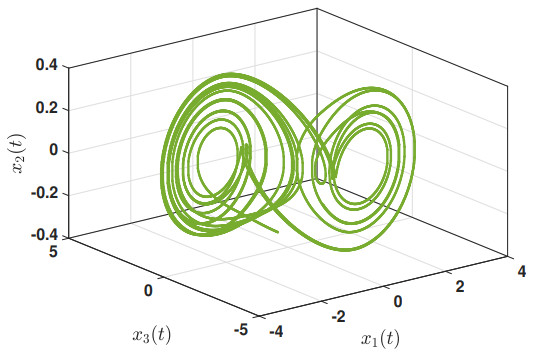
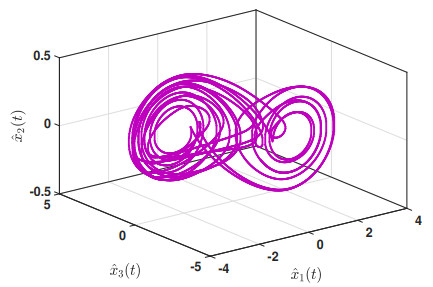
Based on these values and the initial condition $x(0) = [-0.2, -0.33, 0.2]^T$, Figure 1 depicts the responses of the master system, illustrating that the system states move chaotically. Let us look at the simulation results in two scenarios with respect to the proposed control law (2.4), which are as follows:

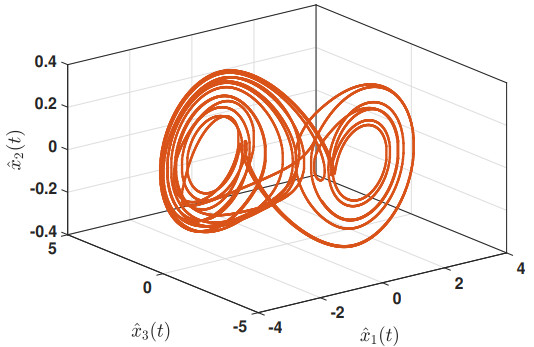
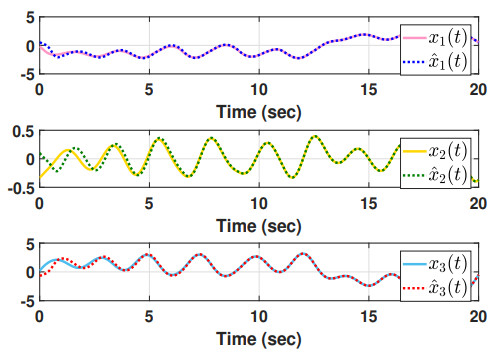
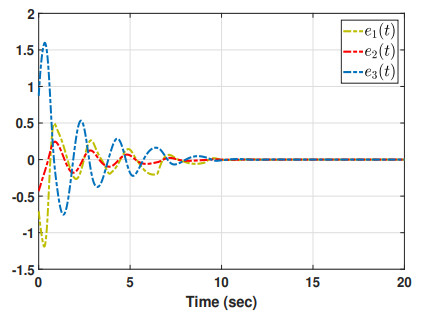
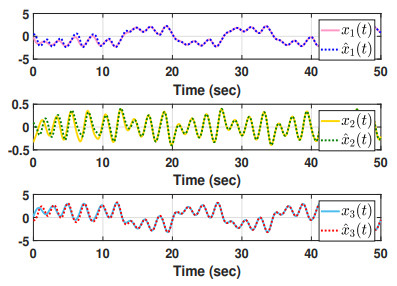
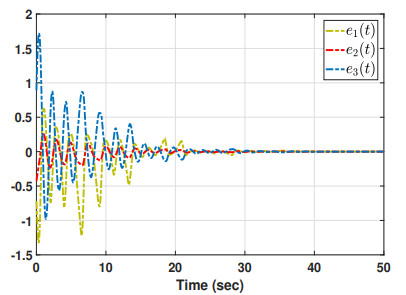
Case 1. (With quantization effect): Choose $\mu_{1} = -0.4$, $\mu_{2} = 0.4$, and $\gamma = 0.6$. Furthermore, consider $\eta_{0} = [\vartheta_{1}, \vartheta_{2}, \vartheta_{3}, \vartheta_{4}, \vartheta_{7}, \vartheta_{9}, \vartheta_{10}, \vartheta_{11}, \vartheta_{12}]$ rather than $\eta_{0} = [\vartheta_{1}, \vartheta_{2}, \ldots, \vartheta_{13}]$ because both scenarios produce the identical results, which are found using the trial and error method. Then, the maximum allowable upper bound (MAUB) in relation to different $\sigma^{1}$ is determined using the results of Theorem 2 and shown in Table 2 along with the corresponding gain matrix because the quantization density $\sigma^{1}$ has such a large influence on the time delay bound $h_{M}$. The results of this table demonstrate that the MAUB $h_{M}$ grows as the quantization density value increases. The following simulation results are shown with the initial condition $\hat{x}(0) = [0.5, 0.1, -0.66]^T$ and using the values $\sigma^{1} = 0.9$ and $h_{M} = 0.2929$. Figure 2 provides the chaotic behavior of the slave system under the proposed quantized control law (2.4). The state responses of the master and slave systems, and the synchronization error responses are depicted in Figures 3 and 4, respectively. These figures show that when the controller (2.4) is used, the required synchronization is achieved in a short period of time. As a result, because the states of the master and slave systems do not synchronize in the absence of a controller, the proposed control law is effective and useful for establishing synchronization of the addressed system (2.1).

Case 2. (Without quantization effect): Using the aforementioned system parameter values, the findings of Theorem 1 are resolved with $\gamma = 3.5$ and $\eta_{0}$ as indicated in the preceding case to obtain the MAUB $h_{M}$ and the corresponding control gain matrix. For comparison purposes, it is assumed that $\mu_{1} = \mu_{2} = 0$. Table 3 shows the results obtained in this paper as well as some recently published ones ^{[3,25,26,27,34,36,38]}, including the MAUB $h_{M}$, control gain matrix $K$, and number of decision variables (DVs) utilized. This table clearly shows that the results of this paper are significantly superior than those of previous works, demonstrating that the proposed method is less conservative. Although it increases computational complexity, the major goal of this paper is to lower the conservatism of the proposed method. In addition, simulation results are provided below based on the values in Table 3 and the initial condition in the prior case. The chaotic behavior of the slave system under the proposed control law (2.4) without the influence of quantization is depicted in Figure 5. Figures 6 and 7, respectively, demonstrate the state responses of the master and slave systems, as well as the synchronization error responses, indicating that the error system (3.1) is asymptotically stable. Based on these simulations, it is concluded that the system (2.1) achieves asymptotic synchronization under the controller (2.4) with no quantization impact.

Remark 4. In the preceding example, $\eta_{0} = [\vartheta_{1}, \vartheta_{2}, \vartheta_{3}, \vartheta_{4}, \vartheta_{7}, \vartheta_{9}, \vartheta_{10}, \vartheta_{11}, \vartheta_{12}]\in \mathbb{R}^{37\times 27}$ is used instead of $\eta_{0} = [\vartheta_{1}, \vartheta_{2}, \ldots, \vartheta_{13}]\in \mathbb{R}^{37\times 37}$ since ^[37] defines $\eta_{0}$ as any vector. Both of these vectors yield the same results, and the vector $\eta_{0}\in \mathbb{R}^{37\times 27}$ is determined by the trial and error approach. As a result, the dimensions of the matrices $X_{a}$ and $Y_{a}$ $(a = 1, 2)$ are chosen to be $\mathbb{R}^{27\times 9}$ rather than $\mathbb{R}^{37\times 9}$, which reduces the number of DVs from 2385 to 2025. It is concluded that any vector in Lemma 1 can be appropriately adjusted to lower the computational complexity of the proposed synchronization criteria.

5.   Conclusions

The quantized master-slave synchronization problem of chaotic Lur'e systems has been addressed in this paper. The goals here are to provide enhanced synchronization criteria and a quantized controller design process. These goals have been met by employing the delay-product-type Lyapunov-Krasovskii functional technique, as well as the generalized free-weighting-matrix technique and augmented zero equality. To be more specific, Theorems 1 and 2 have presented the asymptotic synchronization conditions for the considered system via the time-varying delay feedback controller without and with quantization influence, respectively. These synchronization conditions have been examined using Chua's circuit model parameters, and their usefulness and superiority have been proved through simulations and comparison. It should be noted that finite-time and fixed-time synchronization problems are currently a research hotspot due to their powerful anti-interference properties (for example, see ^[39,40,41]). As a result, it is worthwhile to examine finite-time or fixed-time synchronization for chaotic Lur'e systems, which will be explored further in future research.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence tools in the creation of this article.

Acknowledgments

This work was supported in part by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education under Grant NRF-2020R1A6A1A12047945 and in part by Innovative Human Resource Development for Local Intellectualization program through the Institute of Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (IITP-2024-2020-0-01462, 30%). This work was also supported by Chungbuk National University BK21 program (2023).

Conflict of interest

All authors declare no conflicts of interest in this paper.