On the cooling number of the generalized Petersen graphs

1.   Introduction

Burning number can be used to study the spread of contagion in a network, see ^[1,3,4]. In the past few years, burning number has been widely studied for some families of graphs, for example, circulant graphs ^[7], generalized Petersen graphs ^[19], caterpillars ^[9,14], grid and interval graphs ^[8], t-unicyclic graphs ^[22], hypercube ^[18], theta graphs ^[16], $Q$-graph ^[13], and spiders and path forests ^[6,15]. Mitsche, Prałat, and Roshanbin investigated the burning number of graph products in ^[18] and they also focused on the probabilistic aspects of the burning number in ^[17]. A graph $G$ is said to be $m$-burnable if the burning number of $G$ is at most $m$. Bonato and Lidbetter ^[5] and Das et al. ^[6] proved that every spider of order $m^2$ is $m$-burnable. A tight upper bound on the order of a spider to guarantee that it is $m$-burnable was then determined by Tan and Teh ^[20]. They have also studied the burnability of double spiders and path forests in ^[21].

Recently, Bonato et al. ^[2] introduced a new graph parameter, which is the cooling number. In contrast with burning that aims to minimize the number of rounds to burn all vertices in a graph, cooling attempts to maximize the number of rounds to cool all vertices in the graph. The cooling process on a finite simple, undirected graph $G$ is a discrete-time process. Throughout the cooling process, vertices in $G$ may be either uncooled or cooled.

Initially, in the first round, all vertices are uncooled. At each round $t \geq 1$, one new uncooled vertex is chosen to cool if such a node is available. We call such a chosen vertex a source. If a vertex is cooled, then it remains in that state until the end of the process. Once a vertex is cooled on round $t$, in round $t+1$, its uncooled neighbors become cooled. The source chosen in round $t+1$ cannot be the immediate neighbor of cooled vertex in round $t$. This means that distance between two consecutive sources must be of distance at least 2. If at the beginning of round $t+1$, all uncooled vertices are immediate neighbor (or neighbor) of a cooled vertex in round $t$, then no source is chosen in round $t+1$ and the process ends at round $t+1$. The process ends in a given round when all vertices of $G$ are cooled.

We define the cooling number of $G$, written CL$(G)$, to be the maximum number of rounds for the cooling process to end. Give a graph with CL$(G) = c$ and let $(x_1, x_2, \dots)$ be a set of sources chosen during cooling. To completely cool $G$, it may have $c$ cooling sources in a sequence $(x_1, x_2, \dots, x_c)$ or $c-1$ cooling sources, which we write, $(x_1, x_2, \dots, x_{c-1}, [x_c])$. We call $(x_1, x_2, \dots, x_c)$ or $(x_1, x_2, \dots, x_{c-1}, [x_c])$ the cooling sequence for $G$ with CL$(G) = c$. The latter implies that the whole graph may only be completely cooled in $c$ rounds without positioning the $c$-th cooling source. We have that the burning number of $G$, $b(G) \leq \text{CL}(G)$. Note that a choice of sources that burns the graphs gives an upper bound to the burning number, and a choice of sources that cools the graph gives a lower bound to the cooling number.

In ^[2], Bonato et al. showed the following results on the cooling number of some basic graphs. For all graphs with diameter at most 2, we have that the burning number of $G$, $b(G) = \text{CL}(G)$.

Theorem 1.1. ^[2] For a graph $G$ on $n$ vertices, we have that

Let $u, v \in V(G)$, and $d(u, v)$ is the distance between $u$ and $v$. Then the diameter of $G$, denoted by diam$(G)$, is the max$\{d(v, u) : u, v \in V(G)\}$.

Theorem 1.2. ^[2] For a graph $G$, we have that

For the path $P_n$ and cycle $C_n$ of order $n$, it has been shown in ^[2] that

Theorem 1.3. ^[2]

Theorem 1.4. ^[2]

For the complete caterpillar of length $d$ and $n = 2d-2$, denoted as $CC_d$, (see^[2]), then

Theorem 1.5. ^[2] Let $T$ be a spider with $2m$ legs, each of length $r$. If we have that $m < \left\lceil \log_2 r+1 \right\rceil$, then

They also derived the cooling number of Cartesian grids and studied the cooling number in graphs generated by the iterated local transitivity model for social networks, see ^[2].

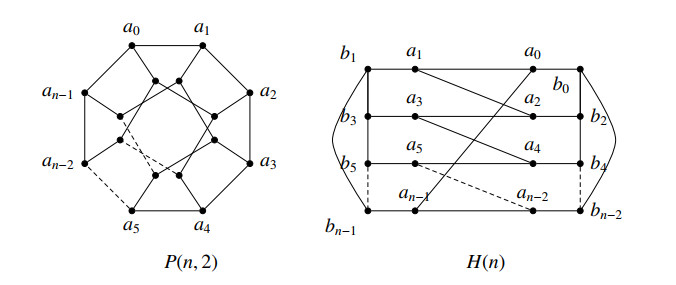
In this paper, we determine completely the cooling number for the generalized Petersen graphs. The generalized Petersen graphs is a classic family of cubic graphs. The Petersen graph is not only the smallest bridgeless 3-regular graph, but it is also a remarkable configuration that serves as a counterexample to many optimistic predictions about what might be true for graphs in general ^[11]. Let $n\geq 3$ and $k\geq 1$ be integers such that $1 \leq k \leq \left\lfloor \frac{n}{2} \right\rfloor$. The generalized Petersen graph $P(n, k)$ is defined to be the graph on $2n$ vertices with vertex set

and edge set

where subscripts are taken modulo $n$. Let $D_1 = \lbrace a_i: i = 0, 1, 2, \dots, n-1 \rbrace$ and $D_2 = \lbrace b_i: i = 0, 1, 2, \dots, n-1 \rbrace$. The subgraph induced by $D_1$ is called the outer rim while the subgraph induced by $D_2$ is called the inner rim. A spoke of $P(n, k)$ is an edge of the form $a_ib_i$ for some $0 \leq i \leq n-1$.

For a graph $G$, for each integer $j\geq 0$, we set

and

Note that if $N(x)$ is the set of vertices adjacent to $x$ in $G$, then

Furthermore, $N_0(x) = \varnothing$ and $N_0[x] = \{x\}$.

2.   Main results

It is worth noting that the main difference when choosing a choice of sources to completely burn or cool a graph is such that we need to carefully choose a cooling source compared to a burning source because the cooling source cannot be a neighbor of a cooled vertex in that particular round, whereas the burning source can be a neighbor of a burned vertex in that round. In the burning number case, where we aim to minimize the number of sources, we just need to make sure a particular vertex that we want is unburned and the choice of vertex will maximize the newly burned vertices at the end of each round. However, in the cooling process, where we aim to maximize the number of sources, we need to carefully choose the cooling sources so that the chosen vertex will minimize the newly cooled vertices at the end of each round. Furthermore, to recall, two consecutive cooling sources cannot be immediate neighbors.

In general, to obtain the lower bound, we can choose a choice of cooling sources in a sequence such that the $(t+1)$-th cooling source is chosen, at best, at distance 2 from the $t$-th cooling source. Besides that, the $(t+1)$-th cooling source, $x_{t+1}$ is best to be chosen with as many neighbors as possible that are contained in $N_1(x_t)$, i.e.,

This will reduce the cooling spread to uncooled vertices in the $(t+1)$-th round.

2.1.   Case for $k=1$

Note that it is fairly straightforward to see that the diameter of $P(n, 1)$ is $\frac{n}{2}+1$ if $n$ is even and $\left\lceil \frac{n}{2} \right\rceil$ if $n$ is odd.

Theorem 2.1. If $n \geq 3$, then $\text{CL}(P(n, 1)) = \left\lfloor \frac{2n+4}{5} \right\rfloor+1$.

Proof. Let $G = P(n, 1)$ with $\text{CL}(G) = k$ and $(x_1, x_2, \dots, x_{k-1}, [x_k])$, or $(x_1, x_2, \dots, x_{k})$ be a cooling sequence of $G$.

First, we show that $k \leq \left\lfloor \frac{2n+4}{5} \right\rfloor+1$. Suppose $k > \frac{2n+9}{5}$. Note that $G$ is vertex-transitive. The first cooling source $x_1$ can be placed at an arbitrary vertex, and we consider the spread of cooling from $x_1$ in $k$ rounds. At the end of the first round, only the vertex $x_1$ is cooled. At the end of the second round, $N_1(x_1)$ which consists of 3 vertices are cooled. Regardless where vertex $x_2$ is positioned, a total of 5 vertices (which are the vertices in $N_1[x_1]\cup \{x_2\}$) are cooled at the end of the second round. After two rounds, it is observed that at the end of each $i$-th round for all $3 \leq i \leq k-1$, at least 5 new uncooled vertices are cooled. In fact, at the beginning of the $i$-th round, the cooled vertices are just the vertices contained in

Recall that $x_{i}$ cannot be a neighbor of a cooled vertex. Therefore,

This implies that

Since $i\leq k-1$, there is still another round before all the vertices are cooled. So, there are four uncooled vertices excluding $x_i$, where two of them are contained in the inner rim and the other two in the outer rim. Thus, at the end of the $i$-th round, at least 5 new uncooled vertices are cooled.

At the $k$-th round, at least one uncooled vertex is cooled. Following this, we have that the number of cooled vertices is at least

a contradiction, as $\vert V(P(n, 1))\vert = 2n$. Thus, $k\leq \frac{2n+9}{5}$. Since $k$ is an integer, we have $k\leq \left\lfloor \frac{2n+9}{5} \right\rfloor = \left\lfloor \frac{2n+4}{5} \right\rfloor+1$.

For the lower bound, we give a choice of sources $(x_1, x_2, \dots, x_{c}, x_{c+1})$ or $(x_1, x_2, \dots, x_{c}, [x_{c+1}])$ where $c = \left\lfloor \frac{2n+4}{5} \right\rfloor$ to cool $G$. Note that all vertices will be cooled at $c+1$ round and $x_{c+1}$ may not need to be positioned in some cases. Without loss of generality, we first place $x_1$ at $a_1$ and $x_2$ at $b_2$. At the end of the second round, $a_0, a_1, a_2, b_1, b_2$ are cooled.

Suppose $\left\lfloor \frac{2n+4}{5} \right\rfloor$ is odd. Let $S_{2j+1} = \{ a_{3j}, b_{3j}, a_{3j+1}, b_{3j+1}, a_{3j+2}, b_{3j+2} \}$ for each $1\leq j\leq \frac{1}{2}\left(\left\lfloor \frac{2n+4}{5} \right\rfloor-1\right)$. We set

for $1\leq j\leq \frac{1}{2}\left(\left\lfloor \frac{2n+4}{5} \right\rfloor-1\right)-1$ and

where $j_0 = \frac{1}{2}\left(\left\lfloor \frac{2n+4}{5} \right\rfloor-1\right)$.

At the end of the third round, $a_3$ and $b_3$ are cooled as they are adjacent to $a_2$ and $b_2$, respectively. Similarly, for each $j$, by the choices of $x_{2j+1}$ and $x_{2j+2}$, all the vertices in $S_{2j+1}$ are cooled. In fact, $a_{3j}$ and $b_{3j}$ are cooled from $a_{3j-1} \in S_{2j-3}$ and $b_{3j-1}\in S_{2j-3}$, respectively; $a_{3j+1}$ and $b_{3j+2}$ are cooled from $b_{3j+1}$.

Now, at the end of the $(2j_0+1)$-th rounds, all the following vertices are cooled:

Besides that, sourced from $x_1 = a_1$, moving toward the opposite direction, the vertices in $\{a_0, a_{n-1}, a_{n-2}, \dots, a_{n-(c-2)}, b_0, b_{n-1}, b_{n-2}, \dots, b_{n-(c-3)} \}$ are cooled at the end of the $c$-th round.

Since $\left\lfloor \frac{2n+4}{5} \right\rfloor$ is odd, $3j_0+1 = 1.5 \left(\left\lfloor \frac{2n+4}{5} \right\rfloor -1 \right)+1$ is an integer. We shall show that by taking $c = \left\lfloor \frac{2n+4}{5} \right\rfloor$,

In fact, the lower bound follows from

and the fact that $\left(n-(c-3)-1.5 \left(\left\lfloor \frac{2n+4}{5} \right\rfloor -1 \right)-1\right)-1$ is an integer, whereas the upper bound follows from

So, we conclude that the number of uncooled vertices in the inner rim is at most 2 at the end of the $\left(2j_0+1\right)$-th round. Therefore, there are two possibilities at the end of the $\left(2j_0+1\right)$-th round,

(a) all vertices are cooled except

in this case, there is exactly one vertex $b_{3j_0+2}$ between $b_{3j_0+1}$ and $b_{n-(c-3)}$.

(b) all vertices are cooled except

in this case, there are exactly two vertices $b_{3j_0+2}, b_{3j_0+3}$ between $b_{3j_0+1}$ and $b_{n-(c-3)}$.

In either case, all these uncooled vertices are adjacent to some cooled vertices. So, no $x_{c+1}$ can be placed and we have the cooling sequence $(x_1, x_2, \dots, x_{c}, [x_{c+1}])$. Hence, $k\geq \left\lfloor \frac{2n+4}{5} \right\rfloor+1$.

Suppose $\left\lfloor \frac{2n+4}{5} \right\rfloor$ is even. Let $S_{2j+1} = \{ a_{3j}, b_{3j}, a_{3j+1}, b_{3j+1}, a_{3j+2}, b_{3j+2} \}$ for each $1\leq j\leq \frac{1}{2}\left(\left\lfloor \frac{2n+4}{5} \right\rfloor-2\right)$. We set

for $1\leq j\leq \frac{1}{2}\left(\left\lfloor \frac{2n+4}{5} \right\rfloor-2\right)$.

At the end of the third round, $a_3$ and $b_3$ are cooled as they are adjacent to $a_2$ and $b_2$, respectively. Similarly, for each $j$, by the choices of $x_{2j+1}$ and $x_{2j+2}$, all the vertices in $S_{2j+1}$ are cooled. In fact, $a_{3j}$ and $b_{3j}$ are cooled from $a_{3j-1} \in S_{2j-3}$ and $b_{3j-1}\in S_{2j-3}$, respectively; $a_{3j+1}$ and $b_{3j+2}$ are cooled from $b_{3j+1}$.

Now, at the end of the $(2j_0+2)$-th rounds where $j_0 = \frac{1}{2}\left(\left\lfloor \frac{2n+4}{5} \right\rfloor-2\right)$, all the following vertices are cooled:

Besides that, sourced from $x_1 = a_1$, moving toward the opposite direction, the vertices in $\{a_0, a_{n-1}, a_{n-2}, \dots, a_{n-(c-2)}, b_0, b_{n-1}, b_{n-2}, \dots, b_{n-(c-3)} \}$ are cooled at the end of the $c$-th round.

Since $\left\lfloor \frac{2n+4}{5} \right\rfloor$ is even, $3j_0+2 = 3\left(\frac{1}{2}\left(\left\lfloor \frac{2n+4}{5} \right\rfloor-2\right)\right)+2 = 1.5 \left(\left\lfloor \frac{2n+4}{5} \right\rfloor -2 \right)+2$ is an integer. We shall show that by taking $c = \left\lfloor \frac{2n+4}{5} \right\rfloor$,

In fact, the lower bound follows from

whereas the upper bound follows from

So, we conclude that the number of uncooled vertices in the outer rim is at most 2 at the end of the $\left(2j_0+2\right)$-th round. Therefore, there are three possibilities at the end of the $\left(2j_0+2\right)$-th round,

(a) all vertices are cooled except

in this case, there are no vertices between $a_{3j_0+2}$ and $a_{n-(c-2)}$.

(b) all vertices are cooled except

in this case, there are exactly one vertex $a_{3j_0+3}$ between $a_{3j_0+2}$ and $a_{n-(c-2)}$.

(c) all vertices are cooled except

in this case, there are exactly two vertices $a_{3j_0+3}, a_{3j_0+4}$ between $a_{3j_0+2}$ and $a_{n-(c-2)}$.

For cases (a) and (b), all these uncooled vertices are adjacent to some cooled vertices. So, no $x_{c+1}$ can be placed and we have the cooling sequence $(x_1, x_2, \dots, x_{c}, [x_{c+1}])$. Hence, $k\geq c+1 = \left\lfloor \frac{2n+4}{5} \right\rfloor+1$. For case (c), we can only set $x_{c+1} = b_{3j_0+4}$ because all other uncooled vertices are adjacent to some cooled vertices. So, we have the cooling sequence $(x_1, x_2, \dots, x_{c}, x_{c+1})$. Hence, $k\geq c+1 = \left\lfloor \frac{2n+4}{5} \right\rfloor+1$.

This completes the proof of the theorem. □

2.2.   Case for $k=2$

Proposition 2.1. Let $3 \leq n \leq 5$. Then CL$(P(n, 2)) = 3$.

Proof. Note that $\text{diam}(P(3, 2)) = \text{diam}(P(4, 2)) = \text{diam}(P(5, 2)) = 2$, and, hence, by Eq (1.1), $\text{CL}(P(3, 2)) \leq 3$, $\text{CL}(P(4, 2)) \leq 3$ and $\text{CL}(P(5, 2)) \leq 3$.

For $n = 3, 4, 5$ the proposition can be verified easily by having a choice of cooling sources, see Table 1. Recall that the cooling sequence of a $P(n, k)$ with $c$ sources may only completely cooled the graph in $(c+1)$ rounds and, hence, $\text{CL}(P(n, k)) = c+1$.

This completes the proof. □

For the rest of the section, we used a similar isomorphic graph of $P(n, 2)$, say $H(n, 2)$, as defined in ^[19] (see Figures 1 and 2).

It has been shown in ^[10] and ^[12] that diameter of $P(n, 2)$ is $O\left(\frac{n}{4} \right)$. Here, we show the exact value. Let $d(x, y)$ be the distance between two vertices $x$ and $y$.

Lemma 2.1. Let $n \geq 6$. Then the diameter of $P(n, 2)$ is $\left\lceil \frac{n}{4} \right\rceil+2$ if $n$ is even and $\left\lceil \frac{n-1}{4} \right\rceil+2$ if $n$ is odd.

Proof. Suppose $n$ is even and $\frac{n}{2}$ is even. By referring to $H(n)$, if we consider only vertices of the outer rim, one of the maximum distances is $d(a_0, a_{\frac{n}{2}}) = 1+\frac{n}{4}+1 = \frac{n}{4}+2$ by first going to $b_0$ and going to in steps of 2 to $b_{\frac{n}{2}}$ and then going to $a_{\frac{n}{2}}$. Note that $d(a_0, a_{\frac{n}{2}}) = d(a_0, a_{\frac{n}{2}-1}) = d(a_0, a_{\frac{n}{2}+1}) = \frac{n}{4}+2$. If we consider one vertex from the outer rim, say $a_0$ with another vertex $b_i$, one of the maximum distances is $d(a_0, b_{\frac{n}{2}+1}) = 2+\frac{n}{4}$ by first going through the path $a_1$, then $b_1$, and going to in steps of 2 in the inner rim to $b_{\frac{n}{2}+1}$. If we consider only any two vertices of the two cycles in the inner rim, one of the maximum distances is $d(b_0, b_{\frac{n}{2}-1}) = 2+\frac{n}{4}$ by first going through path $b_0a_0 a_1 b_1$ and then going to in steps of 2 in the inner rim to $b_{\frac{n}{2}-1}$.

Suppose $n$ is even and $\frac{n}{2}$ is odd. By referring to $H(n)$, if we consider only vertices of the outer rim, one of the maximum distances is $d(a_0, a_{\frac{n}{2}}) = 1+\left \lfloor \frac{n}{4} \right \rfloor +2 = 1+\frac{n-2}{4}+2 = \frac{n+2}{4}+2 = \left\lceil \frac{n}{4} \right\rceil+2$ by first going to $a_1$, then $b_1$, and going to in steps of 2 to $b_{\frac{n}{2}}$ and then going to $a_{\frac{n}{2}}$. If we consider one vertex from the outer rim, say $a_0$ with another vertex $b_i$, one of the maximum distances is $d(a_0, b_{\frac{n}{2}}) = 2+\left\lfloor \frac{n}{4} \right\rfloor = \left\lceil \frac{n}{4} \right\rceil+1$ by first going to $a_1$ followed by $b_1$ and going to in steps of 2 in the inner rim to $b_{\frac{n}{2}}$. If we consider only any two vertices of the two cycles in the inner rim, one of the maximum distances is $d(b_0, b_{\frac{n}{2}}) = 2+\frac{n+2}{4} = \left\lceil \frac{n}{4} \right\rceil+2$ by first going through path $b_0a_0 a_1 b_1$ and then going to in steps of 2 in the inner rim to $b_{\frac{n}{2}}$.

Suppose $n$ is odd and $\frac{n-1}{2}$ is even. By referring to $H(n)$, if we consider only vertices of the outer rim, one of the maximum distances is $d(a_0, a_{\frac{n-1}{2}}) = 1+\frac{n-1}{4}+1 = \frac{n-1}{4}+2$ by first going to $b_0$ and going to in steps of 2 to $b_{\frac{n-1}{2}}$ and then going to $a_{\frac{n-1}{2}}$. Note that $d(a_0, a_{\frac{n-1}{2}}) = d(a_0, a_{\frac{n-1}{2}-1}) = d(a_0, a_{\frac{n-1}{2}+1}) = \frac{n-1}{4}+2$. If we consider one vertex from outer rim, say $a_0$ with another vertex $b_i$, one of the maximum distances is $d(a_0, b_{\frac{n-1}{2}}) = 1+\frac{n-1}{4}$ by first going through the path $a_0$, then $b_0$, and going to in steps of 2 in the inner rim to $b_{\frac{n-1}{2}}$. If we consider only any two vertices of the inner rim, one of the maximum distances is $d(b_0, b_{\frac{n-1}{2}-1}) = 2+\frac{n-1}{4}$ by first going through path $b_0a_0 a_1 b_1$ and then going to in steps of 2 in the inner rim to $b_{\frac{n-1}{2}-1}$.

Suppose $n$ is odd and $\frac{n-1}{2}$ is odd. By referring to $H(n)$, if we consider only vertices of the outer rim, one of the maximum distances is $d(a_0, a_{\frac{n-1}{2}}) = 1+\left \lceil \frac{n-1}{4} \right \rceil+1 = \left\lceil \frac{n}{4} \right\rceil+2$ by first going to $a_1$, then $b_1$, and going to in steps of 2 to $b_{\frac{n-1}{2}}$ and then going to $a_{\frac{n-1}{2}}$. If we consider one vertex from the outer rim, say $a_0$ with another vertex $b_i$, one of the maximum distances is $d(a_0, b_{\frac{n-1}{2}}) = 1+\left\lceil \frac{n-1}{4} \right\rceil$ by first going to $a_1$ followed by $b_1$ and going to in steps of 2 in the inner rim to $b_{\frac{n-1}{2}}$. If we consider only any two vertices in the inner rim, one of the maximum distances is $d(b_0, b_{\frac{n-1}{2}}) = 2+\left\lceil \frac{n-1}{4} \right\rceil$ by first going through path $b_0a_0 a_1 b_1$ and then going to in steps of 2 in the inner rim to $b_{\frac{n-1}{2}}$.

This completes the proof. □

The following corollary follows directly from Eq (1.1) and Lemma 2.1.

Corollary 2.1. Let $n \geq 6$. Then

Now, we are ready to prove the following theorem.

Theorem 2.2. Let $n \geq 28$. Then

Proof. Suppose $n \equiv 0 \mod 4$, i.e., $n = 4k$ for some positive integer $k$. Then $\left\lceil \frac{n}{4} \right\rceil+3 = k+3$. By Corollary 1, $\text{CL}(P(n, 2)) \leq k+3$. To find the lower bound, we need to determine the cooling source $x_i$ in round $i$. We place $x_1 = a_0$, $x_2 = a_2$, $x_3 = a_{4k-3}$, $x_4 = a_{4k-5}$, $x_5 = a_{4k-7}$, and for $6\leq i\leq k+2$, we place $x_i = a_{2i-5}$. Since $n\geq 28$, we have $k\geq 7$. It is not hard to see that at the end of round $k+2$, all vertices are cooled, except $a_{2k}$ and $a_{2k+1}$. The vertex $a_{2k}$ is adjacent to the cooled vertex $b_{2k}$, whereas $a_{2k+1}$ is adjacent to the cooled vertex $b_{2k+1}$. Therefore, we have the cooling sequence $(x_1, x_2, \dots, x_{k+2}, [x_{k+3}])$. Hence, $\text{CL}(P(n, 2)) \geq k+3 = \left\lceil \frac{n}{4} \right\rceil+3$, and the theorem holds for $n \equiv 0 \mod 4$.

Suppose $n \equiv 2 \mod 4$, i.e., $n = 4k+2$ for some positive integer $k$. First, we show that $\text{CL}(P(n, 2)) \leq k+3$. By Corollary 2.1, $\text{CL}(P(n, 2)) \leq \left\lceil \frac{n}{4} \right\rceil+3 = k+4$. Suppose $\text{CL}(P(n, 2)) = k+4$. So, it has a cooling sequence $(x_1, x_2, \dots, x_{k+3}, [x_{k+4}])$ or $(x_1, x_2, \dots, x_{k+3}, x_{k+4})$. This means

Without loss of generality, we may assume that $x_1 = a_0$ or $b_0$. Suppose $x_1 = a_0$. Note that at the end of round $k+2$, all the vertices contained in $N_{k+1}[x_1]$ are cooled. Recall that $x_{k+3}$ cannot be adjacent to a cooled vertex. Therefore, $x_{k+3}\notin N_{k+2}[x_1]$ or, equivalently,

So, we must have $x_{k+3} = a_{2k+1}$. Now,

a contradiction, as $\text{CL}(P(n, 2)) = k+4$. Suppose $x_1 = b_0$. Note that at the end of round $k+2$, all the vertices contained in $N_{k+1}[x_1]$ are cooled. As before, $x_{k+3}\notin N_{k+2}[b_0]$ or, i.e.,

So, we must have $x_{k+3} = b_{2k+1}$. Now,

again, a contradiction. Hence, $\text{CL}(P(n, 2)) \leq k+3$. To find the lower bound, we place $x_1 = a_0$, $x_2 = a_2$, $x_3 = a_{4k-1}$, $x_4 = a_{4k-3}$, $x_5 = a_{4k-5}$, and for $6\leq i\leq k+3$, we place $x_i = a_{2i-5}$. It is not hard to see that at the end of round $k+2$, all vertices are cooled, except

Clearly, $a_{2k+3}$ is adjacent to the cooled vertex $b_{2k+3}$, $a_{2k+2}$ is adjacent to the cooled vertex $b_{2k+2}$, $a_{2k}$ is adjacent to the cooled vertex $b_{2k}$, $a_{2k-1}$ is adjacent to the cooled vertex $b_{2k-1}$, and $b_{2k+1}$ is adjacent to the cooled vertex $b_{2k-1}$. So, at the end of round $k+3$, all vertices are cooled, and we have the cooling sequence $(x_1, x_2, \dots, x_{k+2}, x_{k+3})$. Hence, $\text{CL}(P(n, 2)) = k+3 = \frac{n-2}{4} +3$ and the theorem holds for $n \equiv 2 \mod 4$.

Suppose $n \equiv 1 \mod 4$, i.e., $n = 4k+1$ for some positive integer $k$. Then $\left\lceil \frac{n-1}{4} \right\rceil+3 = k+3$. By Corollary 2.1, $\text{CL}(P(n, 2)) \leq k+3$. To find the lower bound, we need to determine the cooling source $x_i$ in round $i$. We place $x_1 = a_0$, $x_2 = a_2$, $x_3 = a_{4k-2}$, $x_4 = a_{4k-4}$, $x_5 = a_{4k-6}$, and for $6\leq i\leq k+2$, we place $x_i = a_{2i-5}$. It is not hard to see that at the end of round $k+2$, all vertices are cooled, except

The vertex $a_{2k+2}$ is adjacent to the cooled vertex $b_{2k+2}$, $a_{2k+1}$ is adjacent to the cooled vertex $b_{2k+1}$ and $a_{2k}$ is adjacent to the cooled vertex $b_{2k}$. Therefore, we have the cooling sequence $(x_1, x_2, \dots, x_{k+2}, [x_{k+3}])$. Hence, $\text{CL}(P(n, 2)) \geq k+3 = \frac{n-1}{4} +3$ and the theorem holds for $n \equiv 1 \mod 4$.

Suppose $n \equiv 3 \mod 4$, i.e., $n = 4k+3$ for some positive integer $k$. Then $\left\lceil \frac{n-1}{4} \right\rceil+3 = k+4$. By Corollary 2.1, $\text{CL}(P(n, 2)) \leq k+4$. To find the lower bound, we need to determine the cooling source, $x_i$ in round $i$. We place $x_1 = a_0$, $x_2 = a_2$, $x_3 = a_{4k}$, $x_4 = a_{4k-2}$, $x_5 = a_{4k-4}$, and for $6\leq i\leq k+3$, we place $x_i = a_{2i-5}$. It is not hard to see that at the end of round $k+3$, all vertices are cooled, except $a_{2k+2}$. The vertex $a_{2k+2}$ is adjacent to the cooled vertex $b_{2k+2}$. Therefore, we have the cooling sequence $(x_1, x_2, \dots, x_{k+3}, [x_{k+4}])$. Hence, $\text{CL}(P(n, 2)) \geq k+4 = \frac{n-3}{4} +4$ and the theorem holds for $n \equiv 3 \mod 4$.

This completes the proof of the theorem. □

To remark, for $6 \leq n \leq 27$, by using similar choices of cooling sources in the proof of Theorem 2.2, it can be easily seen that $\text{CL}(P(n, 2)) \geq O \left(\frac{n}{4} \right)$. Here, we omitted the choices of the cooling sources for these cases.

2.3.   General case

Lemma 2.2. Let $k \geq 3$ be a fixed positive integer and $n\geq 2k$. Then

Proof. Note that

where $d(x, y)$ is the distance between $x$ and $y$. We consider two cases.

Case 1. Suppose $n = 2sk+r$ where $0\leq r < k-1$. If $y = a_j$ for some $ik\leq j\leq ik+\left\lfloor \frac{k+1}{2}\right\rfloor$ where $0\leq i\leq s-1$, then $d(a_0, y) = 2+i+j-ik$, which can be seen from the path

In particular, if $i = s-1$ and $j = (s-1)k+\left\lfloor \frac{k+1}{2}\right\rfloor$, then

If $y = a_j$ for some $ik+\left\lfloor \frac{k+1}{2}\right\rfloor+1\leq j\leq (i+1)k$ where $0\leq i\leq s-1$, then $d(a_0, y) = 2+(i+1)+(i+1)k-j$, which can be seen from the path

In particular, if $i = s-1$ and $j = (s-1)k+\left\lfloor \frac{k+1}{2}\right\rfloor+1$, then

and

If $y = a_j$ for some $sk\leq j\leq sk+\left\lfloor \frac{r}{2}\right\rfloor$, then $d(a_0, y) = 2+s+j-sk$, which can be seen from the path

Thus, when $j = sk+\left\lfloor \frac{r}{2}\right\rfloor$, we have

This means if $y = a_j$ for $1\leq j\leq sk+\left\lfloor \frac{r}{2}\right\rfloor$, then

By symmetry, if $y = a_j$ for some $sk+\left\lfloor \frac{r}{2}\right\rfloor+1\leq j\leq 2sk+r-1$, then (2.6) still holds.

If $y = b_j$ for some $ik\leq j\leq ik+\left\lfloor \frac{k+1}{2}\right\rfloor+1$ where $0\leq i\leq s-1$, then $d(a_0, y) = j-ik+1+i$, which can seen from the path

In particular, if $i = s-1$ and $j = (s-1)k+\left\lfloor \frac{k+1}{2}\right\rfloor+1$, then

If $y = b_j$ for some $ik+\left\lfloor \frac{k+1}{2}\right\rfloor+2\leq j\leq (i+1)k$ where $0\leq i\leq s-1$, then $d(a_0, y) = (i+1)k-j+3+(i+1)$, which can be seen from the path

In particular, if $i = s-1$ and $j = (s-1)k+\left\lfloor \frac{k+1}{2}\right\rfloor+2$, then

and

If $y = b_j$ for some $sk\leq j\leq sk+\left\lfloor \frac{r}{2}\right\rfloor$, then $d(a_0, y) = j-sk+1+s$, which can be seen from the path

Thus, when $j = sk+\left\lfloor \frac{r}{2}\right\rfloor$, we have

This means if $y = b_j$ for $1\leq j\leq sk+\left\lfloor \frac{r}{2}\right\rfloor$, then

By symmetry, if $y = b_j$ for some $sk+\left\lfloor \frac{r}{2}\right\rfloor+1\leq j\leq 2sk+r-1$, then (2.10) still holds. So, we conclude that

Now, we consider $d(b_0, y)$. If $y = a_j$ for some $ik\leq j\leq ik+\left\lfloor \frac{k+1}{2}\right\rfloor$ where $0\leq i\leq s-1$, then by considering the path in (2.3) (remove $a_0$), we have

If $y = a_j$ for some $ik+\left\lfloor \frac{k+1}{2}\right\rfloor+1\leq j\leq (i+1)k$ where $0\leq i\leq s-1$, then by considering the path in (2.4) (remove $a_0$), we have

If $y = a_j$ for some $sk\leq j\leq sk+\left\lfloor \frac{r}{2}\right\rfloor$, then by considering the path in (2.5) (remove $a_0$), we have

This means if $y = a_j$ for $1\leq j\leq sk+\left\lfloor \frac{r}{2}\right\rfloor$, then

By symmetry, if $y = a_j$ for some $sk+\left\lfloor \frac{r}{2}\right\rfloor+1\leq j\leq 2sk+r-1$, then (2.11) still holds.

If $y = b_j$ for some $ik\leq j\leq ik+\left\lfloor \frac{k+1}{2}\right\rfloor$ where $0\leq i\leq s-1$, then by considering the path in (2.7) (adding $b_0\to a_0$), we have

If $y = b_j$ for some $ik+\left\lfloor \frac{k+1}{2}\right\rfloor+1\leq j\leq (i+1)k$ where $0\leq i\leq s-1$, then by considering the path in (2.8) (remove $a_0$), we have

If $y = b_j$ for some $sk\leq j\leq sk+\left\lfloor \frac{r}{2}\right\rfloor$, then by considering the path in (2.9) (adding $b_0\to a_0$), we have

This means if $y = b_j$ for $1\leq j\leq sk+\left\lfloor \frac{r}{2}\right\rfloor$, then

By symmetry, if $y = b_j$ for some $sk+\left\lfloor \frac{r}{2}\right\rfloor+1\leq j\leq 2sk+r-1$, then (2.12) still holds. So, we conclude that

Hence,

Case 2. Suppose $n = (2s+1)k+r$ where $0\leq r < k-1$. We consider $d(a_0, y)$. If $y = a_j$ for some $ik\leq j\leq ik+\left\lfloor \frac{k+1}{2}\right\rfloor$ where $0\leq i\leq s$, then $d(a_0, y) = 2+i+j-ik$, which can be seen from the path in (2.3). In particular, if $i = s$ and $j = sk+\left\lfloor \frac{k+1}{2}\right\rfloor$, then

If $y = a_j$ for some $ik+\left\lfloor \frac{k+1}{2}\right\rfloor+1\leq j\leq (i+1)k$ where $0\leq i\leq s$, then $d(a_0, y) = 2+(i+1)+(i+1)k-j$, which can be seen from the path in (2.4). In particular, if $i = s$ and $j = sk+\left\lfloor \frac{k+1}{2}\right\rfloor+1$, then

and

This means if $y = a_j$ for $1\leq j\leq (s+1)k$, then

By symmetry, if $y = a_j$ for some $sk+r-1\leq j\leq (2s+1)k+r-1$, then (2.13) still holds.

If $y = b_j$ for some $ik\leq j\leq ik+\left\lfloor \frac{k+1}{2}\right\rfloor+1$ where $0\leq i\leq s$, then $d(a_0, y) = j-ik+1+i$, which can be seen from the path in (2.7). In particular, if $i = s$ and $j = sk+\left\lfloor \frac{k+1}{2}\right\rfloor+1$, then

If $y = b_j$ for some $ik+\left\lfloor \frac{k+1}{2}\right\rfloor+2\leq j\leq (i+1)k$ where $0\leq i\leq s$, then $d(a_0, y) = (i+1)k-j+3+(i+1)$, which can be seen from the path in (2.8). In particular, if $i = s$ and $j = sk+\left\lfloor \frac{k+1}{2}\right\rfloor+2$, then

and

This means if $y = b_j$ for $1\leq j\leq (s+1)k$, then

By symmetry, if $y = b_j$ for some $sk+r-1\leq j\leq (2s+1)k+r-1$, then (2.14) still holds. Thus,

Now, we consider $d(b_0, y)$. If $y = a_j$ for some $ik\leq j\leq ik+\left\lfloor \frac{k+1}{2}\right\rfloor$ where $0\leq i\leq s$, then by considering the path in (2.3) (remove $a_0$), we have

If $y = a_j$ for some $ik+\left\lfloor \frac{k+1}{2}\right\rfloor+1\leq j\leq (i+1)k$ where $0\leq i\leq s$, then by considering the path in (2.4) (remove $a_0$), we have

This means if $y = a_j$ for $1\leq j\leq (s+1)k$, then

By symmetry, if $y = a_j$ for some $sk+r-1\leq j\leq (2s+1)k+r-1$, then (2.15) still holds.

If $y = b_j$ for some $ik\leq j\leq ik+\left\lfloor \frac{k+1}{2}\right\rfloor$ where $0\leq i\leq s$, then by considering the path in (2.7) (adding $b_0\to a_0$), we have

If $y = b_j$ for some $ik+\left\lfloor \frac{k+1}{2}\right\rfloor+1\leq j\leq (i+1)k$ where $0\leq i\leq s$, then by considering the path in (2.8) (remove $a_0$), we have

This means if $y = b_j$ for $1\leq j\leq (s+1)k$, then

By symmetry, if $y = b_j$ for some $sk+r-1\leq j\leq (2s+1)k+r-1$, then (2.16) still holds. Hence,

and

This completes the proof of the lemma. □

Theorem 2.3. Let $k \geq 3$ be a fixed positive integer and $n\geq 2k$. Then

Proof. Let $c = \left\lfloor \frac{n}{2k} \right\rfloor + \left\lfloor \frac{k+1}{2} \right\rfloor$. In order to show the lower bound, instead of providing a cooling sequence $(x_1, x_2, \dots, x_c)$ or $(x_1, x_2, \dots, x_{c-1}, [x_c])$ that can completely cool the whole graph, we provide choices of cooling sources in the cooling sequence so that each assigned cooling source is of $d(x_j, x_i) \geq j-i+1$ for $i = 1, 2, \dots, j-1$. Let $n = sk+r$ for some $0 \leq r \leq k-1$. To ease the explanation, we draw $P(n, k)$ as follows:

(ⅰ) Place the vertices $a_0, a_1, a_2, \dots, a_{k-1}$ horizontally from right to left.

(ⅱ) Then, place the vertices $a_k, a_{k+1}, \dots, a_{sk-1}$ such that $a_{(j+1)k+i}$ is positioned right below $a_{jk+i}$ for each $i = 0, 1, 2, \dots, k-1$ and $j = 0, 1, \dots, s-1$. Place $a_{sk+i}$ below $a_{(s-1)k+i}$ for $i = 0, 1, 2, \dots r-1$. Add edges to form the outer rim cycle $C_n = a_0a_1a_2\dots a_{n-1}$.

(ⅲ) Add the vertex $b_j$ beside $a_j$ for all $j = 0, 1, 2, \dots, n-1$ and then draw the corresponding spoke $a_jb_j$ without any crossing.

(ⅳ) Add the edges of the inner rim induced by the vertices $\{ b_0, b_1, b_2, \dots, b_{n-1} \}$.

Here, we do the following to position each cooling source. Let

(ⅰ) $x_1 = b_{\left\lfloor \frac{n}{2k} \right\rfloor k + \left\lfloor \frac{k-1}{2} \right\rfloor}$;

(ⅱ) $x_i = a_{\left\lfloor \frac{n}{2k} \right\rfloor k + \left\lfloor \frac{k-1}{2} \right\rfloor-(i-1)k}$ for each $i = 2, 3, \dots, \left\lfloor \frac{n}{2k} \right\rfloor +1$;

(ⅲ) $x_{\left\lfloor \frac{n}{2k} \right\rfloor +1+j} = b_{\left\lfloor \frac{k-1}{2} \right\rfloor}+j$ for each $j = 1, 2, \dots, \left\lfloor \frac{k-1}{2} \right\rfloor$.

Hence, $\text{CL}(P(n, k))\geq \left\lfloor \frac{n}{2k} \right\rfloor +1 + \left\lfloor \frac{k-1}{2} \right\rfloor = \left\lfloor \frac{n}{2k} \right\rfloor + \left\lfloor \frac{k+1}{2} \right\rfloor$.

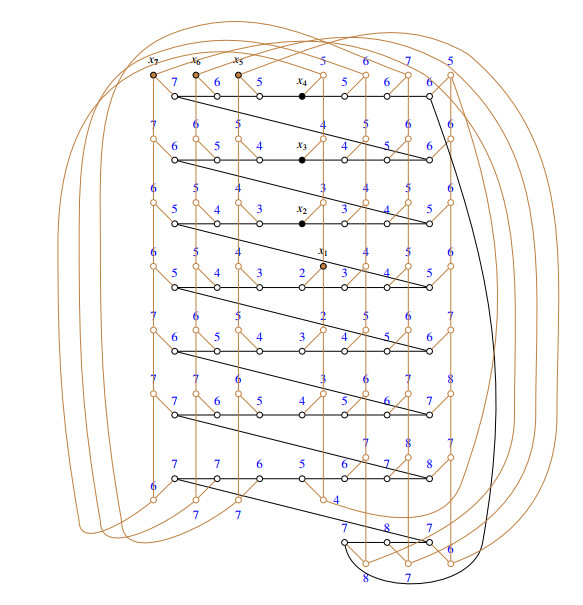
Figure 3 depicts the case for $P(52, 7)$ such that CL$(P(52, 7)) > 7$.

The upper bound follows from Eq (1.1) and Lemma 2.2. □

The following corollary is an immediate consequence of Corollary 2.1 and Theorems 2.2 and 2.3.

Corollary 2.2. Let $k \geq 2$ be a fixed positive integer and $n\geq 2k$. Then

3.   Concluding remark

The cooling number, a relatively new graph parameter, aims to maximize the number of rounds required to cool all vertices in a graph. It is the compelling counterpart to the extensively researched burning number, offering a new perspective on dynamic processes within graphs. We presented the exact results for the cooling numbers of $P(n, 1)$ and $P(n, 2)$, while providing an asymptotic formula for $P(n, k)$ for general $k$.

While this paper focuses on generalized Petersen graphs, it could benefit a discussion on how the results might generalize to other families of graphs or how the use of vertex-transitivity and combinatorial arguments to derive the cooling sequences could be adapted. This would broaden the impact of the results and suggest potential avenues for future research.

Author contributions

Kai An Sim: Conceptualization, investigation, methodology, funding acquisition, writing-original draft, writing-review & editing; Kok Bin Wong: Conceptualization, investigation, methodology, writing-original draft, writing-review & editing. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The author(s) declare(s) that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This project is supported by Publication Support Scheme by Sunway University, Malaysia.

Conflict of interest

All authors declare no conflicts of interest in this paper.