A study of coupled nonlinear generalized fractional differential equations with coupled nonlocal multipoint Riemann-Stieltjes and generalized fractional integral boundary conditions

1.   Introduction

The study of the coupling between free flow and porous media flow has garnered widespread attention in recent years, owing to its diverse applications in geosciences (e.g., karst aquifers, hyporheic flow, contaminant transport), health sciences (e.g., blood flow), and industrial processes; see ^[1,2,3,4,5] and the references therein. Insights derived from a comprehensive understanding of the Navier-Stokes-Darcy equations can be readily employed to tackle various engineering challenges. The typical mathematical analysis on the well-posedness of the associated initial boundary value problem has been done by Layton et al. ^[6] and Discacciati et al. ^[7]. The mathematical analysis of the miscible displacement problem in the subsurface was done in a seminal paper by Alt-Luckhaus ^[8] and by others such as Fabrie-Langlais ^[9], Fabrie-Gallouët ^[10], and Marpeau-Saad ^[11].

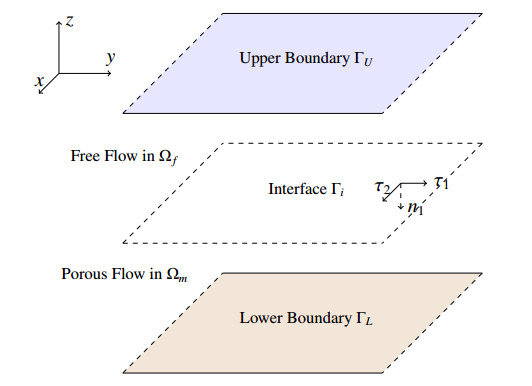
We select a microelement in the fluid-structure coupling system to consider a plane as the research object, which means that the fluid flow on the cross-section of the interface is isotropic. The schematic diagram is shown in Figure 1:

For the fluid flow in the porous medium, we employ the mass conversation law of the porosity medium and Darcy's law ^[12,13] to describe the system as follows:

where $\mathbf{v} = \mathbf{v}(\mathbf{x}, t)\in \mathbb{R}^{3}$ denotes the velocity of the flow in the porosity medium. Obviously, we can get that

where $P_{2} = P_{2}(\mathbf{x}, t)\in \mathbb{R}^{3}$, $\; \mu_{2} > 0$ represents the pressure and the viscosity of the flow in $\Omega_{m}$, respectively, and $\Pi$ denotes the permeability tensor. We use the incompressible Navier-Stokes equations with constant viscosity $\mu_{1} > 0$ to describe the flow in $\Omega_{f}$ as the following equations:

where $\Omega_{f}\subset \mathbb{R}^{3}$ covers the domain of the free flow, $\mathbf{u} = \mathbf{u}(\mathbf{x}, t) = \big(u_{1}, \ u_{2}, \ u_{3}\big)\in \mathbb{R}^{3}$ is the velocity of the free flow, $P_{1} = P_{1}(\mathbf{x}, t)$ represents the pressure of the flow in $\Omega_{f}$, and $\mu_{1}$ is the viscosity of the free flow.

The interface-boundary and initial conditions are given by

where $\alpha$ is an empirically determined coefficient, $\tau_{i}, \; i = \{1, \ 2\}$ represents two orthogonal tangent vectors in the horizontal direction, and $\mathbf{n}_{1}$ denotes the exterior unit vector normal of $\partial \Omega_{f}$ satisfying

$(1.4)_{1}$ is derived by the balance of force in the normal direction and Beavers-Joseph-Saffman-Jones interface boundary condition $(1.4)_{2}$ states the shear force to the tangential stress of the fluid velocity along $\Gamma_{i}$.

We acknowledge the pioneering work of researchers who have contributed to the fields of fluid dynamics in porous media, computational methods for solving coupled equations, and the development of interface-boundary conditions ^{[14,15,16,17,18]}. For the conditions at the sharp interface, a comprehensive review of these interface selections is provided in ^[19]. It is known that there are three options for the shear stress conditions in the tangential velocity: The BJ (Beavers-Joseph) condition ^[14], the BJJ (Beavers-Joseph-Jones) condition ^[17], and the BJSJ (Beavers-Joseph-Saffman-Jones) condition ^[18], which is equivalent to what is known as BJS interface condition in some other literature such as ^[20]. Additionally, two choices are available for the balance of force in the normal direction at the interface: The Lions interface condition and the Rankine-Hudoniot condition.

Research in this domain primarily centers on the classical Navier-Stokes-Darcy equations with sharp interface conditions (refer to ^{[3,6,7,21,22,23,24,25,26,27,28,29,30,31,32,33,34]} and the related references), the Navier-Stokes-Darcy-Boussinesq equations involving temperature variations (refer to ^[35,36] and related references), and the more complex Cahn-Hilliard-Navier-Stokes-Darcy equations with interface mixing (refer to ^{[20,37,38,39,40]} and related references).

However, there have been few achievements in the mathematical analysis, especially in the case of well-posedness of strong solutions ^[41,42]. This is mainly due to the strong coupling of the interface, which makes it difficult to obtain high-order estimates of the system. The convection phenomenon under consideration is notably more intricate than that in a single fluid (see ^[43] for the free-flow and ^[44,45] for fluids in a porous medium).

In recent years, researchers have obtained results on non-stationary weak solutions ^{[30,46,47,48]}. Cui, Dong, and Guo ^[41] have studied the strong solutions and exponential decay in the two-dimensional case, and we have extended these results to the problem in the 3-D Euclidean space in this paper. Our primary objective is to conduct an initial analysis on the global well-posedness of a coupled Navier-Stokes-Darcy model in the context of the Beavers-Joseph-Saffman-Jones interface boundary condition and establishing their uniqueness property.

Definition 1. For any $T\in (0, +\infty]$, we first define a function space $X(0, T)$ as

$(\mathbf{u}, P_2) \in X(0, T)$ is called the strong solution of (1.2)–(1.4), if it satisfies systems (1.2) and (1.3) a.e. in $\Omega \times (0, T)$, and fulfills the conditions (1.2)–(1.4).

Next, we present the main result of this paper.

Proposition 1.1. (Local well-posedness) Let $\mu_{1}, \mu_{2}$ both be positive constants and assume that

the initial data $\mathbf{u}_{0}\in H^{2}(\Omega_{f})$ is divergence free, and the compatibility condition holds as follows

where $u_{t}^{0} = u_{t}\mid_{t = 0}$ and $P_{1}^{0} = P_{1}\mid_{t = 0}$. There exists a time $T > 0$ such that the 3-D coupled Navier-Stokes-Darcy systems (1.2)–(1.4) have a unique strong solution $(\mathbf{u}, P_2)\in X(0, T)$.

Theorem 1.2. (Global well-posedness) The permeability tensor $\Pi$ satisfies (1.5) and the initial divergence free velocity field $\mathbf{u}_0\in H^{2}(\Omega_{f})$ satisfies the compatibility condition (1.6), then there exists a positive constant $C$ depending only on $\mu_{1}, \Omega_{f}$, and $\lambda$, such that if

the three-dimensional coupled Navier-Stokes-Darcy systems (1.2)–(1.4) have a unique global strong solution $(\mathbf{u}, P_2)\in X(0, +\infty)$ as described in Definition 1.

Moreover, the solution $(\mathbf{u}, P_2)$ has a decay rate

where the positive constants are $C = C(\mu_{1}, \; \lambda, \; \Omega_{f}, \; \|\mathbf{u}_{0}\|_{ H^{2}(\Omega_{f})})$ and $c = c(\mu_{1}, \Omega_{f})$.

Remark 1. In divergence from the findings of ^[41,42], this paper makes two primary contributions. First, in terms of analytical techniques, the involvement of more intricate directional derivatives under the three-dimensional model renders estimations challenging and convoluted. Second, regarding outcomes, our research is centered on a strip domain, breaking away from the conventional assumption of periodicity. This marks a pioneering achievement as the first three-dimensional outcome in the rigorous examination of robust solutions for the Navier-Stokes-Darcy system. Notably, our results extend beyond, demonstrating applicability, even in the context of periodic domains.

Furthermore, $\epsilon_{0}$ in Theorem 1.2 will depend on $\|\nabla\mathbf{u}_{0}\|_{L^{2}(\Omega_{f})}$.

Remark 2. The decay rate obtained in (1.7) indicates that after time $t > 0$, the solution $(\mathbf{u}, P_{2})$ is smooth, and all its derivatives decay for any order.

The existence and uniqueness of local solutions to this problem can be obtained similarly to the approach in ^[41]. Therefore, our subsequent focus will be on the a priori estimates of the global solution.

2.   A priori estimates

As is well known, the global strong solution to the nonlinear partial differential equations can be obtained by combining local solutions with global a priori estimates. The local solution is proved similarly to that in ^[41] and is omitted here. Instead, we present the crucial a priori estimates pivotal to establishing global well-posedness below. Note that \(K = \frac{\Pi}{\mu_{2}}\) and \(\mathcal{W} = \frac{\mu_{1}\alpha}{\sqrt{\text{tr}\, \Pi}}\) for convenience in the subsequent discussion.

2.1.   A priori estimates (Ⅰ): Lower order estimates

Proposition 2.1. If $(u, P_2)$ is a smooth solution of the Navier-Stokes-Darcy systems (1.3) and (1.4) satisfying

then the following estimates hold:

and

provided

where $C$ depends only on $\mu_{1}, \Omega_{f}$, and $\lambda$.

The proof of Proposition 2.1 can be successfully summarized by the following Lemmas 2.1–2.4.

Lemma 2.1. Under the conditions of Proposition 2.1, it holds that

Proof. Multiplying $(1.3)_{1}$ by $\mathbf{u}$ and integrating the result equation on $\Omega_{f}$, then multiplying $(1.2)$ by $P_{2}$ and integrating it on $\Omega_{m}$, we add up the two resulting equations to have

where we have used Hölder's inequality, Young's inequality, Gagliardo-Nirenberg inequality, Korn's inequality, and (2.1). Here $C$ depends on the domain $\Omega_{f}$. By integrating (2.5) over $(0, t)$, one gets (2.4) with $\epsilon_{0}\leq \frac{\mu_{1}^{2}}{C^{2}M}$ and (2.1). □

Lemma 2.2. Under the conditions of Proposition 2.1, it holds that

Proof. Multiply $(1.3)_{1}$ by $\mathbf{u}_{t}$ and integrate it over $\Omega_{f}$, while differentiating $(1.2)$ with respect to $t$, then multiply by $P_2$ and integrate it over $\Omega_{m}$. Now, summing up the two resulting equations yields with Hölder's inequality, Gagliardo-Nirenberg inequality, Young's inequality, Korn's inequality, and (2.1):

where $C$ depends on $\mu_{1}$ and $\Omega_{f}$.

Next, we come to estimate $\|\nabla^{2} \mathbf{u}\|_{L^{2}(\Omega_{f})}$. The fact that

tells us to deduce the estimations on $\|D(\mathbf{u}_x)\|_{L^{2}(\Omega_{f})}$ minutely, we omit the details of the estimations on $\|D(\mathbf{u}_y)\|_{L^{2}(\Omega_{f})}$ due to the symmetry in the horizontal direction. We know from (2.8) and (2.23)–(2.28) that

thus, we can get from $C \|\mathbf{u}_{0}\|_{L^{2}(\Omega_{f})}^{\frac{1}{2}} M^{\frac{1}{2}}\leq\frac{1}{2}$ that

Next, taking the partial derivative of $(1.3)_{1}$ with respect to $x$, we get

Multiplying (2.10) by $\mathbf{u}_{x}$ and integrating the result inequality with respect to $\mathbf{x}$ over $\Omega_{m}$, then using Hölder's inequality, Gagliardo-Nirenberg inequality, Young's inequality, Korn's inequality, and (2.1), one can get

and, similarly, we have

Therefore, plugging (2.9) into (2.7) and combining (2.1), (2.11), and (2.12), one gets

where we have used $C (\|\mathbf{u}_{0}\|_{L^{2}(\Omega_{f})} +\|\mathbf{u}_{0}\|_{L^{2}(\Omega_{f})}^{\frac{1}{2}} M^{\frac{1}{2}} +\|\mathbf{u}_{0}\|_{L^{2}(\Omega_{f})}M) \leq\frac{1}{2}$. Integrating (2.13) over $(0, t)$, we can obtain (2.6) with Lemma 2.1, Young's inequality, and

Thus, the proof of Lemma 2.2 is completed. □

While combining Lemmas 2.1 and 2. 2, we have

Therefore, the proof of (2.2) is complete.

Lemma 2.3. Under the conditions of Proposition 2.1, it holds that

Proof. Differentiate $(1.3)_{1}$ with respect to $t$, multiply by $\mathbf{u}_{t}$, then integrate over $\Omega_{f}$. Differentiate $(1.2)$ with respect to $t$, multiply by $\partial_{t}P_{2}$, then integrate over $\Omega_{m}$. Adding up the two result equations, we obtain that

where we have used Hölder's inequality, Young's inequality, Gagliardo-Nirenberg inequality, and Korn's inequality, then we can obtain by Grönwall's inequality that

The proof is completed with the supports of Lemmas 2.1 and 2.2. □

Lemma 2.4. Under the conditions of Proposition 2.1, it holds that

Proof. Put $\partial_{x}$ on $(1.3)_{1}$ and multiply $\mathbf{u}_{t, x}$ by both sides of it, then integrate it on $\Omega_{f}$; meanwhile, apply $\partial_{x}\partial_{t}$ to $(1.2)$, then multiply by $\partial_{x}P_{2}$ and integrate it on $\Omega_{m}$. Adding up the two resulting equations gives that

where we have used Poincaré's inequality, Hölder's inequality, Young's inequality, Gagliardo-Nirenberg inequality, and Korn's inequality. Similarly, we can derive that

then we add up (2.17) and (2.18), and use Grönwall's inequality, Lemma 2.1, and Lemma 2.2 to get

Therefore, know from (2.9) and (2.19) that

and it is easy to get that (see ^[42])

thus, the proof of Lemma 2.4 is complete with (2.4), (2.6), (2.9), (2.14), (2.19), and (2.20). □

The proof of Proposition 2.1 has been finished. Next, we will proceed with the higher-order estimation involving the time weighting.

2.2.   A priori estimates (Ⅱ): Higher order estimates

Let $\sigma(t) = \min\{1, t\}$ and, from now on, the generic positive constant is defined by the right term of (2.3) as $N \triangleq C(\|\mathbf{u}_{0}\|_{H^{2}(\Omega_{f})}^{2}+1) \exp \{\|\mathbf{u}_{0}\|_{H^{1}(\Omega_{f})}^{2} +\|\mathbf{u}_{0}\|_{H^{1}(\Omega_{f})}^{4}\}$.

We have the following third-order estimates.

Lemma 2.5. It holds that

Proof. It follows from the fact that

First, we focus on $\mathbf{u}_{z, z}$. By $(1.3)_{1}$, we have

and taking divergence to $(1.3)_{1}$, the elliptic problem can be obtained as follows:

With the boundary condition obtained by $(1.3)_{2}$ and $(1.4)_{1}$, we have

It is clear to show by Lemma 2.5 ^[41] and the Trace theorem that

The estimation of $\|\mathbf{u}\cdot\nabla\mathbf{u}\|_{L^{2}(\Omega_{f})}^{2}$ can be estimated by Hölder's inequality, Gagliardo-Nirenberg inequality, Young's inequality, and Korn's inequality as follows:

Thus, we can derive with (2.23), (2.27), and (2.21), by Young's inequality, that

Obviously, from (2.23) with Hölder's inequality, Young's inequality, Gagliardo-Nirenberg inequality, Poincáre's inequality, Sobolev inequality, and Korn's inequality we have

where we have used the estimation obtained based on (2.27) as follows:

and, again, using Lemma 2.5 ^[41] together with the Trace theorem to get that

such that we have

Next, we will get the bound of each term at the righthand of (2.31) step by step.

Step 1. Next, we apply $\partial_{x}\partial_{y}$ to $(1.3)_{1}$ and multiply $\mathbf{u}_{t, x, y}$ before integrating the result equations over $\Omega_{f}$; meanwhile, we apply $\partial_{x}\partial_{y}$ to $(1.2)$ and integrate it over $\Omega_{m}$ after multiplying $P_{2, x, y}$ on it. Finally, summing up the two resulting equations would come to (2.32), with the help of Hölder's inequality, Gagliardo-Nirenberg inequality, Young's inequality, and Korn's inequality,

Multiplying (2.32) by $\sigma(t)$ and integrating the result over $(0, t)$, with integration by parts and Young's inequality, obtains that

Similarly, we can get

and

Step 2. For $\|D(\mathbf{u}_{t})\|_{L^{2}(\Omega_{f})}^{2}$, first differentiate $(1.3)_{1}$ with respect to $t$ and multiply by $\partial_{t}^{2}\mathbf{u}$, then integrate it on $\Omega_{f}$. Meanwhile, apply $\partial_{t}^{2}$ to $(1.2)$ and multiply by $\partial_{t}^{2}P_{2}$, then integrate it on $\Omega_{m}$. At last, summing up the two resulting equations with Hölder's inequality, Gagliardo-Nirenberg inequality, and Young's inequality gains that

Multiplying (2.36) by $\sigma(t)$ and integrating the result over $(0, t)$, with Lemma 2.3 and Young's inequality, obtains that

Step 3. Undoubtedly, from (2.25), (2.29), and (2.30), we get that

where we have used the estimation:

and

which are derived by Hölder's inequality, Gagliardo-Nirenberg inequality, and Young's inequality. Thus, from (2.38), we could derive that

Step 4. Apply $\partial_{t}\partial_{x}$ to $(1.3)_{1}$, then multiply $\sigma(t)\mathbf{u}_{t, x}$ and integrate the result equation over $\Omega_{f}$. Meanwhile, apply $\partial_{t}\partial_{x}$ to $(1.2)$, then multiply $\sigma(t)\partial_{t}\partial_{x}P_{2}$ and integrate the result equation over $\Omega_{m}$. Summing up the two resulting equations, we obtain with Hölder's inequality, Gagliardo-Nirenberg inequality, and Young's inequality that

which means that

and, similarly, we have

Finally, conclusions can be derived from Proposition 2.1, (2.21), (2.31), (2.33), (2.34), (2.35), (2.37), (2.40), (2.41), and (2.42) that

So far, it's time to complete the 3-order estimates in the next step.

Step 5. We detailedly display the estimate of $\int_{0}^{t}\sigma(s)\|D(\mathbf{u}_{x, x, y})\|_{L^{2}(\Omega_{m})}^{2}\ ds$ in this step, then the estimates of $\int_{0}^{t}\sigma(s)\|D(\mathbf{u}_{x, x, x})\|_{L^{2}(\Omega_{m})}^{2}\ ds$, $\int_{0}^{t}\sigma(s)\|D(\mathbf{u}_{x, y, y})\|_{L^{2}(\Omega_{m})}^{2}\ ds$, and $\int_{0}^{t}\sigma(s)\|D(\mathbf{u}_{y, y, y})\|_{L^{2}(\Omega_{m})}^{2}\ ds$ can be obtained in a similar derivation.

Apply $\partial_{x}^{2}\partial_{y}$ to $(1.3)_{1}$ and multiply by $\sigma(t)\mathbf{u}_{x, x, y}$ before integrating the resulting equations over $\Omega_{f}$. Meanwhile, apply $\partial_{x}^{2}\partial_{y}$ to $(1.2)$ and multiply $\sigma(t)\partial_{x}^{2}\partial_{y}P_{2}$ on it after that, integrate over $\Omega_{m}$. Finally, summing up the above two resulting equations could come to

the proof of which is reckoned from the Gagliardo-Nirenberg inequality and Young's inequality. It is easy to find that

then, similarly, we have

and it is more concisely to be derived that

so that the proof of Lemma 2.5 is completed with Young's inequality. □

Using a similar argument as that in the proof of Lemma 2.5, we can easily obtain the following fourth-order estimates.

Lemma 2.6. It holds that

Proof. It follows from the fact that

Obviously, from (2.23) with Hölder's inequality, Young's inequality, Gagliardo-Nirenberg inequality, Poincáre's inequality, Sobolev inequality, and Korn's inequality we have that

where

Additionally, we leverage Lemma 2.5 ^[41], coupled with the Trace theorem. The methodology employed here mirrors that of (2.26). We obtain

such that one gets

Step 1. We detail work on $\sigma(t)^{2}\|D(\mathbf{u}_{x, x, y})\|_{L^{2}(\Omega_{f})}^{2}$ in this step to get $\sigma(t)^{2}\|D(\mathbf{u}_{x, x, x})\|_{L^{2}(\Omega_{f})}^{2}$, $\sigma(t)^{2}\|D(\mathbf{u}_{x, y, y})\|_{L^{2}(\Omega_{f})}^{2}$, and $\sigma(t)^{2}\|D(\mathbf{u}_{y, y, y})\|_{L^{2}(\Omega_{f})}^{2}$.

Apply $\partial_{x}^{2}\partial_{y}$ to the Eq $(1.3)_{1}$ and multiply by $\partial_{x}^{2}\partial_{y}\mathbf{u}_{t}$. Meanwhile, apply $\partial_{x}^{2}\partial_{y}$ to $(1.2)$ and multiply by $\partial_{x}^{2}\partial_{y}P_{2}$, integrate the two equations with respect to $\mathbf{x}$ by parts, then add up the resulting formulas to get

then by multiplying by $\sigma(s)^{2}$ and integrating over $(0, t)$, one has

We can get the similar results on $\sigma(t)^{2}\|D(\mathbf{u}_{x, x, x})\|_{L^{2}(\Omega_{f})}^{2}, \; \sigma(t)^{2}\|D(\mathbf{u}_{x, y, y})\|_{L^{2}(\Omega_{f})}^{2},$ and $\sigma(t)^{2}\|D(\mathbf{u}_{y, y, y})\|_{L^{2}(\Omega_{f})}^{2}$; thus, we have

Step 2. For $\|\nabla^{2}\mathbf{u}_{t}\|_{L^{2}(\Omega_{f})}$, we have

First, we apply $\partial_{x}\partial_{t}$ to the Eq $(1.3)_{1}$ and multiply by $\mathbf{u}_{t, t, x}$. Meanwhile, apply $\partial_x\partial_{t}$ to $(1.2)$ and multiply by $\partial_x\partial_t P_{2}$, integrate the two equations with respect to $x$ by parts, then we add up the resulting formulas to get

Multiplying by $\sigma(s)^{2}$ on (2.50) and integrating over $(0, t)$ with (2.3) and (2.22) yields:

then, similarly, we have

Second, we try to get a bound of $\|\mathbf{u}_{t, z, z}\|_{L^{2}(\Omega_{f})}$, and differentiating (2.23) with respect to $t$ shows that

For $\|\mathbf{u}_{t, t}\|_{L^{2}(\Omega_{f})}^{2}$, first apply $\partial_{t}^{2}$ to $(1.3)_{1}$ and multiply by $\sigma(t)^{2}\partial_{t}^{2}\mathbf{u}$. Meanwhile, apply $\partial_{t}^{2}$ to $(1.2)$ and multiply by $\sigma(t)^{2}\partial_{t}^{2}P_{2}$, then integrate it on $\Omega_{m}$. At last, integrate the two resulting equations with respect to $\mathbf{x}$ and $t$ and sum them up to arrive at

where we have used Lemma 2.5. Next, it's time to deal with $\|\nabla\partial_{t} P_{1}\|_{L^{2}(\Omega_{f})}$. We differentiate (2.24) and (2.25) with respect to $t$, and then using the standard $L^2$-estimate for the elliptic system with (2.3), (2.51), and (2.52), we have

Next, plugging (2.54) and (2.55) into (2.53), we can get that

Similarly, we can plug (2.56), (2.51), and (2.52) to (2.49) to obtain

Step 3. We work on $\|\nabla\mathbf{u}_{x, z, z}\|_{L^{2}(\Omega_{f})}^{2} +\|\nabla\mathbf{u}_{y, z, z}\|_{L^{2}(\Omega_{f})}^{2}$ in this step. Applying the gradient operator $\nabla$ to (2.38), then multiplying by $\sigma(s)^{2}$ and integrating over $(0, t)$ yields

where we have used Proposition 2.1, (2.44), (2.47), (2.48), (2.51), and (2.52).

We now estimate $\|\nabla^{2}\partial_{x} P_{1}\|_{L^{2}(\Omega_{f})}^{2} +\|\nabla^{2}\partial_{y} P_{1}\|_{L^{2}(\Omega_{f})}^{2}$. We apply Lemma 2.5 in ^[41] together with the Trace theorem on (2.24) and (2.25), similarly as (2.39), to get that

Now, we respectively apply $\partial_{x}^{2}, \ \partial_{x}\partial_{y}, \ \partial_{y}^{2}$ to (2.23) and multiply by $\sigma(s)^{2}$ to get

where we have used Lemma 2.5, (2.44), (2.51), and (2.52), and it remains to estimate the last three terms on the righthand side. Again, we apply Lemma 2.5 ^[41] together with the Trace theorem on (2.24) and (2.25), similarly as (2.39), to get that

thus, combining the above steps, we can complete the proof of Lemma 2.6. □

3.   Proof of Theorem 1.2

First of all, we know that the systems (1.3) and (1.4) have a unique local strong solution $(\mathbf{u}, P_2)$ on $\Omega\times (0, T_{*}]$ for some $T_{*} > 0$, so it's time to verify the continuity of the strong solution to extend it globally in time with counter-evidence.

It follows from the fact that $\mathbf{u}_{0}\in H^{2}(\Omega_{f})$ and Proposition 1.1 that there exists a $T_{1} \in (0, T_{*}]$ such that (2.1) holds for $T = T_{1}$. Next, we set

then $T^{*}\geq T_{1}\geq 0$. Hence, for any $0 < \tau < T\leq T_{*}$ with $T$ finite, we can get

from Proposition 2.1, and Lemmas 2.5 and 2.6. Thus one can deduce that

from

Now, we suppose that

then $T = T^{*}$ holds by Proposition 2.1 and (2.2). It follows from (3.2) that

thus, the initial data condition in Proposition 1.1 is satisfied, which gives that there exists a $T^{**} > T^{*}$ such that (2.1) holds for $T = T^{**}$. This contradicts the definition of $T^{*}$ in (3.1), so $T^{*} = \infty$.

Finally, to finish the proof of Theorem 1.2, we have from (2.5) that

According to the Poincar inequality for three-dimensional cases, we have

then substituting (3.6) into (3.5), we get

Therefore, we have

Here, the positive constants are $C = C(\mu_{1}, \; \lambda, \; \Omega_{f}, \| \; \mathbf{u}_{0}\|_{ H^{2}(\Omega_{f})})$ and $c = c(\mu_{1}, \Omega_{f})$.

4.   Conclusions

In conclusion, this study has made some progress in understanding the global well-posedness of a coupled Navier-Stokes-Darcy model with the Beavers-Joseph-Saffman-Jones interface boundary condition in three-dimensional Euclidean space. Through our investigation, we have achieved the establishment of a global strong solution for the system, marking a crucial advancement in the field. Moreover, we have demonstrated the exponential stability of this strong solution, further reinforcing its reliability. The implications of our findings extend to the analysis of subsurface flow problems, notably in the realm of karst aquifers, where such coupled systems play a pivotal role. By shedding light on the dynamics and behaviors of these systems, our research contributes to a deeper understanding of fluid flow phenomena in complex geological formations, offering valuable insights for both theoretical developments and practical applications in hydrogeology and related disciplines.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

We wish to acknowledge the support of the National Natural Science Foundation of China (Grant No. 11931013, 12061081), the Natural Science Foundation of Shaanxi Province (Grant No. 2023-JC-QN-0073), the Natural Science Foundation of Yulin (Grant No. CXY-2022-76), and the Natural Science Foundation of Yulin University (Grant No. 21GK07).

Conflict of interest

The authors have no conflicts to disclose.