1.
Introduction
The World Health Organization [1] regards the online game addiction (OGA) as a new disease. The general defining feature of this disease is "persistent and recurrent use of the internet to engage in games, often with other players, leading to clinically significant impairment or distress" (see [2]). OGA is often an addictive mental disease. People with OGA tend to be impulsive, violent, misanthropic and withdrawn. As the number of internet users continues to increase, the number of people addicted to online games, especially children, is also growing. The research on OGA has attracted wide attention. The diagnostic and statistical manual of mental disorders [3,4] proposed some classification criteria for OGA. To better cure and reduce the population of OGA, scholars from all walks of life began to study it from various perspectives. One of the important research methods to reveal the dynamic behavior of OGA is using mathematical models. In recent years, some mathematical workers have made use of various mathematical theories and methods to study the OGA problem. For example, Li and Guo [5,6] studied the stability and optimal control of two kinds of OGA mathematical models. Viriyapong and Sookpiam [7] discussed the stability and qualitative behavior of an OGA model for children and youth in Thailand. Therefore, we try to apply a differential equation model to study the OGA problem in this manuscript.
Inspired by the previous works [5,6,7,8] in terms of population division of online gamers, based on the ideas and methods of the papers [9,10,11,12,13], we put forward a mathematical model to describe the changes and interactions of population density with OGA under unsustainable treatment as follows:
where U(τ) and V(τ) stand for the population densities of moderate gamers and addictive gamers at time τ, respectively. r stands for the proportion coefficient of population density of new gamers. aU(τ) is the population density of stopping gaming for moderate gamers through self-control. bU(τ)V(τ) indicates the number of population density converted from moderate gamers to addictive gamers. βΘ(τ)V(τ) measures the unsustainable treatment for an addictive gamer. r,a,b,β>0 are some constants.
As we all know, the number of moderate and addictive gamers not only depends on time variables τ, but also often shows a certain diffusion in space. Therefore, we modify the system (1.1) to the following diffusion partial differential equation model:
where the practical meanings of U(τ,⋅), V(τ,⋅), r, aU(τ,⋅), bU(τ,⋅)V(τ,⋅) and βΘ(τ,⋅)V(τ,⋅) are the same as in system (1.1). di>0(i=1,2) is the diffusion coefficient. Δ is the Laplacian. Ω⊂R is bounded, and its boundary ∂Ω is smooth. The unsustainable treatment function Θ(τ,⋅) has the following characteristics:
(A1) Θ(τ,⋅) is piecewise continuous with respect to τ∈[0,∞), that is, Θ(τ,⋅) is continuous in the interval I∈[0,∞)∖B, where B={τk∈[0,∞):Θ(τ−k,⋅)<Θ(τ+k,⋅)} is countable. For any compact subset of [0,∞), Θ(τ,⋅) has a finite number of discontinuities. For all τ1,τ2∈[0,∞), Θ(τ1,⋅)≤Θ(τ2,⋅) provided that τ1<τ2. 0<γ≤Θ(τ,⋅), and Θ(0,⋅)=Θ(0+,⋅)=γ.
To study the dynamic behavior of model (1.2), the following initial and boundary conditions are necessary:
where →n is the outward normal vector of ∂Ω. The initial values U0(⋅) and V0(⋅) satisfy the below assumption:
(A2) For ∀x∈Ω, U0(⋅),V0(⋅)>0, and U0(⋅),V0(⋅)∈L∞(Ω).
It is similar to [14,15] that the model (1.2) with initial and boundary conditions (1.3) is rewritten of the form
where ¯[Θ(τ,⋅)]=[Θ(τ−,⋅),Θ(τ+,⋅)], Θ(τ−,⋅)=limτ→τ−Θ(τ,⋅), Θ(τ+,⋅)=limτ→τ+Θ(τ,⋅). Obviously, ¯[Θ(τ,⋅)]=Θ(τk,⋅) provided that Θ(τ,⋅) is continuous at τ=τk.
This paper mainly studies the well-posedness and stability of the solution of the model (1.2) with initial and boundary conditions (1.3) with the help of (1.4). The principal illuminating points of our research work are as below:
(i) By analyzing the mechanism of OGA and considering the unsustainable treatment, we establish a new ordinary differential equation model (1.1). Considering that the population of gamers has a certain diffusion in space, we propose a novel diffusion partial differential equation model (1.2).
(ii) We first convert the model (1.2) with initial and boundary conditions (1.3) into differential inclusion (1.4). Next, we study the boundness and existence of solutions to the model (1.2) with initial and boundary conditions (1.3). Meanwhile, we build some Lyapunov type functionals and prove the global stability of the model. Finally, an example is numerically simulated and analyzed using MATLAB. The numerical simulation is in good agreement with the theoretical results.
(iii) The major outcomes of the paper provide theoretical help for the research and treatment of online game addiction. Our work provides an example for applying mathematical theories and methods to solve social problems such as online game addiction, which makes the study of this kind of problem transform from the qualitative to the quantitative.
The paper's remaining structure is as follows. In Section 2, we prove that the model has bounded solutions. In Section 3, the global stability of the steady states of the model is studied. A numerical example and simulation are given in Section 4. Finally, a brief summary is made in Section 5.
2.
Existence and boundedness
Definition 2.1. Let ϕ1(U,V)=r−aU−bUV, ϕ2(U,V)=bUV−β¯[Θ(τ,⋅)]V. (U,V) is a solution of (1.4) if and only if, for U,V∈C([0,σ],H), ∃Λ1(U,V)∈L1([0,σ],H), Λ2(U,V)∈ϕ2(U,V) within (0,σ) satisfying that (U,V) is a solution in (0,σ) of the following equation:
Set Y=C([0,σ],H)×C([0,σ],H) and define W=(U,V)T∈Y, and then Eq (2.1) is rewritten by
where the operators L and F are defined as
The solution of (2.2) is formulated by
where T(τ)=(T1(τ),T2(τ))T, and T1(τ) and T2(τ) are compact and strong C0-semigroup induced by d1Δ and d2Δ with ∂U(τ,⋅)∂→n=∂V(τ,⋅)∂→n=0, respectively.
Theorem 2.1. Assume that (A1) and (A2) are true. Then, for any solution W(τ,⋅)=(U(τ,⋅),V(τ,⋅)) of system (1.2) with initial and boundary conditions (1.3), there exist the constants N1,N2>0, such that N1≤U(τ,⋅),V(τ,⋅)≤N2, ∀(τ,x)∈[0,∞)×Ω.
Proof. Taking L−1=min{βb, minx∈ΩU0(⋅)}, L+1=max{β(γ+1)b, maxx∈ΩU0(⋅)}, L−2=min{r−aL−1bL−1, minx∈ΩV0(⋅)} and L+2=max{rbL−1, maxx∈ΩV0(⋅)}, we define R by
Obviously, W0(⋅)=(U0(⋅),V0(⋅))T∈R. It is similar to [16] that T(t)W0(⋅)∈R. Define a vector field
On the left of R, choosing U=L−1, L−2≤V≤L+2, one derives from (2.3) and (2.4) that
On the right of R, taking U=L+1, L−2≤V≤L+2, it is similar to (2.5) that
On the below of R, associating with (2.3), (2.4), (A1) and (A2), letting V=L−2, L−1≤U≤L+1, 0<γ≤Θ(τ,⋅), we have
On the above of R, choosing V=L+2, L−1≤U≤L+1, 0<γ≤Θ(τ,⋅), we similarly obtain
From (2.5)–(2.8), similar to [16,17], one knows that R is the invariant set of F. Thereby, taking N1=min{L−1,L−2}, N2=max{L+1,L+2}, one has N1≤U(τ,⋅),V(τ,⋅)≤N2, ∀(τ,x)∈[0,∞)×Ω. The proof is completed. To prove the existence of solutions, we need the below fixed point theorem.
Lemma 2.1. [18,19] Let K be a nonempty and weakly compact subset in a real Hilbertspace H and let E:K→P(K) be such that for each u∈K, E(u) is closed and convex. If the graph Graf(E) of E is weakly × weakly sequentially closed, then E has at least one fixedpoint, i.e., there exists at least one element u∈K such that u∈E(u).
Definition 2.2. [20] Let X be a Lebesgue measurable subset in Rq, q≥1, and E:X→P(H) be a mapping. A function f:X→H is called a selection of E if f(z)∈E(z) a.e. z∈X. The set of all the measurable selections of E is denoted by Sel(E).
Theorem 2.2. The model (1.2) with initial and boundary conditions (1.3) has at least one solution W∗(τ,⋅)=(U∗(τ,⋅),V∗(τ,⋅))∈C([0,∞),H)×C([0,∞),H), for (τ,x)∈[0,∞)×Ω, provided that (A1) and (A2) are true.
Proof. Our proof is thanks to [20,21]. We first prove that the model (1.2) with initial and boundary conditions (1.3) has at least a solution W∗(τ,⋅)=(U∗(τ,⋅),V∗(τ,⋅))∈Y. In fact, from Theorem 2.1 together with (A1) and (A2), one knows that there exist some constants M,R>0 such that max{‖U∗‖H,‖V∗‖H}≤M, and for all (x,y)∈(ϕ1(U,V),ϕ2(U,V)), max{‖U‖H,‖V‖H}≤M+1 implies that max{‖x‖H,‖y‖H}≤R+1. Let
K is nonempty and weakly compact in L2([0,σ],H)×L2([0,σ],H). Define Pσ:K→Y as
where (U∗,V∗) is the unique solution on [0,σ] of (2.1). Adopting fallacy reduction, one easily verifies that max{‖U‖H‖V‖H}≤M+1. Define the operator E:K→P(K) as
where Pσ(Λ1,Λ2)=(U∗,V∗). From Theorem 3.4 of [22], Theorem 2.3.3 of [23], Proposition 3.6 of [22] and Theorem 3.3 of [21], we know that the graph Graf(E) of E is weakly × weakly sequentially closed in K. It follows from Lemma 1 that there is (Λ1,Λ2)∈K such that (Λ1,Λ2)∈E((Λ1,Λ2)), and consequently Pσ(Λ1,Λ2)=(U∗,V∗) is a weak solution of (2.1). Since (Λ1,Λ2)∈L2([0,σ],H)×L2([0,σ],H), Theorem 3.6 of [22] ensures that Pσ(Λ1,Λ2)=(U∗,V∗) is in fact a strong solution of (2.1).
Next, we need to show that this strong solution W∗(τ,⋅)=(U∗(τ,⋅),V∗(τ,⋅)) of (2.1) defined on [0,∞). Indeed, according to the continuation theorem, the maximum existence interval of solution of the strong solution W∗(τ,⋅)=(U∗(τ,⋅),V∗(τ,⋅)) is a form of [0,σ∗). Assume that σ∗<∞, we derive from [24] that
which contradicts he boundedness of W∗(τ,⋅)=(U∗(τ,⋅),V∗(τ,⋅)). Thus, the model (1.2) with initial and boundary conditions (1.3) has a strong solution W∗(τ,⋅)=(U∗(τ,⋅),V∗(τ,⋅)) on [0,∞). The proof is completed.
3.
Global asymptotic stability
It is easy to see that the model (1.2) with initial and boundary conditions (1.3) has two steady states S=(U∗0,V∗0)=(ra,0) and S+=(U∗+,V∗+) determined by
In light of (3.1), we obtain h(V)≜, and the steady state S_+ = (\mathcal{U}^*_+, \mathcal{V}^*_+) is represented by \mathcal{U}^*_+ = \frac{\beta\Theta^*}{b} , \mathcal{V}^*_+ = \frac{rb-a\beta\Theta^*}{b\beta\Theta^*} , where \Theta^*\in\overline{[\Theta(\tau, \cdot)]} . Next, we shall discuss the global asymptotic stability of steady states S and S_+ in \mathcal{R} .
Theorem 3.1. The semi-positive steady state S of the model (1.2) with initial and boundary conditions (1.3) possesses global asymptotic stability in \mathcal{R} , provided that rb < a\beta\gamma .
Proof. Clearly, the steady state S is semi-positive. Build a functional
Obviously, V(\tau) is smooth. Let g(\mathcal{U}) = \mathcal{U}-\frac{r}{a}-\frac{r}{a}\ln\frac{a\mathcal{U}}{r} , and then g'(\mathcal{U}) = 1-\frac{r}{a\mathcal{U}} , which implies that g(\mathcal{U})\geq g(\frac{r}{a}) = 0 . Thus, we have V(\tau) > 0 for all \tau\neq0 and V(0) = 0 . Moreover, according to [15], one knows that the set \{\tau\in\mathbb{R}:V(\tau)\leq\alpha\} is bounded for \alpha\geq0 . Define \mathcal{G}(\mathcal{U}, \mathcal{V}) as
From (1.2), (A_1) and (A_2) , one knows that the set-valued map \mathcal{G}(\mathcal{U}, \mathcal{V}) is upper semi-continuous and non-empty compact convex. For any \zeta = (\zeta_1, \zeta_2)^T\in\mathcal{G}(\mathcal{U}, \mathcal{V}) , there is a \Theta^*\in\overline{[\Theta(\tau, \cdot)]} such that
From (3.2), one calculates (\frac{\partial V}{\partial\mathcal{U}}, \frac{\partial V}{\partial\mathcal{V}})\cdot\zeta as
After simplification, (3.3) gives
By Green's first identity and (1.3), one has
Moreover, from rb < a\beta\gamma , we obtain the following estimation:
Noticing that V(0) = 0 , provided that (\mathcal{U}, \mathcal{V}) = (\frac{r}{a}, 0) , based on [15] and (3.6), one knows that V(\tau) is a Lyapunov function of (1.2). According to the boundedness of (1.2) in Theorem 2.1, the parabolic L^p -theory, the Sobolev Embedding Theorem and the standard compactness argument (see [25]), one knows that there exist some constants M, \tau_0 > 0 such that \|\mathcal{U}(\tau, \cdot)\|_{C^2(\overline{\Omega})}+\|\mathcal{V}(\tau, \cdot)\|_{C^2(\overline{\Omega})}\leq M , for all \tau\geq\tau_0 . Thereby, it follows from the Sobolev Embedding Theorem [20] that (\mathcal{U}, \mathcal{V})\to(\frac{r}{a}, 0) in L^2(\Omega)\times L^2(\Omega) , as \tau\to\infty . Also, \frac{dV}{d\tau} = 0 iff (\mathcal{U}, \mathcal{V}) = (\frac{r}{a}, 0) , which implies that \{(\mathcal{U}, \mathcal{V}):\frac{dV}{d\tau} = 0\} = \{(\frac{r}{a}, 0)\} . Thus, the steady state S attracts all the solutions of system (1.2). The proof is completed.
Theorem 3.2. The positive steady state S_+ of the model (1.2) with initial and boundary conditions (1.3) possesses global asymptotic stability in \mathcal{R} , provided that rb\geq a\beta\gamma .
Proof. When the condition rb\geq a\beta\gamma is true, \mathcal{V}^*_+ = \frac{rb-a\beta\Theta^*}{b\beta\Theta^*} > 0 . Thus, one knows that S_+ is a unique positive steady state of system (1.2). The key of the proof is the construction of Lyapunov functional W(\tau) and the estimation of \frac{dW}{d\tau} . In fact, one can construct the Lyapunov functional W(\tau) as
By (3.7), one has
By simplification, similar to (3.5), one derives from the condition rb\geq a\beta\gamma and (3.8) that
In view of (3.7), (3.9) and the remaining discussion being similar to Theorem 3.1, one concludes that the positive steady state S_+ attracts all the solutions of system (1.2). The proof is completed.
4.
Illustrative example and simulation
This section considers the following reaction-diffusion OGA model:
where \Omega = (0, 10) , d_1 = 0.6 , d_2 = 0.3 , \Theta(\tau, \cdot) = 0.8+\frac{0.2}{\pi}\arctan([\tau]) , \mathcal{U}_0(x) = 1+|\sin(x)| , \mathcal{V}_0(x) = 1+|\cos(x)| , and [\tau] is a function such that only integral numbers are taken for the variable \tau . Obviously, the set of unsustainable points of unsustainable treatment \Theta(\tau, \cdot) is the natural number set \mathbb{N}^+ , which is infinitely countable.
4.1. Theoretical analysis
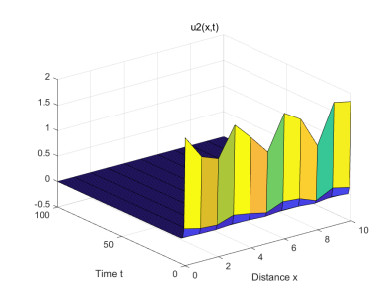
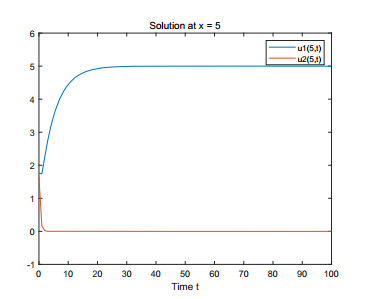
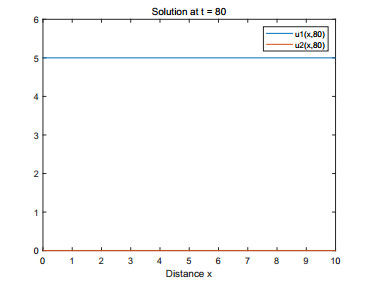
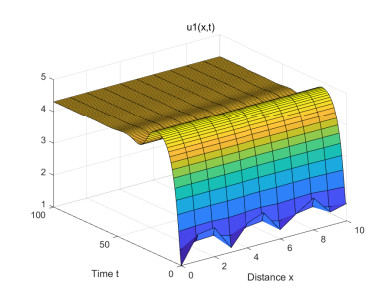
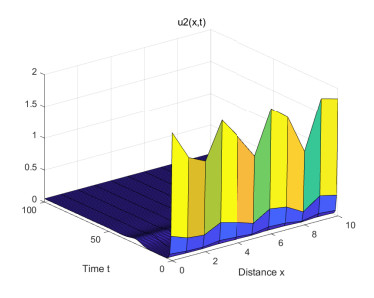
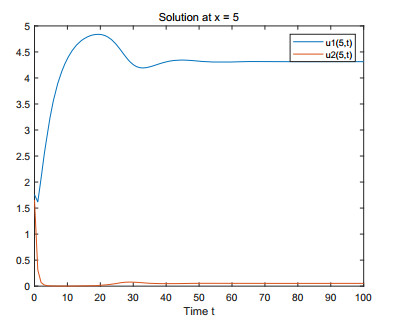
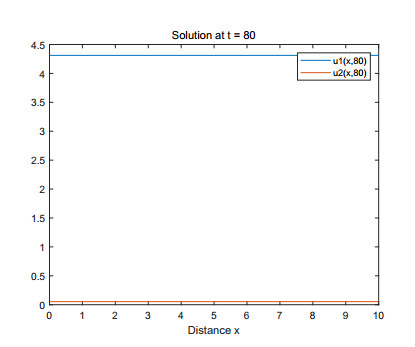
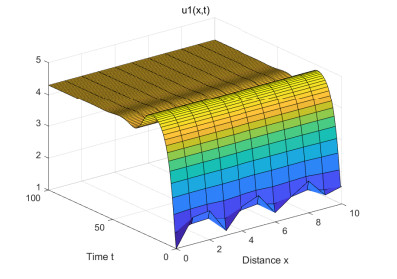
Case 1: Take r = 1 , a = 0.2 , b = 0.6 , \beta = 4 . From (4.1), one has \gamma = 0.8 , \min_{x\in\Omega}\mathcal{U}_0(x) = \min_{x\in\Omega}\mathcal{V}_0(x) = 1 , \max_{x\in\Omega}\mathcal{U}_0(x) = \max_{x\in\Omega}\mathcal{V}_0(x) = 2 , L^-_1 = \frac{20}{3} , L^+_1 = 12 , L^-_2 = 1 , L^+_2 = 2 . By Theorems 2.1 and 2.2, one knows that Eq (4.1) has at least a strong solution \mathcal{W}^*(\tau, \cdot) = (\mathcal{U}^*(\tau, \cdot), \mathcal{V}^*(\tau, \cdot)) , for (\tau, x)\in[0, +\infty)\times(0, 10) , satisfying 1\leq \mathcal{U}^*(\tau, \cdot), \mathcal{V}^*(\tau, \cdot)\leq12 . Moreover, the condition 0.6 = rb < a\beta\gamma = 0.64 is true, and it follows from Theorem 3.1 that the semi-positive steady state S = (\mathcal{U}_0^*, \mathcal{V}_0^*) = (\frac{r}{a}, 0) = (5, 0) of (4.1) has global asymptotic stability.
Case 2: Take r = 1 , a = 0.2 , b = 0.6 , \beta = 3 . Similar to Case 1, \gamma = 0.8 , L_1^- = 5 , L_1^+ = 9 , L_2^- = 1 , L_2^+ = 2 . We conclude from Theorems 2.1 and 2.2 that Eq (4.1) has at least a strong solution \mathcal{W}^*(\tau, \cdot) = (\mathcal{U}^*(\tau, \cdot), \mathcal{V}^*(\tau, \cdot)) , for (\tau, x)\in[0, +\infty)\times(0, 10) , satisfying 1\leq \mathcal{U}^*(\tau, \cdot), \mathcal{V}^*(\tau, \cdot)\leq9 . By the condition 0.6 = rb\geq a\beta\gamma = 0.48 , we know that the positive steady state S_+ = (\mathcal{U}^*_+, \mathcal{V}^*_+) is given by \mathcal{U}^* = \frac{\beta\Theta^*}{b} = 5\Theta^* , \mathcal{V}^* = \frac{rb-a\beta\Theta^*}{b\beta\Theta^*} = \frac{1-\Theta^*}{3\Theta^*} of (4.1), and has global asymptotic stability, where
Remark 4.1. Indeed, in Case 1, when the cure ratio of addictive gamers \beta > \frac{rb}{a\gamma} = 3.75 , mathematically speaking, as long as the cure is powerful enough, the addictive gamers will vanish, and the population density of moderate gamers will tend to \frac{r}{a} = 5 . Unfortunately, this case is difficult to achieve in practice. Generally speaking, the moderate gamers and addictive gamers coexist. People can only reduce the number of addictive gamers through treatment, and this treatment is intermittent and unsustainable. Therefore, Case 2 is more realistic.
Remark 4.2. In Case 2, due to the influence of unsustainable treatment \Theta(\tau, \cdot) = 0.8+\frac{0.2}{\pi}\arctan([\tau]) , the positive steady state S_+ = (\mathcal{U}^*_+, \mathcal{V}^*_+) varies with time variable \tau . By formula (4.2), when \tau\in(0, \infty)\setminus\mathbb{N}^+ , \Theta^* = 0.8+\frac{0.2}{\pi}\arctan([\tau]) , the positive steady state S_+ = (\mathcal{U}^*_+, \mathcal{V}^*_+) is uniquely determined by variable \tau . For example, taking \tau = 1.5 , \Theta^* = 0.8626 , and the positive steady state S_+ = (\mathcal{U}^*_+, \mathcal{V}^*_+)\approx(4.3128, 0.0531) . However, when \tau = n\in\mathbb{N}^+ , \Theta^* belongs to the closed interval \big[0.8+\frac{0.2}{\pi}\arctan(n-1), \, \, 0.8+\frac{0.2}{\pi}\arctan(n)\big] , and then the positive steady state S_+ = (\mathcal{U}^*_+, \mathcal{V}^*_+) is still not unique. For example, taking \tau = 2 , \Theta^*\in[0.8500, \, 0.8705] , and there exist infinite positive steady states S_+ = (\mathcal{U}^*_+, \mathcal{V}^*_+) .
4.2. Numerical simulation
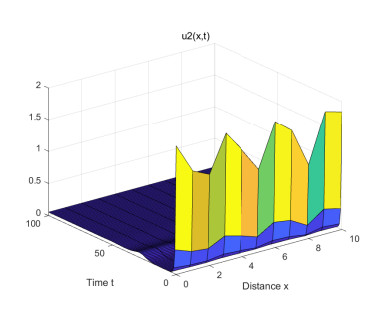
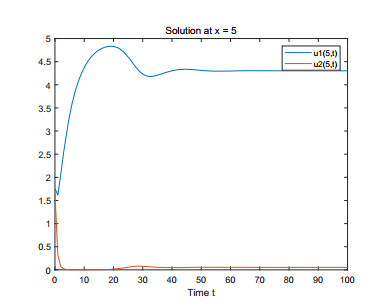
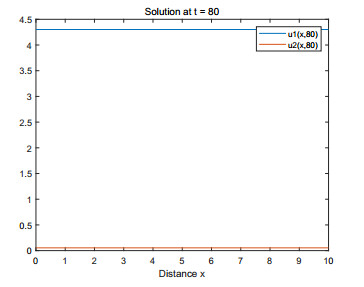
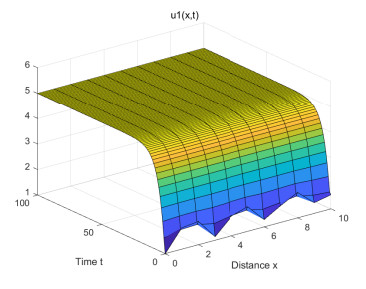
(1) Figures 1–4 are some numerical simulations of Case 1. These simulations show that the equilibrium S = (\mathcal{U}_0^*, \mathcal{V}_0^*) = (5, 0) of example (4.1) has global asymptotic stability. For any initial population density of moderate gamers and addicted gamers, after a long time of discontinuous treatment, the population density of the moderate gamers will be stable at 5 , and the addicted gamers will vanish.
(2) Figures 5–8 are some numerical simulations of Case 2 when \tau = 1.5\in\mathbb{R}^+\setminus\mathbb{N}^+ . These simulations show that the positive steady state S_+ = (\mathcal{U}^*_+, \mathcal{V}^*_+)\approx(4.3128, 0.0531) of example (4.1) has global asymptotic stability. For any initial population density of moderate gamers and addicted gamers, the population densities of the moderate gamers and addicted gamers will be stable at S_+ = (4.3128, 0.0531) .
(3) Figures 9–12 are some numerical simulations of Case 2 when \tau = 2\in\mathbb{N}^+ . In this case, we use the random number generator of MATLAB to get \Theta^* = 0.8605\in[0.8500, \, 0.8705] . A theoretical calculation gives the positive steady state S_+ = (\mathcal{U}^*_+, \mathcal{V}^*_+)\approx(4.3025, 0.0540) of example (4.1). For any initial population density of moderate gamers and addicted gamers, the population densities of the moderate gamers and addicted gamers will be stable at S_+ = (4.3025, 0.0540) .
5.
Conclusions
In the last decade, with the popularity of the internet, the number of internet users has continued to increase. While people enjoy the convenience and benefits brought by the internet, some disadvantages brought by the internet also begin to appear gradually. For example, online game addiction endangers the physical and mental health of players. In particular, many young addictive gamers are trapped in it. Many scholars, including mathematicians, began to pay attention to and study this phenomenon. Through the analysis of the dynamic change process of internet gamers, we put forward a new nonlinear reaction-diffusion model (1.2) of internet gamers having unsustainable treatment in this paper. Utilizing differential inclusion theory and stability theory, we study the existence and boundedness of solutions to the model as well as the global asymptotic stability of the steady states. Based on the MATLAB toolbox, an example is numerically simulated in detail. It is easy to see that the condition rb < a\beta\gamma in Theorem 3.1 and the condition rb\geq a\beta\gamma in Theorem 3.2 are completely opposite. For any initial population density (\mathcal{U}_0(x), \mathcal{V}_0(x)) of moderate gamers and addicted gamers, after a long time of discontinuous treatment, the population density of the moderate gamers will be stable at \frac{r}{a} , and the addicted gamers will vanish in the case of Theorem 3.1. Otherwise, the population densities of the moderate gamers and addicted gamers will be stable at S_+ in the case of Theorem 3.2. Inspired by some recent research works [26,27,28], we can further apply fractional differential equation theory to study the model (1.2) in the future.
Acknowledgments
The work was funded by research start-up funds for high-level talents of Taizhou University.
Conflict of interest
The author declares no competing interest.









 DownLoad:
DownLoad: