1.
Introduction
As we all know, fuzzy model is a extension of deterministic systems, which gives the input, output and state variables definitions on fuzzy sets. Recently, due to the effectiveness in handling the problems of safety control for nonlinear NCSs, fuzzy models have been applied in many research fields, such as fault diagnosis systems, robot control systems and power systems. The ability of fuzzy systems to deal with uncertainty and nonlinear has also attracted much attention in network control, engineering, computer science, and other fields, such as [1,2,3]. The T-S fuzzy methods can approximate the nonlinear systems through a set of local linear systems and a set of IF-THEN rules. Based on the fuzzy systems, many methods of stability and synchronization analysis for linear systems can be extended to the study of nonlinear systems. This provides great convenience undoubtedly for the research of nonlinear NCSs.
Markov jump processes can describe the switch suddenly of system structure parameters due to external disturbance. The transition of the system among the various modes is determined by a set of Markov chains. Recently, SMJSs whose transition rates change with sojourn time have also been investigated. The semi-Markovian processes are similar to the Markov processes generally. However, compared with the Markov processes, the transition time and probability are decided by the time when the system reaches the current state. Recently, more and more researchers have investigated the SMJSs [4,5,6]. In [7], the stable and robust stability conditions for uncertain Markov transition neural networks(NNs) with partially unknown transition probabilities are derived. In [8], the problem of finite-time H∞ fault tolerant control for the T-S SMJSs is investigated. In [9], the asynchronous control problem of a nonlinear MJS based on a method of fuzzy quantization is investigated. Moreover, the designed fuzzy sample controller and the system are asynchronous. The stochastic stability of T-S fuzzy MJSs is guaranteed based on the HMM. In [10], the problem of an elastic asynchronous H∞ control for an uncertain slow sampling discrete-time Markov singular perturbation system (SPS) is investigated. A new conservative sampling controller is proposed to achieve the stability and the H∞ performance of the closed-loop system. In [11], an asynchronous H∞ filter based on an ETM for SMJSs at finite time intervals is designed. In [12], the resilient cooperative output regulation problem of a class of uncertain nonlinear multi-intelligent systems under denial-of-service attacks is studied. A distributed control scheme consisting of a resilient distributed observer and a distributed adaptive controller is proposed. The results show that the control scheme can solve the elastic cooperative output regulation problem for a related class of uncertain nonlinear mathematical models.
As is known to all, time-triggered mechanism and ETM are applied to decrease the network communication burden. Both two communication mechanisms have been introduced into the most NCSs. Based on the previous communication scheme, the signals of the system can be conveyed regularly. For ETM, the data signals of the system can be conveyed unless the given events occur. Meanwhile, ETM can bring more difficulties in constructing the controllers. The advantage over time triggered communication is that ETM can reduce more burden of network communication if it undergoes a little changes for the transmitted signals [13]. In order to make better use of network resources, some strategies on event-triggered communication are proposed for MJSs [14,15,16]. In [17], the guaranteed performance control for T-S fuzzy MJSs with time-varying delays and incompletely unknown transition probabilities is investigated. An ETM related to the system mode is considered at the feedback channel where the network-induced delay occurs randomly. In [18], the safety control problem of the nonlinear unmanned vehicle (UMV) systems is investigated. Sensor-to-controller and controller-to-actuator-side dynamic ETM and an observer-based sliding mode control (SMC) scheme are proposed to stabilize the system under DOS attacks.
Besides ETM, quantization protocol is another method to reduce the burden of network communication [19,20,21]. In [19,20], the robust stability of unknown discrete linear systems with the double quantization strategy is investigated. They also propose some sufficient conditions for closed-loop systems with norm bounded uncertainty and dual quantization. The latter takes into account the phenomenon of the data packets loss. In [21], the problem of quantitative feedback control for uncertain time varying systems based on a sliding mode observer (SMO) is investigated. By constructing a novel L-K function, a time delay-dependent SMO designed criteria is proposed so that the dynamical error system is practically stable.
In [22], the problem of a static output feedback robust H∞ control for the discrete-time singular MJSs is studied. Moreover, the transition probability is incompletely known. In [23], an H∞ tracking control method with adaptive dynamic programming (ADP) for the nonlinear continuous-time SMJSs is proposed. A neural network (NN) detector which includes the input and output of the system signals is designed. In [24], a tracking control problem of nonlinear SMJSs based on T-S fuzzy methods with the incompletely known transition probability is investigated. Furthermore, the designed controller does not fully control the mode that the system maintains at runtime. In this imperfect modal information scenario, a mechanism based on HMM is improved to simulate the defect of modal asynchrony. The main work of [25] is on investigating a class of state output tracking control problem for fuzzy SMJSs. Besides, the affect of both unpredictable external disturbances and uncertainties in the system are also considered. In [26], the location control based on intelligent event triggering in a networked unmanned vehicle (UMV) system based on hybrid attack is studied, where the UMV and the control station are connected through a communication network. The mean square exponential stability condition of the closed loop system and the design method of the controller based on the observer are achieved.
Based on the above analysis of many literatures, this paper investigates a quantitative output feedback control problem of fuzzy tracking control systems under the the influence of the uncertainty and external interference. The main contributions of this paper are summarized as the following:
1) An AETM based on the period data sampling is adopted to relieve the communication burden of the network. The triggered threshold in the AET condition can be adjusted dynamically through an adaptive threshold function ϵ(t), which overcomes the defect of the static ETM. Meanwhile, the size of ϵ(t) can be regulated by an equation related to its derivative ˙ϵ(t);
2) This paper employs a double quantization strategy, which quantizes the controller input and controller output, to compress the network signal. The uncertainty caused by double quantization will increase the difficulties of the research. Therefore, this paper applies two lemmas to deal with this uncertainty.
3) The asynchronous phenomenon is inevitable in realistic situation. In this paper, the time-delay caused by AETM will introduce the asynchronous phenomenon between the controller and the system. Thus, an HMM is established to deal with this problem. Moreover, some sufficient inequality conditions which can ensure the stochastic stability of the system and satisfy the prescribed H∞ tracking performance are derived.
The remainder of this paper is arranged as follows. In Section 2, a controller with AETM and double quantization strategy is constructed for the continuous-time fuzzy SMJSs. In Section 3, some sufficient inequality conditions, which can guarantee the stochastic stability of the system with a prescribed H∞ tracking performance, are derived. Two examples are shown in Section 4 to illustrate the effectiveness of proposed methods. Finally, some conclusions for this paper are summarized in Section 5.
Notations: Rnν represents the nν dimension Euclidean space; Rn×m represents the set of all n×m real matrices; P>0 denotes that P is a positive define matrix; ∗ in matrices represent the symmetric elements for a symmetric matrix; Z+ represents a set of non-negative integers; I and 0 denote unity matrix and zero matrix, respectively; ZT denotes the transpose of Z; sym(AB) represents AB+BTAT; diag{⋅} denotes a diagonal matrix; E{⋅} denotes the mathematical expectation in probability statistics.
2.
Problem formulation
2.1. System dynamics
In consideration of a nonlinear fuzzy SMJS with Markov jump parameter ϕt. Let r be the number of the fuzzy rules. Then, the ith fuzzy rule can be described as follows:
Plant rule i: If η1(℘(t)) is Mi1, η2(℘(t)) is Mi2, ⋯, and ηa(℘(t)) is Mia, then,
where Mi1, Mi2, ⋯, Mia denote the fuzzy sets of the rule i, i∈I={1,2,⋯,r}. ηι(t), ι∈A={1,2,⋯,a} represent the premise variables. ϰ(t)∈Rnν is the system state vector. And u(t)∈Rnu is the input vector which will be designed in this paper. ω(t) denotes the external disturbance which belongs to L[0,+∞]. Ai(ϕt), Bi(ϕt), C(ϕt), Di(ϕt) are known real coefficient matrices which has appropriate dimensions. For notational brevity, these will be denoted by Ais, Bis, Cs, Dis for ϕt=s.
Through the method of fuzzy approach, denote ϕt=s, the description of the system (2.1) can be modified as
where η(t)=[η1(t)η2(t)⋯ηa(t)] and
with Miι(ηj(t)) being the membership grade of ηι(t) in Miι. For i∈I, hi(η(t)) is the membership functions(MFs) of rule i which has been normalized. hi(η(t))≥0 and ∑ri=1hi(η(t))=1. For the symbol simplification, hi replaces hi(η(t)) in the subsequent sections.
Let ϕı, where ı={0,1,2,⋯}, denotes the ıth system mode switch. ˆhı is the residence time from the (ı−1)th switch to the ıth switch. Let ˆh0=0 and ϕt∈S={1,2,⋯,M}. {ϕt,h}t≥0≜{ϕı,ˆhı}ı∈S≥1 can be described as a semi-Markovian process. The matrix of the transition probability Λ(ˆh)=[λisjs(ˆh)]M×M can be written as[5]
where θ>0, limθ→0(o(θ)/θ)=0, λisjs(h)≥0 for ∀is≠js, and λisis(h)=−∑Mjs=1λisjs(h).
Remark 2.1. To avoid notational confusion, it is necessary to clarify that the is and js is a specific value of the system mode s. For example, the λisjs indicates the probability of transfer from modality is to modality js. The is and s represent the same concept. However, it should be noted that the i in is is not the same meaning as the fuzzy rule i previously mentioned in this article.
2.2. Reference model
In order to track the desired signal of the reference output, the following stable reference model is selected. The system output z(t) in (2.2) tracks the reference signals zr(t) :
where ϰr(t), zr(t), r(t) are the state vector, output vector, and the bounded reference input, respectively. Ar, Br, Cr are known real matrices which have appropriate dimensions.
Remark 2.2. The system (2.4) is selected as the reference model of H∞ tracking control. What's more, the reference system is known and stable. In the following research, by letting the system (2.2) track the system (2.4).
2.3. AET mechanism
AETM is a strategy which is applied to save the communication cost and reduce the network bandwidth pressure. The measurement/control signal will be released when the pre-specified triggered condition are met. The AETM is based on the data sampling. We denote τ0<τ1<⋯<τm<⋯ and η=τm+1−τm as the sampling instants and the sampling period. Assume that τ0=0 and η is a constant. Let t0,t1,⋯,tk denote the event triggered instants. Assume that t0=0. For t∈[τm,τm+1), m∈Z+, the asynchronous fuzzy tracking controller related to AET can be constructed as
where
and {φt}t∈R+∈M={1,2,⋯,S}. Due to the existence of the time delay and other external disturbance, the mode switching between the controller and the system is not synchronous at all time. Hence, a hidden process is introduced and its property is defined by
where for ∀s∈S, μ∈M, ϱ∈[0,1], and ∑Sμ=1ϱsμ=1. In (2.5), tk=max{t|t∈{td,d=0,1,⋯,}} denotes the latest event-triggered instants. Kj(φt) and Fj(φt) denote the control gain matrices. For notational brevity, we use Kjμ and Fjμ to denote Kj(φt) and Fj(φt).
The event trigger will work if t=τm(m∈Z+) and the condition (2.6) is violated:
where ξ(τm)=x(τm)−x(tk), ζ(τm)=[xT(τm)xTr(τm)]T. ϵ(t) is a threshold which can be adjusted adaptively. According to [27], ϵ(t) can be adjusted by
where ϵ0 is a given constant.
Remark 2.3. The conditional probability ϱsμ in (2.5) is applied as a mechanism to measure the asynchronous degree. This will be considered in the design of the ultimate controller.
Remark 2.4. The AETM is more effective than traditional ETM in saving bandwidth resources. It can be obtained from (2.7) that the event trigger threshold can be adjusted dynamically. Moreover, if ϵ(0) is 1ϵ0, where ϵ(0) is the initial value of ϵ(t). In this case, ˙ϵ(t)=0 for t≥0, which applies that ϵ(t) is a constant. The AET condition is modified as the traditional ETM [28,29].
2.4. Design of the controller with double quantization
Inspired by [30], this paper quantizes both the controller input and the controller output. Given a vector b=[b1b2⋯bC]T∈Rn, let ˆf(b)=[ˆf1(b1)ˆf2(b2)⋯ˆfC(bC)]T be the quantizer of the controller input. For c=1,2,⋯,C, ˆfc(bc) is described as
where θfc=(1−ρˆfc)/(1+ρˆfc), 0<ρˆfc<1 is defined as the density of the double quantization. ˆucȷ∈Uc is defined as the level of the double quantization, and Uc={±ˆucȷ,ˆucȷ=(ρˆfc)ȷˆuc0,ȷ=±1,±2,⋯,}∪{±ˆuc0}∪{0} with ˆuc0>0.
For the quantization of the controller input, let △ˆf=diag{△ˆf1,△ˆf2,⋯,△ˆfC}, △ˆfc∈[−θfc,θfc], for c∈N={1,2,⋯,C}. Refer to [31], through the approach of the sector bound, ˆf(b) is defined as
For the quantization of the controller output, let △ˆg=diag{△ˆg1,△ˆg2,⋯,△ˆgC}, △ˆgc∈[−θgc,θgc], ˆgc(bc) is described in the same way as ˆfc(bc):
For simplicity, we set θfc=θf and θgc=θg, 0<θf<1 and 0<θg<1. The following two inequalities are specified:
Through mentioned above quantization scheme, the tracking controller in (2.5) can be modified as
Combining (2.8), (2.9) and (2.11), we can rewrite the double quantization controller as
where
Note that Kj(φt)f(ϰ(tk))+Fj(φt)f(ϰr(τm)) is the output of the controller which varies with t. Hence, by the function of g(⋅) and f(⋅), △ˆg and △ˆf also change with t. Thus, we have
For simplicity, △ˆf(t), △ˆg(t), △r1(t) and △r2(t) are abbreviated as △ˆf, △ˆg, △r1 and △r2, respectively. It is necessary to note
Then,
Remark 2.5. To quantify the data which need to be transmitted between the system and the controller, that is, to convert the form of transmitted data from continuous one to discrete one. At this time, less bandwidth resource is required for the data transmission. However, for most network quantization methods, they only consider the single quantization between the system and the controller [32,33].
In this paper, the double quantization between the system and the controller is considered. Therefore, compared with the existing work, this paper adopts the method of double quantization in [34] to design the tracking controller of (2.12) to save more bandwidth resources. Here, double quantization refers to the quantization of the input and output of the controller, that is, from system to controller and from controller to system both require quantization. The advantage of quantizing the input and output of the controller respectively is that it can reduce the communication burden more efficiently. However, there are also some disadvantages, such as this strategy will introduce more uncertainty in the final system. At the same time, it will add more difficulties to the derivation of the paper. Since the states of the original system and the reference system are not identical, two control gain matrices are introduced to fully account for the differences between the two systems. It is necessary to note that the quantization controller contains two different control gain matrices Kjμ and Fjμ corresponding with the system (2.2) and reference system (2.4), respectively.
2.5. Tracking error dynamic system
Denote the tracking error e(t)=z(t)−zr(t) and let ε(t)=t−τm. Then, the following augment tracking error dynamic system can be obtained:
where i,j∈I and
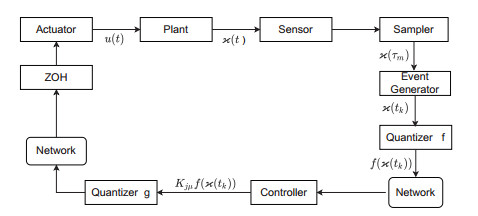
Figure 1 shows the framework of NCS with double quantizers and the AET. As shown in Figure 1, in consideration of the limited capacity of the communication channels and in order to decrease the rate of the data transmission, two quantizers will quantize the signals of the state and control before they are transmitted to the network medium. To this end, the following definitions and some related lemmas are necessary to list here.
Definition 2.1. The system (2.17) will achieve a stochastic stability, if for ∀ˆt, ˉω(ˆt)≡0 and ζ(0)∈Rn, the following inequality holds:
Definition 2.2. For the dynamic tracking error system (2.17), there is a definition for the H∞ norm:
Under the controller (2.12) and the zero initial condition, if system (2.17) satisfies the condition in the Definition 2.1, and ‖Φ‖∞<λ, such that the following inequality holds:
then, it is reasonable to believe that the system (2.17) achieves a stochastic stability and satisfies the given H∞ output tracking performance index λ.
Lemma 2.1. There exists matrices R>0, X is a matrix which has appropriate dimensions, the following inequality can be established under all the circumstance:
Lemma 2.2. For ∀υ>0, there exists matrices ˜Υ1 and ˜Υ2 the following inequality can be established:
Lemma 2.3. For N1≥2n, ℵ∈Rn×n is a semi-positive matrix, and ℵ1∈RN1×N2 is a symmetric matrix which is described as
Then, we can get ℵ≥0.
Remark 2.6. It is necessary to note that the researches about the stochastic stability for the fuzzy SMJSs mostly focus on the field of discrete-time. This paper extends the tracking control problem of T-S fuzzy MJSs to the continuous-time domain compared with the extant researches [35,36].
3.
Results
This section will firstly analyze the stability and H∞ tracking performance of the augment system (2.17) with the AETM and the double quantization strategy.
Theorem 3.1. For some given scalars ρi, ρj, λ>0, the control gain matrices Kjμ and some other matrices Pis>0, Q>0, W>0, Zi=ZTi, Zj=ZTj with appropriate dimensions, the system (2.17) can achieve the defined stochastic stability and satisfy the prescribed H∞ tracking performance λ, if ˆhj−ρjhj≥0, such that for ∀is,js∈S, ∀μ∈M. Meanwhile, ∀i,j∈I, the following inequalities conditions hold:
where
where g(ˆh) is the probability density function (PDF) of the residence time ˆh for the system mode is.
Proof. Suppose ζt(y)=ζ(t+y) for η≤y≤0. For t∈[τm,τm+1), m∈Z+, the following L-K functions are selected as
where
where Psh=∑ri=1hiPsi. For a given small scalar θ which is not the same as θ in θg and θf. Let γ(t)=[ζT(t)ζT(t−ε(t)ζT(t−η)ξT(t−ε(t)]T. The following equalities hold:
where ˉAsh=∑ri=1hiˉAis, ˉBshμ=∑ri=1∑rj=1hiˆhjˉBijsμ, ˉEhsμ=∑ri=1∑rj=1hiˆhjˉEijsμ. Gis(ˆh) represents the cumulative distribution function (CDF) of the residence time h for the mode is, and qisjs represents the probability that the mode of the system changes from is to js, i.e., qisjs=Pr{ϕı+1=js|ϕı=is} and M∑js=1js≠isqisjs=1. λis(ˆh) is the transition rate of the system mode is. λisjs(ˆh)=qisjsλis(ˆh) for is≠js, λisis(ˆh)=−M∑js=1js≠isλisjs(ˆh).
Refer to [5,29], for the semi-Markov process {ζt,s,t≥0} in this paper. Denote J to be the weak infinitesimal operator. For s=is∈S, the derivative of V1(ζt,s,t) along the trajectories of the system (2.17) can be calculated by L:
where F1=[I,0,0,0] and
Take the derivative of V2(ζt,s,t) as follows:
where F3=[0,0,I,0].
Then, we take the derivative of V3(ζt,s,t) as follows:
where Yis=[ˉAshˉBshμ0−ˉEshμ]. By the Jensen-inequality in [37], the second term in the right of (3.11) is modified as
where F2=[0,I,0,0] and
Hence, from (3.11) and (3.12), it follows that
Then, considering the event-triggered condition in (2.6) and (2.7), the derivative of V4(ζt,s,t) is calculated as follows:
where
Combining (3.9), (3.10), (3.13) and (3.14) yields
where Θijis=Ω+Υ, Υ=−1ηFT˜WF and
Then, for (3.1), through the Schur complement, Θijis<0 can be deduced, i.e., JV(ζt,s,t)<0. Through the Dynkin's formula, if JV(ζt,s,t)<0, for a cut-off time T>0 and a constant ϵ>0, the following inequality will hold:
Then, let T→∞, it has
From Definition 2.1, it can be obtained that the system (2.17) have achieved a stochastic stability. Furthermore, the H∞ tracking performance under the condition of external disturbance ˉω(t)≠0 is considered. From (3.15), we can obtain
where ˉγ(t)=[γT(t)ˉωT(t)]T and ˉΘijis=ˆΩ+ˆΥ.
In order to reduce the conservativeness and make full use of the MFs information, we introduce the slack matrices Zi. Due to ∑ri=1hi−∑rj=1ˆhj=0. Then, according to [38,39,40,41], combining (3.2)–(3.4) with the system (2.17) and considering ˆhj−ρjhj≥0, we can get
Then, combining the above formula, we can get
Hence, the condition (3.1) in Theorem 3.1 shows that J<0. i.e.,
From Definition 2.2, it is obvious that the system (2.17) achieves a stochastic stable state and satisfies the prescribed H∞ tracking performance λ.
Thus, the proof is completed.
Remark 3.1. In consideration of reducing the conservatism, referring to [30]. The difference from [30] is that we select the fuzzy Lyapunov matrix Psh=∑ri=1hiPsi as the modal dependency matrix in this paper. This paper studies the stability of the system and H∞ tracking performance, but [30] studies the stability of multi-agent system. For the purpose of making full use of the AET conditions, the quadratic integral term ∫0−η∫0ν˙ζTt(y)W˙ζt(y)dydν related to ζ(t−ε(t) and 12ϵ2(t) related to AET threshold ϵ(t) are all considered in Theorem 3.1, which can decrease the conservatism of the system.
In Theorem 3.1, some sufficient criteria which can ensure the stochastic stability with ˉω(k)=0 and achieve a given H∞ tracking performance for the system (2.17). However, based on the analysis results in Theorem 3.1, it is difficult for us to parameterize the controller gains directly because of the existence of nonlinear terms. For the purpose of using the method of LMIs to solve the problem, the results of the controller construction are summarized in the following achievements.
The matrices in Theorem 3.2 are mainly some equivalent transformations of the final matrix of Theorem 3.1 such as contract transformation and Schur complementary, etc. The matrix separation technique is also used to separate out some uncertain terms. Meanwhile, two lemmas given in the paper are also applied to perform the corresponding deflation without changing the properties of the original matrix. Finally, we can achieve Theorem 3.2.
Theorem 3.2. For some given scalars ρ, η, γ, β, ρi, ρj, λ>0, a1>0, a2>0 and a3>0 and controller gain matrices Kjμ, the system (2.17) can achieve a stochastic stability and satisfy the prescribed H∞ tracking performance, and for some other matrices His>0, ˆQ>0, ˆW>0, Wis>0, ˆKjμ and ˆZi with appropriate dimensions such that, for ∀is∈S, ∀μ∈M, ∀i,j∈I, the following inequalities hold:
where θg and θf are defined in (2.14), αis is the largest eigenvalue of BisBTis. Then, the tracking control gains Kjμ and Fjμ for is∈S, is given by Kjμ=ˆKjμH−1is and Fjμ=ˆFjμH−1is.
Proof. Let His=P−1is. Define Λ=diag{His,His,His,His,His,I}. Then, pre- and post-multiplying (3.1) with ΛT and Λ, respectively, it can be obtained that
Let ˜Ω=ΛTˆΩΛ and ˜Υ=ΛTˆΥΛ. Thus,
Based on Lemma 2.1, we can obtain
and
Integrating (3.24)–(3.26) into (3.23) and using the Schur complement for (3.23). Thus, (3.1) holds if the following condition holds:
where
where
Considering (2.15), (2.16) and (3.27), ˜Ω(1) can be rewritten as
where
From Lemma 2.2, we have
where 0<a1,a2,a3∈R and
Then, considering (3.28) and (3.29), we can obtain that (3.27) holds if
By Lemma 2.1, it is obvious that
Applying Schur complement to (3.21), we have
Considering (3.20), (3.31), (3.32) and ˆKjμ=KjμHis, it can be achieved that
Pre- and post-multiplying (3.33) with H−1is yields KTjμKjμ≤γI. Since KTjμKjμ and KjμKTjμ have same nonzero eigenvalues, thus KjμKTjμ≤γI.
Based on those and (2.15), we can obtain
where αis denotes the largest eigenvalue of BisBTis.
Using similar methods, we can get
Similarly, we can also get
Hence, we can see that BT1rB1r≤B1r, BT2rB2r≤B2r and BT3rB3r≤B3r. Therefore, (3.30) holds if the following holds:
By the Schur complement, (3.35) is equivalent (3.22). In summary, (3.1)–(3.4) hold if (3.17)–(3.22) hold. So far, the proof is completed.
4.
Examples
In order to verify the effectiveness of the theoretical results, a numerical example and a single-link flexible joint manipulator system are selected in this section.
Example 1. In the numerical example, three modes of the system (2.2) are specified. The corresponding three-dimensional transition probability matrix with a semi-Markovian process is chosen as
Through relevant calculations, the mathematical expectation of ˜Λ(ˆh) is
Consider a two-rules T-S fuzzy MJSs of the form (2.1):
Plant rule 1: If ϰ1(t) is −mϕt, then,
Plant rule 2: If ϰ2(t) is mϕt, then,
with its parameters selected as
According to the reference system (2.4), assume a reference model with its parameters:
The parameters of AET condition (2.6) are selected as ϵ0=0.1. The parameters of quantization are chosen as ˆuc0=2, θfc=(1−ρfc)/(1+ρfc)=1.0001, θgc=(1−ρgc)/(1+ρgc)=1.00015 where c∈C={1,2,...,C}. In Theorem 3.2, let γ=1.5, β=0.5. An expected H∞ performance λ∗=0.0052 can be achieved with the results of the controller gains as follows:
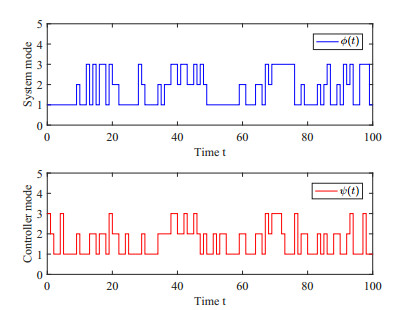
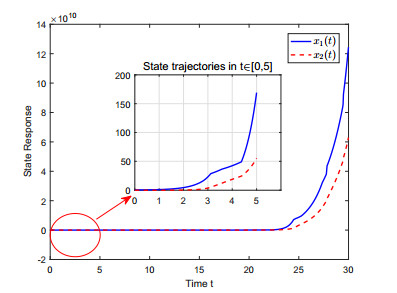
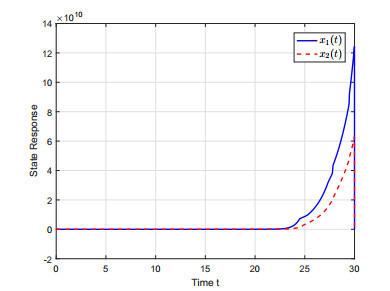
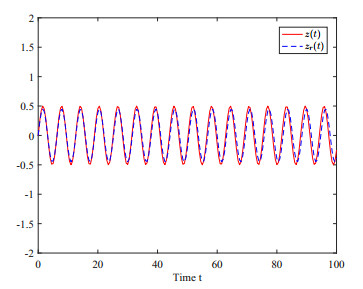
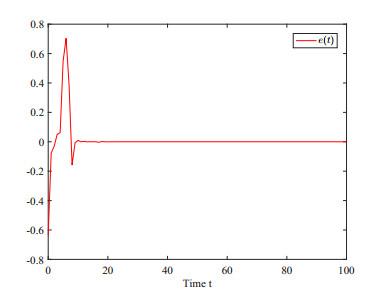
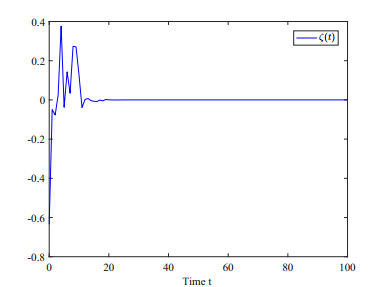
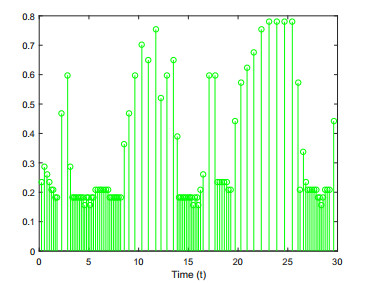
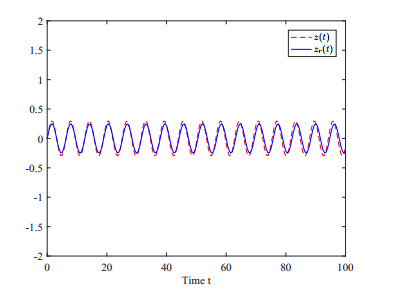
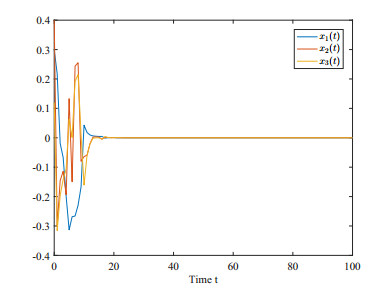
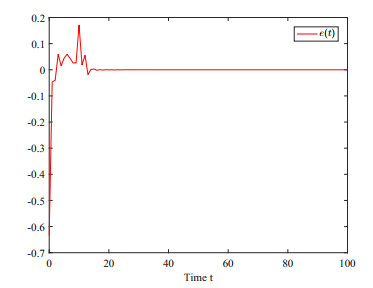
Let the reference input r(t)=sin(t) and the external disturbances w(t)=0.5exp(−t). Figure 2 shows the mode evolution of the system and the controller. The state trajectories of two-rules without a controller are depicted in Figure 3. We can see that the system is unable to achieve a stochastic stability. When the designed controllers (2.12) are added to the system, it is obvious that the system is stable stochastically and the corresponding trajectories are shown in the Figure 4. Figure 5 shows that the output-tracking trajectories of the z(t) and zr(t). It can be seen that the system tracks the reference system perfectly with the controller. Figure 6 depicts that the trajectories of the tracking error with the designed controllers. The value of the tracking error reaches a stochastic stability around the 15th second. Figure 7 is the state trajectory of ζ(t) which also remains stable after the 15th second. Figure 8 demonstrates the AET release instants and intervals. From Figure 5, it can be found that the number of the triggered times is 132. By simple calculation, it implies that there has 10.1% of the sampled data require to be transmitted to the controller. Additionally, it can be calculated that the maximal value of the release interval is 2.109 and the average value of the release interval is 1.046. Next, in order to improve the performance of the network system, it is necessary to analyze that how two quantization parameters θf and θg affect the optimal H∞ tracking performance index λ∗. Through corresponding numerical calculation and simulation, the related results are presented in Table 1.
Due to the limited space of the paper, the data in Table 1 only shows some representative simulation results, and the following conclusions can be obtained through the remaining large number of simulation results. From Table 1, it can be obtained that with the value of output quantization parameter unchanged, the input quantization parameter value increases, λ∗ also increases. Correspondingly, when the value of input quantization parameter remains unchanged, the output quantization parameter value increases, λ∗ also increases. This shows that the smaller both the quantization parameters are, the more superior tracking performance which the original system has.
Example 2. Borrowed from [24], an example of a single-link flexible joint manipulator is selected. The dynamic equation of the system is
where ϰ1(˜t) is the angular position of the arm, ϰ2(˜t) is the angular displacement, ϰ3(˜t) is the angular velocity of the motor, ϰ4(˜t) is the angular velocity. Moreover, ϰ1(˜t)+ϰ2(˜t)∈[−π/2,π/2], Thus, y1(ϰ1(˜t))=sin(ϰ1(˜t)+ϰ2(˜t))ϰ1(˜t)+ϰ2(˜t)∈[y1min,y1max]=[0,1], some related parameters are listed in Table 2.
The MFs are denoted as h1(ϰ1(˜t))=y1(ϰ1(˜t))−y1maxy1min−y1max and h2(ϰ1(˜t))=1−h1(ϰ1(˜t)). The manipulator is considered as a 2-rule fuzzy MJS of system (2.1). Its parameters are selected as
with
Then, the reference model is selected as follows:
By setting the initial value ϰ(0)=[2110]T, ϰr(0)=[0.1110]T, the desired control gains with λmin=1.2456>‖e(˜t)‖2‖ˉω(˜t)‖2=0.0627. The corresponding state and error trajectories are shown in Figures 9–11. It is obtained that the above system can also reaches the stochastic stability under some prescribed conditions. Meanwhile, the manipulator system can also track the desired reference system well under the given H∞ tracking performance index λmin.
5.
Conclusions
In this paper, a class of H∞ tracking control problem for continuous-time fuzzy SMJSs is investigated. The AETM and double quantization strategy for the controller input and the controller output are adopted to compress network communication signals and improve the transmission efficiency. Based on the improved L-K functions and LMI techniques, some sufficient criteria which can enable the system achieve a stochastic stability and satisfy the H∞ tracking performance of the tracking control system are derived. At the same time, a quantitative tracking feedback controller based on fuzzy basis and mode dependence is constructed. Finally, two examples are given to demonstrate the effectiveness and rationality of the above method. In the future work, it is hoped that the results can be extended to other fuzzy SMJSs with the time-varying delay, deception attacks, DOS attacks, and so on. Of course, other quantized strategies are also worth our further research.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under Grant 11661028, the Natural Science Foundation of Guangxi under Grant 2020GXNSFAA159141, Guangxi Philosophy and Social Science Programming Project (2022) under Grant 22BTJ001.
Conflict of interest
The authors declare that they have no conflicts of interest concerning the publication of this manuscript.









 DownLoad:
DownLoad: