An efficient spectral minimization of the Dai-Yuan method with application to image reconstruction

1.   Introduction

The unconstrained optimization basically deals with finding the global maximum or minimum of a continuously differentiable function $f:\mathbb{R}^n\longrightarrow\mathbb{R}$. The general form of an unconstrained optimization problem is as follows:

where the gradient $g(x) = \nabla f(x)$. Solving the complexity of this problem (1.1) would require the use of some symbolic aided algebra system and an effective numerical method that would be able to perform the necessary computations, plot the numerical results and manipulate the mathematical expression in an analytical form. One of the widely and most preferred methods considered for solving (1.1) is the nonlinear conjugate gradient (CG) method because of its robustness and ability to deal with large-scale problems ^[1,2]. The simplicity and efficiency of the CG algorithm has further motivated its application to numerous real-life problems including the feed forward training of neural networks ^[3], robotic motion control ^[4], signal recovery ^[5], regression analysis ^[1,6], image deblurring ^[7,8] and portfolio selection ^[9] among others.

Starting with an initial guess of $x_0\in\mathbb{R}^n$, the CG method generates a sequence of iterates $\left\{ x_k \right\}$ via the following formula:

where $\alpha_k$ represents the step size that is computed along the search direction $d_k$ ^[10]. Usually, a line search procedure is required to obtain the step size ($\alpha_k$) which could either be an exact or inexact procedure. While the exact line search yields the exact minimizer for a given problem, the inexact scheme computes $\alpha_k$ such that it satisfies the Wolfe conditions at each iteration. The most commonly used Wolfe conditions includes the standard Wolfe condition that requires $\alpha_k$ to satisfy

and the strong Wolfe condition is computed such that $\alpha_k$ satisfies (1.3) and

where $0 < \delta < \frac{1}{2},$ $\delta < \sigma < 1$.

Another important component of the CG method is the search direction $d_k$. This component plays an important role in the performance and convergence analysis of any CG method. Also, the search direction distinguishes the classes of different CG algorithms including the spectral and three-term CG methods. The search direction $d_k$ for the classical CG method is computed as follows:

where the coefficient $\beta_k$ characterizes the different CG formulas. Selection of the CG choice parameter and search direction is always crucial in the study of the unconstrained optimization because these two components are responsible for the numerical performance and theoretical analysis of any CG method ^[11].

For any optimization method to fulfill the general optimization criteria and be able to use the line search procedure, it is required to possess the following descent property:

Furthermore, a CG method is said to be sufficiently descending if there exists some constant $c > 0$ such that the following condition holds:

This condition (1.8) plays an important role in the convergence analysis of any nonlinear CG algorithm, which is always preferred over (1.7). Some of the earliest and known CG coefficients that possess this condition (1.8) include those developed by Fletcher and Revees (FR)^[12], Dai and Yuan (DY) ^[13] and Fletcher (conjugate descent (CD))^[14], with formulas as follows:

where $y_k = g_{k+1}-g_k$ and $\left\| \cdot \right\|$ denotes the $\ell_2$ norm. This class of CG methods is characterized by simplicity and less memory requirements under different line search procedures. However, their numerical performance in practical computations is often affected by jamming phenomena. For instance, if any of the above CG algorithm generates a tiny step size from $x_{k}$ to $x_{k+1}$ and poor search direction and as a result if restart is not performed along the negative direction, then, it is likely that the subsequent step size and direction will also have poor performance ^[15].

Due to the challenges reported by the above category of CG algorithms, several studies have shown that the methods possess nice convergence properties (see ^[11,16,17]). To address the issue related to the computational performance, several studies involved constructing new CG formulas by either combining the methods in (1.9) with other efficient formulas or introducing new terms to the set of methods in (1.9) to improve the computational efficiency and their general structure ^[18].

In this study, we are interested in modifying the classical DY CG formula for solving optimization and image restoration problems. The proposed method introduces a new spectral parameter $\theta_k$ to scale the search direction $d_k$ in (1.6) such that it satisfies the Newton search direction and the well-known D–L ^[19] conjugacy condition in Section 2. Section 3 demonstrates how the proposed method satisfies the descent condition and further proves the global convergence under suitable conditions. The preliminary computational results on a set of optimization functions are analyzed in Section 4 while Section 5 reports results related to real-world application problem. The last section summarizes the whole idea related to the study and presents a general conclusion.

2.   Formulation of the spectral algorithm and motivation

The spectral CG methods have been proposed to improve the general structure of CG methods. The methods are based on the works of Raydan ^[20], Barzilai and Borwein^[21] and Birgin and Martínez ^[22]. For some recent results on spectral CG methods, see ^{[8,24,25,26,27,28,29,30,31]}. Similarly, the standard conjugacy condition given by

is crucial in the convergence analysis of these CG methods. The CG methods proposed with this structure (2.1) largely depend on exact line criteria for the choice of step size, $\alpha_k.$ However, this requirement is computationally expensive for large-scale problems. Therefore, denoting $s_{k} = x_{k+1}-x_{k}$, the selection of $\alpha_k$ uses its generalized form called the D–L conjugacy condition introduced in ^[19],

is usually preferable in the design of some nice CG algorithms. The parameter $t,$ called the D-L parameter is capable of ensuring better convergence. Therefore, it must be carefully chosen.

To address some weaknesses associated with the DY method, its modification has been investigated recently. For instance, utilizing the strong Wolfe line search, Jiang and Jian ^[32] proposed the improved DY ^[13] CG parameter with the following structure:

where $r_k = \frac{|g_{k+1}^Td_k|}{-g_{k}^Td_k}.$ Motivated by this idea, Jian et al. ^[33] introduced a spectral parameter that yields the descent direction with

Since $\theta^{JYJLL}_k \geq 1$ it is obvious that $d_k$ is a descent direction. Following the idea in ^[34], they proposed its conjugate parameter as follows:

However, the search direction including the method in (2.5) only satisfies the descent condition, (1.7) and it converges globally based on two cases of ${{{\max \{{\Vert g_{k} \Vert}^2}, \; d_{k}^T y_{k}\}}}$ with the standard Wolfe criteria respectively. According to this formulation, two other modified DY CG methods were proposed in ^[35] with the following forms:

Inspired by these modifications, Zhu et al. ^[36] suggested another DY modification namely, the DDY1 scheme which has the form of

Nonetheless, the method has similar theoretical characteristics with the scheme described by (2.5). Thus, in order to improve the general structure and establish sufficient descent, as given by (1.8) for the DY method, we scale the search direction $d_k$ in (1.6) with a spectral parameter $\theta_k$ such that it satisfies the well-known D–L conjugacy condition (2.2), as well as the Newton search direction in the following form

Pre-multiplying by $y_k^T$, we obtain

Using the above relation with (2.2) gives

Re- arranging implies that

Similarly, in some neighborhood of the minimizer, if the current point $x_{k+1}$ is close enough to a local minimizer and the objective function behaves like a quadratic function, then the optimal search direction to follow is the Newton direction:

where $\nabla^2 f(x_{k+1})$ is the Hessian matrix of $f.$ Thus, the Newton method requires the Hessian matrix, i.e, the second derivative information to update (2.11), which provides a nice convergence rate. Motivated by its quadratic convergence property, we assume that $\nabla^2 f(x_{k+1})$ exists at every iteration and satisfies the conditions of a suitable secant equation; for instance,

Now, equating (2.9) with (2.11) gives

Pre-multiplying by $y_k^T$ and using the secant equation (2.12), we get

After some simple simplification, we obtain

Remark 2.1. Observe that, if $\; t = 1$, then the parameter $\theta_k^{SDL} = \theta_k^{SNM}$, which implies that, the spectral search direction {$d_{k+1}$} does not only satisfy the generalized D-L conjugacy condition it also takes advantage of the nice convergence property of the Newton direction. However, for a sufficient descent condition to hold, we always select $t > 1$ in this paper.

To achieve the sufficient descent of the search direction described by (2.9), we suggest the following modification of (2.10) as follows:

Thus, if $|y_k^T g_{k+1}| > \; d_{k}^T y_{k},$ then (2.14) reduces (2.10). Hence, for ${d_{k}^T y_{k}} > |y_k^T g_{k+1}|,$ we obtain another spectral parameter:

Combining (2.10) and (2.15) implies that the optimal $\theta_k$ can be computed as follows:

Now, we describe the new spectral DY (NSDY) algorithm as follows:

Theorem 2.2. Let $\theta_k^{}$ be given by (2.16) with $0 < \alpha_k \leq \sigma < 1.$ Suppose that the NSDY algorithm generates sequences $\left\{ g_k \right\}$ and $\left\{ d_k \right\},$ where $\alpha_k$ is determined by strong Wolfe rules (1.3)–(1.5); then, there exists a constant $\rho > 0$ for which the condition

holds.

The criterion (2.17) is called the sufficient descent condition, and it ensure that the direction described by (2.9) is indeed sufficient for the minimizer.

Proof. The proof is achieved by mathematical induction. Initially, for $k = 0$ it follows easily that $g_0^T d_0 = -\left\|g_0\right\|^2 \leq -{\rho} {\Vert g_{0} \Vert}^2.$ Suppose that (2.17) holds for index $k$, that is, $d_{k}^T g_{k} \leq -{\rho} {\Vert g_{k} \Vert}^2.$ We now show for $k+1.$ Now, according to the strong Wolfe criterion (1.3), it holds that

i.e.,

Then

Pre-multiplying (2.9) by $g_{k+1}^T$, we have

Using (2.14) with $s_k = \alpha_kd_k$ gives

Obtaining $\beta_k^{DY}$ from (1.9) and applying it with (2.21) and (2.20), we get

where the second to the last and last inequalities follow (2.19) respectively. Now, from (2.18), we get

Combining this with (2.17), we get

The result by the last inequality follows from the induction hypothesis. Finally, using (2.22) and (2.23), we conclude that

Since $\frac{\|g_{k+1}\|^2}{{(1-\sigma) {\rho} {\left\|g_k \right\|}^2}} > 0,$ we have

Denoting $\rho = \bigg(\frac{ \sigma t \alpha_k }{ (1-\sigma) } - \frac{\sigma}{{(1-\sigma)}} \bigg),$ with $t \geq 1.2,$ $\alpha_k \in(0, 0.9]$ and $\sigma \in(0, 0.9]$ the required result is achieved. □

3.   Convergence analysis

The convergence analysis requires the following presumptions.

Assumption 3.1.

1. Given an initial point $x_0,$ the function $f(x)$ is bounded below on the level set $\eta = \{ x\in \mathbb{R}^n: f(x_0) \geq f(x)\}$.

2. Denote $\Gamma$ as some neighborhood of $\eta$, and the function $f$ is smooth with its gradient that is Lipschitz-continuous and satisfying

Note that these assumptions, imply that

The following lemma was taken from ^[17] and is very crucial in our analysis.

Lemma 3.2. Suppose that $\left\{x_k\right\}$ and $\left\{d_k\right\}$ are sequences generated by the NSDY algorithm, where the spectral search direction $d_k$ is descending and $\alpha_k$ satisfies the strong Wolfe conditions; then,

Theorem 3.3. If Assumption (3.1) holds and the sequence of iterations $\left\{x_k\right\}$ is produced by the NSDY algorithm, then

Proof. If (3.5) does not hold, then there exists some constant $r > 0$ so that

Claim: The search direction defined by (2.9) is bounded, i.e., there exists a constant $P > 0$ such that

To proceed with the proof of this claim by induction, we need to show that $\vert \beta_k^{DY}\vert$ and $\vert \theta_k\vert$ are bounded below. According to (2.18), it yields

Combining this with (2.17), we get

Therefore, obtaining $\beta_k^{DY}$ from (1.9) and applying it with (3.2), (3.6) and (3.8), we have

Next, from (2.14), (3.2), (3.8) and (3.9), we obtain

Now, for $k = 0$, we get that $d_{1} = -\theta_1 g_{1} +\beta_1 d_0$ from (2.9), which implies that $d_1 = -\theta_1 g_{1} - \beta_1 g_0,$ since $d_0 = -g_0;$ this yields

that is, the claim (3.7) holds for $k = 0.$ Next we assume that the claim (3.7) is true for $k$, that is, ${\Vert d_{k} \Vert} \leq P.$ To show that it is true for $k+1,$ consider the search direction described by (2.9).

Thus, using (3.2), (3.9) and (3.10), we obtain

therefore, the claim also holds for $k+1$. Now since (3.7) holds for all values of $k,$ then we have

From the above inequality, it follows that

Accordingly, from (2.17), (3.4) and (3.6), it follows that

Therefore, this implies that

It is obvious that, (3.12) and (3.14) cannot hold concurrently. Thus, (3.5) must hold. □

4.   Numerical results

In this part, we present a numerical comparison of the NSDY method versus the classical DY method and three other modifications of the DY method. The evaluations are based on a number of test functions considered from ^[37,38]. For the computation, we consider the dimension ranging from 2 to 100, 000 as presented in Tables 1 and 2. To analyze the results further, the following specifications are considered for the algorithms:

● JYJLL algorithm of Jian et al. ^[33] that uses (2.4) and (2.5) for the search direction described by (2.9) and $\delta = 0.01$ and $\sigma = 0.1$ in (1.3) and (1.4) respectively.

● IDY algorithm of Jiang and Jian ^[32] that uses (2.3) for the search direction described by (1.6) and $\delta = 0.01$ and $\sigma = 0.1$ in (1.3) and (1.4) respectively.

● DDY1 algorithm of Zhu et al. ^[36] that uses (2.8) for the search direction described by (1.6) with $\mu_1 = 0.4$ and $\delta = 0.01$ and $\sigma = 0.1$ in (1.3) and (1.4) respectively.

● DY algorithm of Dai and Yuan ^[13] with $\beta^{DY}_k = \frac{\|g_{k+1}\|^2}{d^T_{k}y_{k}}$ for the search direction described by (1.6) and $\delta = 0.01$ and $\sigma = 0.1$ in (1.3) and (1.4) respectively.

The MATLAB R2022a codes for the numerical experiment were run on a Dell Core i7 laptop with 16 GB RAM and a 2.90 GHz CPU. We set $\delta = 10^{-3}$ and $\sigma = 0.9$ in (1.3) and (1.5) for the NSDY method and $\Vert g_k \Vert \leq 10^{-6}$ as the stopping condition for all schemes. We also use the symbol $***$ to indicate a situation in which the stopping condition is not met. The results from the computational experiments based on number of iterations (NI), number of function evaluations (FE), and CPU time (ET) is presented at the following link https://acrobat.adobe.com/link/review?uri = urn:aaid:scds:US:ed485b92-05e2-40f3-a1f2-6e159858c515.

We will employ the performance profiling technique to interpret and discuss the performance of the methods examined. Let $P$ be the collection of $n_p$ test problems and $S$ be the set of $n_s$ solvers used in the comparison. The performance profiles thus constitute the performance metric for a problem $p\in P$ and a solver $s\in S$, which denote either NI, FE or ET relative to the other solvers $s\in S$ on a set of problems $p\in P$. Then, Dolan and Mor$\acute{e}$^[39] described the measure of performance ratio to compare and evaluate the performance:

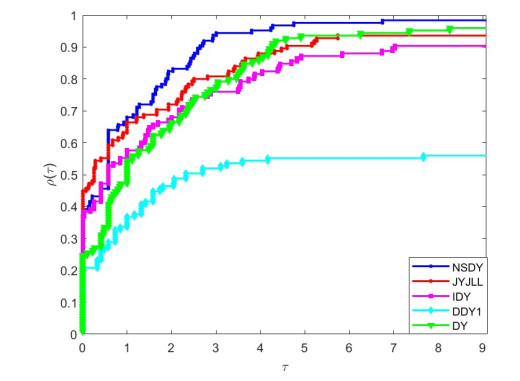
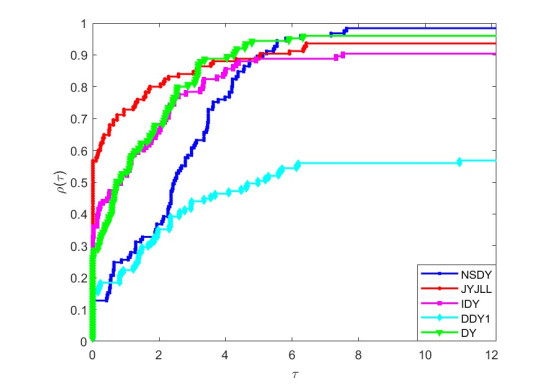
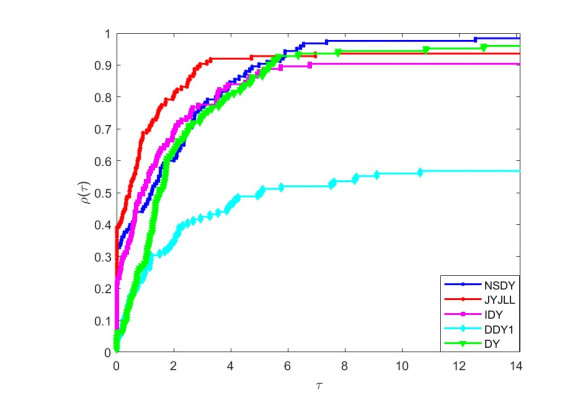
Thus, the best method is indicated by the performance profile plot at the top curve. The experiments can therefore be interpreted graphically by using Figures 1–3 based on numerical performance.

The interpretation of Figure 1 for the value $\tau$ chosen within the $0 < \tau < 0.5$ interval shows that the NSDY method solved the test problems and won in $98\%/38\%$ to be the best, followed by the JYJLL method with $95\%/45\%,$ whereas the DY, IDY and DDY1 methods solved and won in $96\%/25\%,$ $90\%/37\%$ and $55\%/20\%$ of the given problems respectively. Accordingly, if we increase the $\tau$ to an interval $\tau\geq1$, the NSDY method is the best with $68\%$ accuracy, whereas the JYJLL, IDY, DY and DDY1 methods have $66\%,$ $60\%,$ $55\%$ and $40\%$ accuracy, respectively. Similarly, the comparison among the five schemes based on interpretation of Figure 2 shows that the NSDY, DY, JYJLL, IDY and DDY1 methods solved the problems and won in $98\%/12\%,$ $96\%/28\%,$ $94\%/54\%,$ $90\%/30\%$ and $57\%/14\%$ respectively for the value $\tau$ chosen within $0 < \tau < 0.5$. However, increasing the $\tau$ value to the interval $\tau\geq6$ reveals that the NSDY method wins when solving $97\%$ of the test problems compared to JYJLL, IDY, DY and DDY1 methods with $90\%,$ $88\%,$ $96\%,$ and $52\%$ of problems solved to the best respectively. Finally, Figure 3 also shows that for the value $\tau$ chosen within $0 < \tau < 0.5,$ NSDY, DY, JYJLL, IDY and DDY1 methods solved and won in $98\%/33\%,$ $96\%/08\%,$ $94\%/38\%,$ $90\%/22\%$ and $58\%/05\%$ problems, respectively. Alternatively, taking the value of $\tau$ in the interval $\tau\geq6$ reveals that the NSDY method wins when solving $97\%$ of the test problems compared to the JYJLL, IDY, DY and DDY1 methods with $93\%,$ $88\%,$ $92\%,$ and $52\%$ of problems solved to the best, respectively. Therefore, interpretations of Figures 1–3 indicate that the NSDY method is more preferable than other CG methods.

5.   Application of the NSDY algorithm in restoration of corrupted images

The CG method is among the most efficient minimization algorithms used for faster optimization of both linear and non-linear systems because of its rapid solution for large-scale problems. Recently, the CG iterative scheme has been widely considered for solving real-world application problems because of its fewer iterations and less computational resources required to optimize a given problem. Some of the most relevant problems solved by the CG method includes the feed forward training of neural networks ^[3], the problem of motion control of robotic manipulators ^[8], regression analysis ^[1,6], and the restoration of corrupted images ^[8,9].

Image restoration is among the family of inverse problems used to obtain some highly-quality images from those images that have possibly been corrupted during the data acquisition process. Choosing an appropriate algorithm that is capable of restoring these corrupted images is very crucial because knowledge of the degradation system has to be considered in order to achieve better quality images. In this study, we consider restoring some images which that include a building (512 × 512) and camera (512 × 512). These images were possibly corrupted by salt-and-pepper impulse noise during the data acquisition or storage process. For the purpose of this study, the following metrics have been employed to measure the quality of the restored images and evaluate the performance of the algorithms. These metrics include the following

● peak signal-to-noise ratio (PSNR),

● relative error (RelErr),

● CPU time.

The PSNR has widely been used to measure the perceptual quality of restored images because, it calculates the ratio between the power of corrupting noises and the maximum possible power of a signal affecting the fidelity of the representation. This metric is very crucial when evaluating the quality of both corrupted and restored images. It is important to note that a method with higher PSNR will produce images with better quality ^[40]. The PSNR can be obtained as follows

where $MSE$ is used to measure the average pixel differences of the complete images and $MAX_I$ represents the maximum pixel value of the images. Also, an algorithm with higher $MSE$ values will produce greater difference between the original and corrupted images. The $MSE$ values can be obtained via:

where $N$ denotes image size, $E$ is the edge image and $o$ represents the original image.

5.1.   Image restoration problem

Consider the following image restoration problem:

where the edge-preserving potential function $\phi_{\alpha}(t) = \sqrt{t^2+\alpha}$ for some constant $\alpha$ whose value is given as $1$.

The above problem is transformed into the following optimization problem ^[41]

where $x$ is the original $M \times N$ pixel image. Also, $G$ denotes the following index set of noise candidates $x$:

where $i, j \in Q = \{1, 2, \cdot, M\}\times \{1, 2, \cdot, N\}$ its neighborhood is defined as

From (5.3), the maximum and minimum values of the noisy pixel are $s_{\max}$ and $s_{\min}$. Also, $\xi$ is the observed noisy corrupted image whose adaptive median filter is denoted as $\bar{\xi}$.

Next, we present the computational performance of the proposed algorithm in Tables 3, 4, and 5. The performance was compared with that of other similar algorithms with the same characteristics in terms of the PNSR, RelErr, and CPU time to demonstrate the robustness of the algorithm. All computations were carried out under the conditions of the strong Wolfe line search with the restoration noise degrees set as $30, 50$ and $80,$ respectively.

From the results presented in the tables above, it is obvious that all of the methods are very competitive. Starting with the CPU time of the camera image, it can be observed that at $30\%$ noise degree, the CPU time for the proposed method is lower than that of DDY1 and IDY algorithms but higher than that of DY and JYJLL methods. However, at the $50\%$ noise degree, the proposed algorithm outperformed all of the other methods, achieving the shortest CPU time. Also, at the $80\%$ noise degree, our method was superior to all other algorithms except the IDY algorithm which produced the shortest CPU time. Similarly, by considering the Performance of the new method in terms of restoring the building corrupted image also shows that the method is very competitive. Furthermore, overall performance analysis of the methods (see Tables 4 and 5) in terms of the PSNR and RelErr shows that the proposed method performed better because its produced higher values for PSNR and RelErr in most of the noise degrees considered. Based on the previous discussion, the higher the PNSR and RelErr values, the better the quality of the output images. For the graphical representation of the results, we refer the reader to Figures 4 and 5. These results were obtained for the 30%, 50%, and 80% noise degrees, respectively.

Based on Tables 3, 4 and 5 and Figures 4 and 5, we can conclude that the proposed method is more efficient and robust because it restored most of the corrupted images with high accuracy than other existing methods.

6.   Conclusions

In this study, considering the D-L conjugacy condition as well as the Newton search direction, a spectral DY CG method for large-scale unconstrained optimization and image restoration problems is suggested. The proposed method introduces a new spectral parameter $\theta_k$ to scale the search direction $d_k$ such that it satisfies the sufficient descent property and converges globally with strong Wolfe criteria. The preliminary computational results a set of optimization functions analyzed in comparison to those obtained for some DY modifications in literature indicated that the proposed method is efficient and reliable.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence tools in the creation of this article.

Acknowledgments

The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT and Petchra Pra Jom Klao PhD Scholarship of King Mongkut's University of Technology Thonburi (KMUTT), contract No. 52/2564. Moreover, the authors also acknowledged the financial support provided by the Mid-Career Research Grant (N41A640089).

Conflict of interest

The authors declare no competing interests.