1.
Introduction
Non-Newtonian fluids have attracted considerable interest due to their wide array of applications that can be found across many industries. Topics of interest include the structural properties of robust lattice heat, the transfer of atomic waste, the utilization of synthetic synergist reactors, the generation of geothermal energy, the study of groundwater hydrology, the phenomenon of transpiration cooling, and the availability of oil supplies. Numerous models have investigated non-Newtonian liquids but there is not even a prototype that has been constructed that depicts the properties of non-Newtonian fluids. The Casson fluid model is among the various non-Newtonian fluid models, which simulate a variety of fluids, including fruit juices, jelly, honey, soup, and blood. The Casson fluid is a type of non-Newtonian fluid that exhibits shear-thinning behavior and possesses a yielding stress. At infinitely high shear rates, the substance exhibits a viscosity of zero, while at a significantly low shear rate, it demonstrates an infinite viscosity [1]. Numerous scholarly inquiries have been undertaken to investigate the characteristics and behavior of Casson fluid flow such as [2]. Later, Ibrahim and Anbessa [3] examined the characteristics of the three-dimensional magnetohydrodynamic combination convection flow of Casson nanofluid across exponentially stretched sheets. Manvi et al. [4] investigate the flow behavior of non-Newtonian Casson fluids with heat and mass conduction towards extended surfaces.
Magnetohydrodynamics MHD plays a crucial and indispensable function in the domains of engineering and industrial applications. The study of magnetohydrodynamics fluid flow is of significant interest due to its relevance in various applications such as MHD generators, liquid metal cooling system design, MHD pump accelerators, and flow meters. The utilization of magnetic field effects has notable implications in the realms of science and engineering, encompassing various applications such as MHD pumps, geothermal energy extraction, MHD generators, and numerous more. The book by Moreau [5] provides a thorough analysis of magnetohydrodynamics theory and its application in real-world situations. Krupalakshmi et al. [6] a simulation was performed to explore the impact of nonlinear thermal radiation and magnetic fields on the flow of a higher convective Maxwell fluid. The flow was induced by a convectively heated stretched sheet, while dust particles were present. Das et al. [7] investigated the influence of entropy generation on the MHD slip flow of a non-Newtonian Cu-Casson nanofluid while taking heat radiation into consideration. Rashidi et al. [8] analyzed the mass and heat transfer on MHD blood flow of the Casson fluid simulation due to peristaltic motion waves. Recently, Hamarsheh et al. [9] studied MHD and the natural convection effect on the flow of oxide of graphite, carbon nanotubes and methanol-based Casson nanofluids that pass a horizontal circular cylinder. Unsteady Magnetohydrodynamics (MHD) combined convection flow of Non-Newtonian Casson nanofluid with hybrid properties in the stagnation zone of spheres subjected to impulsive spinning was investigated by El-Zahar et al. [10].
The flow of Viscous fluid between two parallel disks or plates is of great interest in modern technologies. Polymer processing, metal liquid lubrication, compression, power transfer through squeezed films, and injection modeling are among their many technological and industrial applications. Squeezing flows are prevalent in polymer processing, including thin sheets, paper, plastic, and metal sheet manufacture. Jackson [11] presented a study of squeezing flow in 1962. Researchers in the literature [12–14] have examined squeeze films. The study of Casson fluid in MHD squeezing flow between a pair of parallel plates is important due to its numerous practical applications in the fields of engineering and science. For example, it can be used to model the flow of blood in arteries, which is important for understanding cardiovascular diseases. It can also be used to model the flow of paints and other materials in manufacturing processes, so studies have been focused on this phenomenon. Naveed et al. [15] studied the effects of the magnetic field in squeezing the flow of a Casson fluid between parallel plates using a variation of parameters method (VPM). Al-Saif and Jasim [16] studied the same fluid using a novel algorithm. Noor et al. [17] investigated the heat and mass transport characteristics within an unstable squeezing flow of a magnetohydrodynamic Casson nanofluid. Divya et al. [18] analyzed the influence of temperature characteristics of peristaltic Casson MHD fluid flow within an irregular channel. The influence of the energy of activation and chemical reactions on the dynamics of unsteady magnetohydrodynamic (MHD) dissipative processes. The study focused on the investigation of the Darcy-Forchheimer squeezing flow of a Casson fluid within a horizontal channel in [19].
In previous studies, the equations governing flow were solved using numerical or analytical methods, but recently, these equations have been solved using fractional calculus. The field of fractional calculus began in 1965. Fractional-order derivatives and integrals are being studied [20]. Researchers like fractional calculus because it includes non-local derivatives and integrals. Fractional calculus effectively explains memory effects [21]. The cognitive capacity helps observe historical events and processes. Because of these advantages, fractional calculus has largely replaced standard calculus. Existing studies on fractional-order partial differential equations show that their results are more precise and comprehensive than integer-order ones [22]. Fractional-order derivatives and integrals are widely used in research and technology, making them a popular and growing calculus subject. Numerous fields use this area [23–26], such as bioengineering, mathematics, finance, and disease dynamics use fractional calculus [27–28]. Ali et al. [29] analyzed nanofluid heat transfer under escalating wall temperatures using fractional derivatives. Thermal radiation effects are included in this research [30] on magnetohydrodynamic Casson fluid-free convection across an oscillating plate. The Caputo fractional derivative showed that fractional parameter values enhance velocity, while thermal radiation and Prandtl number values decrease velocity. Several recent articles have addressed fractional derivatives [31–39].
A review of the literature finds that no attempt has yet been made to investigate the MHD squeezed flow of a Casson fluid via TAM. Thus, the current investigation involves the usage of a fractional transformation to the unsteady Casson fluid model, leading to the development of a more detailed simulation of fluids that incorporates fractional order. The complex model is solved with a semi-analytical iterative methodology. The TAM a method developed by Temimi and Ansari has emerged as a viable approach for solving linear and nonlinear ordinary differential equations (ODEs) as well as partial differential equations (PDEs) [40–42]. The iterative approach has been recently utilized to derive precise as well as approximation solutions for numerous scenarios. As a result, the Technology Acceptance Model (TAM) eliminates the necessity for computationally demanding processes and does not necessitate the use of additional parameters.
The studied case description of this work will be studied in section 2, the full demonstrations and fundamental mechanisms of the used method, TAM, are considered in section 3, while the results and discussion of their numerical examples and the effect of the essential parameters are presented in section 4.
2.
Problem formulation
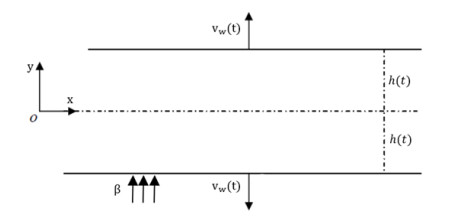
An incompressible fluid flows between parallel plates where the separation distance y=∓L√1−at=∓h(t), and L is the distance between two plates (time t=0). For a greater than zero the plates decrease where the plates contact (t=1/a), while for a less than zero they recede and dilate as shown in Figure 1. In order to analyse the heat creation owing to shear friction caused by the flow, viscous dissipation impacts are also used. Casson fluid rheological expressed by the constitutive equation (the stress tensor and strain rate relation) of the model is described as follows [15]:
where τij is the i, j‑th are the stress tensor components, π=eijeij and eij are the tensor strain rate components, where linear, volumetric, and shear strain are combined in tensor form Py=μb√2πγ is fluid stress, μb is plastic viscosity of Casson fluid, π is the deformation rate component multiplied by itself, and πc is π critical value. In the non-Newtonian flow, πisgreaterthanπc, μ=μb+Py√2π, then the non-Newtonian kinematics viscosity depend on the values of μb, ρ and γ as [43]:
The magnetic field is acting in the y-axis as:
(ⅰ) We can ignore the effects of induced magnetic and electric fields from electrically conducting fluid.
(ⅱ) We can neglect any other electric field.
The equations for maintaining flow under the above constraints are [15]:
where u is the x direction component of the velocity v is the x direction component of the velocity, γ is the parameter of Casson fluid parameter, and β is the magnitude of the imposed magnetic field, σ is fluid electrical conductivity.
Eliminating pressure P from (4), (5) and using the vorticity function ω=∂xv−∂yu, then we have a single momentum equation [15]:
The boundary conditions on the u and v are [15]:
where vw(t)=dh(t)/dt is the velocity of the plates.
In Wang [1], the transform for the flow in two-dimensions is:
Applying similarity transforms (8) in (3), (6), and (7), to an ordinary differential equation that describes the system with boundary conditions is:
The constants S=L2a2ν and M=Lσβh(t)νρ are the squeeze number, and magnetic number, respectively, where the primes denote differentiation with respect to η.
Squeezing number S specifies how the plates move (S>0 indicates that the distance between plates is increasing, and S<0 indicates a decreasing distance). Here our investigation is reported for M=0 and γ→∞. The definition of skin friction coefficient is:
where Cf=νv2w∂tu|y=h(t),Rex=2Lv2wνx√1−at.
3.
The fundamental mechanisms of the TAM
The general fractional differential equation (DE) is a mathematical equation that may be used to represent the essential concepts of the suggested technique as follows:
Along with boundary conditions
where Θ=Dαη=∂α∂ηα is used to represent the fractional Caputo derivative of ϖ(η). The generic linear and nonlinear differential operators are represented by the symbol Ψ,ϖ(η) refers to the unnamed function, the continuous functions are shown as H(η) and the boundary operator is shown by B. The main request made here is for the differential operator Θ, which is general. However, if necessary, we can combine several linear components with nonlinear terms. The following describes how the suggested method operates. The starting condition is obtained by removing the nonlinear portion as
We resolve the following equation to provide the next iteration of the solution
As a result, we have a simple iterative step ϖj+1(η) that successfully resolves a collection of problems that are both linear and nonlinear
It is crucial to remember that each step ϖj+1(η) in this strategy serves as a separate solution for the problem. We confirm that these iterative stages are simple and each solution is an improvement over the previous iteration. To confirm the convergence of solutions, successive solutions are compared to the prior iteration. The analytical solution and the exact solution to the issue converge as more iterations are made. This allows for the development of a suitable semi-analytical solution with an appropriate agreement with the exact solution as
4.
Results and discussion
Now, we can present the impact of following parameters S, γ and M effects on radial ϖ′(η) and normal ϖ(η) components of the velocities.
Table 1 compares the present TAM technique findings to Wang's numerical results published earlier and lately [16, 44]. While Table 2 compares the skin friction coefficient using several values of parameters, the other tables show convergence of results.
The squeeze number effect (in case S>0) and recede number (in case S<0) on the flow under the magnetic field effect is shown in Figure 2. As in |S| increases, ϖ(η) increases. The effect of |S| decreases as we approach the plane. It can be explained by the adhesion forces that occur between the fluid and the plane. The same behavior with the increase in magnetic parameter. However, this increase is greater than in the case of increasing |S|, as in Figure 3. Figure 4 represents the small effect of increasing the Casson parameter in increasing vertical speed, especially when S<0, and this is due to the inverse relationship that relates kinematics viscosity to the Casson parameter (see Eq 2). Figures 5–7 depict the impact of S, M, and γ on radial components of velocity ϖ′(η). Figure 5 shows increases in velocity when |S| increases for 0≤η≤0.5, and ϖ′(η) decreases as we approach the plane with an increase of |S|. The impact of M on radial velocity is shown in Figure 6. This effect is similar to the effect of M on ϖ(η), but less. When the Casson parameter is increased, we note decreases in the radial velocity for 0≤η≤0.5, and it increases as we approach the plane, as in Figure 7.
Physically, the collision occurs between the fluid and the plate's border surface. As a result of the flow retardation near the boundary layer, the fluid velocity decreases. The existence of a magnetic field causes flow to respond with a force, which is known as the Lorentz force. This force is caused by the magnetic field that obstructs fluid flow in the boundary layer when the plates became closer in the squeezing prosses. Now, the flow happens while the plats distance is very small, while the squeezing flow. Inhibiting the Lorentz force produces an inverse stress gradient if they disappear for an extended period of time. As the backflow occurs, there may be a separation point. Furthermore, as M increases, the velocity flow of fluids reduces as the plates move apart. Moreover, when the distance between the plates is increased, the flow takes place and the magnetic number is increased due to free space properties. To avoid the conservation law of mass violation, the fluid is moved at high velocity in that area. As a result, an increased fluid flow is noticed.
5.
Conclusions
In this work, the fractional nun Newtonian condition is studied of Casson fluid where the magnetohydrodynamic and Darcian effect is considered, and the mathematical form of this fluid system is studied by the superior procedure, which was developed by Temimi and Ansari (TAM) which was used for the first time the fluid mechanics. This method is applied in different types of physical and engineering problems and solved this studied system efficiently. The results and the emerging parameters' effects on flow have been numerically tested and tabulated, and illustrated in figures. The validation of this method shows that the results are compared with homotopy perturbation method. After the results were acquired with the applying the Temimi and Ansari method in this studied system, we recommended to use this method in more complicated fluid systems especially when taking the temperature into consideration. Furthermore, we hope it provides the required results when it is used for considering different phenomena in physics and engineering.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R215), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflict of interest
All authors confirm that there are no conflicts of interest.









 DownLoad:
DownLoad:









