Disturbance observer-based adaptive sliding mode synchronization control for uncertain chaotic systems

1.   Introduction

The problem of synchronous control of chaotic systems has become a challenging task due to their complexity and unpredictability, in particular, their sensitivity to initial conditions. Nonetheless, chaotic synchronization has drawn a lot of interest and emerged as a hot topic due to its significant promise for many practical applications ^[1,2,3,4]. For example, in the field of secure communication, the difficulty of deciphering communication signals can be increased with the help of chaotic synchronization scheme, and the security of secure communication can be improved ^[5]. In the field of electrical power systems, the chaotic synchronization scheme can eliminate the chaotic vibrations generated by the power system and enable the system to operate safely and smoothly ^[6]. In the practical engineering field, chaotic synchronization systems can be applied to the fault diagnosis of rolling bearings ^[7]. There are several control techniques to achieve chaos synchronization, including active control, adaptive control, SMC, robust adaptive SMC, DO-based, and so on ^{[8,9,10,11,12,13,14]}.

However, chaotic systems, frequently feature various levels of uncertainty that protrude into and out of the system. The structure and parameters of the mathematical model representing the controlled component are not always precisely known in advance by the designer from the perspective of the interior of the system. It is equivalently defined in terms of a huge number of unanticipated disturbances as the impact of the external environment on the system. It is vital to look into and address how to develop an effective controller in light of these uncertainties so that the system has exceptional dynamic quality and outstanding output performance. Among them, the performance of adaptive control is particularly prominent ^[15]. SMC, as a robust nonlinear control method, is mainly used to solve synchronization problems in chaotic systems ^{[16,17,18,19,20]}. In order to approximate and account for these outside disturbances, DO is frequently utilized ^{[21,22,23,24,25,26]}.

The synchronization control of uncertain chaotic systems has recently made some progress. Reference ^[12] describes the design of two nonlinear control methods. The first technique is a finite-time stable active control that takes into account a few parameters, and the second strategy is a finite-time unbounded adaptive control method that can adjust to parameter uncertainty. A feedback linearization technique based on a DO is suggested in the reference ^[27] for managing chaotic systems when there is an external disturbance. Reference ^[24] offers a succinct introduction to DO and a clear explanation of its functionality. A new design technique for nonlinear DO is introduced in ^[25] for a class of nonlinear systems characterized by input-output differential equations. For the robust trajectory tracking problem of underwater vehicles in the presence of unpredictable external disturbances and parameter uncertainties, a nonlinear DO is set out in ^[26]. The research described above goes into considerable length on this subject. However, the literature does not take into account the inherent uncertainty of chaotic systems and assumes that the boundaries of external disruptions are known in advance ^[28,29,30]. In real-world scenarios, the master and slave systems could not be the same, and it might be challenging to define the limits of outside interference. Consequently, analyzing the synchronization problem for chaotic systems with unclear terms and unknown constraints on external disturbances for real-world applications is more beneficial. In reference ^[9], an adaptive SM controller is designed to address synchronization issues in Duffing-Holmes chaotic systems with uncertainties and external disturbances. However, this paper does not need to understand in advance the boundaries of external disturbance, but to ensure that the external disturbance and derivative bounded uncertainties. In this article, we look into ways to exceed the limit for both the number of external disturbances and the number of their derivatives.

The following constitutes this paper's primary innovative work:

(1) The DO-based SM controller designed in this paper breaks through the restriction that the internal uncertainty of the system is bounded and must be known. At the same time, the time-varying disturbance can be observed, which is rare in previous work. There are two types of DO designs. For constant and bounded disturbances, the linear DO performs well for estimation and has excellent dynamical properties, namely that the observer error tends to zero asymptotically. For time-varying disturbances, nonlinear DO can finitely perform estimation work with bounded observer error.

(2) In this study, a novel SM controller is designed that can handle the synchronization control issue of uncertain chaotic systems with different initial conditions of master and slave systems. The new SM controller is based on adaptive technology and DO.

The article has been set up as follows: The master-slave chaotic synchronization system and the equation of state for the synchronization error are both covered in Section 2. In Section 3, this paper design linear and nonlinear DO for constant and time-varying external disturbances. Based on the DO design, the adaptive SM controller's design process is detailed in Section 4, and the Lyapunov stability theory is used to demonstrate the system's effectiveness. Section 5 presents the simulation findings. This paper is concluded in Section 6.

Notations: In this article, $\mathbb{R}^{n}$ denotes $n$ dimensional real vector space, $\mathbb{R}^{n\times n}$ denotes $n \times n$ real matrices. $\mathbb{R}$ represents the set of real numbers. $\|\cdot \|$ is interpreted as Euclidean norm. The meaning of $|h|$ is the boundary of the function $h$. $\lambda_{\min}(Q)$ is the minimum eigenvalue of $Q$. $diag(\cdot)$ represents a diagonal matrix. $sign(\cdot)$ is the sign function.

2.   System description and problem formulation

In this study, n-dimensional master and slave chaotic systems are considered. The master chaos system is

where $x(t) = [x_1(t), x_2(t), ..., x_n(t)]^T\in {\mathbb{R}}^n$ is the master system state and $h(x, t)$ is a nonlinear function of $x$ and $t$. System (2.1) is commonly used to describe physical systems such as the Duffing-Holmes damping spring system, the Van der Pol system, robot systems and flexible joint institutions. The chaotic system of the slaves is

where $y(t) = [y_1(t), y_2(t), ..., y_n(t)]^T\in {\mathbb{R}}^n$ is the slave system state, $u\in {\mathbb{R}}$ is the control input, $h(y, t)$ is a given nonlinear function of $y$ and $t$, $\triangle h(y, t)$ is an uncertainty term representing the unmodeled dynamics or structural changes of system (2.2) and $d(t)$ is the external disturbance to system (2.2).

This paper supposes that systems (2.1) and (2.2) have unique solutions in time interval $[t_0, +\infty)$, $t_0 > 0$ for any given initial terms $x_0 = x(t_0)$ and $y_0 = y(t_0)$ under $h(x, t)$, $h(y, t)$ and $\triangle h(y, t)$ that satisfy some necessary conditions. The state synchronization errors are denoted as $\xi(t) = [\xi_1(t), \xi_2(t), ..., \xi_n(t)]^T\in {\mathbb{R}}^n$, where $\xi_j\triangleq y_j-x_j$, $j = 1, 2, ..., n$. The synchronization error dynamic equation can be described as:

where $\rho(\xi, t)\triangleq h(\xi+x, t)-h(x, t)$ and $y = \xi+x$.

Remark 1. Given that this paper will design sliding mode controllers that take into account both internal and external disturbances, it is necessary to make assumptions about $\rho(\xi, t), \triangle h(\xi+x)$ and $u(t)$.

Assumption 1. Suppose that $\rho(\xi, t), \triangle h(\xi+x)$ and $u(t)$ have a derivative of time $t$, respectively.

The purpose of this work is to demonstrate that when a slave system is subjected to an external disturbance, master-slave systems starting from various initial circumstances can attain synchronization. The targets are as follows: When the slave system is perturbed by an unknown constant, namely $d(t)\triangleq d_{1}$, where $d_{1}$is an unknown constant, the disturbance is estimated by designing a linear DO and the master-slave system is intended to achieve asymptotic synchronization through the use of a sliding mode control law, that is, $\lim_{t\rightarrow \infty}\|\xi(t)\| = 0$, where $\|\cdot \|$ is the European norm. When the slave system is perturbed by a time-varying disturbance, namely $d(t)\triangleq d_{2}(t)$, where $d_{2}(t)$is an unknown time-varying disturbance, the disturbance is estimated by designing a nonlinear DO and a sliding mode control law is designed to achieve bounded synchronization of the master-slave system, that is, $\lim_{t \rightarrow \infty}\|\xi(t)\|\leq\bar{ \mu}$, where $\bar{\mu}$ is a positive real number. When the slave system is subject to internal uncertainty and an external disturbance, an adaptive DO-based SM controller is designed to achieve bounded synchronization of the master-slave systems.

3.   Design of disturbance observer

In this section, two DOs for different types of disturbances are designed to implement disturbance estimation.

When the constant-type external disturbance $d_1$ is added to the system (2.2), we design a linear DO as:

where $\hat{d}_1$ is the estimated value of the constant-type external disturbance $d_1$ and $l$ is the gain of the linear DO.

Let the observer's error be $\xi_{d1} = \hat{d}_1-d_1$. When the system (2.2) have only suffered external disturbance $d_1$, that is, $\triangle h = 0$. Combining Eqs (2.3) and (3.1), we obtain the derivative of $\xi_{d1}$ as

where $\dot{d}_1 = 0$.

By choosing a positive observation gain, $l > 0$, the disturbance error $\xi_{d1}$ will approach zero when $t \rightarrow \infty$. The $\hat{d}_1$ can asymptotically estimate the constant disturbance $d_1$ of the system (2.2).

When the time-varying type of external disturbance $d_2(t)$ is added to the system (2.2), satisfying:

where ${\omega}(t)\in {\mathbb{R}}^m$ is the interference-generating component, $W\in{\mathbb{R}}^{m\times m}$ and $V^T\in{\mathbb{R}}^{m}$ are gain matrices that will be designed in the following.

We consider the system (2.2) have suffered both external disturbance $d_2(t)$ and internal uncertainty $\triangle h$. Due to the presence of internal uncertainties, the previously designed linear DO does not fit the requirements and the estimation error is not controlled. So, we have to adjust the observer. Here we make the following assumption about the internal uncertainty:

Assumption 2. Let the uncertainty component $\triangle h$ in system (2.2) be bounded and satisfy that $| \triangle h| < \alpha$, where $\alpha$ is a positive constant.

A nonlinear DO for estimating the external disturbance $d_2 (t)$ is given under Assumption 2 as follows:

where $\vartheta\in{\mathbb{R}}^{m}$ is the state of the nonlinear DO, $L\in{\mathbb{R}}^{m}$ is the observer gain, and $\hat{d}_2$ is the estimate of the external disturbance $d_2(t)$. The estimated error is denoted as $\xi_{d2} = \hat{\omega}-{\omega}$.

Taking the derivation of $\xi_{d2}$ and combining it with Eq (3.4):

By choosing appropriate gains $W, L$, and $V$ so that $W+LV$ is Hurwitz, $\xi_{d2}$ of system $\dot{\xi}_{d2} = (W+LV)\xi_{d2}$ is asymptotically stable, that is, $\lim_{t\rightarrow \infty} = 0$. The following lemma has been given for the observer error by designing $W$, $L$, and $V$.

Lemma 1. If the appropriate matrices $W$, $L$, and $V$ are chosen, let $W + LV$ be Hurwitz. Then the nonlinear DO(3.1) can approximate the time-varying external external disturbances well, and the estimated error will not exceed $\mu\|V\|$, where $\mu > 0$.

Proof. Since $W+LV$ is Hurwitz, there are positive matrices $P_d, Q_d\in{\mathbb{R}}^{m\times m}$ satisfied:

Select $V_d = \xi_{d2}^T P_d \xi_{d2}$ as a Lyapunov function, and taking the time derivative of $V_d$:

Substituting Eqs (3.5) and (3.6) into Eq (3.7):

Since $Q_d$ is a positive definite matrix, $\xi_{d2}^T Q_d \xi_{d2}\geq\lambda_{\min}(Q_d)\| \xi_{d2}\|^2$, where $\lambda_{\min}(Q_d)$ is the minimum eigenvalue of the positive definite matrix $Q_d$. The Eq (3.8) can be rewritten as:

By indicating $\| \xi_{d2}\|\geq \frac{4\| P_d\|\| L\|\alpha}{(1-\epsilon)\lambda_{\min}(Q_d)}\triangleq\mu$:

The meaning of the representative of (3.10) is that, when $\|\xi_{d2}\|\geq\mu$, there is a limited time such that $\dot{V}_d < 0$ holds, that is, $\|\xi_{d2}\|\leq\mu$ in a limited time, then $\|\xi_{d2}\|\leq\mu$.

Finally, $\xi_{d2}$ is ultimately uniformly bounded, that is, $|\hat{d}_2-d_2|\leq \mu\|V\|$. □

Remark 2. The convergence rate of the DO error can be adjusted by choosing the value of $\epsilon\lambda_{\min}(Q_d)$. While $W+LV$ is Hurwitz, this design job that is easy to implement in modern control theory. The ultimate estimate error depends on the parameters $\alpha$ and $V$. A Hurwitz matrix, also known as a stable matrix, is a square matrix in which all eigenvalues have negative real parts.

Remark 3. In this section, two DOs were designed to estimate the external disturbances. In order to achieve good synchronization effect, the corresponding disturbance observer is selected according to the type of external disturbance. In practice, disturbances are typically of a fixed type, so the DOs presented in this paper can satisfy most of the system requirements.

Remark 4. In addition, the nonlinear DO presented in this paper considers the system's internal disturbance, which is rare in current chaotic synchronous control systems.

Remark 5. This paper aims to realize the synchronization task of uncertain chaotic systems, which requires the design of suitable controllers. However, SMC is robust as a widely used nonlinear controller. This paper will combine SMC and DO to design the controller.

4.   Design of control strategy and stability analysis

4.1.   Design of adapive sliding mode controller based on disturbance observer

In this section, a smooth controller will be designed that takes into account both DO (3.1) and DO (3.4) as well as the SM surface. Meanwhile, the design of the SM surface is also related to the type of DO. Since both controller design and SM surface design are related to DO, it is necessary to combine the synchronization error system (2.3) with the dynamic system of DO (3.1) or (3.4). In the following, the augmented system with different DOs will be presented and the SM surface will be designed. Considering the internal disturbances of the system (2.2), we would like to implement adaptive parameters and finally design an adaptive SM controller based on DO. Finally, we present the reachability conclusion for the SM surface.

First, $\hat{d}_q$ is denoted by DO, which is linear DO (3.1) as $q = 1$, and is nonlinear DO (3.4) as $q = 2$. $\xi_{d_q}$ is the disturbance error, $q = 1, 2$. Using the concept of the augmented system combined with system (2.3) and the DOs (3.1) and DO (3.4), the error-normalized state space equation under Assumption 1 can be obtained as:

when $q = 1$, $V_1 = 1$; $q = 2$, $V_2 = V$. Notice that the auxiliary scalar

has a derivative about $t$ according to Assumption 1 and DO (3.1) or (3.4).

Next, an integral SM surface will be designed for system (4.1)

where $\xi_{n+1}(0)$ represents the initial value of $\xi_{n+1}$. According to SMC theory, $\dot{\sigma} = 0$ is always valid when the system remains on the SM surface. Therefore, the derivative of equivalent controller is obtained as:

from $\dot{\sigma} = 0$ and system (4.1). The dynamical equation of $\xi_{n+1}$ under the $u_{eq}$ can be described as:

Combining linear DO (3.1) and system (3.2), $\triangle h = 0$, and Eq (4.3), the dynamic equation of SM can be expressed as:

The matrix differential equation of the system (4.4) is:

where $\tilde{\xi} = [\xi_1, \xi_2, ..., \xi_{n+1}, \xi_{d1}]^T\in {\mathbb{R}}^{n+2}$, its initial value is $\tilde{\xi}(0) = [\xi_{1, 0}, \xi_{2, 0}, ..., \xi_{n+1, 0}, \xi_{d1, 0}]^T\in {\mathbb{R}}^{n+2}$, and gain matrix

By choosing appropriate parameters $r_i > 0, i = 1, \cdots, n+1$ and $l > 0$, the asymptotic stability of the system (4.5) can be guaranteed, that is to say, as $t\rightarrow \infty$, the state $\tilde{\xi}$ reaches the equilibrium point zero along the SM surface (4.2). The size of $r_i$ and $l$ affects the speed at which the system state reaches the equilibrium point.

Combining nonlinear DO (3.4), $\triangle h\neq 0$, and Eq (4.3), the dynamic equation of SM can be expressed as:

The matrix differential equation of the system (4.6) can also be expressed as:

where $\xi = [\xi_1, \xi_2, ..., \xi_{n+1}]^T\in {\mathbb{R}}^{n+1}$,

and

Here, we can choose $r_i > 0, r = 1, \cdots, n+1$ to ensure that $\bar{A}$ is the Hurwitz. Next, the crucial conclusion of this paper will be given under Lemma 1.

Theorem 1. Under Lemma 1, if the gain matrix $\bar{A}$ is the Hurwitz, then the state $\xi$ of the system (4.7) is eventually uniformly bounded, and the bound shall not exceed $\bar{\mu}$.

Proof. Since $\bar{A}$ is a Hurwitz matrix, there are positive definite matrices $P, Q\in{\mathbb{R}}^{(n+1)\times (n+1)}$, such that

Choose $V_1 = \xi^T P\xi$ as the Lyapunov function, and its first derivative is

Putting Eqs (4.7) and (4.8) into Eq (4.9):

Since Q is a positive definite matrix,

where $\lambda_{\min}(Q)$ is the minimum eigenvalue of $Q$.

Combining Eqs (4.10) and (4.11):

when

according to Lemma 1,

the following equation can be obtained,

From Eq (4.15), it can be obtained that when $\|\xi\|\geq\bar{\mu}$, there exists a limited time such that $\dot{V} < 0$ holds, that is, $\|\xi\|\leq\bar{\mu}$ in a limited time. That is to say,

Finally, $\xi$ is uniformly bounded, that is, $\|x(t)-y(t)\|\leq\bar{ \mu}$ in a limited time. □

Remark 6. The SM dynamical equation based on linear DO (4.5) can also be written in the form of Eq (4.7) by the block matrix method, that is, $\tilde{\xi} = \bar{A}\xi-l\xi_{d1}$ by choosing $A = {diag}\{\bar{A}, -l\}$ and $\tilde{\xi} = {diag}\{\xi, \xi_{d1}\}$. Therefore, the two augmentation systems used in this paper are essentially the same.

Remark 7. Effectively, the convergence of the augmented system is not invariant. Equation (4.5) converges asymptotically to zero, but Eq (4.7) is only uniformly bounded. The reason is that linear DO dynamic error systems are asymptotically stable, while nonlinear DO dynamic error systems are uniformly bounded.

Remark 8. From Lemma 1 and Theorem 1, the error bound $\bar{\mu}$ relies on the parameter $\alpha$. In this paper, the value of $\alpha$ has been given. From the Assumption 1, we know that $\frac{d}{dt}\triangle h(\xi+x)$ exists, but in order to guarantee the accessibility of the SM, we need to know that it is bounded. When this bound is known, a general approximation law is chosen to ensure SM achieveability. However, when this bound is unknown, estimates of the parameters need to be taken into account. Adaptive techniques are widely used for estimation. The SM approximation laws are considered in combination with adaptive techniques to achieve SM reachability.

Based on the nonlinear DO, an adaptive SM controller will be designed in the following parts.

Assumption 3. Let $|\frac{d}{dt}\triangle h(\xi+x)|$ be bounded, satisfying $|\frac{d}{dt}\triangle h(\xi+x) | < \theta$, where $\theta$ is an unknown positive number.

Taking $\hat{\theta}$ as the estimated parameter of $\theta$ that satisfies the following adaptive law:

where $\hat{\theta}_0$ is the initial condition of $\hat{\theta}$, which is a bounding positive number. Now define the adaptive error as $\tilde{\theta} = \hat{\theta}-\theta$. Since $\theta$ is a constant,

Choosing the SM reaching law as:

where $\text{sign}(\cdot)$ is the sign function, $k$ is a positive number. The law of reaching chosen here includes the law of adaptation.

Combing Eqs (4.2) and (4.19):

Under Eq (4.1), the first derivative of the adaptive SMC signal $u$ is:

The uncertainty component $\triangle h$ is unknown in the actual world. The designed adaptive SMC law under DO can be expressed as:

where the initial value of $u$ is chosen as 0.

4.2.   The reachability of sliding mode surface

In this section, the proposed control scheme (4.22) can drive the system (4.1) into the SM surface (4.2) $\sigma(t) = 0$ in a limited time, that is, the reaching condition $\sigma(t)\dot{\sigma(t)} < 0$ will be satisfied.

Theorem 2. Consider error system (4.1), if the adaptive SMC law (4.22) under nonlinear DO (3.4) is chosen, then the error state reaches the SM surface $\sigma(t) = 0$ in a finite time and maintains on.

Proof. Choosing the Lyapunov function $V = \frac{1}{2}(\sigma^2+\tilde{\theta}^2)$. Under Eqs (4.1), (4.2), and (4.22), the first derivative of $V$ with respect to time $t$ can be obtained as:

Taking Eq (4.18) into Eq (4.23):

Combing with Assumption 3, $\dot{V}$ can be amplified:

Then, we have

As a result, the erroneous state will eventually reach the SM surface $\sigma(t) = 0$ and continue, according to the Lyapunov stability theory. □

Remark 9. In summary, Theorem 2 creates an adaptive SMC law based on the nonlinear DO that permits the augmented error system to reach the SM surface in finite time and remain there. The convergence of the sliding-mode kinetic equation is already provided by Theorem 1, which states that the synchronization error will eventually be uniformly confined. The goal of this study is to synchronize the slave system with the master system. To show the value of the suggested strategy, the give numerical examples will be given.

5.   Simulation examples

Consider the master-slave Duffing-Holmes system as:

and

Let $\xi_1 = y_1-x_1$, $\xi_2 = y_2-x_2$, combining Eqs (5.1) and (5.2), the error state equation of the system can be obtained

Take the gain parameter of SM surface (4.2) as

The adaptive SM controller (4.22) can be designed as

In this paper, two types of DO are designed for different external disturbances, and the SMC law is further designed to synchronize the master-slave system. In the following, the effectiveness of the above method will be verified in three cases.

Case 1: constant disturbance $d(t)\triangleq d_1$.

Take the uncertain component $\triangle h = -0.05y_1$, the constant external disturbance $d_1 = 1$, $l = 10$, $\xi_{d}(0) = 2$, the SM reaching law gain $k = 1$, the step size is taken as 0.001, the initial values of the controller $u(t)$ and the estimated parameter $\hat{\theta}$ are $u(0) = 0$ and $\hat{\theta}_{0} = 0$.

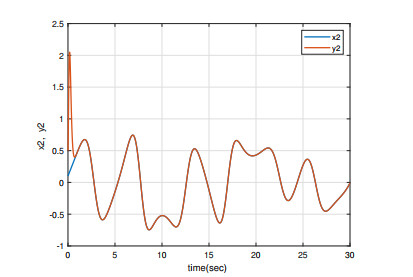
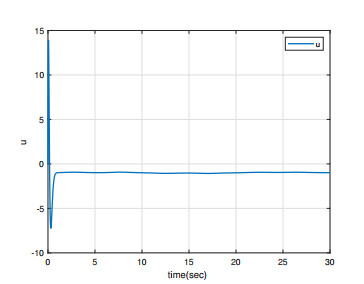
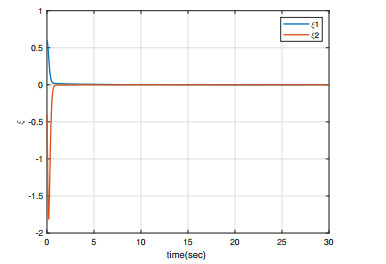
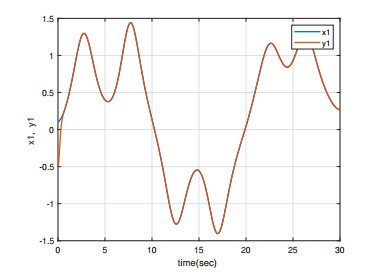
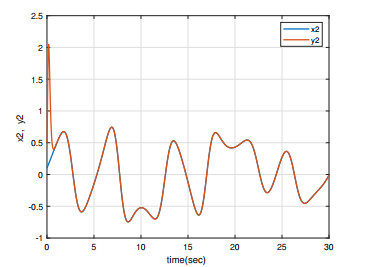
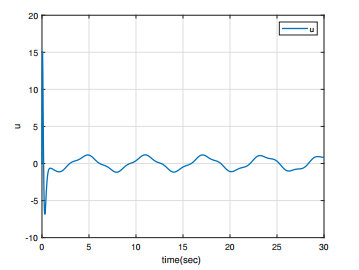
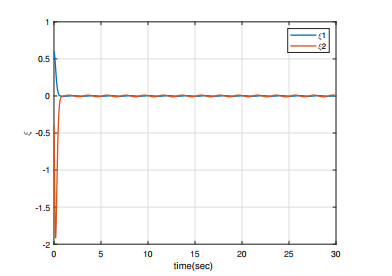
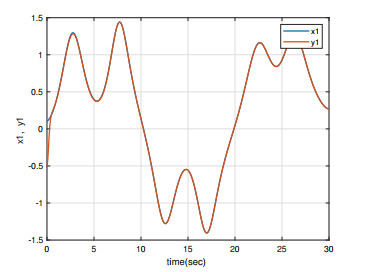
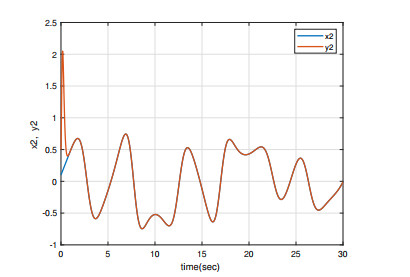
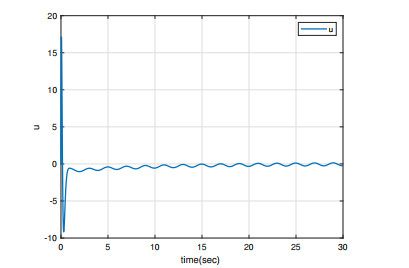
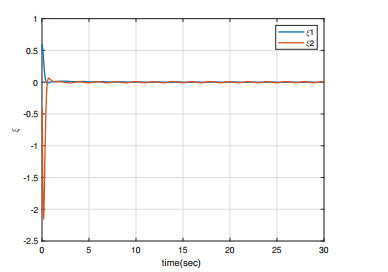
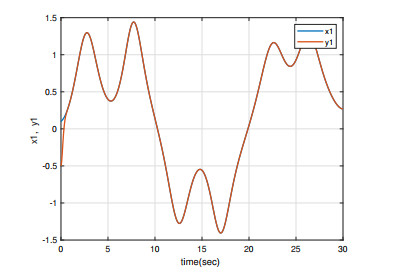
Under the initial conditions $y_1(0) = 0.5$, $x_1(0) = 0.1$, $y_2(0) = -0.5$, and $x_2(0) = 0.1$, the simulation results are shown in Figures 1–4. As can be seen from Figures 1 and 4, the master/slave system can achieve synchronization in less than one second with a fast synchronization rate by employing the adaptive SM controller proposed in this paper. Moreover, the synchronization error remains close to 0 even when the full system contains uncertainties and external disturbances. As can be seen in Figures 3 and 4, the system error states are regulated to zeros asymptotically and the chattering does not appear with this continuous control, even when the overall system is undergoing uncertainty and disturbance.

Case 2: periodic time-varying disturbance $d(t)\triangleq d_2(t)$.

Take the uncertain component as internal uncertainty $\triangle h = 0.2\cos(\pi t)$, the time-varying external disturbance $d_2 = \sin t$; the parameters of nonlinear DO:

the SM reaching law gain $k = 1$; the initial value of the controller $u(0) = 0$; the adaptive parameter initial value $\hat{\theta}_0 = 0$.

The simulation results of the same initial conditions as Case 1 are shown in Figures 5–8. In Figures 5, 6 and 8, it is shown that the master/slave system can also rapidly achieve bounded synchronization by employing the adaptive SM controller proposed in this paper. It can be seen that the synchronization error exists at a certain error even if the entire system contains both uncertainty terms and external disturbances. Also, the continuous control will disappear the chattering; see Figure 7.

Case 3: damped time-varying disturbance $d(t)\triangleq d_2$.

Take the uncertainties and designed parameter terms as $\triangle h = 0.2\cos(\pi t)$, $d_2 = \xi^{-0.1t}$, $W = -0.1$, $L = 1$, $V = -3$, $\xi_{d}(0) = 2$, $u(0) = 0$, $\hat{\theta}_0 = 0$.

The simulation results of the same initial conditions as Case 1 are shown in Figures 9–12. In Figures 9, 10, and 12 it is shown that the master/slave system can also rapidly achieve bounded synchronization by employing the adaptive SM controller proposed in this paper. However, the error in Case 3 is larger than that in Case 2. Also, continuous control does not exhibit chattering; see Figure 11.

Remark 10. The simulation examples show that the control method provided in this paper can achieve the synchronization requirement, but it depends on the type of external disturbance. The above cases all work in the presence of bounded external disturbances, which are common in practical applications. Unbounded external disturbances, which have relatively large effects on the system and few applications, are not designed in this paper.

6.   Conclusions

This paper offers an adaptive DO-based SMC technique to tackle the synchronization control problem and achieve satisfactory control for a class of uncertain chaotic systems. In the presence of ongoing disturbances, it is demonstrated that the suggested controller may asymptotically converge the observer error regime and the synchronization error regime to zero. In the presence of time-varying disturbances, the observer error regime and the synchronization error regime can eventually be uniformly bounded. The error system's stability (or uniformly boundedness) is demonstrated using the Lyapunov approach. According to numerical simulations, the SMC technique developed in this study is effective and does not exhibit chattering.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Shandong Provincial Natural Science Foundation ZR2022MF324 and ZR2021MF003, and the Shandong University of Science and Technology Research Fund 2018 TDJH101.

Conflict of interest

The authors declare that they have no conflicts of interest.