Qualitative study of linear and nonlinear relaxation equations with $\psi$-Riemann-Liouville fractional derivatives

1.   Introduction

Wood-plastic composites (WPC) incorporate lignocellulosic fillers in plastics to generate advantages in terms of stiffness, mechanical strength, cost-benefit ratio and reduced weight. They use lignocellulosic waste to reduce the consumption of natural resources and promote better sustainable practices. These compounds are used to manufacture various products with better advantages than products made of natural wood when used outdoors, such as its resistance to humidity and insect attack.

The use of coupling agents promotes a better interaction between lignocellulosic fillers and the polymeric matrix, which typically exhibit hydrophilic and hydrophobic characteristics, respectively. Maleic anhydride grafted polyolefins are the most widely used coupling agents in WPC when the polymeric matrices are polyethylene or polypropylene. This produces interactions between the components of the WPC, the greatest interaction occurs between the hydroxyl groups of the lignocellulosic fillers and the grafted polyolefins, and the least interaction occurs between the fiber coupling agent with the hydrophobic matrix. A better dispersion of the fiber in the polymer matrix and a better interaction between them are obtained, with greater resistance to humidity and better mechanical properties ^[1,2,3,4].

These abiotic factors, such as ultraviolet (UV) radiation, humidity and temperature, can significantly affect the WPC performance ^[1,2]. The role of lignocellulosic fillers (e.g., wood particles, agricultural residues, agro-industrial wastes natural fibers) in moisture absorption is particularly important. Changes in ambient humidity levels induce cycles of moisture absorption and desorption in the fibers, where hydrogen bonds between water molecules and cellulose chains are continually broken and reformed, making water a plasticizer for wood fillers, promoting compound flow ^[5,6]. A higher deformation in WPC under humidity cycles, attributed to molecular mobility in the amorphous region of wood fillers has been observed ^[7]. Furthermore, it has been suggested that hot and humid climates enhance the water absorption in the material, while exposure to shade or sunlight seems to have a similar effect on moisture absorption ^[8]. This phenomenon in fibers produces stresses resulting from the hygrothermal expansion differences between the polymer matrix and the lignocellulosic fillers, leading to the formation of microcracks ^[9,10,11] and failure at the filler-matrix interface ^[12]. Both facts are responsible for the reduction in strength and rigidity of the material ^[3,4].

We aim to comprehensively analyze the effects of moisture absorption-desorption (AD) cycles, the amount of coupling agent (CA) and UV radiation (UV) on the absorbed-desorption moisture and the flexural and tensile mechanical properties of WPC made of pinewood waste and high-density polyethylene (HDPE). A two-level full factorial experimental design and statistical analysis are used to investigate these effects systematically.

2.   Materials and methods

2.1.   Raw materials

Pine wood residue (PW) obtained from Maderas Bajce (Mérida, Yuc., México) was used as lignocellulosic filler for the WPCs. Extrusion HDPE (Padmex 56035, MFI of 0.3133 g/10 min, from Petroquímica Morelos, Coatzacoalcos, Ver., Mexico) was employed as the thermoplastic matrix. HDPE modified with maleic anhydride (Polybond 3009 from Brenntag México, Cuatitlán Izcalli, México) was included coupling agent (CA). As processing aid (PA), the additive TPW113 (Structure Company of America, Cuyahoga Falls, OH, USA) was added.

2.2.   Methods

2.2.1.   Preparation of PW/HDPE composites

The preparation of PW/HDPE composites involved several steps. First, the pinewood waste was dried for 24 h at 80 ℃ using a convection oven (Fisher Scientific, Pittsburgh, PA) to remove moisture. After drying, the pinewood wastes were ground using a Pagani mill (model 1520, Molino Pagani SpA, Borghetto, Italy) with a mesh with 1 mm diameter holes. The ground particles were then classified using a sieve shaker with a set of Tyler sieves, specifically 20, 30, 40 and 50 mesh sizes, for 5 min. Particles that passed through 30 mesh but were retained on 40 mesh (430 to 600 mm in size) were selected for further use.

High density polyethylene (HDPE), a coupling agent and processing aid, were also processed. They were ground separately using a mill (model TI 880804, C.W. Brabender Instruments, NJ, USA) with a 1 mm diameter mesh. The PW, HDPE and additives were then premixed in a horizontal mixer equipped with a helical agitator (model ML-5; Intertécnica, Mexico City, Mexico). Subsequently, the mixture was dried in a convection oven at 85 ℃ for 24 h before the preparation process.

The basic composite formulation consisted of 40% by weight of PW and 60% by weight of HDPE. In addition, 3% by weight of processing aid based on the pinewood content was added. Different compounds were prepared incorporating 0% and 5% by weight of coupling agent with respect to the pine wood content.

Melting and blending of the compounds was performed using a laboratory twin screw conical extruder (EP1-V5501, C.W. Brabender Instruments, Inc., NJ, USA). The extrusion involved the use of a 4 cm long capillary die with an internal diameter of 5 mm. The screw speed was set at 50 rpm, and the barrel and die temperatures were maintained at 180 ℃. The obtained extrudates were pelletized using a laboratory pelletizer (type 12-72-000, C.W. Brabender Instruments, NJ, USA) for further processing.

2.2.2.   Preparation of tensile and flexural test specimens

The preparation of tensile and flexural specimens involved the use of pellets obtained from the twin screw extrusion process described above. These specimens were prepared according to the geometry and dimensions specified in the ASTM-D638 ^[13] and ASTM-D790 ^[14] standard test methods, respectively, for tensile and flexural specimens.

The pellets were hot-pressed using an automatic hydraulic press (Model 3819, Carver, Inc., IN, USA) at 160 ℃ for 5 min, applying a compression force of approximately 26689 N (6000 lb_f). Molded plates with a thickness of 3.2 mm were obtained. For tensile tests, the pellets were direct molded into V-type test tubes. For flexural tests, the plates were later cut into rectangular sections and then machined to obtain specimens with the required dimensions and geometry.

2.3.   Taguchi experimental design

To evaluate the experimental factors of UV radiation, absorption-desorption cycles and coupling agent content on moisture and mechanical properties of PW/HDPE composites, the following Taguchi-type orthogonal experimental designs were used (Tables 1 and 2).

First, an L8 experimental design was evaluated the contribution of UV radiation (factor A), the presence of MAPE (factor B) and the absorption-desorption cycles (factor C), at two levels, on the tensile and flexural mechanical properties of the PW/HDPE compounds.

Subsequently, only for a statistical analysis, the results of the absorbed moisture (MA) and the desorbed moisture (MD) obtained during the experimental runs that involved only the eight absorption-desorption cycles (experimental runs 3, 4, 7 and 8 from Table 1), were used to evaluate the contribution of UV radiation (factor A) and the presence of MAPE (factor B) on them, using a L4 experimental design (Table 2) derived from the earlier L8 design.

The impacts of the factors listed in Tables 1 and 2 on the above responses were quantified using the commercial software Qualitek-4 (Nutek, Inc., 3829 Quarton Rd Ste 102, Bloomfield Hills, MI 48302, USA).

2.4.   Treatments of PW/HDPE samples

2.4.1.   Accelerated weathering tests

A Uvcon UV accelerated weathering chamber (ATLAS MTT, Moussy Le Neuf, France) was used to expose the PW/HDPE samples to 24 h cycles of continuous UV light irradiation for 16 days at 60 ℃ using UVB-313 type fluorescent lamps (Atlas Electric Devices, Chicago, IL), according to the experimental design in Table 1.

Accelerated UV weathering tests followed the mentioned test methods, including ASTM-D4329 ^[15], ASTM-G151 ^[16] and ASTM-G154 ^[17]. Before exposure, ten samples of each PW/HDPE composite were conditioned following the standard methods ASTM-D618 ^[18] and ASTM-G147 ^[19] (105 ℃ for 24 h).

2.4.2.   Exposure to moisture absorption-desorption cycles

The samples, both UV-irradiated and non-irradiated, were subjected to eight cycles of moisture absorption and desorption as specified in Table 1, following the standard test methods ASTM-D5229 ^[20] and ASTM-D570 ^[21]. Each cycle, called the absorption-desorption (AD) cycle, involved immersing the samples in hot distilled water (60 ℃) for 10 days (240 h) and then drying them for five days (120 h) at a temperature of 60 ℃.

The variation in the percentage of moisture absorbed (MA) and moisture desorption (MD) was measured according to the standard test method ASTM-D5229 ^[20]. Prior to this, the test specimens were conditioned according to the ASTM-D570 standard ^[21].

During absorption-desorption (AD) experiments, the change in sample weight was measured using an analytical balance (Ohaus Voyager Pro, model VP214CN, Parsippany, NJ, USA). The percentage by weight of absorbed moisture (M_A) was calculated using Eq 1:

where m_H is the weight of the sample after exposure to the humid environment and m₀ is its initial weight. The weight percent of desorbed moisture (M_D) was calculated using Eq 2:

where m_S is the weight of the sample after the drying period.

2.5.   Characterization of PW/HDPE samples

2.5.1.   Mechanical characterization

Tensile and flexural tests were conducted using a universal testing machine (Type 5500R, Model 1125, Instron, Norwood, MA, USA). The characterization was performed for irradiated and non-UV irradiated materials, with and without CA, subjected and not subjected to AD cycles. The tensile tests were implemented according to the ASTM-D638 ^[13] standard, using a cross head speed of 10 mm/min. The bending tests were executed in accordance with the ASTM-D790 standard ^[14]. The three-point loading system was used with a crosshead speed of 10 mm/min.

At least ten specimens corresponding to each type of test and PW/HDPE compound were evaluated to obtain the modulus of elasticity in tension and flexion, and the resistance to tension and flexion. All samples were conditioned at 23 ± 2 ℃ and 50 ± 5% relative humidity for at least 40 h before testing conforming to ASTM-D618 ^[18].

2.5.2.   Scanning electron microscopy

The morphological analysis was performed by scanning electron microscopy (SEM) on sample surfaces of the PW/HDPE compounds treated under the experimental conditions indicated in Table 1, as well as on sample surfaces that failed in the mechanical tests. Specimens were cut into small sections and then mounted and coated with sputtered gold (Denton Vacuum Desk II, Moorestown, NJ, USA). Samples were examined with an electron microscope (JSM-6360 LV, Jeol USA, Inc., Peabody, MA) at a voltage of 10 kV.

3.   Results and discussions

The process of the absorption-desorption cycles of the PW/HDPE plastic wood composites was determinant in the resulting physical integrity that affected the tensile and flexural properties obtained ^[5,22] in composites of pinewood waste (PW) and high-density polyethylene (HDPE). This was dependent to a greater or lesser extent on the following experimental factors to which they were exposed: UV radiation ^[7,11], the amount of maleic anhydride grafted polyethylene (MAPE) coupling agent ^[1,23] and water absorption-desorption cycles ^[5,24].

3.1.   Water absorption–desorption in PW/HDPE compounds

The experimental results reveal that degradation and surface damage within PW/HDPE composites lead to high moisture absorption and retention. Clearly, the tension samples show higher maximum moisture values compared to the flexure samples. The influence of the coupling agent MAPP and exposure to UV radiation markedly affect the moisture dynamics. Patterns of change throughout the cycles underscore stabilization trends, with UV radiation increasing values and MAPE hindering the process. These observed behaviors follow an apparent two-step absorption-desorption mechanism described by diffusion, pressure, capillarity and interactions between the composite materials, a proposal supported by the eighth cycle results.

3.1.1.   Absorption–desorption cycles

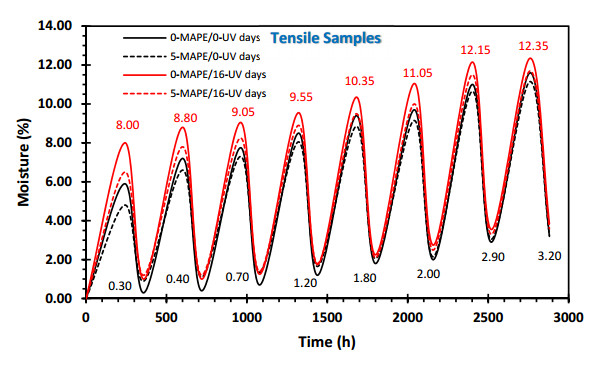
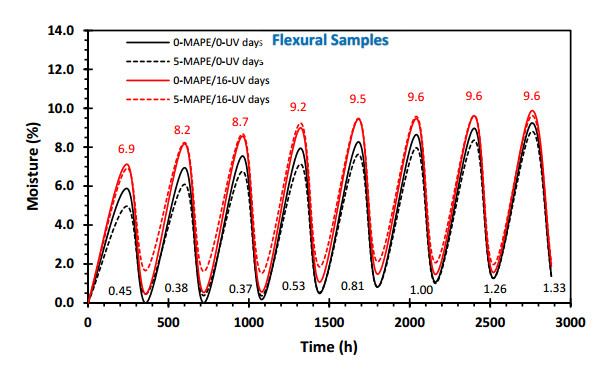
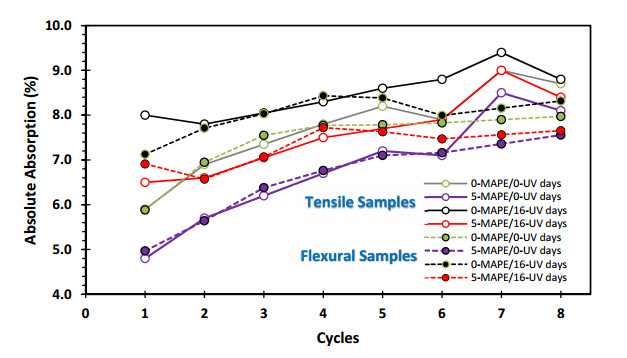
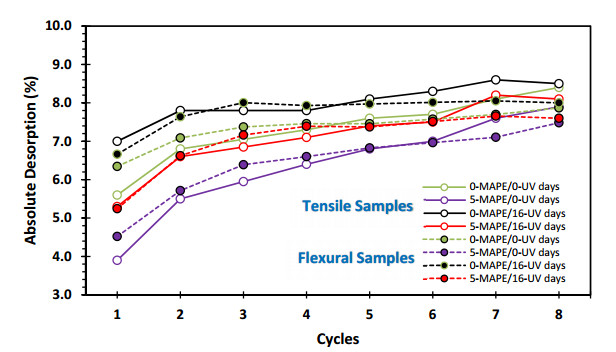
Figures 1 and 2 show the maximum moisture values reached and, from the second cycle, the minimum moisture retained by the four samples, both in tensile and in flexural. All samples are 3.2 mm thick and are subjected to eight water absorption-desorption cycles in the PW/HDPE composite. It is noteworthy that at the end of each cycle, there is an increase in the amount of moisture absorbed and moisture retained, especially in the stress curves (Figure 1). This could be because, in each cycle, there is a marginal increase in the surface exposed to water due to the degradation of the compound ^[3], which produces new damaged surfaces such as microcracks ^[9] or by the loss of the matrix-fiber interface ^[4]. The samples then proceed to the next cycle, with each cycle contributing to the absolute amount of absorption and desorption and adding to the remaining moisture values from the previous cycle. The Figures 1 and 2 present the resulting values obtained from these processes.

In terms of the observed trends, the tensile samples exhibit higher maximum moisture values compared to the flexure samples. This disparity can be attributed to the lower volume of the tensile samples, which amount to approximately one third of the volume of the flexural samples, and mostly to the fact that they have a very narrow section in the middle of the sample, which is susceptible to further degradation and where the absorption and desorption values can continue to increase. A hypothetical cross section would reveal a significant concentration of wood filler in the center, which, once moisture reaches this section through the microcracks from the outside, creates favorable conditions for increased water absorption from the sixth cycle onwards. What obviously does not happen in the bending sample that has the same cross section throughout its length and reaches stable values.

Although there are variations, the water absorption and desorption behaviors exhibit overall similarities among the samples. However, these behaviors can be influenced by the presence or absence of MAPP as well as exposure to UV radiation. The latter degrades the polymeric matrix, producing microcracks ^[25] and also degrades wood, making it more brittle ^[26], due to thermal degradation of hemicellulose and degradation by UV radiation of lignin ^[11]. These additional factors play a role in modifying the water absorption and desorption capacities of the samples, leading to variations in the moisture values observed.

3.1.2.   Maximum moisture and retained moisture

For a more detailed analysis of the values of maximum moisture reached and moisture retained, they are represented as maximum moisture lines and minimum moisture lines in Figures 3 and 4. In both the tensile and flexural samples, it can be observed that the maximum moisture increases progressively, with significantly higher values in the tensile samples compared to the flexural samples. Furthermore, it can be seen that the maximum moisture values exhibit two distinct trends: a more sinuous trend in the tensile samples and a simpler curve in the flexural samples. This difference in trends may indicate that the absorption-desorption process is more complex in tensile samples compared to flexural samples.

It can also be noted that the tensile samples without MAPE and exposed to UV radiation (0-MAPE/16-UV) obtained the highest maximum moisture values. This could be attributed to the fact that these samples experienced greater physical damage ^[7,25], both in tensile and flexural samples, which facilitated water absorption. Following this trend, the samples that follow in descending order are those with UV treatment and the presence of MAPE (5-MAPE/16-UV), followed by the two samples without UV treatment (0-MAPE/0-UV and 5-MAPE/0-UV). In these last samples, the absorption-desorption process can be observed depending solely on the interaction between water and the polymeric matrix. It is evident that the presence of MAPE inhibits this process, resulting in lower moisture values achieved in these samples ^[23].

A similar behavior is observed in the flexing samples, where the maximum moisture values are higher and similar in the samples exposed to UV radiation, specifically the 0-MAPE/16-UV and 5-MAPE/16-UV samples. On the other hand, between the two samples without treatment with UV radiation, the sample containing the coupling agent (5-MAPE/0-UV) presents the lowest maximum humidity values.

Regarding the values of retained moisture, behaviors similar to the maximum moisture are observed. That is, the presence of treatment with UV radiation favors moisture retention, where the highest values are also obtained in the samples with UV treatment (0-MAPE/16-UV and 5-MAPE/16-UV), while the lowest values are obtained in the samples without UV treatment (0-MAPE/0-UV and 5-MAPE/0-UV).

3.1.3.   Absolute absorption–desorption per cycle

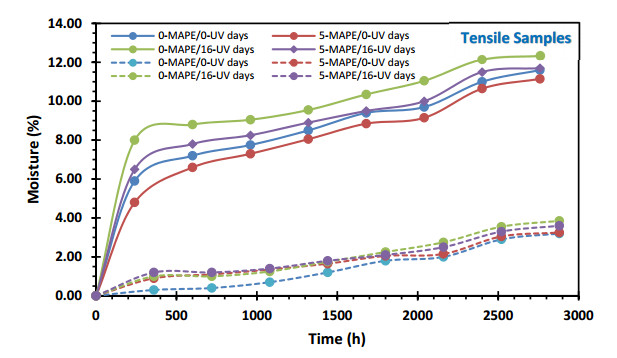
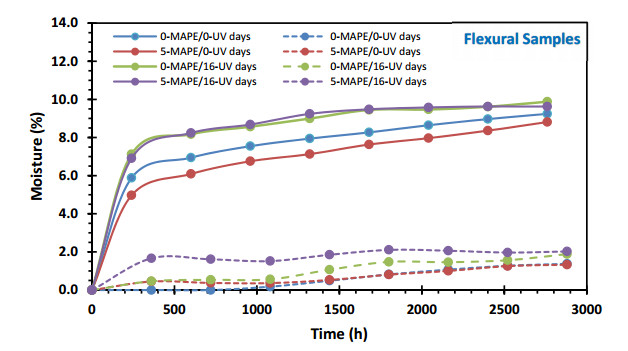
Figures 5 and 6 provide information on the absolute moisture change during the eight cycles of absorption and desorption. These cycles were performed for both tensile and flexural samples of the PW/HDPE composites. The behaviors observed in the four samples exhibit a remarkable similarity. These trends are in line with the previously reported results, demonstrating an asymptotic upward behavior that leads to stabilization from the third cycle on. Initial discrepancies in the first few cycles are clearly noticeable but decrease as more cycles are performed. In addition, an asymptotic behavior is observed between the first and the sixth cycle, observing a small minimum in the sixth cycle, an inflection point that continues with a slight increase in the absorption values during the last two cycles.

The sample without MAPE and exposed to UV radiation (0-MAPE/16-UV) exhibits the highest absorption and desorption values ^[7,11]. Two samples follow: one with MAPE and exposed to UV radiation (5-MAPE/16-UV) and another without MAPE but also without UV radiation (0-MAPE/0-UV). On the contrary, the sample with MAPE and without UV radiation (5-MAPE/0-UV) presents the lowest absorption and desorption values ^[23].

These observed behaviors suggest a two-stage absorption-desorption mechanism ^[27,28], where the parameters involved are moisture diffusion, internal water-fiber pressure back into the polymeric matrix, capillarity, polymer-wood fiber interactions, polymeric matrix relaxation, temperature, time and volumetric factors of the samples, among others.

The first stage demonstrates significant changes in water absorption and desorption, while the second stage exhibits smaller changes that contribute to the stabilization of the process, resulting in convergent absolute values of absorption and desorption for all samples.

3.1.4.   Absolute absorption–desorption of the eighth cycle

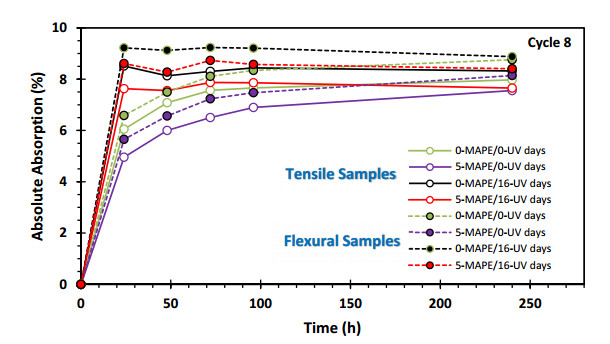
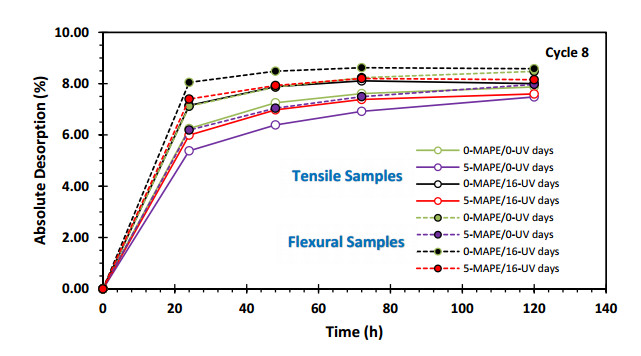
The analysis of the absorption and desorption behavior throughout a complete cycle provides valuable information on the final changes experienced by the samples. The results obtained from the eighth cycle shed light on the comprehensive understanding of these processes.

Figures 7 and 8 represent the values of the absolute moisture change over time in the eighth cycle. During the initial 80 hours, the absorption and desorption curves present the most significant changes, showing notable discrepancies between them. Once again, the samples exposed to UV radiation show the highest absorption and desorption values, with the sample without MAPE (0-MAPE/16-UV) presenting the highest values and following a similar trend. On the contrary, the samples without radiation treatment show the lowest absorption and desorption values, the sample containing MAPE (5-MAPE/0-UV) showing the minimum values. These samples also exhibit consistent trends among themselves.

These findings suggest the attainment of a stable absorption-desorption process, characterized by repeatable trends that reflect the consequences of physical changes occurring in the preceding cycles. Notably, the initial stage of a probable mechanism explaining these processes corresponds to an initial stabilization stage achieved within the first 80 hours. This is followed by a second equilibrium stage where the values tend to converge to the same level across all samples.

3.2.   Statistical analysis of UV and MAPE effects

Statistical analysis of the above results quantifies the impact of UV radiation and MAPE content on moisture dynamics within samples of the PW/HDPE composites. Thus, the maximum absorption of the PW/HDPE compounds depends to a greater extent on exposure to UV radiation, causing an increase in humidity values, with different behaviors in tensile and flexural samples, which determine that the absorption- desorption are performed in two stages. This research emphasizes a complex interplay between UV radiation exposure and the presence of MAPE on moisture behaviors in these composite samples. However, it is the degradation of the samples, mainly due to exposure to UV radiation, which is partially inhibited by the presence of MAPE, which will determine its effect on the performance of the mechanical properties of PW/HDPE compounds.

Thus, the UV radiation increases the absorption and desorption values ^[7,11], while the presence of MAPE decreases these values ^[1,23]. The forms, tendencies and magnitudes differ according to the type of measurement effectuated. In addition, the interaction of UV radiation with the presence of MAPE on the resulting absorption and desorption values was also evaluated, and it was found to have no statistically significant effects.

3.2.1.   Maximum absorption

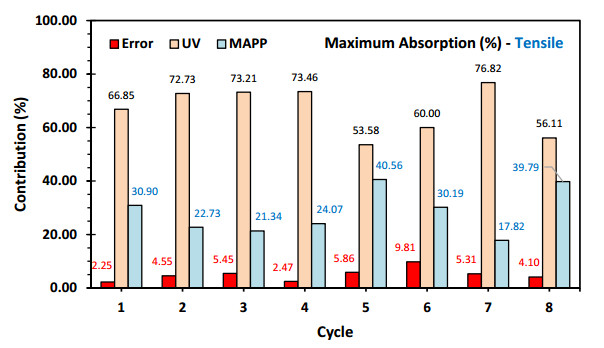
Figures 9 and 10 illustrate the statistical contribution of UV radiation and MAPE content to the maximum moisture reached during these absorption-desorption tests (Figures 1–4). The experimental design presented in Table 2 served as the basis for this analysis. Data were analyzed under the assumption that lower values are preferable.

Both in the tensile and bending samples (Figures 9 and 10), it is observed that UV radiation is the most significant factor in the increase in the maximum humidity value, with different behaviors depending on the type of sample. For the tensile samples, an increasing influence is observed from cycles 1 to 4, with values ranging from 66.86% to 73.46%. It is followed by a minimum value of 53.58% and a maximum value of 76.82% in cycle seven. This is consistent with the curves observed in the behavior of these values in Figure 3. It has been established that this process is complex for stress samples due to its narrow section in the center of the sample. Consequently, the flexure samples exhibit higher and more stable values (ranging from 72.9% to 85.0%), which aligns with the stability of the values shown in Figures 2 and 4–6 during the water absorption and desorption cycles. As mentioned above, irradiated samples are likely to show more damage compared to samples not exposed to UV radiation ^[7,11], as anticipated.

On the other hand, the presence of the coupling agent has the effect of reducing the maximum moisture values ^[1,23] reached by the samples subjected to eight continuous cycles of absorption-desorption. This effect is particularly evident in the tensile samples (Figure 9), where its contribution ranges from 17.82% to 40.56%, with a minimum value of 21.34% in cycle three and a maximum value of 40.56% in cycle five. On the contrary, its contribution is negligible in the flexural samples (Figure 10). This indicates that, although its volumetric expansion is more significant than the tensile samples, in samples of equal thickness, high contributions of UV radiation can be achieved from the first absorption-desorption cycle.

3.2.2.   Absolute absorption–desorption per cycle

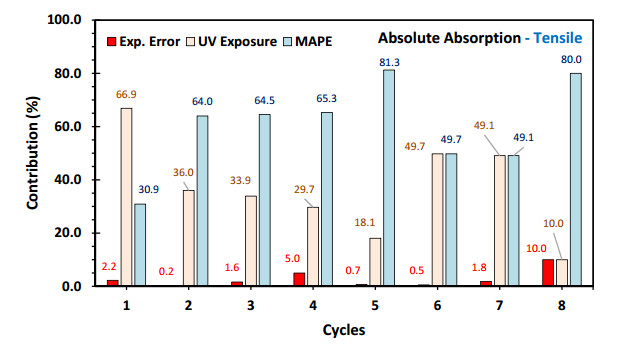
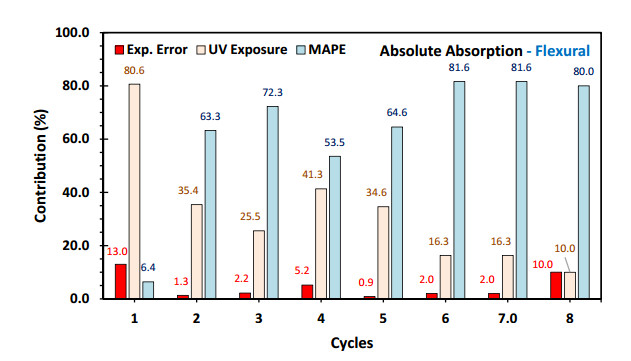
Figures 11–14 present the statistical contribution of UV radiation and MAPP content on the absolute absorption and desorption values of the compounds evaluated (Figures 5 and 6). It is important to highlight that the presence of the coupling agent MAPP reduces the absolute values of absorption and desorption ^[1,23], being the most significant factor in these eight cycles evaluated.

In the tensile samples for absolute absorption (Figure 11), the MAPP contribution values vary from a minimum of 30.69% to a maximum of 81.3% in the fifth cycle, it decreases in cycles 6 and 7 to values of 49% and increases again to 80%. The contribution of UV radiation is inversely related and complementary, adding up to 100% of the contributions since the experimental error of these data was low. In the flexural samples (Figure 12), it is evident that the contribution of MAPP is increasing and significant, varying from 6.4% in the first cycle to a value of 81.4% in the sixth cycle, maintaining high contributions in the two remaining cycles. Similarly, the contribution of UV radiation is less significant.

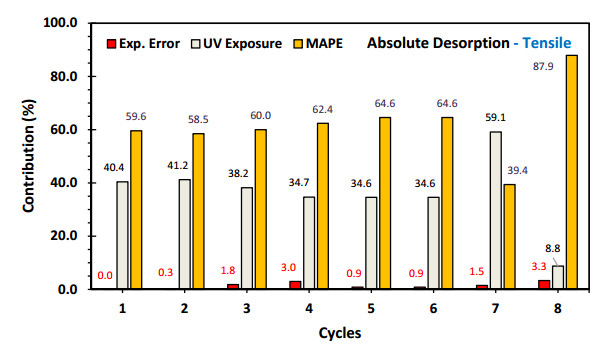
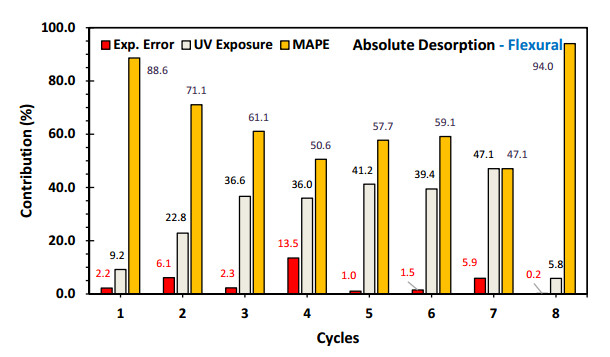
Regarding the absolute desorption, the contributions of MAPP are significant (Figures 13 and 14), since they are much higher in all cycles compared to those of UV radiation ^[7,11]. In the stress samples (Figure 13), an interesting trend is observed where the MAPP contribution remains constant, ranging from 59.6% in the first cycle to 69.6% in the sixth cycle, then reaches a minimum of 39.4% in the seventh cycle, and finally reaches a global maximum of 87.9% in the eighth cycle. UV radiation also affects this absolute absorption, although to a lesser extent, showing stable complementary values from the first to the sixth cycle. On the other hand, in the flexural samples (Figure 14), a high contribution of MAPP is observed, ranging from 88.6% in the first cycle, reaching minimum values of 50.6% in the fourth cycle and 47.1% in the seventh cycle, to later reach a maximum value of 94% in the eighth cycle.

In both types of samples, the trends in the contributions of these factors show inflection points in the fifth and sixth cycles. This supports the idea that these phenomena develop in two stages ^[27,28]: a stage of significant changes from the first to the fifth cycle, and a stage of stabilization from the sixth cycle onwards.

3.2.3.   Absorption–desorption in cycle eight

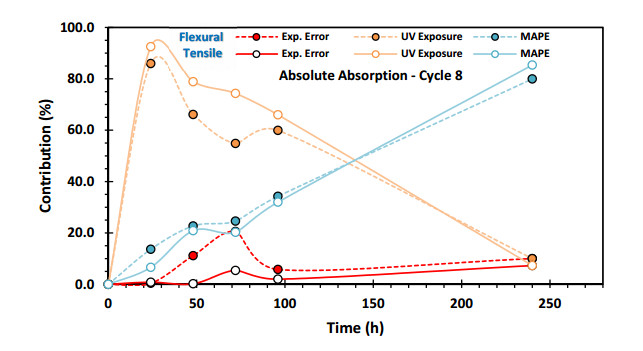
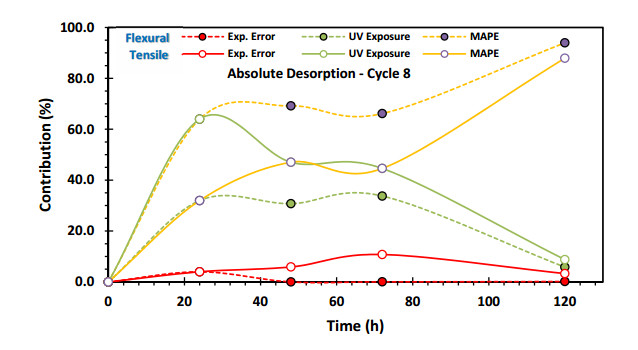
Figures 15 and 16 present the statistical contribution of UV radiation and MAPE on the reported absolute values of absorption and desorption during the development time of the eighth cycle, to which the tensile and flexure samples were subjected (Figures 7 and 8).

In Figure 15, it is evident that the trends in absolute absorption are similar for both tensile and flexure samples, with a maximum contribution from UV radiation at the initial time of result collection, accompanied by a minimum contribution from MAPE. This suggests that, at the beginning of the test, absorption occurs rapidly (Figure 7) in areas where it is easier, such as direct contact of water with lignocellulosic fillers through interactions with the hydroxyl groups of the wood ^{[4,9,10,11,12]}.

To a lesser extent, additional wetting of these soaked fibers continues as they attempt to expand due to the high temperature of the test, 60 ℃. This leads to bulking of all materials, where differences in their expansion coefficients create gaps, interfacial stresses, phase separation and ruptures. In the polymeric matrix, this can be attributed to the relaxation of its molecular chains ^[27] and, to a lesser extent, to the initiation of low molecular weight chain flow at a characteristic temperature known as heat deflection temperature, HDT, which is 56.3 ℃ for the HDPE Padmex in this study ^[29]. Since the temperature of the UV radiation treatments as well as of the absorption-desorption cycles is 60 ℃, it is very possible that this flow of low molecular weight molecules exists.

As a result, moisture partially fills the voids and voids generated by damage from previous cycles of UV radiation. After some time, this reaches a maximum, and only small variations of this phenomenon will depend on new interactions with the available hydrophilic sites found by the wet fiber pool, which is now highly dependent on the action of MAPE ^[1,23]. Therefore, the role of MAPE is to reduce absorption.

On the other hand, Figure 16 shows that in early times, the absolute desorption shows a comparable contribution from both UV radiation and MAPE, which remains constant until around 80 hours. At this time, almost all of the moisture has already been released from the tensile and flex samples, and the remaining, small amount is more easily released as it encounters hydrophobic sites, both within the polymeric matrix and due to the action of MAPE on the lignocellulosic filler ^[1,23].

3.3.   Mechanical properties of PW/HDPE composites

The evaluation of the tensile and flexural properties shows that the samples without exposure treatments to UV radiation or subjection to absorption-desorption cycles exhibit the highest mechanical performance, while those subjected to both UV radiation and absorption-desorption cycles show reduced values. The presence of the coupling agent MAPE leads to marginal improvements in mechanical performance, and the interactions between the experimental factors (i.e., UV radiation, absorption-desorption cycles and presence of MAPE) show minimal influence on mechanical strength. In particular, mechanical stiffness is predominantly dependent on absorption-desorption cycles, underlining its paramount importance.

3.3.1.   Tensile and flexural properties

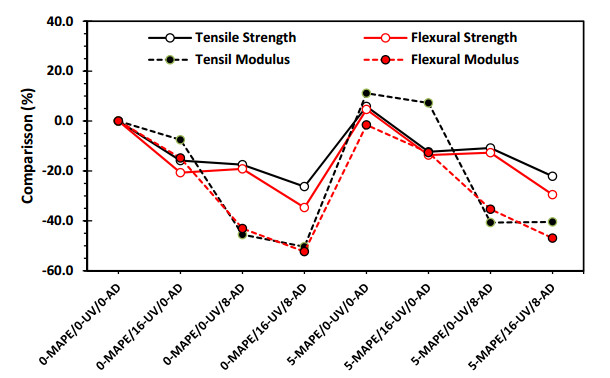
Figures 17 and 18 present the results of the tensile and flexural tests conducted on the samples obtained from the different runs of the experimental design shown in Table 1. It can be observed that the samples without treatments (ERS1 and ERS5) exhibit the highest values for these mechanical properties, with ERS5, which contains the coupling agent, achieving the highest results. Conversely, the sample ERS4, which underwent both treatments, obtained the lowest results, indicating a potential increase in damage caused by these treatments.

Figure 19 shows a comparison of the results obtained for the mechanical properties, taking as reference the sample without coupling agent and treatments, ERS1 (0-MAPE/0-UV/0-AD). As expected, there is a slight increase in mechanical properties by incorporating the MAPE coupling agent into the ERS5 sample (5-MAPE/0-UV/0-AD). On the other hand, a clear decrease in mechanical properties is evident when applying one or both treatments (UV and AD) to all other samples.

This reduction in mechanical properties seems to depend on the damage caused by its type of formulation and by exposure to UV radiation ^[7,11] and the absorption-desorption cycle ^{[9,10,11,12,25]}.

3.3.2.   Statistical analysis of UV and MAPE effects

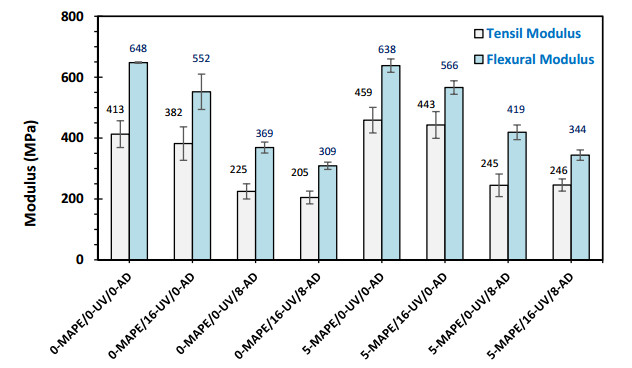
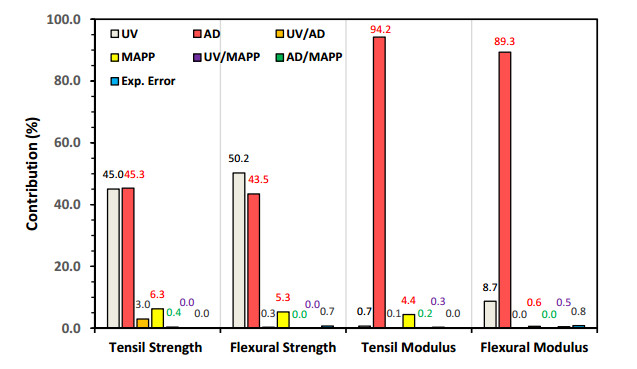
In this analysis, it is also important to mention that when discussing the statistical contribution of the experimental factors, the following can be observed: UV radiation and cycles of absorption and desorption decrease the values of the involved mechanical properties, while the presence of MAPE increases these values. With this consideration, Figure 20 shows the statistical contribution of UV radiation, cycles of absorption-desorption and the presence of MAPE on the evaluated tensile and flexural properties.

It can be observed that both tensile and flexural strength properties are equally affected, with an average of 46% contribution from cycles of absorption-desorption and UV radiation, and a small contribution from the presence of MAPE. The interactions between these experimental factors (i.e., UV/AD, UV/MAPE and AD/MAPE) did not have an effect on these mechanical resistances. On the other hand, the mechanical stiffness of the evaluated composites was only affected by the cycles of absorption-desorption, with a statistical contribution of approximately 92%. Similarly, the interactions between the experimental factors did not have a significant effect on these results.

The above confirms that the mechanical strength properties of the evaluated PW/HDPE composites depend on the interactions between the wood flour and its polymer matrix. It becomes evident that the application of UV radiation and cycles of absorption-desorption affects these interactions, producing changes in the interfacial zone according to the type of experiment involved (Table 1). On the other hand, the stiffness of the evaluated composites depends on the integrity of the compound rather than the interfacial zone, as it was affected by the cycles of absorption-desorption by approximately 90%.

3.4.   SEM micrographs of PW/HDPE composites

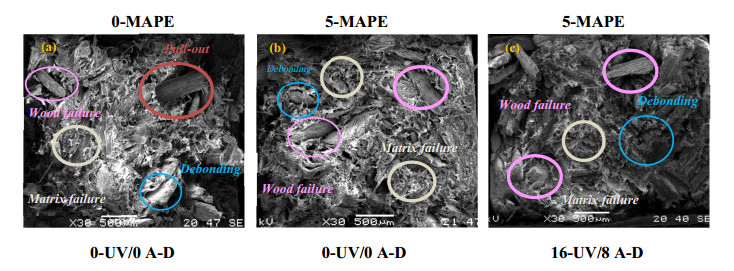
The SEM micrographs show noteworthy evidence of the damage suffered by the PW/HDPE composite samples evaluated, according to the experimental design of Table 1, after being subjected to UV radiation (16-UV) and eight cycles of absorption-desorption treatments (8-AD). Figure 21 shows the surface of the samples evaluated, with and without MAPP, under different conditions.

The micrographs of Figure 21a, b represent the surfaces of the reference samples without treatments, with and without MAPE, respectively, samples ERS5 and ERS1. These surfaces appear mostly smooth with some slight bumps that could be wood chips within the polymer matrix, showing no signs of damage.

The micrographs of Figure 21c, d show how the effect of the absorption-desorption cycles produces some microcracks on the surface of the ERS3 and ERS7 samples, the latter containing MAPE and showing minor damage.

The micrographs in Figure 21e, f demonstrate the effect of UV radiation on the samples. The sample without MAPE (ERS2) exhibits a much higher number of microcracks on its surface, compared to the sample containing MAPE (ERS6). In addition, small superficial detachments of the polymeric matrix (delamination) become visible, exposing the lignocellulosic filler, with a slightly more extensive delamination in the sample without MAPE (ERS2).

Finally, the micrographs in Figure 21g, h reveal the combined effect of both treatments, UV radiation and absorption-desorption cycles, in the ERS4 and ERS8 samples, corresponding to samples without and with MAPE, respectively. Here, the damages are more significant for both samples, compromising the integrity of the surface with larger cracks and delamination of the polymeric matrix, exposing wood particles.

The SEM micrographs in Figure 22 show the samples fractured with and without MAPE, both untreated and treated with UV radiation and absorption-desorption cycles, as specified in Table 1. These samples show similar damage: (1) fibrillated polymeric matrix due to failure; (2) failed pieces of wood with rough surfaces caused by their own breakage; (3) pulled-out wood fibers separated from the polymeric matrix (pull-out) with smooth surfaces; and (4) interfacial voids generated between the wood particles and the polymeric matrix.

As for the sample without MAPE and untreated (ERS1), it presents the aforementioned damage, being the only one with torn wood fibers and larger interfacial spaces compared to the sample with MAPE (ERS5). Furthermore, when comparing the samples with MAPE, both treated and untreated, ERS8 and ERS5 respectively, the former shows a higher number of failed wood particles. This can be attributed to wood degradation caused by water absorption and desorption, which induces mechanical stress in the wood ^[26], eventually leading to its breakage, as observed in this case.

3.5.   Water absorption–desorption mechanism in PW/HDPE compounds and its effect on their mechanical properties

3.5.1.   Proposed water absorption–desorption mechanism in PW/HDPE compounds

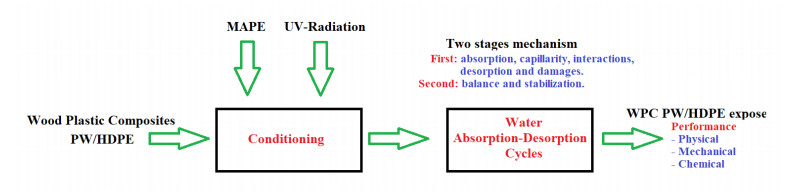
The absorption–desorption behavior of PW/HDPE wood-plastic composites can be explained by a two-stage mechanism involving several factors: UV radiation, MAPE and water exposure (Figure 23).

Stage one includes several steps: initial absorption and delamination; capillary action and polymer-wood interaction; and swelling, fiber-matrix interaction and mechanical damage. This stage occurs during the first four or five absorption-desorption cycles. The stage two involves the balance and stabilization step occurring from cycles five or six, and remains until the final cycle.

Initial absorption and delamination. Exposure to UV radiation causes degradation of the polymeric matrix and wood components, leading to microcracks in the material ^[7,11]. These microcracks create pathways for water to enter the compound. During the initial steps of absorption, water infiltrates these microcracks, interacting with hydrophilic sites on the wood particles ^{[4,9,10,11,12]}. Micrographs show surface delamination and interfacial void formation due to separation between the wood particles and the polymeric matrix (Figure 21g, h). UV radiation accelerates this process, since it degrades both the polymeric matrix and the lignocellulosic filler, increasing water penetration ^[7,11].

Capillary action and polymer-wood interaction. As absorption-desorption cycles continue, more water enters the composite through capillary action and diffusion, filling microcracks and voids ^[9,10,11,12]. The presence of wood flour and the initial damages in the polymer matrix promote capillarity, contributing to greater moisture absorption. The presence of the coupling agent MAPE inhibits water infiltration to some extent, as evidenced by the lower moisture values in samples with MAPE ^[1,23]; however, it improves the interaction between wood and polymer ^[1,2,3].

Swelling, fiber-matrix interaction and mechanical damage. As moisture continues to penetrate, the wood particles absorb water and begin to swell. This swelling puts pressure on the surrounding polymer matrix, which can cause mechanical stress within the material. In the presence of UV radiation, wood degrades and becomes brittle ^[26], increasing the susceptibility of the composite to mechanical damage. This can be observed in micrographs where damaged wood fibers are extracted from the matrix ^[22].

Balance and stabilization. After repeated cycles of absorption and desorption, the compound approaches equilibrium and the moisture content stabilizes, indicating that the absorbed moisture reaches an equilibrium between the polymeric matrix and the wooden floor. Stabilization is due to the complex interplay of factors such as moisture diffusion, polymer relaxation and saturation of available hydrophilic sites.

3.5.2.   Impact on mechanical properties

The mechanical properties of PW/HDPE compounds are significantly influenced by absorption-desorption cycles, UV radiation and the presence of MAPE. Microcracks and delamination caused by UV radiation and water absorption lead to reduced mechanical performance ^[7,11]. SEM images support this observation by showing the formation of microcracks, shedding of wood fibers and interfacial voids (Figures 21g, h and 22). The presence of MAPE mitigates degradation to some extent by improving the interaction between wood and polymer, resulting in slightly better mechanical properties ^[1,23]. However, the combined effects of UV radiation and absorption-desorption cycles dominate the overall reduction in mechanical strength and stiffness, as evidenced by the lower mechanical values in the treated samples ^[17,18].

4.   Conclusions

The results of this study show that high-density polyethylene (HDPE) and pinewood (PW) waste samples, with and without maleic anhydride grafted polyethylene (MAPE) coupling agent, suffer damage when exposed to UV radiation and absorption-desorption cycles, which determined their subsequent mechanical behavior.

Exposure of the PW/HDPE composite to UV radiation led to increased moisture absorption and desorption, resulting in higher maximum moisture content and retained moisture at the end of the eighth absorption-desorption cycle. This was thirty percent more for the tensile samples than the flexure samples, due to a shape factor. On the other hand, the presence of the coupling agent (MAPE) helped to reduce the absorption and desorption of humidity, which contributes to improve the mechanical properties; although its effect was marginal, given the level of damage caused by the other two factors.

The moisture absorption-desorption process follows a two-stage mechanism, with significant changes occurring in the early cycles and a stabilization stage occurring from the sixth cycle onwards.

The mechanical properties of the composites are affected by the interactions between the wood fillers and the polymeric matrix, with UV radiation and humidity cycles causing damage in the interface zone. The damage suffered in the samples was generated to a greater extent during exposure to UV radiation, and to a lesser degree, by the absorption-desorption cycles.

The SEM analysis allowed to identify the damages and their level of extension in the PW/HDPE composites due to UV radiation and exposure to humidity, detected as microcracks, delamination, interfacial voids and failed wood and polymer phases. The presence of the coupling agent (MAPE) helped to mitigate these damages.

Use of AI tools declaration

The authors declare having used Artificial Intelligence (AI) tools in the creation of this article, in particular Google Traductor for better writing.

Acknowledgments

The authors disclosed receipt of the following financial support for the research, authorship and/or publication of this article: This work was supported by the Mexican Council for Science and Technology and the Government of the Yucatan State (grant number YUC-2008-C06-107327).

Gratitude is expressed toward Corrosion Research Center of Autonomous University of Campeche for the assistance provided. Additional thanks are given to Santiago Duarte-Aranda, María Verónica Moreno-Chulim and to Silvia B. Andrade-Canto.

Conflict of interest

The authors declare that there is no conflict of interest.