1.
Introduction
One of the important problems in signal processing is to recover an unknown sparse signal from a few measurements, which can be expressed as follows:
where ‖x‖0 represents the total number of nonzero entries of x∈RN, A∈Rm×N is the measurement matrix with m≪N, and y is the measurement vector. This model has been widely applied in many important areas, including machine learning, compressed sensing, signal processing, pattern recognition, wireless communication, etc. Note that the l0-norm is not continuous and has combinatorial structure. Hence, the problem (1.1) is known to be NP-hard.
Over the past decades, many efficient algorithms have been proposed for solving the model (1.1), including convex relaxation methods, greedy methods, and thresholding-based methods, to name a few. For example, basis pursuit [1,2], lp algorithms [3,4], alternating projections [5] and conjugate gradient adaptive filtering [6] have been proposed by using convex optimization techniques. Greedy methods include orthogonal matching pursuit (OMP) [7,8,9], compressive sampling matching pursuit (CoSaMP) [10] and subspace pursuit (SP) [11,12]. Thresholding-based methods provide a simple way to ensure the feasibility of iteration, which includes iterative hard thresholding [13,14,15], hard thresholding pursuit [16,17,18], soft thresholding [19] and Newton-step hard thresholding [20]. Recently, Zhao [21,22] proposed a new thresholding operator called s-optimal thresholding by connecting the s-thresholding directly to the reduction of the objective function. For more information on theoretical analysis and applications of algorithms for solving sparse signal recovery, see [23,24,25,26].
In this paper, we mainly focus on the hard thresholding algorithms due to their simple structure and low computational cost. One of the key steps in a hard thresholding algorithm is
where Hs(⋅) stands for the hard thresholding operator, keeping the s-largest absolute components of the vector and zeroing out the rest of the components. The main aim in this step is to ensure the feasibility of iteration. However, three possible questions exist for this step. First, the objective function can increase in some iterations, i.e., {‖y−Axn‖2} is not a decreasing sequence. Second, if xn+AT(y−Axn) is a dense vector, only keeping the s-part would lose too much important information. Third, even for a non-dense vector, it is possible that some useful indexes may be missed, as the difference between the s-largest components and (s+j)-largest (with j>0) components of xn+AT(y−Axn) is very small. To the best of our knowledge, the first question can be solved by using the s-optimal thresholding operator introduced by Zhao in [21], and the second question has been discussed recently in [27] by using partial gradient technology, i.e., full gradients AT(y−Axn) are replaced by partial ones Hq(AT(y−Axn)) with q≥s.
Inspired by these works, we continue to study the aforementioned third question in this paper. Precisely, a little greater signal basis, say β, which is greater than s, is selected in each iteration first. This undoubtedly increases the chance of correctly identifying the support set of a signal, particularly for the case of the s-largest components close to the β-largest components. A β-sparse vector un+1 is attained by solving a least-square problem over the subspace determined by the index set Un+1:=Lβ(xn+AT(y−Axn)), where Lβ(x) stands for the index set of the β largest absolute entries of x. Subsequently, the hard thresholding operator Hs(⋅) will be applied to un+1 for reconstructing the s-sparse vector. Finally, to further improve numerical performance, we choose an iteration to seek a vector that best fits the measurements over the prescribed support set by using a pursuit step, also referred to as debiasing or orthogonal projection. This leads to the Compressive Hard Thresholding Pursuit (CHTP) algorithm. Numerical experiments demonstrate that CHTP has better performances when β is slightly greater than s.
The notation used in this paper is standard. For a given set S⊆{1,2,…,N}, let us denote by |S| the cardinality of S and by ˉS:={1,2…,N}∖S the complement of S. For a fixed vector x, xS is obtained by retaining the elements of x indexed in S and zeroing out the rest of the elements. The support of x is defined as supp(x):={i|xi≠0}. Given two sets S1 and S2, the symmetrical difference of S1 and S2 is denoted by S1ΔS2:=(S1∖S2)∪(S2∖S1). Clearly,
The paper is organized as follows. The CHTP algorithm is proposed in Section 2. Error estimation and convergence analysis of CHTP are given in Section 3. Numerical results are reported in Section 4.
2.
Compressive Hard Thresholding Pursuit
In order to solve problem (1.1), Blumensath and Davies [13] proposed the following Iterative Hard Thresholding (IHT) algorithm:
The negative gradient is used as the search direction, and the hard thresholding operator is employed to ensure sparse feasibility. Furthermore, by combining the IHT and CoSaMP algorithms, Foucart [17] proposed an algorithm called Hard Thresholding Pursuit (HTP), which has stronger numerical performance than IHT.
Algorithm: Hard Thresholding Pursuit (HTP).
Input: a measurement matrix A, a measurement vector y and a sparsity level s. Perform the following steps:
S1. Start with an s-sparse x0∈RN, typically x0=0;
S2. Repeat
until a stopping criterion is met.
Output: the s-sparse vector x∗.
In Step (2.1) of HTP, we get |Un+1|=s, which results in only up to s positions being taken as the basis at each iteration in the process of restoring vectors. However, it should be noted that the selected basis of s positions could not accurately represent the full gradient information. From the view of theoretical analysis, the less gradient information of the selected basis there is, the more difficult it is for HTP to achieve good numerical performance. In order to further improve the efficiency of HTP, we propose the following CHTP algorithm. It allows us to choose more elements of gradient information at each iteration. In particular, if β=s, then xn+1=un+1 in CHTP. Hence, CHTP reduces to HTP in this special case.
Algorithm: Compressive Hard Thresholding Pursuit (CHTP).
Input: a measurement matrix A, a measurement vector y and a sparsity level s. Perform the following steps:
S1. Start with an s-sparse x0∈RN, typically x0=0;
S2. Repeat
where β≥s, until a stopping criterion is met.
Output: the s-sparse vector x∗.
The detailed discussion on numerical experiments including special stopping criteria is given in Section 4.
3.
Convergence analysis
Theoretical analysis for CHTP is carried out in terms of the concept of the restricted isometry property (RIP) of a measurement matrix. First, recall that for a given matrix A and two positive integers p,q, the norm ‖A‖p→q is defined as
Definition 3.1. [1] Let A∈Rm×N be a matrix with m<N. The s-th restricted isometry constant (RIC) of A, denoted by δs, is defined as
where AS is the submatrix of A created by deleting the columns not in the index set S.
The s-th restricted isometry constant can be defined equivalently as the smallest number δ>0 such that
In particular, if δs<1, we say that the matrix A has the restricted isometry property (RIP) of order s.
The following inequalities follow from the definition of RIC and play an important role in the theoretical analysis of CHTP.
Lemma 3.1. [23] Given a vector v∈RN and a set S⊆{1,2,…,N}, one has the following statements.
(i). ‖((I−ATA)v)S‖2≤δt‖v‖2 if |S∪supp(v)|≤t.
(ii). ‖(ATv)S‖2≤√1+δt‖v‖2 if |S|≤t.
The following lemma comes from [28], providing an estimate on the Lipschitz constant of the hard thresholding operator. Moreover, [28,Example 2.3] indicates that the constant (√5+1)/2 is tight.
Lemma 3.2. For any vector z∈RN and for any s-sparse vector x∈RN, one has
where S:=supp(x) and Z:=supp(Hs(z)).
The following result is inspired by [28,Lemma 3.3].
Lemma 3.3. Let y=Ax+e. Given an s-sparse vector z and β≥s, define
Then,
where S:=Ls(x) and e′:=Ax¯S+e.
Proof. The case of S⊆V holds trivially due to xS∖V=0. Now, let us consider the remaining case of S⊊V. Define
Since |V|=β≥s=|S|,
Meanwhile, from the definition of V, we know that the entries of the vector z+AT(y−Az) supported on S∖V are not greater than the β largest absolute entries, that is,
Together with (3.3), this leads to
Define
Since y=AxS+e′ with e′=AxˉS+e,
where the last inequality follows from Lemma 3.1 and the fact that
Due to (S∖V)∩(V∖S)=∅, we have
Let us discuss the following two cases separately.
Case 1. ΦV∖S=0. Then, ΦS∖V=0 by (3.4). It follows from (3.2) that (z+AT(y−Az))S△V=0. So,
where the last inequality results from (3.5).
Case 2. ΦV∖S>0. Let
It follows from (3.6) that
Combining (3.7) and (3.8) yields
Furthermore,
On the other hand, it follows from (3.4) and (3.8) that
Putting (3.9) and (3.10) together yields
Thus,
where the last inequality results from
Taking into account (3.5) and (3.11) yields
Lemma 3.4. Let v be a vector satisfying supp(v)⊆T and |T|≤s. For any vector x∈RN, let y=AxS+e′ with e′=Ax¯S+e and S=Ls(x). If z∗ satisfies
then
Proof. According to the definition of z∗, we have
Hence,
By the triangle inequality and Lemma 3.1, we get
where the last inequality is due to |supp(xS−z∗)∪T|≤2s. This means that
i.e.,
This is a quadratic inequality on ‖xS−z∗‖2. Hence,
where the second inequality comes from the fact that √a2+b2≤a+b for all a,b≥0. By Lemma 3.1 and |T|≤s, one has
Note that z∗ˉT=vˉT=0. It follows from (3.12) and (3.13) that
This completes the proof.
Error bounds and convergence analysis of CHTP are summarized as follows.
Theorem 3.1. Let y=Ax+e be the measurement of the signal x and e be the measurement error. If
then the iterate {xn} generated by CHTP approximates x with
where
Proof. For the convenience of discussion, we define tn+1:=Hs(un+1). Then,
It is clear that (tn+1)Un+1=tn+1. Hence,
where the first inequality comes from Lemma 3.2, and the second inequality follows from the fact that [(S∩Un+1)∪Tn+1]⊆Un+1.
Since supp(tn+1)⊆Un+1 and supp(un+1)⊆Un+1, (tn+1)¯Un+1=(un+1)¯Un+1=0. Thus,
where ξ:=(√5+1)/2, and the last step is due to (3.17).
From Step 2 in CHTP, we know that the following orthogonality condition holds:
where y=AxS+e′ and e' = Ax_{\overline{S}}+e . Hence, for any z satisfying supp(z)\subseteq U^{n+1} , we get
Furthermore,
Lemma 3.1 and \left|supp(u^{n+1}-x_S)\cup U^{n+1}\right|\leq s+\beta lead to
Note that
where the third equality comes from (3.19) since supp((u^{n+1}-x_S)_{U^{n+1}})\subset U^{n+1} . Putting (3.20), (3.21) and (3.22) together yields
Therefore,
i.e.,
This is a quadratic inequality on \|x_S-u^{n+1}\|_2 . So,
where the second inequality comes from the fact that \sqrt{a^2+b^2}\leq a+b for all a, b\geq 0 .
Due to supp(u^{n+1})\subseteq U^{n+1} , we obtain (u^{n+1})_{\overline{U^{n+1}}} = 0 . According to Lemma 3.3, we have
Combining (3.23) and (3.24) yields
Hence, it follows from (3.18) and (3.26) that
where the last step is due to the fact that a^2+(b+c)^2\leq (\sqrt{a^2+b^2}+c)^2 for all a, b, c\geq 0 , and \xi^2-1 = \xi since \xi = (\sqrt{5}+1)/2 . Taking the square root of both sides of this inequality and using (3.25) yields
where the third inequality follows from the fact that \|(A^Te')_{U^{n+1}}\|_2\leq \sqrt{1+\delta_{\beta}}\|e'\|_2 by Lemma 3.1.
Note that supp(t^{n+1})\subseteq T^{n+1} , |T^{n+1}|\leq s , and
According to Lemma 3.4 , we have
Combining this with (3.27) , we obtain
where \rho , \tau are given in (3.15) and (3.16) , respectively. Hence,
Since \delta_{s+\beta}\leq \delta_{2s+\beta} and \delta_{2s}\leq \delta_{2s+\beta} , it is easy to get
To ensure \rho < 1 , it suffices to require the right side of the above equation less than 1 , which is guaranteed by the following RIP bound:
This completes the proof.
The corresponding result for the noiseless case can be obtained immediately.
Corollary 3.1. Let y = Ax be the measurement of an s -sparse signal x . If
then the iterative sequence \{x^n\} generated by CHTP approximates x with
where \rho is given in (3.15).
In the noiseless setting, the foregoing result shows that a sparse signal can be identified by CHTP in a finite number of iterations.
Theorem 3.2. If
then any s -sparse vector x\in\mathbb{R}^N can be recovered by CHTP with y = Ax in at most
iterations, where \rho is given by (3.15), \theta: = \min\limits_{i\in S}|x_i| and S: = supp(x) .
Proof. It is sufficient to show that
If (3.28) holds, we can obtain S\subseteq U^{n+1} from the definition of U^{n+1} , which leads to u^{n+1} = x . Furthermore, we can derive T^{n+1} = S and x^{n+1} = x from the CHTP algorithm directly.
Next, we aim to prove (3.28). According to Lemma 3.1 and Corollary 3.1, we yield
It follows that
where \theta = \min\limits_{i\in S}|x_i| , and the last step is due to the fact x_t = 0 for t\in \bar{S} . Taking
we get \sqrt{2}\delta_{2s+\beta}\rho^{n}\|x^0-x\|_2 < \theta . Combining this with (3.29), we conclude that (3.28) holds. This completes the proof.
Now, let us discuss the stability of CHTP. Recall first that the error of the best s -term approximation of a vector x is defined as
In particular, according to [23,Theorem 2.5], we have
Theorem 3.3. Let
Then, for all x\in\mathbb{R}^N and e\in \mathbb{R}^m , the iterate \{x^n\} generated by CHTP with y = Ax+e satisfies
where \rho is given by (3.15), and
Moreover, every cluster point x^* of the sequence \{x^n\} satisfies
Proof. Let T_1: = \mathcal{L}_k(x) , T_2: = \mathcal{L}_t(x_{\overline{T_1}}) , and
where l, r satisfy (l-2)t+k+r = N and r\leq t . According to the structure of T_j , it follows from [23,Lemma 6.10] that
Taking into account Theorem 3.1, one has
It follows from (3.1) and (3.31) that
Hence,
Using (3.30), we get
Putting (3.32) and (3.33) together implies
Since \rho < 1 , taking n\rightarrow \infty in the above inequality yields
This completes the proof.
4.
Numerical experiments
In this section, numerical experiments are carried out to check the effectiveness of CHTP. All experiments were conducted on a personal computer with the processor Intel(R) Core(TM) i5-7200U, CPU @ 2.50 GHz and 4 GB memory. The s -sparse standard Gaussian vector x^*\in\mathbb{R}^N and standard Gaussian matrix A\in \mathbb{R}^{m\times N} with (m, N) = (400,800) are randomly generated, and the positions of non-zero elements of x^* are uniformly distributed. According to [23,Theorem 9.27], if 0 < \eta, \varepsilon < 1 , and
then the restricted isometry constant \delta_s of \frac{1}{\sqrt{m}}A satisfies
with probability greater than or equal to 1-\varepsilon , where
Hence, to satisfy the restricted isometry bound (3.14) with high probability, we replace (1.1) by the following model throughout the numerical experiments:
where \widetilde{A}: = A/\sqrt{m} , and \widetilde{y}: = y/\sqrt{m} . Moreover, the measurement vector y is given by y = Ax^* in the noiseless setting and y = Ax^*+0.005e in the noisy setting, where e\in\mathbb{R}^m is a standard Gaussian random vector. Unless otherwise stated, all algorithms adopt x^0 = 0 as the initial point and the condition
as the successful reconstruction criterion. OMP is performed with s iterations, while other algorithms are performed with at most 50 iterations. For each sparsity level s , 100 random problem instances are tested to investigate the recovery abilities of all algorithms, as shown in Figures 1–3.
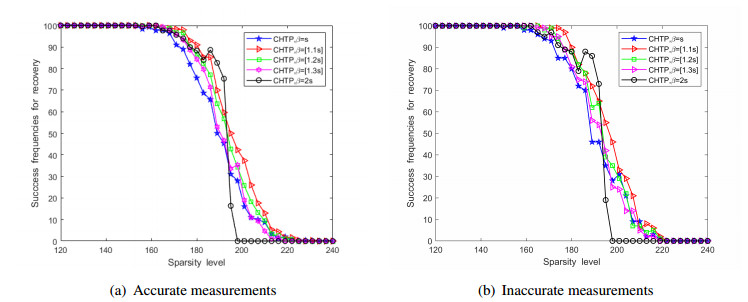
The first experiment is performed to illustrate the effect of the parameter \beta involved in CHTP on the reconstruction ability. Pick the following different values of \beta in \{s, [1.1s], [1.2s], [1.3s], 2s\} and s\in \{120,123, \ldots, 240\} , where [\cdot] denotes the round function. Numerical results with accurate measurements and inaccurate measurements are shown in Figure 1(a) and 1(b), respectively. Since the results shown in Figure 1(b) are similar to those of Figure 1(a), this indicates that CHTP is stable for weak noise. It is also observed that the recovery ability of CHTP is sensitive to the parameter \beta , and it becomes worse with the increase of \beta as \beta\leq [1.3s] . In particular, CHTP reduces to HTP as \beta = s . Thus, CHTP with \beta = [1.1s] , [1.2s] and [1.3s] performs better than HTP in both noiseless and noisy settings. In addition, it should be noted that CHTP with \beta = 2s performs better than HTP as s\leq 190 , and the success rate of the former suddenly drops to zero as sparsity level s approaches m/2 . This phenomenon is similar to the performance of SP in Figure 2. Simulations indicate that the performance of the hard thresholding operator can be improved by introducing a compressive step first.
To investigate the effectiveness of CHTP, we compare it with other four mainstream algorithms: HTP, OMP, CoSaMP and SP. The corresponding results are displayed in Figures 2 and 3. Based on the above discussion on the performances of CHTP, the parameter \beta in this experiment is set as [1.1s] . Sparsity level s ranged from 120 to 258 with stepsize 3 in Figure 2(a), and it ranged from 1 to 298 with stepsize 3 in Figure 2(b). The comparison of recovery abilities for different algorithms is displayed in Figure 2(a) with accurate measurements and in Figure 2(b) with inaccurate measurements. Moreover, Figure 2(c) is an enlarged image of Figure 2(b). Figure 2 indicates that CHTP is competitive with HTP, OMP and SP in both noiseless and noisy scenarios. Furthermore, the recovery ability of CHTP can remarkably exceed that of CoSaMP. Figure 2(b) indicates that the sparse signal reconstruction abilities are significantly weakened in the presence of noise for all algorithms as the sparsity level s\leq 10 .
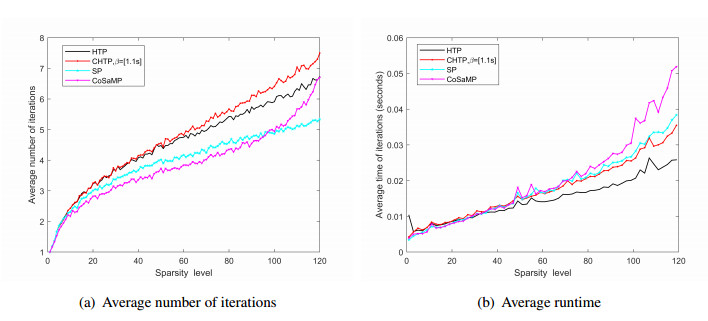
The next problem we examine is the average number of iterations and average recovery runtime for different algorithms with accurate measurements. Due to the number of iterations of OMP being set as s , we just compare all algorithms except OMP in Figure 3, in which s\leq 120 is considered to ensure the success rates of all algorithms are 100%. Figure 3 shows that the larger s is taken, the more average number of iterations and computational time are required for all algorithms. From Figure 3(b), we see that the average recovery runtime for all algorithms are close to each other as s < 50 . Although CHTP needs more iterations than other algorithms in Figure 3(a), it consumes less time than CoSaMP and SP as s\geq 50 in Figure 3(b). From this point of view, CHTP is competitive with the other algorithms mentioned above.
5.
Conclusions
In [21,27], the authors point out that the hard thresholding operator is independent of the objective function, and this inherent drawback may cause the increase of the objective function in the iterative process. Furthermore, they suggest that the hard thresholding operator should be applied to a compressible vector to overcome this drawback. Motivated by this idea, we proposed the CHTP algorithm in this paper, which reduces to the standard HTP as \beta = s . To minimize the negative effect of the hard thresholding operator on the objective function, the orthogonal projection was used twice in CHTP. The convergence analysis of CHTP was established by utilizing the restricted isometry property of the sensing matrix. Numerical experiments indicated that the performance of CHTP with \beta = [1.1s] is better than in other cases. Simulations showed that CHTP is competitive with other popular algorithms such as HTP, OMP and SP, both in the sparse signal reconstruction ability and the average recovery runtime.
Acknowledgments
The second author's work is supported by the National Natural Science Foundation of China (11771255), Young Innovation Teams of Shandong Province (2019KJI013) and Shandong Province Natural Science Foundation (ZR2021MA066). The fourth author's work is supported by the Natural Science Foundation of Henan Province (222300420520) and Key Scientific Research Projects of Higher Education of Henan Province (22A110020).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: