A study of fractional order Ambartsumian equation involving exponential decay kernel

1.   Introduction and motivation

Ambartsumian derived the standard Ambartsumian equation (SAE) ^[1]. The absorption of light by interstellar matter has been defined in this equation. In the theory of surface brightness in the Milky Way, the Ambartsumian delay equation is used. We consider the fractional Ambartsumian equation (FAE) in this paper as ^[2]:

where $\eta$ and $\mu$ are constants and $\mathcal{A}(t)$ represent the fluctuation of the surface brightness in Milky Way. Kato and McLeod have proven and explored existence and uniqueness of Eq (1.1) ^[2]. Because of its use in astronomy, it is important to find an accurate solution to this equation. Very recently, Patade and Bhalekar ^[3] find the analytical solution of Ambartsumian equation using the technique developed in ^[4]. The convergence for all $\left|\eta\right| > 1$ was addressed, where the solution did not occur in the entire domain. Therefore, using the Adomian decomposition method (ADM), which has more precision and validity, a new series solution was deduced. The ADM is a useful tool for the solution of nonlinear differential and integral equations, and IV and BV problems ^[5,6]. In ADM, when we choose a suitable canonical form; the solution converges to an infinite series. Cherruault and Adomian ^[7] have recorded ADM fast convergent and estimate the error terms in the series solution. Bakodah and Ebaid obtained the exact solution for the SAE ^[8]. Alatawi et al., achieve the approximate solution using HPM for the SAE in term of the exponential functions ^[9]. Recently, HTAM is used to find out the approximate solution for the FAE in ^[10].

At present, non-integer order integration and differentiation is a hot area of research. Fractional calculus has many applications in various fields like chemical, mechanical and electrical engineering, medical sciences, electrodynamics, dynamical system, and many more due to memory in heredity properties ^{[11,12,13,14]}. The qualitative analysis of fractional differential equations and their applications has been studied by many researchers^{[15,16,17,18]}. Ullah et al., utilized the Caputo fractional derivative to study the dynamics of childhood diseases ^[19]. Nisar and his coauthors analyzed the transmission of COVID-19 by using the fractional operator in the sense of Caputo ^[20]. Many authors studied it for the existence and uniqueness of solution ^[21,22], using "topological degree theory", "Banach and Leray-Shaudar fixed point theorem", etc. However, many definitions are available in the literature for the fractional derivative with different kernels, which motivates the researches to adopt a best suitable operator, for the considered model. Fractional derivative with non-singular kernel has got great attention among the researchers. Caputo and Fabrizio ^[23] are the ones who define the fractional-derivative in a new scenario. They extend the Caputo fractional derivative having non-singular kernel. This idea has successfully applied in many real-world phenomena ^[24,25]. Baleanu et al., analyzed the dynamics of the human liver model through Caputo-Fabrizio model ^[26]. A Caputo-Fabrizio Rubella disease model has been studied by Baleanu et al., ^[27]. Gao et al., demonstrate the effect of delay terms on the immune system in the Hepatitis B virus model through Caputo-Fabrizio fractional operator ^[28]. Ahmad et al., studied computationally the third-order dispersive PDE with nonsingular fractional operator ^[29].

In the applied analysis, we investigate two types of solutions the analytical and the numerical, for which different analytical and computational techniques are used respectively. To obtain the analytical and the numerical solutions for FDEs is of great interest among the researchers. Therefore, the researchers introduce different methods to solve FDEs. Padey et al., used Homotopy analysis Sumudu transform method to solve the third order dispersive PDE under fractional operator ^[30]. Collocation method was used to solve nonsingular fractional order differential equations by Dumitru with his co-authors ^[31]. In these methods, LADM is the best one for solving nonlinear FDEs. The Laplace transform method and the Adomian decomposition method are combined to form LADM. Like Runge-Kutta and collocation methods LAMD doesn't require any predefined size and discretization of data which require extra memory and time-consuming process. These methods are expensive. Moreover, the homotopy perturbation methods needed the auxiliary parameters which control both the technique and the solution. While in LADM, neither discretization of date nor auxiliary parameters are required ^[32]. It produces the same solution generated by the other methods. Therefore, we considered LADM, an ideal for the solution of the proposed equation. The comparison between ADM and LADM is available in ^[33]. Some of the applications of LADM are also available in ^[34,35]. These motivated us to study the Ambartsumian equation by the aforementioned fractional derivative. The Ambartsumian equation under the Caputo-Fabrizio fractional derivative is given by

In the current article, we study the qualitative and quantitative aspects of the Eq (1.2). We use fixed point results for qualitative analysis of the considered equation. For quantitative approach, we utilize an efficient and accurate analytical method (LADM). We prove the convergence of the suggested method via nonlinear analysis.

2.   Preliminaries

Let $H^{1}[0, t] = \{f:f\in L^{2}[0, T]\, and\, f^{'}\in L^{2}[0, T]\},$ where $L^{2}[0, T]$ is the space of square integrable functions on the $[0, T].$ For the sake of simplicity denote the exponential kernel as $K(t, \varrho) = \exp\left[-\gamma\frac{t-\varrho}{1-\gamma}\right]$.

Definition 2.1. ^[7] If $\mathcal{A}(t)\in H^{1}[0, T], T > 0, \gamma\in(0, 1),$ then the Caputo-Fabrizio derivative is defined as

$\mathscr{M}(\vartheta)$ satisfies $\mathscr{M}(1) = \mathscr{M}(0) = 1, is\; the\; normalization\; function.$ However, if $\mathcal{A}(t)\notin H^{1}[0, T]$, then

Definition 2.2. ^[7] The Caputo-Fabrizio fractional integral is defined as

Definition 2.3. ^[35] Taking $\mathscr{M} = 1,$ the Laplace transform of $^{CF}D_{t}^{\vartheta}\left[\mathcal{A}(t)\right]$ is given by

3.   Existence and stability theory

3.1.   Existence theory

In this section, we use fixed point theory approach to confirm the existence of solution of the proposed equation under the nonsingular fractional derivative. Consider the proposed model as

where

Now using $^{CF}I_{t}^{\vartheta}$, we have

To derive the existence and uniqueness results, we define a Banach space $\mathbb{B} = \boldsymbol{C}\left[\mathscr{P}, \mathbb{R}\right]$; where $\mathscr{P} = [0, \mathrm{T}]$ and $0\leq t\leq\mathrm{T} < \infty.$ We define a norm for Banach space as follows

Let us define an operator $\mathcal{T}:\mathbb{B}\rightarrow \mathbb{B}$ as

We impose growth and Lipschitz condition on $\mathbb{Q}$ as

● Under the continuity of $\mathbb{Q}$, for $K_{\mathbb{Q}} > 0$, we define $\mathbb{Q}:\mathscr{P}\times\mathbb{R}\rightarrow \mathbb{R}$ such that

● There exists $C_{\mathbb{Q}} > 0, L_{\mathbb{Q}} > 0,$and $M_{\mathbb{Q}}$ such that

Theorem 3.1. Assume that the conditions (3.5) and (3.6) hold. Then there is at least one solution of the Eq (3.2), if $\frac{K_{\mathbb{Q}}(1-\vartheta)}{\mathscr{M}(\vartheta)} < 1.$

Proof. Let $\mathbb{E} = \left\{ \mathcal{A}\in\mathbb{B}:\left\Vert \mathcal{A}\right\Vert \leq\kappa, \:\kappa > 0\right\} \subset\mathbb{B}$ be a convex and closed set. Now, we define two operators as

such that $\mathcal{G}\mathcal{A}(t)+\mathcal{H}\mathcal{A}(t) = \mathcal{T}\mathcal{A}(t)$. First, we prove that $\mathcal{G}$ is a contractive mapping, for this let $\mathcal{A}, \overline{\mathcal{A}}\in\mathbb{B}$, one has

By the hypothesis $\frac{(1-\vartheta)}{\mathscr{M}(\vartheta)}K_{\mathbb{Q}} < 1,$ the operator $\mathcal{G}$ is contraction. Next, we show that $\mathcal{H}:\mathbb{E}\rightarrow \mathbb{E}$ is bounded. For this, let $\mathcal{A}\in\mathbb{E}$, one has

It follows that the operator $\mathcal{H}$ is bounded. Next, to show the equi-continuity of $\mathcal{H}$ consider $t_{1} < t_{2},$ one has

when $t_{1}\rightarrow t_{2}$, then $\left|\mathcal{H}\mathcal{A}(t_{1})-\mathcal{H}\mathcal{A}(t_{2})\right|\rightarrow0.$ Also the continuity and boundeness of $\mathcal{H}$ implies that $\left\Vert \mathcal{H}\mathcal{A}(t_{1})-\mathcal{H}\mathcal{A}(t_{2})\right\Vert \rightarrow0$, as $t_{1}\rightarrow t_{2}.$ Thus $\mathcal{H}$ is completely continuous by the "Arzelá-Ascoli theorem". Thus, by "Krasnoselskii's fixed point theorem ^[40]", our proposed equation has at least one solution.

Now, we show that our proposed equation possess at most one solution. To achieve this goal, we will use Banach contraction theorem.

Theorem 3.2. Assume that condition (3.5) holds. Then the proposed equation has at most one solution, if the following condition hold

Proof. Let $\mathcal{A}, \overline{\mathcal{A}}\in\mathbb{B},$ then

By hypothesis (3.9), $\mathcal{T}$ is contraction. Thus by "Banach contraction theorem", the proposed equation has unique solution.

3.2.   Stability theory

The stability of mathematical models is an important aspect of the DEs. To study the different kinds of stability, one can find the most interesting kind is Ulam-Hyers stability introduced by Ulam ^[36], further generalized by Rassias ^[37]. The more general form of this stability is known as Ulam-Hyers-Rassias stability. This stability is studied by many authors in the last few years ^[38,39]. Therefore, in this article, we also use UH stability for the mentioned problem.

3.2.1.   Ulam-Hyers stability

Definition 3.3. Let $\mathcal{A}(t)\in\mathbb{B}$ be any solution. Then the proposed equation is Ulam-Hyers stable if for any $\omega > 0$ with the following inequality

there exists a unique solution $\overline{\mathcal{A}}(t)\in\mathbb{B}$ of the proposed equation with $U_{q} > 0$ such that

Further, if $\exists$ $\varLambda(\omega)\in\boldsymbol{C}\left[\mathbb{R}, \mathbb{R}\right]$ with $\varLambda(0) = 0$ such that $\left\Vert \mathcal{A}-\overline{\mathcal{A}}\right\Vert \leq\varLambda(\omega),$ then the proposed equation is generalized Ulam-Hyers stable.

Remark 3.4. We perturb our proposed equation by taking a small perturbation $\varDelta(t)\in\boldsymbol{C}\left[\mathscr{P}, \mathbb{R}\right]$ which depends on $\mathcal{A}$ and satisfies the following

● For $\omega > 0, \left|\varDelta(t)\right|\leq\omega.$

● $_{0}^{CF}\mathbb{D}_{t}^{\vartheta}\mathcal{A}(t) = \mathbb{Q}\left(t, \mathcal{A}(\frac{t}{\eta}), \mathcal{A}(t)\right)+\varDelta(t).$

The corresponding perturbed equation is given by

Now, we prove an important Lemma, which will be used for further analysis.

Lemma 3.5. The following result holds for the perturbed Eq (3.12)

where $U_{q} = \left(\frac{(1-\vartheta)+\vartheta\mathrm{T}}{\mathscr{M}(\vartheta)}\right).$

Proof. Applying the fractional integral to the perturbed Eq (3.12), we get

Now using Eq (3.4), we have

This complete the required result.

Theorem 3.6. Under the above Lemma 3.5, the solution of the proposed equation is Ulam-Hyers stable and also generalized- Ulam-Hyers stable if $U_{q} < 1$.

Proof. Let $\mathcal{A}, \overline{\mathcal{A}}\in\mathbb{B},$ be any solution and a unique solution of the considered equation respectively. Then

This implies that

Hence, the proposed problem is Ulam-Hyers stable. Consequently, it is generalized Ulam-Hyers stable.

Definition 3.7. Let $\mathcal{A}(t)\in\mathbb{B}$ be any solution. Then the proposed equation is Ulam-Hyers-Rassias stable for $\chi\in\boldsymbol{C}\left[\mathscr{P}, \mathbb{R}\right],$ if for any $\omega > 0$ with the following inequality

there exists a unique solution $\overline{\mathcal{A}}(t)\in\mathbb{B}$ of the proposed equation with $U_{q} > 0$ such that

Further, if $\exists\; \; \chi(\omega)\in\boldsymbol{C}\left[\mathbb{R}, \mathbb{R}\right]$ with $\chi(0) = 0$ such that $\left\Vert \mathcal{A}-\overline{\mathcal{A}}\right\Vert \leq U_{q}\chi(\omega),$ then the proposed equation is generalized Ulam-Hyers-Rassias stable.

Remark 3.8. We perturb our proposed equation by taking a small perturbation $\varDelta(t)\in\boldsymbol{C}\left[\mathscr{P}, \mathbb{R}\right]$ which depends on $\mathcal{A}$ and satisfies the following

● For $\omega > 0,$ $\left|\varDelta(t)\right|\leq\omega\chi(t).$

● $_{0}^{CF}\mathbb{D}_{t}^{\vartheta}\mathcal{A}(t) = \mathbb{Q}\left(t, \mathcal{A}(\frac{t}{\eta}), \mathcal{A}(t)\right)+\varDelta(t).$

Lemma 3.9. The following result holds for the perturbed Eq (3.12)

Proof. The proof is similar to the above Lemma 3.5.

Theorem 3.10. The solution of the proposed problem is Ulam-Hyers-Rassias stable if $U_{q} < 1$.

Proof. Let $\mathcal{A}$ be any solution and $\overline{\mathcal{A}}$ be a unique solution of considered model, then

This implies that

Thus the proposed equation is Ulam-Hyers-Rassias stable. Consequently, it is generalized Ulam-Hyers-Rassias stable.

3.3.   Solution of the proposed equation and simulations

In this section, we will deduce a solution of (1.2) by an efficient analytical technique called Laplace transform. Via Laplace transform, we will find the concerned equation for semi-analytical solution. Now applying the Laplace transform on (1.2), we get

To get approximate solution, we assume the solution in series form as

which gives

The recursion formula (3.18) gives the following result

and so on. Now applying inverse Laplace transform to (3.17) and (3.19), we get

So the first two term of the infinite series solution is given by

Next we prove by fixed point theory that the obtained series solution is a convergent series, i.e., it uniformly converges to the exact solution.

Proposition 3.11. Let $\mathbb{B}$ be a Banach space and $\Omega:\mathbb{B}\rightarrow \mathbb{B}$ be a mapping satisfying the contraction condition, i.e., for all $\mathcal{A}, \mathbb{\bar{\mathcal{A}}\in\mathbb{B}}, \left\Vert \Omega(\mathcal{A})-\Omega(\mathbb{\bar{Y}})\right\Vert \leq\Phi\left\Vert \mathcal{A}-\mathbb{\bar{Y}}\right\Vert,$ where $\Phi\in(0, 1).$ Then $\Omega$ has a unique fixed point $\mathcal{A}$ such that $\mathcal{A} = \Omega\mathcal{A}.$ Moreover, the series solution of the proposed equation can be written as

Consider $G_{\alpha}(\mathcal{A}) = \left\{ \bar{\mathcal{A}}\in\mathbb{B}:\left\Vert \mathcal{A}-\mathbb{\bar{Y}}\right\Vert < \alpha\right\}$ and assume that $\mathcal{A}\in\mathbb{B},$ then $\mathcal{A}_{j}\in G_{\alpha}(\mathcal{A})$ and $\lim_{j\rightarrow \infty}\mathcal{A}_{j} = \mathcal{A}.$

Proof. To prove the required result, we use the concept of mathematical induction, for $j = 1,$ we have

which is true for $j = 1$. Assume that the result is true for $j-1,$ then

Now for $j+1,$ we have

this shows that $\mathcal{A}_{j}\in G_{\alpha}(\mathcal{A}).$ Now, we prove the second part. Since $\left\Vert \mathcal{A}_{j}-\mathcal{A}\right\Vert \leq\Phi^{j}\left\Vert \mathcal{A}_{0}-\mathcal{A}\right\Vert$ and $\Phi\in(0, 1)$, therefore, $\Phi^{j}\rightarrow0$ as $j\rightarrow \infty.$ Consequently, $\left\Vert \mathcal{A}_{j}-\mathcal{A}\right\Vert \rightarrow0$ as $j\rightarrow \infty.$ Thus, $\lim_{j\rightarrow \infty}\mathcal{A}_{j} = \mathcal{A}.$

4.   Conclusions

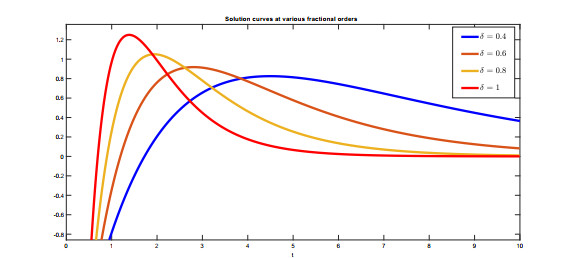
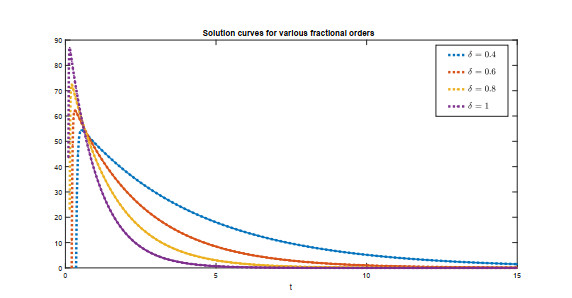
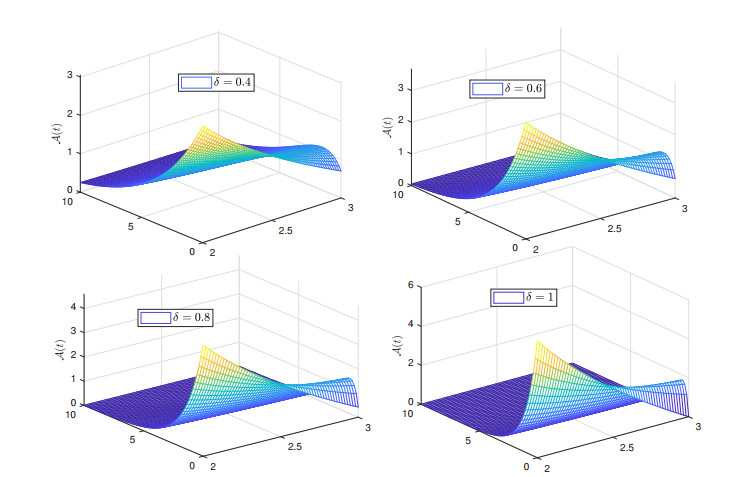
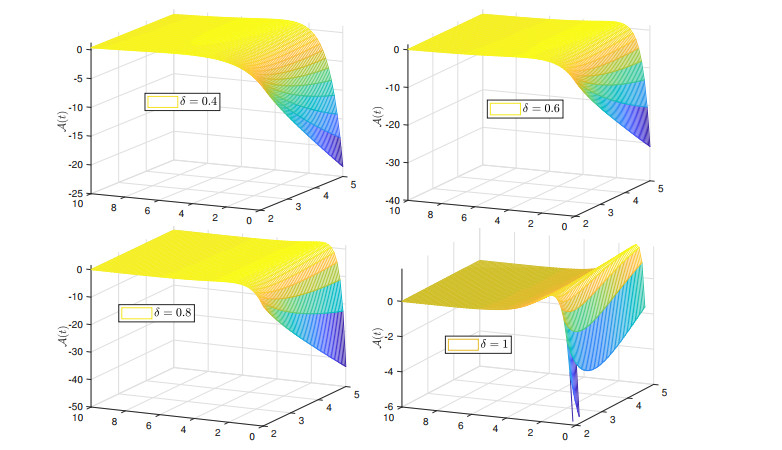
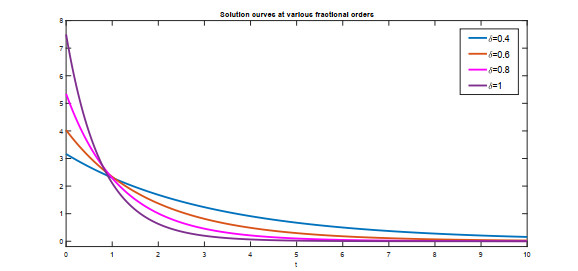
In this paper, we have investigated the Ambartsumian equation under a non-singular fractional operator called the Caputo-Fabrizio operator. We have deduced the existence and uniqueness results by Krasnoselskii's fixed point theorem and Banach fixed point theorem. We have used the notion of functional analysis to show that the proposed equation is Ulam-Hyers and Ulam-Hyers-Rassias stable. We have used an efficient analytical method to find a novel series solution of the proposed equation. We have proved that the series solution is convergent to the exact solution of the equation. Lastly, we have simulated the obtained results for different non-integer orders belongs to (0, 1] in Figures 1–6. We have shown through graphs that when the fractional order tends to unity, then solution curves at non-integer orders tend to solution curves at integer order. Thus, we conclude that nonsingular fractional operators are appropriate for the study of the dynamics of a model at fractional orders. In the future, we will study the concerned equation under more generalized non-integers derivatives.

Acknowledgments

The authors are grateful to the Basque Government by Grant IT1207-19.

Conflict of interest

There exist no conflict of interest regarding to this research work. \newpage