1.
Introduction
In recent years, a useful extension has been proposed from the classical calculus by permitting derivatives and integrals of arbitrary orders is known as fractional calculus. It emerged from a celebrated logical conversation between Leibniz and L'Hopital in 1695 and was enhanced by different scientists like Laplace, Abel, Euler, Riemann, and Liouville [1]. Approaches based on the fractional calculus and fractional differential equations has been widely applied in diffusion equation, polymer physics, medical sciences, bioengineering mathematics, turbulence, fluid flow through porous media and in the model problems of nanoscale flow [2,3,4,5,6,7,8,9,10,11,12]. The concept of this new calculus was applied in several distinguished areas previously with excellent developments in the frame of novel approaches and posted scholarly papers, see [13,14,15,16,17,18,19,20,21,22,23,24,25,26].
Various notable generalized fractional integral operators such as the Riemann-Liouville, Hadamard, Caputo, Marichev-Saigo-Maeda, Riez, the Gaussian hypergeometric operators and so on, are helpful for researchers to recognize real world phenomena. Therefore, the Caputo, Riemann-Liouville and Hadamard were the most used fractional operators having singular kernels. It is remarkable that all the above mentioned operators are the particular cases of the operators investigated by Jarad et al. [27]. The utilities are currently working on weighted generalized fractional operators. Inspired by the consequences in the above mentioned papers, we introduce a new weighted framework of generalized proportional Hadamard fractional integral operator. Also, some new characteristics of the aforesaid operator are apprehended to explore new ideas, amplify the fractional operators and acquire fractional integral inequalities via generalized fractional operators (see Remark 2 below).
Recently, by employing the fractional integral operators, several researchers have established a bulk of fractional integral inequalities and their variant forms with fertile applications (see [28,29,30,31,32,33,34]). These sorts of speculations have remarkable use in fractional differential/difference equations and fractional Schrödinger equations [35].
Our intention is to establish a more general form for the most appealing and noteworthy Pólya-Szegö-Chebyshev type inequalities [36,37] and certain related variants via weighted generalized proportional Hadamard fractional integral that could be increasingly practicable and, also, more appropriate than the existing ones.
In 1882, Chebyshev pondered the noted result [36]:
for integrable functions ˜f and ˜g on [η1,η2] and both the functions are simultaneously increasing or decreasing for the same values of x in [η1,η2], that is,
for any x,y∈[η1,η2].
Butt et al. [38], Rashid et al. [39] and Set et al. [40] established the fractional integral inequalities via generalized fractional integral operator having Raina's function, generalized K-fractional integral and Katugampola fractional integral inequalities similar to the variant (1.1). For more recent literature, (see [41,42,43,44,45,46,47,48,49,50,51]).
The intensively studied Grüss inequality [52] for two integrable functions ˜f and ˜g on [η1,η2] is presented as follows:
where the integrable functions ˜f and ˜g satisfy q≤˜f≤Q and s≤˜f≤S for all x∈[η1,η2] and for some q,s,Q,S∈R.
The Pólya-Szegö type inequality [37] can be stated as follows:
The constant 14 is best feasible in (1.3) make the experience it cannot get replaced by a smaller constant. With the aid of the Pólya-Szegö inequality, Dragomir and Diamond [53] derived the inequality
holds for all x∈[η1,η2] if the mappings ˜f and ˜g defined on [η1,η2] satisfies q≤˜f(x)≤Q and s≤˜g(x)≤S. Here we should emphasize that, inequalities (1.1) and (1.3) are a remarkable instrument for reconnoitering plentiful scientific regions of investigation encompassing probability theory, statistical analysis, physics, meteorology, chaos and henceforth. Nisar et al. [54] proposed the weighted fractional integral inequalities of (1.1) and (1.3) within the weighted generalized fractional integral operator. Shen et al. [55] introduced the time scale version similar to (1.1) and (1.3), respectively. Ntouyas et al. [42] are the ones who contemplated the fractional version of (1.1) and (1.3) via Riemann-Liouville fractional integral operator. For more recent literature, we refer to the readers [56,57,58,59,60,61,62,63] and the references cited therein.
The motivation for this paper is twofold. First, we introduce a novel framework named weighted generalized proportional Hadamard fractional integral operator, then current operator employed to on the Pólya-Szegö-Chebyshev and certain related inequalities for exploring the analogous versions of (1.1) and (1.3). The study is enriched by giving remarkable cases of our results which are not computed yet. Interestingly, particular cases are designed for Hadamard fractional integral, generalized proportional Hadamard fractional integral and weighted Hadamard fractional integral inequalities. It is worth mentioning that these operators have the ability to recapture several generalizations in the literature by considering suitable assumptions of ϖ and φ.
2.
Prelude
This section demonstrates some essential preliminaries, definitions and fractional operators which will be utilized in this paper.
Definition 2.1. ([27]) Let ϖ≠0 bea mapping defined on [η1,η2], ˜g is a differentiable strictly increasing function on [η1,η2]. The space χpϖ(η1,η2),1≤p<∞ is the space of all Lebesgue measurable functions ˜f defined on [η1,η2] for which ‖˜f‖χpϖ, where
and
Remark 1. Clearly we see that ˜f∈χpϖ(η1,η2) ⟹ ϖ(x)˜f(x)(˜g′(x))1/p∈Lp(η1,η2) for 1≤p<∞ and ˜f∈χpϖ(η1,η2) ⟹ ϖ(x)˜f(x)∈L∞(η1,η2).
Now, we show a novel fractional integral operator which is known as the weighted generalized proportional Hadamard fractional integral operator as follows.
Definition 2.2. ([29]) Let ˜f∈χpϖ[1,∞) and ϖ≠0 be a function on [1,∞). Then the left and right-sided weighted generalized proportional Hadamard fractional integral operator of order ℘>0 are described as:
and
where φ∈(0,1] is the proportionality index, ℘∈C,ℜ(℘)>0 and Γ(x)=∫∞0ϕx−1e−ϕdϕ is the Gamma function.
Remark 2. Some particular fractional operators are the special cases of (2.5) and (2.6).
I. Setting ϖ(x)=1 in Definition 2.2, then we get the generalized proportional Hadamard fractional operator introduced by Rahman et al. [62] stated as follows:
and
II. Setting φ=1 in Definition 2.2, then we get the weighted Hadamard fractional operators stated as follows:
and
II. Setting ϖ(x)=1 and φ=1 in Definition 2.2, then we get the Hadamard fractional operator proposed by Samko et al. [18] and Kilbas et al. [19], respectively, stated as follows:
and
Remark 3. (Semi-group property) For ℘,ψ>0,φ∈(0,1] with 1≤p<∞ and let ˜f∈χpϖ(η1,η2). Then
This section consists of some novel Pólya-Szegö type inequalities regarding the generalized proportional Hadamard fractional operators which are also utilized to obtain Chebyshev type integral inequalities and related variants. Throughout the present investigation, for the consequences related to (1.1) and (1.3), it is assumed that all functions are integrable in the Riemann sense.
Theorem 2.3. Let two positive integrable functions ˜f and ˜g defined on [η1,∞). Assume that there exist four integrable functions υ1,υ2,υ3 and υ4 defined on [η1,∞) such that
for all ℓ∈[η1,x](x>η1),η1∈R+0. Then, the inequality
holds for all φ∈(0,1],℘∈C and ℜ(℘)>0 with ϖ>0.
Proof. By means of given hypothesis, we obtain
Thus, we have
which imply that
Here, taking product each side of the above inequality by the following term 1φ℘Γ(℘)exp[φ−1φ(lnxℓ)](lnxℓ)1−℘ϖ(ℓ)ℓ(ℓ∈[η1,x])(x>η1) and integrating the resulting inequality with respect to ℓ on [η1,x], we have
Multiplying both sides of the above equation by ϖ−1(x) and employing Definition 2.2, we have
Taking into account the arithmetic-geometric mean inequality, we have
which leads to the inequality (2.13). This completes the proof.
Corollary 1. Let two positive integrable functions ˜f and ˜g defined on [η1,∞) such that
for all ℓ∈[η1,x](x>η1),η1∈R+0 with ϖ>0. Then, the inequality holds:
Remark 4. Under all assumptions of Theorem 2.3 and Corollary 1:
(1) If we take ϖ(x)=φ=1, then we get the result similar to Lemma 2.1 (by taking κ=1) of [64].
(2) If we take ϖ(x)=φ=1, then we get the result similar to Corollary 1 (by taking κ=1) of [64].
Theorem 2.4. Let two positive integrable functions ˜f and ˜g defined on [η1,∞) such that the assumption (A) satisfying (2.12). Then, for all ℓ,ϕ∈[η1,x](x>η1),η1∈R+0, the inequality
holds for all φ∈(0,1],℘,ψ∈C and ℜ(℘),ℜ(ψ)>0 with ϖ>0.
Proof. By means of assumption (2.12), we have
which imply that
Conducting product each side of the inequality (2.24) by υ1(ϕ)υ2(ϕ)˜g2(ϕ), we get
Here, taking product each side of the above inequality by the following term
and integrating the resulting inequality with respect to ℓ and ϕ on [η1,x]. Then, multiplying both sides of the inequality by ϖ−2(x) and employing Definition 2.2, we obtain
By employing the arithmetic-geometric mean inequality, we have
which leads to the desired inequality (2.22). Hence the proof is complete.
Corollary 2. Let two positive integrable functions ˜f and ˜g defined on [η1,∞) satisfying (2.20). Then for all ℓ,ϕ∈[η1,x](x>η1),η1∈R+0, the inequality
holds for all φ∈(0,1],℘,ψ∈C and ℜ(℘),ℜ(ψ)>0 and I(x) is the identity mapping.
Remark 5. Under all assumptions of Theorem 2.4 and Corollary 2:
(1) If we take ϖ(x)=φ=1, then we get the result similar to Lemma 2.2 (by taking κ=1) of [64].
(2) If we take ϖ(x)=φ=1, then we get the result similar to Corollary 2 (by taking κ=1) of [64].
Theorem 2.5. Under the assumption of Theorem 2.4, then for all x>η1 and ℓ,ϕ∈[η1,x]. Then, the inequality
holds for all φ∈(0,1],℘,ψ∈C and ℜ(℘),ℜ(ψ)>0.
Proof. By means of assumption (2.12), we have
Multiplying both sides of the above equation by ϖ−1(x) and employing of Definition 2.2, we have
By similar argument, we have
Multiplying both sides of the above equation by ϖ−1(x) and employing Definition 2.2, we have
Taking product of the inequalities (2.31) and (2.33) side by side, then we obtain the desired inequality (2.29).
Corollary 3. Let two positive integrable functions ˜f and ˜g defined on [η1,∞) satisfying (2.20). Then for all ℓ,ϕ∈[η1,x](x>η1),η1∈R+0, the inequality
holds for all φ∈(0,1],℘,ψ∈C and ℜ(℘),ℜ(ψ)>0 with ϖ>0.
Remark 6. Under all assumptions of Theorem 2.5 and Corollary 3:
(1) If we take ϖ(x)=φ=1, then we get the result similar to Lemma 2.3 (by taking κ=1) of [64].
(2) If we take ϖ(x)=φ=1, then we get the result similar to Corollary 3 (by taking κ=1) of [64].
Our next result is the Chebyshev type integral inequality within the weighted generalized proportional Hadamard fractional integral operator defined in (2.3), with the aid of Pólya-Szegö type inequality established in Theorem 2.3.
Theorem 2.6. Let two positive integrable functions ˜f and ˜g defined on [η1,∞) such that the assumption (A) satisfying (2.12). Then, for all ℓ,ϕ∈[η1,x](x>η1),η1∈R+0, the inequality
where
and
holds for all φ∈(0,1],℘,ψ∈C and ℜ(℘),ℜ(ψ)>0 with ϖ>0.
Proof. For ℓ,ϕ∈[η1,x] with x>η1, we define Δ(ℓ,ϕ) as
or, equivalently,
Taking product each side of the above inequality by the following term
and integrating the resulting inequality with respect to ℓ and ϕ on [η1,x], then we have
Multiplying both sides of the above equation by ϖ−2(x) and employing Definition 2.2, we have
Thanks to the weighted Cauchy-Schwartz integral inequality for double integrals in (2.41), we can write that
In view of Definition 2.2, we get
Applying Theorem 2.3 and setting υ3(x)=υ4(x)=˜g(x)=1, we find
This implies that
and
Analogously, setting υ1(x)=υ2(x)=˜f(x)=1, we find
and
A combination of (2.42)–(2.48), we get the immediate consequence (2.35). This completes the proof of (2.35).
Remark 7. If we take ϖ(x)=φ=1 in Theorem 2.6, then we get the result similar to Theorem 1 (by taking κ=1) of [64].
The following lemma play a vital role for generating new outcomes by employing weighted generalized proportional Hadamard fractional integral operator
Lemma 2.7. ([65]) Let σ≥0,θ1≥θ2≥0 and θ≠0. Then
Theorem 2.8. For θ1≥θ2≥0,θ1≠0 and let an integrable function ˜f defined on [η1,∞). Moreover, assume that there exist two integrable functions υ1,υ2 defined on [η1,∞) such that
Then, the inequality
holds for all φ∈(0,1],℘∈C and ℜ(℘)>0 with ϖ>0.
Proof. By means of Lemma 2.7 and utilizing the assumption (2.49), for θ1≥θ2≥0,θ1≠0, for any κ>0, it follows that
Taking product each side of the above inequality by the following non-negative term 1φ℘Γ(℘)exp[φ−1φ(lnxℓ)](lnxℓ)1−℘ϖ(ℓ)ℓ(ℓ∈[η1,x],x>η1) and integrating the resulting inequality with respect to ℓ on [η1,x], we have
Multiplying both sides of the above equation by ϖ−1(x) and employing of Definition 2.2, we have
which leads to inequality (c1). Inequality (c2) can be proved by similar argument.
Theorem 2.9. For θ1≥θ2≥0,θ1≠0 and under the assumptions of Theorem 2.3. Then, the inequalities
holds for all φ∈(0,1],℘,ψ∈C and ℜ(℘),ℜ(ψ)>0 with ϖ>0.
Proof. The inequalities (c3)−(c6) can be deduced by utilizing Lemma 2.7 and the following assumptions:
Remark 8. Under all assumptions of Theorem 2.8 and Theorem 2.9:
(1) If we take ϖ(x)=φ=1, then we get the result similar to Theorem 15 of [66].
(2) If we take ϖ(x)=φ=1, then we get the result similar to Theorem 22 of [66].
3.
Particular cases
In the sequel, we derive the certain novel estimates via weighted generalized proportional Hadamard fractional and generalized Hadamard fractonal integral operator as follows.
I. Setting ℘=ψ and considering Theorem 2.6, then we get a new result for weighted generalized proportional Hadamard fractional integral operator.
Corollary 4. Let two positive integrable functions ˜f and ˜g defined on [η1,∞) such that the assumption (A) satisfying (2.12). Then, for all ℓ∈[η1,x](x>η1),η1∈R+0, the inequality
where
holds for all φ∈(0,1],℘∈C and ℜ(℘)>0 with ϖ>0.
II. Considering the assertion (2.20) and Theorem 2.6, then we get a new result for weighted generalized proportional Hadamard fractional integral operator.
Corollary 5. Let two positive integrable functions ˜f and ˜g defined on [η1,∞). Then, the inequality
holds for all φ∈(0,1],℘∈C and ℜ(℘)>0 with ϖ>0.
II. Setting φ=1, then we get a new result for generalized proportional Hadamard fractional integral operator.
Corollary 6. Suppose all assumptions of Theorem 2.8 be satisfied. Then, the inequality
holds for all ℘∈C and ℜ(℘)>0.
IV. Setting φ=1, then we get a new result for generalized proportional Hadamard fractional integral operator.
Corollary 7. For θ1≥θ2≥0,θ1≠0 and under the assumptions of Theorem 2.3. Then, the inequalities
holds for all φ∈(0,1],℘,ψ∈C and ℜ(℘),ℜ(ψ)>0 with ϖ>0.
Example 3.1. Let η1>1,φ,℘>0,p1,q1>1 having p−11+q−11=1, and ϖ≠0 be a function defined on [0,∞). Let ˜f be an integrable function defined on [1,∞) and HϖJφ;℘η1˜f be the weighted generalized proportional Hadamard fractional integral operator. Then we have
and Υ(℘,x)=x∫0e−yy℘−1dy is the incomplete gamma function [68].
Proof. In view of Definition 2.2 and applying modulus property that
for ϕ>1.
By the virtue of the noted Hölder inequality, we have
Substituting ν=ln(xϕ). Then elaborated computations represents
4.
Applications
In the sequel we demonstrate a new methodology for establishing the four bounded mappings and employ them to show certain bounds of Chebyshev type weighted generalized proportional Hadamard fractional integral inequalities of two unknown mappings.
Consider a unit step function χ be defined as
and assuming a Heaviside unit step function χη1(x) defined by
The main characteristic of the unit step function are its frequent use in the differential equations and piece-wise continuous functions when sum of pieces defined by the series of functions. Assume that a piece-wise continuous function υ1(ℓ) defined on [η1,T] can be presented a follows:
where h0,hj∈R(j=0,1,...,i+1) and η1=x0<x1<x2<...<xi<xi+1=T. Analogously, we define the mappings υ2,υ3 and υ4 as follows
where r0=R0=H0=0 and rj,Rj,Hj∈R(j=0,1,...,q).
Suppose an integrable function ˜f defined on [η1,T] satisfying assumption (2.12), (4.1) and (4.2), respectively, then we have hl+1≤˜f(x)≤Hl+1 for every x∈(xl,xl+1)(l=0,1,...,q). Specifically, q=4, the time theory of ˜f presented in (4.1).
The weighted generalized proportional Hadamard fractional integral of ˜f on [η1,T] can be described as follows:
where
Proposition 1. Let two integrable functions ˜f and ˜g defined on [η1,T] satisfying the assumptions (2.12), (4.1) and (4.2), respectively. Then, the inequality
holds for all φ∈(0,1],℘∈C and ℜ(℘)>0 with ϖ>0.
Proof. By employing Definition 2.2, we have
and
Using the fact of Lemma 2.3, inequalities (4.6) and (4.7), the desired inequality (4.5) is established.
Proposition 2. Let two positive integrable functions
˜f and ˜g defined on [η1,T] such that the assumption (A) satisfying (2.12). Then, the inequality
holds for all φ∈(0,1],℘,ψ∈C and ℜ(℘),ℜ(ψ)>0.
Proof. The proof is simple by following (4.1), (4.2) and Theorem 2.4.
Remark 9. The accuracy of the approximated estimates (4.5) and (4.8) depends on the value of q∈N.
5.
Conclusions
This paper proposes a new generalized fractional integral operator. The novel investigation is used to generate novel weighted fractional operators in the Hadamard and generalized proportional Hadamard fractional operator, which effectively alleviates the adverse effect of weight function ϖ and proportionality index φ. Utilizing the weighted generalized proportional Hadamard fractional operator technique, we derived the analogous versions of the weighted Pólya-Szegö-Chebyshev and certain associated type inequalities that improve the accuracy and efficiency of the proposed technique. Contemplating the Remark 2, several existing results can be identified in the literature. It is important to note that our generalizations are refinements of the results obtained by [69]. Some innovative particular cases constructed by this method are tested and analyzed for statistical theory, fractional Schrödinger equation [35]. The results show that the method proposed in this paper can stably and efficiently generate integral inequalities for convexity with better operators' performance, thus providing a reliable guarantee for its application in control theory [67].
Acknowledgments
The authors would like to express their sincere thanks to referees for improving the article and also thanks to Natural Science Foundation of China (Grant Nos. 61673169) for providing financial assistance to support this research. The authors would like to express their sincere thanks to the support of Taif University Researchers Supporting Project Number (TURSP-2020/155), Taif University, Taif, Saudi Arabia.
The work was supported by the Natural Science Foundation of China (Grant Nos. 61673169, 11601140) and the Scientific Research Fund of Hunan Provincial Education Department (Grant No. 16B047).
Competing interests
The authors declare that they have no competing interests.









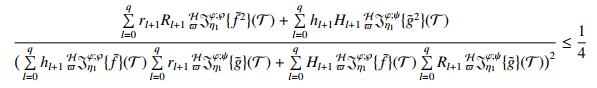




 DownLoad:
DownLoad: