The product property of the almost fixed point property for digital spaces

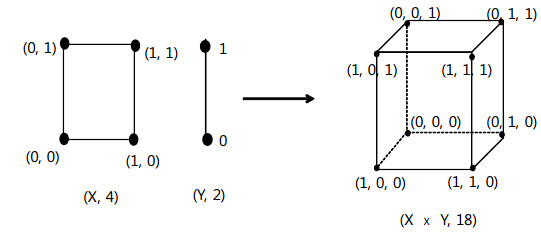
1.   Introduction

Motivated by the Kuratowski's question ^[3,23] on the product property of the fixed point property (FPP for short) on a peano continuum (or a compact, connected, and locally connected metric space), the paper ^[3] studied the FPP for product spaces of which each of the given factor spaces has the FPP. Owing to Borsuk's or Brouwer's fixed point theorem ^[25], it is well known that a compact Euclidean $n$D cube $X \subset {\mathbb R}^n$ has the FPP. Similarly, motivated by the almost fixed point property(AFPP) in the papers ^[4,18,21,26] and its product property (see Brown's work in ^[3]), the present paper studies the product property of the AFPP for digital spaces. Comparing the FPP and the AFPP in the literature ^{[4,12,14,15,18,21,26]}, we observe that their digital versions have own features. To examine the product property of the AFPP for digital spaces, we need to recall basic notions from digital topology and fixed point theory. Let ${\mathbb N}$, ${\mathbb Z}^n$, and ${\mathbb R}^n$ represent the set of natural numbers, points in the Euclidean $n$D space with integer coordinates, and $n$D real numbers, respectively. In this paper we shall use the symbol "$: =$" to introduce new notions without proving the fact.

Unlike the FPP of a compact Euclidean $n$-dimensional cube, it is clear that any digital space $(X, k)$ on ${\mathbb Z}^n$ does not have the FPP for (digitally) $k$-continuous maps ^[28] (for more details, see ^[14,15]). Thus, according to literature, we have followed two approaches. The first one is as follows: After adding certain conditions to $k$-continuous maps, i.e., using more restricted $k$-continuous maps, we study the FPP of a digital space $(X, k)$. For instance, using many types of digital versions of the typical Banach contraction principle and a Cauchy sequence for complete metric spaces, we have also studied this issue which includes the papers ^{[5,6,7,10,11,17,18,19,20,21,24]}. The second one is that we can alternatively study the AFPP because it is the most alternative or closest notion to the FPP from the viewpoint of digital topology. Indeed, the AFPP is broader than the FPP and further, it can strongly contribute to digital topology because a digital space is considered to be a lattice space of ${\mathbb Z}^n$. Hence the study of the AFPP for digital spaces $(X, k)$ on ${\mathbb Z}^n$ plays an important role in digital topology taking a graph-theoretical approach. Indeed, this approach invokes a certain open problem mentioned in the previous part. That is why in this paper we give particular attention to the AFPP for digital spaces and its product property. Hence the present paper may pose the following questions related to the product property of the AFPP for digital spaces:

$\bullet$ Is the AFPP for digital spaces, or is it not necessarily invariant under Cartesian products?

$\bullet$ For two digital spaces $(X_i, k_i), i \in \{1, 2\}$, satisfying the AFPP, under what condition do we have the AFPP for the digital product $(X_1 \times X_2, k)$?

To address these issues, first of all we will use a normal $k$-adjacency for a digital product in ^[8] (see Definition 4.1 in the present paper). Besides, for digital spaces $(X_i, k_i), i \in \{1, 2\}$, let $(X_1 \times X_2, k)$ be a digital product with a normal $k$-adjacency with a certain condition. Then we use some properties of a $k$-continuous self-map of $(X_1\times X_2, k)$.

This paper is organized as follows. Section 2 provides some basic notions from digital topology. Section 3 investigates the AFPP for a digital $n$D cube with $(3^n-1)$-adjacency. Section 4 studies various properties of almost fixed points of $k$-continuous self-maps of a digital product with a normal $k$-adjacency. Furthermore, we prove that for two digital spaces $(X_i, k_i), i \in \{1, 2\}$, satisfying the AFPP, a digital $(X_1 \times X_2)$ with a normal $k$-adjacency such that $N_k^\star(p, 1) = N_k(p, 1)$ for each point $p \in X_1\times X_2$ has the AFPP. Besides, the converse is also proved affirmatively. Section 5 concludes the paper with some remarks and a further work.

In this paper we assume that each digital space $(X, k)$ is $k$-connected and the cardinality of $X$, denoted by $\vert\, X\, \vert$, is greater than or equal to $2$.

2.   Preliminaries

This section recalls basic notions of the graph-theoretical approach of digital topology, i.e., Rosenfeld model ^[27,28]. In relation to the study of digital spaces in ${\mathbb Z}^n$, in the case we follow the Rosenfeld model, a digital picture is usually represented as a quadruple $({\mathbb Z}^n, k, \bar{k}, X)$, where $n \in {\mathbb N}$, a black points set $X \subset {\mathbb Z}^n$ is the set of points we regard as belonging to the image depicted, $k$ represents as an adjacency relation for $X$ and $\bar {k}$ represents an adjacency relation for white points set ${\mathbb Z}^n \setminus X$. We say that the pair $(X, k)$ is a digital image in a quadruple $({\mathbb Z}^n, k, \bar{k}, X)$. Thus, motivated by the $4$- and $8$-adjacencies of $2$D digital images and, $6$-, $18$-, and $26$-adjacencies of $3$D digital images ^[22,27], the $k$-adjacency relations of ${\mathbb Z}^n$ were established to study a high-dimensional digital image. Indeed, these are induced by the following operator ^[8]: For a natural number $m$ with $1 \leq m \leq n$, the distinct points

are $k(m, n)$-adjacent if at most $m$ of their coordinates differ by $\pm1$ and the others coincide. According to this statement, the $k(m, n)$-adjacency relations of ${\mathbb Z}^n, n \in {\mathbb N}$, were formulated ^[8,13]), as follows:

For instance, $(m, n, k) \in \{(1, 4, 8), (2, 4, 32), (3, 4, 64), (4, 4, 80);$ $(1, 5, 10),$ $(2, 5, 50)$, $(3, 5,130)$, $(4, 5,210)$, $(5, 5,242)\}$ ^[8].

Owing to the digital $k$-connectivity paradox of a digital space $(X, k)$ ^[22], we remind the reader that $k \neq \bar k$ except the case $({\mathbb Z}, 2, 2, X)$. For $\{a, b\} \subset \mathbb Z$ with $a \lneq b$, $[a, b]_{\mathbb Z} = \{m \in {\mathbb Z} \, \vert \, a\leq m \leq b\}$ is considered in $({\mathbb Z}, 2, 2, [a, b]_{\mathbb Z})$. However, the present paper is not concerned with the $\bar k$-adjacency of ${\mathbb Z}^{n}\setminus X$.

At this moment we need to further recall the notion of a digital space defined by Herman ^[16], as follows:

Definition 2.1. ^[16] A digital space is a pair $(X, \pi)$ where $X$ is a nonempty set and $\pi$ is a binary symmetric relation on $X$ such that $X$ is $\pi$-connected.

In Definition 2, 1, we say that $X$ is $\pi$-connected if for any two elements $x$ and $y$ of $X$ there is a finite sequence $(x_i)_{i\in [0, l]_{\mathbb Z}}$ of elements in $X$ such that $x = x_0$, $y = x_l$ and $(x_j, x_{j+1}) \in \pi$ for $j \in [0, l-1]_{\mathbb Z}$. In Definition 2.1 we can consider the relation $\pi$ according to the situation such as the digital $k$-adjacency relation of (2.1), which is a symmetric relation because the $k$-adjacency relation of the digital space $(X, k)$ guarantees $(X, k)$ to be a digital space.

We say that a digital space $(X, k)$ is $k$-connected if it is not a union of two disjoint non-empty sets that are not $k$-adjacent to each other ^[22]. We say that two subsets $(A, k)$ and $(B, k)$ of $(X, k)$ are $k$-adjacent to each other if $A \cap B = \emptyset$ and there are points $a\in A$ and $b \in B$ such that $a$ and $b$ are $k$-adjacent to each other ^[22]. For a digital space $(X, k)$ and a point $x\in X$, we say that the maximal $k$-connected subset of $(X, k)$ containing the point $x\in X$ is the $k$-(connected) component of a point $x\in X$ ^[22]. Thus a singleton set with $k$-adjacency is $k$-connected. For a digital space $(X, k)$, two points $x, y \in X$ are $k$-connected if there is a $k$-path from $x$ to $y$ in $X \subset {\mathbb Z}^n$. Given a $k$-adjacency relation of (2.1), a simple $k$-path from $x$ to $y$ in ${\mathbb Z}^n$ is assumed to be the sequence $(x_i)_{i \in [0, l]_{\mathbb Z}}\subset {\mathbb Z}^n$ such that $x_i$ and $x_j$ are $k$-adjacent if and only if either $j = i+1$ or $i = j+1$ ^[22] and further, $x_0 = x$ and $x_l = y$. The length of this simple $k$-path, denoted by $l_k(x, y)$, is the number $l$. A simple closed $k$-curve with $l$ elements in ${\mathbb Z}^n$, denoted by $SC_k^{n, l}$ ^[8,22], is a sequence $(x_i)_{i \in [0, l-1]_{\mathbb Z}}$ in ${\mathbb Z}^n$, where $x_i$ and $x_j$ are $k$-adjacent if and only if $\vert i-j\vert = \pm1(mod\, l)$ ^[22].

In relation to the study of both digital continuity and various properties of a digital space, we have often used the following digital $k$-neighborhood. Using the above adjacency relations of (2.1), we say that a digital $k$-neighborhood of $p$ in ${\mathbb Z}^n$ is the set ^[27]

For a digital space $(X, k)$ let us recall a digital $k$-neighborhood which is a generalization of $N_k(p)$ ^[8]. Namely, the digital $k$-neighborhood of $x_0 \in X$ with radius $\varepsilon$ is defined in $X$ to be the following subset of $X$

where $l_k(x_0, x)$ is the length of a shortest simple $k$-path from $x_0$ to $x$ and $\varepsilon\in \mathbb N$.

Indeed, for $X \subset {\mathbb Z}^n$ we obtain ^[8,12]

This notation (2.3) can be used to represent the AFPP for digital spaces (see Definition 3.1). Let us investigate some properties of maps between digital spaces. To map every $k_0$-connected subset of $(X, k_0)$ into a $k_1$-connected subset of $(Y, k_1)$, the paper ^[28] established the notion of digital continuity. Motivated by this continuity, we can represent the digital continuity of maps between digital spaces, which can be more convenient than the earlier version of ^[28].

Proposition 2.2. ^[8,12] Let $(X, k_0)$ and $(Y, k_1)$ be digital spaces on ${\mathbb Z}^{n_0}$ and ${\mathbb Z}^{n_1}$, respectively. A function $f: X \to Y$ is $(k_0, k_1)$-continuous if and only if for every $x\in X$, $f(N_{k_0}(x, 1))\subset N_{k_1}(f(x), 1)$.

In Proposition 2.2 in the case $n_0 = n_1$ and $k_0 = k_1$, we call it $k_0$-continuous to abbreviate "$$$ (k_0, k_1) $-continuous". Besides, the digital continuity of Proposition 2.2 has the transitive property.

Based on these concepts, let us consider a digital topological category, denoted by DTC, consisting of the following two data ^[8] (see also ^[12]):

$\bullet$ the set of $(X, k)$ on ${\mathbb Z}^n, n \in {\mathbb N}$ as objects, denoted by $Ob(DTC)$;

$\bullet$ for every ordered pair of objects $(X, k_0)$ and $(Y, k_1)$, the set of $(k_0, k_1)$-continuous maps as morphisms. In DTC, in the case $n_0 = n_1$ and $k_0 = k_1: = k$, we will particularly use the notation DTC(k) ^[12] and use $Ob(DTC(k))$ to indicate the set of its objects.

Since a digital space $(X, k)$ is considered to be a set $X \subset {\mathbb Z}^{n}$ with one of the adjacency relations of (2.1), we use the terminology a "$$$ (k_0, k_1) $-isomorphism" as used in ^[9] rather than a "$$$ (k_0, k_1) $-homeomorphism" as proposed in ^[2].

Definition 2.3. ^[2,9] For two digital spaces $(X, k_0)$ on ${\mathbb Z}^{n_0}$ and $(Y, k_1)$ in ${\mathbb Z}^{n_1}$, a map $h : X \to Y$ is called a $(k_0, k_1)$-isomorphism if $h$ is a $(k_0, k_1)$-continuous bijection and further, $h^{-1}: Y \to X$ is $(k_1, k_0)$-continuous.

In Definition 2.3, in the case $n_0 = n_1$ and $k_0 = k_1$, we can call it a $k_0$-isomorphism.

3.   The AFPP for an $n$D digital cube with $(3^n-1)$-adjacency

Since every singleton obviously has the FPP, in studying the FPP from the viewpoint of digital topology, hereafter all digital spaces $(X, k)$ are assumed to be $k$-connected and their cardinalities $\vert X \vert \geq 2$. Indeed, the fixed point property plays an important role in applied topology. It is obvious that a digital space $(X, k)$ on ${\mathbb Z}^n$ does not have the FPP in $DTC(k)$ ^[12,28]. Thus we need to consider the AFPP for digital spaces in $DTC(k)$ ^[28] because the AFPP is weaker than the FPP. We can represent the AFPP for digital spaces in ^[28] by using a digital $k$-neighborhood of (2.3) as follows:

Definition 3.1. For a digital space $(X, k)$ on ${\mathbb Z}^n$ and every $k$-continuous map $f : X \to X$, if there exists a point $x \in X$ satisfying $f(x) \in N_k(x, 1)$, then we say that $X$ has the AFPP.

In Definition 3.1, the phrase "$f(x) \in N_k(x, 1)$" can be equivalent to the property '$x \in N_k(f(x), 1)$'. Since the property "$f(x) \in N_k(x, 1)"$ of Definition 3.1 is equivalent to the property "$f(x) = x$ or $f(x)$ is $k$-adjacent to $x$", it is clear that in $DTC(k)$ the AFPP is broader than the FPP.

Example 3.1. Consider a digital space $({\mathbb Z}, 2)$. Let $f : {\mathbb Z} \to {\mathbb Z}$ be a map defined by the following:

Then, whereas $f$ is a $2$-continuous map, there is no point $x \in {\mathbb Z}$ such that $f(x) \in N_2(x, 1)$. Namely, $({\mathbb Z}, 2)$ does not have the AFPP.

Rosenfeld ^[28] studied the AFPP (or a general fixed point property in ^[28]) for a digital picture $I \subset {\mathbb Z}^2$ from the viewpoint of metric fixed point theory (see Theorems 4.1 and 6.2 in ^[28]). Thus it turns out that a bounded Euclidean digital plane with an $8$-adjacency, denoted by $(I, 8)$, has the AFPP as follows:

Theorem 3.2. ^[28] Let $I$ be a digital picture in ${\mathbb Z}^2$, i.e., $I: = [a, b]_{\mathbb Z} \times [c, d]_{\mathbb Z}$, and let $f$ be a continuous function from $I$ to $I$. Then, there is a point $p \in I$ such that $f(p) = p$ or is a neighbor or diagonal neighbor of $p$.

Example 3.2. (1) (One dimensional case) Consider a digital interval $(X: = [0, 2m-1]_{\mathbb Z}, 2)$ on ${\mathbb Z}$, where $m \in {\mathbb N}$. Let $f: X \to X$ be a map defined by

While $f$ is a $2$-continuous map, there is no point $x \in X$ such that $f(x) = x$. Thus $X$ does not have the FPP. However, there exists a point $m$ such that $f(m) \in N_2 (m, 1)$.

(2) (Two dimensional case) Consider the set $X \subset {\mathbb Z}^2$, where $X = \{(x_1, x_2)\, \, \vert\, \, x_1 \in [0, 5]_{\mathbb Z}$ $\, \, {{and}}$ $\, \, x_2 \in [0, 3]_{\mathbb Z} \}$ in ${\mathbb Z}^2$. Let $f : X \to X$ be a map given by

Let us examine if the AFPP of $(X, k)$ holds, $k \in \{4, 8\}$.

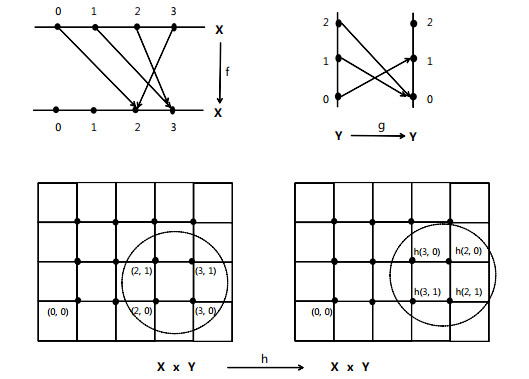
(1-1) Assume a $4$-adjacency for $X$, i.e., a digital space $(X, 4)$. While the map $f$ of (3.1) is a $4$-continuous map, there is no point $x \in X$ such that $f(x) \in N_4(x, 1)$ (see Figure 1(a)), which implies that $(X, 4)$ does not have the AFPP.

(1-2) Assume an $8$-adjacency for $X$, i.e., a digital space $(X, 8)$. Then, for every self-$8$-continuous map $g$ of $(X, 8)$, there is a point $x$ in $X$ such that $g(x) \in N_8(x, 1)$. For instance, the map f of (3.1) has the property $f(x) \in N_8(x, 1)$ at the four points $x \in X$, where $x \in \{(3, 1), (3, 2),$ $(4, 1), (4, 2)\}$.

Besides, suppose there is a self-map $h$ of $(X, 8)$ which does not have the point $x \in X$ satisfying $g(x) \in N_8(x, 1)$. Then, the given map $h$ cannot be an $8$-continuous map.

Let us now consider the AFPP for a three dimensional case.

Example 3.3. (Three dimensional case) Consider the set $Y = [0, 1]_{\mathbb Z} \times [0, 1]_{\mathbb Z}\times [0, 1]_{\mathbb Z} \subset {\mathbb Z}^3$. Let $g : Y \to Y$ be a map given by

Let us investigate certain possibility of the AFPP of $(Y, k), k \in \{6, 18, 26\}$.

(1-1) In the case we take a $6$-adjacency for $Y$, i.e., a digital space $(Y, 6)$, we see that the map $g$ of (3.2) is a $6$-continuous map. Then we observe that there is no point $y \in Y$ such that $g(y) \in N_6(y, 1)$, which implies that $(Y, 6)$ does not have the AFPP.

(1-2) In the case we assume an $18$-adjacency for $Y$, i.e., a digital space $(Y, 18)$, it is clear that the map $g$ of (3.2) is an $18$-continuous map. But there is no point $y\in Y$ such that $g(y) \in N_{18}(y, 1)$ (see Figure 1(b)), which implies that $(Y, 18)$ does not have the AFPP either.

(1-3) In the case we take a $26$-adjacency for $Y$, i.e., a digital space $(Y, 26)$, consider any $26$-continuous maps $g$ such as the map $g$ of (3.2). Then it is clear that each point $y\in Y$ satisfies the property $g(y) \in N_{26}(y, 1)$ (see Figure 1(b)).

Besides, suppose a self-map $h$ of $(Y, 26)$ which does not have a point $y \in Y$ such that $h(y) \in N_{26}(y, 1)$. Then the map $h$ cannot be a $26$-continuous map, which concludes that $(Y, 26)$ has the AFPP.

Using the method used in Theorem 3.2 and Example 3.3, we obtain the following as a generalization of the AFPP of the $2$-dimensional digital picture in ^[28] (see Theorem 4.1 of ^[28]).

Proposition 3.3. ^[14] Consider the set $X: = \prod_{ i = 1}^n [0, 1]_{\mathbb Z} \subset {\mathbb Z}^n$ and a digital space $(X, 3^n-1)$. Then $(X, 3^n-1)$ has the AFPP. Naively, only the $(3^n-1)$-adjacency instead of the $k(\neq 3^n-1)$-adjacency supports the AFPP for $X$.

4.   Characterizations of the product property of the AFPP for digital spaces

This section deals with the problem of whether the AFPP for digital spaces is, or is not necessarily invariant under Cartesian product. In details, as referred to in Examples 3.2 and 3.3, consider the set $\prod_{i = 1}^{n}[m_i, {m_i}+1]_{\mathbb Z} \subset {\mathbb Z}^{n}$ with a $k$-adjacency of (2.1), where $m_i\in {\mathbb Z}$. Then it turns out that $(\prod_{i = 1}^{n}[m_i, {m_i}+1]_{\mathbb Z}, k)$ has the AFPP if $k = 3^n-1$ (see Proposition 3.3). Since the digital space $([m_i, {m_i}+1]_{\mathbb Z}, 2)$ has the AFPP, as a more general case of $[m_i, {m_i}+1]_{\mathbb Z}$, consider certain digital spaces $(X_i, k_i)$ in ${\mathbb Z}^{n_i}, i \in \{1, 2\}$, such that each of $(X_i, k_i), i \in \{1, 2\}$, has the AFPP. Then, we have the following query. Under what adjacency of the Cartesian product $X_1 \times X_2$ does the digital product have the AFPP? Moreover, as a more general case of Proposition 3.3, for digital spaces $(X, k_i), i \in \{1, ..., n\}$, we need to study the AFPP for the so-called digital product such as $\prod^n_{i = 1}X_i$ with some $k$-adjacency. As a digital topological version of the strong adjacency in ^[1] from the viewpoint of typical graph theory, the following notion was initially established ^[8].

Definition 4.1. (^[8]) For two digital spaces $(X, k_0)$ on ${\mathbb Z}^{n_0}$ and $(Y, k_1)$ on ${\mathbb Z}^{n_1}$, we say that $(x, y) \in {X \times Y} \subset {\mathbb Z}^{{n_0 +n_1}}$ is normally $k$-adjacent to $(x^{\prime}, y^{\prime}) \in {X \times Y}$ if and only if

(1) $y$ is equal to $y^{\prime}$ and $x$ is $k_0$-adjacent to $x^{\prime}$, or

(2) $x$ is equal to $x^{\prime}$ and $y$ is $k_1$-adjacent to $y^{\prime}$, or

(3) $x$ is $k_0$-adjacent to $x^{\prime}$ and $y$ is $k_1$-adjacent to $y^{\prime}$.

Remark 4.2. (1) Hereinafter, for our purposes, in relation to Definition 4.1, we will use the following notation. For a point $p \in X \times Y$,

and further,

Then we call $N_k^\star(p, 1)$ a normally $k$-neighborhood of $p$.

Indeed, it is clear that $N_k^\star(p)$ need not be equal to $N_k^\ast(p)$, where $N_k^\ast(p): = \{q \in X \times Y\, \vert \, q \, \, {{is}}\, \, k \;{{-adjacent\; to}}\, \, p\}$ in ^[22].

(2) Consider digital spaces $(X, k_1)$ on ${\mathbb Z}^{n_1}$ and $(Y, k_2)$ on ${\mathbb Z}^{n_2}$ satisfying the AFPP. Not every $k$-adjacency for the digital product $X \times Y \subset {\mathbb Z}^{n_1+n_2}$ supports the AFPP for $(X \times Y, k)$ in $DTC(k)$.

To guarantee Remark 4.2(2), we examine the following:

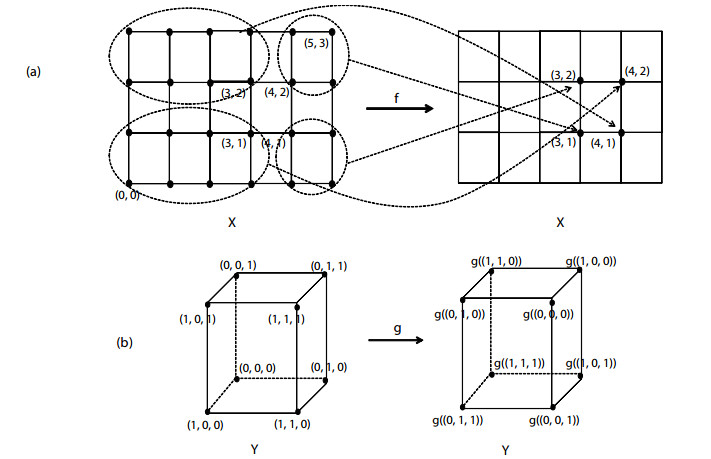
Example 4.1. Consider the following sets $X = \{(0, 1), (0, 0), (1, 0)\}$ and $Y = \{(0, 0), (1, 0), (1, 1),$ $(2, 1)\}$ in ${\mathbb Z}^2$ (see Figure 2(a)). Since the digital space $(X, 4)$ is $(4, 2)$-isomorphic to a digital line $[0, 2]_{\mathbb Z}$ and $(Y, 4)$ is also $(4, 2)$-isomorphic to a digital interval $[0, 3]_{\mathbb Z}$, motivated by Example 3.2, each of $(X, 4)$ and $(Y, 4)$ has the AFPP for $4$-continuous self-maps of the given spaces.

(Case 1) Assume an $8$-adjacency for the Cartesian product $X \times Y = \{(x, y)\, \vert\, \, x \in X \, \, {\rm{and}} \, \, y\in Y\} \subset {\mathbb Z}^4$ (see Figure 2(b)). Let $f : X \to X$ be a map defined by

and $g : Y \to Y$ be a map given by

Then it is clear that both $f$ and $g$ are $4$-continuous maps. Furthermore, the points $(0, 0), (0, 1)$ are almost fixed points in $X$ by the map $f$ and the points $(1, 0), (1, 1)$ are also almost fixed points in $Y$ by the map $g$.

Meanwhile, let us now consider the map $h : = f \times g : {X \times Y} \to {X \times Y}$ given by $h(x, y): = (f(x), g(y))$ which is an $8$-continuous map. Then, since

we conclude that $(X \times Y, 8)$ does not have the AFPP (see Figure 2(b)).

(Case 2) In the case of the map $h$ above, there is a certain point $p\in X\times Y$ such that $h(p) \in N_k(p, 1), k \in \{32, 64, 80\}$ (for instance, see the points $h(1, 0, 1, 0)$ and $h(1, 0, 1, 1)$ in the above data). Thus we need to further examine if all $k$-continuous self-maps of $X\times Y$ has the property related to the AFPP (see Theorem 4.4).

Remark 4.3. Let $(X, k_0)$ be a digital space on ${\mathbb Z}^{n_0}$ and $(Y, k_1)$ be a digital space on ${\mathbb Z}^{n_1}$. If either $(X, k_0)$ or $(Y, k_1)$ does not have the AFPP, then the AFPP for $(X \times Y, k)$ depends on the situation of the $k$-adjacency of ${\mathbb Z}^{n_0+n_1}$.

To guarantee Remark 4.3, let us consider the following:

Example 4.2. Consider the sets $X = \{(0, 0), (0, 1), (1, 0),$ $(1, 1) \}$ in ${\mathbb Z}^2$ with $4$-adjacency (see Figure 3) and $Y = \{0, 1\}$ in ${\mathbb Z}$ with $2$-adjacency. Let $f : X \to X$ be a map defined by

While the map $f$ is $4$-continuous map, for each point $x \in X$, it is clear that $f(x) \notin N_4(x, 1)$, which implies that $(X, 4)$ does not have the AFPP. By using the method used in Example 3.1, it is clear that $(Y, 2)$ has the AFPP. Using a method similar to the assertion of Example 3.3, we see that while $(X \times Y, k)$ does not have the AFPP, $k \in \{6, 18\}$ (see Figure 3), $(X \times Y, 26)$ has the AFPP. In particular, assume $X \times Y$ with the normal $18$-adjacency, i.e., consider the points in $X \times Y$ with the normal $18$-adjacency instead of the typical $18$-adjacency. Then it is clear that $X \times Y$ with the normal $18$-adjacency, denoted by $(X \times Y, 18)$, does not have the AFPP either. To guarantee this assertion, consider a two-clicks rotation of $(X \times Y, 18)$ in Figure 3 such as $(0, 0, 1)\to (1, 1, 1, ), (0, 0, 0) \to (1, 1, 0)$, and so on.

Motivated by Remark 4.3 and Example 4.2, we may pose the following query: Under what condition do we have the product property of the AFPP?

For convenience, let us use the notation. Given a digital space $(X, k)$,

Let us now address this issue, as follows:

Theorem 4.4. Assume two $k_i$-connected digital spaces $(X, k_1)$ and $(Y, k_2)$ and a digital product $X \times Y$ with a normal $k$-adjacency such that $N_k^\star(p, 1) = N_k(p, 1)$ for each point $p \in X\times Y$. Each of $(X, k_1)$ and $(Y, k_2)$ has the AFPP if and only if $(X \times Y, k)$ has the AFPP.

Proof: According to the hypothesis, since both $(X, k_1)$ and $(Y, k_2)$ have the AFPP, we obtain that for any $k_1$-continuous self-map $f$ of $(X, k_1)$

and for any $k_2$-continuous self-map $g$ of $(Y, k_2)$

Besides, for a digital product with a normal $k$-adjacency $(X \times Y, k)$, it turns out that for any point $(x, y)$ in $(X \times Y, k)$ we have the following property which is equivalent to the $k$-normal adjacency of Definition 4.1.

With the hypothesis of the normal $k$-adjacency of the digital product $X \times Y$ and the property (4.1) and (4.2), for the sake of contradiction, let us now suppose that $(X \times Y, k)$ does not have the AFPP. Namely, there is a certain $k$-continuous self-map $h$ of $(X \times Y, k)$ such that every point $(x, y) \in X \times Y$ has the property (see the hypothesis)

Then, we obtain

Since $X$ and $X \times \{y\}$ are indeed assumed to be $k_1$-isomorphic and $Y$ and $\{x\} \times Y$ are assumed to be $k_2$-isomorphic, there exist $f \in Con_{k_1}(X)$ and $g \in Con_{k_2}(Y)$ satisfying $h \vert_{X \times \{y\}}(x, y) = (f(x), y)$ and $h \vert_{\{x\} \times Y} = (x, g(y))$. Thus, $f(x) \notin N_{k_1}(x, 1)$ or $g(x) \notin N_{k_2}(y, 1)$ which contradicts to the properties of (4.1) or (4.2).

Let us now prove that the AFPP of $(X \times Y, k)$ implies the AFPP of each of $(X, k_1)$ and $(Y, k_2)$. Using reductio ad absurdum, without loss of generality, with the hypothesis we may assume that $(X, k_1)$ does not have the AFPP. Naively, for a certain map $f \in Con_{k_1}(X)$, every point $x \in X$ has the property $f(x) \notin N_{k_1}(x, 1)$. Let us now consider any map $F \in Con_{k}(X\times Y)$. Then, for any point $(x, y)\in X\times Y$ we have the map $F\vert_{X \times \{y\}} \in Con_{k_1}(X)$, where $F\vert_{X \times \{y\}}$ means the restriction of $F$ to $X \times \{y\}$. Indeed, owing to Proposition 2.2 and the above property (4.3), any map $f \in Con_{k_1}(X)$ can be represented by a certain $F\vert_{X \times\{y\}}$, where $F \in Con_{k}(X\times Y)$. Since $F\vert_{X \times \{y\}} \in Con_{k_1}(X)$, owing to the non-AFPP of $(X, k_1)$, every point $x \in X$ has the property $(f(x), y): = F\vert_{X \times \{y\}}(x, y) \notin N_{k_1}(x, 1) \times \{y\}$ for a certain $f \in Con_{k_1}(X)$. Hence every point $(x, y) \in X\times Y$ has the property

for a certain $F \in Con_{k}(X\times Y)$, which implies the non-AFPP of $(X\times Y, k)$. Thus the proof is completed.

Remark 4.5. (The importance of the hypothesis of $N_k^\star(p, 1) = N_k(p, 1)$) As we can see the property in (4.5), without this hypothesis, we cannot support the property of (4.5).

As a generalization of the property (4.3), for given digital spaces $(X_i, k_i)$ on ${\mathbb Z}^{n_i}, i \in \{1, 2, ..., m\}$, we define a normal $k$-adjacency for the digital product $\prod^m_{i = 1}X_i \subset {\mathbb Z}^{n_1+...+n_m}$ as follows:

Definition 4.6. For digital spaces $(X_i, k_i)$ on ${\mathbb Z}^{n_i}, i \in \{1, 2, ..., m\}$, consider $X: = \prod^m_{i = 1}X_i: = (\prod^{m-1}_{i = 1}X_i) \times X_m \subset {\mathbb Z}^{{n_1}+ \, \, \cdots\, \, + {n_m}}$. Then, for two disctinct points $x: = (x_1, x_2, ..., x_m), y: = (y_1, y_2, ..., y_m) \in X$, we say that $y$ is normally $k$-adjacent to $x$ if and only if $y \in N_k^\star(x)$, where

In Definition 4.6, we call $N_k^\star(x, 1)$ a normally $k$-neighborhood of $x$. In view of Definition 4.6, we see that a point $x^\prime: = (x_1^\prime, x_2^\prime, ..., x_m^\prime) \in \prod^m_{i = 1}X_i \subset {\mathbb Z}^{n_1+...+n_m}$ is normally $k$-adjacent to $x: = (x_1, x_2, ..., x_m) \in \prod^m_{i = 1}X_i$ if and only if the points $x^\prime$ and $x$ satisfies the property of Definition 4.6.

Corollary 4.7. Let $(X_i, k_i)$ have the AFPP, where $X_i \subset {\mathbb Z}^{n_i}$ and $i \in \{1, 2, ..., m\}$. Assume a digital product $X: = \prod^m_{i = 1}X_i \subset {\mathbb Z}^{{n_1}+\, \cdots \, + {n_m}}$ with a normal $k$-adjacency such that $N_k^\star(x, 1) = N_k(x, 1), x \in X$. Then, each $(X_i, k_i), i \in \{1, 2\}$, have the AFPP if and only if $(\prod^m_{i = 1} X_i, k)$ has the AFPP.

Example 4.3. Consider the digital intervals $X = [0, 3]_{\mathbb Z}$ and $Y = [0, 2]_{\mathbb Z}$ on $({\mathbb Z}, 2)$. By Definition 4.1, the digital product $X \times Y = \{(x, y)\, \vert\, \, x \in X \, \, {{and}} \, \, y\in Y\}$ has the only normal $8$-adjacency on ${\mathbb Z}^2$. Let $f : X \to X$ be a map defined by $f(0) = 2, \, \, f(1) = f(2) = 3, \, \, f(3) = 2$ and $g : Y \to Y$ be a map defined by $g(0) = 1, \, \, g(1) = g(2) = 0$. Then $f, g$ are $2$-continuous maps and the map $h : = f \times g : {X \times Y} \to {X \times Y}$ defined by $h(x, y) = (f(x), g(y))$ is an $8$-continuous map. The points $(2, 0), (2, 1), (3, 0), (3, 1)$ in $X \times Y$ are almost fixed points for an $8$-continuous map $h$ (see Figure 4).

Lemma 4.8. Only the $(3^m -1)$-adjacency of the digital product $X: = \prod^m_{i = 1}X_i \subset {\mathbb Z}^m$ of the digital intervals $(X_i, 2)$ is normal such that $N_k^\star(x, 1) = N_k(x, 1)$, $i \in \{1, 2, ..., m\}, x \in X, k: = 3^m -1$.

Proof: Since the digital intervals $[m_i, m_i+p_i]_{\mathbb Z}$ and $[0, p_i]_{\mathbb Z}$ are $2$-isomorphic to each other, where $m_i \in {\mathbb Z}$ and $p_i \in {\mathbb N}$, without loss of generality, we may consider $[m_i, m_i+p_i]_{\mathbb Z}$ to be the digital interval $[0, p_i]_{\mathbb Z}$ for $i \in \{1, 2, ..., m\}$, where $m \in {\mathbb N}$.

First of all, it is clear that any $k$-adjacency of $X \subset {\mathbb Z}^m$, $k \neq 3^m-1$, cannot satisfy the property $N_k^\star(x, 1) = N_k(x, 1)$.

Let us now prove this assertion in terms of mathematical induction, as follows:

(Case 1) For the digital spaces $(X_1, 2)$ and $(X_2, 2)$, it is clear that $X_1 \times X_2$ has an normal $8$-adjacency such that $N_8^\star(x, 1) = N_8(x, 1)$.

(Case 2) Assume that $\prod_{i = 1}^m X_i$ has a normal $(3^m-1)$-adjacency such $N_k^\star(x, 1) = N_k(x, 1), k = 3^m-1$. Then we need to prove that $\prod_{i = 1}^{m+1} X_i$ has a normal $(3^{m+1}-1)$-adjacency such that $N_k^\star(x, 1) = N_k(x, 1), k = 3^{m+1}-1$. According to Definition 4.6, we obtain that the product $(\prod_{i = 1}^{m} X_i, 3^m-1) \times (X_{m+1}, 2)$ has the normal $(3^{m+1}-1)$-adjacency such that $N_k^\star(x, 1) = N_k(x, 1), k = 3^{m+1}-1$, which completes the proof. $\Box$

Indeed, in the proof of Lemma 4.8, we may prove the existence of the normal $(3^m -1)$-adjacency of $\prod_{i = 1}^m [0, 1]_{\mathbb Z}$ such that $N_k^\star(x, 1) = N_k(x, 1)$.

Hereafter, let us study the AFPP for digital $n$D cubes, denoted by $\prod^n_{i = 1}[m_i, {m_i}+{p_i}]_{\mathbb Z} \subset {\mathbb Z}^n, m_i \in {\mathbb Z}, p_i \geq 2$, as a Cartesian product of finite digital intervals $[m_i, {m_i}+{p_i}]_{\mathbb Z}$. Motivated by Example 3.3 and Proposition 3.3, we obtain the following (see also Theorem 1 of ^[14]):

Theorem 4.9. Consider the set $X: = \prod^n_{i = 1}[m_i, m_i+p_i]_{\mathbb Z} \subset {\mathbb Z}^n$ with $k$-adjacency, where $m_i \in {\mathbb Z}$ and $p_i \in {\mathbb N}-\{1\}$. Then, only $(X, 3^{n}-1)$ has the AFPP.

Proof: Using Theorem 4.4 and Lemma 4.8, the proof is completed because only $k = 3^{n}-1$ has the property $N_k^\star(p, 1) = N_k(p, 1)$ for each point $p \in X$. $\Box$

5.   Summary and further works

We have studied the product property of the AFPP of digital spaces in the graph-theoretical approach (Rosenfeld model). Namely, it turns out that a normal $k$-adjacency of a digital product with the property $N_k^\star(p, 1) = N_k(p, 1)$ for each point $p$ of a digital product plays an important role in studying the product property of the AFPP of digital spaces. Based on this approach, as a further work we can find some digitization functors transforms AFPP of spaces in a certain category into that of spaces in another category.

Acknowledgments

We would like to thank the referees for valuable suggestions that helped improve the original manuscript in its present form. The corresponding author (S.-E. Han) was supported by the Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education, Science and Technology (2019R1I1A3A03059103).

Conflict of interest

The authors declare no conflict of interest.