A class of impulsive vibration equation with fractional derivatives

1.   Introduction

In 1969, the Lassa fever disease was first identified in a town called Lassa in the Yedseram River Valley, part of the Borno State in Northern Nigeria ^[1]. The first affected person was Laura Wine ^[2], a 65-year-old female nurse who worked at the Lassa Mission Hospital, now known as the "Bingham University Teaching Hospital" in Borno State, Nigeria. Since then, the disease has spread significantly across Africa, becoming a significant health concern in the region ^[3].

Lassa Fever is endemic to numerous countries in West Africa, where Mastomys natalensis rodents are frequently present. These countries, which include Sierra Leone, Liberia, Guinea and Nigeria are collectively known as the "Lassa belt" owing to the high prevalence of Lassa fever in these areas ^[4].

Lassa fever is a viral hemorrhagic fever caused by the Lassa virus, a single-stranded RNA virus transmitted by a mouse species called Mastomys natalensis ^[5]. This zoonotic disease results from contact with infected Mastomys natalensis ^[6]. These rodents are known for their high reproduction rates during the rainy season. They are commonly found in human households and food storehouses, facilitating the transmission of viruses like the Lassa virus ^[7].

Lassa virus mainly spreads to humans through contact with Mastomys rodents' urine, droppings or contaminated items. Eating tainted food or having open cuts can also lead to infection. Inhaling tiny airborne particles with rodent excretions during cleaning is another way it spreads. Person-to-person transmission occurs when someone is exposed to an infected person's blood, tissue, secretions or excretions. This mainly happens in healthcare settings without proper protective gear or through contaminated medical equipment like needles. Casual contact doesn't spread the virus ^[6].

Lassa fever is diagnosed by isolating the virus from blood, throat swabs or urine in a BSL-4 laboratory or by detecting virus-specific antibodies. Viremia can persist for up to two weeks, and the virus can also be found in urine and semen for 2 to 3 months ^[8]. Consequently, sexual transmission can be a route of Lassa virus transmission ^[9].

The incubation period for Lassa fever, from the time of contact with the Lassa virus to the manifestation of symptoms, typically ranges from 1 to 3 weeks. The initial signs of the infection are mild and may include a low-grade fever, weakness and headaches. However, as the illness progresses, more severe symptoms may emerge such as hemorrhaging in the gums, nose, eyes, along with persistent and severe vomiting, swelling of the face, chest, back and abdominal pain ^[6].

As of now, there is no available vaccine for Lassa fever ^[10]. Therefore, infection control measures are critical in limiting disease transmission among people. Since eradicating the rodent population is impractical, preventing the spread of the disease involves promoting good hygiene practices at home to avoid contact with waste products from infected rats and establishing well-equipped medical facilities for efficient patient screening, diagnosis, and treatment. Ribavirin, an antiviral medication, treats Lassa fever when used at the first sign of the illness ^[11].

Mathematical models have been crucial in studying specific communities' disease patterns over the past decade. Mathematical modeling has experienced significant growth, employing various techniques to analyze real-world problems related to bacterial and viral diseases, among other topics. Numerous disease-specific models have been developed, such as those referenced in ^{[12,13,14,15,16,17,18,19]}, contributing valuable insights into the epidemiology of the conditions under investigation.

Ibrahim et al. ^[20] and Bakare et al. ^[21] presented a periodic model to understand Lassa fever transmission dynamics. Their findings suggest the need for interventions to eliminate the Lassa virus from the community. However, their models did not incorporate optimal control analysis of intervention measures ^[20]. Bakare et al. ^[21] further emphasized the potential effectiveness of a combination of intervention measures, such as treating Lassa fever with Ribavirin, educating the community on practicing environmental hygiene, isolating infected Lassa fever patients and possibly culling rodents if found. Implementing these measures could lead to a marginal reduction in the prevalence of Lassa virus.

Ibrahim et al. ^[20], Peter et al. ^[22] and Onah et al. ^[23] previously introduced optimal control models for Lassa fever. However, their works did not include a gender-wise division of the human population. Onuorah et al. ^[24] developed a model employing gender-wise split populations to investigate Lassa fever transmission through sexual activity in opposite genders. They also proposed controls to reduce Lassa virus transmission but did not include graphical illustrations of the efficacy of these controls, which sets the uniqueness of this article.

This study presents a novel seven-compartmental model, building upon the work of Onah et al. ^[23] and Onuorah et al. ^[24]. This modified model employs a system of ordinary differential equations to investigate the transmission of the Lassa virus within human and rodent populations while incorporating gender-based distinctions within the human population focused on the transmission of the virus between opposite genders via sexual activities.} The model has undergone rigorous scrutiny, ensuring the properties of a positively invariant region, disease-free equilibrium, basic reproduction number, stability and sensitivity of parameters. Furthermore, this study devises and examines control strategies, such as using Ribavirin, implementing mobile health technology and considering natural predators like barn owls, cats and dogs to reduce the virus's transmission rate.

2.   Formulation of the model

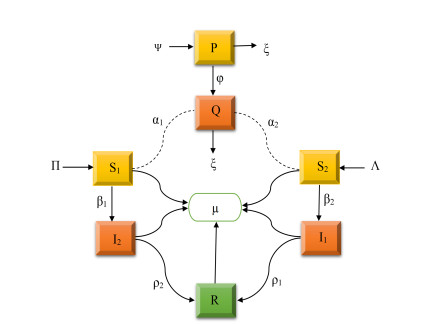
The formulation of this model involves considerations from a deterministic model and an assumption of constant human and rodent population sizes, denoted as $H(t)$ and $M(t)$, respectively. To explore Lassa virus transmission between opposite genders due to sexual activities, the human population is divided into distinct categories: susceptible females denoted as $S_1(t)$, infected females as $I_1(t)$, susceptible males as $S_2(t)$, infected males as $I_2(t)$, and individuals that have recovered as $R(t)$. The entire human population can be expressed as follows:

The rodent population is divided into susceptible rodents, represented by $P(t)$, and infected rodents, represented by $Q(t)$, where the entire rodent population can be expressed as:

It is assumed that individuals enter the susceptible classes $S_{1}(t)$ and $S_{2}(t)$ through birth with rates $\Pi$ and $\Lambda$, respectively. The potential mode of transmission encompasses the interaction between rodents and humans, whereas the virus can also be transmitted through human-to-human contact, specifically via sexual activities ^[9]. The infection rates for females and males through rodents are denoted as $\alpha_{1}$ and $\alpha_{2}$, respectively. In contrast, the infection rates for female and male human-to-human transmission are denoted as $\beta_{1}$ and $\beta_{2}$, respectively. Infected females $I_{1}(t)$ and males $I_{2}(t)$ recover at rates $\rho_{1}$ and $\rho_{2}$, respectively.

The model incorporates the assumption that rodents enter the susceptible class through birth at a rate $\Psi$. Susceptible rodents can contract the Lassa virus by contacting another infected rodent $Q(t)$ at a rate $\phi$. The natural death rates in human and rodent populations are represented by $\mu$ and $\xi$, respectively. Based on the assumptions and descriptions above, the system of differential equations given in (2.1) has been formulated to represent the biological problem. Additionally, Figure 1 illustrates the flow diagram of the model (2.1).

2.1.   Invariant region

The invariant region for the system (2.1) is defined as $\Omega = \Omega _{h}\times \Omega_{r}\in \mathbb{R}_{+}^{5}\times \mathbb{R}_{+}^{2}$, where

and

The local invariant set theorem ^[25,26] confirms that the region $\Omega$ is positively invariant. It implies that the mathematical and epidemiological definition of the model (2.1) holds within the region $\Omega$.

2.2.   The basic reproduction number $(R_{0})$

By taking the infected classes and their derivatives to zero in the model (2.1), the disease-free equilibrium (DFE) can be determined, which is expressed as follows:

At this equilibrium point, all populations remain susceptible and no infected individuals or rodents exist.

To calculate the basic reproduction number ($R_{0}$) of the Lassa fever-free model (2.1), the next generation matrix method, as used in ^[27], is employed and yields

where

Here, $R_{h}$ and $R_{r}$ represent the basic reproduction numbers for humans and rodents, respectively, which are significant epidemiological indicators.

2.3.   Stability analysis of the disease-free equilibrium

The local stability of DFE determines the short-term behavior of Lassa fever ^[27,28]. To analyze this, the Jacobian matrix $J^{0}$ of the model (2.1) at the DFE is calculated as

The eigenvalues of the Jacobian matrix $J^{0}$ are

It is evident that $\lambda _{1}$ and $\lambda _{2}$ are both negative, and if $R_{r} < 1$, $\lambda_{3} < 0$ as well. Additionally, $\lambda_{4}$ and $\lambda_{5}$ are negative if $R_{h} < 1$. Negative eigenvalues indicate that the disease dynamics will eventually decay over time, leading to a stable disease-free equilibrium. Consequently, the following theorem holds:

Theorem 2.1. DFE of model (2.1) exhibits local asymptotic stability when $R_{0} < 1$, and it becomes unstable when $R_{0} > 1$.

Theorem 2.1 has significant epidemiological implications for eradicating Lassa fever. If the basic reproduction number, $R_0 < 1$, and the initial infected population falls within the region of attraction of DFE, Eq (2.4), it becomes feasible to eliminate the disease from the entire population. However, if $R_0 > 1$, the infection will persist.

To ensure the eradication of the disease, regardless of the initial size of the infected population, it is crucial to examine the global stability at the DFE. The global stability result presented by Castillo-Chavez et al. ^[29] is used in this regard.

Theorem 2.2. When $R_{0} < 1$, the DFE of the model (2.1) exhibits global asymptotic stability.

Proof. To analyze the global asymptotic stability of the DFE, it is sufficient to confirm that the conditions ($H_{1}$) and ($H_{2}$), outlined in the global stability theorem proposed by Castillo-Chavez et al. in ^[29], are satisfied when $R_{0} < 1$. In model (2.1), the state variables are denoted as $X_{1} = (S_{1}, S_{2}, P)$, $X_{2} = (I_{1}, I_{2}, Q)$ and the DFE is represented as $X_{1}^{\ast } = \left(\frac{\Pi }{\mu}, \frac{\Lambda }{\mu}, \frac{\Psi }{\xi }\right).$ By solving the linear system

We have

The above equations converge to $\frac{\Pi }{\mu }$, $\frac{\Lambda }{\mu }$ and $\frac{\Psi }{\mu }$ respectively, as $t\rightarrow \infty$, irrespective of the initial values of $S_{1}(0)$, $S_{2}(0)$ and $P(0)$. Therefore, $X_{1}^{\ast} = \left(\frac{\Pi }{\mu }, \frac{\Lambda }{\mu }, \frac{\Psi }{\mu }\right)$ is globally asymptotically stable. Additionally, it can be stated that

We define $A$ and $AX$ as follows:

The matrix $A$ has non-negative off-diagonal entries, making it an $M$-matrix. Consequently, $\hat{G}$ can be obtained as $AX-G$:

It is evident that $G(X_{1}, X_{2})\geq 0$ since $0\leq S_{1}\leq H$, $0\leq S_{2}\leq H$, and $0\leq P\leq M$. The proof is now complete. □

3.   Estimating parameters and fitting data

Estimating the values of parameters accurately is crucial for making accurate predictions in epidemiological research. Compatibility of the developed model with real-world data is essential to ensure relevant model outcomes. It may be accomplished by fitting the proposed model to actual data, which informs about its accuracy and ability to predict achievable results. Lassa fever-reported cases from Nigeria are used to estimate parameters obtained from the NCDC database ^[30]. The data covers 65 weeks, starting from the first week of January 2020 and continuing onward.

It is vital to note that the number of confirmed Lassa fever cases continues to rise as the weeks pass, highlighting the necessity for effective control techniques to limit the disease's spread in the community. The values of the parameters are evaluated individually for females and males. According to current information, Nigeria's average human life expectancy for the year 2020 is $52.9$ years ^[31]. Additionally, it is reported that the total population of Nigeria in $2020$ consisted of $103.08$ million females and $105.24$ million males, resulting in an entire human population of $208.3$ million.

Supposing the entire rodent population is $500000$, the model (2.1) is calibrated to match the actual number of reported cases, estimating eight parameter values. {Figure 2 illustrates the count of confirmed cases, sourced from ^[30,32], categorized by gender based on the male and female population ratio.

Tables 1 and 2 display the parameter values obtained through the model calibration with the actual data of the female and male populations, respectively. Figure 3 illustrates the number of actual and estimated confirmed cases, categorized by gender.

By analyzing the weekly count of confirmed Lassa fever cases recorded in the NCDC database ^[30] from January 2020 to 65 weeks later, the reproduction number for human-to-human and rodent-to-human transmissions is evaluated based on gender. The estimated reproduction number for the female population ranges from $0.0232702$ to $3.02437$, while for the male population, it ranges from $0.0760725$ to $3.02437$. The reproduction number for rodents falls between $0.125$ to $3.125$.

4.   Sensitivity analysis

The purpose of conducting sensitivity analysis in this study is to assess the potential risk of Lassa virus disease spreading within a population. The primary objective is to investigate and understand the factors that play a crucial role in the transmission and persistence of this illness within the community. Since eradicating the Lassa virus from society is not feasible, this analysis focuses on identifying the key parameters contributing to high infection levels.

4.1.   Sensitivity indices of $R_0$

The sensitivity indices quantify the impact of parameter variations on changes in the stated variable of the problem. The methodology outlined in ^[33,34] is utilized to calculate sensitivity index $\Gamma _{p}^{R_{0}}$ for each parameter in the reproduction number $R_{0}$, which is following equation:

The values of the corresponding sensitivity indices are presented in Tables 3 and 4, and their graphical representations can be seen in Figure 4. It is crucial to remember that every positive index that increases due to the sensitivity analysis would immediately raise the disease's threshold quantity and vice versa.

The analysis of Tables 3 and 4 reveals a positive correlation between the expansion of Lassa fever and the increasing trends observed in the parameters $\beta_{1}$, $\beta_{2}$ and $\phi$. Moreover, it is evident that the spread of Lassa fever is inversely related to the negative values exhibited by the parameters $\rho_{1}$, $\rho_{2}$ and $\xi$. The sensitivity indices indicate that the parameter $\xi$, which represents the mortality rate of rodents, shows the most pronounced negative value.

The sensitivity analysis indicates that the parameter $\phi$, which represents the rodent-to-rodent transmission rate, has a positive sensitivity index of $+1$. This means that a $1%$ increment or decrement in its value will result in a $1%$ rise or drop in the reproduction number. Similarly, the parameter $\xi$, which represents the natural death rate of rodents, has a negative sensitivity index of $-2$. A $1%$ increase or decrease in the value will result in a $2%$ drop or rise in the reproduction number.

4.2.   Influence of threshold parameters on $R_{0}$

By simultaneously changing two parameters, reproduction dynamics can be seen using a 2-D contour plot, as shown in Figure 5.

In Figure 5(a), a correlation is depicted between the rates of infection in female and male humans, represented by $\beta_{1}$ and $\beta_{2}$ respectively, and their effect on the reproduction number. The results demonstrate that to sustain $R_{0} < 1$, it is crucial to decrease the female human infection rate to a value below $1.\times10^{-8}$ and ensure a continuous decline in the male human infection rate, keeping it below $4.29007\times10^{-9}$. Similarly, Figure 5(b) demonstrates the impact of the female human infection rate, represented by $\beta_{1}$, and the female human recovery rate, expressed by $\rho_{1}$, on the reproduction number. The findings suggest that reducing the female human infection rate below $1.\times10^{-8}$ and increasing the female human recovery rate above $2.04076\times10^{-3}$ can help maintain the reproduction number below unity. Figure 5(c)–(g) also provide similar results regarding the values required to keep the reproduction number below unity.

The results suggest that a control strategy that reduces both female and male human infection rates through humans ($\beta_{1}$ and $\beta_{2}$, respectively) and increases the recovery rates ($\rho_{1}$ and $\rho_{2}$, respectively) of infected female and male humans is essential to sustain $R_{0} < 1$. Any increase in the transmission probabilities would lead to a rise in $R_{0}$. Conversely, decreasing both $\beta_{1}$ and $\beta_{2}$ while keeping $\rho_{1}$ and $\rho_{2}$ constant would lead to a decrease in the reproduction number.

Thus, to keep $R_{0} < 1$, it is necessary to reduce the rates of infection in both female and male humans to values below $\beta_{1} < 1.\times10^{-8}$ and $\beta_{2} < 4.29007\times10^{-9}$, respectively. The findings indicate that reducing only one of the transmission probabilities would not be sufficient in decreasing $R_{0}$, and implementing control strategies that reduce both human-to-human and rodent-to-rodent transmission probabilities could help reduce the virus transmission in the community.

5.   Optimal control

To optimize the control of the model (5.1), four time-varying control variables denoted as $c_{1}$, $c_{2}$, $c_{3}$ and $c_{4}$ are introduced into the existing model (2.1). The descriptions of these time-dependent control variables are as follows:

● The variables $c_{1}$ and $c_{2}$ act as control measures aimed at halting virus transmission from infectious rodents to susceptible female and male human populations, respectively. These preventive measures involve various approaches, including educational campaigns to promote good personal hygiene, discouraging the consumption of rats, environmental fumigation, condom usage, early disease diagnosis, and ensuring access to appropriate medications like Ribavirin. It is crucial to note that the effectiveness of these control strategies in preventing infection relies on setting both $c_{1}$ and $c_{2}$ equal $1$. Conversely, if both variables are assigned a value of $0$, the strategies would fail to prevent transmission. Therefore, properly implementing these preventive measures is of utmost significance in eradicating Lassa fever.

● The control variable $c_3$ signifies the control strategy of utilizing mobile health technology to enable immediate reporting of suspected Lassa fever cases from remote or underserved regions. This can be accomplished through mobile apps or SMS-based reporting systems, which empower healthcare workers and individuals to promptly report potential issues. Early reporting facilitates a swift response and efficient allocation of resources to control outbreaks before they escalate.

● The control variable $c_4$ specifies a comprehensive approach to reduce virus transmission from infected to susceptible rodents. This specific approach encompasses a variety of control measures, including the sealing of fissures and openings in structures, the setup of wire mesh on doors and windows, the capturing and elimination of rodents (ideally using live traps), the usage of rodenticides, the fumigation of plagued zones and the potential consideration of natural predators like barn owls, cats and dogs.

Taking into account the above descriptions, an optimal control model for Lassa fever can be established, comprising four variables that are dependent on time, as follows:

Including the four controls, we aim to reduce the number of affected individuals and rodents transmitting the Lassa virus within the community while maintaining cost-effectiveness. An objective functional is defined as follows to attain this goal:

where $t_f$ denotes the control's ultimate execution time, and $t \in [0, t_f]$. The constant weight factors $A_1$, $A_2$, $A_3$, $A_4$ and $B_i$ ($i = 1, \ldots, 4$) represent the total expenses related to the control variables $c_i$ for $i = 1, \ldots, 4$. In this study, the cost-control functions have a quadratic form, which is significant, where $\frac{B_1 c_1^2}{2}$ and $\frac{B_2 c_2^2}{2}$ represent the cost-control functions for good personal hygiene and earlier medication through educational campaigns targeting female and male human individuals, respectively. Similarly, the terms $\frac{B_3 c_3^2}{2}$ and $\frac{B_4 c_4^2}{2}$ represent cost control functions related to the implementation of mobile health technology and rodent control measures, respectively. To solve the following minimization problem, it is necessary to determine the optimal control quadruplet $c^* = \left(c_1^*, c_2^*, c_3^*, c_4^*\right)$:

Here, a non-empty control set is defined as

Pontryagin's maximum principle transforms the control minimization problem (5.3) within the optimal control system (5.1) into a pointwise Hamiltonian minimization problem. This transformation has been extensively discussed in ^[35], and the resulting Hamiltonian equation is expressed as $\mathbb{H}$.

Here, $\lambda_i$ for $i = 1, \ldots, 7$ represents the adjoint functions associated with the state variables of the optimal control model, and $M_i$ for $i = 1, \ldots, 7$ represents the right-hand side of the differential equations governing the state variables in the system (5.1). The Hamiltonian equation in extended form is as follows:

The following theorem describes the control $c^*$ that satisfies the minimization problem (5.3). It is worth mentioning that the methodology employed here builds upon the techniques outlined in ^[36,37].

Theorem 5.1. If there exists an optimal control set $c_{1}^*, c_{2}^*, c_{3}^*, c_{4}^* \in \omega$ that satisfies (5.3) with respect to the corresponding state system (5.1), then $\exists$ a set of adjoint functions $\lambda_1(t), \lambda_2(t), \ldots, \lambda_7(t)$ that satisfies the following system of equations:

subject to the transversion conditions $\lambda_i(t_f) = 0$ $\forall$ $i = 1, 2, \ldots, 7$. Hence, the optimal control quadruplet $c^* = \left(c_1^*, c_2^*, c_3^*, c_4^*\right)$ is given by

Proof. Building upon the methodology outlined in ^[36], the optimal control problem's existence conditions can be determined by applying Pontryagin's maximum principle. This principle involves evaluating the partial derivatives of the Hamiltonian function concerning the state variables, enabling us to derive the adjoint variables that need to meet the following conditions:

Subject to the transversion conditions $\lambda_i(t_f) = 0$ $\forall$ $i = 1, 2, \ldots, 7$, the behavior of the controls can be established by differentiating the Hamiltonian $\mathbb{H}$ w.r.t the optimal control quadruplet $c^* = \left(c_1^*, c_2^*, c_3^*, c_4^*\right)$ within the control set $\omega$.

Now, the controls can be characterized by imposing constraints on their values using essential arguments, such that

where

This completes the proof. □

The numerical solution to the problem is implemented, and the effectiveness of the applied controls is observed. It is assumed that the optimal campaign will span 65 weeks, utilizing the values provided in Tables 1 and 2. The positive weights are assigned as $A_{1} = 1, \; A_{2} = 5, \; A_{3} = 10, \; A_{4} = 15$, $B_{1} = 3, \; B_{2} = 6, \; B_{3} = 9, \; B_{4} = 12.$ The initial conditions are set to $S_{1}(0) = 103084231, \; I_{1}(0) = 9$, $S_{2}(0) = 105243174, \; I_{2}(0) = 9, \; R(0) = 50, P(0) = 500000, Q(0) = 10000.$ By adopting all of the controls, the goal is to minimize the number of victims, and a rise in recovered individuals can be achieved, as illustrated by graphical visualizations.

5.1.   Optimal control under lowest baseline parameter values

Figure 6 shows the optimal control at the lowest baseline parameter values. Figure 6(a) and (b) demonstrate that by applying preventive measures initially, susceptible female and male individuals get transition into other compartments, so the number of susceptible individuals decreases, and after some time, the susceptible female and male human population become stable.

By implementing these controls, a significant reduction in the number of infected female and male humans is achieved, as depicted in Figure 6(c) and (d), respectively.

A noticeable increase in individuals recovering from the infection is observed upon implementing the control strategies, as shown in Figure 6(e). Furthermore, Figure 6(f) demonstrates a decline in the population of susceptible rodents following the implementation of controls, which means rodents are transitioning into the infected compartments, and after some time, the susceptible rodent population becomes stable. Figure 6(g) displays a significant decrease in infected rodents. Figure 6(h) presents numerical results demonstrating the effectiveness of different optimal controls in managing the transmission of the Lassa virus. The results indicate the efficiency of each control strategy in controlling the virus transmission over specific durations. It reveals that control $c_{1}$, which is applied for $16$ weeks, reduces the transmission by an impressive $75%$. Control $c_{2}$ has a $62%$ reduction when implemented for $4$ weeks. Control $c_{3}$ proves effective, achieving a $71%$ reduction over $28$ weeks. Lastly, control $c_{4}$ has a significant impact, leading to a $75%$ reduction when applied for $64$ weeks. These results demonstrate the potential effectiveness of various control measures in managing the spread of the Lassa virus.

5.2.   Optimal control under highest baseline parameter values

Figure 7 illustrates the optimal control at the highest baseline parameter values.

Figure 7(a) and (b) indicate that after implementing precautionary measures initially, susceptible female and male individuals get transitioned into other compartments, so the susceptible individuals decrease, and after some time the susceptible female and male human population become stable. While Figure 7(c) and (d) represent a significant reduction in infected female and male populations, respectively.

Upon implementing the control strategies, initially, there is a noticeable increase in the number of individuals who have recovered from the infection, followed by stabilization, as shown in Figure 7(e).

Additionally, Figure 7(f) demonstrates a decline in the population of susceptible rodents following the implementation of controls, while Figure 7(g) displays a significant decrease in the number of infected rodents. Figure 7(h) presents numerical results demonstrating the efficacy of optimal controls in controlling the transmission of the Lassa virus. These findings exhibit the efficiency of each control strategy in managing virus transmission over specific time intervals. Control $c_{1}$ is administered for $2$ weeks, remarkably reducing virus transmission by $75%$. When control $c_{2}$ is implemented for the same duration of $2$ weeks, it reduces transmission $10%$. Additionally, control $c_{3}$ effectively achieves a $75%$ reduction over $5$ weeks. Lastly, control $c_{4}$ has a remarkable impact, resulting in a $75%$ reduction when utilized for an extended period of $64$ weeks. These outcomes offer valuable insights into the potential impact of diverse control measures in managing the spread of the Lassa virus.

6.   Conclusions

This study offers a comprehensive mathematical analysis of the dynamics of Lassa fever, focusing particularly on its transmission through sexual activities and the pursuit of optimal epidemic control strategies. The study unfolds in several key phases, starting with developing and qualitatively examining a mathematical model. This model is then applied to real-world data segregated by gender to shed light on the intricate dynamics of Lassa virus transmission. Additionally, sensitivity analysis is conducted to pinpoint the critical parameters significantly influencing the virus's spread.

The study goes beyond mere analysis and delves into optimal control theory. This theoretical framework is harnessed to evaluate various control strategies based on the estimated parameter values. The results are visually represented, offering practical guidance for disease control efforts. This graphical evaluation is a noteworthy contribution to the research. Integrating mathematical modeling, stability analysis, sensitivity analysis, and optimal control strategies highlights the importance of interdisciplinary approaches in effectively addressing the complex public health challenges posed by the Lassa virus.

Moreover, this study significantly enriches our understanding of infectious disease dynamics. It provides invaluable insights for policymakers and public health authorities, emphasizing the importance of evidence-based interventions and the pivotal role of mathematical modeling in disease control endeavors. In addition to shedding light on control strategies, the study explores innovative approaches. These include the potential integration of Ribavirin, the implementation of mobile health technology and considering natural predators such as barn owls, cats, and dogs. These novel ideas lay the groundwork for more effective control measures to reduce the prevalence of Lassa fever.

Looking forward, future research avenues are outlined. These avenues aim to refine the mathematical models, enhance parameter estimation techniques, validate findings with diverse data sources, assess the economic impacts of control strategies, explore the development of vaccines, consider the influence of human behavior, adopt a One Health approach, leverage mobile health technology further, conduct comparative studies, provide policy recommendations, and engage in longitudinal studies. Collaboration and adequate funding are critical to advancing knowledge in Lassa fever dynamics and epidemic control.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to acknowledge the financial support received in the form of the Center For Research & Innovation (CORI) from Universiti Kuala Lumpur.

Conflict of interest

The authors declare no conflict of interest for this manuscript.